Free Energy of Sickle Hemoglobin Polymerization: A Scaled-Particle Treatment for Use with Dextran as a Crowding Agent

Abstract

Fundamental to the analysis of protein polymerization is the free energy of association, typically determined from solubility. It has been previously shown that concentrated 70 kDa dextran lowers the solubility of sickle hemoglobin, due to molecular crowding, and provides a useful ranking tool for the effects of inhibitors and molecular modifications. Because hemoglobin occupies a substantial volume as well, crowding effects of both hemoglobin and dextran contribute to the nonideality of the solution. We show how scaled-particle theory can be used to account for both types of crowding, thus allowing the determination of solubility in the absence of dextran, given data measured in its presence. The approach adopted approximates dextran as a sphere with a volume that decreases as the concentration of dextran increases. We use an asymptotic relation to describe the volume, which decreases nearly linearly by a factor of two over the range studied, from 60 to 230 mg/ml. This compression is similar to previously observed compression of sephadex beads and ficoll solutions. In the limit of low hemoglobin concentrations, the theory reduces to the previously-used approach of Ogston. Our method therefore provides a means of measuring the free energy of association of molecules that occupy significant volume fractions, even when assisted by the crowding of dextran and we present a tabulation of all known free energies of polymerization of sickle hemoglobin measured in the presence of dextran.

INTRODUCTION

The pathology of a number of diseases, of which perhaps the most prominent members are Alzheimer's and Mad Cow disease, is related to protein assembly into large, fibrous structures. Fundamental to understanding protein assembly diseases is a measure of the interaction of the molecules within the aggregate, and the free energy of interest can be learned from the measurement of solubility. The formation of aggregates may also occur in crowded environments (1), a finding that has inspired the study of assembly in the presence of crowding agents such as high-molecular-weight dextran. Moreover, it is possible by adjustment of crowding conditions to promote aggregation (2–4) and thus induce aggregation under conditions that might otherwise not be amenable to protein association. Although crowding may be a natural part of some processes, a molecular understanding requires that energetics of the assembled polymer or fibril be known independent of the crowding process.

Sickle hemoglobin polymerization is the basis of the oldest known assembly disease, sickle cell disease, and occurs once the concentration of monomers exceeds a concentration variously designated as c_sat or as solubility, c_s. Under conditions near physiological, this solubility is ∼160 mg/ml (5). Investigation of the propensity to form such polymers therefore typically requires a significant mass of hemoglobin, and, particularly if mutant proteins are to be studied, this requirement can be difficult to achieve. Smaller amounts of protein can be employed if the solubility is reduced by dramatically increasing the ionic strength of the solution, (6,7) but such a strategy often raises questions of whether intrinsically important ionic interactions have been modified by the changed ionic strength. An alternative is to adjust the protein activity by adding inert molecules, thus crowding the solution, and altering the activity coefficients that formally account for solution crowding. By using 100–120 mg/ml of 70 kDa dextran, the HbS solubility can be reduced to 30–40 mg/ml, in striking validation of the concept (4). The fibers produced in the presence of the dextran are indistinguishable by electron microscopy from those found in its absence (4).

Despite the utility of the approach, as evidenced by its widespread use (4,8–11) and the conceptual clarity of its origin, no quantitative thermodynamic connection has been shown between solubility measured without dextran and solubility determined in the presence of this crowding agent. Dextran has been used in other studies on protein association and folding (3,12–14), and in those studies it has typically been successfully described by a model developed by Ogston (15). However, in Ogston's model it is assumed that only the dextran has significant volume crowding, and thus the theory cannot be employed when any other species occupies a substantial volume as well, as is the case in hemoglobin polymerization. The absence of a successful theory for dextran effects on hemoglobin polymerization is particularly limiting if one wishes to deduce free-energy changes, in which case activity coefficients must be known. Moreover, it is important if experiments executed under one set of conditions need to be compared to those executed under another set. For example, a mutant Hb that might be a candidate for gene therapy could be assayed in the presence of dextran, but its actual efficacy needs to be known under physiological conditions. Although the dextran results provide a proper ranking tool (showing what changes increase or decrease solubility, for example), the thermodynamic connection is not present.

In this article, we use scaled-particle theory, a particularly successful theory for relating hard-sphere exclusion between spheres of any size, to account for solution crowding of dextran and hemoglobin molecules in the same solution in which solubility is measured. In using the hard-sphere calculation it is necessary to vary the volume of the dextran particles, depending on the final dextran concentration. This is rationalized as the consequence of interpenetration of the dextran.

MATERIALS AND METHODS

Hemoglobin was purified chromatographically, as described elsewhere (16). Buffers were 0.15 M phosphate, pH 7.35. Dextran was obtained from Sigma, and used without further preparation. Hemoglobin concentrations were obtained by measuring optical absorption spectra in the Soret region (400–450 nm), and fitting the entire spectrum to known standards. For one set of experiments, C-14 was used to track the composition of the supernatant.

A series of experiments was analyzed, for which results have been previously reported, in which conventional centrifugation methods were used to separate the gel formed in dextran (4). In addition, we employed a newly developed photolytic method (17). This procedure uses an emulsion of COHbS in castor oil placed between microscope coverslips. A particular droplet is selected and subjected to continuous laser photolysis except for a small spot at the droplet center. This spot serves as a reservoir from which monomers will be drawn into the photolyzed, polymerizing region until solubility in the reservoir is reached. Droplets were 200–300 μm in diameter and a few micrometers thick, and the masked area at their center is 4–5% of the total area. The spectrum of the reservoir is measured using an Ocean Optics (Dunedin, FL) 2000 spectrometer. Photolysis is achieved using a Lambda-Pro green solid-state laser. The sample is observed with 15× reflecting microscope optics (Ealing, Holliston, MA). As shown below, the new method gives results that agree with the conventional approach. However, the new method uses only a few microliters of sample per experiment, can be repeated a number of times, and can readily measure solubility at a number of different temperatures.

Theory

The central theoretical concept is that solution monomers with chemical potential μ_S, are in equilibrium with a polymer phase of chemical potential μ_P. This implies equality of the chemical potentials, i.e.,

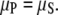(1)

The polymers are treated in a crystal approximation (18), and thus

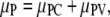(2)

where PC denotes the contribution from molecular contacts and PV the contribution from vibrations of the molecules in polymers, moving about their center of mass. The solution has translational and rotational freedom, and thus

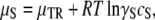(3)

where S subscripts have been added, anticipating that we are considering the solution at solubility. γ is an activity coefficient that depends on concentration, and thus has an S subscript as well. We have found that for hard spheres such as hemoglobin, a simple yet accurate expression is (19)

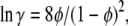(4)

where φ is the volume fraction, which is given for simple hemoglobin (Hb) solutions by the equation φ = V_Hbc.

Thus, the monomer-polymer equilibrium is described by a solubility, c_S, which satisfies the equation

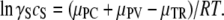(5)

Since the righthand side of this equation does not change as the solution is crowded, it is evident that changes in the activity coefficient are offset by changes in solubility. If γ′_Sc′_S represents activity in a crowded milieu, then

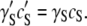(6)

To calculate γ′_S requires a specific prescription for incorporating crowding. An effective way is scaled-particle theory, which allows similarly shaped particles to be employed in the calculation of their mutual crowding (20). The activity coefficient for Hb, taken as a hard sphere in the presence of dextran, also taken as a spherical crowding agent, is denoted as γ_sp and is given by Minton (20) as

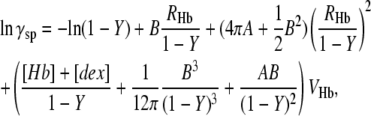(7)

in which Y is the fraction of space occupied, and is given by

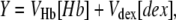(8)

and the auxiliary constants A and B are given by

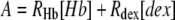(9)

and

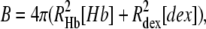(10)

and V_Hb is the specific volume of Hb, with 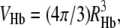and similarly for dextran. It is convenient to factor the hemoglobin volume, and to write V_dex as multiples of V_Hb. Thus, we define v_dex as the ratio V_dex/V_Hb. Because spherical objects are assumed, once V_dex is determined, the radius, R_dex, can be deduced. Other approaches have been used for dextran, and will be compared in the Discussion section. For now, it is sufficient to point out that in the other approaches that have been used, the particle crowded (e.g., Hb) was much more dilute than the crowder. That assumption cannot be made here.

Since dextran does not go into the polymer, it is necessary to correct the final dextran concentration in supernatant solution, which is done by simple mass conservation according to

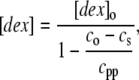(11)

in which [dex]_o is the initial concentration of dextran, c₀ is the initial concentration of Hb, and c_pp is the concentration of Hb in the polymer phase, which is the inverse of the specific volume of the polymer phase.

RESULTS AND DISCUSSION

Using Eq. 11, we computed the expected final concentration of dextran in each sample. This was compared with the radiolabeled dextran which, taken from the supernatant, gives a direct measurement. The results are shown in Table 1. As can be seen, agreement is excellent, using c_pp = 55 g/dl (21). The average difference is a mere 0.019 g/dl, ∼0.1%.

TABLE 1.

Comparison of measured and predicted dextran concentrations

Measured [dex] (g/dl)	Predicted [dex] (g/dl)
12.5	12.7
12.5	12.7
13.0	13.0
13.0	13.0
12.9	13.0
13.2	13.0
14.3	14.3
14.1	14.3
13.3	13.0
13.4	13.0

Dextran concentration was predicted based on Eq. 11.

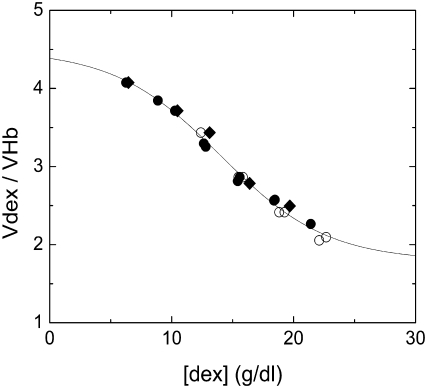
To determine the appropriate specific volume for use in Eq. 8, we first employed a volume determined by density measurement of the dextran, which yielded 0.664 ml/g, in good agreement with published values (22) This is equal to 0.0465 L/mmol, which is within a few percent of the specific volume for Hb, 0.0482 L/mmol. When used in the scaled-particle theory, this did not yield good agreement. We therefore reversed the procedure, and determined a specific volume that would suffice to reconcile the dextran-free solubility with that measured in various dextran concentrations. This yielded a series of volumes that depended on the initial dextran concentration, as shown in Fig. 1, and decreased as dextran concentration increased. These volumes are all given relative to the volume of Hb, and are therefore dimensionless.

FIGURE 1.

Relative specific volume of dextran as a function of final dextran concentration. Dextran volume is measured relative to the volume of hemoglobin. Volume was determined by using Eq. 7 for the scaled-particle activity coefficient to determine the volume that gave the solubility, as listed in Table 2. (Open circles) 22°C data published previously (4); (solid circles) 22°C data determined here; (diamonds) 37°C data determined here. The curve is the best fit of the empirical function of Eq. 12.

To explore this behavior further, we obtained additional data at 22°C and 37°C. The solubility data is shown in Table 2, along with the published data (4) for comparison. Typical reproducibility of the solubility data was 3%, and in no case worse than 4%. The dextran volume determined by analysis of this data is shown in Fig. 1, and is in generally excellent agreement with the published 22°C data, while extending its range. It is noteworthy that both temperatures give the same effective volume.

TABLE 2.

Solubilities of sickle hemoglobin with dextran

[dex]o (g/dl)	[dex] (g/dl)	Csat (g/dl)	[Hb]o (g/dl)	Temperature (°C)
Measured by centrifuge
21	22.10	1.27	4	22
18	18.81	1.63	4	22
15	15.47	2.32	4	22
21	22.66	0.96	5	22
18	19.25	1.42	5	22
15	15.84	2.09	5	22
12	12.39	3.28	5	22
Measured by droplet and mask
21	21.40	0.97	2.01	22
18	18.46	1.38	2.75	22
18	18.40	1.44	2.62	22
15	15.58	2.25	4.31	22
15	15.42	2.50	3.99	22
12	12.79	3.37	6.77	22
12	12.63	3.41	6.17	22
10	10.27	4.75	6.17	22
8	8.87	6.08	11.45	22
6	6.25	9.10	11.34	22
18	19.69	0.78	5.49	37
15	16.39	1.50	6.16	37
12	13.11	2.10	6.77	37
10	10.47	3.70	6.17	37
6	6.45	7.50	11.34	37

Published data at 37°C (4) was not used because the accepted protocol for this method is to gel the sample at 37°C, but to centrifuge it at room temperature. (4,8–10) This raises the possibility that some of the gel will dissolve during sedimentation and processing, and that the effective temperature is neither 37°C nor room temperature. We will return to this issue in the discussion.

The dimensionless volume ratio data of Fig. 1 was fit by the empirical equation

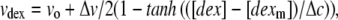(12)

in which v_o, Δv, [dex_m] and Δc are constants determined by fitting to the data. From the fit, it is found that v_o = 1.79 and Δv = 2.70, and [dex_m] = 14.01 g/dl, and the width Δc = 8.75 g/dl. As can be seen in Fig. 1, the function, selected to have high and low asymptotes, provides a good fit.

The consistency of the variable volumes used for dextran, independent of temperature and Hb concentration suggested that the approach had validity. Moreover, other workers have observed the compressibility of dextran (23), as well as the closely related Ficoll (12). Quantitatively, the size variation of dextran volume appears reasonable. This can be seen by considering the asymptotic values of the empirical function (Eq. 12). As described above, the volume of the hemoglobin, insofar as it excludes water, is the same as 70 kDa dextran, so we expected the volume of dextran (per mmol) to be at least as great as that of Hb. Thus, it is likely that the ratio v_dex > 1. At the high [dex] asymptote, 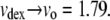The low [dex] asymptote corresponds to highly dilute conditions, where a number of investigators have measured the effective hydrodynamic radius of dextran (treating it as a sphere). Typical results are 6.49 nm (24), 6.39 nm (25), and 6.2 nm (26). For Hb, the radius is 3.2 nm (27). Thus, from hydrodynamics, one would expect the maximum v_dex to be ∼(6.35/3.2)³ = 8. At the low [dex] asymptote (i.e., 0), we find 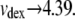Hence, the asymptotes of the function employed appear well within the bounds of what is known about dextran.

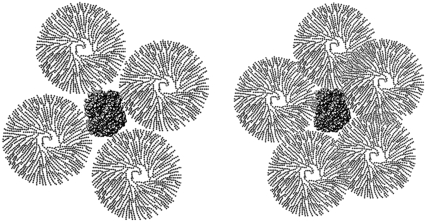
The variation of volume is rationalized by the observation that dextran is not a densely packed object, since its hydration volume is similar to that of Hb whereas its hydrodynamic volume is eight times that of Hb. At the highest concentrations used here (21 g/dl), dextran of specific volume eight times that of Hb would overfill the available volume, i.e., overlapping would be required to allow it to fit. If we take the well known filling factor of hard spheres of 0.74, and assume the dextran to be hard spheres with 8Hb volume, the solution is completely packed at 12 g/dl. In other words, at concentrations of 12 g/dl and above, the dextran must overlap. For concentrations from 6 g/dl to 12 g/dl, though space filling considerations don't require overlap, it is evident that some overlap must occur by the random encounter of the dextrans. Fig. 2 illustrates the effect this has on excluded volume. As the concentration of dextran rises, even though the number of dextran molecules encountered by a Hb molecule rises, each dextran denies less effective volume to the Hb thanks to their overlap.

FIGURE 2.

Schematic of dextran overlap. The picture illustrates dextran with a hydrodynamic radius twice that of Hb, in agreement with measurements, surrounding Hb. Dextran is drawn schematically, and, unlike Hb, is not a compact object. As the concentration increases, the dextrans surrounding Hb each exclude less volume because of their overlap. Though only one Hb is shown, the neighboring Hb molecules will be roughly one dextran diameter away.

The empirical function of Eq. 12 contains asymptotes that are limited, but not specified, by external data. Consequently, it is possible to imagine a different function that might have different asymptotes. The data itself are close to linear, and a linear fit is quite acceptable. However, the asymptotic form provides a better fit even when the effects of the extra parameter are taken into account. Specifically, the sum of the squared deviations divided by the degrees of freedom (number of data points minus number of parameters minus number of equations) is 5.3 × 10⁻³ (g/dl)² for the asymptotic fit and 7.5 × 10⁻³ (g/dl)² for the linear fit.

Unlike proteins, dextrans exhibit polydispersity of molecular weight (28–30). The dextran used here did not have a range specified by the manufacturer, but similar products have a distribution width of ∼10% of the mean (e.g., Pharmacosmos Dextran Standards, Pharmacosmos, Holbaek, Denmark.) We examined the results of using a mixture of two equal concentrations of dextran at the upper and lower standard deviations, i.e., 63 kDa and 77 kDa. There was no significant change in ln γ by using this extremely bimodal distribution, and thus we conclude that polydispersity does not have a significant effect on the approach taken here.

The approach using scaled-particle theory differs from that of Ogston (15), subsequently employed by others (e.g., (14)) in the analysis of dextran's influence on protein behavior. Ogston's approach involved considering dextran as an assemblage of polymeric rods of radius a (rod length does not enter into the formalism). The rods exclude a spherical particle, in this description, of radius r. If the dextran occupies a volume fraction φ_d (= V_dex[dex]), then

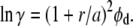(13)

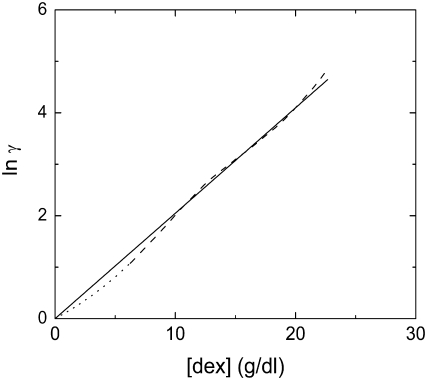
Minton (31) has used a = 0.7 nm for dextran, and r = 3.2 nm for Hb (27). We can compare the result of our analysis with scaled-particle theory in the limit where the concentration of Hb is small, and this is shown in Fig. 3. The agreement is excellent, validating further the variable volume approach. It is also interesting to note that the Ogston approach is specifically immune to issues of overlap of the dextran particles.

FIGURE 3.

Activity coefficient γ, as a function of dextran concentration, for trace concentrations of Hb. The theory of Ogston (15) (Eq. 13) is represented by the straight line, whereas the scaled-particle theory, employed here, is represented by the dashed undulating curve. Dotted lines show the theoretical curve in regions where volume data (Fig 1) was not collected, but which depend on the empirical function.

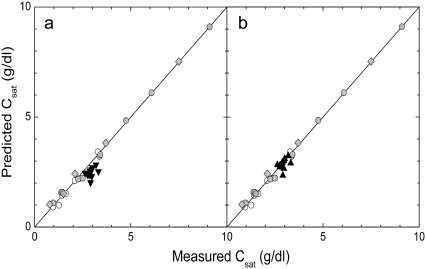
With the accuracy of the method established, it is interesting to return to the data of Bookchin et al. (4) collected at 37°C gelation with room temperature (22°C) centrifugation, which we shall label 37(−) data for convenience. Fig. 4 shows a correlation of the solubility computed using Eq. 1 of Li et al. (32), the volume function of Eq. 12, and measured solubility. In the left panel, the 37(−) data is used as if the temperature were continuously held at 37°C. As can be seen, this data, while close, fails to correlate as well as the other points. If, however, we adjust the temperature (which adjusts the solubility used in Eq. 6), we find a good correlation for an apparent temperature of 25°C, as seen in the right panel of Fig. 4. Because this apparent temperature is likely to depend on procedural details, it is uncertain how universally applicable this particular finding is, and it would be far more useful, in future analysis of HbS solubility, to centrifuge and gel at a single temperature. In such future reports, it would also be important to tabulate the initial Hb concentration of samples, so as to allow accurate determination of the final dextran concentration from Eq. 11.

FIGURE 4.

Correlation of predicted and measured solubility. (Left) The data gelled at 37°C and measured at 22°C are shown as solid triangles, using the assumption that the correct temperature is the gelation temperature, 37°C. As can be seen, the points are not so well correlated as the other data. (Right) The correlation resulting when the appropriate temperature is taken to be 25°C. Light gray symbols represent the data from Table 2. (Open circles) 22°C data published previously (4); (solid circles) 22°C data determined here; (diamonds) 37°C data determined here.

Finally, in Table 3, we have tabulated the calculated dextran-free solubilities and the free energies of association for all the mutant hemoglobins that have been studied by the dextran method to date. We can compare our predicted solubilities for two cases in which solubilities without dextran had also been determined (33,34). Those experiments used the Benesch method, which assigns solubility to the concentration at which there is a change in the slope of p50 plotted as a function of concentration (35). The values shown in Table 3 are somewhat below those inferred in the original publications, but would actually be consistent with the data from which the values were generated (cf. Martin de Llano and Manning (33), Fig. 8, and Himanen et al. (34), Fig. 6). This demonstrates the power of the present method, since a single dextran measurement suffices to ascertain the solubility with significantly greater precision. Especially important for future work will be the degree to which various mutations do not show additive free energies (e.g., the effects of L88A and K95I, comparing their separate and joint energies), indicating some effective interactions between the mutations' effects on polymerization.

TABLE 3.

Solubilities and free energies of hemoglobins studied with dextran

		Dextran	Predicted non-dextran
HbS mutant	Co (g/dl)	Csat (g/dl)	Csat* (g/dl)	ΔΔG† (kcal/mol)	Reference
E6V(β)/L88A(β)	7.68	6.86	26.4	0.24	(10)
E6V(β)/K95I(β)	9.90	8.97	30.4	0.32	(10)
E6V(β)/L88A(β)/K95I(β)	13.21	9.21	32.0	0.36	(10)
E6V(β)/E121R(β)	4.43‡	2.43 ± .03	15.4 ± .1	−0.08	(11)
D75Y(α)/E6V(β)/E121R(β)	2.18‡	1.18 ± .04	9.5 ± .2	−0.37	(11)
D6A(α)/D75Y(α)/E6V(α)/E121R(β)	1.70‡	0.70 ± .06	6.6 ± .4	−0.59	(11)
A19G(α)/A21G(α)/E6V(β)	8.01	5.36 ± .07	23.9 ± .2	0.18	(8)
A19Aib(α)/A21Aib(α)/E6V(β)	7.70	2.78 ± .06	17.7 ± .2	0.00	(8)
A19G(α)/A21G(α)/A78H(α)/E6V(β)	7.26	2.80 ± .05	17.7 ± .2	0.00	(8)
A19G(α)/A21G(α)/A78Q(α)/E6V(β)	7.25	4.96 ± .14	22.8 ± .3	0.15	(8)

^*At 25°C.

^†ΔΔG relative to HbS.

^‡The initial concentration value is assumed as this value.