Molecular Dynamics Simulations of Asymmetric NaCl and KCl Solutions Separated by Phosphatidylcholine Bilayers: Potential Drops and Structural Changes Induced by Strong Na⁺-Lipid Interactions and Finite Size Effects

Abstract

Differences of ionic concentrations across lipid bilayers are some of the primary energetic driving forces for cellular electrophysiology. While macroscopic models of asymmetric ionic solutions are well-developed, their connection to ion, water, and lipid interactions at the atomic scale are much more poorly understood. In this study, we used molecular dynamics to examine a system of two chambers of equal ionic strength, but differing amounts of NaCl and KCl, separated by a lipid bilayer. Our expectation was that the net electrostatic potential difference between the two chambers should be small or zero. Contrary to our expectation, a large potential difference (−70 mV) slowly evolved across the two water chambers over the course of our 172-ns simulation. This potential primarily originated from strong Na⁺ binding to the carbonyls of the phosphatidylcholine lipids. This ion adsorption also led to significant structural and mechanical changes in the lipid bilayer. We discuss this surprising result in the context of indirect experimental evidence for Na⁺ interaction with bilayers as well as potential caveats in current biomembrane simulation methodology, including force-field parameters and finite size effects.

INTRODUCTION

Membranes are among the most basic structures of cells and subcellular organelles. Direct interactions of cations with membranes have been extensively studied due to the prevalence of ions in biological milieu and the significant effects of ions on membrane properties such as phase transitions (1–4), aggregation and fusion (5), surface charge densities and potentials (6,7), structure and mechanical strength (4,8,9), and lipid mobilities (2). The nature of ion-lipid interactions has been studied by several methods, including infrared spectroscopy (1,10), ζ-potential measurements (11), x-ray standing wave experiments (12), NMR spectroscopy (13,14), atomic force microscopy (8,9), small angle x-ray diffraction (4), and molecular simulations (2,15–19). Most of these studies conclude that higher valency ions have greater affinity and larger effects on biomembranes (1,4); however, recent results have suggested that monovalent cations can also interact with biomembrane lipid moieties and alter bilayer properties (1,2,4,9,15,17,19).

Previous reports (16,17,20) have indicated that asymmetric Na⁺ and Cl⁻ concentrations around bilayer systems can generate electrostatic potential differences as large as −85 mV across lipid bilayers in molecular dynamics simulations. These reports, in part, motivated the current study which was originally designed as a control for studying asymmetric applications of salicylate around bilayers to extend our previous work in this area (21). To this end, we designed a simulation that contained two bilayer-separating chambers with differing NaCl and KCl concentrations but the same net ionic strength. Simple analysis of this system on the basis of ion activities and the symmetries of the solutions suggests that, at steady state, the Nernstian transmembrane potential (e.g., the potential drop at infinite separations of the two bilayers) for this system should be negligible. However, as discussed in detail throughout the remainder of this article, we observed a significant potential drop across dipalmitoylphosphatidylcholine (DPPC) bilayers due to selective Na⁺ binding to the lipid carbonyls. Although there is some indirect experimental evidence which may suggest some degree of Na⁺-carbonyl interactions (10), both the finite size of our simulation and the nonequilibrium nature of the system caution against overinterpretation of these observations. This article addresses the possible effect due to the finite size on the calculation of membrane potentials and the issue on the force-field parameters of ions on the electric properties and structures of membranes.

METHODS

Molecular dynamics simulations

GROMACS 3.2.1 (22) was used for the molecular dynamics (MD) simulations and preparation of the starting structures; GROMACS 3.3.1 was used for all analyses. Dipalmitoyl-phosphatidylcholine (DPPC) lipids were simulated using the parameters of Berger and Lindahl (23) together with SPC water (24) and Straatsma-Berendsen sodium, potassium, and chloride ion parameters (25). This combination of force-field parameters have been successfully used in a number of previous studies (21,23,26,27) and show good agreement with experimental observables such as area per lipid headgroup and tail order parameters.

Following the work of Sachs et al. (17), Gurtovenko (16), and Vernier et al. (18), the starting structure of the DPPC double-bilayer system shown in Fig. 1 was generated by duplicating a previously-equilibrated DPPC single-bilayer system of 9.5 nm × 8.5 nm × 10.0 nm dimensions (21) along the bilayer-normal direction. The hydration level of 60 waters per lipid provided a spacing of ∼6 nm between the two bilayers. These two bilayers, together with the periodic boundary conditions used in this simulation, provided two separated water chambers, denoted N and K (see Fig. 1). Ions were inserted into the two water chambers by replacement of existing water molecules. In particular, 100 random water molecules in the N chamber were replaced by 48 Na⁺, 2 K⁺, and 50 Cl⁻ ions while 100 water molecules in the K chamber were replaced by 2 Na⁺, 48 K⁺, and 50 Cl⁻ ions. This placement of ions resulted in an electroneutral system with solutions of ∼150 mM ionic strength in both chambers but with different species ratios. The final simulation system was comprised of 512 DPPC, 30568 SPC water, 50 Na⁺, 50 K⁺, and 100 Cl⁻ molecules. The membrane system was equilibrated as described previously (21): the starting structure was subject to an energy minimization followed by a series of MD simulations to increase the system temperature to 323 K. After the system reached 323 K, the MD simulation was continued for 172 ns.

FIGURE 1.

Diagram of double-bilayer simulation geometry with approximate dimensions along the z axis labeled. Left and right boundaries are periodic (e.g., K is a single contiguous chamber in the simulation). As described in the text, the N chamber contains 48 Na⁺, 2 K⁺, and 50 Cl⁻ ions while the K chamber contains 2 Na⁺ (blue), 48 K⁺ (green), and 50 Cl⁻ (orange) ions.

All MD simulations were performed with Lennard-Jones interaction cutoffs of 1 nm. Long-range electrostatic interactions were calculated using the particle-mesh Ewald method (28) with conducting boundary conditions and a direct space cutoff of 1 nm. Simulations were performed in an isobaric-isothermal ensemble (NpT). The system pressure was maintained at 1 atm with a Parrinello-Rahman barostat (29) using a 2-ps coupling time. The temperature was maintained at 323 K through a Nosé-Hoover thermostat (30) with 0.5-ps coupling frequency. All bonds between hydrogen and heavy atoms were constrained using the SHAKE algorithm (31) which permitted a 2-fs time step. The simulations were performed on Intel Xeon cluster nodes at the National Biomedical Computation Resource and at the Texas Advanced Computing Center. Snapshots from the simulations were stored for analysis at 16-ps intervals.

To determine the effect of the monovalent cations, the properties of our present double-bilayer system were compared with those of an ion-free DPPC membrane simulation which has been described previously (21). The ion-free system is equivalent to the half of the double-bilayer system along the z axis and was simulated for 50 ns at the same conditions with this simulation. The last 20-ns portion of the trajectory was used to analyze equilibrium observables for this system.

Statistical tools

Time averages were used to calculate expectation values for system observables. In general, these averages were computed over the 62-ns stationary portion of the 172-ns simulation, as described in Reaching Steady State. To compare the measured quantities between different systems or between different parts within the same system, the statistical errors of each quantity were calculated as explained below.

To estimate errors, the trajectory was divided or resampled into statistically independent smaller blocks. To determine the size of these blocks for a particular observable, the autocorrelation time (32) of the observable was calculated for different delay times τ using the equation

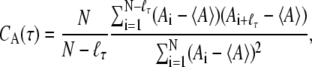(1)

for N time points 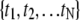with equal spacing Δt = t_i+1 − t_i and a lag ℓ_τ such that τ = ℓ_τΔt. This autocorrelation function is for an observable A with mean value 〈A〉 evaluated at each of the time points such that 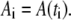A characteristic correlation time τ_A was calculated for each observable A as the smallest |τ| for which C_A(τ) = e⁻¹. We wish to point out that, due to the use of an NpT ensemble for our molecular dynamics calculations, these correlation times are used strictly for resampling purposes and not intended for a description of the dynamics of this bilayer system.

To ensure statistical independence, decorrelation times of 2τ were used to generate new datasets for calculating observable statistics. In particular, following similar analyses by Chen and Pappu (33), bootstrap-style sampling-with-replacement (34) was used to generate new resampled datasets of size 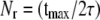(rounded to the nearest integer) given the original evenly-spaced snapshots from a trajectory of length t max. Each resampled set was used to estimate averages for system observables. The distribution of these averages over all resampled sets was then used to estimate the variability of the observables and calculate variances and confidence intervals. Finally, the statistical significance between any two samples was assessed by the Student t-test with a 99.5% confidence interval, using the error and the size of the resampled datasets.

RESULTS

Reaching steady state

The nonidentical nature of the N and K chambers throughout our simulation indicate that we are studying a nonequilibrium system at steady state rather than the equilibrium observations associated with most molecular dynamics simulations. Monitoring macroscopic thermodynamics parameters is a standard procedure to verify the equilibrium or steady state of the system. In our simulation, parameters such as temperature, box pressure, and total energy of the system reached stationary values at an early stage of the simulation (e.g., <10 ns); however, several other system properties took much longer to stop drifting. Previous reports have shown that adsorption and coordination of cations by carbonyl oxygens is one of the slowest processes in the simulation of salt-containing zwitterionic bilayer systems (2,16,35). Given these observations, we examined the time course of absorption and coordination of Na⁺ and K⁺ by the DPPC headgroups using the methods described below (see Eq. 2 and description in Ion-Lipid Interactions). As shown in Fig. 2, A and B, the total number of lipid-coordinated ions and the average coordination number increased throughout the initial 65 ns of the simulation; no significant drift was observed after 65 ns. For our simulation, however, the most slowly-converging observables were net water flux across the bilayers (see Ion and Water Distributions and Fig. 4) and box area (see Lipid Structure: Headgroup Area and Tail Order Parameters and Fig. 5), which reached the steady state only after 110 ns. Although the changes in area were very small, they occurred over the same timescales as water flux through the membrane. While such small area changes alone may not warrant concern about simulation convergence, their appearance together with other slowly-relaxing properties led us to confine our analysis to the last 62 ns of our 172-ns trajectory.

FIGURE 2.

(A) Total number of lipid-coordinated ions as a function of time for Na⁺ (blue) and K⁺ (green). (B) Average lipid-ion coordination numbers, defined in Eq. 2, as a function of time for Na⁺ (blue) and K⁺ (green). (C) Lipid/ion ratios for coordinated Na⁺ (blue) and K⁺ (green) ions. The average fraction of the complex comprised of five DPPC molecules is 0.003 ± 0.007, so the bar is not visible in the figure. (D) Example of a representative four-coordinate lipid carbonyl-ion interaction. Any residues within 3.2 Å from an Na⁺ ion are displayed. The carbonyl oxygens coordinating the ion are shown as red spheres.

FIGURE 4.

Water distribution in the double-bilayer system. Number of waters in each chamber (K solid, N dashed) as a function of simulation time.

FIGURE 5.

Plot of simulation box cross-sectional area (in the bilayer planes) over the course of the molecular dynamics run. Figure includes individual snapshots (every 16 ps, dots) and 1.6-ns running average (line).

Ion-lipid interactions

To assess the specific interaction of each cation with the lipid, the average DPPC-cation coordination number (c_X) for each cation (X is Na⁺ or K⁺) was calculated in a manner similar to Gurtovenko (16) by

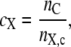(2)

where n_C is the number of carbonyls within a cutoff distance r_{X, c} of any ion of species X and n_{X, c} is the number of ions of species X within a cutoff distance r_{X, c} of any lipid carbonyl group. We chose r_{c, Na⁺} = 0.322 nm and r_{c, K⁺} = 0.375 nm as determined from the first minima of the Na⁺- or K⁺-DPPC carbonyl oxygen radial distribution function (data not shown). The results from this analysis are illustrated in Fig. 2 and summarized in Table 1. Na⁺ coordination numbers varied from 3.11 ± 0.03 in the N chamber to 3.2 ± 0.4 in the K chamber while K⁺ coordination numbers were much smaller: 0.008 ± 0.002 in the N chamber and 1.2 ± 0.1 in the K chamber. The distribution of ion coordination states is shown in Fig. 2 C. The primary mode of Na⁺ coordination was via DPPC carbonyl oxygens, as illustrated in Fig. 2 D.

TABLE 1.

Ion-carbonyl coordination statistics calculated according to Eq. 2

Chamber	Ion	Correlation time (ps)	Coordination number (average ± error)
N	Na+	2131	3.11 ± 0.03
N	K+	42	0.008 ± 0.002
K	Na+	12592	3.2 ± 0.1
K	K+	832	1.2 ± 0.1

Averages and standard errors determined using the bootstrap resampling procedure described in the text with the specified correlation times.

Our average Na⁺-lipid coordination number (3.11 ± 0.03) is comparable to the results of Gurtovenko (16). However, we also observed complexes involving four and five lipid molecules and found that four-coordinate Na⁺ was the most common. Gurtovenko observed three-coordinate Na⁺ most frequently and did not report any five-coordinate complexes. There are a number of potential reasons for these differences; the most likely is sampling (45 ns for Gurtovenko versus 172 ns here). In particular, five-coordinate lipid-Na⁺ complexes were observed only after 130 ns of simulation, suggesting a much slower rate of formation.

Ion and water distributions

Fig. 3 shows number densities for water and lipid moieties (Fig. 3 A) as well as individual ion species (Fig. 3 B) as a function of distance along the bilayer normal. These figures clearly demonstrate significant adsorption of Na⁺ to the polar region of the DPPC bilayers. This adsorption is quantified in Table 2, which summarizes the numbers of ions observed in each region of the simulation domain. As discussed below, the specific association of Na⁺ with the bilayer appears to be due to coordination by the DPPC carbonyl oxygens (Ion and Water Distributions) and leads to a significant dipole moment at the interface of the N chamber DPPC leaflets (Electrostatic Potential).

FIGURE 3.

Relative number densities depicting fraction of total species as a function of distance along the bilayer normal (see Fig. 1 for coordinate definition). (A) Distribution of lipid moieties (polar portion of lipid, solid; nonpolar portion of lipid, dashed; total lipid density, dotted) and water (dashed-dotted). (B) Distribution of ions (Na⁺, solid; K⁺, dashed; Cl⁻, dotted) with specific regions labeled for binding analysis (see text).

TABLE 2.

Ion distributions across the regions labeled in Fig. 3 B as obtained from the 110–172 ns portion of the simulation

Region	Ion	Correlation time (ps)	Number (average ± error)
N1	Na+	3968	16.2 ± 0.3
N1	K+	256.6	0.03 ± 0.01
N1	Cl−	31.7	0.51 ± 0.02
N2	Na+	5571.2	15.5 ± 0.5
N2	K+	160	1.95 ± 0.01
N2	Cl−	28.8	48.68 ± 0.03
N3	Na+	5332	16.2 ± 0.5
N3	K+	98.5	0.188 ± 0.005
N3	Cl−	28.5	0.82 ± 0.02
K1	Na+	—	2 ± 0
K1	K+	—	48 ± 0
K1	Cl−	—	50 ± 0

Unlisted correlation times imply no change in ion numbers during this simulation time. Averages and standard errors determined using the bootstrap resampling procedure described in the text with the specified correlation times.

Time-dependent changes in water distribution in the double-bilayer system are illustrated in Fig. 4. Over the first 110 ns of the simulation, water was redistributed from the initial configuration of 15,284 water molecules in each chamber to 15,271 ± 3 in the N chamber and 15,297 ± 3 in the K chamber. Even though the ionic strengths of the two chambers were the same, adsorption of Na⁺ ions onto membrane likely generated an osmotic imbalance between the two chambers. This argument is supported by the observation that the net water flux started at ∼10 ns, which is after a significant number of Na⁺ ions had adsorbed onto the membrane. By 110 ns, a net of 13 ± 3 water molecules (0.083% of total) had transferred across the membrane; after this time, fluctuations in N and K chamber water numbers were observed but without a net change over the last 62 ns of simulation. Note that this net water flux is small and, unlike similar work with stronger fields and ion asymmetries (18,20), not related to the formation of pores in the bilayer structure.

Lipid structure: headgroup area and tail order parameters

The area per headgroup 〈A〉 is a fundamental characteristic of the membrane and provides an important comparison to available experimental structural data (26,36,37). The area per headgroup was calculated by dividing the projected box area in the xy-plane by the 128 lipids in each leaflet. As shown in Fig. 5, the area per headgroup started at 0.6295 nm² and, over a period of ∼110 ns, decreased very slightly to a value of 0.6255 ± 0.0001 nm² (as calculated over the last 62-ns trajectory by using the bootstrap method with a correlation time of 16 ps). In our simulation, this drift occurs over a much longer period than the 65 ns required for steady-state ion binding and, instead, has timescales similar to the transfer of water between the N and K chambers (see Fig. 4). Despite this small change in bilayer area due to Na⁺ binding, the range of 〈A〉 is in reasonable agreement with experimental data (37) and previous simulations (21,38). Other simulations of lipid bilayers in the presence of aqueous Na⁺ ions have reported a much larger decrease in membrane area associated with Na⁺ binding (2,16,38) than the small contraction observed in this work. These differences are discussed in more detail in Finite Size Effects.

The lipid tail order parameters of the two acyl chains of DPPC were calculated for comparison against published data (39). The order parameters were calculated separately for each leaflet to distinguish the effect of different local ion concentrations in the N and K chambers. The algorithms for calculating order parameters and descriptions of their interpretations have been described previously (21,40). We generated order parameters from our simulation data using the resampling method described above, using every snapshot of the trajectory. This statistical independence was identified by examining the correlation time of 〈A〉, an important determinant of lipid tail order. This area correlation time was shorter than the sampling rate of 16 ps, allowing us to use every snapshot of the simulation in our analysis. As shown in Fig. 6, the overall shapes of the order parameter profiles are similar among the three different leaflet environments (N chamber, K chamber, and a DPPC bilayer in pure water) and are reasonably close to experimentally measured order parameters (39). The SN-1 tail of DPPC was disordered in the N and K chamber leaflets relative to the DPPC bilayer in pure water near the carbonyl oxygens (Student t-test, 99.5% confidence interval). On the other hand, the SN-2 tails of N leaflet lipids showed slight ordering of carbons near the carbonyl oxygens (Student t-test, 99.5% confidence interval), presumably due to the higher participation of SN-2 carbonyl oxygens in coordination of Na⁺ (data not shown).

FIGURE 6.

DPPC (A) SN-1 and (B) SN-2 tail order parameters for N chamber DPPC leaflets (dotted), K chamber DPPC leaflets (dashed), and a DPPC bilayer surrounded by pure water (solid).

Electrostatic potential

The membrane potential was calculated from the total charge density to examine the effect of the asymmetric ion distributions on the electrostatic properties of the membrane. Given the zero potential difference boundary conditions implied by conducting-boundary particle-mesh Ewald electrostatics (28,41), the electric displacement was calculated according to

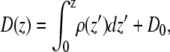(3)

and the potential difference was calculated according to

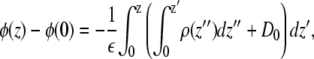(4)

where ε is a homogeneous dielectric constant and ρ(z) is the charge density. For a net neutral system with the boundary conditions described above, the displacement constant D₀ is defined by

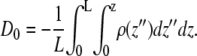(5)

This constant D₀ is related to the total polarization of system and is similar to that obtained by Sachs et al. (17). For our simulation, D₀ = 0.0142 z × nm⁻¹ = 2.27 × 10⁻¹² C × m⁻¹.

The simulation box was divided into 200 slabs parallel along the bilayer normal (z) direction. Potentials calculated at every 16 ps showed no correlation between snapshots at every slab along the z axis, which implies that the correlation time is much smaller than 16 ps. To verify this short correlation time, an additional short simulation was performed with a much more frequent output rate of 4 fs. From this simulation, the correlation times of membrane potential were determined to be <1 ps at all slabs, indicating a rapidly-fluctuating potential across the entire membrane system. Since the correlation time was much shorter than the sampling rate (16 ps), all snapshots were statistically independent from each other, and the bootstrap resampling protocol described above was performed with all 4062 snapshots of the trajectory. Charge densities (Fig. 7 A) were used to calculate the potential (Fig. 7 B) by trapezoidal rule integration (42) according to the formulae above with L = 20 nm and ε = ε₀, the permittivity of free space.

FIGURE 7.

Electrostatic potentials in the double-bilayer system. (A) Charge density components of bilayer system; the entire system (solid), lipids (dashed), water (dotted), and ions (Na⁺, K⁺, and Cl⁻; dashed-dotted) (B) Total electrostatic potential (thick line) with standard deviations (thin lines) calculated as described in the text. The potential drop across the bilayer is calculated from the potential value of −70 mV (−0.07 V) at z = 10 nm. (C) Electrostatic potential components due to the lipids (dashed), water (dotted), ions (Na⁺, K⁺, and Cl⁻; dashed-dotted), and the entire system (solid). (D) Electric field components due to lipids (dashed), water (dotted), ions (Na⁺, K⁺, and Cl⁻; dashed-dotted), and the entire system (solid).

The resulting potentials were averaged and plotted in Fig. 7 B, which shows a net potential drop across the bilayers of −70 ± 10 mV between the K and N chambers. Fig. 7 C decomposes this potential into separate contributions from lipid, water, and ions. This figure demonstrates that both lipids and water contribute to a net positive potential drop while the ions provide a large negative contribution. The origins of the negative ion contribution can be deduced from Fig. 3 B, which shows a clear layering or separation of Na⁺ and Cl⁻ ions at the membrane-water interface of leaflets in the N chamber, leading to a large surface dipole moment. On the other hand, K⁺ and Cl⁻ ions in the K chamber are much more uniformly mixed and generate smaller surface dipoles. These differing surface dipoles are clearly evident in Fig. 7 A, which plots charge densities across the simulation domain.

Membrane mechanics

Ions are known to affect membrane fusion and phase transitions (43,44). Divalent ions have also been demonstrated to change the bulk modulus of DPPC bilayers (45). Such effects can be quantified in our simulations by calculating mechanical moduli related to the deformation of membrane in different modes such as membrane bending and volume fluctuation. To compare the effects of different ionic environments, all mechanical measurements were made on each leaflet separately and then averaged over the two leaflets which share the same water chamber (see Fig. 1).

The bending modulus denotes the energy required to bend the membrane and was calculated on a per-leaflet basis, therefore including both peristaltic and undulatory types of motion (46). The methods to describe the calculation of bending modulus have been described previously (21,27), although these previous studies focused on mechanics of bilayers rather than individual leaflets. Briefly, a per-leaflet height function was constructed by the position of the glycol carbon (C12) of each lipid. These heights were mapped on a 0.5-nm grid which was then Fourier-transformed to give 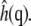Each resulting 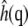field was averaged over the two leaflets sharing the same water chamber. The bending modulus k_c was calculated according to

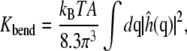(6)

where k_B is Boltzmann's constant, T is the temperature, A is the (average) area, and 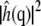is the square modulus of 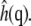Fig. 8 illustrates the differences in bending modulus for the lipid leaflets facing the N and K chambers and for a DPPC bilayer in pure water. All numbers are in reasonable agreement with the experimental bending modulus of 1.0 × 10⁻¹⁹ J (47). Fig. 8 shows large and significant differences (Student t-test, 99.9% confidence interval) in the N leaflet bending modulus when compared to the K leaflets or the leaflets of the DPPC bilayer in pure water. Conversely, differences between the K leaflet and the pure water DPPC bending moduli are much smaller, although still statistically significant. Errors on the bending modulus were calculated using the bootstrap method described above with 78- (single DPPC bilayer leaflets), 177- (N chamber leaflets), and 96- (K chamber leaflets) snapshot sample sizes based on 128- (single DPPC bilayer leaflets), 176- (N chamber leaflets), and 240- (K chamber leaflets) picosecond correlation times for the integral of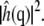

FIGURE 8.

(A) Bending and (B) bulk moduli for leaflets facing the N and K chambers in the double-bilayer setup (see Fig. 1) and for leaflets of a 128-lipid DPPC bilayer in pure water. Brackets and asterisks denote differences which are statistically significant (Student t-test, ≥99.9% confidence level).

The bulk modulus describes the (volume) compressibility of the membrane and can be determined from the fluctuation of the membrane volume through the relationship (48)

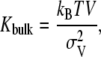(7)

where K_bulk is the bulk modulus, V is the average volume of a leaflet, k_B is Boltzmann's constant, T is the temperature, and 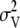is the variance in leaflet volume. The volume of the membrane was calculated for each leaflet separately by multiplying the box area with the thickness of each leaflet. The thickness of a leaflet was determined from the average distance between phosphorus atom and the center of bilayer (37,49). Based on Student t-tests with a 99.9% confidence interval, the average volume of the leaflets were significantly different: 308.16 ± 0.04 nm³ for the single DPPC bilayer system, 305.8 ± 0.1 nm³ for the N chamber leaflets, and 305.2 ± 0.1 nm³ for the K chamber leaflets. This volume data was used to calculate the bulk modulus according to Eq. 7 above with errors assessed using the resampling methods described above with 1250- (single bilayer), 324- (N chamber), and 243- (K chamber) snapshot sample sizes based on 8- (single bilayer), 96- (N chamber), and 128- (K chamber) ps correlation times for volume. Fig. 8 shows the bulk moduli and associated errors for each of the leaflets; both the N and K chamber leaflets showed significant differences with respect to the pure water DPPC bilayer leaflets. The N and K leaflets had significantly different bulk moduli, although these differences were much smaller than deviations from the pure water DPPC bilayer.

DISCUSSION

Our results show that the asymmetric distributions of different NaCl and KCl solutions within our small double-bilayer system can generate net potential differences across DPPC membranes. In our simulation, this potential drop arose from imbalances in the magnitudes of induced dipoles on both sides of the membrane caused by differing levels of adsorption of monovalent cations to the DPPC bilayer surfaces. The process of monovalent ion adsorption was slow, requiring 65 ns before our nonequilibrium simulation reached an apparent steady state. Furthermore, water flux across the membrane persisted for 110 ns of the simulation. Very long equilibration times and slow sampling in membrane systems have previously been observed by a number of groups (50–53) and the current relaxation times of 65 ns are not particularly surprising, given the strong Na⁺-headgroup interactions and asymmetry in this system. At steady state, we observed high levels of Na⁺ bound to the headgroup region of the DPPC bilayers through coordination by lipid carbonyl groups. Adsorption of Na⁺ to the headgroup region was accompanied by accumulation of Cl⁻ at the membrane surface, leading to a net dipole on N chamber leaflets of the double bilayer system (see Fig. 3). K⁺ ions showed significantly less affinity for the bilayer and thus created a much smaller surface dipole moment. The net result of these dipoles was a field across the bilayer which, in turn, led to the observed −70 ± 10 mV potential drop.

Other observations of membrane cation binding

As observed in previous computational simulations, we saw extensive coordination of Na⁺ ions by DPPC carbonyl oxygens (2,20) throughout our simulations resulting in high densities of Na⁺ ions at the lipid carbonyl region of the membrane-water interface (2,38,54). Conversely, K⁺ showed significantly less coordination by lipid carbonyl oxygens and, as a result, was distributed more uniformly away from the carbonyl region of the lipid-water interface. Finally, as observed in previous simulations (2,38), Cl⁻ ions were largely excluded from the interface region.

Recent experimental work has also observed specific monovalent ion-lipid interactions, some of which provide indirect support for the interactions observed in our simulations.

First, recent atomic force microscope work by Fukuma and co-workers (9) revealed specific interactions of Na⁺ ions with the headgroups of gel-phase DPPC lipids. The primary site of these interactions appears to be the DPPC phosphate groups, a mode of Na⁺-DPPC interaction not observed in our molecular dynamics simulations but observed in other molecular dynamics simulations of Sachs et al. using the CHARMM force field in a different thermodynamic ensemble (19). However, Fukuma and co-workers observed interesting regions of interactions between neighboring DPPC molecules at heights below the sites of Na⁺-phosphate interactions (9); these lower-height interactions could be due to water molecules or Na⁺ ions bridging adjacent DPPC carbonyls (S. P. Jarvis, personal communication, 2007).

Second, infrared spectroscopy measurements were made on 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) vesicles in solutions of various metal chlorides. Addition of LiCl, NaCl, and KCl to highly-hydrated POPC vesicles showed decreases in C=O vibrational frequencies but little change in the asymmetric PO₂ stretching mode frequencies, indirectly suggesting possible interactions between the cations and POPC carbonyls. Note that these experiments revealed significant effects for Li⁺, Na⁺, and K⁺, while our simulations only showed significant carbonyl association for Na⁺ (Li⁺ was not included in our simulations). These differences in putative carbonyl association could be due to a number of reasons, including differences between POPC and DPPC and possible simulation artifacts (discussed below). However, it is important to note that these experiments were carried out at ion/lipid mole ratios of 1.6, which are much higher than the 0.2 ion/lipid (or 0.1 Na⁺/lipid and 0.1 K⁺/lipid) ratios used in our simulations.

Third, Böckmann et al. (2) used excess heat capacity measurements to demonstrate how increasing NaCl concentrations shift POPC gel-to-liquid phase transition temperatures to higher temperatures and broaden the overall calorimetric profile. Such broadening suggests decreased cooperativity of the phase transition due to the presence of NaCl (55). The same authors also studied the diffusion constant of POPC molecules at different NaCl concentration. The appearance of populations of lipids with much lower diffusion constants was matched to the complexation of the lipids by coordinating Na⁺ ions. Finally, Pabst et al. (4) used small angle x-ray diffraction to observe structural and mechanical changes in POPC bilayers, albeit at higher concentrations (>1 M) than used here.

Force-field sensitivity

The proper force-field parameters are critical to reproduce the chemico-physical properties of the ions during the simulations (33). The Lennard-Jones interaction parameters for Na⁺ and K⁺ ions were obtained from the GROMACS FFGMX force field (22) which contains parameters loosely related to values from Straatsma and Berendsen (25), in which the parameters of these ions were fit to reproduce the gas-phase energetics for ion monohydrates calculated by ab initio self-consistent field calculations. These parameters were implemented in the GROMACS force field and have been widely used for ion-membrane interactions (16,38,56,57), despite problems accurately describing K⁺-protein interactions when used with protein GROMOS force field parameters (58). Additionally, although popular, these Straatsma-Berendsen parameters yield ion solvation free energies, which are significantly more negative than experimental values (25,59). As shown in Table 3, these FFGMX parameters used in our simulations are significantly different from the Åqvist parameters often used in protein and nucleic acid simulations (59) and also differ from the modified ion parameters of Roux (60). It is possible that these particular ion parameters may have contributed to the strong adsorption of Na⁺ ions to the membrane. Comparative analysis of ion force-field effects on these results is underway; however, interested readers should also refer to the recent work of Gurtovenko and Vattulainen for similar comparisons (20).

TABLE 3.

Lennard-Jones interaction parameters of Na⁺ and K⁺ ions

	FFGMX		Åqvist		CHARMM
Ion	σ (nm)	ε (kJ mol−1)	σ (nm)	ε (kJ mol−1)	σ (nm)	ε (kJ mol−1)
Na+	0.25752	6.17743 × 10−2	0.33305	1.15980 × 10−2	0.24299	1.96290 × 10−1
K+	0.64541	5.66508 × 10−5	0.49346	1.37235 × 10−3	0.35275	3.64251 × 10−1

The FFGMX parameters were obtained from the GROMACS package (22). We have also included Åqvist (59) and CHARMM parameters for comparison. The Åqvist parameters are reproduced from Chen et al. (33). The CHARMM parameters for Na⁺ are obtained from Gurtovenko et al. (20), and the modified CHARMM parameters for K⁺ are from Roux (60).

Another potential source of concern lies in the high dipole moment of the lipid carbonyl group (see Table 4) used in our and many other GROMACS-based simulations (2,16,20,35,54,61–63). The high partial charges associated with the lipid headgroup were determined by ab initio self-consistent field calculations and resulted in good agreement with experimental areas per headgroup when simulated in constant pressure ensembles (64,65). However, it is possible that this high carbonyl dipole moment could also influence Na⁺ interaction with the lipid headgroups and lead to the high surface dipoles observed in the current simulations. Comparison of GROMACS lipid parameters with other force fields is currently underway.

TABLE 4.

Partial charges for lipid carbonyl atoms

	FFGMX		CHARMM
	SN-1	SN-2	SN-1	SN-2
Ester oxygen	−0.7	−0.7	−0.34
Carbonyl carbon	0.8	0.7	0.63
Carbonyl oxygen	−0.6	−0.7	0.52

Partial charges (in e) for lipid carbonyls were adapted from Chandrasekhar et al. (65) for FFGMX parameters and from Heller et al. (72) for CHARMM parameters.

Of course, most fixed charged force fields are faced with a fundamental flaw: their inability to predict, accurately, transfer-free energies for multiple types of media (e.g., water, vacuum, protein, lipid, etc.) simultaneously due to their lack of atomic polarizability (66–69). One consequence of this lack of atomic polarizability in the context of lipid bilayers is an artificially low dielectric coefficient in the lipid tail region. In particular, the neutral united-atom alkane model used in the current fixed-charge lipid force field yields an effective dielectric coefficient of 1 for the lipid tail region; however, a polarizable model for the alkane tails would yield an dielectric coefficient for this region of ∼2 (66). Such differences in dielectric coefficients have been shown to significantly affect ion permeation through gramicidin A channels (58,66,70) and clearly will have an impact on the localization of ions in the DPPC bilayers considered here. Another potential consequence of the fixed charge force field is an incorrect affinity of Na⁺ and K⁺ for the lipid headgroup region; a symptom of the inaccurate transfer free energies of fixed-charge force fields discussed above. The inclusion of polarizability in a force field comes at the expense of additional computation time, which would have made the 172 ns of simulation reported here prohibitively expensive. However, we look forward to the advances in polarizable force-field simulation methodology and computational power, which should make the routine use of polarizable force fields feasible in the near future.

Finite size effects

Our double-bilayer system was relatively large. We included 256 lipids per bilayer (512 lipids total), to allow for reasonable membrane undulations (27). Additionally, we used much larger water chambers than other recent double-bilayer studies (16–18). However, despite these precautions, there are important finite size artifacts that affect this work and should serve as a precaution to other groups interested in simulating asymmetric aqueous solutions in similar double-bilayer configurations.

Electrostatic properties

One finite size artifact in this simulation arises from the finite extent of our water chambers between lipids, despite their relatively large size as compared to recent simulations (16–18). Both the ion distributions and the water polarization data presented earlier demonstrate the influence of finite size effects. The counterion distributions (Fig. 3 B) do not reach bulk or constant values anywhere within the simulation domain. Given large enough water chambers, we would expect a region of nearly constant ion densities between the bilayers, corresponding to a weak electrostatic field and nearly constant ion concentrations. Likewise, the electric field (Fig. 7 D) also lacked a region of constant (small) values and, instead, was zero only at the center of the water chambers. Since the electric field due to the water molecules is expected to be proportional to their polarization, this implies that the water in these systems was strongly influenced by their proximity to the bilayer surfaces. As such, it is highly unlikely that our current simulation is measuring Nernst transmembrane potentials; e.g., the net drop in potential observed in bulk solution at some distance from the membrane surface associated with net differences in ion chemical potentials. Instead, it is much more probable that the results of this simulation reflects a combination of surface potentials due to 1), asymmetric double layers induced by strong DPPC-Na⁺ interactions in the GROMACS force field; and 2), potential artifacts from the finite size of the simulations.

Structural properties

A second finite size artifact in this simulation arises from the finite number of lipids in the bilayer leaflets. Other simulations of lipid bilayers in the presence of aqueous Na⁺ ions have reported a much larger decrease in membrane area associated with Na⁺ binding (2,16,38) than the small contraction observed in this work. It is important to keep in mind that our system was set up with equal numbers of lipids in the N and K chambers, unlike recent work by Gurtovenko and Vattulainen (71) on lipids of asymmetric composition, but similar to the pore formation simulations of Gurtovenko (20) as well as past simulations of asymmetric ionic solutions by Sachs et al. (17), Gurtovenko (16), and Vernier et al. (18). However, significant ion binding was only observed for leaflets in the N chamber. The periodicity of our system, together with its relatively small size, prevents an asymmetric compression of the N and K chamber leaflets in response to ion binding. This finite size artifact is present in common double-bilayer setups where asymmetric aqueous solutions are expected to induce asymmetric structural changes in bilayer leaflets but are unable to do so due to periodic constraints and (relatively) small system size. In this case, the finite number of lipids in our setup prevented the asymmetric change in area between the N and K chamber leaflets, resulting in the observed area decrease, which was much smaller than previous symmetric Na⁺ solution simulations. Note that this lack of change in area could also possibly compound the finite size effects on electrostatic properties described above by alternating the dipole moment densities associated with each leaflet. This finite area artifact could likely be overcome in future simulations by simulating systems with fewer lipids in the K chamber leaflet, in a manner similar to the simulations by Gurtovenko and Vattulainen (71) on bilayers of asymmetric composition. We are exploring configurations for future simulations.

CONCLUSIONS

An atomic-detail MD simulation has been used to demonstrate the influence of ion imbalance on the properties of a lipid membrane while maintaining electroneutrality and equal ionic strength in each water chamber surrounding the lipid bilayer. The unexpected effects of the ions on the structural and electrical properties of the membrane mainly originated from the strong adsorption of Na⁺ ions. Even though some experimental observations indirectly support specific interactions of Na⁺ ions with the zwitterionic lipid headgroup, the extensive binding and concomitant −70 mV potential drop observed in our simulations also suggests cautious examination of force field parameters and finite size effects. Finally, it is important to note the extremely long equilibration time required for this asymmetric (and nonequilibrium) system to reach steady state. In particular, slow processes related to Na⁺ headgroup binding, small changes in the bilayer area and, water permeation across the lipid bilayers resulted in relaxation times of ∼110 ns. Overall, our results show that potential drops across membrane interfaces can be highly sensitive to both ion species and concentration due to specific lipid-ion interactions. This work also suggests that, while the multilamellar membrane simulation methodology pioneered by Sachs et al. (17) is an excellent mechanism for simulating asymmetric membrane solution environments and electrostatics, care must be taken in assessment of force-field parameterization, finite size effects, and sampling artifacts when interpreting the simulation results.