Structure of the Alamethicin Pore Reconstructed by X-Ray Diffraction Analysis

Abstract

We reconstructed the electron density profile of the alamethicin-induced transmembrane pore by x-ray diffraction. We prepared fully hydrated multiple bilayers of alamethicin-lipid mixtures in a condition where pores were present, as established previously by neutron in-plane scattering in correlation with oriented circular dichroism. At dehydrated conditions, the interbilayer distance shortened and the interactions between bilayers caused the membrane pores to become long-ranged correlated and form a periodically ordered lattice of rhombohedral symmetry. To resolve the phase problem of diffraction, we used a brominated lipid and performed multiwavelength anomalous diffraction at the bromine K edge. The result unambiguously shows that the alamethicin pore is of the barrel-stave type consisting of eight alamethicin helices. This pore structure corresponds to the stable pores detected by neutron in-plane scattering in fully hydrated fluid bilayers at high peptide/lipid ratios, which are the conditions at which alamethicin was tested for its antibacterial activity.

INTRODUCTION

Pore formation in membranes is the mode of action utilized by the ubiquitous antimicrobial peptides and pore-forming proteins. Antimicrobial peptides (1), such as alamethicin and magainin, and the bacterial toxins colicins (2) form transmembrane (TM) pores to exert their cytotoxic function. The apoptosis regulator Bax (3,4) activates pore formation in the outer mitochondria membrane to release the apoptotic factor cytochrome c (3,4). Despite the consensus on such pore-forming activities, so far there has not been a direct observation of the pores. The main evidence for the pore formation has been the peptide-induced ion conduction across the membranes (2,4–9) and the peptide-induced molecular leakage into or out of lipid vesicles (10–14). From the magnitude of the single channel ion conductance (6,8,14) and from the size of the largest dye molecules leaking through the membranes of lipid vesicles (10–12), one can roughly estimate the size of a peptide- or protein-induced pore. A more precise estimate of pore size was carried out by neutron in-plane scattering that directly measured the internal and external pore diameters (15–18). Here we report the first attempt, to our knowledge, to reconstruct the electron density profile of a peptide-induced TM pore by x-ray diffraction. Specifically, we obtained the image of the pore structure produced by one of the best known antimicrobial peptides, alamethicin (19).

Accumulated experimental results suggest that there may be two types of peptide-induced pores (18) depending on the peptides that induce them. One is a TM structure consisting of a cylindrical array of parallel peptide helices with a water-filled central lumen, like the staves of a barrel, and hence called the barrel-stave model (5). This model resembles a TM ion channel. Whether the lipid bilayer is distorted to accommodate the peptide barrel is unknown. For a long time, all peptide-induced pores were assumed to be of such a TM structure. However several lines of evidence (18) have suggested that most pore-forming peptides create another type of pore that resembles a pore formed in a pure lipid bilayer when subject to an external tension. When a pore is formed in a pure lipid bilayer, the lipid molecules along the edge of the pore must reorient to merge the two monolayer leaflets to shield the hydrocarbon chains from direct contact with water (20,21). The extra energy for the formation of the edge incurs line tension. The second type of peptide-induced pore was proposed (17,22) to be like a pure lipid pore except that the edge of the pore is partially made of peptides. The peptide binding to the edge of the pore is analogous to the action of surfactant (23) that serves to lower the line tension, which is one of the factors stabilizing the pore (24). In this second model, the two lipid monolayers merge through the pore in the fashion of a toroidal hole (or a wormhole), and the pore is lined by both the peptides and the lipid headgroups. This was named the toroidal (wormhole) pore (17).

The pore structure is important because it is closely related to the mechanism of pore formation by the peptide. Therefore a definitive determination of the pore structure is essential for the functional analysis of the peptide. This structural problem is significantly different from that of protein crystallography for three reasons. First, the lipid-peptide complex is of a soft matter structure lacking the rigidity of a protein crystal. The structure is described by an electron density distribution, not by the atomic positions. Second, the sizes of the pores are of the order of a few nanometers (16–18), close to the limits of various imaging methods. Third, the condition under which the peptides form pores is a thermodynamic phase of the peptide-lipid system (25); therefore, one needs a very specific sample condition for observing the pores. All of these reasons present challenges to existing imaging methods, such as transmission electron microscopy.

In recent years, we developed a new method for imaging lipidic structures. We found that lipidic structures could be long-ranged correlated into periodically ordered lattices that are amenable to diffraction analysis (26–28). Although the inherent disorder within the unit cells limits the x-ray diffraction to a relatively low resolution, the reconstructed electron density nevertheless provides solid evidence for the lipidic structure. In our first application, we analyzed a lipidic structure that was induced in membrane multilayers by osmotic pressure and found that the unit cell consists of two lipid bilayers merged in an intermediate state of membrane fusion (29). The discovery of this lipid structure validated the stalk-pore hypothesis for membrane fusion (30). We now extend the technique to resolve the lipidic structure induced by a peptide.

As in protein crystallography, the phase problem is the main obstacle for the reconstruction of electron density. But for two basic reasons, the well-developed phasing methods for protein crystallography are mostly inapplicable to lipidic structures (31). First, as stated above, a lipidic structure is described by an electron density distribution, not by atomic positions. Second, although most proteins are not centrosymmetric, a lipidic structure most likely is. This is because the lipid-peptide samples are prepared from a homogenous mixture from which symmetric lipid bilayers are usually formed. The phasing methods of protein crystallography are based on atomicity and are often specifically for noncentrosymmetric structures (31). Thus a routine technique for phasing the diffraction amplitudes from lipidic structures is yet to be developed. In the case here, we used multiwavelength anomalous diffraction (MAD) to simplify the phasing problem to that of heavy atoms alone. For this reason, we used a brominated lipid, 1,2-distearoyl(9-10dibromo)-sn-glycero-3-phosphocholine, which has two bromine atoms on each chain. We let alamethicin/lipid mixtures form periodically ordered lattices under the condition alamethicin forms pores. After we extracted the diffraction intensities belonging to bromines alone, we modeled the distribution of bromines to obtain the phases. We demonstrate that this is a sensible method for solving the phase problem for lipid structures. The result for the alamethicin-induced pore confirms the barrel-stave model that has been speculated since 1974 (5).

MATERIALS AND METHODS

Lipid and peptide

1,2-Distearoyl(9-10dibromo)-sn-glycero-3-phosphocholine (abbreviated di18:0(9,10Br)PC) was purchased from Avanti Polar Lipids (Alabaster, AL). Alamethicin was purchased from Sigma-Aldrich Chemical (St. Louis, MO). The Sigma product is a mixture of components, principally alamethicin I (85% by high-performance liquid chromatography) and alamethicin II (12%), which differ by one amino acid (19). This product has been used in a great number of previous investigations. Silicon wafers (〈100〉 surface, P-doped), 300 μm thick, were purchased from Virginia Semiconductor (Fredericksburg, VA). The materials were used as delivered.

The peptide/lipid mixtures of the desired molar ratios were first dissolved in a 1:1 trifluoroethanol-chloroform solvent and then uniformly deposited onto a thoroughly cleaned silicon (for x-ray) or quartz (for oriented circular dichroism; OCD) substrate. The organic solvent was evaporated in vacuum or open air for ∼1 h. The deposit was then hydrated with saturated water vapor and incubated in an oven at 35°C for several hours until the sample films looked visibly uniform, smooth, and flat. The result was 1 mg of lamellar phase lipid spread over an area of 10 × 20 mm², with an average thickness of 5 μm. For both x-ray and OCD experiments, the sample was kept inside a humidity-temperature chamber (32). The chamber was covered by a double-layer insulating wall with kapton windows for the passage of x-ray (quartz windows for ultraviolet). Between the two layers, a resistive heating coil maintained the surface temperature of the chamber above that of the sample to prevent water condensation on the windows.

Oriented circular dichroism

OCD is a simple method for detecting the orientation change of peptides embedded in lipid bilayers using a conventional circular dichroism (CD) machine especially for α-helical peptides (33,34). A Jasco J-810 spectropolarimeter was used for this experiment (Jasco, Tokyo, Japan). The procedure of OCD measurement is the same as that for the conventional CD measurement, except that an aligned multilayer sample is used. For most experiments as in this one, normal (rather than oblique) incidence OCD is sufficient for spectral analysis (34). The sample mount for OCD (housed in a temperature-humidity chamber) was allowed to rotate around an axis normal to the surface of the sample substrate and coincident with the incident light. If OCD changes with the rotational angle, it implies that the signal contains artifacts due to linear dichroism; in that case a rotational average can remove the artifacts (34). In this experiment, the OCD of our samples did not change with the rotational angle.

X-ray experiment

Grazing-angle x-ray anomalous diffraction was performed at the beamline X21 of the National Synchrotron Light Source, Brookhaven National Laboratory (Upton, NY). The setup was similar to the one described in Yang and Huang (32). The sample was positioned to let a beam of size 0.5 × 0.3 mm² incident at ∼0.3° relative to the substrate. Diffraction patterns were recorded on a MarCCD detector (Mar USA, Evanston, IL) vertical to the incident beam. A helium beam path between the sample chamber and the detector was used to reduce air scattering. A niobium (Nb) attenuator was used to keep strong reflection orders from saturating the detector. The intensity of the incident beam was monitored by a Bicron scintillation detector (Saint-Gobain Crystals, Newbury, OH) that measured the elastic scattering from a 0.9-μm-thick polyethylene film inserted in the incident beam; the detector measured the 90° scattering in the direction perpendicular to the incident polarization.

The technical detail for MAD measurement has been described in previous works (35,36). The initial steps included measuring the wavelength dependence of the detectors and the absorption spectrum of bromine in the actual sample. By a standard procedure described in Wang et al. (36), both the real 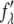and imaginary 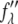parts of the bromine atom's anomalous scattering factor were obtained from the measured absorption spectrum. The results are shown in Fig. 1 of Pan et al. (35). The energy of the bromine K-edge is 13.474 keV. Ten subedge x-ray energies were chosen such that the values of 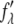at successive energies differ by 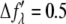in the unit of electron (Table 1). The grazing-angle diffraction patterns were recorded at each of these chosen x-ray energies. In addition, to obtain the complete diffraction patterns, the meridional peaks were measured by θ − 2θ scan (32).

FIGURE 1.

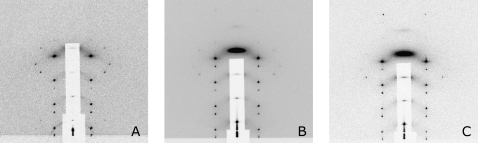
Diffraction patterns of (A) pure di18:0(9.10Br)PC at 40% < RH < 52%, (B) alamethicin/di18:0(9.10Br)PC P/L = 1:30 at 40% < RH < 55%, and (C) alamethicin/di18:0(9.10Br)PC P/L = 1:20 at 40% < RH < 55%, all at 25°C. The patterns are of rhombohedral symmetry (space group R 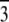). The dimensions of the unit cells are in (A) c = 5.40 nm, a = 6.96 nm, in (B) and (C) c = 4.95 nm, a = 5.94 nm. The detector images are raw data. The lighter background of (C) was due to a shorter exposure time.

TABLE 1.

Anomalous scattering factor at 10 sub-K edge x-ray energies (K edge at 13.474 keV)

No.	En(eV)	f′	f″
1	13470.7	−7.53	0.87
2	13468.1	−6.98	0.68
3	13464.8	−6.51	0.59
4	13459.0	−5.99	0.54
5	13449.8	−5.50	0.51
6	13434.8	−5.00	0.50
7	13409.1	−4.50	0.51
8	13366.3	−4.00	0.52
9	13294.1	−3.50	0.51
10	13156.7	−3.00	0.52

As previously described in our method work (36), we took precaution to avoid radiation damage to the sample. The x-ray beam was blocked between scans so the sample was exposed to radiation only during data collection. After the completion of 10 energy recordings, the diffraction pattern of the first energy was recorded again to compare with the initial recording. Then we displaced the substrate to a previously unexposed sample position to repeat the same measurement in the reverse order of the x-ray energies. We made sure there was no change in the diffraction pattern by this double-checking procedure, indicating no deterioration effect from radiation damage. More extensive tests on radiation damage have been established in previous experiments (36).

Data reduction and MAD analysis

The rhombodedral diffraction pattern in Fig. 1, B or C, is on a lattice described by the set of reciprocal vectors and 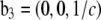indexed by 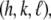which correspond to the crystal axes 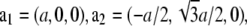and 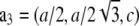(32). a₁, a₂, a₃ define the primitive unit cell. The lattice constants a and c are 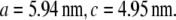Equivalently, the lattice is described by the reciprocal vectors 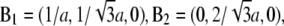and 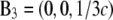indexed by 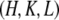and the crystal axes 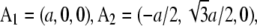and 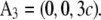The cell defined by A₁, A₂, A₃ contains three primitive unit cells positioned at (0,0,0), 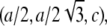and

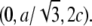
Diffraction peaks were integrated from the raw data after carefully removing the background. The integrated intensities were then reduced to the relative magnitudes of the diffraction amplitude 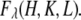These procedures have been previously described in detail (32,35,37). Twelve independent peaks, listed in Table 2, have integrated intensities substantially above the background. The symmetry-related peaks are grouped as one independent peak and their intensities averaged. Four visible but very weak diffraction peaks at (1,1,9), (0,2,10), (1,1,12), and (1,0,13) were not included for analysis. Their magnitudes could not be determined accurately, and they were small enough that they would not make any significant contribution to the electron densities shown below.

TABLE 2.

Results of MAD analysis (symmetry-related peaks are grouped as one independent peak)

No.	(H,K,L)	|F2|	|F0|	−F0/F2	r(linear correlation)	ɛ(std of |F2|)	F2 model phase
1	(0,0,3)	207.28	58.90	0.284	0.99589	6.67	+1
2	(0,0,6)	90.62	50.60	−0.558	−0.98613	5.39	−1
3	(0,0,9)	99.55	50.91	−0.511	−0.99816	2.14	−1
4	(0,0,12)	60.03	58.79	−0.979	−0.95204	6.82	−1
5	(1,0,1)(−1,1,1)(0,−1,1)	65.90	142.50	−2.163	−0.86739	7.86	−1
6	(0,1,2)(−1,0,2) (1,−1,2)	18.85	8.63	0.458	0.99423	0.72	−1
7	(1,0,4)(−1,1,4)(0,−1,4)	16.16	15.56	−0.963	−0.95272	1.82	−1
8	(0,1,5)(−1,0,5) (1,−1,5)	21.83	21.89	−1.003	−0.94241	2.74	−1
9	(1,0,7)(−1,1,7)(0,−1,7)	32.07	19.43	−0.606	−0.98254	2.15	+1
10	(0,1,8)(−1,0,8) (1,−1,8)	42.52	21.90	−0.515	−0.98122	2.96	+1
11	(1,0,10)(−1,1,10)(0,−1,10)	6.36	8.25	−1.453	−0.91197	1.01	+1
12	(0,1,11)(−1,0,11) (1,−1,11)	42.70	52.29	−1.225	−0.93385	5.78	+1

MAD analysis follows the procedure given by Wang et al. (36). First, we express the diffraction amplitude of a system containing atoms with anomalous scattering factor 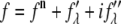as

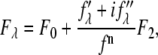(1)

where 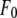is the normal diffraction amplitude of the whole system, 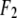is the normal diffraction amplitude of the anomalous atoms alone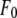, and and 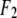are functions of q, independent of the x-ray wavelength λ. The lipidic structure under consideration was started from a symmetric lipid bilayer. Its average molecular distribution in the unit cell is most likely centrosymmetric. We will assume this is the case. Then the amplitudes F₀ and F₂ are real quantities, and Eq. 1 is absolute squared to a simple expression 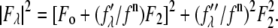On the right-hand side of this equation, the second term is ∼1% of the first term because at energies below the absorption edge the values of are ∼10% of 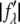(Table 1). Therefore, we obtain the approximate relation

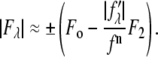(2)

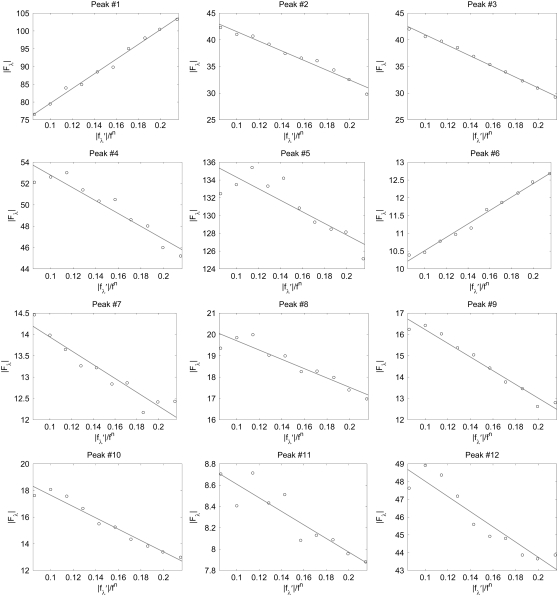
For each independent peak listed in Table 2, the value of 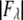is plotted as a function of 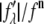in a panel in Fig. 2. The data in all the panels appear to follow a linear relation. The linearity shown by all 12 peaks justifies the assumption that led to Eq. 2, i.e., that the unit cell structure is centrosymmetric. From the straight-line fit in each panel, the intercept of the fitted line gives 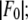the magnitude of the slope gives 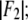and the sign of the slope gives the sign of 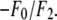In Table 2, we listed for each of the 12 independent peaks the values of 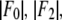the ratio 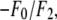the linear-correlation coefficient r for the straight-line fitting, and ɛ, the standard deviation for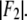

FIGURE 2.

MAD analyses for the detected peaks. For each independent peak, the square root of the integrated intensity, 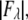is plotted as a function of 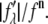The data are fit with a straight line, from which 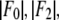and the ratio 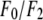are obtained. The results are in Table 2.

RESULTS

Orientation of alamethicin in lipid bilayers and pore formation

Alamethicin forms an α helix when bound to a lipid bilayer, as indicated by its CD spectrum (25,38,39) and is in agreement with its crystalline molecular structure (40). By a combination of CD and neutron experiments, we previously correlated the orientation of alamethicin helices with pore formation (15,16).

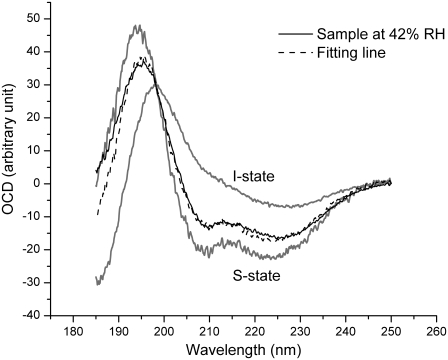
The orientation of the helices in lipid bilayers is most easily monitored by OCD (34) because of the distinct CD spectra for helices parallel and perpendicular to the light (Fig. 3). This is done by measuring the CD of the peptides in aligned multiple bilayers at normal incidence. Extensive studies by OCD (25,38,39) showed that the peptide orientation changes systematically as a function of concentration. At low concentration (expressed as the peptide/lipid molar ratio; P/L), alamethicin is oriented with its helical axis parallel to the plane of the bilayer. But as the concentration P/L increases above a certain critical value, P/L*, an increasing fraction of peptides reorient to the perpendicular orientation. This critical value P/L* depends on the lipid compositions of the bilayers (25,38,39). In saturated lipids such as di12:0PC or di14:0PC, the values of P/L* are so low that alamethicin is always inserted perpendicular to the bilayers in all measurable concentrations. In unsaturated lipids, we have seen P/L* varying from 1:30 to 1:200 (41). To utilize the MAD method, we chose to use the lipid di18:0(9.10Br)PC, which has two bromine atoms on each chain. Although it is a saturated lipid, the two extra Br atoms on each chain make the lipid behave similarly to an unsaturated lipid. (It has been reported that a bromine atom can often replace a methyl group isomorphously in a hydrocarbon chain (42).) The OCD in Fig. 3 shows that at P/L = 1:100 in full hydration, alamethicin is in the parallel orientation (the S state), whereas at P/L = 1:30 and 1:20 in full hydration alamethicin is in the perpendicular orientation (the I state). Thus the P/L* in di18:0(9.10Br)PC is between 1:100 and 1:30; the exact value is irrelevant to this experiment.

FIGURE 3.

OCD of alamethicin in aligned multiple bilayers of di18:0(9.10Br)PC, measured at normal incidence. The I state was measured at full hydration at P/L = 1:20, representing the OCD of alamethicin orienting perpendicular to the bilayer. The S state was measured at full hydration at P/L = 1:100, representing the OCD of alamethicin orienting parallel to the bilayer (33,37). The sample P/L = 1:20 measured at 42% RH has the spectrum shown by a solid line, which is fit by a linear combination of S and I (dash line), indicating that 30% of the alamethicin helices were oriented perpendicular to the substrate (see Ding et al. (37) for details).

Previously, pore formation was shown by neutron in-plane scattering (on the same OCD samples), which detected TM water channels in the bilayers whenever P/L > P/L*, but no channels were detected for P/L < P/L* (15,16,18). This indicates that alamethicin parallel to a bilayer does not form pores. Pores are associated with alamethicin orienting perpendicular to the membrane.

In fully hydrated multiple bilayers, the neutron scattering patterns showed that alamethicin pores diffused freely in each bilayer like a two-dimensional liquid, and there were no interbilayer correlations (27,28). However, it was subsequently discovered that at dehydrated conditions, the interbilayer distance shortened and the interactions between bilayers could cause the membrane pores to become long-ranged correlated and form a periodically ordered lattice (27,28). This is what we found in the mixtures of alamethicin and di18:0(9,10 Br)PC. At 25°C the systems (both P/L = 1:20 and 1:30) remained in the lamellar phase between 100% and 60% RH. Below 55% RH the system transformed to a rhombohedral phase (Fig. 1). OCD shows that under this condition (P/L = 1:20, 42% RH), 30% of alamethicin peptides remained perpendicular to the substrate (Fig. 3). As we will see below, not all the lipids and peptides in the sample transformed into the rhombohedral phase.

Crystallization and diffraction pattern

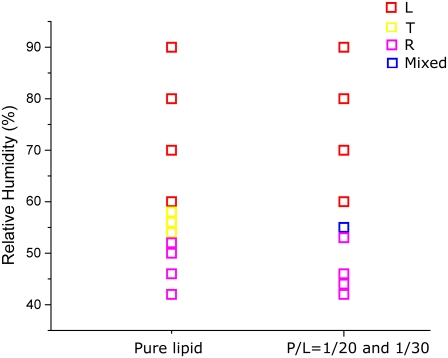
Pure di18:0(9,10Br)PC is in a lamellar (L) phase from RH 100%–60%, transformed to a newly discovered tetragonal phase (space group I4₁) between RH 58% and 54%, and below 52% RH to a pure rhombohedral (R) phase. (There were two phase coexistence regions between phases; see the phase diagram in Fig. 4.) This R phase of a pure lipid (Fig. 1 A) has been analyzed (29). Its unit cell is a structure of two bilayers merged to an intermediate state of membrane fusion called a stalk. The R phase of the alamethicin/lipid mixture is clearly different. Both the mixtures, one of P/L = 1:30 and another of P/L = 1:20, transformed from an L phase to a pure R phase below 55% RH (Fig. 4). The important difference is in the lattice constants: the pure lipid R phase has c = 5.40 nm, and a = 6.96 nm (Fig. 1 A), but both alamethicin/lipid mixtures have c = 4.95 nm, and a = 5.94 nm (Fig. 1, B and C). Although the two mixtures were prepared at different P/L, their diffraction patterns are the same within experimental errors, both having the same lattice constants and the same relative integrated peak intensities. This implies that the actual P/Ls in the R phase are not the same as the P/Ls in the samples. That means that there were excess lipids or peptides which were not part of the R phase, yet there were no extra diffraction peaks. This phenomenon is often seen in lipid phase transitions. For example, it has been demonstrated (43) that during the phase transitions of lipid/water mixtures when there is a change of the lipid/water ratio between phases, the excess lipids are often in a coexisting phase that do not diffract. These excess lipids are considered to be in a unstructured, or nondiffracting, phase (43).

FIGURE 4.

Phase diagram of pure di18:0(9,10Br)PC and its mixture with alamethicin at the P/Ls 1:20 and 1:30. Three phases were detected: lamellar L, tetragonal T (space group I4₁), and rhombohedral R (space group R 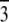). There were relatively narrow coexistence regions (1%–2% RH) between phases for pure lipid. The T phase was absent, and the coexistence region between L and R was 4%–5% RH for the mixtures. (Note that the accuracy of commercial RH sensors is 1%–2% (32).)

However, we are not aware of a possible lipid structure that does not diffract. One possible explanation for not seeing extra diffraction peaks is that the coexisting phase is lamellar, has the same lamellar spacing as the R phase, and has the same hydration dependence as the R phase from 40% to 55% RH. This is unlikely because we have seen that both pure lipid and alamethicin-lipid mixtures transformed from a lamellar phase at high hydrations to a R phase at low hydrations, and pure lipid and mixtures have different lattice constants. Furthermore, between P/L = 1:20 and P/L = 1:30 samples, the 1:30 sample has more lipids for the same amount of peptide and therefore should have a greater amount of excess lipids in this coexisting lamellar phase. Yet there was no noticeable difference between the 1:20 and 1:30 samples on their relative peak intensities. What happens to the extra lipids during a phase transition is a puzzle worthy of further investigation.

If there was a coexisting nondiffracting phase with the R phase, how the alamethicin molecules were distributed between the R phase and the coexisting phase is also unclear. Although OCD is very sensitive to the difference between the perpendicular and parallel orientations, it is not sensitive to the difference between the parallel orientation and the randomly distributed orientation. Theoretically a solution (or randomly oriented) spectrum is equal to the sum of 1/3 of the I (perpendicular) state and 2/3 of the S (parallel) state (proven experimentally in Wu et al. (34)). Because the amplitude of the S state is much larger than the I state, the S spectrum is not very different from the solution spectrum (34). As the following analysis shows, the unit cell of the R phase contains a pore. We know from the correlated study of neutron and OCD experiments (15,16) that the 30% of alamethicin that were in the I state should be associated with pore formation, therefore were in the R phase. But the remaining 70% of alamethicin could be in the S state with the R phase or randomly oriented in the unstructured, nondiffracting phase.

The diffraction patterns of the R phase of alamethicin/lipid mixtures did not vary within the range 40%–55% RH. As a result, it is not possible to use the swelling method (32,44) for determining the phases. From all of the practically same diffraction patterns of the P/L = 1:30 and 1:20 samples measured at many points between 55% RH and 40% RH, we chose to analyze the anomalous diffraction patterns of P/L = 1:20 measured at 42% RH.

Reconstruction of the unit cell structure

As shown in Materials and Methods, anomalous diffraction allows us to obtain the diffraction amplitudes of the Br atoms alone 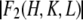and the diffraction amplitudes of the whole lipid 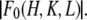It is much simpler to obtain the phases for 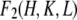than for 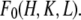Furthermore, once the phases of F₂ are determined, so are the phases of F₀, because their relative phases have been determined by the MAD analysis (Table 2). We use the following method to determine the phases and reconstruct the electron density of the unit cell.

Patterson synthesis

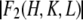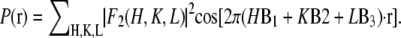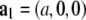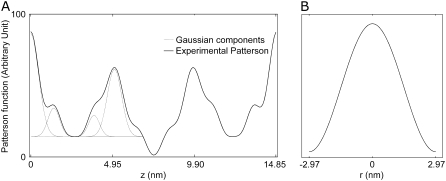
First, we use the absolute amplitudes to construct the Patterson function Fig. 5 A shows the Patterson map along the c axis (this is the z axis, vertical), P(z), and Fig. 5 B along the direction, 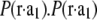shows a single self-correlation peak, indicating that there is a structure in the unit cell, and its horizontal dimension is about the width of the peak, ∼4 nm. P(z) exhibits fine structures within a repeat distance of 3c, c being the vertical height of a primitive unit cell. To understand the Patterson function, P(z), we recall that the rhombohedral lattice consists of two-dimensional hexagonal lattices stacking up in the ABCABC… fashion (29). That is why P(z) is not symmetric within the period of one primitive unit cell from 0 to c. Within a primitive unit cell (0 to c), the positions of the peaks in the Patterson function P(z) can be reproduced by a model of two Gaussian peaks, 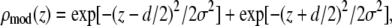positioned symmetrically with respect to the midplane (z = 0) in the unit cell. This model produces three peaks from z = 0 to c: one self-correlation peak which is split to two halves, one-half at z = 0 and another half at z = c; and two intercorrelation peaks, at z = d and at z = c − d. From the Gaussian decomposition of Fig. 5 A, we obtain d = 1.42 nm.

FIGURE 5.

Patterson maps. (A) P(z) along the c axis, from z = 0 to 3c (c = 4.95 nm). Gray lines show the Gaussian decomposition from z = 0 to c. (B) 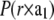along the 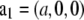direction, from x = − a/2 to a/2 (a = 5.94 nm).

We draw two important conclusions from the Patterson function: 1), the Br distributions are concentrated on two z planes separated by 1.42 nm, as in a lipid bilayer; and 2), there is a structure in the lipid bilayer (e.g., it can have a hole) whose horizontal dimension is ∼4 nm.

Model fitting and phases

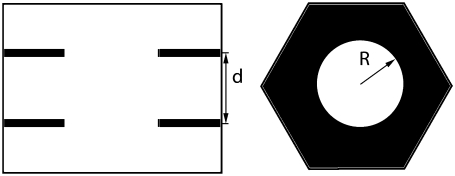
One possible way of determining the phases of diffraction amplitudes is to make use of a model that reproduces the experimental data (45). Based on the conclusions from the Patterson function, we built a model of two parallel Br planes with a central hole (Fig. 6). We let the distance between the two planes, d, and the radius of the central hole, R, be the adjustable parameters. The model diffraction amplitudes were calculated from

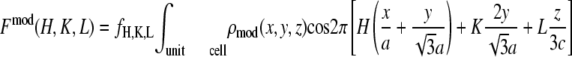(3)

with

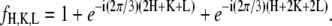(4)

We used the T function defined below (35,46,47) to measure the agreement between the model and the experimental data:

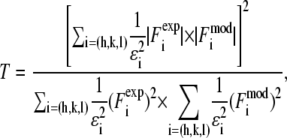(5)

where ɛ_i is the standard deviation for 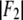given in Table 2. We varied d (∼1.42 nm) and R until we reached the highest T factor (71.23%). The model gave rise to many high-order diffraction peaks which were absent in the measured diffraction pattern. We believe the reason is that the actual distribution of Br atoms is much more diffused than the simple model and the unit cells may fluctuate from one lattice site to another. To keep the model simple, we used one Debye-Waller factor in the z direction 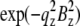and one Debye-Waller factor in the horizontal plane 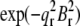(where 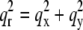) to represent these effects. We varied the B factors as well as d and R until we obtained the maximum T factor (91.01%). Our best result for this model was d = 1.42 nm, R = 1.94 nm, B_z = 0.29 nm, B_r = 0.71 nm.

FIGURE 6.

Model for the Br distribution. (Left) Side view of the unit cell. (Right) Top view of the unit cell. Position fluctuations, or equivalently the Debye factors, were imposed on this simple model to reproduce the experimental diffraction intensities.

Next we tried the model in which the Br distribution was Gaussian in both the z and r directions.

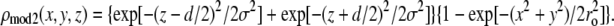(6)

The adjustable parameters were d, σ, and r_o. The best results were d = 1.46 nm, σ = 0.41 nm, r_o = 0.58 nm, which gave a value of T = 90.24%. These two models were similar and they gave the same phases for the diffraction amplitudes listed in Table 2. This set of phases gave the best result, consistent with a structure composed of lipid monolayers. That the T factor is not higher than 91% is most likely due to the density variations caused by the lattice constraint, i.e., the unit cells are confined in a hexagonal lattice; this is visible in the top view of Fig. 6 below. For example, the effect of lattice constraint on the density distribution in the inverted hexagonal phase has been analyzed previously (35,45). Such density variations caused by lattice constraint would be absent if the pore were formed in a planar lipid bilayer. Thus we believe that the lipid assembly for an alamethicin pore in a planar bilayer is very close to the simple model.

We also tried various models resembling a toroidal model, but the resulting phases did not produce a structure resembling a possible assembly of lipid monolayers.

Structure of the unit cell

The model phases were used to construct the electron density maps of the unit cell

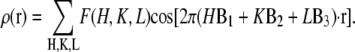(7)

The results are shown in Fig. 7 for the Br distribution and for the whole lipid distribution. Fig. 8 shows a three-dimensional view of the unit cell. The basic feature of this structure is robust in the sense that if a few phases randomly changed signs, the main feature would remain the same; i.e., the unit cell is a planar lipid bilayer with a central hole.

FIGURE 7.

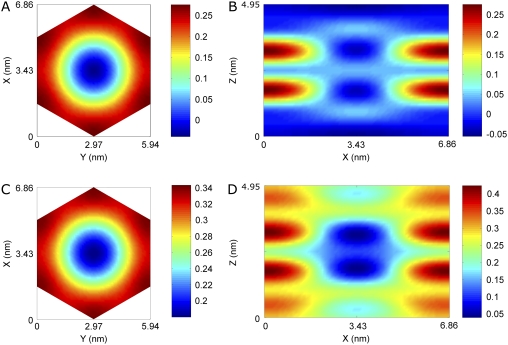
Electron density distributions in a unit cell of (A and B) bromine atoms and (C and D) the whole lipid system. Top view (A) is the plane through the maximum of the Br layer (z ≈ 2.1 nm). Top view (C) is the plane through the maximum of the phosphate layer (z ≈ 0.6 nm). The side views (B and D) are a cut through the long diagonal of the hexagon.

FIGURE 8.

Three-dimensional view of a unit cell. One sixth of the unit cell is removed to show the interior. The surface of electron density distribution is chosen at a density value such that the central hole has a radius of 2.0 nm, according to the model. The low-resolution diffraction essentially reveals the layers of phosphate groups (top and bottom layers) and the layers of bromine atoms (two interior layers). An alamethicin channel of eight monomers arranged in the barrel-stave fashion fits the hole perfectly.

The low resolution diffraction reveals only the high density regions of the electron distribution, viz., the phosphate groups and the bromine atoms. There is an obvious hole in the center, but otherwise there is no visible perturbation to the remaining bilayer. We notice that the hole region where the density should be more or less uniformly low is in fact not uniform and contains a number of relatively high density horizontal fringes as well as deep minima. We believe these are due to incomplete cancellation from the limited number of diffraction peaks. Some of their integrated intensities, particularly those of weak peaks, might contain errors from background removal.

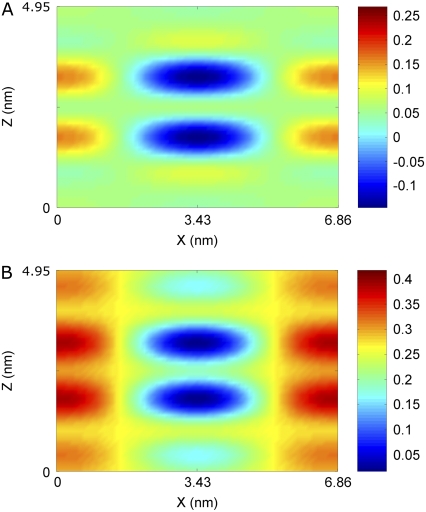
Because we could not exclude the possibility of a coexisting lamellar phase, even though it is unlikely, as discussed above, we would like to know if the nonuniform density seen in the hole region, such as the high density horizontal fringes, could be caused by a coexisting lamellar phase. To this end we constructed the electron density without the contribution of the diffraction amplitudes on the z axis, hence excluding the contribution of a coexisting lamellar phase, if any. The results are shown in Fig. 9. It is clear from a comparison with Fig. 7 that the nonuniformity was due to the limited number of rhombohedral peaks, not due to a possible coexisting lamellar phase.

FIGURE 9.

Electron density constructed from the side peaks. The (0,0,L) peaks were excluded to examine the origin of nonuniformity in the central hole region.

The distributions of the phosphoryl headgroups and bromine atoms are planar and parallel. This is contrary to the case of the membrane fusion intermediate state (29,32) and the case of pores induced by other antimicrobial peptides (S. Qian, W. Wang, L. Yang, H. W. Huang, unpublished data) where the monolayers were obviously curved. Although alamethicin is invisible due to its electron density being practically indistinguishable from that of water or the methylenes, the configuration of the lipid leaflets is unambiguously clear. It is that of a barrel-stave model. Due to the large Debye-Waller factor in the horizontal direction, as estimated by the model fitting, we take the size of the central hole in the model as the most reliable measure of the outside pore radius, i.e., R = 1.94 nm.

Normalization

The result of Eq. 7 needs to be normalized to represent the true electron density as shown in Figs. 7 and 8. The experimental densities 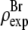and 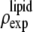from Eq. 7 are related to the true densities 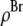and 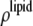by the two equations: 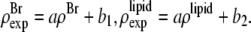The second relation can be replaced by the density of the lipid without bromine atoms, 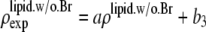where 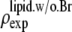was obtained from 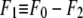by using Eq. 7. For the purpose of normalization, 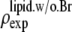has an advantage over 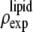in that the former contains no dominating effect of the heavy atoms. Thus we chose to normalize 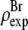and 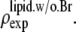Obviously once b₁ and b₃ are determined, so is b₂: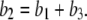

We need three conditions to determine the three constants a, b₁, and b₃. From the unnormalized lipid density distribution, we obtained the phosphate peak-to-phosphate peak distance, PtP = 4.15 nm. We know that, to a good approximation, the thickness of the hydrocarbon region is 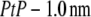(48–50). The hydrocarbon chain volume per lipid is 1.214 nm³ (51), including four bromine atoms (each has a volume about the same as that of CH₃ (42)). Thus we determined the average cross section per lipid to be 0.77 nm². Using the model above, we estimated that there are 54 lipids, hence 216 Br atoms, in each unit cell. The three conditions for determining a, b₁, and b₃ are 1) 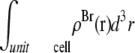= total Br electrons in unit cell, 2) 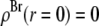along the central axis of the unit cell (we took the average of the density along the line 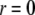), and 3) in the midplane of the density is that of the methyl group 0.17 electrons/ų (51). We did not use the integration of the lipid density because of the uncertainty in the number of water molecules.

DISCUSSION

For the first time, to our knowledge, the alamethicin pore is directly imaged by reconstructing its electron density based on x-ray diffraction. Because the molecular assembly of the pore is defined by the atomic distribution rather than by atomic positions, and also because soft-matter structures have a high intrinsic disorder, the diffraction pattern of the pore lattice is limited to relatively small q values. Only the high density parts are clearly revealed by the low-resolution diffraction. The clearly visible regions include the distribution of phosphate groups of the lipids and the distribution of the heavy atoms bromines that are bound to carbon 9 and 10 of each hydrocarbon chain. Unfortunately, the peptide alamethicin does not possess high electron density; therefore, their positions are not visible. Nevertheless, the lipid assembly is unambiguously defined by the distributions of the phosphate group and the bromines bound to carbons 9 and 10. The lipid assembly for the alamethicin pore is unmistakably that of a barrel-stave construction.

This lipid assembly accommodates a channel made of n alamethicin helixes. From the crystallographic data (40), we know that an alamethicin monomer is a cylinder 3.2 nm long and 1.1 nm in diameter. A channel of eight alamethicin helices gives an outside radius of 1.95 nm that fits the lipid assembly (16). The same size for the alamethicin pore was found in fluid lipid bilayers in full hydration under the condition that P/L exceeded a critical ratio, P/L* (15,16). In fully hydrated, fluid lipid bilayers, neutron in-plane scattering essentially yielded two length parameters, i.e., the diameter of the water column through the pore (∼1.8 nm) and the contact distance between pores (∼4.0 nm), which are consistent with an eight-monomer channel (15,16). Note that this is different from single channels formed at extremely low alamethicin concentrations (6,8). Single channels were found to have varying sizes from n = 5 to n = 10, with a transient lifetime of seconds or less at each level. The biological function of alamethicin is antibacterial. It exerts its function at high peptide concentrations (∼100 μM) (52). Thus the antibacterial activity of alamethicin is achieved by forming a massive number of stable pores, similar to the structure found here, in the bacterial membranes.

As pointed out in the Crystallization section above, P/L in the rhombohedral lattice is unknown but is at least 8:54. This is higher than the P/Ls 1:20 and 1:30 used to prepare the samples. Yet the two samples prepared at different ratios gave the same diffraction pattern. This implies that the pore size is determined by the free energy of formation, not by the P/Ls in the bilayers. This is consistent with the finding that both in the rhombohedral lattice and in fully hydrated fluid bilayers, the pores were found to have the same size.

The analysis shows that the Debye-Waller factor for the horizontal positions is considerably larger than that for the vertical positions (B_r ≈ 0.7 nm compared with B_z ≈ 0.3 nm). We believe that the horizontal disorders include the variability of the pore's horizontal position within the unit cell. It is the combination of the variability of the pore position within the cell and the variability of atomic positions within the pore structure that diminishes the diffraction intensities in the in-plane direction, limiting the in-plane diffraction to two orders (the third order was visible but too weak for numerical analysis). If this were the inherent nature of soft matter lattices, we could have reached the limitation of resolution already. This does not diminish the significance of this approach, for the resolution is still sufficiently high to unambiguously identify or confirm the key features of lipid structures, as in the cases of the membrane fusion intermediate state (29) and the alamethicin pore here.