Abstract
Head movements during magnetoencephalography (MEG) recordings may lead to inaccurate localization of brain activity. This can be particularly problematic for studies with children. We quantified head movements in 8–12 year old children performing a cognitive task and examined how the movements affected source estimation. Each child was presented auditory word stimuli in five four-minute runs. The mean change in the MEG sensor locations during the experiment ranged from 3–26 mm across subjects. The variation in the head position was largest in the up-down direction. The mean localization error in equivalent current dipole (ECD) simulations was 12 mm for runs with the most head movement, with the frontal cortex appearing to be most prone to errors due to head movements. In addition, we examined the effect of head movements on two types of source estimates, ECDs and minimum-norm estimates (MNE), for an auditory evoked response. Application of a recently introduced signal space separation (SSS) method to compensate for the head movements was found to increase the goodness-of-fit of the ECDs, reduce the spatial confidence intervals of the ECDs, and enhance the peak amplitude in the MNE. These results are indicative of the SSS method being able to compensate for the spatial smoothing of the signals caused by head movements. Overall, the results suggest that MEG source estimates are relatively robust against head movements in children, and that confounds due to head movements can be successfully dealt with in MEG studies of developmental cognition.
Introduction
Magnetoencephalography (MEG) allows non-invasive recording of brain activity related to cognitive processes (Cohen and Halgren, 2003; Hämäläinen et al., 1993). In an evoked-response study, stimuli are presented repeatedly and the data are subsequently averaged over many trials, time locked to the stimulus. By averaging evoked responses in this manner, one typically assumes that the position of the head relative to the sensor array does not change throughout the recording session. However, this assumption is not always valid, particularly when recording in children.
Several factors affect the signal-to-noise ratio (SNR) of MEG in children. Children tend to tire more easily under long recording sessions commonly required for EEG and MEG studies, resulting in less focused attention and more frequent eye movements and blinks (Phillips, 2005). These effects can be remediated, at least partially, by experimental designs that incorporate detailed instructions, training and practice, and frequent rest periods during the recording. Additionally, children have a smaller head size compared with adults. This may affect the SNR in two ways. First, the spatial sampling may be suboptimal when using MEG sensor arrays designed to fit the adult head. The SNR of sources in different parts of the brain depends critically on the position of the head with respect to the sensor array, even with adults (Marinkovic et al., 2004). Second, a small head size allows for head movements inside the measurement helmet during the experiment (Fig. 1A), which can lead to a loss of spatial details and inaccurate localization of the brain activity. Head movements can be reduced by placing foam padding around the head or by the use of a bite bar; however, these methods are often uncomfortable for children and may adversely affect performance on the task. Such approaches may not be required if the child’s head position is monitored continuously during the measurement and this information is taken into account in the data analysis (de Munck et al., 2001; Uutela et al., 2001; Wilson, 2004). In the present study, we examined the amount of head movements in children during MEG recordings and the effect of these movements on MEG source estimation.
Figure 1.
Head position within MEG sensor array. A) The scalp surface for an adult (left) and a child (right) subject is shown within a representation of a helmet-shaped array of MEG sensor elements (gray squares). The sensor array is immersed in liquid helium Dewar (not shown), which imposes a minimum distance between the head and the sensor array. However, there is typically room for the head to move with respect to the sensors, especially for children with a small head. B) The head-based coordinate system, defined by three anatomical landmarks: right and left pre-auricular points (1 & 2) and nasion (3).
In MEG, the position of the head can be monitored with the help of three or more small coils attached to the head (Ahlfors and Ilmoniemi, 1989; Fuchs et al., 1995; Incardona et al., 1992). By feeding currents to the coils whose frequencies are outside of the frequency range of the brain activity of interest, the magnetic field of the coils can be filtered out before analyzing the brain signals, thereby allowing continuous head localization during the MEG recording (de Munck et al., 2001; Uutela et al., 2001; Wilson, 2004). The required coordinate transformation for relating the head position to the sensor array is achieved by determining the locations of the coils with respect to anatomical landmarks (typically using a 3D digitizer) before the MEG recording, and to the sensor array during the recording.
Continuous head position information can be used to compensate for effects of the head movement on the MEG data. Effectively, the data can be extrapolated to a virtual sensor array fixed with respect to the subject’s head. Two approaches have been suggested: one is to construct a distributed source estimate (MNE) from which the measured data can be extrapolated to a standard representation (Burghoff et al., 2000; de Munck et al., 2001; Hämäläinen and Ilmoniemi, 1994; Numminen et al., 1995), the other is to use a spherical harmonics expansion (Taulu and Kajola, 2005; Wilson, 2004). In the MNE approach, the calculations can be quite time consuming as forward and inverse solutions need to be constructed at each time instant. The amount of calculation can be reduced by averaging the original epochs as usual and by computing an average forward model over the different head positions (Uutela et al., 2001). In the signal-space separation (SSS) method the field patterns originating from outside a sphere encompassing the sensor array are separated from those originating inside the head. Thus, SSS uses spherical harmonics to obtain field patterns specifically generated by source distributions inside the head, but without constructing an explicit source estimate. Previously, the applicability of SSS as an effective movement compensation method has been tested with simulations and in a study with infants (Cheour et al., 2004; Taulu et al., 2005). Here we evaluate the SSS method in a study with older children performing a cognitive task.
In the present study we measured and quantified the head motion of children during a cognitive MEG experiment, examined the effect of this realistic head motion on equivalent current dipoles (ECD) using simulations, and evaluated the effectiveness of the SSS method to compensate for the effect of head movements on ECD and MNE source estimates.
Methods
Quantitative assessment of head movement in children
To assess the amount of head movement in children in MEG, we used data from a cognitive study, the results of which are reported elsewhere (Wehner et al., 2007). Data from nineteen children 8–12 years of age were analyzed (one participant was excluded due to inadequate quality of the head movement data because some of the head position indicator coils were too far from the sensors during some runs). The children had no history of neurological or psychological problems, and they had normal or corrected to normal vision, and normal hearing. All children had English as their primary language. Written informed assent/consent was obtained from all subjects/parents in accordance with the Human Subjects Committee at Massachusetts General Hospital and the Massachusetts Institute of Technology.
A typical protocol for collecting MEG data was used. MEG was recorded using a 306-channel (204 first-order planar gradiometers, 102 magnetometers) VectorView MEG system (Elekta-Neuromag Ltd., Helsinki, Finland) in a magnetically shielded room, with the subjects comfortably sitting in a chair. Vertical and horizontal electrooculograms (EOG) were recorded to detect large eye movements and blinks. To co-register the MEG data with each subject’s MRI, the locations of anatomical landmarks (nasion and preauricular points), four head position indicator (HPI) coils, and about 50 additional points along the surface of the head were determined with a 3D digitizer (Polhemus, Colchester, VT) before the MEG recording. The three anatomical landmarks defined our head-based MEG coordinate system such that the x-axis passes through the two auricular points with positive direction to the right, the y-axis is perpendicular to the x-axis and passes through the nasion with positive direction to the front, and the positive z-axis points up (Fig. 1B). The additional points are helpful for the co-registration with anatomical magnetic resonance images (MRI). The HPI coils were attached on an EEG cap over frontal, parietal, and left and right temporal scalp (in the vicinity of the 10–20 electrode locations Fz, Pz, T3, and T4). To ensure an accurate localization of the coils using the MEG sensors, the coils were positioned such that each of them was under the sensor array, covered by multiple sensors, but at the same time placed far from each other to ensure reliable determination of a coordinate system on the basis of the HPI coils positions.
Auditory evoked MEG data were recorded as subjects performed an oddball detection task. Subjects were presented with 300 embedded deviant words (bat, cat, rat) in a train of 1000 standard word (pat) stimuli. The subjects were to press a button if they detected a deviant, and not to press a button otherwise. The experiment was divided into five four-minute sections or “runs” to give the subjects frequent breaks to rest. Continuous MEG signals were sampled at 601 Hz after filtering from 0.03 to 200 Hz. Responses related to each stimulus condition were averaged offline using an epoch from −100 to 800 ms. Trials containing eye movements, blinks, or other channel artifacts (peak-to-peak amplitude >150 μV in EOG or >500 fT/cm in gradiometers) were rejected. Averaged epochs were low-pass filtered with a cutoff at 40 Hz, and the zero level in each channel was taken to be the mean value in the 100-ms pre-stimulus baseline. Here we only examined the brain responses evoked by the standard word “pat”.
While recording MEG, low-amplitude sinusoidal continuous currents (at 154, 158, 162, and 166 Hz) were fed to the four HPI coils positioned on the subject’s head. The position and orientation of the head with respect to the sensor array was computed at 200 ms intervals, using software provided by the MEG manufacturer. In the localization procedure, each coil was approximated as a magnetic dipole with 6 parameters (position and dipole moment vectors in the sensor coordinate system), determined using a least-squares fit. Knowledge of the coil positions in both the head-based and sensor-based coordinate systems allows the determination of the coordinate transformation matrix T between the two coordinate systems (Besl and McKay, 1992; Fuchs et al., 1995):
| (1) |
where R is the rotation matrix, and r0 = [x0 y0 z0 ]T is the associated translation vector. Using these data, the locations of the MEG sensors, originally given in a coordinate system fixed to the MEG device, were transformed to an anatomically-based coordinate frame that was defined by the digitized locations of fiducial landmarks on the head: rh = Trd, where rh = [xh yh zh 1]T and rd = [xd yd zd 1]T are the augmented sensor location vectors in head-based and device-based coordinate system, respectively. We computed the mean displacement of the MEG sensors between the beginning of the experiment and each subsequent time point as
| (2) |
where is the location of the kth sensor in head coordinates at time t and Ns is the number of sensors. To quantify the amount of head movement for each subject over time, the average and standard deviation of D were calculated over 10-second time bins. To also quantify the head movement in different directions, the mean change in the components x0, y0, and z0 of the translation vector within each time bin were computed.
Dipole localization error due to head movements
Head movements affect the sources estimates in two ways. On one hand, a change in the mean position of the head will cause a net bias in the estimated location of the source. On the other hand, head movements will smooth the measured averaged field patterns and effectively increasing the noise in the measurements. We will first quantify the location bias using simulated current dipoles, as described below. Subsequently (under Movement compensation using the Signal Space Separation method), we will examine the variability in the source estimates due to head movements, before and after the application of movement compensation methods.
To investigate the effect of head movement on equivalent current dipoles, which are commonly used to model the sources of MEG data, we simulated the magnetic signals from dipole sources and computed the error in the estimated dipole locations due to the head movement. The locations of the simulated dipoles were chosen to be on an anatomically realistic representation of the cortex, determined from MR images. For each subject, high-resolution structural T1-weighted MRIs were acquired on a 3T Siemens Allegra or Trio head scanner (TR = 2530 ms, TE = 3.25 ms, flip angle = 7°, 128 slices, slice thickness = 1.3 mm, voxel size = 1.3 × 1.0 × 1.3 mm3). The MEG data was aligned with the MRI by using digitized head information. A surface representation for the cerebral cortex was constructed using the FreeSurfer software (Dale et al., 1999; Fischl et al., 1999). The cortical surface was decimated with spacing of about 5 mm between dipoles to yield approximately 7000 sources.
Forward solutions were calculated using a boundary element model (BEM) representing the inner surface of the skull (Hämäläinen and Sarvas, 1989; Oostendorp and van Oosterom, 1989). Each column of a forward matrix describes the signal pattern generated by a unit dipole oriented normal to the cortical mantle at one location on the surface. Forward matrices A(t) were calculated at one-second intervals using the sensor array position given by the HPI. These forward solutions were treated as simulated data, and current dipoles were fitted to the field patterns corresponding to each dipole in the forward solution for the initial head position and each of the subsequent forward solutions. However, in all cases the sensor positions corresponding to the initial HPI measurement obtained from the beginning of the run was used in the fitting algorithm. No cortical location or orientation constraint was used in the fitting. An initial guess for the ECD location was determined by evaluating the least-squares error function in a volumetric grid within the cranial volume. This initial guess was refined with the nonlinear Nelder-Mean simplex algorithm (Nelder and Mead, 1965), first using a spherically symmetric conductor model, then the boundary-element model, to find the final optimal location.
The dipole fits to the initial forward solution provided an estimate of the methodological error, whereas dipole fits to the subsequent forward solutions provided information about the localization error due to a change in the head position. Dipole localization error was calculated as the distance between the estimated and the actual source locations (Uutela et al., 2001). The mean and standard deviation of the localization error for each source location was calculated and displayed on an inflated cortical surface for five subjects.
Movement compensation using the Signal Space Separation method
We examined the effect of SSS-based head movement compensation on the ECD and MNE source estimates of auditory evoked response. Specifically, we compared the goodness-of-fit and variability of the ECDs as well as the amplitude of the MNEs, with and without head movement compensation.
The SSS method takes advantage of the oversampling of the measured magnetic field present in modern large-array MEG devices (Taulu and Kajola, 2005). SSS represents the magnetic field as a truncated basis function expansion. Any measured signal vector φ = [φ1,…,φNs ] can be approximated as
| (3) |
where alm and blm are vectors containing the inside and outside basis functions respectively, αlm and βlm are scalar coefficients. The terms with the inside basis functions describe signals generated by sources within the head, the terms with the outside basis functions correspond to signals from sources external to the sensor array. We used the cutoff values Lin = 8 and Lout = 3, which have been found to provide a reliable representation of the data in practice (Taulu and Kajola, 2005). Eq. (3) can be written in compact matrix form
| (4) |
where Sin = [a1,−1,..., aLinaLout]T, Sout = [b1, −1,..., bLinbLout], xin = [α1, −1,..., αLinLout]T, and xout = [β1, −1,..., βLinLout]T. A least-squares estimate x̂ is given by
| (5) |
where S† is the pseudoinverse of S. A reconstruction of the biomagnetic signals can then be performed by leaving out the contribution of sources external to the sensor array
| (6) |
The separation of sources inside the brain from those outside of the sensor array allows for the suppression of external interference signals such as heartbeat artifacts in MEG data collected from children and infants (Cheour et al., 2004; Pihko et al., 2004).
Of particular interest to the present study is that SSS can be used to extrapolate the measured signals from different head positions to a virtual array that is fixed with respect to the subject’s head (Taulu et al., 2005). The extrapolated signals are obtained by ϕ̑v = Sv,in x̂in, where Sv,in correspond to the internal subspace of the SSS base of the virtual array (Taulu and Kajola, 2005). One way to accomplish this is to average the estimated moments x̂ generated for each data epoch, rather than averaging epochs directly from the original data. This approach requires the calculation of a pseudoinverse for each epoch, and therefore can be quite time consuming. Here we used a faster method in which the original data are averaged over all epochs with the SSS basis averaged over all head positions, updated in our case every 200 ms, to generate the virtual signals corresponding to a desired reference head position. This method is based on the assumption that the head movements and magnetic fields are independent random variables (Taulu and Kajola, 2005). This assumption is valid as long as there are no head movements synchronized to the stimulus event; this could, however, be of a concern in some somatosensory and motor studies.
We evaluated the effect of head movement compensation on two different source estimates, ECD and MNE, of the magnetic N100 response (N100m) to the repeated stimulus “pat”. To quantify the effect of SSS compensation on ECD localization, a dipole was fitted at the peak of the auditory event-related N100m response with and without SSS movement compensation. A single dipole model was used for each hemisphere, fitting the ECD to the left and right hemisphere sensors, respectively. A spherically symmetric conductivity model for the head was used with the origin at x = y = 0 mm, z = 40 mm in the head coordinate system. The N100m is an obligatory response to auditory stimuli (Naatanen and Picton, 1987), and its neural generators are expected to remain relatively constant across trials. Generators of the N100m have been localized to the supra-temporal plane within Heschl’s gyri (Reite et al., 1994). However, we expected to observe spatial smearing of the magnetic field pattern due to the head movements, which would result in a lower goodness-of-fit for the ECDs. The goodness-of-fit was defined as
| (7) |
where φ and φ̂ are the measured and model signal vectors, respectively. We hypothesized that a reduction in spatial variance when SSS was applied would lead to an increase in the goodness-of-fit of the ECD compared with when SSS was not applied. The Wilcoxon signed-rank test was used to determine significant differences between the SSS-corrected and uncorrected data for ECDs fit to each hemisphere of all twenty subjects.
In addition to the goodness-of-fit measure, we examined the effect of the SSS compensation on the confidence limits of the ECD location using a bootstrap method (Darvas et al., 2005). Data from two runs of a single subject were used: one with minimal head movement, and one with considerable movement. The data were averaged and epochs with blink or other artifacts were rejected, giving approximately n = 100 trials of the standard stimulus “pat” in each run. Two-hundred bootstrap samples were generated by randomly selecting and averaging n epochs from the raw data (with replacement); epochs with artifacts were excluded from the analysis. A single dipole was fit at the peak of the N100m response to each bootstrap sample, with and without SSS movement compensation. This resulted in two clusters of dipoles (one with and one without SSS-compensation) for each of the two runs. We hypothesized that the application of SSS will reduce the variance in the ECD locations caused by the head movement. To quantify this variance, we calculated confidence volumes for each dipole cluster. The dipole locations r1,…,r200 were transformed to the center of mass, and the principle axes of the confidence volume ellipsoid were calculated using the singular value decomposition (r1,…,r200) = UΩVT, where U and VT are unitary matrices and Ω = diag(λ1, λ2, λ3 ), with λ1,λ2,λ3 as the singular values. The values λ1,λ2,λ3 were converted into standard deviations as , where m is the number of bootstrap resamples; in our case m = 200. Assuming a Gaussian distribution for the dipole clusters, a 95% confidence interval along each axis of the ellipsoid was calculated as ±2σ = 4σ. The 95% confidence volumes for each dipole cluster were then calculated as 43 (σ1σ2σ3).
We also examined the effect of SSS head motion compensation on a distributed source estimate, MNE (Hämäläinen and Ilmoniemi, 1994). The MNE was calculated by constructing a linear inverse operator AT (AAT + γC)−1, where A is the forward matrix, C is the noise covariance matrix, and γ is a regularization parameter. The same source locations and orientations on the cortical surface that were generated for the dipole simulations were also used to calculate the MNE solution. To assess the impact of SSS on MNE we computed the forward solution under four conditions, incorporating different amounts of head movement information: (1) uncorrected-run1, using the initial head position from the first run only, (2) uncorrected-all runs, averaging the forward solutions obtained using the initial head position at the beginning of each run (Uutela et al., 2001), (3) SSS-each run, using the averaged forward solution as in (2), but with the data for each run transformed to the head position at the beginning of that run using SSS, and (4) SSS-entire experiment, full SSS-correction where the forward solution from (1) was used with all data transformed to the head position at the beginning of the experiment.
Conditions (1) and (2) correspond to the common practice of measuring the head position at the beginning of an experimental run in MEG studies when continuous head position monitoring is not available. Condition (1) is accurate if there is no head movement during the whole experiment. Condition (2) takes into account changes in the head position between runs, whereas condition (3) also incorporates information about head movements during the runs. Condition (4) attempts also to eliminate the smoothing of the measured field patterns due to averaging over the different head positions in each run. Thus, comparison of (3) vs. (2) is expected to indicate the effect of within-run compensation with SSS, whereas comparison of (4) vs. (3) is expected to characterize the smoothing effects due to averaging of the forward solutions across runs. The difference between the conditions was evaluated with paired t-test comparisons by determining the mean MNE amplitude difference within a small cortical patch surrounding the MEG response corresponding to the peak N100m response in each subject for the four forward solution conditions. We hypothesized that compensating for the head movements would result in a larger amplitude of the MNE response corresponding to the N100m due to the decrease in spatial smearing of the MEG signals.
Results and Discussion
Quantitative assessment of head movement in children
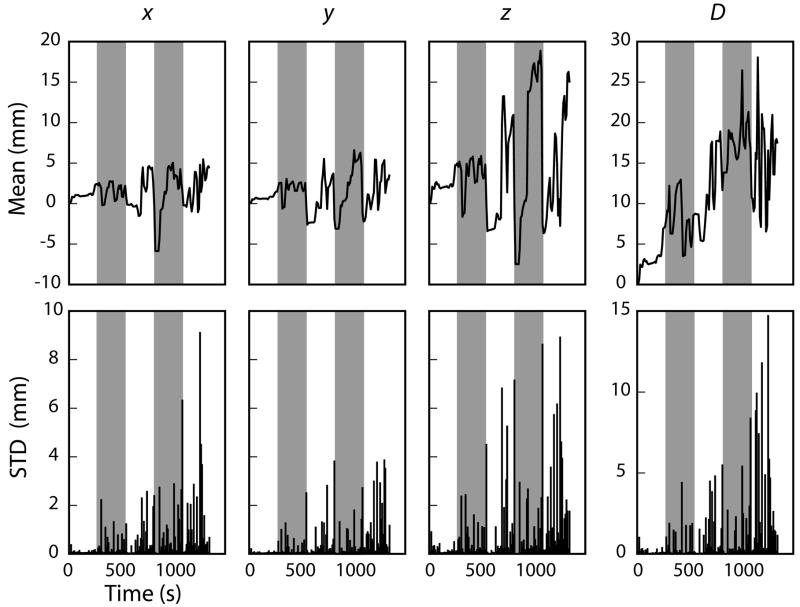
Head movement statistics for one child performing the cognitive task during the MEG recording are plotted in Fig. 2. On average, the mean displacement of the MEG sensors from the position at the beginning of the experiment was 12 mm (range: 3–26 mm). The changes in the head position were largest in the z (up-down) direction, and tended to increase toward the end of the experiment. The average standard deviation was 3.7 mm in the x-direction, 15 mm in the y-direction, and 23 mm in the z-direction. A planned series of paired t-tests comparing the magnitude and variance of head movement in each direction (e.g., x-direction vs. y-direction) indicated that there was more variation in head movement for the z-direction than the x- and y-directions (p < 0.01, and p < 0.05 respectively), and more variation in head movement in the y-direction than the x-direction (p < 0.01).
Figure 2.
The mean (top) and standard deviation (bottom) head movement in 10-second bins for one child over the course of the entire 25-minute experiment. The left three columns describe the relative head movement in the x (right-left), y (front-back), and z (up-down) directions, whereas the rightmost column indicates the mean displacement of the MEG sensors in the head-based coordinate system relative to the positions at the beginning of the experiment. The five runs are indicated with the alternating unshaded/shaded intervals.
A likely explanation for the movement to be largest in the z-direction (up-down) is that over the course of the experiment, most subjects begin to slouch in the seat, thereby lowering their head inside the measurement helmet. Although a particularly salient problem for children, this downward movement has also been seen in adults (Wehner, unpublished data). The second largest head motion was in the y-direction (front-back). As a child’s head is smaller than the inside of the helmet containing the measurement sensors, there is ample opportunity for front-back head movement should the child sneeze, cough, or simply lean forward or backward. Different positioning of the head in the front-back direction with respect to the MEG sensor array has been shown to strongly affect the detection of frontal activity in adults (Marinkovic et al., 2004); the effect is expected to be even larger in children. The amount of empty space on the sides of the head is usually less, reflected in the smallest amount of head movement in the x-direction (side-to-side). Rotations of the head, particularly “nodding” the head forward and downward as sometimes happens when the subject is tiring, would also show head movement in the y- and z-directions in our analysis but not in the x-direction.
In the present study, the subjects were sitting under the helmet-shaped MEG sensor array. One way to reduce the amount of head movements is to record MEG data in a supine position. In this case only rotational sideways (left-right) and up-down movements are expected, with the largest displacements occurring frontally, in the x- and z-directions. The supine position, however, is often less comfortable for the subject, especially when EEG electrodes are attached on the back of the scalp. Also, some subjects tend to fall asleep in the quiet conditions in the shielded room. Therefore, sitting position is preferred in most cognitive experiments.
Overall, the results indicate that a fair amount of head motion occurs over the course of a typical 25-minute MEG experiment with children. In the next section we will examine the effect of this head movement on source estimation.
Dipole localization error due to head movements
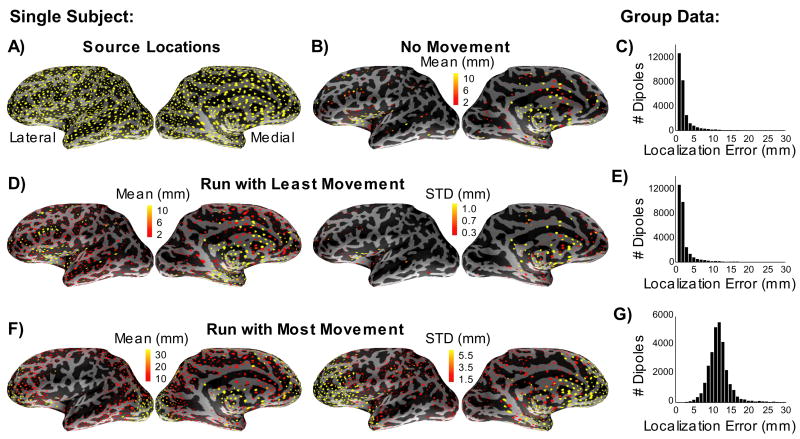
The effect of realistic head motion on the source localization error was examined using simulated dipoles distributed throughout the cerebral cortex (Fig. 3A). The localization error introduced by the dipole fitting method in the absence of noise or head movement is shown in Fig. 3B. The automated dipole-fitting algorithm was able to localize the majority of sources accurately in this ideal case; most of the localization errors were below 5 mm (Fig. 3C). Largest errors typically occurred deep in the sulci and on the medial surface of the hemispheres. Inclusion of simulated EEG data in combination with the MEG data could help to lower this methodological error in these problematic locations.
Figure 3.
Dipole source localization errors due to head movements. A) Locations of the sources used in the simulations (yellow dots) are shown on the inflated cortical surface of the left hemisphere for one subject. B) Dipole sources that had a localization error larger than 2 mm in the absence of noise and head movements using the automated dipole fitting procedure. The amount of localization error is indicated by the color scale. C) The histogram shows group data (5 subjects) indicating the total number of dipoles with different localization errors. D) Dipole localization errors in a single five-minute run with small head movements: mean (left) and standard deviation (right) for one subject. E) The corresponding histogram of group data. F) and G) Dipole localization errors in a five-minute run with large head movements.
The effect of head motion on the dipole localization errors throughout the cortex is shown in Figs. 3D–G. For the run with least head movement (Fig. 3D,E), the mean localization errors were only slightly larger than those in the no movement case. However, for the run with the largest amount of movement (Fig. 3F,G), the mean localization error was about 12 mm.
The largest localization errors induced by the head movement in the subject shown in Fig. 3 resided in the frontal lobe. This could result from the subject rotating the head forward and down during the course of the experiment, as the points with the most movement would correspond to those farthest from the center of rotation. Similarly, if the head were to rotate around the vertical axis (e.g., from side to side), the locations on the head with the most movement would be points on the lateral temporal regions as well as those in the frontal and occipital cortices.
The dipole localization error due to the head movement was of the same order of magnitude than errors previously reported due to other sources of uncertainty, including measurement noise (Hari et al., 1988; Mosher et al., 1993; Supek and Aine, 1993) and forward modeling (Cohen et al., 1990; Cuffin, 1990; Leahy et al., 1998). This suggests that head movement compensation methods could potentially improve the quality of MEG recordings and reduce the error in source estimates.
Movement compensation using the Signal Space Separation method
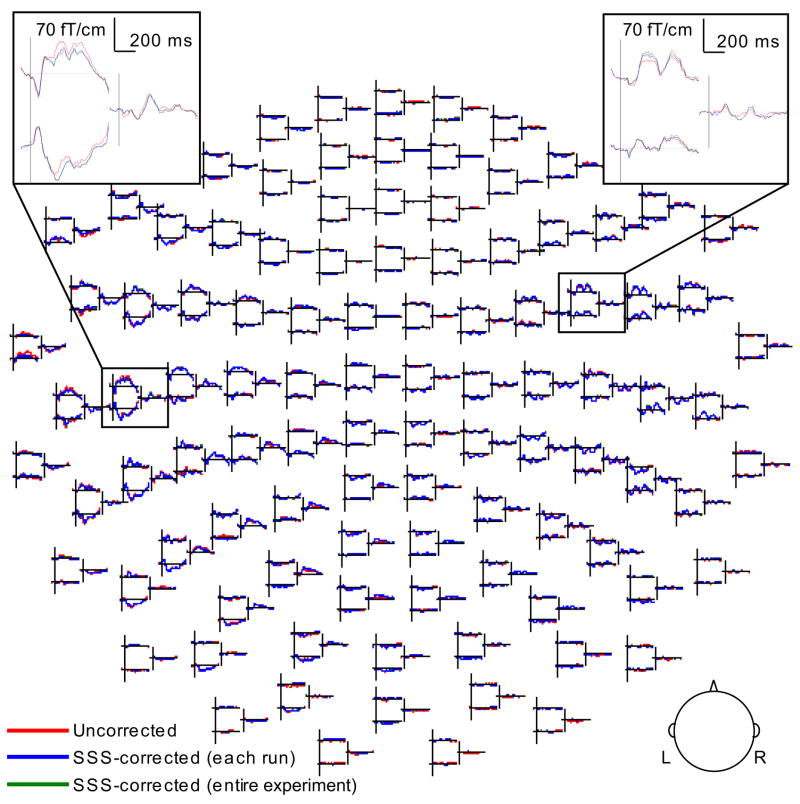
Averaged event-related magnetic fields with and without head movement compensation are illustrated in Fig. 4. The overall similarity of the original and transformed signals suggests that the MEG data is moderately robust against head movements that are small.
Figure 4.
Event-related magnetic fields for one child. The averaged responses in the uncorrected, SSS-corrected for each run separately (compensating for head movements within but not between runs), and SSS-corrected for the entire experiment cases are superimposed. The spatial distribution of the signal waveforms in 204 gradiometer and 102 magnetometer sensors is shown (L: left hemisphere, R: right).
To quantify the effect of head movement compensation on the ECDs, we calculated the mean change (SSS corrected for the entire experiment – uncorrected, using the initial head position from the first of the five runs) in the location and the goodness-of-fit of dipoles for the N100m response in each hemisphere for all subjects. The average change in the location was 5.0 mm in the left hemisphere, and 5.6 mm in the right hemisphere. Since we do not have independent information about the true location of the sources, we cannot determine whether the ECD localization after SSS correction was actually more accurate. However, the ECD goodness of fit increased after SSS correction for 15 (of the 19) subjects in the left hemisphere and 14 in the right hemisphere. The average change in the goodness-of-fit was 1.5% for the left hemisphere and 1.0% for the right hemisphere. After the SSS-correction, the ECD goodness-of-fit was significantly greater for the left hemisphere ECDs (Wilcoxon signed-rank test, p < 0.01), but not for the right hemisphere ECDs (p > 0.1). Successful compensation of the head movement is expected to improve the ECD goodness-of-fit by reducing the modeling error: head movements are likely to smooth the spatial patterns of the averaged MEG signals such that the pattern cannot be fully explained with an ECD, even if the true brain source were focal, and as such could be well modeled with a dipole in the absence of head movement. However, for small head movements the change in the goodness-of-fit is expected to be minor, and therefore, only modest conclusions can be made from these results. To complement the goodness-of-fit analysis we will next discuss the effect of the SSS compensation on the precision of the estimated ECD locations
The spread of the locations of ECDs fit to the N100m was examined with a bootstrap approach in one subject (we only examined the dipole clusters in the right hemisphere, which showed stronger signals in this subject). In the run with the most movement (in which the mean displacement from beginning of run was 17.5 mm) the 95% confidence volume was reduced after SSS compensation: for uncorrected data the confidence limits were σ1 = 3.3 mm, σ2 = 2.8 mm, σ3 = 2.1 mm, and the confidence volume = 1240 mm3, whereas for the SSS-corrected data the values were σ1 = 3.2 mm, σ2 = 2.6 mm, σ3 = 1.9 mm, confidence volume = 1010 mm3. Note that the total error in the uncorrected case is likely to be larger than that given by the estimated confidence limits, as the results do not include a potential bias between the true location of the source and the mean location of the estimated ECDs. No improvement was found in the run with the least amount of movement (mean displacement 2.7 mm): uncorrected: σ1 = 2.1 mm, σ2 = 1.7 mm, σ3 = 1.2 mm, confidence volume = 274 mm3, SSS-corrected: σ1 = 2.2 mm, σ2 = 1.7 mm, σ3 = 1.3 mm, confidence volume = 311 mm3. This may be due to a minimal effect of the head movement in this case, compared to other sources of uncertainty in the data. In general, head movements can be considered as contributing to the measurement noise, and therefore, compensation for the movements is expected to reduce the uncertainty in the ECD parameters estimated from the data when the effective noise due to head movements is equal or larger than other sources of noise in the data.
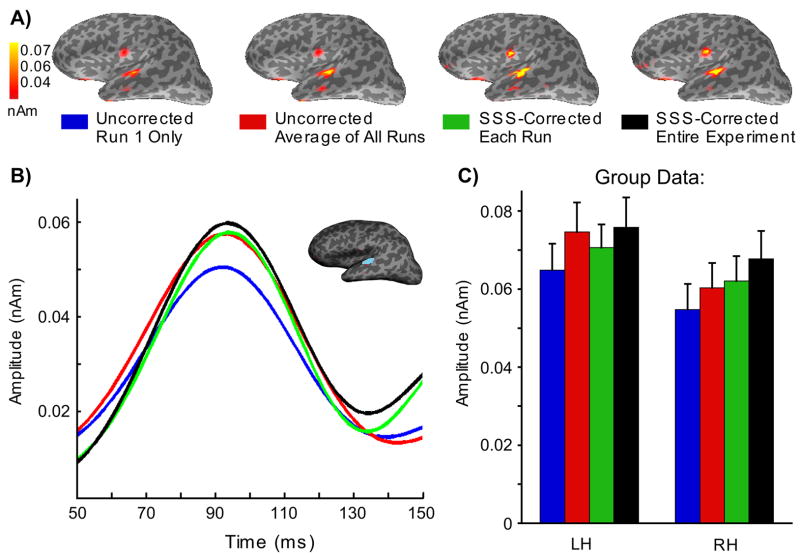
To assess the impact of SSS on a distributed source estimate, the MNE, we examined four different levels of head movement compensation (Fig. 5). The location of the estimated activation was similar across the different cases, being maximal at the superior temporal regions (Fig. 5A), consistent with sources in the auditory cortex (Reite et al., 1994). The MNE maps for the N100m response suggest that the estimated source amplitudes were larger when increasing amounts of information about the head position were taken into account. The mean MNE amplitude within a small patch of cortex surrounding the peak response for each of the four conditions for one subject is shown in Fig. 5B. Group data representing the peak MNE response across all subjects is shown in Fig. 5C. A series of pairwise t-tests indicated that the peak N100m response in the left hemisphere was significantly larger for all three conditions that were tested (uncorrected-all runs; SSS-each run; SSS-entire experiment) relative to the uncorrected-run1 condition (p < 0.01, p < 0.09, and p < 0.03, respectively). There was a trend toward larger N100m amplitudes for the SSS-each run relative to the uncorrected-all runs, although this difference was not significant (p = 0.14). There was, however, a significant difference (p < 0.04) in the peak N100m amplitudes for the two SSS conditions, with larger amplitudes for the SSS-entire experiment relative to the SSS-each run. The right hemisphere peak N100m responses again yielded significantly larger amplitudes for the three tested conditions (p < 0.02, p < 0.01, p < 0.02, respectively) relative to the uncorrected-run1. In addition, there were significantly larger N100m amplitudes for the SSS-entire experiment compared to the SSS-each run (p < 0.04) and the uncorrected-all runs (p < 0.04).
Figure 5.
Effect of SSS head movement compensation on a distributed source estimate. A) Minimum Norm Estimates (MNE) at the peak latency of the N100m response in one child, calculated using forward solutions with four different levels of head movement compensation: (1) uncorrected data using the initial head position only, (2) the average of forward solutions computed for the initial head position at the beginning of each run, (3) averaged forward solution with data corrected using SSS within each run, and (4) full SSS-correction with all data transformed with respect to the initial head position. B) The corresponding source waveform in the left hemisphere. The patch of cortex that was used for comparison of the different forward-solution conditions is outlined in blue. C) Group data (n=19) for the peak MNE response in the left hemisphere (LH) and right hemisphere (RH) region.
The enhanced MNE amplitude is in accordance with the hypothesis that the SSS compensation would reduce the spatial smoothing caused by the head movements to the MEG signals and subsequently derived source estimates. The averaged forward solution proposed by Uutela et al. (Uutela et al., 2001) also provided good results. This method assumes that there are movements only between the runs; due to the linearity of the forward model, the average forward solution takes the between-run movements into account, albeit with some smoothing, as there is no actual compensation for the movement, unlike in the SSS-based approaches. Often the between-run changes in the head position are larger than within-run changes, as the subjects have a tendency to relax and stretch during the breaks between the runs. Within-run movements can be considerable, however, as suggested by the present head displacement data on children. The present analysis did not show a significant difference between the uncorrected-all runs vs. SSS-each run conditions, which was expected to reveal the effect of within-run head movements. The full SSS compensation, however, appears to be beneficial, taking into account effects due to head movements during the whole recording period, as well as reducing the smoothing effect due to the averaging of the forward models across runs.
In the analyses it was assumed the MNE peak amplitude will increase after compensation for the spatial smoothing of the field patterns caused by head movements; however, the relationship between the smoothing and amplitude is not straightforward, and therefore, caution is necessary in interpreting the results based on the amplitude measure.
In the present study auditory activity in the temporal lobe was chosen to be analyzed because of the high SNR of the MEG signals. However, the dipole simulation (cf. Fig. 3) suggested that the largest errors were expected in the frontal lobe. Therefore, the benefits of the SSS compensation may appear modest here, as the error in the auditory N100m source estimates due to head movements was rather small to begin with. Furthermore, we did not evaluate of the SSS compensation on the overall accuracy of the source estimates for the N100m, which would include the bias in the estimated source locations due to a change is the mean position of the head; here we only evaluated the effect of spatial smoothing on the precision of the source estimates. It is worth noting that greater improvements are expected when the head movements are larger (Taulu et al., 2005), as is likely to be the case with very young children (Cheour et al., 2004; Pihko et al., 2004) and patient populations such as children with attention deficit hyperactivity disorder.
Conclusions
MEG source estimates were found to be relatively robust against head movements in children. The results suggest that, by careful control of experimental conditions and the use of appropriate data analysis methods such as SSS, confounds due to head movements can be successfully dealt with in MEG studies of developmental cognition.
Acknowledgments
We thank Surina Basho and Deirdre Von Pechmann for their assistance with data collection, Dr. Elfar Adalsteinsson for helpful comments on the manuscript, and Samu Taulu of Elekta Neuromag for providing the Maxfilter software for head movement compensation. The research was supported by funding to Maria Mody (NIH: DC00159, HD056355), and in part by the National Center for Research Resources (P41RR14075) and the Mental Illness and Neuroscience Discovery (MIND) Institute. Daniel Wehner was also supported in part by an NIH Training Grant (DC00038) to the Speech and Hearing Biosciences and Technology Program (HST), and by an NIH Neuroimaging Training Program Fellowship (5T32EB001680; PI: Bruce Rosen). We thank all the children and parents for their willingness to participate in the study.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ahlfors S, Ilmoniemi R. Magnetometer position indicator for multichannel MEG. In: Williamson SJ, Hoke M, Stroink G, Kotani M, editors. Advances in Biomagnetism. Plenum; New York: 1989. pp. 693–696. [Google Scholar]
- Besl PJ, McKay ND. A Method for Registration of 3-D Shapes. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1992;14:239–255. [Google Scholar]
- Burghoff M, Nenonen J, Trahms L, Katila T. Conversion of magnetocardiographic recordings between two different multichannel SQUID devices. IEEE Transactions on Biomedical Engineering. 2000;47:869–875. doi: 10.1109/10.846680. [DOI] [PubMed] [Google Scholar]
- Cheour M, Imada T, Taulu S, Ahonen A, Salonen J, Kuhl P. Magnetoencephalography is feasible for infant assessment of auditory discrimination. Experimental Neurology 190 Supplement. 2004;1:S44–51. doi: 10.1016/j.expneurol.2004.06.030. [DOI] [PubMed] [Google Scholar]
- Cohen D, Cuffin BN, Yunokuchi K, Maniewski R, Purcell C, Cosgrove GR, Ives J, Kennedy JG, Schomer DL. MEG versus EEG localization test using implanted sources in the human brain. Annals of Neurology. 1990;28:811–817. doi: 10.1002/ana.410280613. [DOI] [PubMed] [Google Scholar]
- Cohen D, Halgren E. Magnetoencephalograpy (Neuromagnetism) In: Adelman G, Smith BH, editors. Encyclopedia of Neuroscience. Elsevier; Amsterdam: 2003. [Google Scholar]
- Cuffin BN. Effects of head shape on EEG’s and MEG’s. IEEE Transactions on Biomedical Engineering. 1990;37:44–52. doi: 10.1109/10.43614. [DOI] [PubMed] [Google Scholar]
- Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis. I. Segmentation and surface reconstruction. Neuroimage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Darvas F, Rautiainen M, Pantazis D, Baillet S, Benali H, Mosher JC, Garnero L, Leahy RM. Investigations of dipole localization accuracy in MEG using the bootstrap. Neuroimage. 2005;25:355–368. doi: 10.1016/j.neuroimage.2004.09.045. [DOI] [PubMed] [Google Scholar]
- de Munck JC, Verbunt JP, Van’t Ent D, Van Dijk BW. The use of an MEG device as 3D digitizer and motion monitoring system. Physics in Medicine and Biology. 2001;46:2041–2052. doi: 10.1088/0031-9155/46/8/301. [DOI] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Dale AM. Cortical surface-based analysis. II: Inflation, flattening, and a surface-based coordinate system. Neuroimage. 1999;9:195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
- Fuchs M, Wischmann HA, Wagner M, Kruger J. Coordinate system matching for neuromagnetic and morphological reconstruction overlay. IEEE Transactions on Biomedical Engineering. 1995;42:416–420. doi: 10.1109/10.376136. [DOI] [PubMed] [Google Scholar]
- Hämäläinen MS, Hari R, Ilmoniemi R, Knuutila J, Lounasmaa OV. Magnetoencephalography - theory, instrumentation, and applications to noninvasive studies of the working human brain. Reviews of Modern Physics. 1993;65:413–497. [Google Scholar]
- Hämäläinen MS, Ilmoniemi RJ. Interpreting magnetic fields of the brain: minimum norm estimates. Medical and Biological Engineering and Computing. 1994;32:35–42. doi: 10.1007/BF02512476. [DOI] [PubMed] [Google Scholar]
- Hämäläinen MS, Sarvas J. Realistic conductivity geometry model of the human head for interpretation of neuromagnetic data. IEEE Transactions on Biomedical Engineering. 1989;36:165–171. doi: 10.1109/10.16463. [DOI] [PubMed] [Google Scholar]
- Hari R, Joutsiniemi SL, Sarvas J. Spatial resolution of neuromagnetic records: theoretical calculations in a spherical model. Electroencephalography and Clinical Neurophysiology. 1988;71:64–72. doi: 10.1016/0168-5597(88)90020-2. [DOI] [PubMed] [Google Scholar]
- Incardona F, Narici L, Modena I, Erne SN. Three-dimensional localization system for small magnetic dipoles. Reviews of Scientific Instrumentation. 1992;63:4161–4166. [Google Scholar]
- Leahy RM, Mosher JC, Spencer ME, Huang MX, Lewine JD. A study of dipole localization accuracy for MEG and EEG using a human skull phantom. Electroencephalography and Clinical Neurophysiology. 1998;107:159–173. doi: 10.1016/s0013-4694(98)00057-1. [DOI] [PubMed] [Google Scholar]
- Marinkovic K, Cox B, Reid K, Halgren E. Head position in the MEG helmet affects the sensitivity to anterior sources. Neurology and Clinical Neurophysiology. 2004;2004:30. [PMC free article] [PubMed] [Google Scholar]
- Mosher JC, Spencer ME, Leahy RM, Lewis PS. Error bounds for EEG and MEG dipole source localization. Electroencephalography and Clinical Neurophysiology. 1993;86:303–321. doi: 10.1016/0013-4694(93)90043-u. [DOI] [PubMed] [Google Scholar]
- Naatanen R, Picton T. The N1 wave of the human electric and magnetic response to sound: a review and an analysis of the component structure. Psychophysiology. 1987;24:375–425. doi: 10.1111/j.1469-8986.1987.tb00311.x. [DOI] [PubMed] [Google Scholar]
- Nelder JA, Mead R. A Simplex Method for Function Minimization. Computer Journal. 1965:308–313. [Google Scholar]
- Numminen J, Ahlfors S, Ilmoniemi R, Montonen J, Nenonen J. Transformation of multichannel magnetocardiographic signals to standard grid form. IEEE Transactions on Biomedical Engineering. 1995;42:72–78. doi: 10.1109/10.362916. [DOI] [PubMed] [Google Scholar]
- Oostendorp TF, van Oosterom A. Source parameter estimation in inhomogeneous volume conductors of arbitrary shape. IEEE Transactions on Biomedical Engineering. 1989;36:382–391. doi: 10.1109/10.19859. [DOI] [PubMed] [Google Scholar]
- Phillips C. Electrophysiology in the study of developmental language impairments: Prospects and challenges for a top-down approach. Applied Psycholinguistics. 2005;26:79–96. [Google Scholar]
- Pihko E, Lauronen L, Wikstrom H, Taulu S, Nurminen J, Kivitie-Kallio S, Okada Y. Somatosensory evoked potentials and magnetic fields elicited by tactile stimulation of the hand during active and quiet sleep in newborns. Clinical Neurophysiology. 2004;115:448–455. doi: 10.1016/s1388-2457(03)00349-3. [DOI] [PubMed] [Google Scholar]
- Reite M, Adams M, Simon J, Teale P, Sheeder J, Richardson D, Grabbe R. Auditory M100 component 1: relationship to Heschl’s gyri. Brain Research: Cognitive Brain Research. 1994;2:13–20. doi: 10.1016/0926-6410(94)90016-7. [DOI] [PubMed] [Google Scholar]
- Supek S, Aine CJ. Simulation studies of multiple dipole neuromagnetic source localization: model order and limits of source resolution. IEEE Trans Biomed Eng. 1993;40:529–540. doi: 10.1109/10.237672. [DOI] [PubMed] [Google Scholar]
- Taulu S, Kajola M. Presentation of electromagnetic data: The signal space separation method. Journal of Applied Physics. 2005;97:124905. [Google Scholar]
- Taulu S, Simola J, Kajola M. Applications of the Signal Space Separation Method. IEEE Transactions on Signal Processing. 2005;53:3359–3372. [Google Scholar]
- Uutela K, Taulu S, Hämäläinen M. Detecting and correcting for head movements in neuromagnetic measurements. Neuroimage. 2001;14:1424–1431. doi: 10.1006/nimg.2001.0915. [DOI] [PubMed] [Google Scholar]
- Wehner DT, Ahlfors SP, Mody M. Effects of phonological contrast on auditory word discrimination in children with and without reading disability: A magnetoencephalography (MEG) study. Neuropsychologia. 2007;45:3251–3262. doi: 10.1016/j.neuropsychologia.2007.06.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson HS. Continuous head-localization and data correction in a whole-cortex MEG sensor. Neurology and Clinical Neurophysiology. 2004;2004:56. [PubMed] [Google Scholar]