Abstract
An analytical expression is derived for time-harmonic calculations of the near-field pressure produced by a circular piston. The near-field pressure is described by an efficient integral that eliminates redundant calculations and subtracts the singularity, which in turn reduces the computation time and the peak numerical error. The resulting single integral expression is then combined with an approach that divides the computational grid into sectors that are separated by straight lines. The integral is computed with Gauss quadrature in each sector, and the number of Gauss abscissas in each sector is determined by a linear mapping function that prevents large errors from occurring in the axial region. By dividing the near-field region into 10 sectors, the raw computation time is reduced by nearly a factor of 2 for each expression evaluated in this grid. The grid sectoring approach is most effective when the computation time is reduced without increasing the peak error, and this is consistently accomplished with the efficient integral formulation. Of the four single integral expressions evaluated with grid sectoring, the efficient formulation that eliminates redundant calculations and subtracts the singularity demonstrates the smallest computation time for a specified value of the maximum error.
I. INTRODUCTION
The impulse response of a circular piston1–3 defines a linear input–output relationship of a single transducer with a closed-form single integral expression. This expression implicitly summarizes the temporal and spatial characteristics of a particular transducer geometry in a framework that is convenient for pulsed and time-harmonic acoustic field computations. These computations ordinarily assume that the velocity profile across the surface of the transducer is spatially uniform, although certain other models permit some radial variation in the velocity profile.4,5 The impulse response is primarily used for pulsed mode calculations in the near-field region; however, this model is also suitable for time-harmonic pressure calculations in the near field.
Two other equivalent single integral expressions are described by Archer-Hall et al. 6 and Hutchins et al.7 specifically for time-harmonic near-field calculations of the pressure generated by a circular piston. The expression in Archer-Hall et al.6 applies a cylindrical coordinate system with a movable origin2 to the solution of the Kirchhoff integral. These geometric manipulations convert a double integral into a simplified single integral. A similar expression derived by Hutchins et al.7 computes the velocity potential for a circular piston driven by a sinusoidal excitation. The velocity potential is expressed as a double integral containing Bessel functions, and this result is simplified using Hankel transform tables. The resulting single integral expression7 is closely related to the result of Archer-Hall et al.6 Although these single integral expressions are all analytically equivalent, the numerical properties of these expressions are quite different. The single integral expressions of Archer-Hall et al.6 and Hutchins et al.7 are particularly amenable to certain numerical improvements.
After three single integral expressions for time-harmonic near-field pressures produced by a circular piston are briefly reviewed, an efficient single integral expression is derived from the results of Archer-Hall et al.6 and Hutchins et al.7 A sector-based technique for spatially varying the number of Gauss abscissas applied to each integral is also introduced. Results of near-field beam patterns produced by each expression are then compared for a fixed number of Gauss abscissas. All four expressions are evaluated and compared with a grid sectoring technique that varies the number of Gauss abscissas as the spatial grid coordinates change. The results show that the peak errors increase significantly when the impulse response and the expression derived in Archer-Hall et al.6 are evaluated with grid sectoring. The peak errors increase over a limited range of values if the single integral expression of Hutchins et al.7 is computed with grid sectoring. These numerical problems are avoided altogether in near-field calculations that combine the efficient expression and grid sectoring. The efficient formulation, which combines the best features of the Archer-Hall et al.6 and Hutchins et al.7 expressions, achieves the smallest peak errors in the shortest time for calculations in a single sector. For near-field calculations evaluated in multiple sectors, the efficient single integral expression also demonstrates the smallest computation time for a specified value of the peak error.
II. SINGLE INTEGRAL EXPRESSIONS
The impulse response for a circular piston,1–3 defined here as h(r,z;t), is a function of temporal and spatial parameters. The impulse response of a circular piston is also applicable to time-harmonic pressure calculations once the Fourier transform, H(r,z;k) = ℱ{h(r,z;t)}, is evaluated. The Fourier transform of the impulse response is related to the steady-state pressure p generated by a circular piston according to
| (1) |
where ω is the excitation frequency in radians per second, ρ is the density of the medium, υ is a constant normal velocity evaluated at the surface of the circular piston, k is the wavenumber, and t is the elapsed time. As indicated in Eq. (1), H(r,z;k) is directly proportional to the pressure distribution, and all of the spatial variations in the pressure field are represented by the expression H(r,z;k). Therefore, the quantity H(r,z;k) is computed in the analysis that follows. The relationship between each computed pressure field and the circular piston is shown in Fig. 1, where the center of the circular piston is the origin of the cylindrical coordinates (r,z), and the positive z direction is coincident with the normal at the center of the circular piston. In Eq. (1), the Fourier transform of the impulse response H is represented as a function of the wavenumber k = ω/c, which is implicitly related to the excitation frequency f = ω/(2π). This notation simplifies the following expressions for H, which is computed for a circular piston with several analytically equivalent but numerically dissimilar single integral expressions.
FIG. 1.
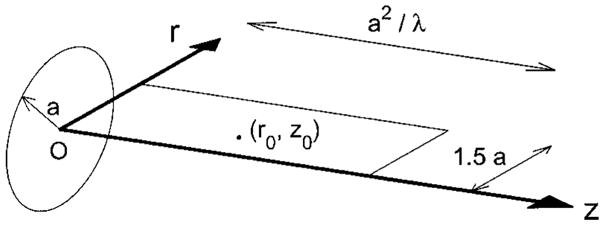
Definition of coordinate axes for acoustic field calculations. The origin (O) of the coordinate system is defined as the intersection between the z and r axes in a cylindrical coordinate system. The z axis is coincident with the piston normal, and individual field coordinates are indicated by the pair (r0,z0). The radius of the circular piston is designated by a, the extent of the field calculation in the radial direction is 1.5a, and the extent of the computed field in the axial direction is a2/λ. These are the same coordinates used by Zemanek (Ref. 8) and Lockwood and Willette (Ref. 3) for calculations of pressure fields generated by circular pistons.
A. Oberhettinger,1 Stepanishen,2 and Lockwood and Willette3
In pressure field calculations for pulsed excitations, the impulse response is convolved with a temporally dependent excitation function, and therefore the corresponding convolution integral is necessarily evaluated with respect to the time variable. For sinusoidal excitations, however, distance is a more convenient variable. Therefore, the notation describing the time limits in Lockwood and Willette3 is adapted to distance limits here. The distance values required for time harmonic pressure field calculations using the impulse response are
| (2) |
These limits are then applied to the Fourier transform of the impulse response,
| (3) |
where the integral I1 is defined as
| (4) |
These expressions, which describe the pressure field produced by a sinusoidal excitation, are valid at all grid coordinates where z ≥ 0. Equations (3) and (4) are obtained from the impulse response presented in Oberhettinger,1 Stepanishen,2 and Lockwood and Willette3 after the change of variable t = β/c is applied, where c represents the speed of sound.
B. Archer-Hall et al.6
An equivalent expression for Eq. (3), which applies the coordinate geometry suggested by Stepanishen2 to the integral of the time-harmonic Green’s function evaluated over the face of a circular piston, is derived in Archer-Hall et al.6 This expression is presented in condensed form7 as
| (5) |
where I2 is the integral expression defined by
| (6) |
In Eq. (5), only the (1/jk)e−jkz term is multiplied by 1, 1/2, or 0, depending on the location of the radial coordinate r relative to the edge of the piston. The integral I2 is evaluated numerically in all off-axis locations. At r = 0, the cos ψ contributions disappear from Eq. (6), and the resulting value of I2 is . This result is exactly equal to the corresponding on-axis term in Eq. (3).
C. Hutchins et al.7
Another analytically equivalent expression is derived from a Green’s function approach7 that generates a double integral containing Bessel functions. This result is simplified using Hankel transform tables, which produces
| (7) |
As noted in Hutchins et al.,7 the ratio (a − re−jψ)/(a2 + r2 − 2ar cos ψ) in Eq. (7) is analytically equivalent to (a − rejψ)−1. Of these two choices, the former is preferred for numerical calculations in languages (such as C) that fail to provide explicit compiler support for complex arithmetic.
III. NUMERICAL TECHNIQUES
Several techniques improve the numerical performance of these single integral expressions for the Fourier transform of the impulse response evaluated for a circular piston. Some of these techniques are applicable to all of the formulations, and others are only applicable to specific expressions. Each integral is evaluated with Gauss quadrature, and normalized errors are computed for each result.
A. Efficient formulation
Although H2 and H3 are analytically equivalent, each expression possesses unique numerical properties. By combining the best numerical features of H2 and H3, an efficient single integral formulation with improved numerical performance is obtained. The derivation of the efficient expression begins either with H2 or H3, and each converges to the same result, yielding a fourth equivalent single integral expression for the Fourier transform of the impulse response.
One derivation begins with the expressions for H2 and I2 in Eqs. (5) and (6), respectively. The integral I2 contains a numerical singularity that is encountered whenever r ≈ a and ψ ≈ 0, and this singularity is responsible for increasing the numerical errors in all spatial locations where r ≈ a. The numerical errors increase whenever a very small number in the denominator of the integrand in I2 is divided into a much larger number in the numerator. Although division by zero is avoided either with a simplified expression for the integrand or with the selection of a numerical integration method that excludes the end points of the interval (such as Gauss quadrature), increased numerical errors are guaranteed with the Archer-Hall et al.6 expressions for H2 and I2 in all locations where r ≈ a. The numerical problems are eliminated by subtracting a singularity9 from the exponential term in the numerator of I2. The required term e−jkz is obtained from a series expansion and then subtracted from the complex exponential term in I2. The resulting expression, which instead divides a small number by a small number when r ≈ a and ψ ≈ 0 and therefore reduces the error where r ≈ a, is retained for numerical calculations. This same term is also added to the complex exponential term in I2 and evaluated analytically. The analytical result exactly cancels the term on the far right-hand side of H2 in Eq. (5), yielding the efficient formulation
| (8) |
The same result is also obtained from H3 through manipulations which are very similar to those presented by Hutchins et al.7 in a derivation that equates H3 and H2. That derivation eliminates the e−jkz term from the integrand; however, this term is retained here because subtracting the singularity reduces the error in all locations where r ≈ a. The first step in this derivation notes that the real part of the ratio γ = (a − re−jψ)/(r2 + a2 − 2ar cos ψ) in H3 is an even function. Likewise, the imaginary part of γ is an odd function with respect to ψ for all values of a and r. Furthermore, both the real and the imaginary parts of the difference in H3 are even functions with respect to ψ for all values of a, r, and z. The integral with respect to ψ of the imaginary part of γ (an odd function) multiplied by the difference between the two complex exponential functions (an even function), evaluated from − π to π, is equal to zero. Thus, the imaginary part of γ is eliminated. The second step notes that the integral with respect to ψ of the real part of γ (an even function) multiplied by the difference between the two complex exponential functions (an even function), evaluated from −π to π, is equal to twice the integral of the same expression from 0 to π. The result of these manipulations again yields the efficient expression H4 in Eq. (8). Although the expressions H2, H3, and H4 are similar in appearance, the numerical performance of each expression is quite different, especially when grid sectoring schemes are defined for numerical integration.
B. Grid sectoring
In each of the expressions H1, H2, H3, and H4, the spatial distribution of the numerical error is nonuniform when the integrand is evaluated with a constant number of abscissas in all field locations. This suggests that the integrand is oversampled in some regions and undersampled in others. Increasing the number of abscissas in regions where the error is large and decreasing the number of abscissas in regions where the error is small improves the efficiency of near-field pressure calculations. This result is ordinarily accompanied by a reduction in the computation time.
Grid sectoring, when applied to certain integral formulations, reduces the time required for pressure field calculations without increasing the maximum numerical error. This approach divides the computational grid in Fig. 1 into sectors, and the number of abscissas utilized in the numerical evaluation of the integral expression for H(r,z;k) is determined by the sector in which a particular grid point is located. Grid sectoring only maintains the maximum error value for integral expressions that avoid numerical singularities.
A similar multirate sampling scheme in Orofino and Pedersen10 defines regions based on contours that are extracted from the argument of the exponential term in I1. This scheme, expressed here in terms of the parameters required for time-harmonic calculations using the impulse response, notes that the argument of e−jkβ in Eq. (4), evaluated from β2 to β3, ranges from to . The extent of this range is then , and a proportional number of abscissas N is specified according to
| (9) |
where λ is the wavelength and C is a scale factor.
The grid sectoring approach employed here improves the multirate scheme of Orofino and Pedersen10 by replacing curved contour boundaries with sectors defined by straight lines. The expression for the linear sector boundaries is derived from
| (10) |
which is an asymptotic approximation to Eq. (9). Equation (10) is obtained after a binomial expansion is evaluated for both square root terms in Eq. (9). The approximation r2 + z2 ≫ a2 is applied to the result. In Eq. (10), the spatially varying term , is exactly equal to sin θ in the coordinate system of Fig. 1. Constant values of θ, which are indicated by straight lines emanating from the center of the circular piston and are measured with respect to the piston normal, define sector boundaries between successive values of N. Incremental changes in N are therefore related to θ through the sin−1 function. Likewise, tan θ = r/z in Fig. 1, so the boundaries between adjacent sectors are expressed by
| (11) |
Equation (11) evaluates the argument of sin−1 at equal increments of the range of (r,z) pairs considered, and the boundaries thus defined are a series of nl lines which divide the computational grid in Fig. 1 into ns = nl − 1 sectors.
Figure 2 contains a comparison of the contours indicated by Eq. (9) and the sectors specified by Eq. (11). The solid lines are evaluated according to Eq. (11) for ns = 10 sectors. In Fig. 2, two of the nl = 11 solid lines are coincident with the r and z axes, and therefore only 9 of the solid lines are apparent. The solid lines are asymptotically related to the 9 contours indicated by the dashed lines in Fig. 2. These contours, which are computed directly from Eq. (9), are equally spaced over the range of values generated by Eq. (9). In Fig. 2, the solid lines from Eq. (11) are consistently closer to the z axis than the corresponding dashed contours from Eq. (9). This increases the size of the regions that require the most abscissas, which in turn reduces the errors near the boundaries between adjacent sectors. Also, Eq. (11) is more convenient than Eq. (9) for numerical calculations performed on a rectilinear grid. Intersections between grid lines and the lines defined in Eq. (11) are easily converted into limits defined for loop constructs, both for aligned and rotated grid orientations with respect to the piston source.
FIG. 2.
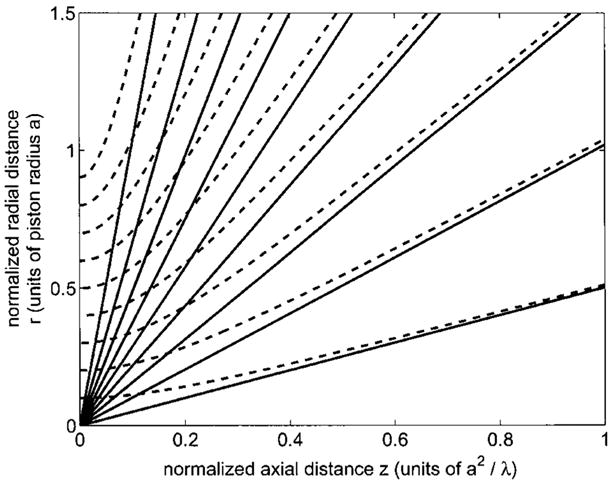
Equation (11) predicts the asymptotic behavior of Eq. (9) for a circular piston with radius a = 5λ. Here, the solid lines define the asymptotes indicated by Eq. (11) for nl = 11 straight lines dividing the computational grid into ns = 10 separate sectors. Two of the lines are coincident with the z and r axes, respectively, so only 9 straight lines are evident. The asymptotes are superposed over a contour plot of Eq. (9) evaluated for the same piston radius. The dashed lines show where 9 equally spaced contours are located in the same computational grid. The solid lines obtained from Eq. (11), which are easier to compute than the dashed contours, define an efficient grid sectoring scheme for pressure field calculations.
The numerical error is also reduced by increasing the number of abscissas in the axial region. Equations (9) and (10) underestimate the number of abscissas required for near-field pressure calculations in the axial region, which motivates the construction of an expression that specifically increases the number of abscissas in the sectors nearest the piston normal. This is achieved with a linear mapping function
| (12) |
where S ∈ [0,1] is a scale factor, Nmax is the specified largest number of Gauss abscissas, ns is the total number of sectors defined by Eq. (11), and M is the number of abscissas in the ith sector. With Eq. (12), the number of abscissas in each sector ranges from a minimum value of NmaxS to a maximum value of Nmax. For a piston with radius a = 5λ, S = 0.3 is an appropriate value for calculations with ns = 10 sectors. Likewise, the number of sectors ns defined in the near-field region typically ranges from 5 to 15, depending on the value of S as well as the piston and grid geometry.
C. Gauss quadrature
The Gauss quadrature rule11 evaluates the integrals in Eqs. (3), (5), (7), and (8). Gauss quadrature achieves lower errors than the trapezoidal rule, Simpson’s rule, and other standard numerical integration schemes using the same number of abscissas. For results normalized to a specified maximum error value, Gauss quadrature is generally faster than other numerical integration methods, including adaptive methods (e.g., Romberg integration, etc.) which sometimes fail to converge for impulse response calculations where r ≈ a. The Gauss quadrature rule is defined according to the descriptions given by Davis and Rabinowitz11 and Abromowitz and Stegun.12 The Gauss rule computes the abscissas gi and weights wi of the N point Gauss–Legendre integration rule for the interval [−1,1], and the abscissas are then converted by a linear mapping function12 defined for an arbitrary input interval [αmin, αmax] according to
| (13) |
where the Gauss weights wi are multiplied by the scalar quantity (αmax − αmin)/2. In Eq. (13), the pair [αmin, αmax] represents for evaluations of H1 in Eq. (3), [αmin, αmax] represents [0, π] for H2 and H4 in Eqs. (5) and (8), respectively, and [αmin, αmax] represents [−π, π] for H3 in Eq. (7).
D. Error calculations
The numerical error η (r,z) in the computed acoustic field is defined here as the normalized absolute value of the difference between a specific beam pattern and a separate reference beam pattern. The spatial distribution of the error is represented by
| (14) |
and the maximum error is defined as
| (15) |
In Eqs. (14) and (15), Href(r,z) represents the reference beam pattern, and H(r,z) describes the Fourier transform of the impulse response that is compared to the reference field. Although these expressions implicitly depend on the wavenumber k, the wavenumber is constant in all of the calculations that follow, so only the spatial coordinates are included. Here, H(r,z) is interchangeable with the pressure distribution p(r,z) since all results are normalized and the leading constant terms in Eq. (1) cancel in the numerator and denominator of Eqs. (14) and (15). The scalar normalization factor in both equations prevents division by zero and avoids exaggerating differences where the field amplitudes are relatively small. The resulting spatial variations in the error η (r,z) are presented in mesh plots where peak values indicate the presence of possible numerical singularities.
IV. SIMULATION RESULTS
All simulations routines were written in the C programming language. The simulations were performed on a generic 800 MHz Pentium III personal computer running the Red Hat Linux 7.1 operating system. On this computer, all simulations were run sequentially, and outside processes were limited to maintain similar load conditions at all times. The compiler switches were set to a standard level of optimization for all expressions and then left alone. No other optimization settings were examined.
A. Reference beam pattern
An example of a simulated beam pattern generated by a circular piston is presented in Fig. 3. The radius of the circular piston is a = 5λ, which is the same value used in Fig. 8 of Lockwood and Willette,3 Fig. 2(b) in Hutchins et al.,7 and Fig. 6 in Zemanek.8 In Fig. 3, the acoustic field is evaluated in the half-plane bounded by the line r = 0 in one direction and the line z = 0 in the other direction. This figure, which evaluates the impulse response expression H1 at every field coordinate with 80 000-point Gauss quadrature, is the reference beam pattern for all error calculations. Larger maximum normalized differences are encountered if fewer Gauss abscissas are applied to H1, whereas the maximum normalized difference never exceeds ηmax = 10−13 as the number of Gauss abscissas increases above M = 80 000. In addition, the results of the other three equations evaluated with 80 000-point Gauss quadrature are indistinguishable from Fig. 3. The expressions H1, H2, H3, and H4 generate solutions that are within at most ηmax = 10−13 of one another at all points in the simulated field presented in Fig. 3, which indicates that all four expressions converge to the same result if the pressure field is computed with 80 000 or more Gauss abscissas.
FIG. 3.
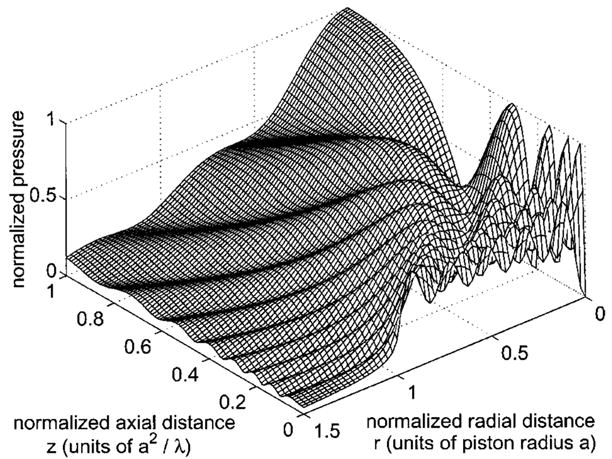
Simulated acoustic field generated when 80 000-point Gauss quadrature is applied to the impulse response calculation described in Eq. (3) and represented by H1. The wavelength of the acoustic excitation is equal to λ, and the radius of the circular piston is a = 5λ. The spatial axes are normalized in the radial direction with respect to the piston radius a and in the axial direction with respect to a2/λ. This simulation result is the reference for all subsequent error calculations in Figs. 4, 6, and 8–11.
B. Errors and times for a single sector (ns = 1)
The convergence of H1, H2, H3, and H4 is established with 80 000 Gauss abscissas; however, acceptable time-harmonic calculations of the near-field pressure are obtained with a smaller number of Gauss abscissas. This is demonstrated in Fig. 4, which displays the peak error values ηmax computed for a circular piston with a = 5λ using all four single integral expressions. For each value plotted in Fig. 4, the entire near-field pressure distribution is computed with the same number of Gauss abscissas at each grid coordinate, and peak error values are calculated with Eq. (15). In Fig. 4, near-field calculations are repeated for each of the expressions H1, H2, H3, and H4, and for each expression, the entire near field is computed with one Gauss abscissa, then two Gauss abscissas, and so on up to 200. The resulting peak errors ηmax are then plotted for calculations performed in a single sector (ns = 1) as a function of the number of Gauss abscissas applied to H1, H2, H3, and H4.
FIG. 4.
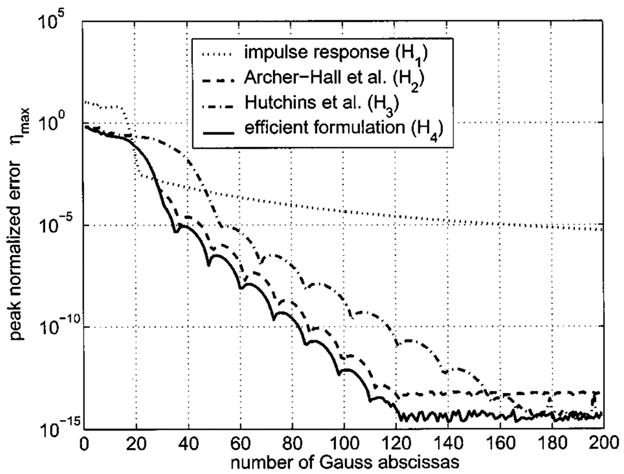
A comparison of the peak normalized errors ηmax obtained from beam patterns computed with H1, H2, H3, and H4 and evaluated for a constant number of Gauss abscissas in a single sector. Each beam pattern is computed for a circular source with radius a = 5λ. The errors are computed relative to the reference in Fig. 3. The efficient formulation H4 (solid line) generally produces the smallest peak errors ηmax, and the peak errors obtained with the Archer-Hall et al. (Ref. 6) formulation H2 (dashed line) are very similar if the same number of Gauss abscissas are applied across the entire computational grid. Likewise, the peak errors obtained with the Hutchins et al. (Ref. 7) formulation H3 (dot dash) are consistently larger than those obtained with H2 and H4. The errors obtained with the impulse response H1 (dotted line) are similar to those achieved with the efficient method H4 over a very small range of values, although for most values, the peak errors ηmax are largest with the impulse response H1.
Figure 4 shows that, for a given number of Gauss abscissas, the efficient formulation H4 (solid line) produces the smallest peak errors ηmax overall. The peak errors are reduced relative to H1, H2, and H3 because a singularity is subtracted from the numerator in H4 and because the limits of integration are selected such that all redundancies are eliminated from the integral expression in H4. If the near-field pressure distribution is computed with a constant number of Gauss abscissas at all grid points as in Fig. 4, the peak errors obtained with the Archer-Hall et al.6 formulation H2 (dashed line) are likewise relatively small. This result suggests that, for computations using a constant number of Gauss abscissas, the errors produced by the singularity in H2 are dominated by errors in other locations. In this case, the largest error values are encountered in locations where is large. However, if the region near the radiating surface of the piston is excluded, the largest error values occur wherever r ≈ a as a result of the singularity. In Fig. 4, the peak errors obtained with the Hutchins et al.7 formulation H3 (dot dash) are consistently larger than those obtained with H2 and H4 because H3 doubles the range over which the integrand is evaluated. The integral in H3 is evaluated over the range [−π, π], but the integrand is an even function, so the abscissas within the interval [−π,0] are redundant. This redundancy increases the error relative to H4 and H2 because H3 samples the integrand half as often within the range [0, π]. Figure 4 also demonstrates that the errors obtained with the impulse response H1 (dotted line) are similar to those achieved with the efficient method H4 over a very small range of values. However, the peak errors ηmax are larger with the impulse response H1 than any of the other single integral expressions for most values. The errors produced by the impulse response are the result of a rapid change in the impulse response where r ≈ a.
Figure 5 illustrates the computation times, plotted as a function of the number of Gauss abscissas, that are associated with the peak errors depicted in Fig. 4. In Fig. 5, the same number of Gauss abscissas are applied throughout the entire pressure field for calculations using the expressions H1, H2, H3, and H4, and the computation times are measured for each pressure field distribution. Figure 5 shows that, if the number of Gauss abscissas remains constant throughout the computational grid depicted in Fig. 1, H2 and H4 compute near-field pressure distributions in the shortest times by almost a factor of 3. This result evaluates only the raw computation times for the same number of Gauss abscissas without considering the peak error ηmax. In Fig. 5, the Hutchins et al.7 formulation H3 is somewhat slower because of the additional complex term in the numerator of Eq. (7). Nevertheless, the expressions H2, H3, and H4 are all nearly three times faster than the impulse response solution H1 for the a = 5λ circular source and computational grid evaluated here. The impulse response H1 is slower than the other expressions in part because of the additional time required to compute the inverse trigonometric function in Eq. (4) and in part because the other three expressions exploit the values that are repeated within the limits of integration and the integrand.
FIG. 5.
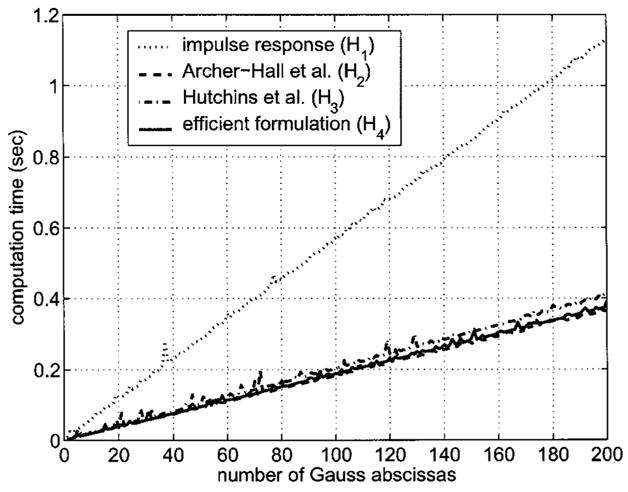
A comparison of measured computation times for beam patterns calculated with a constant number of Gauss abscissas using the expressions H1, H2, H3, and H4. As in Fig. 4, each beam pattern is computed on the same spatial grid as Fig. 3 for a piston with radius a = 5λ. A single sector that covers the entire computational grid in Fig. 1 is defined for these computations. A comparison of the raw computation times indicates that, for the same number of Gauss abscissas, the times required to compute the pressure field using the expressions in H2, H3, and H4 are roughly the same, although H3 (dot dash) is somewhat slower because of the additional complex term in the numerator of Eq. (7). Likewise, for the source geometry and computational grid evaluated here, the expressions H2, H3, and H4 are all nearly three times faster than the impulse response solution H1 (dotted line).
If the computation times in Fig. 5 are normalized with respect to the peak error values in Fig. 4, the resulting reduction in computation time achieved by the efficient formulation H4 depends on the value of the specified peak value ηmax. This normalized value, evaluated in a single sector that encompasses the entire computational grid depicted in Fig. 1, compares the numerical performance of H4 with that of the other single integral expressions H1, H2, and H3 and summarizes the result with a single number. For example, the efficient formulation H4 first achieves a peak error value below 10% in Fig. 4 with 19 Gauss abscissas, and the impulse response H1 first reaches a peak error less than 10% in the same figure with 20 Gauss abscissas. The computation time for the efficient formulation H4 using 19 Gauss abscissas with ns = 1 is then divided into the computation time for the impulse response using 20 Gauss abscissas with ns = 1, and the result indicates that the efficient method in H4 is 3.2 times faster than the impulse response H1 for a specified peak error value of 10%. For the same specified peak error, H2 and H4 are computed in roughly the same time (H2 is marginally faster), whereas H4 is 1.7 times faster than H3. Similarly, for a peak error value of 1%, H4 is 2.5 times faster than H1, H4 is roughly the same speed as H2 (H2 is again marginally faster), and H4 is again 1.7 times faster than H3. Finally, for a peak error value of 0.1%, H4 is 3.6 times faster than H1, H4 is roughly the same speed as H2, and H4 is once again 1.7 times faster than H3. These ratios are specific to the grid and source geometry considered here, and any changes in the size of the piston or the extent of the computational grid are expected to modify all of the calculated values.
C. Errors and times for multiple sectors (ns = 10)
The results of the grid sectoring strategy outlined in Eqs. (11) and (12), applied to a piston with a = 5λ and ns = 10, are summarized in Figs. 6 and 7. Figure 6 contains the peak computed errors for H1, H2, H3, and H4, and Fig. 7 displays the corresponding computation times. Figure 6 shows that, with 10 sectors defined, the efficient formulation H4 (solid line) again achieves the smallest peak errors ηmax overall. The peak errors computed for 10 sectors with H4 in Fig. 6, compared to the peak errors computed with (ns = 1) in Fig. 4, are virtually unchanged for all values of Nmax. Thus, grid sectoring successfully maintains the peak error value for H4 by applying the largest number of Gauss abscissas in the sector adjacent to the piston face and an incrementally smaller number of Gauss abscissas in successive sectors. For H4 and the remaining single integral expressions, the peak errors ηmax obtained with the maximum number of Gauss abscissas in Fig. 6 are compared to the peak errors ηmax obtained with a constant number of Gauss abscissas in Fig. 4. With respect to the single sector (ns = 1) results presented in Fig. 4 for the same source and grid geometry, grid sectoring results with ns = 10 applied to H3 (dot dash) generally produce the same peak error values ηmax for all values of Nmax except 60⩾ Nmax⩾ 40. In contrast, the impulse response H1 (dotted line) evaluated in ns = 10 sectors increases the peak errors ηmax by a factor of 2 or more for all values of Nmax > 20. Furthermore, the peak errors ηmax computed for the Archer-Hall et al.6 formulation H2 increase by several orders of magnitude for values of ns = 10 and Nmax > 20. With ns = 10, the peak error values in H1 and H2 are significantly increased, whereas H3 and the efficient formulation H4 maintain similar or equal peak error values, respectively.
FIG. 6.

A comparison of the maximum normalized errors ηmax for beam patterns computed with H1, H2, H3, and H4 and the grid sectoring approach defined in Eqs. (11) and (12) with ns = 10 sectors. Each beam pattern is computed for a piston radius a = 5λ and compared to the reference beam pattern in Fig. 3. Peak error values ηmax are plotted as a function of the maximum number of Gauss abscissas Nmax. The number of Gauss abscissas M in each sector varies according to Eqs. (11) and (12) so that M ranges from 0.3Nmax to Nmax across 10 sectors. Relative to the errors computed in Fig. 4 for single sector (ns = 1), the peak errors ηmax are maintained when grid sectoring with ns = 10 is combined with the efficient formulation H4 (solid line). For the same combination of input values, grid sectoring combined with H3 (dot dash) generally results in unchanged peak error values outside of the range 60 ⩾ Nmax⩾ 40. For ns = 10 and Nmax > 20, a noticeable increase in the peak error ηmax is indicated for sectored results computed with the impulse response H1 (dotted line), and the peak errors ηmax computed with H2 (dashed line) increase dramatically.
FIG. 7.
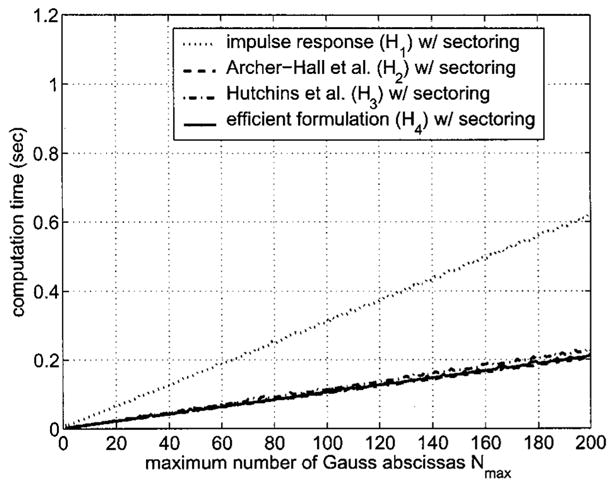
A comparison of computation times for beam patterns calculated with H1, H2, H3, and H4 combined with the grid sectoring approach defined in Eqs. (11) and (12) and plotted as a function of the maximum number of Gauss abscissas Nmax. Each beam pattern is computed for a piston radius a = 5λ on the same spatial grid as the reference in Fig. 3. The number of Gauss abscissas M in an individual sector ranges from 0.3Nmax to Nmax across the ns = 10 sectors indicated in Fig. 2. The axes are the same as in Fig. 5, so grid sectoring achieves roughly a factor of 2 reduction in the raw computation time for each integral formulation evaluated on this computational grid. Since grid sectoring reduces the computation time for each integral expression by nearly a factor of 2, H2, H3, and H4 are again approximately three times faster than the impulse response solution H1.
Figure 7 shows that, for a circular piston with a = 5λ evaluated on the grid depicted in Fig. 1, grid sectoring with ns = 10 applied to H1, H2, H3, and H4 cuts the raw computation time in half. The times in Fig. 7 correspond to the errors in Fig. 6, where the values illustrated in these two figures are obtained from the same set of calculations. In Fig. 7, the grid and source geometries are the same as in previous figures, and the measured times in Fig. 7 are plotted on the same axes as Fig. 5 for purposes of comparison. The measured times for each expression in both Fig. 5 and Fig. 7 are linearly proportional to the number of Gauss abscissas and the maximum number of Gauss abscissas, respectively. As in Fig. 5, the time required to compute pressure fields with the expressions H2, H3, and H4 is reduced by almost a factor of 3 in Fig. 7 relative to time required for impulse response calculations with H1.
If the computation times in Fig. 7 are normalized with respect to the peak error values in Fig. 6, the reduction in computation time achieved by the efficient formulation H4 again depends on the value of the specified peak value ηmax. This normalized value, evaluated for ns = 10, compares the numerical performance of H4 with that of the other single integral expressions H1, H2, and H3 and summarizes the result for grid sectoring with a single number. For example, the efficient formulation H4 initially achieves a peak error value below 10% in Fig. 6 where Nmax = 19, and the impulse response H1 first reaches a peak error less than 10% in the same figure where Nmax = 20. The computation time for the efficient formulation H4 with ns = 10 and Nmax = 19 is then divided into the computation time for the impulse response H1 with ns = 10 and Nmax = 20, and the result indicates that the efficient method in H4 is 3.1 times faster than the impulse response H1 for a specified peak error value of 10%. For the same specified peak error, H2 and H4 are computed in roughly the same time (now with H4 marginally faster), whereas H4 is 1.7 times faster than H3. For a peak error value of 1%, H4 is 2.4 times faster than H1, H4 is 1.7 times faster than H2 (H4 and H2 are no longer similar), and H4 is again 1.7 times faster than H3. Finally, for a peak error value of 0.1%, H4 is 4.7 times faster than H1, H4 is 2.1 times faster than H2, and H4 is 1.7 times faster than H3. Once again, these values are for a specific grid and source geometry, and any modifications in the grid or source are expected to change these computed values.
These normalized computation times show that, if grid sectoring is applied, the efficient formulation H4 computes the near-field distribution more quickly than any of the other single integral expressions. This result is expected, since the peak errors and the computation times are smallest with the efficient formulation, both for results computed in a single sector (Figs. 4 and 5) and in 10 sectors (Figs. 6 and 7). However, the relationship between the peak errors computed with H4 and H2 changes dramatically with 10 sectors, and for peak errors of 1% and smaller, the normalized computation time required for the Archer-Hall et al.6 expression H2 actually increases with ns = 10. Thus, grid sectoring is not recommended for pressure field calculations with H2 that require errors less than 1%, although grid sectoring reduces the normalized computation time for all of the other expressions (H1, H3, and H4).
D. Spatial distribution of the error
If a single sector (ns = 1) is defined for near-field pressure calculations, the spatial distribution of the error η(r,z) changes for each single integral expression as the number of Gauss abscissas is increased. Initially, the largest errors are increasingly concentrated away from the piston normal and toward the piston face (where is largest) until the complex exponential terms in each integrand are adequately sampled. For a circular piston with a = 5λ evaluated across the range of coordinate values depicted in Fig. 1, the large errors adjacent to the piston face disappear if near-field pressures are evaluated with 20 or more Gauss abscissas are applied to H1, H2, and H4 and if more than 30 Gauss abscissas are applied to H3. When H1 and H2 are evaluated with additional Gauss abscissas, numerical singularities appear in locations where r ≈ a. Examples of the spatial distribution of the error η(r,z) for a single sector (not shown) are easily obtained for each of the single integral expressions in H1, H2, H3, and H4.
Illustrations of η (r,z) evaluated in multiple sectors (ns = 10) are demonstrated in Figs. 8, 9, 10, and 11. These figures show that the expressions H1, H2, H3, and H4 produce four distinct error distributions and that grid sectoring with Nmax = 50 has a different effect on each expression. In Figs. 8, 9, 10, and 11, the error distribution in the sector adjacent to the piston face is the same as that obtained if Nmax = 50 is applied throughout the computational grid. The error distributions in the remaining sectors differ from those obtained with Nmax = 50 because the number of Gauss abscissas decreases in successive sectors. The error distributions η (r,z) in Figs. 8, 9, and 10 demonstrate that the peak values ηmax for H1, H2, and H3 are located in sectors away from the piston face, which indicates that these three expressions increase the peak error value relative to that obtained when Nmax Gauss abscissas are applied throughout the entire grid. If the peak error value η max occurs in the sector adjacent to the piston face (where Nmax Gauss abscissas are applied) as in Fig. 11, then the peak error value is the same as that obtained when Nmax Gauss abscissas are applied throughout the entire grid. In this example, H4 maintains the peak error with values of ns = 10 and Nmax = 50, while the expressions H1, H2, and H3 increase the peak error with the same parameters.
FIG. 8.
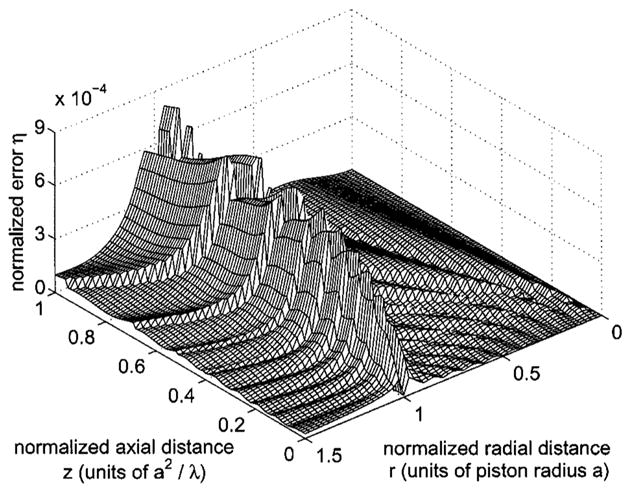
Normalized difference between the reference beam pattern in Fig. 3 and the results of the impulse response H1 evaluated with grid sectoring as defined by Eqs. (11) and (12). For this simulation, the near-field region is divided into ns = 10 sectors, and the scale factors C = 5 and S = 0.3 specify the largest and smallest number of abscissas as 50 and 15, respectively. The integrand is evaluated with the largest number of Gauss abscissas in the sector adjacent to the piston face and the smallest number of Gauss abscissas in the sector adjacent to the piston normal. When these values are applied to H1 for a circular piston with radius a = 5λ, the maximum normalized error is ηmax = 8.33 × 10−4 relative to the reference in Fig. 3. As the number of Gauss abscissas decreases in each sector evaluated along the line r/a = 1, the computed numerical error grows larger with increasing values of z. Numerical errors are encountered along the line r/a = 1 because of the large slopes produced by the cos−1 term in the impulse response.
FIG. 9.
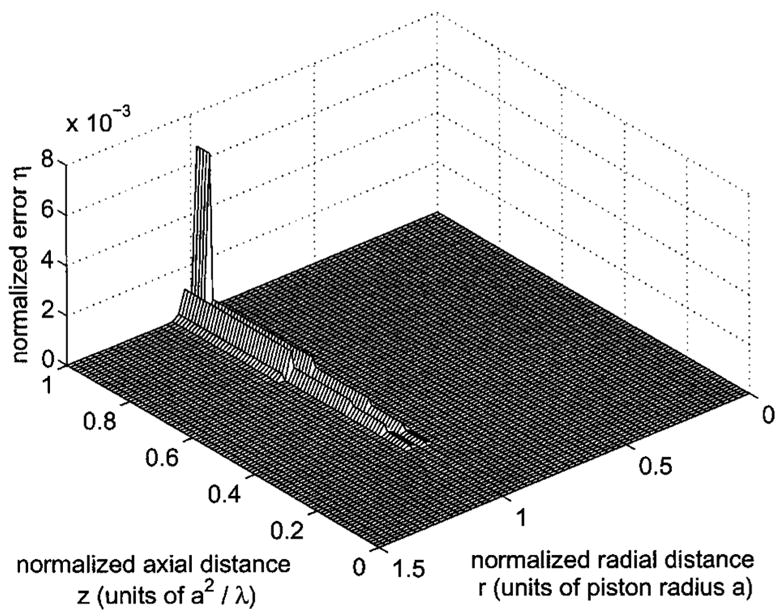
Normalized difference between the reference beam pattern in Fig. 3 and the results of the Archer-Hall et al. (Ref. 6) formula H2 evaluated with grid sectoring as defined by Eqs. (11) and (12). For this simulation, the near-field region is divided into ns = 10 sectors, and the scale factors C = 5 and S = 0.3 specify the largest and smallest number of abscissas as 50 and 15, respectively. The integrand is evaluated with the largest number of Gauss abscissas in the sector adjacent to the piston face and the smallest number of Gauss abscissas in the sector adjacent to the piston normal. When these values are applied to H2 for a circular piston with radius a = 5λ, the maximum normalized error is ηmax = 6.63 × 10−3 relative to the reference in Fig. 3. The errors shown here grow substantially larger with increasing z near the line r/a = 1. These errors are produced by a numerical singularity in H2.
FIG. 10.
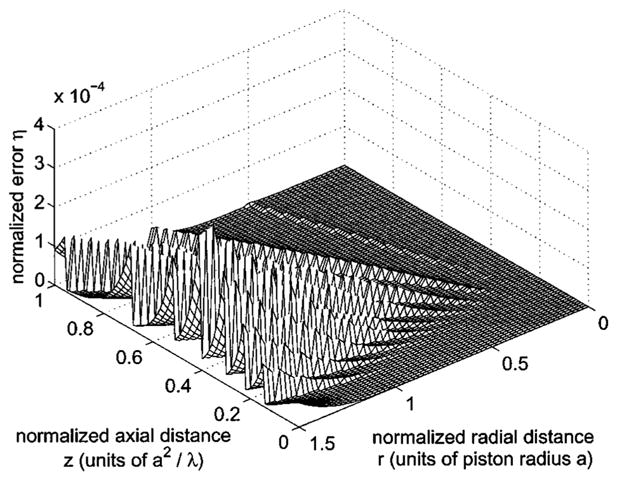
Normalized difference between the reference beam pattern in Fig. 3 and the results of the Hutchins et al. (Ref. 7) formula H3 evaluated with grid sectoring as defined by Eqs. (11) and (12). In this simulation, the near-field region is divided into ns = 10 sectors, and the scale factors C = 5 and S = 0.3 specify the largest and smallest number of abscissas as 50 and 15, respectively. The integrand is evaluated with the largest number of Gauss abscissas in the sector adjacent to the piston face and the smallest number of Gauss abscissas in the sector adjacent to the piston normal. When these values are applied to H3 for a circular piston with radius a = 5λ, the maximum normalized error is ηmax = 3.67×10−4 relative to the reference in Fig. 3. Similar to the result in Fig. 8, the sectoring strategy increases the maximum error value somewhat relative to the peak value obtained if the results are evaluated with 50 Gauss abscissas throughout the field; however, no singularity is present along the line r/a = 1 because a singularity is subtracted within the integrand of H3.
FIG. 11.
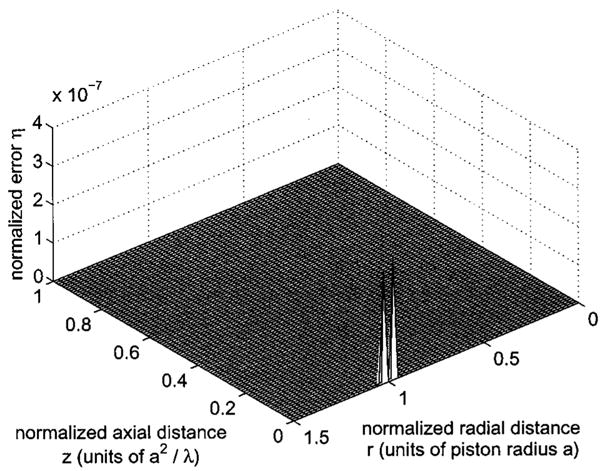
Normalized difference between the reference beam pattern in Fig. 3 and the results of the numerically efficient formulation H4 evaluated with grid sectoring as defined by Eqs. (11) and (12). In this simulation, the near-field region is divided into ns = 10 sectors, and the scale factors C = 5 and S = 0.3 specify the largest and smallest number of abscissas as 50 and 15, respectively. The integrand is evaluated with the largest number of Gauss abscissas in the sector next to the piston face and the smallest number of Gauss abscissas in the sector adjacent to the piston normal. When these values are applied to H4 for a circular piston with radius a = 5λ, the maximum normalized error is ηmax = 3.20×10−7 relative to the reference in Fig. 3. As in Fig. 10, and in contrast to the results shown in Figs. 8–10, the sectoring strategy maintains a maximum error that is the same as that obtained if 50 Gauss abscissas are applied to all points in the field. The maximum error value is maintained because the limits of integration are minimized and a singularity is subtracted from H4.
In Fig. 8, the normalized error η (r,z) is computed for the impulse response H1 evaluated with ns = 10 sectors and Nmax = 50 Gauss abscissas for a circular piston with radius a = 5λ. Figure 8 contains an example of the numerical singularity produced by the impulse response which appears adjacent to the line r/a = 1. This singularity is observed well beyond the grid boundaries depicted in these figures. The numerical artifact in this region is caused by the slope of the term in the impulse response H1, which is infinite at the values for β2 and β3 specified in Eq. (2). These infinite slopes are encountered in calculations of the impulse response at all grid coordinates, and the errors near line r/a = 1 are amplified by other rapid changes that are caused by the cos−1 term in I1. In Fig. 8, the errors caused by the singularity grow larger as the value of z increases, and several discrete jumps are evident along the line r/a = 1. These jumps, which appear at the sector boundaries defined by Eq. (11), occur as the number of Gauss abscissas applied within each sector decreases. In subsequent sectors encountered as the z coordinate increases along the line r/a = 1, the errors rise rapidly at each sector boundary, then decay until the next sector boundary is reached. This pattern is repeated in subsequent sectors. The error distribution in Fig. 8 suggests that additional Gauss abscissas are required near r/a = 1, whereas grid sectoring reduces the number of Gauss abscissas with increasing z values in this location. Grid sectoring nevertheless reduces the normalized computation time for the impulse response H1 evaluated on the computational grid in Fig. 1, though the improvements diminish for values of Nmax > 20.
Figure 9 depicts the error distribution η (r,z) computed for the Archer-Hall et al.6 expression H2 with ns = 10 sectors and Nmax = 50 Gauss abscissas. Figure 9 contains an example of η (r,z) calculated with H2 for a circular piston with radius a = 5λ, where the error increases along the line r/a = 1 as the z coordinate moves away from the face of the piston. This error distribution, which produces larger errors as the number of samples is reduced by grid sectoring, is the result of the numerical singularity in H2. The singularity originates in I2, where the denominator of the integrand in Eq. (6) approaches zero as the value of r approaches a. As with the impulse response H1, the numerical error computed with the expression H2 jumps at each sector boundary encountered along r/a = 1 as z increases, suggesting that H2 requires additional abscissas in this location. However, grid sectoring reduces the number of Gauss abscissas in each subsequent sector, and the errors computed with H2 increase where r ≈ a. As a result, the singularity in H2 limits the effectiveness of grid sectoring in Fig. 1, especially for values of Nmax > 20.
Figure 10 shows the spatial distribution of η (r,z) for the Hutchins et al.7 expression H3 with ns = 10 sectors and Nmax = 50 Gauss abscissas. Unlike the error distributions presented in Figs. 8 and 9 for H1 and H2, respectively, the errors depicted in Fig. 10 for a circular source with a = 5λ demonstrate that H3 eliminates the singularity along the line r/a = 1. However, as the value of z increases in successive sectors and as the number of Gauss abscissas is therefore reduced, the peak value of the error observed in each sector gradually rises at first until a maximum value is reached and then slowly diminishes. This error distribution indicates that the linear mapping defined for ns = 10 sectors in Eq. (12) underestimates the number of Gauss abscissas required for calculations with H3 within intermediate sectors, particularly for values of 60⩾ Nmax⩾ 40. Outside of this range of values for Nmax, where the exact range of values for Nmax is a function of the source and grid parameters, the peak errors consistently decrease from one sector to the next as z increases. Although Fig. 10 indicates that, for certain parameters, H3 increases the numerical error obtained with grid sectoring, the overall numerical performance of H3 is improved by subtracting the singularity and eliminating the numerical problems along the line r/a = 1.
Figure 11 contains the distribution of computed error values η(r,z) for the efficient formulation H4 evaluated with ns = 10 and Nmax = 50. Figure 11 shows that, for this combination of values evaluated on the grid in Fig. 1, the errors obtained with H4 are substantially smaller than those produced by H1, H2, and H3 in Figs. 8, 9, and 10, respectively. In Fig. 11, the computed errors are confined to a small region where z≈0 and r≈a. Although some errors remain after the numerical singularity of H2 shown in Fig. 9 is removed in H4, the remaining errors in Fig. 11 are insignificant. Likewise, by selecting limits of integration that remove all redundant function evaluations, the efficient formulation also avoids the numerical problems illustrated in Fig. 10. Figure 11 shows that, although ns = 10 sectors are defined for H4, the sector boundaries observed in previous mesh plots are not present. The sector boundaries disappear from the plot of η(r,z) whenever the errors in subsequent sectors are significantly smaller than the errors in the sector adjacent to the circular source. Thus, for grid sectoring defined with ns = 10 and Nmax = 50, the efficient formulation H4 maintains the same peak error value obtained when 50 Gauss abscissas are applied throughout the computational grid. A comparison of Figs. 4 and 6 indicates that the efficient expression H4 maintains the same peak error for all values of Nmax.
V. DISCUSSION
A. Single sector
The single integral expressions H1, H2, H3, and H4 are all analytically equivalent; however, the numerical properties of each vary widely. For computations that define a single sector (ns = 1) so that the number of Gauss abscissas remains constant across the entire computational grid, the Archer-Hall et al.6 expression H2 and the efficient expression H4 produce pressure fields with approximately the same peak errors in roughly the same amount of time. This result is restricted to near-field pressures calculated in the grid depicted in Fig. 1. For other grid geometries that include points with r≈a and exclude the region near the surface of the circular piston, the peak error obtained with H2 increases relative to that obtained with H4. Therefore, the normalized computation time for H2 evaluated in a single sector is approximately the same as that for the efficient formulation H4 only in certain circumstances. The normalized computation times for H4 are consistently less than or equal to those for H2, so the overall numerical performance of H4 is superior to that of H2, even for calculations performed within a single sector.
As indicated in Figs. 4 and 5, the efficient formulation H4 consistently produces smaller errors in less time than the Hutchins et al.7 expression H3. The normalized computation times, which condense these results into a single value, show that H4 is 1.7 times faster than H3 for specified errors of 10%, 1%, and 0.1%, where the exact value of this ratio varies as a function of the grid and source geometry. For calculations in a single sector, H3 consistently requires more time than H4 to achieve a specified peak error. This is due to the additional term in the numerator of Eq. (7), which increases the raw computation time, and the duplicated values in the integrand, which increase the error relative to that obtained with H4.
Figure 5 also shows that, for pressure field calculations performed in a single sector that covers the entire grid in Fig. 1, the computation times measured with the impulse response H1 are significantly larger than those obtained with the same number of Gauss abscissas applied to the efficient formulation H4. Although the peak errors produced by H1 are slightly smaller than those generated by H4 if the number of Gauss abscissas falls within a certain restricted range, comparisons of normalized computation times demonstrate that the efficient formulation H4 is consistently faster than the impulse response H1. In calculations performed on a 61 by 101 point grid, H4 is 3.1, 2.4, and 4.7 times faster than H1 for peak error values of 10%, 1%, and 0.1%, respectively. In computational grids that contain a larger number of points, the efficient formulation H4 is even faster relative to H1 because calculations involving common terms in Eq. (8) are exploited in even more locations.
The impulse response H1 consistently requires more time for pressure field calculations than the other three single integral formulations because the values for the limits of integration β2 and β3 are constantly changing and because the only expression repeated in I1 is (β2−z2). By computing new values for β2 and β3 at every new value of r and z, the computational overhead is increased relative to that required for H2, H3, and H4. In contrast, the other three single integral expressions compute the limits of integration once and then repeatedly apply the result at every point in the computational grid. H2, H3, and H4 also share some other repeated expressions that are very similar. These three single integral formulations, which all include integrals that are evaluated with respect to ψ, contain the term r2+a2−2ar cos ψ in both the denominator and an exponent of the integrand. This term is independent of the z coordinate and is therefore computed once for each value of r and then applied repeatedly at each z value that shares the same radial coordinate. Similarly, H2, H3, and H4 each contain ratios of terms that are strictly functions of r, a, and ψ and therefore independent of z. These expressions are also evaluated once for each value of r and then applied repeatedly at each z coordinate. In addition, the value of e−jkz is calculated once for each z coordinate in the grid and then applied throughout the computational grid wherever that z value is encountered. Even without these time-saving measures, pressure field calculations are completed more quickly with H2, H3, and H4 than with the impulse response H1 because of the extra time required to compute the inverse cosine function. These improvements apply equally to computations with a single sector and computations with multiple sectors, as demonstrated by the consistent relationships between computation times demonstrated in Figs. 5 and 7.
B. Multiple sectors
In pressure fields computed with multiple sectors, the Archer-Hall et al.6 expression H2 produces larger errors than the efficient formulation H4. This is clearly demonstrated in a comparison of the peak errors ηmax depicted in Fig. 6. For calculations with Nmax>20 and ns = 10 in a 61 by 101 point grid, the peak errors computed with H2 are several orders of magnitude greater than those computed with H4. Although the specific error values change with the number of sectors and the value of Nmax, the peak errors produced by H2 are consistently larger than those obtained with H4 whenever the pressure field is sampled near r/a = 1. In this region, the errors grow larger as the sampling of the integrand is reduced because of the singularity in H2, and H4 avoids these errors by subtracting the singularity in Eq. (8). The results indicate that H2 and H4 achieve an error of 10% in approximately the same amount of time; however, this result only applies to the grid geometry in Fig. 1. Other grid geometries that evaluate the pressure at some distance from the surface of the circular piston show that H4 is faster than H2 unless values near r/a = 1 are avoided completely. The ratios of normalized computation times corresponding to peak errors of 1% and 0.1% measured for the same grid show that H4 is 1.7 and 2.1 times faster than H2, respectively. These values also depend on the grid and source geometry. Relative to results computed with a single sector (ns = 1) defined for the entire grid in Fig. 1, the normalized computation time for H2 actually increases with ns = 10 sectors for specified peak errors less than or equal to 0.1%. This result indicates that grid sectoring applied to H2, by reducing the number of Gauss abscissas in sectors away from the face of the circular piston, shifts samples away from locations where a singularity dominates the peak error values. Grid sectoring therefore is primarily applicable either to grid coordinates that avoid the singularities or integral formulations that eliminate singularities in all coordinate locations.
A comparison between the expression H3 derived by Hutchins et al.7 and the efficient formulation H4 shows that expressions that subtract the singularity obtain consistent numerical results. Whether the specified peak error is 10%, 1%, or 0.1%, the efficient expression H4 evaluated on the 61 by 101 point grid defined in Fig. 1 is 1.7 times faster than H3. The ratio of normalized computation times changes as the source and grid parameters vary, but the results are much more consistent for different error values computed with the same source and grid parameters if the singularity is subtracted as in H3 and H4.
Relative to the peak errors ηmax obtained from near-field pressure calculations that apply the same number of Gauss abscissas to the impulse response H1 at every grid point in Fig. 1, the peak errors increase for H1 with ns = 10 sectors whenever Nmax>20. As shown in a comparison of the peak errors for H1 computed with one and ten sectors in Figs. 4 and 6, respectively, the peak error obtained with H1 increases by at least a factor of 2 up to a factor of 8 for this range of Nmax values. As with all of the other results, the exact ratios are a function of the source and grid parameters. The peak error values for H1 in Fig. 6, which are calculated with ns = 10 sectors, are larger that those computed with the Archer-Hall et al.6 expression H2 for values of Nmax>80, where both peak errors are about 0.03%. In terms of normalized computation times, H2 is 3.0, 1.4, and 2.2 times faster than H1 for specified peak errors of 10%, 1%, and 0.1%, respectively, for pressure field calculations evaluated in ns = 10 sectors. Therefore, even with ns = 10 sectors defined for grid sectoring, the impulse response is the slowest of the four single integral expressions for this combination of parameters. Overall, for near-field calculations performed in single or multiple sectors, the fastest and most consistent performance is demonstrated by the efficient method H4 in Eq. (8).
C. Parameters for grid sectoring
Each of the near-field pressure distributions computed with grid sectoring defines ns = 10 sectors for the grid outlined in Fig. 1. For this grid, any value of ns between 5 and 15 achieves approximately the same factor of 2 reduction in the computation time demonstrated in a comparison between Figs. 5 and 7. With fewer sectors, errors at the sector boundaries can exceed the peak error in the sector next to the surface of the radiating source, and values of ns>15 reduce the number of repeated calculations in each sector for H2, H3, and H4. Outside of this range of values for ns, grid sectoring achieves some reduction in the normalized computation time, but the values 15⩾ns⩾5 demonstrate the best performance for the computational grid evaluated here. The specific range of values depends on the source and grid geometry, so grid sectoring is defined for different values of ns with each new combination of parameters.
The linear mapping function defined in Eq. (12) eliminates the large errors that otherwise appear in sectors located near the piston normal. Although near-field pressure calculations in the axial region require fewer Gauss abscissas than other nearfield locations, Eq. (9) underestimates the number of Gauss abscissas required near the piston normal. For example, with Nmax = 10 and ns = 10, Eq. (9) correctly employs 10 Gauss abscissas in the sector adjacent to the piston face, but Eq. (9) also applies one Gauss abscissa in the sector adjacent to the piston normal. If one Gauss abscissa is applied throughout this sector, the resulting errors are much larger than those obtained in the sector adjacent to the piston face. To prevent the errors in the axial region from increasing the peak error, the number of Gauss abscissas is computed with Eq. (12) instead of Eq. (9). In this example, Eq. (12) with S = 0.3 employs three Gauss abscissas throughout the sector adjacent to the piston face, and additional abscissas are specified in subsequent sectors until the maximum value Nmax = 10 is reached. The value S = 0.3 is used for grid sectoring with each of the single integral expressions evaluated in Figs. 6–11; however, other values are required for different grid and source geometries.
D. Near-field/far-field transition
The pressure field in Fig. 3 and the error distributions in Figs. 8–11 are evaluated strictly in the near-field region; however, the single integral expressions H1, H2, H3, and H4 are also useful for pressure calculations well beyond the near-field/far-field transition distance. As demonstrated in the text by Kinsler et al.,13 the far-field approximation for a circular piston produces substantial errors at the far-field transition distance a2/λ. These errors continue well beyond the location of the near-field/far-field transition, out to at least 5 transition distances. The errors are characterized by discrete jumps in the computed pressure that are clearly evident on a linear scale that is normalized to the peak value of the axial pressure. On this scale, these jumps are no longer visible after six or seven transition distances for most circular piston geometries. Thus, the far-field approximation is only appropriate for locations that are at least six or seven times the transition distance a2/λ. The efficient formulation H4 combined with grid sectoring is also effective well beyond six or seven transition distances, which eliminates the need for two different calculation methods in grids that extend into both regions.
E. Large aperture phased arrays
The single integral calculations H1, H2, H3, and H4 are all substantially faster than any method that superposes point sources (e.g., Zemanek8) or rectangular radiators (e.g., Ocheltree and Frizzell14). In particular, near-field calculations that combine the efficient formulation H4 with grid sectoring can reduce the computation time by as much as an order of magnitude or more relative to point source or rectangular radiator calculations. Shorter run times are especially useful in calculations of three-dimensional fields generated by large ultrasound phased arrays designed for thermal therapy. For example, pressure fields are repeatedly calculated in evaluations of sparse ultrasound phased arrays15–17 designed for noninvasive surgery. Pressure field computations for large sparse arrays are very time-consuming, and the efficient formulation H4 combined with grid sectoring achieves a significant reduction in the computation time relative to these other methods.
An expression similar to H4 is also available for square or rectangular sources,18 and this expression is likewise faster than any calculation that uses point sources, rectangular radiators, or the impulse response. With or without grid sectoring, the efficient formulation H4 derived for a circular piston is faster than any of these expressions for rectangular sources. Calculations utilizing H4 in repeated pressure field calculations save time by evaluating a single one-dimensional integral instead of a two-dimensional integral or multiple one-dimensional integrals, and because H4 reduces the computation time, this expression is recommended for preliminary designs of sparsely and densely populated therapy arrays.
VI. CONCLUSION
In a comparison of four analytically equivalent single integral expressions that describe the near-field pressure produced by a circular piston, the efficient formulation H4 in Eq. (8) achieves the smallest numerical errors in the shortest time. The efficient formulation H4, which eliminates redundant calculations and subtracts a singularity, exploits the best features of the Archer-Hall et al.6 expression H2 and the Hutchins et al.7 expression H3. The single integral expression H4 is also amenable to grid sectoring, where the computational grid is divided into sectors, and the number of Gauss abscissas is adjusted from one sector to the next. In the sector adjacent to the piston face, the pressure is evaluated with the largest number of Gauss abscissas, and in the sector adjacent to the piston normal, pressure calculations employ the smallest number of Gauss abscissas. Sector definitions are improved with a scheme that defines straight lines emanating from the center of the circular piston. Grid sectoring is also improved with a linear mapping function that avoids sampling problems in the axial region. Grid sectoring applied to the efficient formulation H4 successfully reduces the computation time by nearly a factor of 2 without increasing the peak error value.
Near-field pressure distributions are evaluated on a 61 by 101 point grid for a circular piston with radius a = 5λ, and the results obtained for the single integral expressions H1, H2, H3, and H4 are evaluated both in a single sector and in ns = 10 sectors. If all pressure field values are calculated in a single sector that extends up to the piston face or if the computational grid avoids all locations where r≈a, the Archer-Hall et al.6 expression H2 and the efficient formulation H4 obtain nearly the same errors in approximately the same amount of time. Otherwise, the peak error values calculated with H2 are greater than those obtained with H4. For calculations utilizing multiple sectors, the efficient formulation H4 also demonstrates superior performance. For example, the peak error increases dramatically with ns = 10 sectors for the Archer-Hall et al.6 expression H2, and the singularity in H2 prevents grid sectoring from achieving significant reductions in computation times that are normalized with respect to the peak errors. The peak errors obtained with the impulse response H1 are also amplified in ns = 10 sectors, though grid sectoring nevertheless reduces the normalized computation time for H1 because the peak errors increase by less than an order of magnitude relative to calculations performed in a single sector. The peak errors obtained with the Hutchins et al.7 expression H3 increase somewhat over a small range of values for Nmax in calculations with ns = 10 sectors, and despite this moderate increase in the peak error, grid sectoring achieves a consistent reduction in the normalized computation time. Likewise, the peak errors evaluated with the efficient formulation H4 are effectively unchanged in calculations with ns = 10 sectors, so grid sectoring combined with H4 consistently reduces the normalized computation time. Results evaluated in a 61 by 101 point grid divided into ns = 10 sectors for a piston with radius a = 5λ show that pressures are calculated by the efficient formulation H4 in about the same time as H2 for a peak error value of 10%, whereas H4 is 3.1 times faster than the impulse response H1 and 1.7 times faster than H3. For a peak error value of 1%, the efficient formulation H4 is 2.4, 1.7, and 1.7 times faster than H1, H2, and H3, respectively. For a peak error value of 0.1%, the efficient formulation H4 is 4.7, 2.1, and 1.7 times faster than H1, H2, and H3, respectively. As demonstrated by these ratios of normalized computation times, the impulse response H1 is the slowest of these four single integral expressions, and the efficient formulation H4 is the fastest. The ratios of normalized computation times change as the grid and source parameters vary; however, H4 consistently achieves the best overall performance.
Acknowledgments
This work was funded in part by a Biomedical Engineering Research Grant from the Whitaker Foundation, NIH Grant 5PO1 CA42745, and NIH Grant 1R01 CA093669. The authors would like to thank Jeremy D. Hoff of the Department of Radiation Oncology in the Duke University Medical Center for his helpful comments and suggestions.
Contributor Information
Robert J. McGough, Department of Electrical and Computer Engineering, Michigan State University, East Lansing, Michigan 48824.
Thaddeus V. Samulski, Department of Radiation Oncology, Duke University Medical Center, Durham, North Carolina 27710
James F. Kelly, Department of Mathematics, Michigan State University, East Lansing, Michigan 48824
References
- 1.Oberhettinger F. On transient solutions of the ‘baffled piston’ problem. J Res Natl Bur Stand, Sect B. 1961;65B:1–6. [Google Scholar]
- 2.Stepanishen PR. Transient radiation from pistons in an infinite planar baffle. J Acoust Soc Am. 1971;49:1629–1638. [Google Scholar]
- 3.Lockwood JC, Willette JG. High-speed method for computing the exact solution for the pressure variations in the near field of a baffled piston. J Acoust Soc Am. 1973;53:735–741. [Google Scholar]
- 4.Harris GR. Transient field of a baffled planar piston having an arbitrary vibration amplitude distribution. J Acoust Soc Am. 1981;70:186–204. [Google Scholar]
- 5.Verhoef WA, Cloostermans MJTM, Thijssen JM. The impulse-response of a focused source with an arbitrary axisymmetric surface velocity distribution. J Acoust Soc Am. 1984;75:1716–1721. [Google Scholar]
- 6.Archer-Hall JA, Bashter AI, Hazelwood AJ. Means for computing the Kirchhoff surface integral for a disk radiator as a single integral with fixed limits. J Acoust Soc Am. 1979;65:1568–1570. [Google Scholar]
- 7.Hutchins DA, Mair HD, Puhach PA, Osei AJ. Continuous-wave pressure fields of ultrasonic transducers. J Acoust Soc Am. 1986;80:1–12. [Google Scholar]
- 8.Zemanek J. Beam behavior within the near field of a vibrating piston. J Acoust Soc Am. 1971;49:181–191. [Google Scholar]
- 9.Davis PJ, Rabinowitz P. Numerical Integration. Academic; New York: 1975. p. 139.p. 140. [Google Scholar]
- 10.Orofino DP, Pedersen PC. Multirate digital signal-processing algorithm to calculate complex acoustic pressure fields. J Acoust Soc Am. 1992;92:563–582. [Google Scholar]
- 11.Davis PJ, Rabinowitz P. Numerical Integration. Academic; New York: 1975. pp. 73–77.pp. 87–89.pp. 369 [Google Scholar]
- 12.Abramowitz M, Stegun IA. Handbook of Mathematical Functions, with Formulas, Graphs, and Mathematical Tables. Dover; New York: 1972. pp. 887–889.pp. 916–919. [Google Scholar]
- 13.Kinsler LE, Frey AR, Coppens AB, Sanders JV. Fundamentals of Acoustics. 4. Wiley; New York: 2000. p. 179. [Google Scholar]
- 14.Ocheltree KB, Frizzell LA. Sound field calculation for rectangular sources. IEEE Trans Ultrason Ferroelectr Freq Control. 1989;36:242–248. doi: 10.1109/58.19157. [DOI] [PubMed] [Google Scholar]
- 15.Goss SA, Frizzell LA, Kouzmanoff JT, Barich JM, Yang JM. Sparse random ultrasound phased array for focal surgery. IEEE Trans Ultrason Ferroelectr Freq Control. 1996;43:1111–1121. [Google Scholar]
- 16.Gavrilov LR, Hand JW. A theoretical assessment of the relative performance of spherical phased arrays for ultrasound surgery. IEEE Trans Ultrason Ferroelectr Freq Control. 2000;47:125–139. doi: 10.1109/58.818755. [DOI] [PubMed] [Google Scholar]
- 17.Pernot M, Aubry JF, Tanter M, Thomas JL, Fink M. High power transcranial beam steering for ultrasonic brain therapy. Phys Med Biol. 2003;48:2577–2589. doi: 10.1109/TMI.2010.2076829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.McGough RJ. Rapid calculations of time-harmonic nearfield pressures produced by rectangular pistons. J Acoust Soc Am. 2004;115:1934–1941. doi: 10.1121/1.1694991. [DOI] [PMC free article] [PubMed] [Google Scholar]


