Abstract
As the most diverse group of early tetrapods, temnospondyls provide a unique opportunity to investigate cladogenetic patterns among basal limbed vertebrates. We present five species-level supertrees for temnospondyls, built using a variety of methods. The standard MRP majority rule consensus including minority components shows slightly greater resolution than other supertrees, and its shape matches well several currently accepted hypotheses of higher-level phylogeny for temnospondyls as a whole. Also, its node support is higher than those of other supertrees (except the combined standard plus Purvis MRP supertree). We explore the distribution of significant as well as informative changes (shifts) in branch splitting employing the standard MRP supertree as a reference, and discuss the temporal distribution of changes in time-sliced, pruned trees derived from this supertree. Also, we analyse those shifts that are most relevant to the end-Permian mass extinction. For the Palaeozoic, shifts occur almost invariably along branches that connect major Palaeozoic groups. By contrast, shifts in the Mesozoic occur predominantly within major groups. Numerous shifts bracket narrowly the end-Permian extinction, indicating not only rapid recovery and extensive diversification of temnospondyls over a short time period after the extinction event (possibly less than half a million years), but also the role of intense cladogenesis in the late part of the Permian (although this was counteracted by numerous ‘background’ extinctions).
Keywords: Temnospondyli, supertree, diversification, Stereospondyli, Permian, Triassic
1. Introduction
The origin and early radiation of limbed vertebrates (or tetrapods) are the focus of much renewed interest and interdisciplinary research at the interface between evolutionary and developmental biology. Outstanding palaeontological discoveries continue to refine the complex picture of character acquisition and transformation that accompanied vertebrate terrestrialization. At the same time, phylogeny-based macroevolutionary studies are beginning to decipher quantitative and qualitative aspects of early tetrapod diversification (e.g. Laurin 2004; Ruta et al. 2006; Wagner et al. 2006; Marjanovic & Laurin 2007). In the present work, we examine for the first time models of cladogenesis (i.e. branch subdivision) in Temnospondyli, the largest group of primitive tetrapods. Our focus is the identification of portions of the temnospondyl phylogeny that underwent significant changes in lineage splitting. This is achieved through analyses of the degree of asymmetry (i.e. imbalance), count of taxa and overall shape of the two branches that descend from each internal node in the phylogeny. Throughout, we employ the term ‘branching’ in the sense of multiplication of lineages. In this context, ‘branching’ is more appropriate than ‘diversification’, as our analysis revolves exclusively around tree topology and is not concerned with measures of morphological character change or with the tempo and mode of evolutionary transformations (e.g. Simpson 1944).
Comprehensive temnospondyl phylogenies are still unavailable. Compilation of an exhaustive data matrix for all described species is unrealistic at present. However, several species-level trees have been published for nearly all families or superfamilies of temnospondyls. Thus, given a set of partially overlapping input trees, supertree techniques can be used to combine these trees and generate a synthetic ‘consensus’ phylogeny (e.g. Pisani & Wilkinson 2002; Wilkinson et al. 2005a; Pisani et al. 2007). Here, we present various supertrees for temnospondyls built using different methods and employ them for an analysis of cladogenetic patterns. Temnospondyls are particularly amenable to this kind of analysis and to macroevolutionary studies in general, given their sheer diversity and their broad stratigraphical and geographical distributions, with records from all continents and spanning approximately 210 Myr (Early Carboniferous–late Early Cretaceous; Milner 1990).
Temnospondyls are of great zoological significance because they are implicated in the current debate on amphibian origins (e.g. Ruta & Coates 2007), although this is disputed by a number of researchers (e.g. Vallin & Laurin 2004). Regardless of their systematic affinities, temnospondyls present an interesting case study for elucidating macroevolutionary patterns in species-rich fossil groups.
We address two main questions: (i) which portions of temnospondyl phylogeny underwent a significant branching shift (i.e. a significant change in lineage multiplication)? and (ii) what was the distribution of shifts immediately before and after the end-Permian extinction? The end-Permian extinction (Benton 2003; Benton et al. 2004; Erwin 2006) had by far the most dramatic impact on terrestrial and marine life of all known mass extinctions and continues to play an unrivalled role in our understanding of the consequences that large-scale biological crises have for faunal turnovers, ecological remodelling and adaptive radiations.
2. Material and methods
(a) Input trees
Temnospondyl phylogenies (see appendix 1a in the electronic supplementary material) were chosen according to several criteria (Ruta et al. 2003; Bininda-Emonds et al. 2004). First, current knowledge of the large-scale interrelationships of temnospondyls relies extensively on Milner's (1990) overarching family-level study, which was therefore selected as the starting point for our survey. Second, we included trees with four or more temnospondyl taxa (either species or supraspecific units). Third, if an original tree included different tetrapod groups, then only its temnospondyl portion was used as an input tree. Fourth, if several trees were obtained from an original analysis, we used either their strict consensus (if presented) or the tree selected by the original author(s) (in the absence of a consensus). Last manually generated trees were considered only if accompanied by apomorphy lists. Original data were not reanalysed (for supraspecific taxon replacement, see ‘a’ in the electronic supplementary material).
(b) Supertree analyses
Input trees were built using MacClade 4 (Maddison & Maddison 2005). Baum & Ragan's (1993) and Purvis' (1995) codings were employed to generate matrix representations of these trees and to build standard and Purvis MRP supertrees, respectively. In addition, we used the Baum and Ragan's matrix to generate a split-fit supertree (SFIT; Wilkinson et al. 2005b). Finally, we built a most similar supertree (MSS; Creevey et al. 2004) and a combined consensus of the standard plus Purvis MRP supertrees (for details of methods, see ‘b’ in the electronic supplementary material). All supertrees represent Majority Rule consensus topologies including minority components (see appendix 1b–f in the electronic supplementary material).
For the MRP analyses, we carried out two independent searches, using Quicke et al.'s (2001) strategy for estimating large phylogenies and Nixon's (1999) parsimony ratchet (implemented in perlRat.pl v. 1.0.9a; Bininda-Emonds 2004). Both of these methods produced trees of identical minimal length. A maximum of 100 000 trees were retained owing to computer memory limitations. A standard plus Purvis MRP supertree was built from 200 000 trees (i.e. using 100 000 trees from each of the standard and Purvis MRP analyses).
Methodological artefacts are common in phylogenetic reconstruction (e.g. Delsuc et al. 2005). As the standard and Purvis MRP methods show different properties and opposite shape-related biases (e.g. Wilkinson et al. 2005b), we conjecture that nodes present in the consensus of the combined standard plus Purvis MRP are less likely to be artefactual. Therefore, we regard this consensus (see appendix 1f and g in the electronic supplementary material) as the most conservative estimate of temnospondyl phylogeny, given available data, although it is obviously less resolved than both the standard and the Purvis MRP supertrees.
PAUP* v. 4.0b10 (Swofford 1998) was used to run all the parsimony analyses and to calculate consensus topologies. We employed the following programs: MIX (Felsenstein 2000) for the SFIT analysis (1000 random additions; threshold parsimony set to 1.8); Clann (Creevey & McInerney 2005) for the MSS analysis (default settings); and MeSA (http://www.agapow.net) to calculate Colless’ imbalance index (Colless 1995) for the standard MRP supertree.
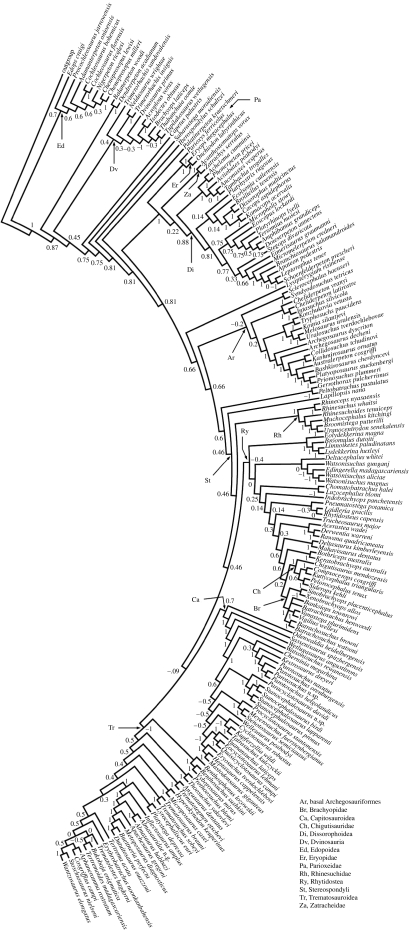
Node support, shown here only for standard MRP (figure 1) and for the consensus of standard plus Purvis MRP (see appendix 1g in the electronic supplementary material), is expressed using Wilkinson et al.'s (2005a) V1 index. Values of this index range from +1 to −1 and show different degrees of support between supertree and input trees, i.e. from complete support to total conflict. Our dataset is not amenable to input tree bootstrapping (Creevey et al. 2004; see also Burleigh et al. 2006) due to sparse taxon sampling (Moore et al. 2006).
Figure 1.
Standard MRP majority rule consensus supertree with minority components; V1 support values (Wilkinson et al. 2005a) are reported for each node.
Wilkinson et al. (2005b) have shown that biases occur in most supertree methods, and within the limits of feasibility, method dependence of results should be assessed. No approach exists for ranking a set of supertrees based upon their fit to the input trees (as in the standard Shimodaira's (2002) approximately unbiased test). Therefore, we employed a tree-based randomization test (see Rodrigo et al. 1993) to evaluate the degree of similarity of our supertrees (see appendix 1b–f in the electronic supplementary material; figure 1) relative to a set of random trees of identical size (i.e. having the same number of taxa). In PAUP*, we calculated pairwise tree-to-tree distances among our supertrees using Robinson & Foulds' (1981) symmetric difference. For two trees, the symmetric difference is the number of splits present on one tree but not on the other (a split is the partition of a set of taxa into two non-empty subsets; Thorley & Page 2000). We thus generated 1000 random trees of the same size as our supertrees (173 taxa) and calculated tree-to-tree distances for each pair of random trees. Finally, we plotted the distribution of these distances and tested whether our supertrees are more similar to one another than are 99% of the random trees. In addition, we used the Templeton (1983) test to assess whether topological differences among our supertrees are significant when evaluated against the standard MRP matrix. The application of this test is not dissimilar from that in character-based analyses. As used here, the test evaluates statistically significant differences in supertree topologies against a matrix in which ‘characters’ represent nodes in the input trees rather than biological traits.
(c) Diversification analyses
Chan & Moore (2002, 2005) and Moore et al. (2004) devised a tree topology-dependent method for detecting diversification rate shifts (i.e. significant changes in lineage branching, based upon differences in the number of taxa and degree of imbalance on the left and right branches subtended by tree nodes) and for calculating whole-tree tests of rate variations. This method is implemented in SymmeTREE v. 1 (http://www.phylodiversity.net/bmoore/software_symmetree.html). Briefly, in the triplet (A(BC)), the probability that a shift occurred along the internal branch that subtends BC is calculated through a statistic termed Δ1. This is expressed as a function of two likelihood ratios that compare the probabilities of obtaining observed differences in diversity at the internal and basal node of the triplet under a homogeneous (equal rate model, ERM) and a heterogeneous (unequal branching rates) diversification (for SymmeTREE search settings, see appendix 1h in the electronic supplementary material). A rate shift (if present) refers to the more speciose of the two branches that descend from a node for which Δ1 and associated p values are output. A difficulty with the application of SymmeTREE to cladograms incorporating extinct taxa is that the method, as currently implemented, assumes that the terminal taxa on the two branches descending from a node are of the same age (but note that SymmeTREE does not require information on the relative or absolute times of clade divergence; see Chan & Moore 2002, 2005; Moore et al. 2004). In an attempt to circumvent the problem of non-coeval terminal taxa, we adopted the following approach (but note that at present, there is no satisfactory solution to the problem of relaxing the time component for calculations of shifts). First, each of the five supertree topologies was ‘time sliced’ based upon occurrences of terminals in various stages. Second, SymmeTREE was applied to each pruned topology deriving from the original supertree following removal of terminals that are older than a given stage. All taxa used in this study are grouped by stage occurrences in appendix 1i in the electronic supplementary material (for alternative applications of tree ‘time slicing’, see Upchurch et al. (2002)). Attribution of taxa to stages is often problematic; as far as possible, we have taken into account revisions in the recent literature (e.g. Ward et al. 2006).
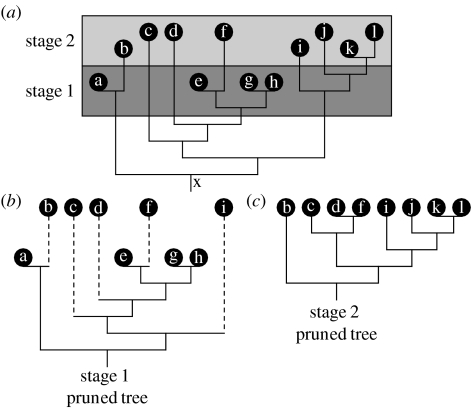
Figure 2 illustrates this approach. First, we considered all taxa that belong to a given stage and kept their relationships in the same relative order in which they appear in the supertree. We then deleted all taxa that belong to earlier stages, but included the ghost lineage extensions (see Norell 1992; Smith 1994) of taxa that belong to later stages. These ghost lineages imply unrecorded portions of temnospondyl phylogeny, based upon overall supertree shape, and thus add to overall taxonomic diversity for a stage. This procedure is repeated for all stages. If several taxa belong to a more recent stage (or stages) than the time interval being examined and form a monophyletic sister group to an older taxon (or an older group of taxa) in a supertree, then we assume that only one of these more recent taxa (the oldest if they differ in age) had its ghost lineage extended back in time to the stage of interest (figure 2). Similarly, if a more recent taxon (or groups of taxa) forms a paraphyletic array relative to an older taxon (or an older group), then we consider each of the more recent taxa (or groups of taxa) to have a ghost lineage extension.
Figure 2.
(a) Hypothetical tree consisting of taxa a–l plotted on a time scale with stages 1 and 2, illustrating the time-slicing approach (see text). (b,c) Pruned trees related to stages 1 and 2. The internal branches and most inclusive (more basal) nodes of the tree have been drawn mostly outside the two stages in which taxa a–l occur to avoid line crowding. In fact, the age of node ‘x’ subtending taxa a–l should be placed correctly in stage 1; as additional examples, the node subtending taxa c–h belongs to stage 1 while the node subtending taxa i–l belongs to stage 2.
To sum up, each pruned topology for a given stage consists exclusively of taxa that belong to that stage, to which we add ghost lineages for younger taxa. The age of the internal nodes in each pruned topology is based upon the original supertree, as explained in §2d.
Although the time-slicing approach removes taxa (and, therefore, tree shape information) that are older than those belonging to a given time interval, it satisfies the ERM requirements for the application of SymmeTREE. ‘SymmeTREE does not require information on the absolute/relative timing of internal nodes (divergences), [but] it does assume that [two] sister clades have had an equal opportunity to diversify, and this assumption is valid when all tips are coeval’ (M. Laurin & B. Moore 2007, personal communication).
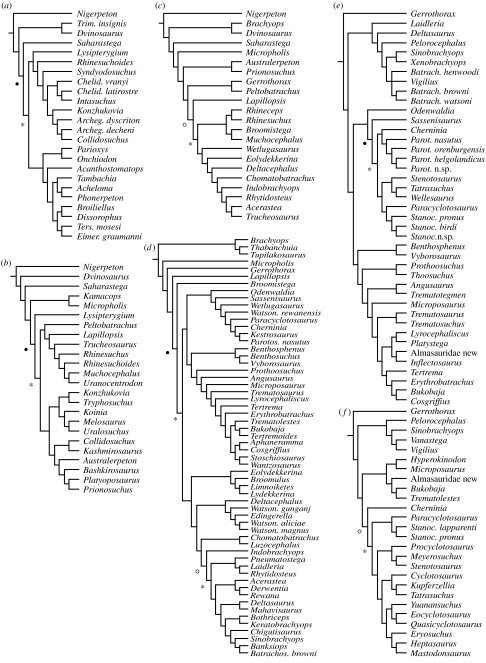
Figure 1 illustrates the standard MRP supertree. Appendix 1b–f in the electronic supplementary material shows supertrees obtained with other methods. The time-sliced standard MRP supertree is reported in figures 3 and 4 and in appendix 1j in the electronic supplementary material as a set of pruned topologies, one for each stage. Significant (p<0.05) and informative (0.05<p<0.1) shifts are indicated by filled and open circles, respectively. For brevity, we provide only results of SymmeTREE for the standard MRP supertree. Results for all other supertrees (as input MacClade and Excel files) are available upon request. Pruned topologies related to stages in which neither significant nor informative shifts were detected are shown in appendix 1j in the electronic supplementary material.
Figure 3.
Pruned, stage-related topologies deriving from the standard MRP supertree: (a) Moscovian and (b) Asselian. Stage names refer to the age of the terminal units plus ghost lineage extensions of younger taxa, such as are inferred from the supertree. Filled and open circles indicate significant and informative shifts, respectively. Asterisks mark branches along which a significant or informative change in lineage splitting takes place.
Figure 4.
Pruned, stage-related topologies deriving from the standard MRP supertree: (a) Sakmarian, (b) Kazanian, (c) Tatarian, (d) Induan, (e) Olenekian and (f) Anisian. Stage names refer to the age of the terminal units plus ghost lineage extensions of younger taxa, such as are inferred from the supertree. Filled and open circles indicate significant and informative shifts, respectively. Asterisks mark branches along which a significant or informative change in lineage splitting takes place.
(d) Node age and temporal distribution of shifts
In order to assign each node in the standard MRP supertree to a stage, we employed conservative fossil-based estimates of the time of origin of different temnospondyl groups. Thus, the age of a group is assumed to coincide with that of its earliest known, confidently assigned member. The age of a node connecting two sister groups is dated using the estimated age of the basal node of the older group. The earliest known members of each superfamily or family are all represented in our taxon sample. From the complete supertree, it is easy to derive minimum ages for all internal nodes in the stage-based pruned topologies. We note that in figure 2a, both internal branches and most inclusive (more basal) nodes of a hypothetical tree have been drawn mostly outside the two stages in which taxa a–l occur. This is to avoid crowding of lines in the illustration. However, based upon fossil estimates, the age of the most inclusive node ‘x’ subtending taxa a–l should be placed correctly in stage 1; as additional examples, the node subtending taxa c–h belongs to stage 1 while that subtending taxa i–l belongs to stage 2.
We calculated the mean of all the absolute Δ1 values (output in SymmeTREE) associated with internal nodes of the same age in a pruned topology; significant differences (if any) in |Δ1| means (one value of |Δ1| mean for each internal node age in a pruned topology) were assessed through a one-way ANOVA. This method is similar to that used by Jones et al. (2005) for supertrees that include extant terminals, and in which internal nodes are dated using either fossils or molecular clocks. We confine our discussion to pruned topologies that have direct relevance to the Permian extinction and pattern of post-extinction recovery (figure 4b–f).
3. Results
(a) Supertree shape and balance
The standard MRP supertree (figure 1), used only as a ‘guide tree’ for comparing distributions of branching shifts in various time intervals, is 620 steps long with 171 internal nodes and a Colless’ imbalance index of 0.168369. A Templeton test shows that the various supertrees (see appendix 1b–g in the electronic supplementary material) differ significantly from each other (p<0.0001) but are more similar to one another than a set of randomly generated trees of identical size (p<0.01). Note that the length of the supertree has the same meaning as in character-based analyses, i.e. the total number of character-state changes, where a change refers to a transition between node absence and node presence in the input trees. Node support for the standard MRP supertree is higher than that for other supertrees, except the combined standard plus Purvis MRP supertree.
Appendix 1k in the electronic supplementary material shows nodes common to all supertrees. Using the standard MRP as a reference, we identified each of its nodes with a pair of taxa bracketing the group subtended by the node of interest. Nodes that consist of the same taxa with the same mutual relationships as in the standard MRP are marked with tick marks. The topology of the standard MRP conforms largely to Milner's (1990) arrangement of major temnospondyl groups but contradicts Yates & Warren's (2000) alternative hypothesis of large-scale interrelationships. Three monophyletic groups of mostly Carboniferous and/or Permian species occur in order of increasing distance from the supertree root: Edopoidea, Dvinosauria and an assemblage of Parioxeidae, Eryopidae and Dissorophoidea. Two remaining groups complete the picture of temnospondyl diversity, namely the basal Archegosauriformes and the Stereospondyli. The latter are the most species rich of all temnospondyls and represent a predominantly Mesozoic (especially Lower and Middle Triassic) radiation. The stereospondyls consist of Rhinesuchidae, Rhytidostea, Capitosauroidea and Trematosauroidea (figure 1). For an overview of temnospondyls, the reader is referred to Milner (1990) and Schoch & Milner (2000).
(b) Temporal distribution of branching shifts
The temporal distribution of branching shifts is discussed with reference to stage-related pruned topologies derived from the complete standard MRP supertree (figures 3 and 4; see also appendix 1l in the electronic supplementary material). However, it is also useful to consider the age of the branch along which a particular shift takes place, as that branch may be older than the stage being examined. This is important for an assessment of differences in the temporal distribution of Δ1 values (see above). It is likewise useful to remember that if a node has undergone a rate shift (i.e. a significant change in lineage splitting), the shift itself is related to the more diverse of the two branches subtended by that node (Chan & Moore 2002, 2005). For instance, in figure 4d, the filled circle identifies a node with a significant shift, subtending all taxa comprised between Broomistega and Batrachosuchus browni. The shift proper has thus occurred along the branch (marked with an asterisk) including all taxa comprised between Odenwaldia and B. browni. The branch in question (or, more conveniently, the node at the end of the branch that is placed further away from the root of the tree) is Kazanian in age, as is the node marked by the open circle. In this example, terminal taxa (including range extensions for younger taxa) are Induan in age.
In this section, all branching shifts in each pruned topology are presented with reference to the stratigraphical stages in which terminal taxa occur in that topology (figures 3 and 4). For instance, the Induan pruned tree (figure 4d) shows Induan taxa as well as more recent taxa with a range extended back into that stage. In §3c, shifts are discussed with reference to the age of the branches on which they take place. Asterisks (figures 3 and 4) mark such branches.
SymmeTREE located the following nine shifts: one in the Carboniferous (Moscovian); four in the Permian (Asselian, Sakmarian, Kazanian and Tatarian); and four in the Triassic (two Induan, one Olenekian and one Anisian). In the Moscovian (figure 3a), a significant shift occurs along the branch subtending dissorophoids (Stegops to Doleserpeton). In the Asselian (figure 3b), an informative shift marks the group bracketed by Lysipterygium and Schoenfelderpeton. A significant shift in the Sakmarian (figure 4a) subtends basal archegosauriforms (Lysipterygium to Collidosuchus, but including also the early stereospondyl Rhinesuchoides) as well as a group consisting of eryopoids, parioxeids and dissorophoids (Parioxys to Eimerisaurus). The Kazanian is marked by a significant shift (figure 4b) along a branch that leads to an assemblage of archegosauriforms (Konzhukovia to Prionosuchus) and of peltobatrachids plus basal stereospondyls (Peltobatrachus to Uranocentrodon). In the Tatarian, an informative shift (figure 4c) is observed near the base of the stereospondyls (Rhineceps to Trucheosaurus). In the Induan (figure 4d), a significant shift marks the radiation of stereospondyls other than rhinesuchids (Odenwaldia to Batrachosuchus browni). In this radiation, two sister groups are recognized, i.e. rhytidosteans (Eolydekkerina to B. browni) and capitosaurians (Odenwaldia to Wantzosaurus). An informative shift within rhytidosteans occurs along the branch that subtends all taxa between Pneumatostega and B. browni. The last two shifts to be considered, in the Olenekian (figure 4e) and in the Anisian (figure 4f), underpin two radiations within capitosauroid stereospondyls (Cherninia to Stanocephalosaurus birdi and Paracyclotosaurus to Mastodonsaurus, respectively).
(c) Analysis of variance in the temporal distribution of shifts
The pruned topologies that have yielded shifts can now be looked at, in a more general way, as a frame of reference for investigating temporal variations in lineage splitting. For this purpose, we consider the differences in the |Δ1| means for each topology. We assess the overall significance of these differences through a one-way ANOVA and seek to pinpoint significant differences in pairwise comparisons of sampled |Δ1| values through a post hoc J. W. Tukey's (1953, unpublished manuscript) honestly significant differences (HSD) test. Where possible, we have lumped together samples of |Δ1| values for different stages, especially when only one or very few nodes in a pruned tree belong to a certain stage (as is generally the case for the most inclusive tree nodes).
For the Kazanian pruned tree (figure 4b), we have 15 Kazanian, 1 Sakmarian, 2 Asselian and 4 Moscovian nodes. Differences among the means of |Δ1| values, related to Kazanian, Sakmarian plus Asselian, and Moscovian, are marginally non-significant (F=3.4209; p=0.051758).
For the Tatarian pruned tree (figure 4c), there are 9 Tatarian, 6 Kazanian, 1 Asselian and 5 Moscovian nodes. Differences among means of |Δ1| values for Tatarian, Kazanian and Asselian plus earlier stages are significant (F=3.9422; p=0.038029), although a post hoc HSD Tukey's test does not highlight significant differences in any of the pairwise comparisons for the selected time intervals.
For the Induan pruned tree (figure 4d), ages of nodes are distributed as follows: 47 Induan, 6 Tatarian, 4 Kazanian, 1 Moscovian and 1 Viséan. Differences among means of |Δ1| values relate to Induan, Tatarian and Kazanian plus earlier stages and appear to be significant (F=17.1205; p<0.0001). A post hoc HSD Tukey's test shows that significant differences between means of |Δ1| values concern comparisons between Induan and Tatarian and between Induan and Kazanian plus earlier stages (p<0.01). More specifically, the mean |Δ1| value in the Induan is significantly lower than those associated with the other time intervals.
For the Olenekian pruned tree (figure 4e), node ages are distributed as follows: 18 Olenekian, 19 Induan, 2 Tatarian and 1 Kazanian. There are significant differences among the means of |Δ1| values for Olenekian, Induan and Tatarian plus earlier stages (F=3.9976; p=0.026567), and a post hoc test shows that the significant difference relates to the comparison between Olenekian and Tatarian plus earlier stages (p<0.05). In the Olenekian, the mean |Δ1| value is significantly lower than in the Tatarian plus earlier stages.
For the Anisian (figure 4f), node ages are distributed as follows: 13 Anisian, 2 Olenekian, 8 Induan and 3 Kazanian. Differences among means of |Δ1| values for Anisian, Olenekian and Induan plus earlier stages are not significant (F=3.0898; p=0.064783).
4. Discussion
(a) Branching shifts and secular diversification trends in temnospondyls
In the majority of pruned trees with Palaeozoic species (figures 3b and 4a–c), shifts take place along branches that connect major groups, thus marking the separation between distinct radiations. For example, the shift in figure 3b, dating back to the Moscovian, underpins the radiation of all post-edopoid and post-dvinosaur temnospondyls. The shift in figure 4a marks approximately the same radiation although the latter shows only a partial taxonomic overlap with that in figure 3b. Taken together, these shifts testify to the rapid diversification of some of the most diverse among all groups of Permo-Carboniferous temnospondyls. The shifts in figure 4b,c are observed near the base of stereospondyls. In these two figures, either a separation of basal archegosauriforms from basal stereospondyls or a split between basal and ‘higher’ stereospondyls (sensu Schoch & Milner 2000; see also Yates & Warren 2000) is highlighted.
The pattern of ‘between-groups’ shift distribution that characterizes most Palaeozoic pruned trees contrasts with a ‘within-group’ shift distribution in one Palaeozoic (figure 3a) and all of the Triassic (figure 4d–f) pruned trees. The Palaeozoic shift occurs within a subset of dissorophoids, whereas shifts in figure 4d–f underpin lineage-splitting events within assorted stereospondyls, in particular rhytidosteans and capitosauroids.
(b) Temnospondyls and the end-Permian extinction
The chronology of the four shifts in figure 4d–f (highlighted by asterisks) is interesting. Two of these shifts (figure 4e,f) took place in the Induan, one (figure 4d, open circle plus asterisk) in the Tatarian and one (figure 4d, filled circle plus asterisk) in the Kazanian. Together, the four shifts bracket narrowly the end-Permian extinction: in particular, the Induan shifts took place about half a million years after the extinction. This suggests that temnospondyls underwent a relatively rapid post-extinction recovery with the appearance of several new lineages shortly after their catastrophic decline (in terms of observed diversity values). However, the Late Permian shifts also testify to an increase in lineage splitting, which took place over a period of approximately 18 Myr before the extinction (an additional Kazanian shift is highlighted in figure 4e).
The pattern of temnospondyl diversification near the end of the Palaeozoic thus appears to be complicated by an interplay between multiple ‘background’ extinctions in the late Permian and a series of interspersed cladogenetic events. Milner (1990) noted that the Upper Permian record of temnospondyls includes late range extensions of Lower Permian groups, rather than early range extensions of Lower Triassic groups. This observation led Milner (1990) to argue in favour of an extinction-driven pattern of diversification and against a gradual decline in diversity throughout the Permian. A gradual decline would also imply a slow emergence of Triassic lineages, a model that is not supported by the explosive nature of the stereospondyl radiation and by the location of branching shifts in the Induan.
However, we note that diversification shifts occurred also on branches preceding the Permian extinction, as early as three million years before the extinction event proper. These finds may not be reconciled with Milner's (1990, p. 335) hypothesis of a ‘… cessation of appearance of families’ in the Upper Permian, for which Milner (1990) invoked taphonomic artefacts. In this scenario, extinction was responsible for the decimation of several Upper Permian temnospondyl groups in Laurasia. However, in Gondwana, some other groups survived into the Triassic. The distribution of shifts in relation to the geographical occurrences of taxa is noteworthy in this respect. Thus, several basal members that belong to groups underpinned by shifts in figure 4c,d are found in South Africa. Furthermore, most of the taxa in the bottom half of the tree in figure 4d occur in Gondwana.
The biogeographic implications associated with the distribution of shifts are that, although a large number of temnospondyls went extinct across Laurasia before the end-Palaeozoic, a series of speciation bursts occurred in rapid succession in the late Permian, which led to the appearance of several new families in the Southern Hemisphere. Dispersal probably involved spread into the southeastern portions of Gondwana and subsequent colonization of Laurasia. Additional work is needed to correlate shifts with profiles of observed and inferred (i.e. corrected with ghost lineage extensions) diversities for the group as a whole across the Permo-Triassic boundary. Research in progress suggests (although results are still preliminary) that the ‘burst’ of diversification in the aftermath of the end-Permian extinction is significantly mitigated by inclusion of ghost lineages. Furthermore, pre- and post-extinction shifts imply the occurrence of ‘pulses’ of diversification with a distinct geographical ‘fingerprint’. It will therefore be interesting to explore the impact of ancestral area distributions and dispersal routes on profiles of diversity across the Palaeozoic–Mesozoic transition.
Acknowledgments
This research is funded by NERC grant NE/C518973/1 to M.R. and M.J.B., Marie Curie Intra-European Fellowship MEIF-CT-2005-010022 and an award from the Center for Theoretical Physics of the University of Michigan both to D.P., and NERC studentship NER/S/A/2004/12222 to G.T.L. We thank Michel Laurin, Brian Moore and two anonymous referees for useful exchanges and constructive criticism.
Supplementary Material
The additional electronic resources consist of Supplementary Materials and Appendix. The Supplementary Materials include the following sections: (a) replacement of supraspecific taxonomic units; (b) brief descriptions of various methods of supertree construction and accompanying references to relevant literature. The Appendix includes the following sections: (a) list of source trees used in this study, accompanying references to relevant literature, and a note explaining which of the most recently published trees were excluded; (b–g) various supertrees built using different methods; (h) search settings in SymmeTREE applied to all supertrees; (i) temnospondyl species used in this study grouped by stage; (j) pruned trees derived from the standard MRP supertree and for which neither significant nor informative diversification rate shifts are found; (k) distribution of internal nodes common to all supertrees used here in tabulated format; (l) diversification shift statistics for pruned trees derived from the standard MRP supertree and for which significant and/or informative diversification rate shifts are detected
References
- Baum B.R, Ragan M.A. Reply to A. G. Rodrigo's “A comment on Baum's method for combining phylogenetic trees”. Taxon. 1993;42:637–640. doi:10.2307/1222541 [Google Scholar]
- Benton M.J. Thames & Hudson; London, UK: 2003. When life nearly died: the greatest mass extinction of all time. [Google Scholar]
- Benton M.J, Tverdokhlebov V.P, Surkov M.V. Ecosystem remodelling among vertebrates at the Permo-Triassic boundary in Russia. Nature. 2004;432:97–100. doi: 10.1038/nature02950. doi:10.1038/nature02950 [DOI] [PubMed] [Google Scholar]
- Bininda-Emonds, O. R. P. 2004 PerlRat.plversion 1.0.9a Program distributed by the author. Friedrich-Schiller-Universität Jena, Germany: Institut für Spezielle Zoologie und Evolutionsbiologie mit Phyletischem Museum.
- Bininda-Emonds O.R.P, Jones K.E, Price S.A, Cardillo M, Grenyer R, Purvis A. Garbage in, garbage out. Data issues in supertree construction. In: Bininda-Emonds O.R.P, editor. Phylogenetic supertrees: combining information to reveal the tree of life. Kluwer Academic Publishers; Dordrecht, The Netherlands: 2004. pp. 267–280. [Google Scholar]
- Burleigh J.G, Driskell A.C, Sanderson M.J. Supertree bootstrapping methods for assessing phylogenetic variation among genes in genome-scale data sets. Syst. Biol. 2006;55:426–440. doi: 10.1080/10635150500541722. doi:10.1080/10635150500541722 [DOI] [PubMed] [Google Scholar]
- Chan K.M.A, Moore B.R. Whole-tree methods for detecting differential diversification rates. Syst. Biol. 2002;51:855–865. doi: 10.1080/10635150290102555. doi:10.1080/10635150290102555 [DOI] [PubMed] [Google Scholar]
- Chan K.M.A, Moore B.R. SymmeTREE: whole-tree analysis of differential diversification rates. Bioinformatics. 2005;21:1709–1710. doi: 10.1093/bioinformatics/bti175. doi:10.1093/bioinformatics/bti175 [DOI] [PubMed] [Google Scholar]
- Colless D.H. Relative symmetry of cladograms and phenograms: an experimental study. Syst. Biol. 1995;44:102–108. doi:10.2307/2413487 [Google Scholar]
- Creevey C.J, McInerney J.O. Clann: investigating phylogenetic information through supertree analyses. Bioinformatics. 2005;21:390–392. doi: 10.1093/bioinformatics/bti020. doi:10.1093/bioinformatics/bti020 [DOI] [PubMed] [Google Scholar]
- Creevey C.J, Fitzpatrick D.A, Philip G.K, Kinsella R.J, O'Connell M.J, Pentony M.M, Travers S.A, Wilkinson M, McInerney J.O. Does a tree-like phylogeny only exist at the tips in the prokaryotes? Proc. R. Soc. B. 2004;22:2551–2558. doi: 10.1098/rspb.2004.2864. doi:10.1098/rspb.2004.2864 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delsuc F, Brinkmann H, Philippe H. Phylogenomics and the reconstruction of the tree of life. Nat. Rev. Genet. 2005;6:361–375. doi: 10.1038/nrg1603. doi:10.1038/nrg1603 [DOI] [PubMed] [Google Scholar]
- Erwin D.H. Princeton University Press; Princeton, NJ: 2006. Extinction: how life on Earth nearly ended 250 million years ago. [Google Scholar]
- Felsenstein, J. 2000 Phylipversion 3.6 alpha Seattle, WA: Department of Genetics, University of Washington.
- Jones K.E, Bininda-Emonds O.R.P, Gittleman J.L. Bats, clocks, and rocks: diversification patterns in Chiroptera. Evolution. 2005;59:2243–2255. [PubMed] [Google Scholar]
- Laurin M. The evolution of body size. Cope's Rule and the origin of amniotes. Syst. Biol. 2004;53:594–622. doi: 10.1080/10635150490445706. doi:10.1080/10635150490445706 [DOI] [PubMed] [Google Scholar]
- Maddison, D. R. & Maddison, W. P. 2005 MacClade4: analysis of phylogeny and character evolution version 4.08 OS X. Sunderland, MA: Sinauer Associates.
- Marjanovic D, Laurin M. Fossils, molecules, divergence times, and the origin of lissamphibians. Syst. Biol. 2007;56:369–388. doi: 10.1080/10635150701397635. doi:10.1080/10635150701397635 [DOI] [PubMed] [Google Scholar]
- Milner A.R. The radiations of temnospondyl amphibians. In: Taylor P.D, Larwood G.P, editors. Major evolutionary radiations. Clarendon Press; Oxford, UK: 1990. pp. 321–349. [Google Scholar]
- Moore B.R, Chan K.M.A, Donoghue M.J. Detecting diversification rate variation in supertrees. In: Bininda-Emonds O.R.P, editor. Phylogenetic supertrees: combining information to reveal the tree of life. Kluwer Academic Publishers; Dordrecht, The Netherlands: 2004. pp. 487–533. [Google Scholar]
- Moore B.R, Smith S.A, Donoghue M.J. Increasing data transparency and estimating phylogenetic uncertainty in supertrees: approaches using nonparametric bootstrapping. Syst. Biol. 2006;55:662–676. doi: 10.1080/10635150600920693. doi:10.1080/10635150600920693 [DOI] [PubMed] [Google Scholar]
- Nixon K.C. The parsimony ratchet, a new method for rapid parsimony analysis. Cladistics. 1999;15:407–414. doi: 10.1111/j.1096-0031.1999.tb00277.x. doi:10.1111/j.1096-0031.1999.tb00277.x [DOI] [PubMed] [Google Scholar]
- Norell M.A. Taxic origin and temporal diversity: the effect of phylogeny. In: Novacek M.J, Wheeler Q.D, editors. Extinction and phylogeny. Columbia University Press; New York, NY: 1992. pp. 88–118. [Google Scholar]
- Pisani D, Wilkinson M. Matrix representation with parsimony, taxonomic congruence and total evidence. Syst. Biol. 2002;51:151–155. doi: 10.1080/106351502753475925. doi:10.1080/106351502753475925 [DOI] [PubMed] [Google Scholar]
- Pisani D, Cotton J.A, McInerney J.O. Supertrees disentangle the Chimerical origin of eukaryotic genomes. Mol. Biol. Evol. 2007;24:1752–1760. doi: 10.1093/molbev/msm095. doi:10.1093/molbev/msm095 [DOI] [PubMed] [Google Scholar]
- Purvis A. A modification to Baum and Ragan's method for combining phylogenetic trees. Syst. Biol. 1995;44:251–255. doi:10.2307/2413710 [Google Scholar]
- Quicke D.L.J, Taylor J, Purvis A. Changing the landscape: a new strategy for estimating large phylogenies. Syst. Biol. 2001;50:60–66. doi:10.1080/106351501750107477 [PubMed] [Google Scholar]
- Robinson D.F, Foulds L.R. Comparison of phylogenetic trees. Math. Biosci. 1981;53:131–147. doi:10.1016/0025-5564(81)90043-2 [Google Scholar]
- Rodrigo A.G, Kelly-Borges M, Bergquist P.R, Bergquist P.L. A randomisation test of the null hypothesis that two cladograms are sample estimates of a parametric phylogenetic tree. N. Zeal. J. Bot. 1993;31:257–268. [Google Scholar]
- Ruta M, Coates M.I. Dates, nodes and character conflict: addressing the lissamphibian origin problem. J. Syst. Palaeontol. 2007;5:69–122. doi:10.1017/S1477201906002008 [Google Scholar]
- Ruta M, Jeffery J.E, Coates M.I. A supertree of early tetrapods. Proc. R. Soc. B. 2003;273:2107–2111. doi: 10.1098/rspb.2003.2524. doi:10.1098/rspb.2006.3577 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruta M, Wagner P.J, Coates M.I. Evolutionary patterns in early tetrapods. I. Rapid initial diversification followed by decrease in rates of character change. Proc. R. Soc. B. 2006;270:2507–2516. doi: 10.1098/rspb.2006.3577. doi:10.1098/rspb.2003.2524 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schoch R.R, Milner A.R. Pfeil; Munich, Germany: 2000. Handbuch der Paläoherpetologie: Teil 3B, Stereospondyli. [Google Scholar]
- Shimodaira H. An approximately unbiased test of phylogenetic tree selection. Syst. Biol. 2002;51:492–508. doi: 10.1080/10635150290069913. doi:10.1080/10635150290069913 [DOI] [PubMed] [Google Scholar]
- Simpson G.G. Columbia University Press; New York, NY: 1944. Tempo and mode in evolution. [Google Scholar]
- Smith A.B. Blackwell Scientific Publications; London, UK: 1994. Systematics and the fossil record: documenting evolutionary patterns. [Google Scholar]
- Swofford, D. L. 1998 PAUP*: phylogenetic analysis using parsimony (*and other methods) version 4.0b10 Altivec. Sunderland, MA: Sinauer Associates.
- Templeton A. Phylogenetic inference from restriction endonuclease cleavage site maps with particular reference to the evolution of humans and the apes. Evolution. 1983;37:221–224. doi: 10.1111/j.1558-5646.1983.tb05533.x. doi:10.2307/2408332 [DOI] [PubMed] [Google Scholar]
- Thorley J.L, Page R.D.M. RadCon: phylogenetic tree comparison and consensus. Bioinformatics. 2000;16:486–487. doi: 10.1093/bioinformatics/16.5.486. doi:10.1093/bioinformatics/16.5.486 [DOI] [PubMed] [Google Scholar]
- Upchurch P, Hunn C.A, Norman D.B. An analysis of dinosaurian biogeography: evidence for the existence of vicariance and dispersal patterns caused by geological events. Proc. R. Soc. B. 2002;269:613–621. doi: 10.1098/rspb.2001.1921. doi:10.1098/rspb.2001.1921 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vallin G, Laurin M. Cranial morphology and affinities of Microbrachis, and a reappraisal of the phylogeny and lifestyle of the first amphibians. J. Vert. Paleontol. 2004;24:56–72. doi:10.1671/5.1 [Google Scholar]
- Wagner P.J, Ruta M, Coates M.I. Evolutionary patterns in early tetrapods. II. Differing constraints on available character space among clades. Proc. R. Soc. B. 2006;273:2113–2118. doi: 10.1098/rspb.2006.3561. doi:10.1098/rspb.2006.3561 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward P, Labandeira C, Laurin M, Berner R.A. Confirmation of Romer's Gap as a low oxygen interval constraining the timing of initial arthropod and vertebrate terrestrialization. Proc. Natl Acad. Sci. USA. 2006;103:16 818–16 822. doi: 10.1073/pnas.0607824103. doi:10.1073/pnas.0607824103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilkinson M, Pisani D, Cotton J.A, Corfe I. Measuring support and finding unsupported relationships in supertrees. Syst. Biol. 2005a;54:823–831. doi: 10.1080/10635150590950362. doi:10.1080/10635150590950362 [DOI] [PubMed] [Google Scholar]
- Wilkinson M, et al. The shape of supertrees to come: tree shape related properties of fourteen supertree methods. Syst. Biol. 2005b;54:419–431. doi: 10.1080/10635150590949832. doi:10.1080/10635150590949832 [DOI] [PubMed] [Google Scholar]
- Yates A.M, Warren A.A. The phylogeny of the ‘higher’ temnospondyls (Vertebrata: Choanata) and its implications for the monophyly and origins of the Stereospondyli. Zool. J. Linn. Soc. 2000;128:77–121. doi:10.1006/zjls.1998.0184 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The additional electronic resources consist of Supplementary Materials and Appendix. The Supplementary Materials include the following sections: (a) replacement of supraspecific taxonomic units; (b) brief descriptions of various methods of supertree construction and accompanying references to relevant literature. The Appendix includes the following sections: (a) list of source trees used in this study, accompanying references to relevant literature, and a note explaining which of the most recently published trees were excluded; (b–g) various supertrees built using different methods; (h) search settings in SymmeTREE applied to all supertrees; (i) temnospondyl species used in this study grouped by stage; (j) pruned trees derived from the standard MRP supertree and for which neither significant nor informative diversification rate shifts are found; (k) distribution of internal nodes common to all supertrees used here in tabulated format; (l) diversification shift statistics for pruned trees derived from the standard MRP supertree and for which significant and/or informative diversification rate shifts are detected