Abstract
Intraspecific cooperation and interspecific mutualism often feature an asymmetry in the scope for exploitation. We investigate the evolution of indirect reciprocity in an asymmetric game, loosely modelled on interactions between cleaner fishes and clients, in which ‘actors’ can choose to help or to exploit a ‘recipient’ that approaches them, while recipients can only choose whether or not to approach an actor (based on the observation of its behaviour towards others). We show that when actors vary in state over time, in a manner that influences the potential gains from exploitation, an equilibrium is possible at which recipients avoid actors whom they have observed exploiting others in the past, and actors help when the potential gains from exploitation are low but choose to exploit when the potential gains are high. In this context, helping is favoured not because it elicits reciprocal altruism (‘help so that you may be helped’), but because it facilitates profitable exploitation (‘help so that you may gain the opportunity to harm’). The cost of helping one recipient is thereby recouped through exploitation of another. Indirect reciprocity is thus possible even in asymmetric interactions in which one party cannot directly ‘punish’ exploitation or ‘reward’ helping by the other.
Keywords: indirect reciprocity, image scoring, social prestige, altruism, asymmetric game, tactical deception
1. Introduction
Humans often help unrelated individuals even when it is unlikely that the recipient will reciprocate such favours in the future. Alexander (1987) proposed that apparently altruistic behaviour may prove beneficial under these circumstances if the helper gains an improved ‘image’, which increases the probability that some other individual will help the original helper in the future. Reciprocity in this case is not direct between helper and recipient but indirect between helper and third parties. Similarly, Zahavi (1995) and Roberts (1998) used Zahavi's handicap principle (Zahavi 1975) to argue that apparent altruism may serve as an honest signal of quality, which increases the ‘prestige’ of the helper, and may increase its mating success or encourage others to interact favourably with it.
The idea of ‘image scoring’ has been formalized by Nowak & Sigmund (1998a,b) and Leimar & Hammerstein (2001), who have shown that indirect reciprocity is indeed evolutionarily plausible (although it is necessary that changes in an individual's image or standing reflect not only whether or not it is seen to help, but also the standing of those whom it helps or refrains from helping). Similarly, Lotem et al. (2003) have modelled the idea of social prestige, demonstrating that when individuals vary in state, such that some find helping more costly than others, then those for whom the costs are low may profit by helping recipients that cannot reciprocate, because in doing so they advertise their state and thereby attract potential partners that are capable of reciprocation. Empirical support for indirect reciprocity among humans was first obtained in experiments conducted by Wedekind & Milinski (2000), who examined the behaviour of undergraduate students in a game based on the model of Nowak & Sigmund (1998a), and found that individuals who were more altruistic also received more help from others and ended up with a higher net pay-off than those who were less helpful (see Semmann et al. 2004, 2005 for further evidence).
The above models assume, however, that all players have similar behavioural options, and are thus capable of reciprocation. In reality, by contrast, many examples of intraspecific cooperation or interspecific mutualism feature marked asymmetries between partners in the opportunity for exploitation (see references in Bshary & Grutter (2002) and Bshary & Bronstein (2004)). The first evidence for image scoring in species other than our own, for instance, comes from work on a cleaning mutualism involving the cleaner wrasse Labroides dimidiatus (Bshary 2002; Bshary & D'Souza 2004; Bshary & Grutter 2006), in which opportunities for exploitation are entirely one-sided. In this mutualism, ‘client’ reef fishes visit cleaners at their small territories (cleaning stations) so that the latter may remove ectoparasites (reviewed by Côté (2000)). Conflict arises because cleaners prefer to eat client tissue and mucus rather than ectoparasites (Grutter & Bshary 2003). While cleaners do not exploit predatory clients in this way, non-predatory clients are often exploited (Bshary 2001), and a minority of cleaners may switch back and forth between a cleaning and a biting strategy (Bshary 2002; Bshary & D'Souza 2004). The clients in question lack the capacity to retaliate in kind. Nevertheless, a way to avoid cleaners in biting mood is to watch the interaction of a cleaner with its current client and to invite inspection if no conflict is observed but otherwise to avoid the cleaner. The Cleaners have up to 2300 interactions per day (Grutter 1995), so interactions often take place in the presence of bystanders that could gain the relevant information (i.e. they form part of a communication network in which eavesdropping is possible; see McGregor 1993, 2005). The experimental evidence supports the idea that clients pay attention to ongoing interactions as well as to the consequent prediction that cleaners should be more cooperative to their current client in the presence of bystanders (Bshary & Grutter 2006).
The cleaner wrasse example suggests that image scoring may be important even when helpful (or exploitative) acts cannot be directly rewarded (or punished) by third-party help (or exploitation), but instead influence whether or not an individual will gain the opportunity for further interactions. To address this possibility, we explore in §2 the dynamics of indirect reciprocity in an asymmetric game that is loosely based on cleaner–client interactions, but is relevant also to many other instances of intraspecific cooperation and interspecific mutualism that involve two distinct classes of traders, only one of which has the option to help or harm the other.
2. The model
Our model focuses on pairwise interactions between ‘actors’ (cleaners) and ‘recipients’ (clients), over a large number of rounds. In each round, actors and recipients are paired at random (we assume that the possibility of repeated encounters between the same two individuals is negligible), and the recipient in each pair decides whether to evade or to approach the actor. Evasion yields a pay-off of zero for both players; if the recipient approaches, the pay-offs that each obtain depend upon the subsequent behaviour of the actor, which may choose to ‘help’ or to ‘harm’.
The pay-off to the recipient is assumed to be positive if the actor helps and negative if the actor harms; the solution of the model depends only on the cost (to the recipient) of harm relative to the benefit of help, which we will denote c. The pay-off to the actor, however, depends not only on its action but also on its ‘state’ (which is not directly observable by the recipient). For simplicity, we assume that only two states are possible (1 or 2) and that there is some probability of switching between them from one round to the next; the probability of switching from state i to the alternative is denoted si (where 0<si<0.5). We will assume that harming the recipient yields an exploitative benefit to the actor, the magnitude of which is denoted xi when in state i; while helping entails a cost, the magnitude of which is denoted yi when in state i. We assume (without loss of generality) that the temptation to exploit is greater when in state 1, so that x1>x2.
Finally, we assume that if an actor harms a recipient in any given round, this is observed with probability e (where 0<e<1) by the recipient with whom it is paired during the next round.
(a) Solving the model
We are interested in the possibility of an equilibrium at which the behaviour of actors is conditional upon their state, such that they help recipients only when in state 2 (when exploitation is less profitable) and harm recipients only when in state 1 (when exploitation is more profitable), and in which recipients only approach an actor if it was not seen to harm a recipient in the previous round.
Suppose, then, that actors and recipients adopt these strategies. Let fi+(n) denote the probability that an actor is in state i at the start of round n and was not observed harming a recipient in the previous round; fi−(n) denotes the probability that an actor is in state i and was observed harming a recipient in the previous round. The probabilities f1+(n), f1−(n), f2+(n) and f2−(n) will then change from one round to the next according to the following difference equations:
| (2.1a) |
| (2.1b) |
| (2.1c) |
and
| (2.1d) |
Note that an actor that was observed harming a recipient in the previous round will not be approached, and therefore has no opportunity to harm a recipient in the current round. As a result, a ‘negative image’ cannot persist from one round to the next, which is why the expressions for f1−(n+1) and f2−(n+1) given in equations (2.1b) and (2.1d) contain no terms involving f1−(n) or f2−(n).
The above probabilities converge, over time, to the values
| (2.2) |
The pay-off to a recipient from approaching an actor that was not seen to harm its partner in the previous round thus converges to
| (2.3) |
while the pay-off from approaching an actor that was seen to harm its partner in the previous round converges to
| (2.4) |
Taking the long-term average pay-off per round (over a large number of rounds) as our measure of fitness, the conditional approach strategy adopted by recipients is therefore strictly optimal if and only if
| (2.5) |
To assess the stability of the conditional helping strategy adopted by actors requires slightly more calculation. In appendix A, however, we show that if we take the long-term average pay-off per round (over a large number of rounds) as our measure of fitness once again, then the conditional helping strategy is strictly optimal if and only if
| (2.6) |
Provided, therefore, that conditions (2.5) and (2.6) are both satisfied, an equilibrium does indeed exist at which actors help recipients only when in state 2 (when exploitation is less profitable) and harm them when in state 1, and at which recipients only approach an actor if it was not seen to harm its partner in the previous round.
(b) Impact of model parameters
Conditions (2.5) and (2.6) are less easily satisfied when x2 and/or y2 are larger relative to x1, implying that harming the recipient yields relatively larger benefits and/or helping entails relatively larger costs to the actor when in state 2. The reason for this pattern is intuitively obvious—the greater the temptation to exploit even when in state 2 (in which the benefits of exploitation are smaller), the less likely a strategy of conditional helping is to prove stable. In addition, conditions (2.5) and (2.6) are less easily satisfied when e is smaller, implying that harmful behaviour is less likely to be observed. The reason is once again clear—it is the possibility that harmful behaviour will be observed, leading to a negative image and hence to avoidance by recipients, that stabilizes helping; consequently, the greater the chance that harm will go unnoticed, the less likely a strategy of conditional help is to prove stable.
The impact of the other parameters, c, s1 and s2, is not so simple. If c, the cost of harm to a recipient (relative to the benefit of help), is too large, then it can pay recipients simply to avoid all interaction; conversely, if the cost is too small, then it can pay to approach any and all actors, regardless of their image. Conditional approach thus proves stable only for intermediate costs. Turning to the probability of switching states, increasing values of s1 and s2 favour conditional helping. Greater switching probabilities mean that an actor that helps when in state 2 (low temptation to exploit) and thereby attracts a recipient in the following round has a greater chance of switching to state 1 (high temptation) and gaining a large benefit from exploitation. On the other hand, if the probability of switching states is too high, then an actor's behaviour in the previous round provides a poor guide to its probable behaviour in the current round, and a strategy of conditional approach based on image is unlikely to prove stable.
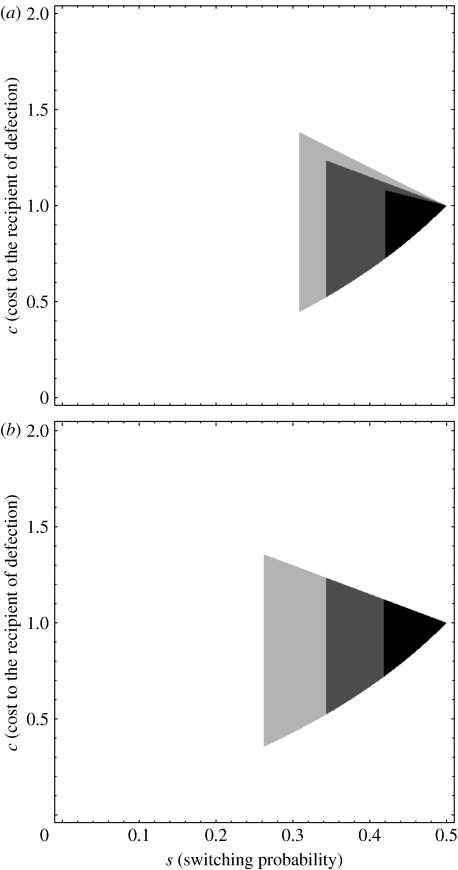
The above patterns are illustrated in figure 1, which focuses on the special case in which s1=s2=s, so that the probabilities of switching from each state to the other are the same, and actors consequently spend equal amounts of time (over the long term) in each state. Figure 1a shows the range of values of s (switching probability) and c (cost to recipients of harm, relative to the benefit of help) over which conditional helping and approach prove stable, for different values of e (the probability that harmful behaviour is observed), and figure 1b for different values of x2/x1 (the temptation to harm when in state 2 relative to that in state 1. Crudely, figure 1 shows that, as stated above, stability is most likely for intermediate values of c and s, and for higher values of e and lower values of x2/x1.
Figure 1.
Regions of parameter space in which conditional helping and approach are stable. (a) The range of values of s (the probability of switching state, here assumed equal for both states) and c (the cost to the recipient of harm, relative to the benefit of help) over which an equilibrium of the kind considered in the text proves stable, for three different values of e, the probability that harmful behaviour is observed: successively darker shading corresponds to successively lower values of e, 1, 0.75 and 0.5, respectively. In all cases, x2/x1=0.1 and y2/x1=0.05. (b) Equivalent regions of stability for three different values of x2/x1, the temptation to harm when in state 2 relative to that in state 1 successively darker shading corresponds to successively greater values of x2/x1, 0.05, 0.1 and 0.15, respectively. In all cases, e=0.75 and y2/x1=0.05.
3. Discussion
Our model shows that image scoring of individuals that have the potential to exploit their partners, by individuals that cannot retaliate but that control the occurrence of interactions, can indeed support a form of indirect reciprocity. Under these circumstances, potential exploiters may do best to refrain from exploiting current interaction partners when the benefits of doing so are smaller, and even to incur short-term costs by acting helpfully towards them, so as to avoid a negative image that would entail less scope for interaction in the future. Thus, indirect reciprocity is possible even when the capacity for exploitation is entirely one-sided, as in the interaction between cleaner wrasse and non-predatory clients described in §1 (and in many other asymmetrical relationships; see Bshary & Grutter 2002 and Bshary & Bronstein 2004). Note that under such circumstances, only members of the potentially exploitative class have an image or prestige.
We have previously shown that in such asymmetrical interactions, potential victims that lack the ability to retaliate against exploitation might nevertheless exert a degree of control over their partners' behaviour through their ability to terminate an encounter (Johnstone & Bshary 2002). The current model demonstrates an additional mechanism by which such apparently ‘powerless’ individuals may exert control. The two mechanisms are not incompatible, and it appears, for instance, that in the cleaning mutualism, clients employ both tactics, avoiding cleaners whom they observe exploiting others (Bshary & D'Souza 2004) and also terminating encounters earlier in response to exploitation (Bshary & Grutter 2002).
The form of indirect reciprocity we have analysed is different from that previously modelled, although it fits well the verbal arguments of Zahavi (1995) and Roberts (1998). Previous analyses have typically dealt with a single class of players who in principle have the same behavioural options (although they may play different roles on different occasions). In particular, all players are capable on at least some occasions of helping or harming a recipient, and all are on at least some occasions potential recipients of help (e.g. Nowak & Sigmund 1998a,b; Leimar & Hammerstein 2001; Lotem et al. 2003). Under these circumstances, helping behaviour is favoured (when possible) because it tends to elicit help from others. In our model, by contrast, ‘clients’ cannot choose to help or harm; it is always the ‘cleaner’ that determines the outcome of an interaction (whether it is beneficial or harmful for the cleaner itself and for the client). Cleaners do not, therefore, act helpfully in order to elicit help in turn from observers; rather, they do so to encourage clients to approach in the future, and thereby gain the opportunity for exploitation at a time when it will potentially be more profitable. This form of indirect reciprocity could be summed up, not as ‘help so that you may be helped’, but as ‘help so that you may gain the opportunity to (profitably) harm’. The costs of helping one client are, in our model, recouped only by exploiting another.
As the above description makes clear, the stability of this kind of indirect reciprocity depends on actors gaining occasional opportunities for exploitation. From the recipient's perspective, this implies that an actor's past behaviour must be an imperfect guide to its future actions. Since the actor's state may have changed, it cannot be relied on to refrain from exploitation simply because it was observed to do so before. Despite this risk, the frequency of exploitation at equilibrium may be low enough that on average it pays recipients to approach actors that have a positive image; at the same time, the benefits of occasional exploitation to actors outweigh the costs of the helping behaviour that attracts recipients, because exploitative behaviour tends to occur on those occasions when the benefit is greatest (it is worth emphasizing that helping when the potential benefits of exploitation are low cannot increase the overall frequency with which an actor is able to exploit recipients; rather, the strategy pays because it increases the probability that the actor is able to exploit when it is more profitable to do so). Thus, both actors and recipients benefit on average from their interaction.
Although occasional switching in state is necessary for the stability of indirect reciprocity of the kind described above, it cannot occur too frequently; there must be sufficient consistency in an actor's behaviour from one round to the next to make it worthwhile for recipients to attend to past actions when deciding whether or not to approach. Previous models of reciprocity, both indirect and direct, have stressed the need for variation in the propensity to cooperate in order to maintain conditional behaviour (e.g. Lotem et al. 1999; Sherratt & Roberts 2001; McNamara et al. 2004; Foster & Kokko 2006)—if no one ever cheats, there is nothing to be gained by behaving in a discriminatory manner, and reciprocators (of whatever form) can be replaced, through random drift, by naive cooperators. Most commonly, models have incorporated such variation in the form of occasional strategic mutation (e.g. Nowak & Sigmund 1997) or consistent inter-individual differences in ‘quality’ that supports a quality-dependent strategy (e.g. Lotem et al. 2003). Fewer analyses have concentrated on intra-individual variation in state that supports a state-dependent strategy (though see Leimar 1997 for a model of state-dependent direct reciprocity, and Leimar & Hammerstein 2001 for a partial analysis of a model of state-dependent indirect reciprocity). We have concentrated on such intra-individual differences in state, partly because there is evidence that these play a role in the cleaner wrasse mutualism (Bshary & D'Souza 2004), and partly because they are necessary (in the asymmetric context with which we are concerned) to account for the costly helping behaviour. While both inter- and intra-individual differences in the propensity of actors to exploit can favour conditional approach based on image by recipients, selection will not favour consistent helping on the part of an actor. As we have stressed above, helping is only favoured as a means to obtain the opportunity for profitable exploitation.
It is also worth pointing out that our treatment of individual variation in state differs slightly from that of most previous analyses. Existing models have mostly emphasized individual differences in the capacity to cooperate or help others, assuming that individuals may occasionally be unable to cooperate (e.g. Sherratt & Roberts 2001), or may find it more expensive to do so (e.g. Leimar & Hammerstein 2001; Lotem et al. 2003). This perhaps reflects the emphasis in Zahavi's (1975) and Roberts' (1998) discussions of apparent altruism as an honest and costly signal of quality. But the handicap principle is applicable to signals of need as well as of quality (Godfray 1991; Maynard Smith 1991) and, accordingly, we have emphasized state-dependent variation in the potential benefits of exploitation, rather than in the costs of helping (see Leimar & Hammerstein 2001 for a previous analysis of state-dependent benefits). In our case, helping behaviour signals not that an actor is of high quality (i.e. finds helping cheap), but that it currently has little need to engage in exploitation (perhaps because it is less hungry, for instance) and thus can be trusted to help rather than harm a recipient. In fact, condition (2.6) above implies that an equilibrium is only possible when the benefits of exploitation are state dependent; a state-dependent difference in the costs of helping alone cannot (given our model assumptions) support image scoring. We have also assumed that actors are always capable of exploitation, and stand to gain at least some immediate benefit thereby. In other words, there is always a temptation to cheat; it is only the magnitude of this temptation that varies according to state. Thus, actors do not merely forego exploitation when there is nothing to be gained thereby; it pays them to sacrifice the potential benefits of exploitation when these are positive but small, i.e. to engage in behaviour that in the short term is altruistic, in order to gain the opportunity for exploitation when the potential benefits are greater.
It is interesting to speculate that state-dependent helping, and changes in individual state, might account in a very simple way for some reports of tactical deception, in which an exploiter produces a signal to attract and exploit a bystander (Hauser 1997). Were internal changes in state apparent to the observer, it might emerge that the signal in some of these cases was not produced out of context. A potential exploiter, for instance, may simply cooperate as long as it is satiated but switch to exploitation as it becomes hungrier, giving rise to the appearance of tactical forethought. While one can argue that sudden changes in state are unlikely to occur, they might explain some of the largely anecdotal evidence for tactical deception in the primate literature (Byrne & Whiten 1988; Whiten & Byrne 1997). Although these observations have led to the development of the so-called ‘Machiavellian intelligence’ hypothesis, the notion that the complexity of social life has favoured the evolution of sophisticated social cognitive abilities like the capacity to use tactical deception (Byrne & Whiten 1988), several authors have argued that one must separate a phenomenon (i.e. the production of a signal out of context) from the mechanism that produces the phenomenon (Strum et al. 1997; Heyes 1998; Bshary et al. 2002). A switch in internal state would be one very simple mechanism that could lead to the production of signals seemingly out of context, without implying any understanding on the part of the signaller as to why that might yield benefits at the expense of the recipient.
We end by emphasizing that although our model was prompted by the cleaner wrasse mutualism, the same form of indirect reciprocity may operate in any other, similarly asymmetrical system. For instance, a case that has several similarities with our model is that of food calling by domestic cockerels. Often, such calls are produced when cockerels find a food source, and they offer the food to their hens. Hens never reciprocate such food sharing. However, cocks sometimes utter the call when there is no food and quite often copulate with approaching hens (Hauser 1997). This suggests a situation similar to that proposed in our analysis, in which the cockerels altruistically supply food, with no hope of reciprocation, in order to obtain the occasional opportunity for selfish mating. Our suggestion is that apparent altruism may often serve, not to elicit reciprocal help, but rather to facilitate subsequent exploitation of observers.
Acknowledgments
We thank Oistein Holen and Arnon Lotem for their helpful comments and discussion. This research was supported by NERC grant NER/A/S/2002/00898.
Appendix A.
Suppose that in the population under consideration, a rare mutant actor type arises, which harms when in state i with probability pi, and otherwise helps. Let denote the probability that such an actor is in state i at the start of round n and was not observed harming a recipient in the previous round, and let denote the probability that such an actor is in state i and was observed harming a recipient in the previous round. These probabilities change from one round to the next according to the difference equations
| (A1a) |
| (A1b) |
| (A1c) |
| (A1d) |
converging to the values
| (A2) |
The long-term average pay-off per round to the mutant therefore converges to
| (A3) |
Differentiating Wm with respect to p1, we find that
| (A4) |
which (since x1>x2) must be positive, so we may restrict our attention to mutants for which p1=1. Differentiating Wm(1, p2) with respect to p2, we then find that
| (A5) |
which is of the same sign as
| (A6) |
It follows that the established strategy of conditional help, for which p1=1 and p2=0, is strictly optimal if and only if
| (A7) |
as stated in the text.
References
- Alexander R.D. Aldine de Gruyter; New York, NY: 1987. The biology of moral systems. [Google Scholar]
- Bshary R. The cleaner fish market. In: Noë R, van Hooff J.A.R.A.M, Hammerstein P, editors. Economics in nature. Cambridge University Press; Cambridge, UK: 2001. pp. 146–172. [Google Scholar]
- Bshary R. Biting cleaner fish use altruism to deceive image scoring clients. Proc. R. Soc. B. 2002;269:2087–2093. doi: 10.1098/rspb.2002.2084. doi:10.1098/rspb.2002.2084 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bshary R, Bronstein J.L. Game structures in mutualisms: what can the evidence tell us about the kind of models we need? Adv. Stud. Behav. 2004;34:59–101. [Google Scholar]
- Bshary R, D'Souza A. Cooperation in communication networks: indirect reciprocity in interactions between cleaner fish and client reef fish. In: McGregor P, editor. Communication networks. Cambridge University Press; Cambridge, UK: 2004. pp. 521–539. [Google Scholar]
- Bshary R, Grutter A.S. Asymmetric cheating opportunities and partner control in a cleaner fish mutualism. Anim. Behav. 2002;63:547–555. doi:10.1006/anbe.2001.1937 [Google Scholar]
- Bshary R, Grutter A.S. Image scoring and cooperation in a cleaning mutualism. Nature. 2006;441:975–978. doi: 10.1038/nature04755. doi:10.1038/nature04755 [DOI] [PubMed] [Google Scholar]
- Bshary R, Wickler W, Fricke H. Fish cognition: a primate's eye view. Anim. Cogn. 2002;5:1–13. doi: 10.1007/s10071-001-0116-5. [DOI] [PubMed] [Google Scholar]
- Byrne R.W, Whiten A. Clarendon Press; Oxford, UK: 1988. Machiavellian intelligence. [Google Scholar]
- Côté I.M. Evolution and ecology of cleaning symbioses in the sea. Oceanogr. Mar. Biol. Annu. Rev. 2000;38:311–355. [Google Scholar]
- Foster K.R, Kokko H. Cheating can stabilize cooperation in mutualisms. Proc. R. Soc. B. 2006;273:2233–2239. doi: 10.1098/rspb.2006.3571. doi:10.1098/rspb.2006.3571 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Godfray H.C.J. Signalling of need between parents and offspring. Nature. 1991;352:328–330. doi:10.1038/352328a0 [Google Scholar]
- Grutter A.S. Relationship between cleaning rates and ectoparasite loads in coral reef fishes. Mar. Ecol. Prog. Ser. 1995;118:51–58. doi:10.3354/meps118051 [Google Scholar]
- Grutter A.S, Bshary R. Cleaner wrasse prefer client mucus: support for partner control mechanisms in cleaning interactions. Proc. R. Soc. B. 2003;270:S242–S244. doi: 10.1098/rsbl.2003.0077. doi:10.1098/rsbl.2003.0077 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hauser M.D. Minding the behaviour of deception. In: Whiten A, Byrne D.W, editors. Machiavellian intelligence II. Cambridge University Press; Cambridge, UK: 1997. pp. 112–143. [Google Scholar]
- Heyes C.M. Theory of mind in non human primates. Behav. Brain Sci. 1998;21:101–148. doi: 10.1017/s0140525x98000703. doi:10.1017/S0140525X98000703 [DOI] [PubMed] [Google Scholar]
- Johnstone R.A, Bshary R. From parasitism to mutualism: partner control in asymmetric interactions. Ecol. Lett. 2002;5:634–639. doi:10.1046/j.1461-0248.2002.00358.x [Google Scholar]
- Leimar O. Reciprocity and communication of partner quality. Proc. R. Soc. B. 1997;264:1209–1215. doi:10.1098/rspb.1997.0167 [Google Scholar]
- Leimar O, Hammerstein P. Evolution of cooperation through indirect reciprocity. Proc. R. Soc. B. 2001;268:745–753. doi: 10.1098/rspb.2000.1573. doi:10.1098/rspb.2000.1573 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lotem A, Fishman M.A, Stone L. Evolution of cooperation between individuals. Nature. 1999;400:226–227. doi: 10.1038/22247. doi:10.1038/22247 [DOI] [PubMed] [Google Scholar]
- Lotem A, Fishman M.A, Stone L. From reciprocity to unconditional altruism through signaling benefit. Proc. R. Soc. B. 2003;270:199–205. doi: 10.1098/rspb.2002.2225. doi:10.1098/rspb.2002.2225 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maynard Smith J. Honest signaling: the Philip Sidney game. Anim. Behav. 1991;42:1034–1035. doi:10.1016/S0003-3472(05)80161-7 [Google Scholar]
- McGregor P.K. Signaling in territorial systems: a context for individual identification, ranging and eavesdropping. Phil. Trans. R. Soc. B. 1993;340:237–244. doi:10.1098/rstb.1993.0063 [Google Scholar]
- McGregor P.K, editor. Animal communication networks. Cambridge University Press; Cambridge, UK: 2005. [Google Scholar]
- McNamara J.M, Barta Z, Houston A.I. Variation in behaviour promotes cooperation in the Prisoner's Dilemma game. Nature. 2004;428:745–748. doi: 10.1038/nature02432. doi:10.1038/nature02432 [DOI] [PubMed] [Google Scholar]
- Nowak M.A, Sigmund K. Tit for tat in heterogeneous populations. Nature. 1997;355:250–252. doi:10.1038/355250a0 [Google Scholar]
- Nowak M.A, Sigmund K. Evolution of indirect reciprocity by image scoring. Nature. 1998a;393:573–577. doi: 10.1038/31225. doi:10.1038/31225 [DOI] [PubMed] [Google Scholar]
- Nowak M.A, Sigmund K. The dynamics of indirect reciprocity. J. Theor. Biol. 1998b;94:561–574. doi: 10.1006/jtbi.1998.0775. doi:10.1006/jtbi.1998.0775 [DOI] [PubMed] [Google Scholar]
- Roberts G. Competitive altruism: from reciprocity to the handicap principle. Proc. R. Soc. B. 1998;265:427–431. doi:10.1098/rspb.1998.0312 [Google Scholar]
- Semmann D, Krambeck H.J, Milinski M. Strategic investment in reputation. Behav. Ecol. Sociobiol. 2004;56:248–252. doi:10.1007/s00265-004-0782-9 [Google Scholar]
- Semmann D, Krambeck H.J, Milinski M. Reputation is valuable within and outside one's own social group. Behav. Ecol. Sociobiol. 2005;57:611–616. doi:10.1007/s00265-004-0885-3 [Google Scholar]
- Sherratt T.N, Roberts G. The role of phenotypic defectors in stabilizing reciprocal altruism. Behav. Ecol. 2001;12:313–317. doi:10.1093/beheco/12.3.313 [Google Scholar]
- Strum S.C, Forster D, Hutchins E. Why Machiavellian intelligence may not be Machiavellian. In: Whiten A, Byrne D.W, editors. Machiavellian intelligence II. Cambridge University Press; Cambridge, UK: 1997. pp. 50–85. [Google Scholar]
- Wedekind C, Milinski M. Cooperation through image scoring in humans. Science. 2000;288:850–852. doi: 10.1126/science.288.5467.850. doi:10.1126/science.288.5467.850 [DOI] [PubMed] [Google Scholar]
- Whiten A, Byrne R.W, editors. Machiavellian intelligence II. Cambridge University Press; Cambridge, UK: 1997. [Google Scholar]
- Zahavi A. Mate selection—a selection for a handicap. J. Theor. Biol. 1975;53:205–214. doi: 10.1016/0022-5193(75)90111-3. doi:10.1016/0022-5193(75)90111-3 [DOI] [PubMed] [Google Scholar]
- Zahavi A. Altruism as a handicap: the limitations of kin selection and reciprocity. J. Avian Biol. 1995;26:1–3. doi:10.2307/3677205 [Google Scholar]