The use of site-directed fluorophore labeling and donor–donor energy migration to investigate solution structure and dynamics in proteins

Abstract

The use of molecular genetics for introducing fluorescent molecules enables the use of donor–donor energy migration to determine intramolecular distances in a variety of proteins. This approach can be applied to examine the overall molecular dimensions of proteins and to investigate structural changes upon interactions with specific target molecules. In this report, the donor–donor energy migration method is demonstrated by experiments with the latent form of plasminogen activator inhibitor type 1. Based on the known x-ray structure of plasminogen activator inhibitor type 1, three positions forming the corners of a triangle were chosen. Double Cys substitution mutants (V106C-H185C, H185C-M266C, and M266C-V106C) and corresponding single substitution mutants (V106C, H185C, and M266C) were created and labeled with a sulfhydryl specific derivative of BODIPY (=the D molecule). The side lengths of this triangle were obtained from analyses of the experimental data. The analyses account for the local anisotropic order and rotational motions of the D molecules, as well as for the influence of a partial DD-labeling. The distances, as determined from x-ray diffraction, between the C_α-atoms of the positions V106C–H185C, H185C–M266C, and M266C–V106C were 60.9, 30.8, and 55.1 Å, respectively. These are in good agreement with the distances of 54 ± 4, 38 ± 3, and 55 ± 3 Å, as determined between the BODIPY groups attached via linkers to the same residues. Although the positions of the D-molecules and the C_α-atoms physically cannot coincide, there is a reasonable agreement between the methods.

Many studies in structure biology and biochemistry depend on physical techniques to measure distances in macromolecules, such as proteins and nucleic acids. X-ray crystallography and multidimensional NMR spectroscopy are powerful methods for determining the three-dimensional structure. However, the former technique relies on the cumbersome preparation of crystals of high quality, and the NMR experiments suffer from spectral resolution as the proteins are larger. NMR is also relatively insensitive, typically demanding protein concentrations in the range of millimoles per cubic decimeter. As a consequence, questions concerning aggregation need consideration.

Electronic energy transfer between a donor (D) and an acceptor (A) molecule, so called donor–acceptor energy transfer (DAET, frequently also denoted by FRET), can be used to determine distances in macromolecules (1, 2). However, this requires the specific attachment of one donor, and one acceptor group within the same macromolecule. In practice, this is usually a very difficult task, which can be circumvented by a recently developed method based on site-directed fluorophore labeling and donor–donor energy migration (DDEM) (3). DAET and DDEM have the same physical origin (4), with the difference that DDEM is a reversible process. As a consequence for observing DDEM, fluorescence depolarization experiments must be performed whereas fluorescence lifetime experiments are sufficient for monitoring DAET.

In particular, Cys residues are useful for specific covalent attachments of fluorescent D-molecules in proteins. They allow for using sulfhydryl specific reagents, such as the BODIPY (Molecular Probes) derivative used in present work (see Fig. 1). From fluorescence depolarization experiments with DD-labeled proteins, the rate of DDEM can be extracted if proper account is taken for the influence of local anisotropic order and rotational motions of the D molecules, as well as the global rotation of the macromolecule (3). Independent information about rotational motions and order is determined from experiments with the D-labeled single Cys-mutated forms of the protein. The closer distances between the interacting D molecules, the faster is rate of energy migration and thereby the polarization decay. The DDEM method possesses similarities to the electron paramagnetic resonance methods previously described (5–9). The electron paramagnetic resonance methods are limited to determining distances shorter than ≈25 Å, which is, however, valuable because it complements the range of 20 to 100 Å, typically covered by the DDEM and DAET methods.

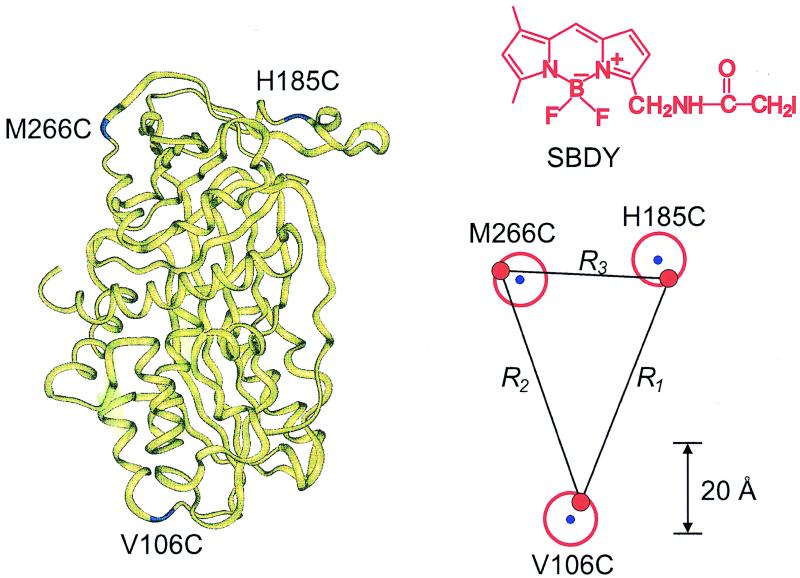
Figure 1.

Structure of latent PAI-1, illustrating the labeled Cys-mutated positions M266C, H185C, and V106C. The average distances (R₁ − R₃ in units of angstroms) obtained between the donors are indicated, and their positions are shown by red dots. The blue dots forming corners of the triangle denote the positions of the C_α-atoms of Cys-mutated amino acids. The red circle indicates a sphere that includes the center of mass of BODIPY. The structure formula of the sulfhydryl specific derivative of BODIPY (denoted by SBDY) is inserted.

In present work, we demonstrate an experimental approach to use the DDEM method for mapping the three-dimensional extension of a protein and for establishing structural changes induced by, for example, cofactors and specific target molecules. Three positions that form the corners of a triangle in the latent form of plasminogen activator inhibitor type 1 (PAI-1) were selected. Because PAI-1 lacks Cys, site-specific mutagenesis can be used to introduce unique specific positions as reactive sites for D-labeling. After a pairwise labeling of these positions, all side lengths of the triangle were obtained from DDEM experiments. The side lengths and angles obtained were in reasonable agreement with the distances determined from the known crystal structure (10).

Materials and Methods

Fluorescent Probe.

A sulfhydryl specific derivative of BODIPY, N-(4, 4-difluoro-5, 7-dimethyl-4-bora-3a, 4a-diaza-s-indacene-3-yl)methyl iodo-acetamide (SBDY) was used as the donor molecule (for the chemical structure, see Fig. 1.). SBDY is commercially available from Molecular Probes.

Construction, Expression, and Labeling of PAI-1 Cys-Mutants.

The plasmid pDL06(11) designed for expression of the human PAI-1 in Escherichia coli was used as the template DNA. Site-directed mutagenesis was performed by using the QuickChange site-directed mutagenesis kit (Stratagene). Two single PAI-1 mutants (V106C and M266C), and three double mutants (V106C-H185C, H185C-M266C, and M266C-V106C) were created. The construction of single mutant H185C has been described previously (3). The mutant proteins were expressed in E. coli strain SG20043 Δ lon⁻ and were purified to homogeneity as described (12). The activity of the mutants was tested by a chromogenic assay and by a stable complex formation with the urokinase type plasminogen activator (uPA) (3, 13). The inhibitory activity of the mutants was similar to that of the wild type of PAI-1. The fractions of double BODIPY-labeled mutants varied between 62 and 100%. The degree of labeling was obtained from the absorption spectra of BODIPY and the protein. Glycerol was added (50% wt/wt) to eliminate the influence of global rotational motion of PAI-1.

Fluorescence Measurements and Data Analysis.

The fluorescence spectra and steady-state anisotropies were determined on a SPEX fluorolog 112 instrument equipped with Glan-Thompson polarizers. The excitation and emission bandwidths were set to 5.6 and 2.8 nm, respectively.

The single photon counting experiments were performed on a PRA 3000 system (Photophysical Research, London, Ontario, Canada). The excitation source was a thyratron-gated flash lamp (Model 510C, Photophysical research) filled with deuterium gas and operated at ≈30 kHz. The excitation and emission wavelengths were selected by interference filters (Omega/Saven AB, Stockholm) centered at 500 nm (half bandwidth = 12.1 nm) and 550 nm (half bandwidth = 40 nm), respectively. The instrument response function was determined with a light scattering solution (LUDOX, Merck). Further details of the fluorescence depolarization experiments, as well as the analysis of data, are given elsewhere (3).

Theoretical Model

The most important equations used in the analysis of fluorescence anisotropy data are summarized below. A more elaborate presentation is given elsewhere (3, 14). The time-resolved fluorescence anisotropy decay [r(t)] of a partly labeled protein is described by the following equation:

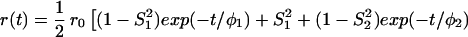1

In Eq. 1, the mole fraction of D-labeled Cys mutant is denoted by f_j. The subscript j (= 1 and 2) refers to numbering of the two D-molecules. The local orientational order of the BODIPY group is described by an effective order parameter (S_j, where −1/2 ≤ S_j ≤ 1,  j = 1 and 2). The parameter S_δ = (3cos²δ − 1)/2 describes the projection between effective symmetry axes of the two orientational distributions. The rotational correlation times of the D molecules are denoted by φ_j, and the limiting anisotropy, r₀ = 0.370 for the BODIPY fluorophore (13).

The probability that the excitation is located on the initially excited donor at a time t after excitation is denoted by ρ(t), and it is related to the rate of DDEM (ω) according to:

2

Eq. 2 is the first order cumulant approximation of the extended Förster theory of energy migration (15). Moreover, for the systems considered here,

3a

3b

Here τ, R, and R₀ denote the fluorescence lifetime, the distance between the center of mass of interacting D molecules, and the Förster radius, respectively. For BODIPY, R₀ = 57 ± 1 Å (13).

Results and Discussion

Three double Cys mutants of the latent form of PAI-1 (V106C-H185C, H185C-M266C, and M266C-V106C) as well as the corresponding single Cys mutants were studied. The location of these mutation sites is indicated in the structure of latent PAI-1, and the distances R₁, R₂, and R₃ are between the BODIPY groups that are attached to the mutated amino acids V106C-H185C, H185C-M266C, and M266C-V106C, respectively (see Fig. 1). The suitability of BODIPY as a donor molecule has previously been demonstrated (13). Here, a sulfhydryl-specific BODIPY derivative (SBDY, see Fig. 1) was used for the covalent labeling of PAI-1.

Local Rotational Motions and Order.

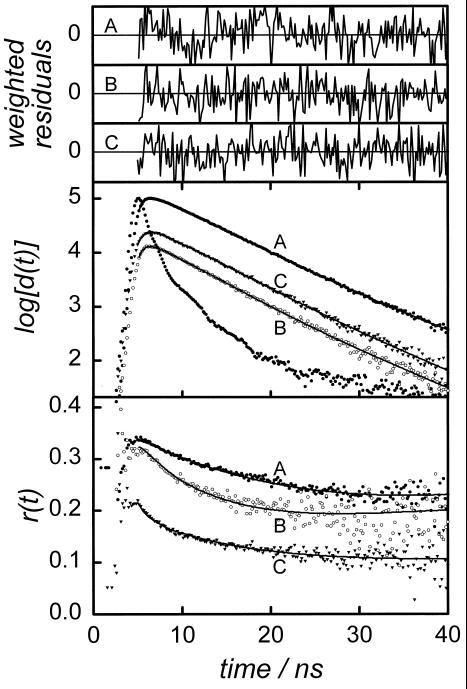
The time-resolved fluorescence anisotropy experiments with D-labeled PAI-1 show that the local rotational motions of the BODIPY group are slow in all mutants studied. This is obvious from a qualitative inspection of the anisotropy decays exemplified in Fig. 2 by the D-labeled H185C and M266C mutants of latent PAI-1. Typically, the rotational correlation times range between 7 and 12 ns (see Table 1). For all D-systems examined, the initial anisotropy value of r(0) ≈ 0.33 is significantly less than the limiting fluorescence anisotropy r₀ = 0.37 (13). The lower value is compatible with the presence of rapid rotational motions, presumably on the sub-nanosecond timescale, which is beyond the time-resolution of the experiments.

Figure 2.

Anisotropy decays [r(t); Bottom], difference curves [d(t); Middle]. and weighted residual-to-fit graphs (Top) obtained for the single mutants H185C (A), M266C (B). and the double mutant H185C-M266C (C) of latent PAI-1 at 277 K. A d(t) curve is defined by the difference in intensity of fluorescence light polarized parallel and perpendicular to the excitation polarization. The d(t) decays are used to judge on the quality of fittings to data, for which the weighted residuals range between −2 and +2.

Table 1.

The studied forms of latent PAI-1 are the double mutants V106C-H185C, H185C-M266C, and M266C-V106C and the corresponding single mutants V106C, H185C, and M266C

Mutant	rs	r(0)	φ/ns	ρ0	Sj	Sδ	ω/ns−1	〈κ2〉	R/Å	RC/Å
V106C	0.303	0.332	12  ±  1		0.80  ±  0.02
H185C	0.306	0.343	12  ±  1		0.78  ±  0.02
M266C	0.264	0.329	7  ±  1.5		0.69  ±  0.01
V106C-	0.272	0.340		0.81		0.17	0.6  ±  0.1	1.5	54  ±  4	60.9
H185C
H185C-	0.167	0.329		−0.26		−0.36	2.1  ±  0.3	0.6	38  ±  3	30.8
M266C
M266C-	0.22	0.333		0.40		0.06	0.4  ±  0.1	1.3	55  ±  3	55.1
V106C

The fluorescence steady-state anisotropy, the initial anisotropy, and the rotational correlation time are denoted by r_s, r(0), and φ, respectively. R and R_c denote the distance between the center of mass of the BODIPY groups and the C_α-atoms of the mutated amino acids obtained from the x-ray structure, respectively. The local order of the BODIPY moieties (j = 1 and 2) is described by the order parameter S_j, and S_δ accounts for the mutual projection of the symmetry axes of the local orientational distributions. ρ₀ is the maximum contribution to the fluorescence anisotropy from secondary excited donors. The rate of DDEM is ω, and 〈κ²〉 accounts for the angular part of dipole–dipole coupling. Further explanation to the notation is given in the text (see Theoretical Model) and elsewhere (3, 14). The results represent average values obtained from two to three experiments, using independently prepared samples. 

The local order of BODIPY (S_j) is strongly restricted, as is evident from the high values of the residual fluorescence anisotropy, exemplified in Fig. 2. As compared with the maximum value of S_j = 1, the values obtained range between 0.7 and 0.8, as can be seen from Table 1. A high order is compatible with an insertion of the BODIPY group into the PAI-1 molecule. Such a location is also expected because of a low solubility of BODIPY in water.

Fluorescence Relaxation of BODIPY.

To apply the theoretical model described above, the fluorescence relaxation of both donors needs to be very similar. For this reason, fluorescence lifetime experiments were performed with all labeled forms of mutants. A perfect description of the photophysics’ decay is obtained by fitting two lifetimes. A longer lifetime of ≈5.6 ns is dominating, and it contributes with >98% to the total fluorescence intensity whereas the remaining intensity is attributable to a lifetime component of ≈1 ns. The average lifetimes of all mutants are within 5.56 ± 0.09 ns. For SBDY or other BODIPY derivatives in liquid solutions, the shorter lifetime was not observed (13). No evidence for quenching of SBDY from neighboring amino acids was found.

Rate of DDEM and Intramolecular Distances.

The rate of DDEM (ω) within a DD-labeled Cys double mutant is determined from a global analysis of fluorescence depolarization data, which includes the relevant D-labeled single mutants. Further details about the analysis are given elsewhere (3, 16). Typical anisotropy decays obtained for one of the double mutants examined (H185C-M266C) and the corresponding single mutants (H185C and M266C) are displayed in Fig. 2. The more rapid initial decay of r(t) for the DD-labeled PAI-1 is compatible with intraprotein DDEM. The rates of DDEM determined for the different mutants, as well as the local motion and order, are summarized in Table 1.

In calculation of the intramolecular distance (R) from ω, account is taken for the angular part of dipole–dipole coupling (〈κ²〉), i.e., Eq. 3b. This depends on the local order parameters, which can be extracted from the residual plateau values of the anisotropy decays. To calculate R from Eq. 3a, the fluorescence lifetime is needed. A lifetime of 5.56 ± 0.09 ns was used, which was calculated as an average lifetime that included all samples investigated. Taking also local order parameters into account (Eqs. 1–3), we obtain the following intramolecular DD-distances (cf. Fig. 1): R₁ = 54 ± 4, R₂ = 38 ± 3, and R₃ = 55 ± 3 Å, which are summarized in Table 1. With the DDEM method, the distance between the center of mass of the interacting BODIPY cores is determined. Because these specific distances cannot be determined from the x-ray structure, a perfect agreement between the two methods cannot be expected. Nevertheless, the distances agree reasonably well with those of 60.9, 30.8, and 55.1 Å obtained from the x-ray structure of latent PAI-1. These distances were calculated between the relevant C_α-atoms of the amino acids in the wild type of latent PAI-1.

According to the law of cosines, the angle (α_ij) between any sides of a triangle can be calculated, provided all side lengths are known (R_i, R_j, and R_k). By using the side lengths obtained from the DDEM experiments, the angles were calculated and compared with those determined from the crystalline structure (see Table 2). The angles determined from the x-ray structure were those of the triangle that is defined by the C_α-atoms of V106, H185, and M266 of latent PAI-1. To further illustrate the triangle predicted by the DDEM method, it is compared with that defined by the C_α-atoms in Fig. 1. The red dots represent the spread in the center of mass of each BODIPY moiety. The blue dots are the positions of the C_α-atoms. Because the BODIPY groups are attached to the C_α-atoms by a linker, the overlap between the two triangles cannot, of course, be perfect. As shown in Fig. 1, the results of the DDEM method are compatible with the x-ray structure because the location of each BODIPY group is enclosed by the volume of a sphere centered at each C_α-atom with a radius equal to the length of the linker. The linker length is the average distance between a C_α-atom and center of mass of the BODIPY group. This distance was estimated to be 5.8 Å by using Monte Carlo simulations and an MM2 force field approximation (3).

Table 2.

Calculated angles (α₁₂, α₁₃, α₂₃) of a triangle obtained from DDEM experiments on the BODIPY-labeled latent PAI-1 Cys-mutants: V106C, H185C, M266C, V106C-H185C, H185C-M266C, and M266C-V106C

From R1, Å	DDEMR2, Å	Experiments R3, Å	Calculated angle (°) from DDEM	Calculated angle (°) from x-ray
54 ± 4	38 ± 3	55 ± 3	α12 = 68 ± 12°	85.3°
54 ± 4	38 ± 3	55 ± 3	α23 = 71 ± 13°	64.5°
54 ± 4	38 ± 3	55 ± 3	α13 = 41 ±  6°	30.2°

The results are compared to angles determined from the crystalline structure of latent PAI-1 (10). The triangle considered in the x-ray structure is defined by the positions of the C_α-atoms of the amino acids V106, H185, and M266. R_j(j = 1, 2, and 3) are the distances defined in FIg. 1. The three angles (α_ij) were calculated by in different ways combining the R_j distances (shown in the column to the left) in the law of cosines. 

Comparing Distances Determined with DDEM and X-Ray Methods.

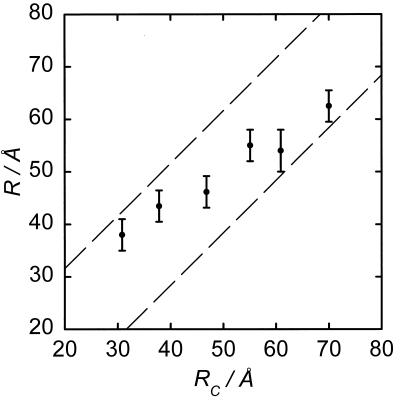
In addition to the present results, several distances in PAI-1 (3, 16) have been measured by using SBDY and DDEM. The distances determined, which range between ≈30 and 70 Å, are plotted as a function of the distance between the correspondingly labeled C_α-atoms (see Fig. 3). For a perfect agreement, a straight line with the slope of 45° is expected, which is obviously not the case. However, as was pointed out in the previous paragraph, the reference positions (i.e., the C_α-atoms) are physically distinct from those of the BODIPY core. Hence, the possible displacement between the BODIPY core and the C_α-atom involved is limited by a sphere with a radius of ≈5.8 Å for SBDY. If account for possible deviations is taken, the actually allowed distances are between the two dashed lines in Fig. 3. Thus, deviations between all distances obtained with the DDEM and x-ray methods are geometrically allowed.

Figure 3.

Distances (R) obtained with the DDEM method (●) for various of SBDY-labeled Cys double mutants of PAI-1 at 277 K. The distances (R_C) between the corresponding C_α-atoms calculated from the x-ray structure of latent PAI-1 are given on the abscissa. The area between the dashed lines represents possible DD-distances calculated when account is taken for the maximum distance from C_α-atoms to the center of mass of the BODIPY core. The errors are based on averages over two to three independent experiments with new preparations.

Applications Using DDEM.

To explore the geometrical extension of a protein molecule, it is appropriate to label Cys-mutated amino acids located at the protein surface. The principles for this are given in present study whereas a detailed description is found elsewhere (3, 16). For a protein of unknown structure, the surface-located amino acids are usually not known from the primary structure. It means one has to combine a trial-and-error approach with independent information, such as sequence homologies with related proteins for which the structure is known. This may be time consuming, which is, however, often also the case when using NMR and x-ray techniques, which involve far from rapid and straightforward procedures.

For D-labeling of amino acids located in the interior of a protein, small and preferentially hydrophobic fluorophores would be useful. With the BODIPY fluorophore, distances typically between 30 and 70 Å can be determined. However, it is valuable to measure shorter as well as longer distances. For this purpose, a variety of different donors are needed. Currently, we are investigating new fluorescent derivatives suitable for DDEM experiments with proteins.

The present study clearly demonstrates a potential applicability of the DDEM method in exploring protein structures. Although the DDEM method cannot provide distances with atomic resolution, the present work strongly supports its applicability for exploring the overall geometry of protein structures. For instance, in the case of PAI-1, the outlined approach is currently being used to reveal whether there are any major structural differences between the latent and active forms of PAI-1. To answer this question, the DDEM method appears valuable because, hitherto, all attempts to prepare crystals of the active form of wild-type PAI-1 have failed. In ongoing research, the method is also used to establish structural changes of PAI-1 as well as its localization in complexes formed with plasminogen activators (17).

Abbreviations

DDEM

donor–donor energy migration

PAI-1

plasminogen activator inhibitor type 1

DAET

donor–acceptor energy transfer

SBDY

N-(4, 4-difluoro-5, 7-dimethyl-4-bora-3a, 4a-diaza-s-indacene-3-yl)methyl iodo-acetamide