Odor space and olfactory processing: Collective algorithms and neural implementation

Abstract

Several basic olfactory tasks must be solved by highly olfactory animals, including background suppression, multiple object separation, mixture separation, and source identification. The large number N of classes of olfactory receptor cells—hundreds or thousands—permits the use of computational strategies and algorithms that would not be effective in a stimulus space of low dimension. A model of the patterns of olfactory receptor responses, based on the broad distribution of olfactory thresholds, is constructed. Representing one odor from the viewpoint of another then allows a common description of the most important basic problems and shows how to solve them when N is large. One possible biological implementation of these algorithms uses action potential timing and adaptation as the “hardware” features that are responsible for effective neural computation.

More is different (1). There are fundamental differences between the behaviors of small systems made from elementary components and the behaviors of large ones made from the same components. Large systems can have collective properties that are not displayed in small ones—e.g., the sharp boiling point of a liquid. Buck and Axel (2, 3) recently discovered that rodents have ≈2,000 olfactory receptor genes, and each receptor cell expresses only one of them. The large number of receptor cell types introduces the possibility of algorithms explicitly based on that fact.

The generalist olfactory system is believed to recognize a particular odor by the pattern of excitation that the odor generates in the olfactory receptor cells (4–8). The mathematical nature of this pattern recognition has not been well described. The visual determination of color is its closest analogy in well understood sensory processing. The color of a uniform visual field presented immediately after seeing a normal color scene‡ is determined by the relative excitation strengths of the red, green, and blue cones. Recognizing a color independent of light intensity is like recognizing an odor independent of the odor strength. I believe that this analogy to color vision misleads because the large number of odor receptor cell types allows computational algorithms and the use of neural hardware in ways that would not be effective in a system having only a small number of receptor cell types. My thesis is that in olfaction more, once again, is different.

As Marr (9) emphasized, it is useful to separate the analysis of a sensory system into several stages. I thus begin with a description of the problems that must be solved by the olfactory system and the sensory information available to it. From this, I construct a representation of the problems that shows how to solve them simply when the number of receptor types is large. Finally, I show how a transformation that is key to solving the most difficult-seeming of the problems can be directly accomplished by a population of adapting neurons.

Computational Problems of Olfaction.

A highly olfactory animal uses odor both as a proximal sense and for remote sensing. For remote objects, an animal uses scents brought by the wind to identify the direction and approximate distance of odor sources. It can remember odors for comparison and identification, can identify known components in mixtures, and can separate a mixture of unknown odors into individual odor objects. Basic computational tasks that must be performed include:

1.  Odor memory and recognition. The scent of an isolated object (i.e., one dominating the olfactory scene) must be stored so that the object can later be recognized independent (approximately) of odor intensity. The time-varying odor intensity, due to turbulent mixing or active exploration, is also an essential measurement for guiding behavior.

2.  Background elimination. When a weak known odor is thoroughly mixed with an unknown background, the known odor can be identified and its intensity measured.

3.  Component separation. When a few known odors are thoroughly mixed (eliminating relative fluctuations), an animal can identify the component odors and their intensities.

4.  Odor separation. When odors from different objects are mixed by air turbulence, the fluctuations of the relative contributions to the mixture can be used to separate the odors of multiple unknown objects in the environment.

Only by understanding how all these tasks can be performed, in the presence of defective data due to residual adaptation or residual odorant binding to many of the sensory cell types, can I understand the ordinary behaviors of highly olfactory animals. Studies of olfactory processing most often emphasize the first and most elementary of these tasks. Simple methods of solving the first task are generally incapable of dealing with the set of essential problems. Other tasks such as olfactory hyperacuity (e.g., distinguishing between the urine of two genetically similar animals) lie beyond the scope of the present analysis.

The Logarithmic Distribution of Odorant Binding Constants.

The threshold for the perceptual detection of pure compounds varies over an immense range (11). In a study of 529 odorants (12), the distribution of the logarithms of binding constants was approximately Gaussian (i.e., the distribution of free energies of binding is Gaussian.) The ± 2σ range within which most olfactants lay was 6.8 log10 units, with the extremes separated by 10 log10 units. Detection necessitates the binding of odorants to receptor proteins. To reach the threshold of detection of a particular pure odorant, some minimal coverage, cov_min, of the odorant receptors of a given type (or more probably, a few types) will be necessary. If I assume that cov_min is the same for all odorants, then the range of thresholds reflects the range of binding constants. There is no direct experimental information as to whether cov_min is the same for all odorants, for few binding constants have been measured (13).

Each glomerulus receives axons from a single type of receptor cell (2, 3). The pattern of excitation across the glomeruli describes an odor. To understand such patterns, it is necessary to describe the binding constants of a particular ligand for receptors that do not bind it maximally. Because the best-fit ligand-receptor pairs have a range of binding free energies of 9 kcal and of range of binding constants of >10⁶, the same kind of stereochemistry should produce a similar range of binding constants and binding free energies below the maximal ones. While odors differ markedly in behavior, there is a typical psychophysical range of a factor of, 1,000 over which the odor seems to have the same quality, and over which the relationship between the perceived intensity and the actual concentration is approximately a low power law or logarithmic. An odor presented at the concentration where nonlinearities begin drives the cells having the highest affinity receptors into response saturation. For this driving strength, I would expect, from the above numbers, that ≈1/3 of the cell types would show responses to that odorant and ≈2/3 would show no obvious response at the individual cell level. Glomeruli pool information from many receptor cells, which can presumably extend the system dynamic range to lower concentrations.

There is no quantitative summary of experimental information in this regard. Threshold concentrations for a single receptor cell for different odorants have been measured as different as a factor of 1,000, and, often, a cell simply does not respond to an odor. Assays are available from studying responses of many cells for an array of odorants, both by conventional electrophysiology (4) and by cell biology techniques (8). For the concentrations of odorants used, 1/4–1/2 of the cells showed some level of response to a particular odorant. These qualitative experiments are similar to the expectations described in the previous paragraph.

Modeling Pure and Mixed Odors.

A specific model of binding constant distributions is used for analysis. I assume that a glomerulus has a dynamic range§ of 1,000 in odorant concentration and that the probability distribution of binding constants of the less-than maximal cell classes is uniformly spread (on a log scale) over a range 10⁶ below the binding constant of the most sensitive cell type. However, while the model is specific, most of the qualitative conclusions of the present analysis rely chiefly on the model being consistent with the experimental fact seen directly in the data of Sicard and Holley (4) and of Malnic et al. (8), namely that, for unrelated odorant pairs a,b, there will be hundreds of cell types that respond chiefly to a, hundreds that respond chiefly to b, and hundreds more that respond to both.

I presume that the receptor cell sends a signal related to its ligand coverage and that the ligand coverages due to different ligands are additive. However, the real situation is much more complicated than the modeling. The responses may not be additive. The latency of sensory cell response can be odorant specific. The mucous layer and the proteins it contains may play some role in kinetics and in odorant clearance. The situation is reminiscent of the depth perception computation in vision. There are at least five different computations that are involved, including binocular stereopsis, shape from shading, linear perspective, occlusion, and structure from motion. While the neural hardware for these may be shared, at the algorithmic level, they are very different. Visual studies have gained much by analyzing each separately. Similarly, for olfaction, it is useful to analyze how concentrations and binding can be used alone.

At threshold concentration c_thres,λ of ligand λ, only one glomerulus responds in a minimally detectable fashion. This glomerulus has a coverage of cov_min, so it has a binding constant of cov_min/c_thresh,λ. The coverages of all other receptor cell types will lie in a range of 10⁶ below the cov_min, which is reached by the most responsive cell at concentration unity. When the concentration is raised to 10 c_thres,λ, then 1/6 (2,000) = 333 glomeruli should respond. These glomeruli correspond to cell types that happen to have their binding constants in the range of 0.1–1× the binding constant of the most strongly binding cell types. As the concentration is raised further, more cell types respond, until at concentration 1,000 (in units of the threshold concentration), about half of the glomeruli types will be responding.

Unrelated molecules have no particular relationship of their binding contacts and binding energies for a given receptor type. Each glomerular type is independently assigned binding constants for each odorant by the prescription above. Odors can be related, either because they have dominant chemicals of similar structure (e.g., ethanol and isopropanol) or because they are mixtures in different ratios of the same chemicals (orange and tangerine). While related odors can be described within the present context, doing so requires knowing details of the mixtures and the binding patterns of receptors.

Statistical Response Patterns for Tasks 1–3.

An appropriate representation of a problem is essential to understanding procedures or algorithms than can solve the problem. I develop a representation that describes an odor-induced excitation pattern across glomeruli from the viewpoint of a target odor. For simplicity, let the target, t, be a single odorant species, and the background be a different single species, b. Following the odor model above, the coverage of receptors of type i in the presence of concentrations c_t and c_b is given by

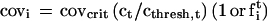1

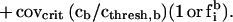In the first term parenthesis, a 1 is used if it happens that i is the glomerulus that maximally binds t, and otherwise an f^t_i is chosen at random in the range between 1 and 10⁻⁶, with a uniform probability distribution in the logarithmic domain. The same is true for the second parenthesis and odorant b.

The response of a sensory cells and glomeruli to the coverage should be a monotonic increasing function that is “known to the system.” For a known odor t, this means that the system has implicit knowledge of c_thresh,t and f^t_i. If only odorant t is present, then, from each glomerulus i that is appreciably driven, the system can “calculate” the concentration, c_t, from Eq. 1. When an unknown odor, u, is presented that generates a pattern of coverage, cov^u_i, then, for each i that would be driven by the target odor, we can calculate the concentration of t that would yield that level coverage for cells of type i, namely

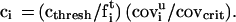2

c_i is the apparent concentration of t deduced from the saturation level caused by the unknown odorant in a single channel i. The observation of cov^u_i is a “vote” for the presence of t at concentration c_i.

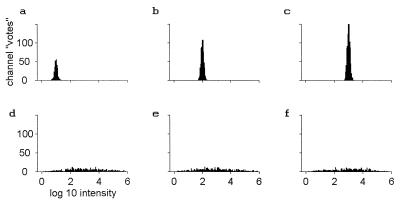
Fig. 1 a–c shows histograms of all the votes c_i when odor u is in fact t, presented at a concentration 10, 100, and 1,000 (in units of the threshold concentration). A logarithmic scale is used because of the large range of concentrations involved. This scale is also particularly apt for systems that show an approximately logarithmic response as a function of intensity, as many sensory systems do. A glomerular Gaussian noise level of ±26% (±0.1 log10 units) introduces width to the histograms¶. Because the unknown odor u is in fact t, each channel deduces (within noise) the correct concentration from its value of cov^u_i. Of the 2,000 receptor cell types, ≈333, 667, and 1,000 are driven to observable levels by odorant t at these concentrations respectively, corresponding to the total numbers of votes. The concentration of t can be read from the peak positions, located as expected. As the concentration is decreased another decade, the number of responding glomeruli approaches one.

Figure 1.

Histograms of the number of glomerular channels that vote for various dimensionless intensities (or concentrations) of the target odor. Units of odor strengths are on a logarithmic scale; one unit is a factor of 10 in intensity. Threshold intensity for an odorant corresponds to intensity 1, logI = 0. (a–c) The target odor itself at concentrations of 10, 100, and 1,000. (d–f) Three different nontarget odors at concentrations of 1,000.

Fig. 1 d–f shows histograms of the same sort, using the same 1,000 channels that are potentially activated by t but calculated for three different odors, b, unrelated to t, each at its saturation level of 1,000c_thresh,b. Only those having more than the minimal detectable coverage respond. For each channel, there is a probability of 0.5 of this occurring. Because there is no relationship between k_u(n) and k_t(n), there is a wide spread of events within these histograms, and no sharp peak. A histogram for a weaker presentation of b would be similar, but with fewer events.

Target and nontarget odors are highly distinguishable in this representation. Even when the target odor is at a strength of only at 3c_{thresh, t} the peak in such a histogram for odor t alone has ≈150 votes spread over a total concentration range of 0.4 on a logarithmic scale. The probability that an unrelated odor u at a concentration 1,000c_thresh,u produces a total number of events >100 in such a range is less than 10⁻⁶. When the target odor t is at strength 10c_thresh,t, it becomes astronomically unlikely to confuse t with a random strong odor. In this representation, task 1 (pure odor recognition) can be solved by merely thresholding the total number of votes in a bin of appropriate width.

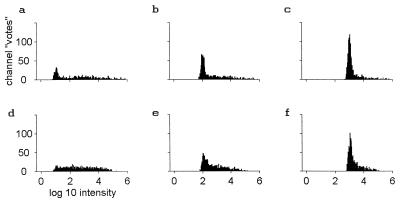
Task 2 (background elimination) is examined in Fig. 2 a–c. These histograms were generated from an odor mixture in which the target odorant at strengths 10, 100, and 1,000c_thresh,t is mixed with an unrelated background odorant b at strength 1,000c_thresh,b. The area of the peak in the histogram is decreased, but a simple threshold on the number of events in a suitable bin width will still distinguish between when the target odor is present and when it is not. The target begins to be detected when its concentration is greater than 3c_thresh,t, even in the presence of the saturating concentration of an unknown odor. Task 2 can be solved by the same means as task 1.

Figure 2.

Histograms as in Fig. 1 a–c, but with the simultaneous presence of a background of strength 1,000c_thresh,b. d–f have a more complex background of total strength 400 in terms of the relevant thresholds, made up of an equal mixture of four nontarget odors.

The statistics of large numbers and the chance occurrence of non-interference make identification in the presence of strong unknown odors possible. No glomerulus is specific—each has a probability of 0.5 of being at least somewhat activated by a saturating concentration of any odor. This translates to ≈333 channels being noticeably driven when odor t alone is presented at low concentration, 10c_thresh,t. However, each channel also has a probability of 0.5 of being negligibly driven by odor b at strength 1,000c_thresh,b. Thus, ≈167 ± 13 channels are still expected to respond to t at concentration 10c_t in essentially the same way as they would have in the absence of the unknown background odor, and many more will do so at higher c_t. These channels are responsible for the lowered but appropriately located histogram peaks in Fig. 2 a–c compared with Fig. 1 a–c. Channels that have responses that are distorted by the presence of the strong background odor produce the broad background.

Fig. 2 d–f are like figures Fig. 2 a–c except that the background odor is made up of a mixture of four unknown odorants each at a strength 100 (in terms of its threshold). The total strength of the background is now 400. It is much harder to recognize a known single-molecular species in the presence of this complex background, but identification and quantification of a single odorant against a complex background that is several times stronger can still be done by the same method.

Task 3 (component separation) can also be solved in this same fashion. The fact that we could identify a known component of strength 100 in the presence of four unknown chemicals each of strength 100 indicates that a complex mixture of five known molecular components could be separated into its five components. When the number of components is raised to seven, this method will no longer result in separation. While it is mathematically possible to separate seven or more known components, it requires more complex processing.

The effects of erroneous data can be understood in terms of these simulations. Sensory channels that are to some extent stuck “on” are equivalent to channels that have additional input and have effects exactly like those of a background odor, contributing a wing to the right in Fig. 2. Sensory channels that are strongly adapted contribute a wing to the left. Such effects on 50% of the channels produce little impact on performance other than a slight rise in the detection threshold and a slight decrease in background rejection capability.

The special case of an odor made from comparable (in terms of saturation concentration) amounts of two unrelated odorants A and B is often studied. If recognition is based simply on finding a peak in the histogram, then a recognizer of A + B will also recognize each of B and A separately. There are, however, subtle inconsistencies in the histogram that could be used to show that A is not identical to A + B.

On the Large Number N of Glomeruli: More Is Different.

The size of N is qualitatively important. We have intuitive feelings for the case N = 3 from color vision. If light from different sources are mixed together, all three channels will usually be mixed, and there is no reliable way to tell whether a “target” hue is present or not. For example, light of 5,100 Å and of 4,900 Å wavelengths are quite distinguishable shades of green but drive chiefly green and blue cones. Because of this, a particular mixture of 5,100- and 4,500-Å light produces an exact visual color match to 4,900-Å light. N = 3 is a small number.

In the case of olfaction, if N = 5 and random binding constants picked in the prescribed range, 6% of odors will have significant binding to only one channel. Odors can then be divided into a set that drives more than one channel, and five sets each containing ≈1% of all molecules. Within each 1% set, all members are utterly indistinguishable. Appropriate levels of five primary odorant chemicals could duplicate any odor. For any primary odorant, unknown backgrounds that drive that unique odorant receptor (and ≈50% of backgrounds will do so) completely prevent the reliable detection of the target. About 25% of odors will drive two receptor types. For these, the ratio of the bindings can be used, generating some reliability, but there is only one ratio, and ≈4% of odors will drive those two receptors in the same ratio. Benefits of large numbers are beginning to appear, but the statistics are not reliable. For N = 100, many ratios are always available, and the statistics already reliable (for example, the probability at saturation of driving <25 channels is <10⁻⁶). Were it to turn out that the 2,000 receptor types were composed of 100 different families with strong interfamily similarity, the large N algorithms would still work quite well. Similarly, ablation of 90% of the glomeruli at random would little compromise the basic performance. A range of 10⁶ in binding constants is not essential—a range of 10⁴ is sufficient to yield adequate non-interference with N = 100. However, the situation should be contrasted with many “artificial nose” projects in which the range of responses to different odorants is much less and/or the number of channels small.

Large N is especially useful when the binding constants are broadly distributed, producing a naturally sparse representation and appreciable probability of non-interference of two compounds, and thus leaving a statistically significant number of channels that are receiving unambiguous information about each compound. This basic idea is not limited to olfaction (18, 19).

Task 4: Separating Unknown Odors Using Fluctuations.

When two or more unknown odors are mixed in a time-dependent fashion, the time-dependent fluctuations of the relative amounts of the different odors in principle allow the separation of the two odors when N is large. Without fluctuations, the task is impossible. I will describe how, using the odor model and representation already described, a “two-sniff” paradigm can discover the presence of two or more objects. Previous algorithms (20) require a study of the fluctuating odors over a considerable time.

Suppose that two different odors, x and y, are in the environment, each due to its own single molecule type. A first sniff contains the combination a*x + b*y. A second sniff is due to α*x + β*y, where a, b, α, and β are the intensities of x and y.

Construct a “virtual target” odor on the basis of the first sniff. The second sniff is then analyzed with the first sniff as the target odor, using the histogram representation as before. I anticipate the appearance of the histogram by noting that many of the channels are dominated by odor x, and will contribute just as they would have if a*x were the target and α*x the second odor, and produce a peak to the histogram at that α/a. Many other channels are dominated by y and generate a peak in the histogram at β/b. A third set of channels is of a mixed character.

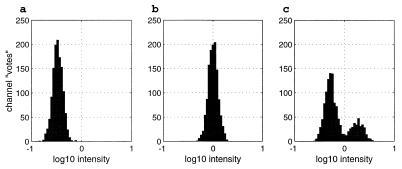
Fig. 3 shows simulation results for a situation representing a weak “object” (a = 25) in the presence of a stronger “background” (b = 1,000). Fig. 3b shows the result when the second sniff is identical to the first. The location of the histogram peak is at 0, (representing an intensity ratio of 1 between the first and second sniffs), and its area represents the contribution of ≈1,200 channels. Fig. 3a shows the result when the second sniff is α = 8.3, β = 333. Both odors have decreased in strength by a factor of 3. This would happen if there were really a single object for which all components track in parallel. The peak has shifted by −0.48 [or log₁₀(1/3)], corresponding to the decrease in intensity of the second sniff compared with the first.

Figure 3.

A first sniff consists of a mixture of two unknown odorants x and y and is the particular mixture 25x + 1,000*y. This first sniff is used as the target in the histograms a–c. (b) The second sniff is the same mixture as the first. (a) The second sniff is 8.3*x + 333*y. It contains the same ratio of the two components but is lower in intensity by a factor of 3. (c) The second sniff is 50*x + 500*y. The weaker component has increased in intensity by a factor of 2, while the stronger component has decreased by a factor of 2. The noise Gaussian noise level is 0.10log10 units.

Fig. 3c shows the result with the same first sniff but when the second sniff is α = 50, β = 500. The two odors have changed in intensity relative to each other by a factor of 4, resulting in a histogram with two peaks. The smaller peak is due to channels that chiefly respond to the weaker odor, and the larger peak is due to channels that chiefly respond to the stronger odor. The location of the smaller peak at about +0.3 is due to the increase of the intensity of the weak target by a factor of 2 [0.30 = log₁₀(2)]. The position of the larger peak near −0.3 corresponds to the decrease of the stronger odor intensity by a factor of 2. The channels can now be divided into two groups, corresponding to the two odors. Each group responds to more sniffs by showing a single peak whose location and height varies in the expected way with the strength of its particular component.

The Two-Sniff Representation and Adapting Neurons.

The representation essential to the two-sniff paradigm can be generated by simple neurons that adapt. For adapting integrate-and-fire neurons, the cell potentials, u_I, obey

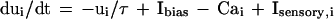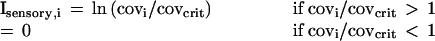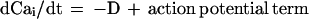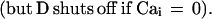The sensory input current of a driven channel is proportional to the logarithm of the coverage of the odorant receptors driving that channel. When u_i reaches a threshold, an action potential of negligible duration is generated, and u_i is then reset to u_thresh − δ. The Ca_i term represents an inward K⁺ current proportional to the internal Ca²⁺ concentration. The internal Ca²⁺ is depleted at a fixed rate D by a Ca²⁺ pump and is resupplied by an inward fixed aliquot of Ca²⁺ (due to high potential Ca²⁺ channels or to the Na⁺ channels themselves) that enters cell i each time it generates an action potential.

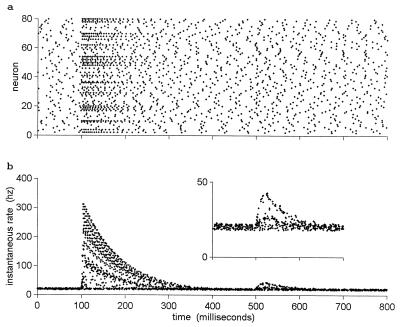
Fig. 4a shows the spike rasters of 80 model neurons responding to two sniffs of a mixed odor. At t = 100 msec, a constant odor mixture a*x + b*y was introduced, with a = 50 and b = 1,000 in terms of saturation strengths. This mixture might represent a background y that is 20× as strong as an object, x. About 65 of the neurons are visibly driven by this odor mixture, fire briefly at a high rate, and then adapt back to their baseline level in spite of the continued presence of the odor. At t = 500 msec, a second sniff, α*x + β*y, is taken, with the object now 50% stronger in intensity and the background 10% stronger (i.e., with α = 75, β = 1,100). The suggestible reader may see a subtle change in the raster patterns around that time. This odor remains fixed for the rest of the time, and the neurons again adapt to their basal firing rate.

Figure 4.

Eighty adapting integrate-and-fire neurons are exposed to two sniffs of an odor mixture in which the relative components have changed between the two sniffs. No odor was present before 100 msec. The time period 100–500 has a mixed odor present of the form 50*x + 1,000*y. At 500 msec, the odor shifts to 75*x + 1,100*y (i.e., the weak odor goes up by 50%, the strong component goes up by 10%, and their ratio changes by a factor of 1.36). (a) Raster plots of the spikes of the 80 neurons. The sniff at 100 msec strongly activates more than half the neurons, after which they adapt. The changed sniff at 500 msec is almost invisible. (b) The same data as in a, but the y axis is the instantaneous firing rate at the time of each action potential. The second sniff is now clearly visible, and most spikes appear to belong to one of three patterns. A 20% spread in D was included to produce parameter-spread noise. matlab programs to explore all figures are available at www.hopfield.net/∼john.

Fig. 4b shows the same data in a different representation. With each spike is associated an interspike interval (the interval to the previous spike of that neuron) and an instantaneous frequency (the reciprocal of that interspike interval). Each spike of Fig. 4a is plotted in Fig. 4b. The data after t = 500 chiefly fall on three lines. The neurons that are negligibly driven by both odors lie on the bottom straight line. The neurons that are chiefly driven by the stronger odor y generate the low arc. The smaller numbers of neurons that are chiefly driven by the weak object x generate the top arc. In this representation of the firing pattern, the fact that there are two objects is completely obvious, in spite of the fact that the raster plot looks devoid of interest in the relevant time interval. This plot presents a neural representation of the separation visible in Fig. 3c. An arc in Fig. 4b goes up (or down) because the intensity of its corresponding odor went up (or down). If the odors had fluctuated in opposite directions, separation would have been easier. Because reasonable plotting requires representing only a small fraction of the 2,000 channels, Fig. 4 has been presented without measurement noise so that what is happening is visible without massive statistics being necessary. The threshold for detectable fluctuations depends entirely on noise issues. However, the noise level may be quite modest (see the third footnote).

These results can be simply understood on the basis of three essential features: namely, existence of a significant number of non-interfering channels, logarithmic encoding, and adaptation. Because there are many non-interfering channels, many neurons will be driven only by one of the odors. Consider a simple adapting cell that has a basal firing rate f_basal then responds to a step input current I by briefly firing at a rate f_basal + I*h, where h is some constant, and then adapts back to firing at f_basal. If the input is now stepped to the value I′, the neuron will briefly fire at the rate f_basal + (I − I′)*h, then will relax back to the basal rate. This sort of behavior is not uncommon in adapting neurons.

Now consider the case I_i = ln (x_i*a) and I_i′ = ln (x_i*α). The firing rate immediately after I′ starts is now f_basal + (I_i − I_i′)*h = f_basal + ln(α/a)*h, independent of x_i. Thus, all neurons that respond chiefly to x have a common value of α/a = 1.5 and will also have a common input current step, and a common firing-rate versus time trajectory in an adapting system. The neurons that respond chiefly to y have a common value of β/b = 1.1 and have their own (lower) common trajectory.

Recognition Algorithms.

An elementary algorithm that merely looks for a high peak in an appropriate histogram calculated from glomerular responses can adequately address three of the basic tasks described. A system was previously described for solving the olfactory “analog match” problem (18, 20) by using action potential timing relative to an underlying rhythm as the encoding of channel intensity and using a time-delay network to organize the recognition of a particular odor. The time-dependent input to a recognition neuron during one period of the underlying rhythm is exactly the histogram of Figs. 1, 2, and 3, with the intensity axis representing time. The time at which each action potential arrives is its vote in this histogram. If the near-simultaneous arrival of perhaps 50 action potentials is necessary to drive a receiving cell to fire, then that cell is performing a thresholding operation on the histogram. Thus, recognition units using time-delays and phase coding of intensity automatically solve tasks 1, and 2, and 3, in the presence of noise. Undoubtedly, there are other neural schemas that also can produce an effective implementation of these tasks. And while neurobiology is not based on “grandmother cells,” this representation does show how easy it would be to solve the problem using a few basic mechanisms available to neurobiology. The central point is that simple schemes can use non-interfering, uncorrupted channels to evaluate the situation, utilizing the fact that, in a large system, there will be many such channels. The situation is totally unlike a problem in which there is equivalent interference in all glomerular channels.

For task 4, the next interesting question is how to recognize the existence of the arched trajectories as seen in Fig. 4b. One potential way is through the synchronization of action potentials. Each of these trajectories represents a set of neurons whose effective input (after adaptation) is due to the changing intensity of one odor as a function of time. They will therefore have firing rate patterns over time that is the same except for the phasing of when action potentials occur. Even though not periodic, such activity patterns would be easily synchronized by direct or indirect weak couplings between the neurons. It would be easiest to accomplish this if the adapted firing rate of the nondriven cells is very small. The distinct olfactory objects (by definition, the components of a single olfactory object all fluctuate together), represented by the trajectories of Fig. 3, would then be identified by groups of cells that tend to synchronize their action potentials (21–23).

Sniffs before full adaptation and sniffs after adaptation are expected to encode different information, and large experimental differences are observed^∥. Experiments (25, 26) showing strong synchronization effects often analyze data only subsequent to the first sniff. If those experiments represent full adaptation, and if only one odor is truly present, then there should be a set of neurons that all have a common firing rate as a function of time, while others fire at some other rate unaffected by puffs of the adapted odor.

The patterns of “arcs” in Fig. 4b are easily seen when many neurons are simultaneously observed. In a freely behaving animal environment, and recording from only a few neurons, the necessity to collect statistics by summing over what would effectively be different independent sniffs with different values of a and b would wipe out all relevant structure. Unless simultaneous recording from a large number of neurons is available, such arcs can be anticipated only in a tightly controlled laboratory protocol.

The answer to “why are there so many channels?” seems to be found in the ease of constructing a “neural computer” that solves the essential olfactory problems when N is large. A second conundrum, “why does the system have such complex adaptation?” (24), may be answered from the usefulness of adaptation as a computational device in algorithms seeking to separate the olfactory world into separate objects. The universal sensory principle that “what moves together is an object” seems particularly simple to implement for the olfactory system.