Sound pressure distribution and power flow within the gerbil ear canal from 100 Hz to 80 kHz

Abstract

Sound pressure was mapped in the bony ear canal of gerbils during closed-field sound stimulation at frequencies from 0.1 to 80 kHz. A 1.27-mm-diam probe-tube microphone or a 0.17-mm-diam fiber-optic miniature microphone was positioned along approximately longitudinal trajectories within the 2.3-mm-diam ear canal. Substantial spatial variations in sound pressure, sharp minima in magnitude, and half-cycle phase changes occurred at frequencies >30 kHz. The sound frequencies of these transitions increased with decreasing distance from the tympanic membrane (TM). Sound pressure measured orthogonally across the surface of the TM showed only small variations at frequencies below 60 kHz. Hence, the ear canal sound field can be described fairly well as a one-dimensional standing wave pattern. Ear-canal power reflectance estimated from longitudinal spatial variations was roughly constant at 0.2–0.5 at frequencies between 30 and 45 kHz. In contrast, reflectance increased at higher frequencies to at least 0.8 above 60 kHz. Sound pressure was also mapped in a microphone-terminated uniform tube—an “artificial ear.” Comparison with ear canal sound fields suggests that an artificial ear or “artificial cavity calibration” technique may underestimate the in situ sound pressure by 5–15 dB between 40 and 60 kHz.

I. INTRODUCTION

A. Spatial variations in sound within the ear canal

This paper is part of a study to investigate high-frequency sound transmission through the external and middle ear of the Mongolian gerbil Meriones unguiculatus and has ramifications for similar investigations in humans and other species. In studies of auditory function, the auditory input is generally taken as the sound pressure in the ear canal (EC) just lateral to the tympanic membrane (TM), and explorations of auditory function at any point along the auditory pathway (middle ear, cochlea, auditory nerve and beyond) generally require an accurate assessment of this input. At low frequencies, sound pressure is approximately uniform throughout the ear canal, and auditory input can be estimated accurately from a sound pressure measurement anywhere within the ear canal. At high frequencies, however, sound pressure can vary considerably within the ear canal and across the TM, and accurate measurement of auditory input is problematic.

At such high frequencies, spatial variations in the sound field related to the wave nature of sound can be described in terms of modal patterns with local maxima and minima in sound pressure magnitude and differences in phase that occur along the length or across the diameter of the ear canal. Sound pressure variations along the ear canal length L can become significant at frequencies where the sound wavelength λ < ~ 10L.¹ Variations across the ear canal diameter d can become significant near changes in ear canal cross-section or mechanical properties (such as near the TM; e.g., Rabbitt and Holmes, 1988). The first mode that creates these transverse variations can propagate along the ear canal at frequencies where λ<d/0.59 (Morse and Ingard, 1968, p. 511; Stinson and Khanna, 1994), lower if the ear canal cross section is noncircular. The mechanisms of these frequency-dependent spatial variations in ear-canal sound pressure are discussed in more detail in Sec. II.

Such spatial variations in EC sound pressure are usually significant at audible frequencies. For example, for the human ear canal with length L=22.5 mm (Shaw, 1974) and EC area ≈TM area=60 mm² (Wever and Lawrence, 1954), λ< 10L above 500 Hz, d≈8.7 mm, and λ<d/0.59 above 24 kHz. Considering that the range of human hearing is 20 Hz–20 kHz (Sivian and White, 1933), it is clear that longitudinal sound pressure variations exist in the ear canal well below the upper frequency limit of hearing. The frequency range of gerbil hearing has been described as 210 Hz–46 kHz (threshold within 30 dB of best threshold; Rosowski, 1992). In a gerbil preparation in which the cartilaginous ear canal has been removed (as in many physiological experiments), the length of the remaining bony ear canal is about 4 mm. The EC diameter is 2.3 mm near its midpoint but about 5 mm near the TM [mean of Lay (1972) and Ravicz (1990)]. With these dimensions, λ < 10L above 8 kHz and λ < d/0.59 near the TM above 40 kHz. Therefore, substantial sound pressure variations could exist both along the EC length and across the EC diameter at frequencies below the 46-kHz upper limit of gerbil hearing. Similarly, sound pressure can vary throughout the ear canal of other species within their audible range.

Several techniques have been developed to estimate the middle-ear input at high frequencies. One common approach in nonhuman ears is to use a probe-tube microphone to measure the sound pressure at a point just lateral to the TM. This method is difficult both in a clinical setting as well as in small animals with narrow ECs. In some animal experiments, a portion of the ear canal is removed to shorten the effective length of the ear canal between the measurement location and the TM (as described earlier for gerbil). A second approach is to use measurements of the sound pressure in a convenient location relatively distant from the TM to estimate the sound pressure at the TM using a mathematical model of the ear canal (e.g., Stevens et al., 1987; Huang et al., 2000). A third and probably the most common approach for studies of human hearing is to calibrate the earphone output in an “artificial ear” that mimics the essential dimensions of the ear canal as well as the load impedance of the TM on the ear canal. Such an approach has been used to calibrate audiometric earphones (Zwislocki et al., 1988).

A variation of this third approach has been used in recent studies of high-frequency hearing and auditory mechanics in small mammals (Pearce et al., 2001; Overstreet and Ruggero, 2002; Overstreet et al., 2003). In these studies, the stimulus earphone was calibrated against a reference microphone that was coupled to the earphone via an excised ear canal or a short tube of dimensions similar to the ear canal—an “artificial cavity calibration.” There are problems with this approach: In particular, the acoustic impedance of the reference microphone terminating the artificial ear is a high-magnitude stiffness that is unlikely to be representative of the impedance of the intact TM. While the impedance at the TM is not well described in any animal at frequencies above about 20 kHz, various authors have suggested that the high-frequency TM impedance in cats is resistive and approximately matched to the characteristic impedance of the ear canal [Lynch, 1981; Lynch et al., 1994; inferred from Allen (1986) and Puria and Allen (1998)]. It should be noted, however, that in none of these studies did the frequency range of measurement approach the upper frequency limit of hearing. If the terminating impedance is larger than that of the TM, the sound field within the ear canal will be altered from the natural case, and the calibration may be biased, as we demonstrate in this paper.

B. Sound field measurements in gerbil ear canals

The topics of variations in EC sound pressure and EC sound pressure calibration difficulties at medium to high frequencies have been addressed previously for humans and cats for frequencies as high as 20 kHz (Stinson et al., 1982; Lawton and Stinson, 1986; Khanna and Stinson, 1985; Stinson and Khanna, 1994). Here we extend the discussion to higher frequencies in the Mongolian gerbil, a common subject for auditory measurements whose ear canals are smaller than those of cat or human. The frequency range of measurements includes the entire range of gerbil hearing.

This paper contains measurements of spatial variations in sound pressure within the gerbil ear canal near the TM. Sound pressure variations were also measured in a cylindrical artificial ear terminated by a reference microphone. Measurements were obtained from two different laboratories using two different sound-pressure measuring devices of different size and sensitivity: a probe-tube microphone, and a fiber-optic miniature pressure sensor (Olson, 1998), which acts as a miniature microphone in air. Most of the probe-tube measurements in ear canals and in the artificial ear were performed in the Eaton-Peabody Laboratory at the Massachusetts Eye and Ear Infirmary (MEEI), while the fiber-optic miniature microphone measurements in ear canals were performed at Princeton University (early experiments) and the Fowler Laboratory at Columbia University (later experiments). The more extensive ear-canal sound pressure maps were made with the probe-tube system; results with the smaller fiber-optic microphone confirm those findings and establish that the probe tube did not affect the sound field significantly.

Our measurements address the following questions: (1) How does the sound pressure vary in the terminal portion of the gerbil ear canal? (2) Do sound-field measurements in a calibration cavity provide an accurate estimate of the sound pressure near the umbo at the center of the pars tensa of the TM? (3) What fraction of the sound energy in the ear canal is reflected at the TM at different frequencies? Our findings can be generalized to other species by a simple scaling, using the anatomical dimensions for the gerbil ear canal provided here.

II. THEORY

A. Sound pressure distribution and standing waves in a model ear canal

For the purposes of the analysis in this paper, it will be convenient to consider the ear canal as a uniform cylindrical tube of length L and diameter d. The tube is coupled to a sound source at one end (x=−L) and terminated with the TM at the other end (x=0). Consider a source-generated forward-traveling uniform plane sound wave p_i(x,t) (fundamental mode) with frequency f described by p_i(x,t) =A cos(ωt−kx), where ω=2πf, t is time, k is the wave number=2π/λ, and x is the longitudinal dimension. At the termination (the TM), part of the incident (forward-traveling) wave is absorbed and part is reflected. The reflected wave p_r(x,t) travels backward along the ear canal toward the source (in the -x direction) and is described by p_r(x,t) =B cos(ωt+kx+θ ), where θ is the phase difference at the TM between the incident and reflected waves. The resulting sound field in the ear canal is the sum of the sound pressures of the incident and reflected waves:

$$\begin{array}{l}p(x,t)=p_i(x,t)+p_r(x,t)\\ =Acos(\omega t-kx)+Bcos(\omega t+kx+\theta ).\end{array}$$ (1)

At frequencies where λ is greater than 10L, spatial variations in sound pressure within the ear canal are small, and the ear canal can be considered a lumped element. However, at higher frequencies (shorter wavelengths), sound pressure will vary substantially longitudinally along the ear canal (e.g., Kinsler et al., 1982). Similarly, at frequencies where λ <d/0.59, the sound pressure can vary substantially transversely across the EC diameter; these transverse variations (higher-order modes) will be considered later.

The relative magnitude B and relative phase of the reflected wave θ are determined by the nature of the EC termination. If the TM is perfectly reflecting, such that all sound power incident on the TM is reflected backward toward the source, then A=B, and the sound field in the ear canal is a standing wave in which the amplitude varies spatially as |P| =2A cos(kx+θ/2). (If the TM were not only perfectly reflecting but also perfectly rigid, θ=0.) If all of the sound power incident on the TM is absorbed (transmitted into the middle ear), there is no reflected wave, B=0, and the sound field is described by the forward traveling wave A cos(ωt−kx) in which the sound amplitude=A for all x throughout the ear canal and the phase increases as kx. If the incident wave is partially absorbed and partially reflected, the EC sound field has features of both traveling and standing waves (e.g., Kinsler et al., 1982).

Figure 1(a) illustrates how the longitudinal distribution of ear canal sound pressure magnitude |P| and phase ∠P varies in a model ear canal for different values of B/A, the amount of reflection at the TM (pressure reflection coefficient). In this model, the EC length is 5 mm and the EC diameter is small enough that we need consider only uniform plane waves. Values of B/A between 0 and 0.9 correspond to varying the magnitude of the TM impedance between the characteristic impedance of the tube Z₀ = ρ₀c/S and about 20 × Z₀ (nearly rigid). [c is the propagation velocity of sound in air, ρ₀ is the density of air, and S is the EC cross-section area=πd2/4, e.g., Kinsler et al., (1982)]. Curves were generated from

FIG. 1.

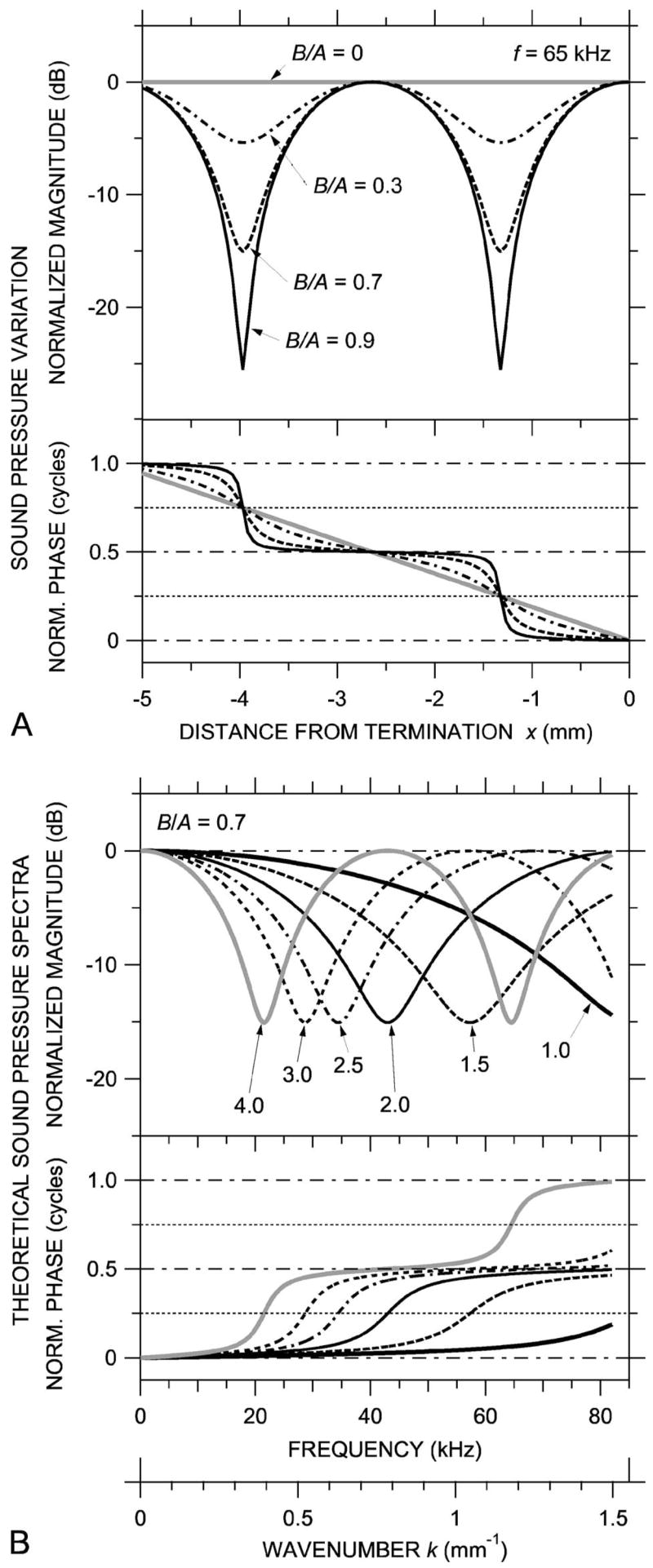
Theoretical standing waves in a uniform cylindrical tube. (A) Spatial variations in sound pressure magnitude (top) and phase (bottom) at a given frequency for different values of B/A, the ratio of the amplitude of a sound wave reflected from the termination to the incident sound wave amplitude. (B) Computed broadband sound pressure spectra at different locations for B/A=0.7. If B/A changes slowly with frequency, the spectra are equivalent to the spatial sound pressure distribution—see lower horizontal scale in wave number k=2πf/c.

$$|\mathbf{P}(x)|={[1+{(B/A)}^2+2(B/A)cos(2kx-\theta )]}^{1/2}$$ (2a)

$$\angle \mathbf{P}(x)=\frac{\theta }{2}+arctan\left[\frac{1-(B/A)}{1+(B/A)}tan\left(kx-\frac{\theta }{2}\right)\right]$$ (2b)

[from Stinson, (1985a), Eqs. (30) and (32)]. The magnitude of each curve in Fig. 1(a) is normalized by the maximum sound pressure achievable within the tube (B+A), and the phase is normalized by the phase at the termination.² The sound frequency is 65 kHz, so the wavelength is 5.3 mm. For simplicity, we set θ=0.

When B/A=0 [zero reflection, total transmission; the thick gray line in Fig. 1(a)], the sound pressure amplitude is uniform throughout the tube and the phase of the sound varies linearly with distance from the TM (∠P slope is constant with position). The sound field in the ear canal is a uniform traveling wave.

For nonzero reflection (e.g., B/A=0.3, dot-dashed line), broad local maxima and narrow local minima (notches) appear in the spatial |P| distribution, and ∠P shows slight increases and decreases from the constant slope of the zero-reflection case. The local |P| maxima occur where the incident and reflected waves combine constructively; this is also where the ∠P slope is shallowest and equal to 0, 0.5, or 1 cycle, in this model ear canal at x=0 and −2.65 mm. The |P| notches occur where the incident and reflected waves combine destructively, in this model ear canal at x=−1.33 and −3.98 mm, where x=λ/4 (a “quarter-wave resonance”) and 3λ/4. These locations are also where the ∠P slope is steepest, where ∠P=0.25 or 0.75 cycles. To state the rule, |P| notches occur and ∠P=(2n−1)/4 cycles where kx =π/2, 3π/2, 5π/2,…, (2n−1)π/2 [after Stinson (1985a)].

As B/A increases toward 1 [in our model ear canal, as the magnitude of the TM impedance increases further; Fig. 1(a), dashed and solid curves], the |P| notches deepen and the spatial ∠P distribution becomes more step-like. If B/A =1 (total reflection, zero transmission), |P| is zero at the minima, and the sound field in the ear canal is a pure standing wave. For 0<B/A<1, the sound field can be thought of as a combination of a traveling wave and a standing wave: Some of the incident wave is transmitted into the TM and some is reflected to form a pattern of |P| maxima and minima and associated ∠P changes.

In this uniform ear canal, sound power reflectance at the TM ℜ is related to the standing wave ratio (SWR), the ratio of |P| maximum to minimum, by

$$\Re ={(B/A)}^2={[(\text{SWR}-1)/(\text{SWR}+1)]}^2$$ (3)

(e.g., Magnusson, 1965; Kinsler et al., 1982; Stinson et al., 1982).

In addition to the fundamental-mode uniform plane waves discussed earlier, higher-order-mode nonuniform plane waves may also be present in a tube and may propagate down the ear canal. These nonuniform plane waves reflect off the tube or EC walls and cause transverse variations in sound-pressure magnitude and phase across the tube or EC diameter (Morse and Ingard, 1968, p. 511; Fletcher, 1992, p. 198). Higher-order modes may be induced by a nonuniformity in the source generating the wave, the reflecting termination, or the tube itself. A large potential source for transverse variations in ear canal sound pressure is the tympanic membrane, which is known to vibrate in complicated patterns (e.g., Khanna and Tonndorf, 1972; Rabbitt and Holmes, 1988; Furlong et al., 2006; Rosowski et al., 2006). At frequencies where λ >d/0.59, any nonuniform plane wave that is generated by the TM will decay exponentially³ within a short distance of the TM. For example, in the terminal portion of the gerbil ear canal at frequencies less than 37 kHz, the lowest nonuniform mode generated at the TM will decay by more than 3 dB at 0.5 mm from the TM and by 20 dB at 3 mm from the TM. At higher frequencies, nonuniform modes do not decay but propagate back up the ear canal. The resultant EC sound field in the ear canal is the sum of incident and reflected waves of all modes present.

Such transverse spatial sound pressure variations complicate the estimation of power reflection in the ear canal: Though the notches in the uniform-plane-wave standing wave pattern in a tube or ear canal with a reflective termination may be quite deep, the sound pressure associated with higher-order modes may fill in the deepest part of the notches, thereby decreasing their apparent depth and causing the SWR and hence the power reflectance to be underestimated. Higher-order modes may also cause phase irregularities in the standing wave pattern. (Microphone or environmental noise could have a similar effect.) In this way, higher-order modes limit the maximum SWR and ear canal reflectance that we could measure.

B. Sound pressure spectra at various locations in the model ear canal

Because the spatial term of the wave equation [Eq. (1)] depends on both location x and sound frequency f (via the wave number k=2πf/c), we can prepare a “dual” of the standing wave pattern in Fig. 1(a) (which shows the sound pressure at many locations in the ear canal at one frequency) by plotting the sound pressure at one location at many frequencies (spectrum). Figure 1(b) shows such dual sound pressure spectra (magnitude and phase) for B/A=0.7 at six locations in the model ear canal (at 1, 1.5, 2, 2.5, 3, and 4 mm from the TM). The common feature in Figs. 1(a) and 1(b) is the pattern of repeated magnitude notches and 0.5 cycle phase changes. Such simple relationships between the spatial and frequency dependence will occur as long as B/A varies slowly with frequency. The lower abscissa scale in Fig. 1(b), which scales the patterns in k, emphasizes this duality.

III. METHODS

A. Animal preparation

1. At Massachusetts Eye and Ear Infirmary (MEEI)

The preparation of the experimental animals was approved by the MEEI Institutional Animal Care and Use Committee and is similar to that described previously (e.g., Ravicz et al., 1992). Thirteen young adult Mongolian gerbils were used. The animals were anesthetized with an intraperitoneal injection of sodium pentobarbital (Nembutal, 40 mg/kg) together with intramuscular Ketamine injections (25 mg/kg). A tracheal cannula was inserted. The soft tissue was removed from the surface of the skull around the opening of the bony ear canal. Two or three small holes were made in the wall of the auditory bulla to preclude a buildup of static pressure within the middle-ear cavity and to provide visual access to the stapes.

The intact gerbil ear canal is long, curved, and narrow and flares near the TM, which has a diameter approximately twice that of the ear canal (5 mm vs 2.3 mm; see previous text) and is oriented nearly parallel to the axis of the more distal ear canal (Fig. 2). Consequently, bringing a probe tube near the TM is difficult. To shorten the ear canal, the pinna flange and cartilaginous EC were removed, and as much as possible of the ventro-lateral wall of the bony EC opening was removed without breaking into the middle-ear cavity. A short cylindrical brass tube [3.2 mm inside diameter (i.d.) × 3–5 mm length] was cemented around the bony EC opening with dental cement or cyanoacrylate glue [Fig. 2(a)]. The tube permitted reliable coupling and recoupling of the ear to the high-frequency sound source [Fig. 2(b)]. In earlier experiments the sound coupler was left square-ended and covered part of the opening in the lateral EC wall. In the six later experiments, in which most of the data presented here were taken, the coupler end was beveled and notched to widen the opening between the coupler and the lateral-wall remnant [Fig. 2(a)].

FIG. 2.

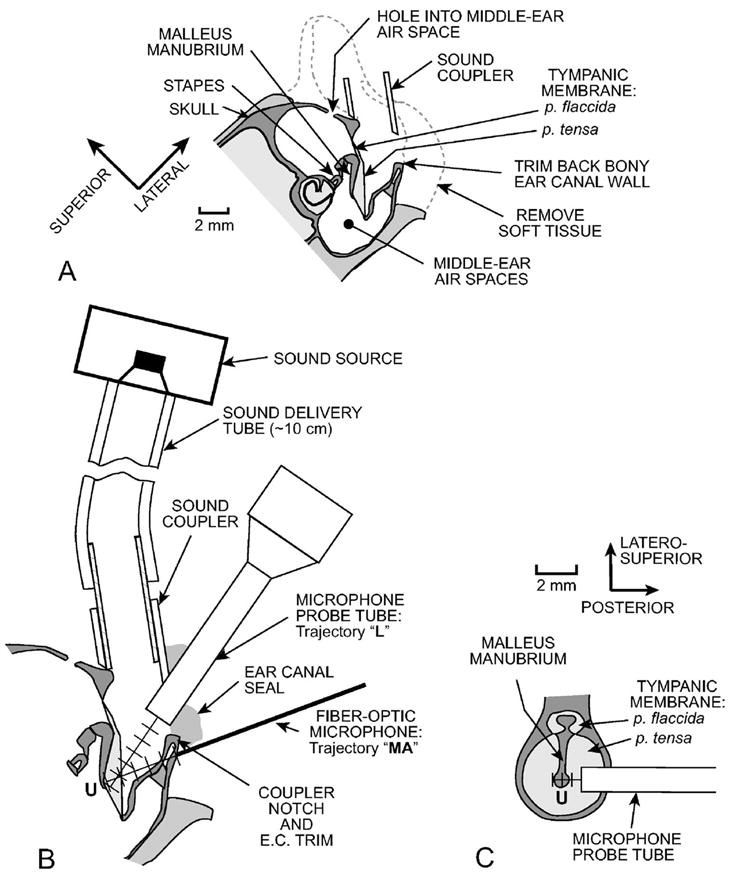
Schematic section through a gerbil head showing preparation methods and measurement trajectories. (A) Coronal section. The external ear and soft tissue were removed, the lateral wall of the bony ear canal (EC) opening was trimmed back, and a brass tube sound coupler was placed at the opening of the bony ear canal. A reflector was placed on the stapes posterior crus, and the laser vibrometer beam was shined through one or more holes in the middle ear wall toward the reflector. (B) Details of the coronal EC section showing EC sound pressure (P_EC) measurement trajectories. The microphone probe tube (MEEI) or fiber-optic microphone (Princeton and Columbia) was introduced through a notch in the coupler wall and advanced in 0.5-mm steps toward the umbo “U” along an approximately longitudinal trajectory “L.” P_EC was also measured with the fiber-optic microphone along an medio-axial trajectory through the middle-ear wall “MA” toward the umbo. (C) Section perpendicular to the coronal section in panel (B). P_EC was also measured along a transverse trajectory across the ear canal over the umbo approximately 0.5 mm from the tympanic ring.

2. At Princeton and Columbia

The preparation of the experimental animals was approved by the Institutional Animal Care and Use Committees of Princeton University and Columbia University as applicable. Anesthesia and animal monitoring were as described in Olson (1998) except that 40 mg/kg Ketamine was administered preoperatively instead of acepromazone.⁴ Three young adult Mongolian gerbils were used; one was just postmortem when measurements commenced.

B. Experimental methods

The experiments were conducted in a sound-isolation booth. Heart rate was monitored throughout the experiment, and body temperature was maintained at 37±1 °C with a heating pad. Anesthesia boosters at half the initial surgical dose were provided as necessary to suppress the withdrawal reflex. The animal’s head was held securely in a custom snout clamp. At the conclusion of the live experiment the animal was euthanized with a fatal dose of anesthesia.

Sound was produced by an electrostatic earphone (TDT EC1 and amplifier ED1, Tucker-Davis Technologies, Alachua, FL) and delivered to the ear canal via a flexible sound delivery tube (Tygon) approximately the same i.d. (2.4 mm) as the ear canal and about 10 cm in length [Fig. 2(b)], with a short brass section that allowed the sound delivery tube to be removed and replaced repeatably. Sound pressure P_EC was measured at various locations within the remaining ear canal with the measurement microphone [the probe-tube microphone (MEEI) or the miniature fiber-optic microphone (Princeton/Columbia)] mounted in a micromanipulator (Narishige or Marzhauser). Both the magnitude and phase of P_EC relative to the stimulus were measured. The probe tube was introduced into the ear canal through the notch in the sound coupler, and P_EC was measured in various locations as the probe tube was advanced and retracted in 0.25–0.5 mm steps along an approximately longitudinal trajectory down the ear canal toward the umbo [trajectory “L” in Fig. 2(b)]. Measurements were made with the gap between the probe tube and the sound coupler left unsealed and with the gap sealed with saturated cotton, which was effectively acoustically rigid. The probe tube was advanced until changes in microphone output and stapes velocity (see the following) suggested that it had touched the TM. (Sound pressure measured at this position is not included.) The innermost probe tube position was confirmed by viewing scuff marks on the TM through an operating microscope after the probe tube had been withdrawn.

In two early experiments (at Princeton), the miniature fiber-optic microphone was introduced into the ear canal via natural cracks in the bone of the EC lateral wall (Olson, 1998) and advanced toward the umbo in an approximately medio-axial direction intermediate between longitudinal and horizontal [trajectory “MA” in Fig. 2(b)]. In the third experiment (at Columbia), the MEEI sound coupler was used, and the microphone was introduced and advanced approximately longitudinally along trajectory L as described earlier. In all experiments, the microphone was advanced directly toward the umbo, which was visible throughout the experiment. Low-frequency fluctuations in the fiber-optic microphone output signaled that the microphone tip had touched the TM. The third experiment was performed just post-mortem.

Stapes velocity was measured simultaneously with P_EC in the longitudinal-trajectory MEEI experiments to evaluate the effect of the probe tube on the sound field within the ear canal. The velocity of small reflectors placed on the posterior crus of the stapes was measured with a laser-Doppler vibrometer (OPV 501/2600, Polytec PI, Waldbronn, Germany) focused through one of the bulla holes (usually posterior to the ear canal—Rosowski et al., 1999; Ravicz and Rosowski, 2004). Stapes velocity was also used to monitor the position of the probe tube: When the probe-tube tip touched the TM, stapes velocity decreased at low frequencies.

In three ears, P_EC was also measured at various points spaced at 0.5 mm along a transverse trajectory [Fig. 2(c)] from the ear canal wall just lateral to the posterior tympanic ring to a point in the ear canal just lateral to the anterior tympanic ring. This trajectory passed approximately 0.5 mm lateral to the umbo. For these measurements, a hole was chipped in the posterior wall of the ear canal just lateral and posterior to the tympanic ring [Fig. 2(c)]. This access was obstructed by the animal’s shoulder in intact animals, so these measurements were performed post-mortem after separating the head from the body.

C. Stimulus generation and response measurement

1. At MEEI

In the MEEI experiments, custom software (written in LABVIEW 7.1, National Instruments, Austin, TX) on a desk-top computer synthesized stimuli, controlled equipment, acquired and averaged responses synchronously with the stimulus, and computed the transfer function between the response (microphone or laser-Doppler vibrometer) and the stimulus. Acoustical and mechanical responses were produced by sound stimuli delivered to the earphone via a signal generator (HP 33120A, Hewlett-Packard, Palo Alto, CA). The stimulus was a computer-generated broadband chirp with evenly spaced components from 50 Hz to 99 kHz. For some measurements, the spectrum of the chirp stimulus was modified to reduce the level at frequencies below 5 kHz by 20 dB, so as to produce more equal stimulus sound pressures over a broader frequency range. Stimulus levels were set by a computer-controlled attenuator (TDT PA5) and the output amplifier stage of a reconstruction filter (Krohn-Hite 3901, Avon MA). Responses were digitized synchronously to the stimulus signal by a National Instruments PCI-4451 A-D card triggered by the signal generator.

2. At Princeton and Columbia

The stimulus generation and response measurement system was similar but made use of a sequence of pure tones (step size 10–15 pts./octave at Princeton, 500 Hz at Columbia). The responses to the tones were digitized synchronously with signal generation by a paired D-to-A/A-to-D converter (Princeton: TDT System II DD1; Columbia: TDT System 3 RX6; includes attenuator and driver amplifier). Sound stimuli in early experiments were delivered to the ear canal by a dynamic earphone (based on Radio Shack 40-1377, Ft. Worth, TX).

D. Probe tube and miniature fiber-optic microphone design and calibration

1. Probe-tube microphone (at MEEI)

The probe-tube microphone used at MEEI comprised a $\frac{1}{2}$ in. condenser microphone (2530, Larson-Davis, Provo, UT) and a short (13 mm) probe tube constructed of commercially available hypodermic tubing [18-gauge thin-wall, 0.97 mm i.d., 1.27 mm outer diameter (o.d.)] coupled to the microphone via a short (7 mm) exponential horn and phase plug. Experimentation showed that the 0.97 mm i.d. was sufficient to transmit sound up to 80 kHz without unacceptably large viscous losses. The receptive field of the probe tube microphone extends approximately 0.3–0.4 mm beyond its tip (~0.6 × the probe tube radius; Ando, 1968; Beranek, 1986).

2. Miniature fiber-optic microphone (at Princeton and Columbia)

The miniature fiber-optic microphone has been described previously (Olson, 1998). It consists of a glass capillary of 170 μm o.d., tipped with a gold-coated polymer diaphragm that is a fraction of a micrometer thick. Light from an infrared light-emitting diode is delivered via an optical fiber inserted into the capillary and reflects from the diaphragm. The amount of light returning through the optical fiber to a photodetector varies linearly with the pressure-induced motion of the diaphragm (Hu et al., 1992). The receptive area of the diaphragm is 100 μm in diameter, so the receptive field extends less than 0.1 mm from the diaphragm.

3. Calibration coupler and reference microphone

Both microphones were calibrated in a custom calibration coupler that positioned the measurement microphone at grazing incidence within 1 mm of the diaphragm of an $\frac{1}{8}$ in. reference pressure microphone (G.R.A.S. 40-DP, N. Olmstead OH) of known sensitivity—see Fig. 3(a). The i.d. of the coupler near the reference microphone was 2.3 mm. The tip of the measurement microphone protruded approximately 0.25 mm past the wall. The calibration coupler was also used as an artificial ear [Fig. 3(b)] and for an artificial cavity calibration—discussed in Sec. IV D.

FIG. 3.

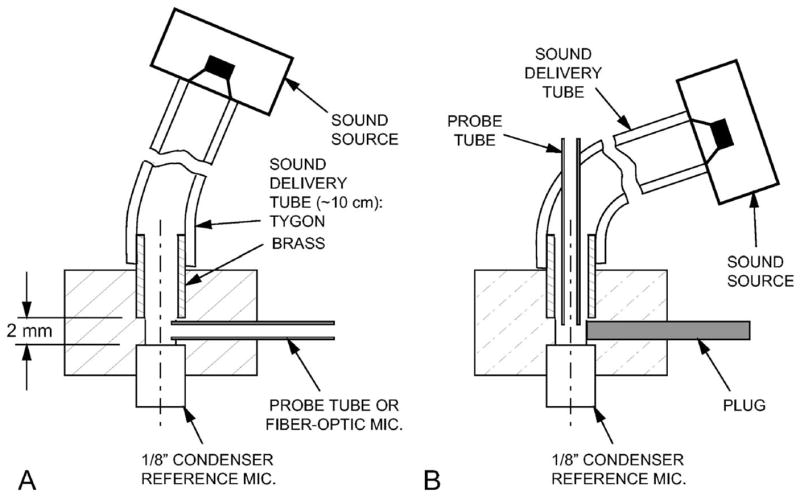
Section through the calibration coupler used (A) for microphone calibrations and (B) as an “artificial ear.” The sound delivery tube was 2.4-mm i.d. Tygon with a 2.4 mm i.d. ×6 mm long brass section that fit into the acrylic body of the calibration coupler (2.3 mm diameter in front of the $\frac{1}{8}$-in. reference microphone). For the “artificial ear calibration,” the setup in (A) was used, the probe tube was replaced with a plug as in (B), and the brass tube was withdrawn about 3 mm from the position shown.

4. Microphone calibrations

The microphone calibrations are shown in Fig. 4. The magnitude and phase of the probe-tube microphone frequency response (solid line) varied substantially with frequency. The frequencies of the magnitude peaks and the phase accumulation (equivalent to a 60-μs delay) are generally consistent with the 20-mm length of the probe-tube assembly. When the probe-tube tip was plugged, the probe-tube microphone output decreased by at least 30 dB (except at isolated frequencies near 60 kHz, where the reduction was 15–20 dB), which implies that probe-tube acoustic artifact (sound conducted through the probe tube walls) was negligible. The microphone noise floor was 5–10 dB below the acoustic artifact.

FIG. 4.

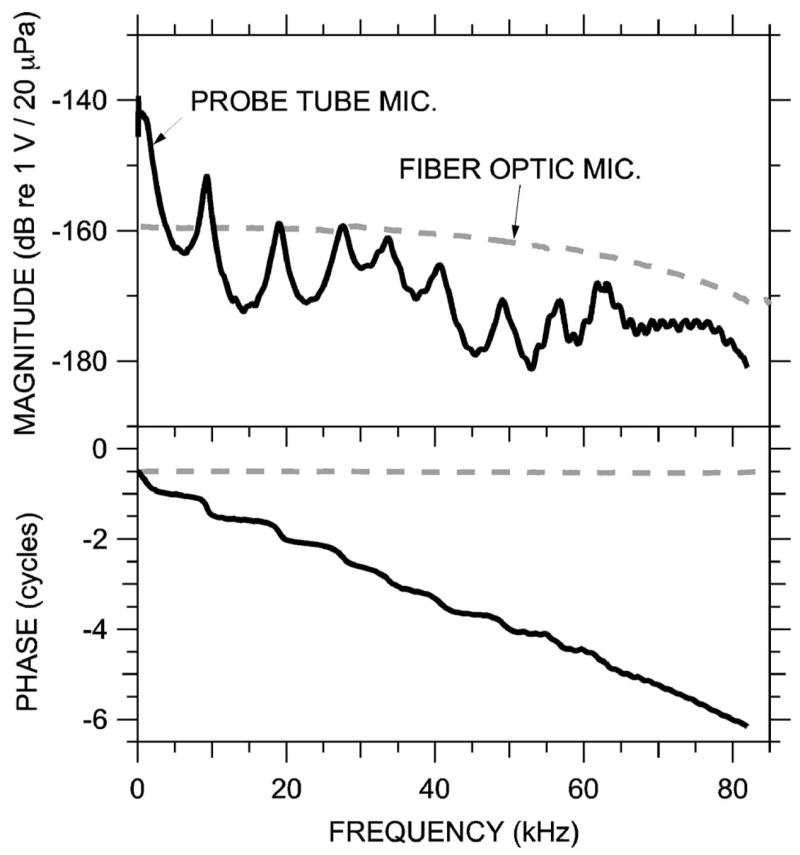
Sensitivity and frequency response of the probe-tube microphone (MEEI, solid curve) and miniature fiber optic microphone (Princeton and Columbia, dashed curve). Top: Magnitude; bottom: phase relative to sound pressure condensation.

Because the fiber-optic microphone has no probe tube and employs a very small receptive membrane, it is expected to have a flat frequency response to high frequencies. Its response in Fig. 4 (dashed line) was quite flat to 50 kHz but displayed a gradual decrease in sensitivity at the higher frequencies that reduced the response ~6 dB at ~70 kHz. The fiber-optic microphone had a higher noise floor than the probe tube microphone; its output for P_EC measurements was generally only ~20 dB above its noise floor.

Longitudinal and transverse variations in the sound field within the calibration coupler and across the diaphragm of the reference microphone impose a high-frequency limit on the accuracy of the microphone calibrations. Differences in sound pressure between the measurement microphone location and the reference microphone due to longitudinal waves were expected to be less than 2 dB below 35 kHz, <6 dB below 60 kHz, and ~12 dB at 80 kHz with the measurement microphone located 1 mm from the nearly rigid reference microphone diaphragm.⁵ These differences limit the frequency range of absolute sound pressure measurements (Fig. 14) but do not affect ratios of ear canal sound pressure (Figs. 5–13).

FIG. 14.

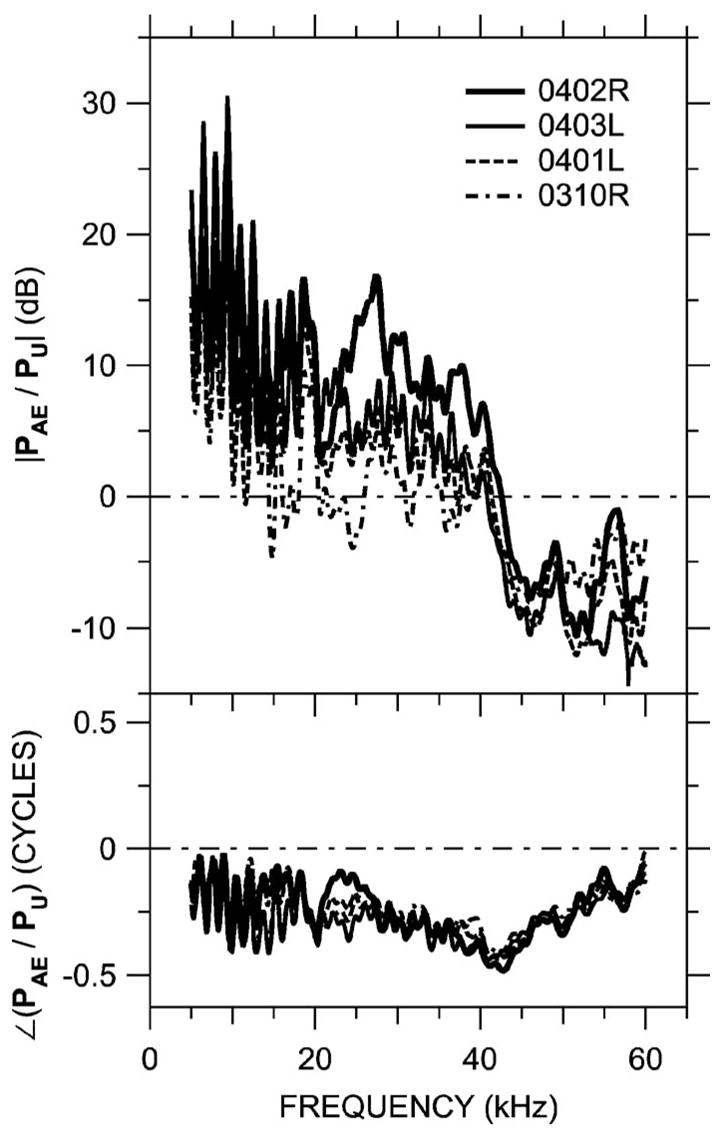
Ratio of sound pressure P_AE measured at the terminating microphone of the artificial ear to P_U measured near the umbo in four gerbil ears. The length of the artificial ear was adjusted to mimic the length of the gerbil bony ear canal. Data are not shown below 5 kHz because leaks between the probe tube and the ear canal influence the results. Top: Magnitude; bottom: phase. The artificial ear calibration overestimates P_U at low frequencies and underestimates P_U between 40 and 60 kHz.

FIG. 5.

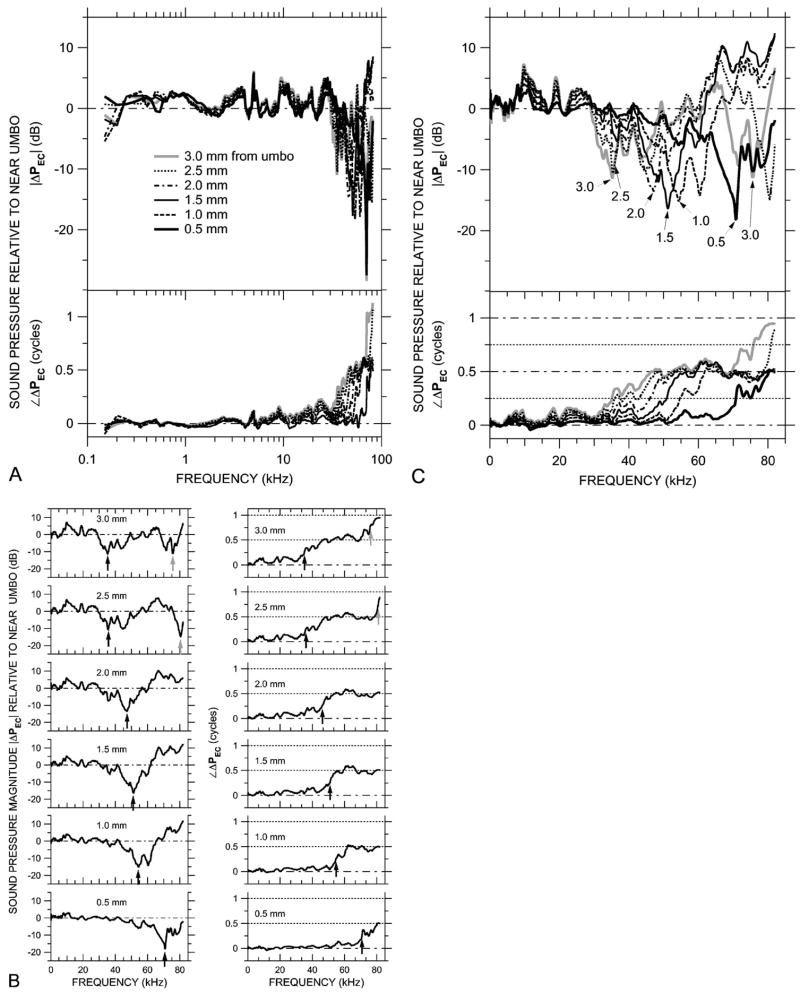
Variations in ear canal sound pressure P_EC measured in 0.5-mm steps along trajectory L [see Fig. 2(b)] in ear 0402R with the probe tube microphone (MEEI) in response to a chirp stimulus. Shown is ΔP_EC, the ratio of P_EC in various locations along the trajectory to P_EC near the umbo. (A) ΔP_EC at six locations, plotted on a logarithmic frequency scale. Variations in ΔP_EC are small below 30 kHz. Top: Magnitude ratio in decibels; bottom: phase difference. (B) ΔP_EC in the six locations, shown individually on a linear frequency scale. Left: Magnitude ratios in decibels; right: phase differences. Arrows indicate frequencies of |ΔP_EC| notches and frequencies where ∠ΔP_EC crosses 0.25 or 0.75 cycles. (C) The ΔP_EC curves from (B) superposed, plotted on a linear frequency scale. Top: Magnitude ratio in decibels; bottom: phase difference.

FIG. 13.

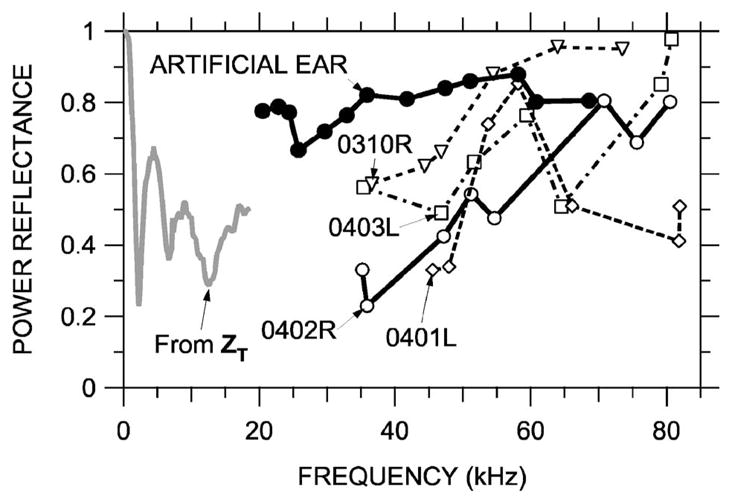
Power reflectance ℜ computed from standing wave patterns in the artificial ear and in several gerbil ear canals. Shown are: ℜ_AE in the artificial ear (thick solid line and closed symbols), computed from standing wave patterns of Fig. 11(b); ℜ_EC in ear 0402R (thick solid line, open symbols), computed from standing wave patterns of Fig. 11(a); ℜ_EC in other MEEI ears (thin dashed lines and open symbols), computed in a similar fashion; and ℜcomputed from the mean middle-ear input impedance Z_T between 100 Hz and 18 kHz in 5 gerbil ears (gray line, from Ravicz et al., 1996).

Transverse variations in sound pressure across the coupler diameter due to higher-order modes needed to be taken into account because the measurement location is near their source at the reference microphone diaphragm (e.g., Keefe and Benade, 1981). The position of the sound delivery tube along the coupler axis and the close match between the coupler and sound delivery tube i.d.s minimized antisymmetric and axisymmetric higher-order modes, respectively. Differences in sound pressure across the coupler diameter were generally antisymmetric: <3 dB for the fiber-optic microphone, <5 dB below 68 kHz for the probe tube microphone. For calibration, we computed the area-averaged sound pressure (sum of pressure measured at different radial points normalized by the area of an annulus at that radius), as suggested in Keefe and Benade (1981). (The reference microphone output follows the average pressure over its area.)

IV. RESULTS

The MEEI experiments are emphasized because they included more experimental animals and approach angles, they sampled the frequency very finely (50 Hz), and the signal-to-noise ratio was higher; unless noted, results are from MEEI. The fine frequency sampling is particularly important to computations of sound reflection. The Princeton and Columbia results using the miniature fiber-optic microphone are shown in three animals and primarily provide confirmation of the MEEI results. A possibly important difference between the MEEI and Princeton/Columbia experimental methods was the size of the pressure measuring device: the 1.27-mm-diam probe-tube microphone was larger relative to the 2.3-mm-diam ear canal than the 170 μm-diam fiber-optic microphone. The similarity of the results with the two methods is consistent with the larger probe tube having no significant effect on the sound field.

A. Sound field longitudinally within the bony ear canal

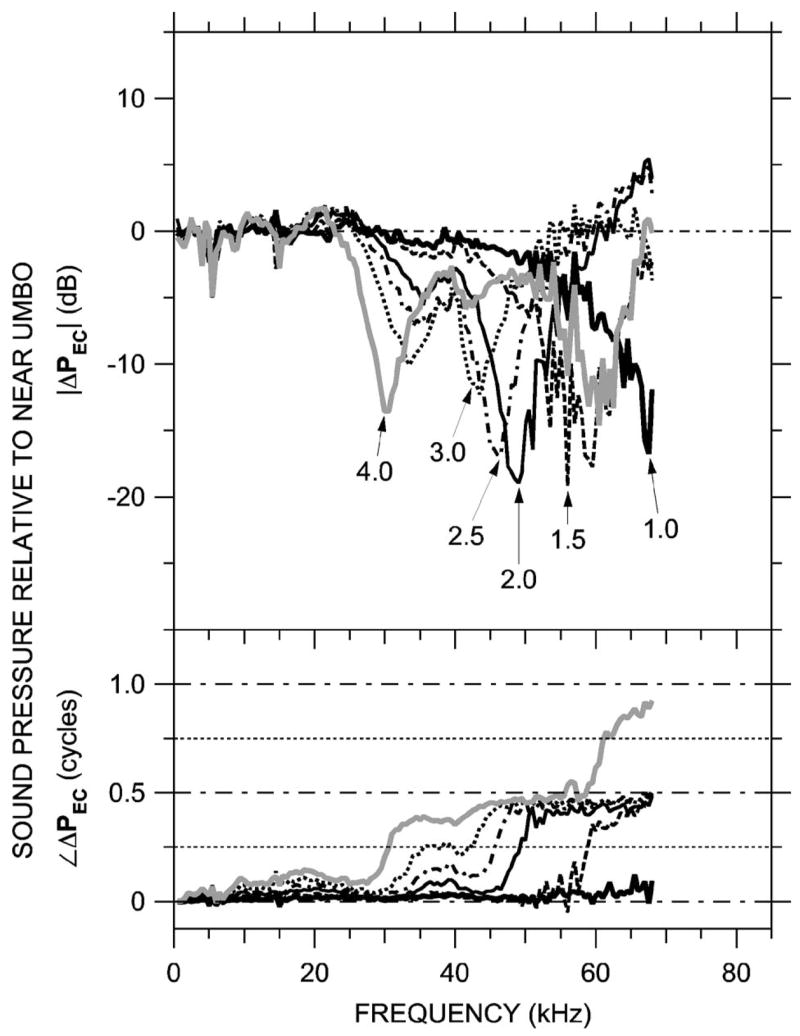
The sound pressure P_EC within the bony terminal portion of the ear canal was measured approximately longitudinally along the ear canal by advancing the probe tube along trajectory L from the lateral wall of the ear canal to a point close to the umbo, as shown in Fig. 2(b). The receptive field of the probe tube microphone extends 0.3–0.4 mm beyond the tip (see Sec. III), so for measurements of the sound field near the umbo P_U (0-mm reference location), the probe tip was actually approximately 0.5 mm from the umbo. Because we are interested in spatial variations in P_EC, we examine the ratio of P_EC measured at various locations along the trajectory to P_U. Such ratios are denoted as ΔP_EC. The top panel of Fig. 5(a) shows the magnitude of the spatial variations in sound pressure |ΔP_EC| in an ear canal (0402R); the bottom panel shows the corresponding variations in phase ∠ΔP_EC. Microphone and physiological noise were at least 30 dB below |ΔP_EC| maxima and about 10 dB below |ΔP_EC| minima. At frequencies below 30 kHz, the variations in ΔP_EC along the trajectory were less than 6 dB in magnitude and 0.2 cycles in phase. The sound pressure was lowest near the umbo: |ΔP_EC| was generally greater than 0 dB. Below 10 kHz the phase differences were less than 0.1 cycle; between 10 and 30 kHz, ∠ΔP_EC became more negative as the distance from the umbo increased, consistent with sound wave propagation along the trajectory. Above 30 kHz, |ΔP_EC| varied between +10 and −25 dB and ∠ΔP_EC varied up to 1 cycle. At this 30-kHz break frequency, the 3-mm distance between the EC wall and the reference location near the umbo corresponds to about one-quarter of the sound stimulus wavelength.

These high-frequency variations in ΔP_EC magnitude and phase can be seen more clearly when each ΔP_EC measurement is plotted separately on a linear frequency scale. Figure 5(b) shows ΔP_EC magnitude (left panels) and phase (right panels) as the probe tube was moved from the lateral EC wall (top) toward the umbo (bottom). Each |ΔP_EC| curve shows one or more pronounced notches, and each ∠ΔP_EC curve shows one or more 0.5-cycle steps. The frequencies of the first magnitude notch (black arrows in left panels) correspond closely (within 5%) to the frequencies midway in the first phase step (where ∠ΔP_EC is 0.25 cycles—black arrows in right panels). The notch frequencies increased as the measurement location approached the umbo. (The curve for ΔP_EC 1.0 mm from the umbo shows a double magnitude notch and a dip in ∠ΔP_EC near 0.25 cycles. Sound pressure at this location was most variable among ears—discussed in Sec. V C.) A second magnitude notch and phase step were observed in the two measurements most distant from the umbo. In these measurements, the frequencies of the second magnitude notch (gray arrows in top left panels) correspond to the frequencies midway in the second phase steps (where ∠ΔP_EC is 0.75 cycles—gray arrows in top right panels). These notches and phase steps indicate that the sound field becomes more complex at high frequencies but also indicate that the field has an ordered structure.

It will be convenient for comparisons of these results acquired at the MEEI to results acquired at Columbia to condense the curves of Fig. 5(b) into a single pair of panels (magnitude and phase). Figure 5(c) superposes the ΔP_EC magnitude (top) and phase data (bottom) from Fig. 5(b). The changes in the ΔP_EC magnitude notch and phase step frequencies with measurement location can be seen clearly. At frequencies where |ΔP_EC| notches occur, the difference between the maximum and minimum |ΔP_EC| among the measurement locations increases as the notch frequency increases.

Figure 6 shows data taken similarly at Columbia with the miniature fiber-optic microphone in the bony ear canal of animal ESO3 along a similar trajectory L [Fig. 2(b)], using the same sound coupler at the bony EC entrance. The results are very similar to those of Fig. 5. The sound pressure was measured over a wider spatial range than the measurements in Fig. 5 (to 4 mm from the umbo as opposed to 3 mm),⁶ and the magnitude notch and phase change at the measurement locations furthest from the umbo occurred at a lower frequency (30 Hz vs 35 kHz in 0402R). There are many similarities between the two data sets: Both sets are clearly separable into low- and high-frequency regions, with the low-frequency regions (<25 kHz in Fig. 6) characterized by little variation in magnitude (<6 dB) or phase (<0.1 cycle) and the high-frequency region characterized by spatial variations of 10–20 dB. The |ΔP_EC| minima occur at approximately the same frequencies where ∠ΔP_EC crosses 0.25 or 0.75 cycles (±15%). In Fig. 6, as in Fig. 5, the difference between the maximum and minimum |ΔP_EC| tended to increase above about 45 kHz. The noise floor in the fiber optic microphone was sufficiently high that |ΔP_EC| at the notches should be considered as an upper bound at frequencies above 40 kHz, where the sound source output and thus the microphone signal-to-noise ratio were lower.

FIG. 6.

Variations in ear canal sound pressure P_EC measured in 0.5-mm steps along trajectory L [see Fig. 2(b)] in ear ESO3 just post-mortem with the miniature fiber optic microphone (Columbia) in response to a series of tones. Shown is ΔP_EC at six locations, computed as in Fig. 5 and plotted on a linear frequency scale. Top: Magnitude ratio in decibels; bottom: phase difference. Variations in ΔP_EC with position and frequency are similar to those in Fig. 5.

These same patterns (high-frequency ΔP_EC magnitude notches and phase steps that increase in frequency as the measurement position approaches the umbo) were observed in three other ears at MEEI in which P_EC was measured near the umbo. Figure 7 shows ΔP_EC computed from measurements made at the bony EC entrance and near the umbo from five animals—four at the MEEI (including 0402R, the animal in Fig. 5) and ESO3 (from Fig. 6). In these five ears the pressure transformation from the EC entrance to near the umbo was similar: |ΔP_EC| in all ears had a minimum of 12–15 dB and an associated phase transition near 35 kHz, and |ΔP_EC| in three ears had a 6–10 dB maximum near 60–65 kHz. (The 3-mm distance between umbo and EC entrance is approximately $\frac{1}{4}$ wavelength at 30 kHz and $\frac{1}{2}$ wavelength at 60 kHz.) Figure 7 shows that the bony ear canal produces a pressure gain from EC entrance to umbo of 6–15 dB between 30 and 50 kHz. The similarity between MEEI and Columbia data indicates that the larger probe tube used for the MEEI measurements had little effect on the EC sound field.

FIG. 7.

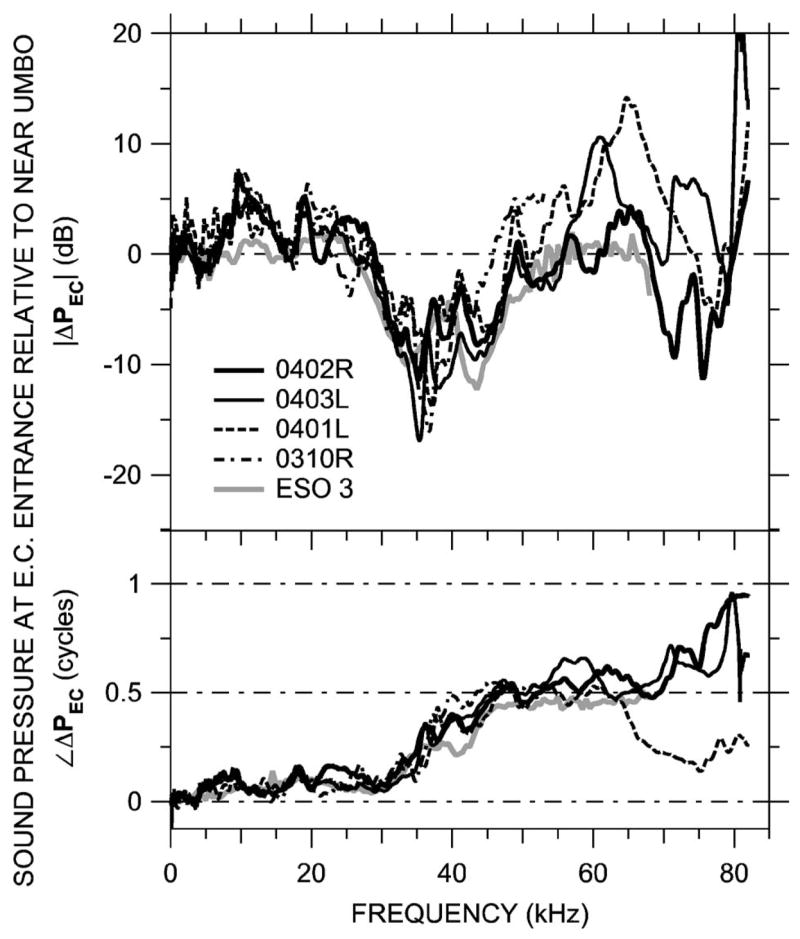
ΔP_EC near the opening of the bony ear canal in five ears measured at MEEI and Columbia. Top: Magnitude ratio in decibels; bottom: phase difference.

B. Sound field medio-axially and transversely across the ear canal

The sound field was also measured along two other trajectories across the ear canal. P_EC was measured in two animals at Princeton along a medio-axial trajectory “MA:” The sensor was placed in the ear canal through a small hole in the bony lateral wall and was advanced until it touched the umbo—see Fig. 2(b). This trajectory was more perpendicular to the tympanic ring than the approximately longitudinal trajectory L measured in the previous section. The results, shown for one animal as ΔP_EC (computed as earlier) in Fig. 8, show similarities to those obtained from trajectory L (Figs. 5 and 6): There was <6 dB spatial variation in P_EC at frequencies below 30 kHz, and local minima in |ΔP_EC| of up to 19 dB appeared at frequencies between 43 and 53 kHz. The minima were accompanied by a half-cycle increase in ∠ΔP_EC. (The upper frequency limit of these measurements was 58 kHz.) The ΔP_EC curves in Fig. 8 generally resemble those in the third and fourth rows of Fig. 5(b), measured 2.0 and 1.5 mm from the umbo, respectively. Figure 2(b) shows that the trajectory MA samples the same section of the ear canal as the medial extent of trajectory L, so the similarity in ΔP_EC measured along these two trajectories is not surprising.

FIG. 8.

Variations in ear canal sound pressure P_EC measured in 0.6-mm steps along a medio-axial trajectory “MA” [see Fig. 2(b)] in ear ESO2 with the miniature fiber optic microphone (Princeton) in response to a series of tones. Shown is ΔP_EC at five locations, computed as in Fig. 5 and plotted on a linear frequency scale. Top: Magnitude ratio in decibels; bottom: phase difference. Variations in ΔP_EC with position and frequency resemble those in Figs. 5 and 6 at locations 1.5 and 2.0 mm from the umbo.

Ear canal sound pressure was measured in three postmortem animals (due to anatomical constraints in the live ear—see Sec. III) at MEEI along the transverse trajectory shown in Fig. 2(c). The low height of the TM over the ear canal limited measurements to ±1 mm from the umbo. The results, shown normalized by P_U as in earlier figures for one animal in Fig. 9, are very different from ΔP_EC along the longitudinal and medio-axial trajectories. Variations with position were less than 2 dB in magnitude and 0.05 cycles below 70 kHz, except slightly larger (~4 dB) near the EC wall above 40 kHz. Between 40 and 70 kHz the variations 0.5 mm away from the umbo are symmetric: for |ΔP_EC| in decibels and ∠ΔP_EC in cycles, ΔP_EC at +0.5 mm≈ −ΔP_EC at −0.5 mm. Similar results were obtained in two other animals. These results suggest that the largest variations in the sound field within the terminal portion of the bony ear canal occur along the ear canal axis—variations in the transverse direction due to higher-order modes are small.

FIG. 9.

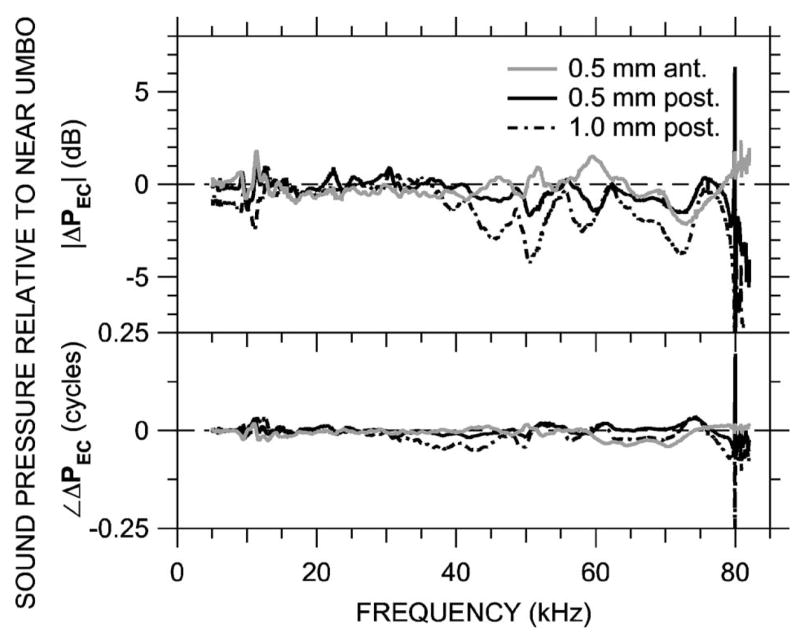
Variations in ear canal sound pressure P_EC measured in 0.5-mm steps along an transverse trajectory 0.5 mm from the tympanic ring [see Fig. 2(c)]in ear 0305L (just post-mortem) with the probe-tube microphone (MEEI) in response to a chirp stimulus. Shown is ΔP_EC at three locations, computed as in Fig. 5 and plotted on a linear frequency scale. Variations in ΔP_EC are small below 70 kHz. Top: Magnitude ratio in decibels; bottom: phase difference.

C. Stapes velocity with probe tube in various places in ear canal

The similarity of EC sound field measurements with the 1.27-mm-diam probe tube and the 0.17-mm-diam fiber optic microphone (Figs. 5–7) supports the idea that the probe tube did not disturb the sound field substantially. Another estimate of the perturbation of the EC sound field is the degree of variation in measured stapes velocity when the probe tube was advanced along the longitudinal trajectory within the ear canal. In the same ear in which the longitudinal ΔP_EC was shown (g0402R—Fig. 5), stapes velocity was virtually unaffected by the position of the probe tube below 60 kHz: Variations were less than a factor of 2.

The above-described example was the “best case;” in the other MEEI ears shown in Fig. 7, the results were similar but the effects on stapes velocity occurred at lower frequencies (as low as 50 kHz). Our interpretation is that variations in probe-tube position within the ear canal caused the effect of the probe tube on the sound field to be larger or extend to lower frequencies in some ears compared to others. Another explanation of some of this variability in stapes velocity may be complexity in stapes motion at high frequencies (Olson and Cooper, 2000; Decraemer et al., 2007). Our results show that it is possible to measure P_EC at frequencies up to 60 kHz with a probe tube that is relatively large compared to the ear canal cross-section area (~30%) with little perturbation of the EC sound field near the umbo.

D. Sound field in an artificial ear

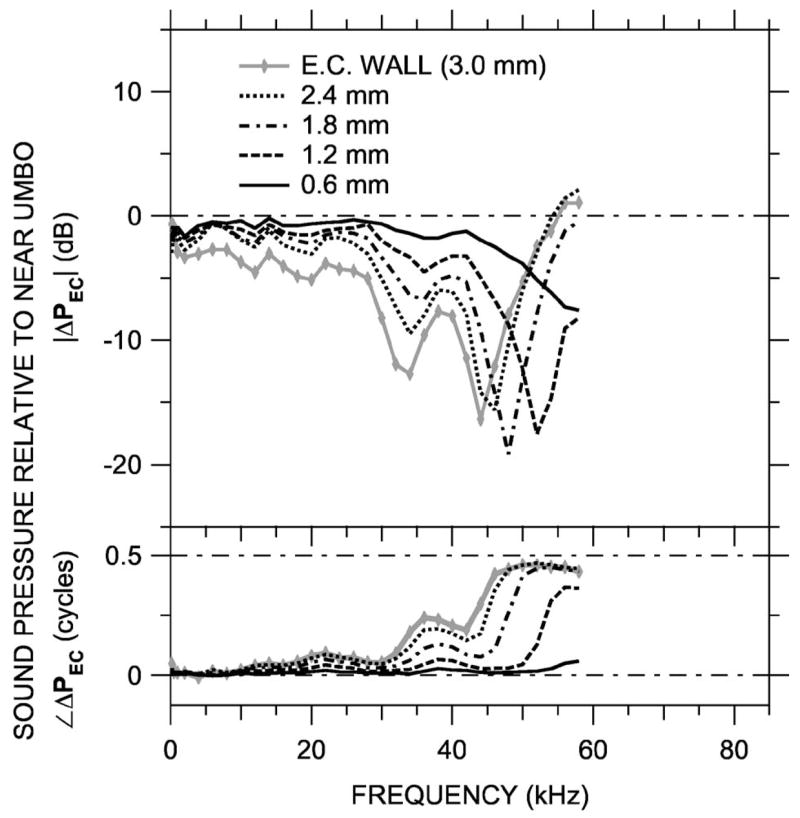
As a further test of the effects of the probe tube on the sound field in the ear canal, as well as a comparison of probe-tube measurements to other methods of estimating sound pressure at the TM, the sound pressure distribution was measured with the probe tube (at MEEI) in a simple artificial ear: the calibration coupler in the arrangement shown in Fig. 3(b). The earphone, sound delivery tube, and stimulus type (chirp) used were the same as for the EC measurements of Figs. 5, 7, and 9.

Two sets of measurements were made: In the first set, the flexible portion of the sound delivery tube was bent so the same probe tube used for P_EC measurements could be introduced through a hole in the wall and advanced axially toward the terminating microphone [Fig. 3(b)]. In this way, the sound pressure field P_AE within the artificial ear could be sampled in much the same way as P_EC was measured within the ear canal. In this setup, P_AE was measured at finer spatial increments (0.25 mm) than in the ear canal; representative measurements at 0.5-mm spacing normalized by P_AE near the terminating microphone (ΔP_AE) are shown in Fig. 10(a). A comparison with ΔP_EC in Fig. 5(b) shows a similar ordered structure for measurements 2.0 mm or more from the termination: each such |ΔP_AE| curve (left panels) shows one or more pronounced notches, and each such ∠ΔP_AE curve (right panels) shows one or more 0.5-cycle steps. Frequencies of the first magnitude notch (black arrows in left panels) correspond closely (within 2%) to the frequencies midway in the first phase steps (where ∠ΔP_AE is 0.25 cycles—black arrows in right panels). The notch frequencies increased as the distance from the probe tube to the termination decreased. A second notch and corresponding phase shift were observed in the more distal measurements (gray arrows). The depth of the first |ΔP_AE| notches (measured maximum-to-minimum) was about 27 dB and roughly constant across frequency. Figure 10(b) shows the curves superposed as in Fig. 5(c).

FIG. 10.

Variations in sound pressure P_AE measured axially in 0.5-mm steps within an artificial ear with the probe-tube microphone (at MEEI) in response to a chirp stimulus. The artificial ear was terminated with a $\frac{1}{8}$-in. condenser microphone. (A) ΔP_AE, the ratio of P_AE at six locations to P_AE near the termination, shown individually on a linear frequency scale. Left: Magnitude ratios in decibels; right: phase differences. Arrows indicate frequencies of |ΔP_AE| notches and frequencies where ∠ΔP_AE crosses 0.25 or 0.75 cycles. (B) The ΔP_AE curves from (A) superposed, plotted on a linear frequency scale. Top: Magnitude ratio in decibels; bottom: phase difference.

During these first measurements, the output of the $\frac{1}{8}$- in. reference microphone was recorded as well to estimate the effect of the probe tube on the sound field in the artificial ear and, by extension, in the ear canal. Changes in reference microphone output were generally about 3 dB below 60 kHz. Between 60 and 80 kHz variations were slightly larger (5 dB) and showed a decrease in |P_AE| consistent with shadowing. The magnitude of these effects was substantially less than the longitudinal P_AE variations, which suggests that the probe tube did not disrupt the sound field substantially.

In the second set of measurements, the probe tube microphone [Fig. 3(a)] was replaced with a plug, and the brass portion of the sound delivery tube was withdrawn approximately 3 mm from the calibration coupler. The dimensions of this extra space approximated the gerbil ear canal dimensions for a “uniform-tube calibration” (Pearce et al., 2001) or “artificial-cavity calibration” (Overstreet and Ruggero, 2002). The sound pressure at the termination measured with the reference microphone is compared with P_U in Sec. V F.

V. DISCUSSION

A. Basic description of EC sound field from measurements in situ

Our in situ measurements of sound pressure P_EC at multiple points within the bony gerbil ear canal (Figs. 5–9) lead to the following description of how sound pressure varies in the ear canal near the tympanic membrane:

1. The measurements along approximately longitudinal trajectories indicate that at frequencies below 30 kHz the spatial dependence of the measured sound pressure is small [Figs. 5(a) and 7]. P_EC measured at any frequency in this range is relatively independent of axial position: Spatial variations are less than ~5 dB in magnitude and 0.1 cycles in phase. At frequencies above 30 kHz, spatially dependent variations in P_EC were observed that were > 15 dB in magnitude and 0.25–1 cycle in phase. Therefore, measurements of the sound pressure at a single point within the bony ear canal provide a reasonably accurate estimate of sound pressure at the TM at frequencies less than 30 kHz, but above 30 kHz the accuracy of a remote TM sound pressure estimate diminishes (see the discussion in Dong and Olson, 2006).

2. The sound pressures measured along our longitudinal trajectories show pronounced minima in the frequency domain that coincide with half-cycle phase transitions (Figs. 5 and 6). The frequencies of the minima and phase transitions vary with axial position: Minima occurred at 30–35 kHz in measurements 2.5–3.0 mm from the umbo (near the opening in the lateral EC wall) and at 55–60 kHz in measurements within 1 mm of the umbo. P_EC along a medio-axial trajectory (Fig. 8) had a frequency dependence that was similar but compressed in frequency. As will be discussed in Sec. C, the frequency and location dependence of these minima and their associated phase changes suggest the presence of standing waves in the terminal portion of the ear canal.

3. Sound pressures measured along a transverse trajectory in the plane of the tympanic ring about 0.5 mm from the umbo are generally uniform, varying by less than 4 dB in magnitude at frequencies up to ~70 kHz (Fig. 9). This result suggests that below 70 kHz, the concept of a stimulus sound pressure “at” the gerbil TM is reasonable. This result also suggests that the sound field in other species with simpler ear canals is likely to be simple near the TM.

B. Effects of measurement conditions on ear canal sound field

The conclusions drawn about the nature of the ear canal sound field rely on an assumption that any effect the probe tube has on the sound field is small: Neither occlusion of the ear canal nor any sound shunt path provided by the probe tube is significant. The probe tube occluded the EC cross-section area by about 30%. Several lines of evidence suggest that the effect of the probe tube on the sound field was minor: (1) In general, stapes velocity changed by less than a factor of 2 below about 60 kHz as the probe tube was moved into and out of the ear canal. (2)When the probe tube was introduced into the calibration coupler or advanced in the artificial ear (as for Fig. 10), the output of the terminating microphone changed by less than 3 dB. (3) The diameter of the miniature microphone (used at Princeton and Columbia) was only 15% of that of the probe tube (used at MEEI), yet longitudinal sound pressure variations measured with the miniature microphone (Fig. 6) were nearly identical to those measured with the probe tube (Fig. 5). (4) The spatial locations of |P_AE| notches in the artificial ear match their theoretical location, and the depth of |P_AE| notches was independent of probe tube location (see Sec. V C). These lines of evidence suggest that the presence of the probe tube did not change the nature of the sound field in the ear canal.

Though the measurements at MEEI along a longitudinal trajectory were made in a live preparation, the longitudinal measurements at Columbia were made post-mortem, as were measurements at MEEI along a transverse trajectory. Past studies have shown little effect of death on middle-ear input or transmission properties: For instance, Rosowski et al. (1990) demonstrated that the middle-ear input admittance of guinea pigs was not greatly affected by the death of the animal. While post-mortem changes in active cochlear mechanics are large, passive intracochlear pressure and BM motion change little post-mortem as long as the cochlear fluid is not depleted (Olson, 2001; Ren and Nuttall, 2001; Cooper, 2000), so there should be little effect on middle-ear input impedance or P_EC. Measurements of longitudinal sound pressure patterns in one ear at MEEI post-mortem versus alive showed only small differences except above 50 kHz: |P_EC| notch depths were within 1 to 2 dB of those in live ears below 50 kHz and 5 dB or so less at higher frequencies.

C. Evidence for longitudinal standing waves within the ear canal

The sound pressure spectra measured at various locations along an approximately longitudinal trajectory in the ear canal (Figs. 5 and 6) have much in common with the theoretical frequency dependencies associated with a standing wave pattern [Fig. 1(b)]. In each case, spectra at locations far from the TM have two magnitude notches and a 0.5-cycle phase step at the notch frequencies, and the notch/phase step frequencies increase as the observation location is moved toward the TM. A comparison of Fig. 5(c) with Fig. 1(b) suggests that the sound field in the ear canal is a combination of a traveling wave and a standing wave, with B/A≈0.7 near 30 kHz.

The ear-canal and artificial-ear spectra of Figs. 5, 6, and 10 also have some features that are not present in the theoretical curves of Fig. 1(b): Fig. 5(c) shows double |ΔP_EC| notches and ∠ΔP_EC ripple at 1.0 mm from the umbo (and to a lesser extent, 2.5 mm), and Figs. 6 and 10 show |ΔP_EC| >0 dB and ∠ΔP_EC<0.5 cycles at higher frequencies. These differences suggest the presence of higher-order modes at high frequencies, possibly generated by the TM or by changes in ear canal cross section. We will discuss the limitations of higher-order modes on reflectance estimates in the next section.

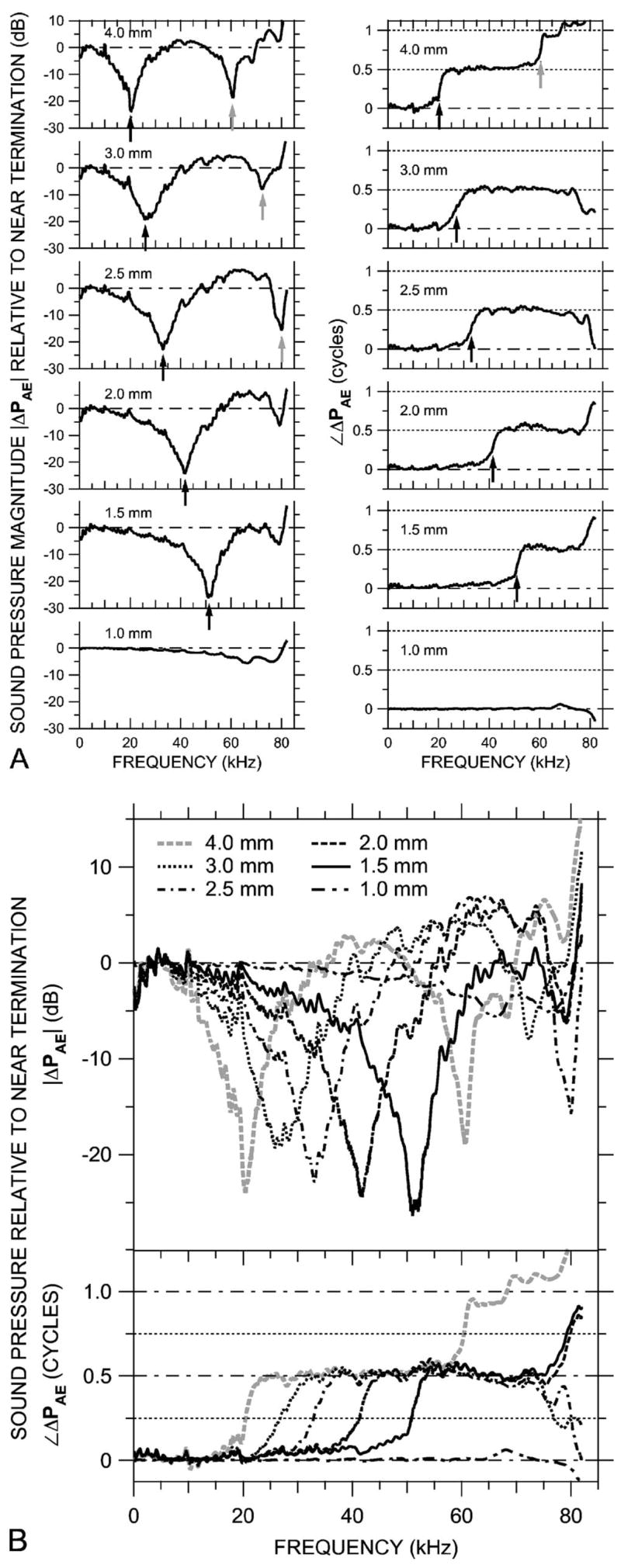
Another more descriptive demonstration of the similarity between our measurements and the theoretical standing wave patterns of Fig. 1 is provided by constructing the spatial dependence of the sound pressure field from spectra measured at various locations within the ear canal or the artificial ear. Each curve in Fig. 11(a) shows the spatial distribution of ΔP_EC at a frequency where one of the ΔP_EC spectra in Fig. 5(c) had a magnitude minimum. Each such isofrequency curve was constructed from the data in Fig. 5(c) in the following manner: (1) Frequencies at which |ΔP_EC| had a clear minimum at any measurement position were identified; (2) |ΔP_EC| at these frequencies at each measurement position was extracted; (3) the maximum |ΔP_EC| among the measurement positions at each of the frequencies was identified and used to normalize the other |P_EC| measurements at that frequency; and (4) the normalized |ΔP_EC| values at each frequency were plotted as a function of measurement position in the top panel of Fig. 11(a). A similar procedure was used to prepare the plots of ∠ΔP_EC versus position in the bottom panel of Fig. 11(a), though the minimum ∠P_EC was used as the normalization factor. Figure 11(b) shows similar curves at the frequencies of the magnitude minima in the ΔP_AE spectra in Fig. 10. (Note that these frequencies are not intrinsically special; if different axial positions had been sampled, the minima would have occurred at different frequencies.) The data in Figs. 5 and 10 were finely sampled in frequency (50-Hz spacing within the chirp), so it was possible to choose a frequency where a pronounced dip was present and be sure that the depth of the minimum was captured.

FIG. 11.

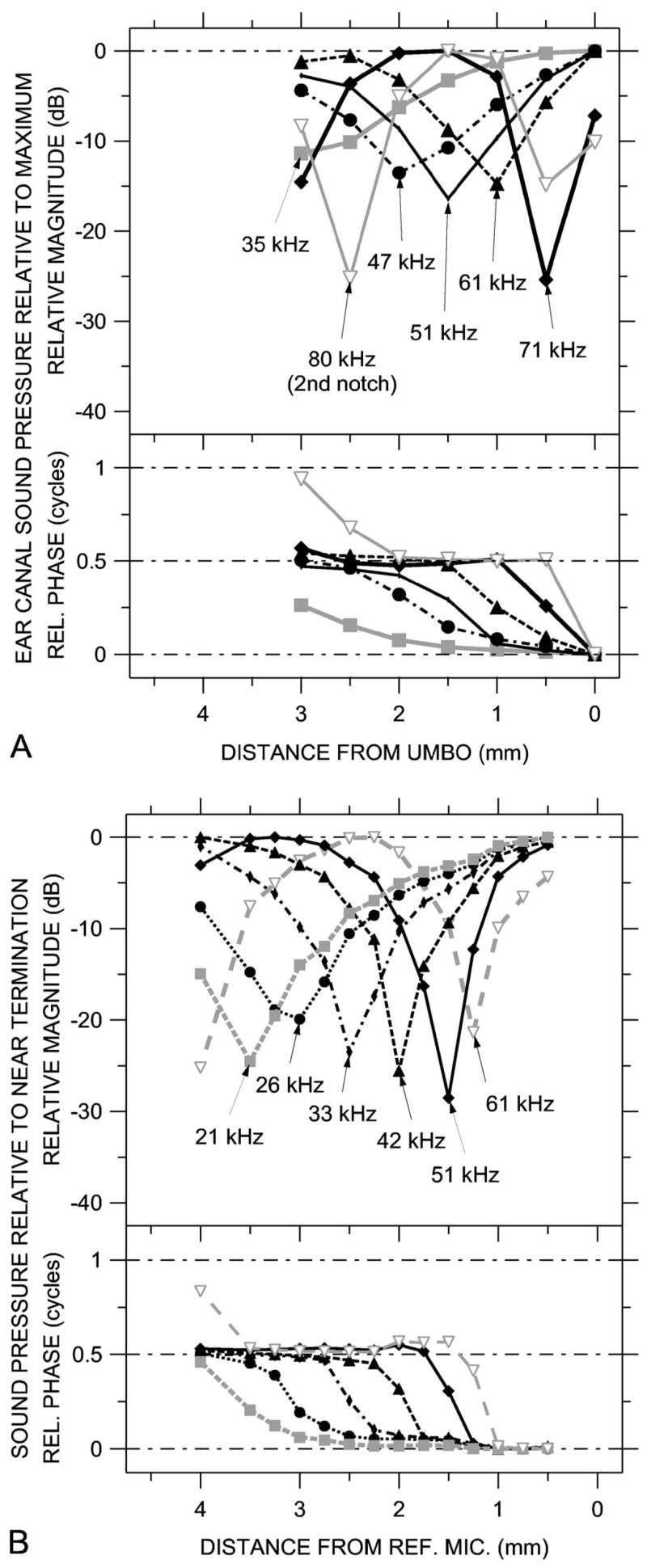
Standing wave patterns at frequencies of notches in sound pressure spectra, constructed from sound pressure spectra measured at various locations. Because the MEEI data were taken with a chirp (broadband) stimulus, the frequencies at which notch minimums occurred could be identified reliably. (A) Standing wave patterns in ear 0402R computed from ΔP_EC at various EC locations, from Fig. 5(c). (B) Standing wave patterns in the artificial ear computed from ΔP_AE at various locations, from Fig. 10(b). Top: Magnitude at frequencies of magnitude notches; bottom: Phase at frequencies of magnitude notches.

The spatial sound pressure distributions in Fig. 11 show that the sound fields in the ear canal and the artificial ear have the same basic structure as the theoretical standing wave patterns of Fig. 1(a). Specifically, the spatial distributions of both ΔP_EC in Fig. 11(a) and ΔP_AE in Fig. 11(b) show a pronounced magnitude notch and a half-cycle phase accumulation from one side of the notch to the other. At the highest frequencies an additional magnitude notch and half-cycle phase accumulation can be seen at the measurement point most distant from the umbo or termination. In the ear canal, the notches at the high frequencies of 71 and 80 kHz are deeper than the notches at lower frequencies (35–61 kHz); in the artificial ear, the depth of the notches is roughly constant. A comparison of Fig. 11(a) with Fig. 1(a) suggests that the magnitude of the pressure reflection coefficient B/A in the ear canal is approximately 0.9 near 70 kHz and closer to 0.7 at lower frequencies. The similarities of both the EC sound pressure spectra and spatial distributions to the theoretical spectra and standing wave patterns of Fig. 1 support the notion that the sound field in the ear canal is a combination of a traveling wave and a standing wave.

A more quantitative comparison of the salient features of ΔP_EC and EC standing wave patterns to the theoretical sound field is shown in Fig. 12. In Fig. 12, the frequencies of the first (lowest-frequency) |ΔP_EC| and |ΔP_AE| notches at the various measurement locations are compared to the theoretical location of the first sound pressure null in the artificial ear. We assume that the reference microphone is a rigid termination (see Sec. V D), so the distance from the null to the termination is equal to λ/4 (e.g., Kinsler et al., 1982). The locus of |ΔP_AE| notch frequencies in the artificial ear [Fig. 12(a)—closed symbols] matches the theoretical curve quite well in location and shape.

FIG. 12.

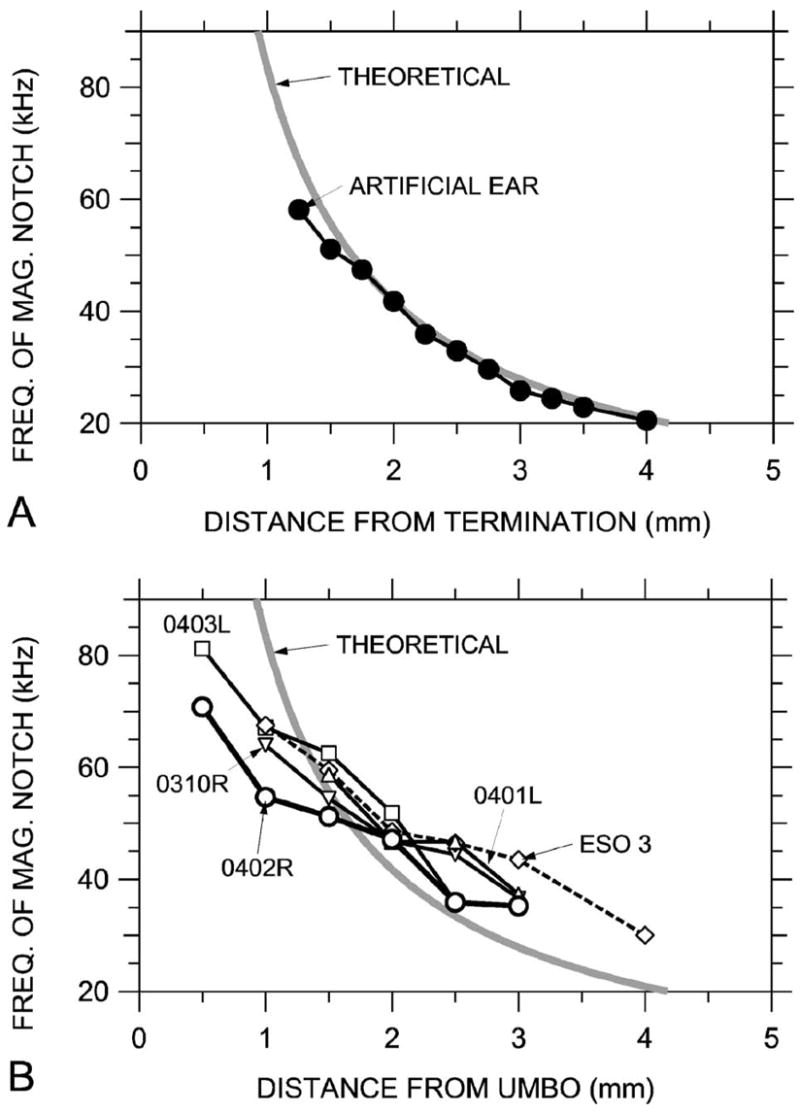
Comparison of the frequencies of sound pressure magnitude notches at measurement locations to the theoretical $\frac{1}{4}$-wave notch frequencies and locations in a rigidly terminated uniform tube (thick gray line). (A) In the artificial ear terminated by a reference microphone, 0.25 mm spacing—closed symbols. (B) In five ear canals.

Frequencies of |ΔP_EC| notches [Fig. 12(b)—open symbols] vary somewhat from the theoretical: At locations fairly remote from the umbo, where the first notch occurs below about 40 kHz, the slope of the notch frequency versus distance curve is similar to the theoretical. The curves are offset to the right, which implies that the effective length of the ear canal was less than its actual length. At locations closer to the umbo, where the notch occurs between 45 and 55 kHz, the slope is shallower, as if the effective length of the ear canal were increasing. Possible reasons for this apparent stretching of the standing-wave pattern include the following (1) Variations in the ear canal cross-section area. These variations affect the acoustics in ways that can be interpreted as changing the effective EC length (Benade, 1990, pp. 473–476). (2) A change in the nature of the TM impedance. If the TM impedance became more compliance-dominated or less mass-dominated as frequency increased, a phase shift in the sound wave reflected from the TM could make the ear canal appear longer.⁷ (3) A mismatch between the trajectory of the probe tube and the effective axis of the curved ear canal. If the probe-tube trajectory is along the outside of the curve (so that normal planes evenly spaced along the axis diverge), the spacing between magnitude notches could be larger than along the EC axis (e.g., Stinson, 1990). (4) Effects of the EC flare and curvature near the TM that limit the utility of a description of the ear canal as a (nearly) uniform tube with a normal termination. In cat and human, the TM terminates the ear canal obliquely so that the TM may be considered a compliant section of EC wall, and this oblique termination increases the complexity of the standing wave pattern (Stinson and Khanna, 1989; Stinson, 1990). The EC geometry in gerbil is even more complicated than in these two species, so a simple one-dimensional model may not be adequate to predict |P_EC| notch locations to a high degree of accuracy; a 3D model may be necessary.

D. Computation of middle-ear power reflectance and absorption from standing wave patterns

The standing wave ratios from standing wave patterns of Fig. 11(a) and spectra of Fig. 5 are used in Eq. (3) to compute the ear-canal sound power reflectance ℜ_EC, the fraction of the incident sound power that is reflected at the tympanic membrane (and not transmitted into the middle ear). We also compute the reflectance ℜ_AE from SWRs in the artificial ear [Fig. 11(b)], and we compute the theoretical reflectance ℜ_theo of the calibration coupler from its characteristic impedance Z₀ =4ρ₀c/πd² (from Sec. II) and the impedance of the terminating microphone Z_mic by

$${\Re }_{\text{theo}}={\left(\frac{{\mathbf{Z}}_{\text{mic}}-Z_0}{{\mathbf{Z}}_{\text{mic}}+Z_0}\right)}^2$$ (4)

(e.g., Kinsler et al., 1982).⁸ Discrepancies between the measured and theoretical reflectances are used to estimate errors and limits of ear-canal reflectance measurements.

Figure 13 shows that ℜ_AE computed from standing wave patterns in the artificial ear is about 0.7–0.8 [from Fig. 11(b)—thick line and closed circles]. This value is somewhat lower than the theoretical reflectance ℜ_theo≈1 across the frequency range. Because ℜ_AE was computed from the depth of the |ΔP_AE| notches, this discrepancy implies that real or apparent sound pressure not associated with the incident or reflected plane wave was present at the notch frequencies, thereby making |ΔP_AE| at the notch greater than it would be were this other sound pressure not present. A closer look at Fig. 10(b) shows that some of the |ΔP_AE| spectral notches appear flattened at the bottom, in contrast to the sharp tips in the theoretical spectra in Fig. 1(b). The presence of extra sound pressure at the |ΔP_AE| notches would cause the SWR and hence ℜ_AE to be underestimated and puts an upper bound of about 0.8 on the reflectance measurable by this method.

Possible mechanisms for notch-flattening include: apparent sound pressure from environmental noise, microphone self-noise, or probe tube artifact (see Sec. III D); and real sound pressure from higher-order modes. We examine these possibilities in turn: (1) The noise floor (includes environmental and microphone noise) was 5–10 dB below the probe tube artifact, which was itself at least 30 dB below the microphone signal in the calibration (see Sec. III). If the SWR is limited by artifact to a maximum of 30 dB (ratio of |P_AE| at notch to |P_AE| at maximum=0.03), the maximum measurable ℜ_AE [by Eq. (3)] is 0.89. This result suggests that there is some other source of the extra sound pressure. (2) Higher-order modes may be generated at the termination and decay over a small but finite distance that increases at frequencies close to the propagation frequency (88 kHz for the 2.3-mm calibration coupler). These higher-order modes do not transmit energy below their propagation frequencies (Pierce, 1981, p. 316), but their presence complicates estimates of the standing wave ratio. A maximum measurable ℜ_AE of 0.8 suggests [by rearranging Eq. (3)] that the sound pressure contributed by higher-order modes in the artificial ear is ~0.1A (the sound pressure in the incident plane wave) or ~26 dB below the maximum |P_AE|. The result that transverse P_EC variations near the TM are small (1 to 2 dB; see Fig. 9) implies that the contribution of higher-order modes to EC sound pressure is comparable to that in the artificial ear. This implies in turn that, though measurement of reflectances >0.8 are problematic, reflectances below 0.8 can be measured accurately.

Figure 13 also shows the power reflectance ℜ_EC computed from standing wave patterns in ear canals. ℜ_EC in animal 0402R [from Fig. 11(a)—thick line and open circles] was relatively low at the lower frequencies (0.2–0.3 near 35 kHz) and increased at higher frequencies to a value comparable to that measured in the artificial ear (0.7–0.8 near 70 kHz). Because 0.8 is the maximum reflectance we can measure, it is possible that ℜ_EC is even higher at high frequencies. Similar results were obtained in three other animals (thin lines and open symbols). The variability in ℜ_EC was about 0.1 among several measurement sets in animal 0402R and about 0.2 in the other ears. In all ears ℜ_EC was low at 35–45 kHz and increased with frequency.⁹

Figure 13 also includes the power reflectance ℜ_T computed by Eq. (4) from previous measurements of gerbil middle-ear input impedance Z_T at lower frequencies (Ravicz et al., 1992, 1996—gray line). ℜ_T at the highest frequency computed by this measure (~0.5 at 18 kHz) was similar to ℜ_EC at the lowest frequencies computed from standing wave patterns (~30 kHz). ℜ_T increased to ~1 below 1 kHz. Figure 13 indicates that more incident sound power is transmitted into the gerbil middle ear (less incident sound power is reflected) in the middle frequencies than at very low (<100 Hz) or high frequencies (>50 kHz).

The result that ℜ_EC is comparable to ℜ_T near 30 kHz and increases at higher frequencies suggests that the gerbil |Z_T| increases with frequency. Because the reflectance is a measure of the impedance mismatch between the terminating impedance and the frequency-independent characteristic impedance Z₀ [Eq. (4)], a large reflectance implies a large difference between the magnitude of the terminating impedance and Z₀. Similarly, increasing Z_T artificially (for example, by replacing the TM with a nearly rigid microphone diaphragm) can be expected to cause an increase in reflectance and spatial P_EC variations at lower frequencies.

As mentioned earlier, the fraction of incident sound power that enters the middle ear is equal to 1-ℜ_EC. Over much of our measurement range ℜ_EC was 0.2–0.6, which means that 40%–80% of the power in the ear canal between 6 and 50 kHz entered the middle ear. At higher frequencies, ℜ_EC⩾0.8, which means that at most 20% of the EC power entered the middle ear. The increase in ℜ_EC means that less energy is available to be transmitted to the cochlea at higher frequencies (Rosowski et al., 1986, 1988).

The detection of sound requires both transmission of a sound signal to the cochlea and activation of sensory cells within the cochlea (e.g., Dallos, 1996). Ruggero and Temchin (2002) point out that the high-frequency limit of hearing (the audiometric limit) corresponds to the upper extent of the cochlear sensitivity map. We have shown here that ear canal reflectance also increases as sound frequency approaches the audiometric limit, which indicates that sound transmission to the cochlea decreases. It is likely that the frequency ranges of sound transmission to the cochlea and the cochlear sensitivity map are similar so that the capabilities of one do not greatly surpass the limitations of the other.

E. Comparisons to ear canal sound pressure field and reflectance in other species

Our ΔP_EC data are similar to the standing wave patterns measured previously in human (Stinson, 1985b; Lawton and Stinson, 1986; Stinson, 1990; Chan and Geisler, 1990) and cat (Khanna and Stinson, 1985; Stinson and Khanna, 1994) in a fashion similar to that described here, though not to nearly such high frequencies. The frequencies of standing-wave notches we observed in gerbil are higher than those observed in ear canals of these other species, consistent with the shorter remaining gerbil ear canal.

Our estimates of gerbil ℜ_EC in Fig. 13 show the same frequency dependence as ℜ computed previously in human, chinchilla, and cat (in healthy ears). The reflectance computed for human from Z_T by Eq. (4) (Voss and Allen, 1994; Margolis et al., 1999) was ~1 at 250 Hz and below, decreased to 0.3–0.5 near 1 kHz, and increased again to about 0.7 from 7 to 10 kHz (the highest frequency of reliable measurements), while ℜ computed from SWR increased from about 0.25 near 4 kHz (the lowest frequency measured) to 0.7 near 8 kHz [and decreased slightly as frequency increased further to 13 kHz, the highest frequency measured; Stinson (1990)]. Chinchilla ℜ was similar to human except that ℜ was high below 2 kHz (Margolis et al., 2001). Previous estimates of cat ℜ are more variable: Cat ℜ computed from Z_T (Lynch et al., 1994; Puria and Allen, 1998) was ~1 below 300 Hz, decreased to ≤0.3 at 1.5 kHz, and remained nearly constant (except for a peak near 4 kHz in the Lynch et al. data) to the highest frequency measured (22 kHz, Lynch et al.; 32 kHz, Puria and Allen). Cat ℜ computed from SWR (Stinson and Khanna, 1994) was quite variable at high frequencies: Ears with TMs in poor condition had high ℜ, but the others showed ℜ generally low (<0.3) at 10 kHz (the lowest frequency measured) and increasing sharply between 23 kHz and the highest frequency measured (generally 32 kHz), in contrast to ℜ computed from Z_T by the other authors. Our results suggest that ear canal reflectance in gerbil is representative of ℜ in other species: relatively low over a wide middle frequency range, with higher values at low and high frequencies.

F. Comparison with ear canal sound pressure estimated by other methods

Our data allow us to compare the accuracy of the three methods of estimating TM sound pressure described in Sec. I: shortening the ear canal and using a probe tube to measuring the sound close to the TM, mathematically modeling the ear canal, and using an artificial ear.

It should be noted that alternatives to sound pressure as a measure of middle-ear input have been proposed: For example, ear-canal sound intensity (e.g., Neely and Gorga, 1998), in part because the spatial distribution of intensity in the ear canal, is much more uniform than the sound pressure field (Neely and Gorga, 1998). A disadvantage of using intensity as input is that the determination of intensity from sound pressure measurements requires knowledge of the TM impedance (e.g., Keefe et al., 1993; Neely and Gorga, 1998), a quantity that may not be easily measurable at high frequencies (e.g., Stinson et al., 1982; Khanna and Stinson, 1985). Also, analysis of middle-ear mechanics requires knowledge of stimulus phase; when intensity is computed from sound pressure, ∠P_EC information is lost. The use of P_U to specify the middle-ear input preserves the phase information present in the ear-canal stimulus. For these reasons as well as the relative simplicity of the measurement, ear canal sound pressure remains the most commonly used measure of middle-ear input.

We shortened the gerbil ear canal and measured the sound pressure near the ear canal entrance and umbo (the first method mentioned previously) and found that longitudinal and transverse P_EC variations were less than 6 dB at frequencies less than 30 kHz. This result implies that P_EC measured at the entrance of the bony ear canal is a fairly accurate and repeatable estimate of the sound pressure input to the middle ear at frequencies below 30 kHz, which includes much but not all of the gerbil range of hearing. The larger longitudinal P_EC variations at 40 kHz and above indicate that measurements of middle-ear function at these high frequencies should measure the sound pressure near the umbo if possible, and if that is not practical, must be interpreted with the measurement location in mind.

The only other EC sound pressure distribution data in gerbil of which we are aware were measured by Maki and Furukawa (2005a, Fig. 2i) with a probe tube introduced down an intact ear canal post-mortem. For these measurements the TM was stiffened with cyanoacrylate adhesive. Notches were observed in the EC transfer function of apparently 16–23 dB at 14–32 kHz, deeper than the 12- to 15-dB notches we observed near 35 kHz. Though the location of their probe-tube tip relative to the TM is not known, the lower notch frequency suggests that it was lateral to the bony ear canal. The increased notch depth may be due to the stiffening of the TM, which probably increased the middle-ear input impedance and therefore EC reflectance and, as a result, increased P_EC variations.

The second method, mathematical modeling of the gerbil bony ear canal, is difficult due to the complex shape of the ear canal: If the EC axis is considered to terminate at the umbo, then the axis curves sharply near the TM; and if the EC axis is considered to extend to the medial edge of the tympanic ring, then the TM forms part of the EC wall (see Fig. 2). The ear canal also flares as it nears the TM. A simple model that neglects EC curvature and considers the TM to terminate the ear canal (Ravicz et al., 1996) fit Z_T data fairly well up to 18 kHz, but its applicability at higher frequencies is unknown, and we did not pursue this model further. Stinson (1990) developed a model of the human ear canal that successfully predicted sound pressure at the TM from more lateral P_EC measurements and an accurate representation of the ear canal shape. The more complicated shape of the gerbil ear canal may render this approach more difficult.

Regarding the third method, use of an artificial ear, our data show that the location and range of P_EC variations are affected by the shape and termination of the ear canal. For much of the frequency region in which |P_EC| notches were apparent, they were shallower than those in the artificial ear. The result in this frequency region highlights the greater power reflectance of the artificial ear, a difference that is expected to produce a bias when a calibration performed in an artificial ear [a uniform-tube calibration (Pearce et al., 2001) or artificial-cavity calibration (Overstreet and Ruggero, 2002)] is used to set sound stimulus levels in an actual ear (e.g., Siegel, 1994).

Figure 14 shows the ratio of P_AE (measured by the terminating microphone in the artificial ear) to P_U in each of the real ears, for the same broadband drive signal level to the sound source. Each of these P_AE/P_U curves can be thought of as an earphone calibration in that they indicate how an earphone drive voltage must be set to deliver a sound pressure stimulus to an experimental ear that is constant in level across frequency. Below 40 kHz, P_AE/P_U >0 dB, which means that the artificial ear calibration would call for a lower stimulus than is needed to produce the desired sound pressure level in the real ear. Between 40 and 60 kHz, P_AE/P_U <0 dB, which means that the artificial ear calibration would call for a larger stimulus than is needed to produce the desired sound pressure level in the real ear. Throughout the frequency range there are ripples in magnitude and phase introduced by a mismatch in acoustic length between the artificial ear and the real ear. Together these factors introduce a substantial frequency-dependent bias in artificial ear calibrations across a wide frequency range.

Such bias will clearly influence high-frequency measurements that use P_U as an input, e.g., middle-ear transmission or auditory bandwidth. Quantities such as stapes velocity or cochlear or neural responses, when normalized by ear canal sound pressure, would appear artificially low by 5–20 dB below 40 kHz and artificially high by 5–15 dB in the 40- to 60-kHz range. For these reasons, artificial ear calibrations should be used with caution.

The similarity of ΔP_EC at the ear canal entrance among the five ears (from two laboratories) in Fig. 7 suggests that a simple average EC sound pressure correction is possible. The variation in ΔP_EC in Fig. 7 is less than P_AE/P_U in Fig. 14, so an average ear canal correction leads to a more accurate estimation of middle-ear input than an artificial ear calibration.

VI. SUMMARY AND CONCLUSIONS

1. The sound field in the gerbil bony ear canal can be described as (a) primarily uniform below 30 kHz and (b) a combination of uniform traveling and standing plane waves at higher frequencies. |P_EC| variations along the ear canal were on the order of 15 dB above 35 kHz and at least 20 dB above 60 kHz. Transverse variations across the ear canal at the TM were much smaller: about 2 dB.

2. Sound pressure could be measured sufficiently near the umbo that no frequency-dependent notches in ear canal sound pressure were seen there over the frequency range of measurements (0.1–82 kHz). The result that variations across the TM were small means that the middle-ear input can be specified as sound pressure measured near the umbo at frequencies up to at least 60 kHz.

3. The probe tube used to measure the sound pressure variations in some ear canals occluded ~30% of the ear canal but had a reasonably small effect on sound pressure near the umbo up to at least 60 kHz.

4. Sound power reflectance computed from standing wave patterns indicates that 40%–80% of incident sound power at the TM enters the middle ear below 50 kHz, comparable to ℜ in cat, chinchilla, and human at lower frequencies. The ear canal power reflectance increases at higher frequencies. This increase in ℜ_EC as frequency increases is consistent with previous results in chinchilla and human and some previous results in cat, both at lower frequencies, and is consistent with the idea that the boundaries of the audiometric range are influenced by sound transmission into and through the middle ear.

5. Sound pressure measured near the umbo in a real ear differed from the sound pressure measured at the termination of an artificial ear. If P_AE is used to set ear canal sound stimulus levels, these differences would bias stimulus levels downward below 40 kHz and upward between 40 and 60 kHz. These systematic biases throw into question the validity of the artificial ear calibration technique at high frequencies.