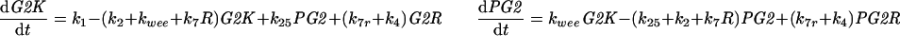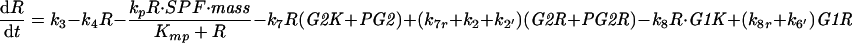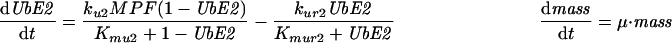Modeling the control of DNA replication in fission yeast

Abstract

A central event in the eukaryotic cell cycle is the decision to commence DNA replication (S phase). Strict controls normally operate to prevent repeated rounds of DNA replication without intervening mitoses (“endoreplication”) or initiation of mitosis before DNA is fully replicated (“mitotic catastrophe”). Some of the genetic interactions involved in these controls have recently been identified in yeast. From this evidence we propose a molecular mechanism of “Start” control in Schizosaccharomyces pombe. Using established principles of biochemical kinetics, we compare the properties of this model in detail with the observed behavior of various mutant strains of fission yeast: wee1⁻ (size control at Start), cdc13Δ and rum1^OP (endoreplication), and wee1⁻ rum1Δ (rapid division cycles of diminishing cell size). We discuss essential features of the mechanism that are responsible for characteristic properties of Start control in fission yeast, to expose our proposal to crucial experimental tests.

The molecular events that coordinate DNA synthesis and mitosis in eukaryotic cells are beginning to be unraveled by elegant physiological, genetic, and biochemical studies of fission yeast (1, 2) and budding yeast (3, 4). For instance, Russell and Nurse (5) found that fission yeast cells carrying two mutant genes, wee1⁻ cdc25^OP, initiate mitosis before they have finished replicating their DNA; this lethal mistake is a failure of the G₂ checkpoint controls that normally delay mitosis until DNA synthesis is complete. A molecular mechanism and mathematical model of these controls has been proposed (6). The opposite mistake, reinitiating DNA synthesis without intervening mitoses to produce viable polyploid cells, is a failure of the G₁ control point to check that mitosis has occurred. Endoreplication has been observed by Nurse and his colleagues in mutants of cdc2 [coding for the sole cyclin-dependent kinase (CDK) in fission yeast] (7, 8), in chromosomal-deletion mutants of cdc13 (coding for the only essential mitotic cyclin) (9), in mutants that overexpress the wild-type gene rum1 (coding for a stoichiometric inhibitor of Cdc13/Cdc2 dimers) (10, 11), and in mutants that overexpress cdc18 (coding for a putative licensing factor for DNA synthesis) (12, 13). From the clues provided by these and other mutants we have constructed a mechanism of the G₁ checkpoint in fission yeast and fused it to our previous model of G₂ checkpoint controls.

Model for G₁ and G₂ Checkpoint Controls

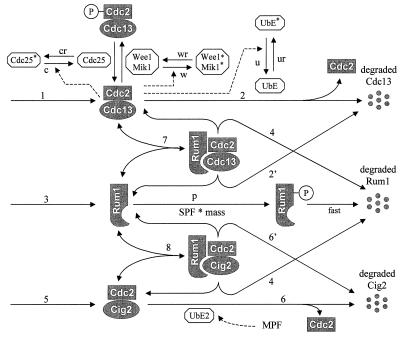
Although our mechanism for cell cycle control in fission yeast (Fig. 1) looks formidable, it is built of simple modular pieces. The two crucial initiation events of the cell cycle (for DNA synthesis and mitosis) are triggered by Cdc2 in conjunction with one of three different B-type cyclins, Cdc13, Cig1, or Cig2 (2, 14). S-phase promoting factor (SPF) is a weighted sum of all three CDK activities, whereas only Cdc13-dependent kinase is essential for M-phase promoting factor (MPF). Step 1, in Fig. 1, represents a constant rate of synthesis of Cdc13 (15) followed immediately by association with free Cdc2 (from a large pool of inactive kinase subunits) and phosphorylation of Thr-167 of Cdc2 to form active Cdc13/Cdc2 dimers (16). Active dimers, however, are quickly inactivated by phosphorylation of Tyr-15 of Cdc2 by two kinases, Wee1 and Mik1 (17). The inactivating phosphate group can be removed by Cdc25. Furthermore, Cdc13/Cdc2 dimers can be destroyed by ubiquitin-mediated proteolysis (UbE) of Cdc13 (step 2). Net activity of MPF is controlled by three feedback signals: MPF activates Cdc25 and UbE, and it inactivates Wee1. This part of the mechanism is similar to our earlier description of G₂/M control in fission yeast, which is supported by considerable experimental evidence (6).

Figure 1.

A model of G₁/S and G₂/M controls in fission yeast. See text for an explanation.

The rest of the mechanism replaces the “automaton model of Start” in our earlier work (6) by molecular interactions between Rum1 and the cyclin/Cdc2 dimers. Step 3 describes Rum1 synthesis and step 7 the reversible binding of Rum1 to Cdc13/Cdc2, resulting in a trimer with no kinase activity. The trimer can be disrupted by degradation of Rum1 (step 4) or Cdc13 (step 2′). Because Rum1 and Cdc13 show alternating patterns of expression (Rum1 is high and Cdc13 low in G₁ phase, and vice versa in S+G₂+M phase) (18), we assume that each protein stimulates the degradation of the other. Thus, the rate constant for Cdc13 degradation from trimers (k_2′) is assumed to be larger than the background degradation rate of Cdc13 by the UbE system in interphase (V_2′). In addition, we assume that SPF can phosphorylate free Rum1 (step p) and Rum1P is rapidly degraded. Growth regulation enters the model here in the assumption that the rate of Rum1 phosphorylation is dependent on cell size as well as SPF activity.

Step 5 represents Cig2 synthesis followed by rapid dimerization with Cdc2, and step 6 is Cig2 proteolysis by another ubiquitin-ligating enzyme (UbE2). Rum1 binds to and inhibits Cig2/Cdc2 (step 8), and the trimers are disrupted by degradation of Rum1 (step 4) or Cig2 (step 6′). In contrast to Cdc13, Cig2 accumulates in G₁ and peaks during S phase (19, 20). This suggests that, unlike Cdc13, Cig2 is stabilized by binding to Rum1 and is degraded after Rum1 disappears, so we choose rate constants satisfying the inequality k_6′ < V_6′.‡

The assumptions we have made in this part of the model are supported directly and indirectly by recent experimental observations. It is well established that Rum1 binds strongly to Cdc13/Cdc2 and Cig2/Cdc2 and inhibits their activities (19, 21, 22). Nonphosphorylable Rum1 is more stable than wild type (18), suggesting that phosphorylation renders Rum1 more susceptible to proteolysis. Furthermore, in vitro, Rum1 is efficiently phosphorylated by Cig1/Cdc2, a heterodimer that is not inhibited by Rum1 (18). Cdc13/Cdc2 and Cig2/Cdc2 do not phosphorylate Rum1 significantly in vitro (18), as might be expected, because they are inhibited by Rum1; however, when present in excess, they may be effective Rum1 kinases. The phenotype of cdc10^ts rum1Δ cells (11, 21) suggests that Rum1 destabilizes Cdc13: although Cdc13 level is normally low in G₁ phase, it accumulates in the double mutant strain, driving the cells into M phase with unreplicated DNA.

Using standard principles of biochemical kinetics, we convert the mechanism in Fig. 1 into a set of differential equations (Table 1) describing how the concentrations of the major control variables change with time. In writing these equations we must introduce a number of rate constants and Michaelis constants that characterize the kinetic properties of the component reactions. Few of these parameters can be estimated directly from experimental data. The values assigned in Table 1 represent a possible set of kinetic constants, consistent with observed features of the fission yeast cell cycle. To obtain more confident estimates of these parameters is a job for future experimentation and modeling.

Table 1.

A mathematical model of the proposed mechanism (Fig. 1) for cell cycle control in fission yeast

Concentration variables

G2K = [Cdc13/Cdc2], PG2 = [Cdc13/P-Cdc2], R = [Rum1], G1K = [Cig2/Cdc2], G1R = [Cig2/Cdc2/Rum1], G2R = [Cdc13/Cdc2/Rum1], PG2R = [Cdc13/P-Cdc2/Rum1], IE = “Intermediary enzyme,” SPF = MPF + α⋅G1K + Cig1, MPF = G2K + β⋅PG2 (all concentration variables are scaled to be dimensionless numbers of order 1)

Differential equations*

Rate functions

k2 = V2′(1 − UbE) + V2UbE, k6 = V6′(1 − UbE2) + V6UbE2, kwee = Vw′(1 − Wee1) + VwWee1, k25 = V25′(1 − Cdc25) + V25Cdc25

Switches

(i) When SPF crosses 0.1 from below, S phase is initiated (Start). (ii) When UbE crosses 0.1 from above, the cell divides functionally (mass → mass/2), although visible cytokinesis may be delayed. (iii) 60 min after Start, kp is divided by 2, and at cell division kp is multiplied by 2.†

Rate constants (all have dimensions min−1)‡

k1 = 0.015, k2′ = 0.05, k3 = 0.09375, k4 = 0.1875, k5 = 0.00175, k6′ = 0, k7 = 100, k7r = 0.1, k8 = 10, k8r = 0.1, kc = 1, kcr = 0.25, ki = 0.4, kir = 0.1, kp = 3.25, ku = 0.2, kur = 0.1, ku2 = 1, kur2 = 0.3, kw = 1, kwr = 0.25, V2 = 0.25, V2′ = 0.0075, V6 = 7.5, V6′ = 0.0375, V25 = 0.5, V25′ = 0.025, Vw = 0.35, Vw′ = 0.035, μ = 0.00495

Michaelis and miscellaneous constants (dimensionless)§

Kmc = Kmcr = 0.1, Kmi = Kmir = 0.01, Kmp = 0.001, Kmu = Kmur = 0.01, Kmu2 = Kmur2 = 0.05, Kmw = Kmwr = 0.1 α = 0.25, β = 0.05, Cig1 = 0

^*One component in the model, IE, does not appear in the mechanism; it is an intermediary enzyme between MPF and UbE, necessary to introduce a time lag between MPF activation and Cdc13 degradation. The variable “Wee1” represents the active form of both tyrosine kinases, Wee1 and Mik1. Each of the variables “Cdc25, UbE, UbE2, IE” represents the fraction of an enzyme in the more active form. For simplicity we ignore fluctuations in the activity of Cig1-dependent kinase. In fact, usually we set [Cig1] = 0. Our model does not explicitly account for changes in amount and activity of licensing factor(s) because these events seem to be strictly “downstream” of the network of cyclins, Cdc2, and Rum1; that is, CDK activity affects the state of licensing factor but not vice versa. As kinase activities fluctuate according to this mechanism, the state of the licensing-factor machinery changes, which determines whether a cell is in G₁ phase or G₂ phase, as described in refs. 1, 2, and 23. 

^†The value of k_p is modified periodically (in G₂ phase and at cell division) to mimic a gene-dosage effect on the phosphatase that counteracts SPF in the phosphorylation of Rum1. This signal provides a mechanism for size control of Start during endoreplication cycles. 

^‡Parameter values for a wee1⁻ strain. To simulate the wild-type cell cycle, we put a G₂ size control signal on Cdc25 and increase the rate constants for Tyr-15 phosphorylation: V_w = 1, V_w′ = 0.1. The results (data not shown) are nearly identical to our earlier study of mitotic control in fission yeast (6). 

^§Because we choose these Michaelis constants all to be considerably smaller than 1, the corresponding enzyme activities, IE … Cdc25, operate as “ultrasensitive” switches (24)—i.e., they tend to be either “on” (activity = 1) or “off” (activity = 0). This switch-like behavior is important for G₂ checkpoint controls (25, 26) but is not essential for the Start transition. 

Simulations, Analysis, and Comparison with Experiments

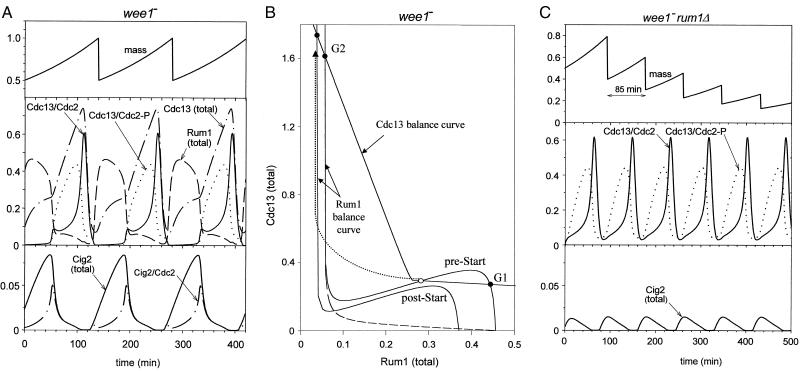
Fission yeast cells have two size requirements: one enforced at S-phase initiation and the other before entering M phase. In wild-type cells, the larger of the two size requirements (governing the G₂/M transition) is operative; at birth, cells are already large enough to initiate DNA synthesis, so the G₁/S size requirement is cryptic (27). In wee1⁻ cells, the G₂/M size control is inoperative, permitting cells to divide at an abnormally small size, which brings the G₁/S size control into play. That is, wee1⁻ cells maintain balanced growth and division at about half the size of wild-type cells by operation of a size control mechanism over the Start transition. Our model (Fig. 1 and Table 1) is designed for wee1⁻ mutants: it has no size control over the Cdc2 tyrosine-phosphorylation reactions, and the rate constants for the Wee1+Mik1-catalyzed reactions are chosen to represent a wee1⁻ strain. A typical simulation of this model is illustrated in Fig. 2A. G₁ phase, during which Rum1 level is high and CDK activity is low, lasts for roughly 65 min, whereas S+G₂+M phase (about 75 min in duration) is shorter than in wild-type cells (130 min) and incompressible. That is, if we decrease the specific growth rate, μ, the cycle time increases by lengthening G₁ phase; the duration of S+G₂+M is independent of μ. These are characteristic features of wee1⁻ cells, whose division cycle is governed by a size requirement in G₁ phase (27).

Figure 2.

(A) The wee1⁻ cell cycle. Simulated time courses for the major components. Parameters given in Table 1. Rum1 (total) = R + G1R + G2R + PG2R, Cdc13 (total) = G2K + G2R + PG2 + PG2R, Cig2 (total) = G1K + G1R. The cycle time is 140 min, identical to the mass doubling time. (B) Phase portrait of the Start transition. As explained in the Appendix, we select from Fig. 1 only those steps involved in the synthesis, degradation, and interactions of Cdc13 and Rum1, thereby reducing the complete system to just two differential equations (A6, A7). The properties of this two-dimensional subsystem are conveniently portrayed as balance curves (solid lines) in the phase plane (28). The dashed curve shows how the activity of Cdc13/Cdc2 is quenched as Rum1 accumulates. In pre-Start, the balance curves intersect in two stable steady states (the • labeled G₁ and G₂) and an intermediate unstable steady state (○). In post-Start, the balance curves intersect only in the G₂ steady state. As the cell grows, the Rum1 balance curves moves down, causing the G₁ state to disappear (by a saddle-node bifurcation) and the system to proceed along the dotted trajectory to the G₂ state. (C) Unbalanced growth and division in wee1⁻ rum1Δ mutants. Parameter values as in Table 1, except k₃ = 0 (therefore, R = G1R = G2R = PG2R = 0). Both size controls, at G₁/S and G₂/M, are inoperative. There is no stable steady state (checkpoint) at which the cycle can pause to query cell size. Instead the control system executes autonomous (limit cycle) oscillations with a division time (85 min) shorter than the mass doubling time (140 min). Hence cells get smaller each cycle.

The timing of Start in these cells is sensitive to cell size because we assume that the rate of Rum1 phosphorylation is proportional to (SPF activity) × (cell mass). Perhaps Rum1 phosphorylation occurs within the nucleus, where CDKs accumulate as the cell grows. There are other ways to imagine how cell growth could trigger a loss of stability of the G₁ steady state. Until experiments pinpoint where cell size feeds into the G₁ checkpoint machinery, we present this possibility as a working hypothesis.

The simulation in Fig. 2A indicates that Cig2 is much less abundant than Cdc13, as seems to be the case (P. Russell, personal communication). Nonetheless, cell size at Start, when wee1⁻ cells commit to DNA synthesis, is determined equally by Cig2 and Cdc13, because (in our model) wee1⁻ cig2Δ cells execute Start at about twice the size of wee1⁻ cig2⁺ cells (simulation not shown), similar to observations by Martin-Castellanos et al. (19).

Numerical simulations alone cannot give us an intuitively useful understanding of how a molecular mechanism works. In earlier publications (28) we have stressed the utility of “phase plane portraits” to guide thinking about cell cycle control systems. In the Appendix we show how to simplify the equations in Table 1 to just two variables, [total Rum1] and [total Cdc13], and construct the portrait in Fig. 2B. In this figure, the Cdc13 balance curve describes conditions for which Cdc13 synthesis is exactly balanced by its degradation, so that everywhere along this curve total Cdc13 level is unchanging. Similarly along the Rum1 balance curve, total Rum1 level is unchanging. Therefore, wherever the two curves intersect, we have a steady state of the control system. Given the Cdc13 and Rum1 interactions we have hypothesized, Fig. 2B illustrates that, in pre-Start, the two balance curves intersect at two stable steady states: a G₁ state with lots of Rum1 and little Cdc13-dependent kinase activity, and a G₂ state with little Rum1 and lots of active Cdc13/Cdc2 dimers.§

Clearly, in this model Rum1 and Cdc13 cannot coexist, because they are antagonistic proteins: binding of Rum1 to Cdc13 enhances Cdc13 degradation, and Cdc13-dependent kinase phosphorylates Rum1 and destabilizes it. In G₁ phase Rum1 wins. But, as the cell grows, the rate of Rum1 phosphorylation by Cdc13-dependent kinase increases (because we assume that this rate is proportional to cell mass), causing the steady-state level of Rum1 to decrease and the local maximum of the Rum1 balance curve to drop (Fig. 2B). When the cell reaches a critical size, the G₁ steady state disappears by fusing with the intermediate (unstable) steady state. When the G₁ steady state is lost, the control system must switch to the only remaining steady state at G₂. As Rum1 is degraded, Cdc13 accumulates and Cdc13-dependent kinase activity appears (the dotted trajectory in Fig. 2B). Rising levels of both Cig2- and Cdc13-dependent kinases (SPF) trigger DNA synthesis. Loss of the G₁ steady state by growth-driven rearrangement of the balance curves corresponds to the Start transition. Later, as Cdc13/Cdc2 activity (MPF) reaches very high levels, mitosis is initiated (15). After M phase, CDK activity drops precipitously due to degradation of B-type cyclins, cell size is halved by cytokinesis, the Rum1 balance curve moves back into its pre-Start position, and the control system returns to the G₁ steady state, waiting for cell growth to start the whole process anew.

In our simulation of the double mutant strain wee1⁻ rum1Δ (Fig. 2C), the cycle of DNA replication and cell division proceeds more rapidly than the mass-doubling process, and cells get progressively smaller each cycle, as observed (10, 11). Clearly these cells lack any mechanism to coordinate cell growth and division (29). The cell cycle in wee1⁻ rum1Δ is analogous to the autonomous oscillations of MPF in frog egg extracts (25, 30), which drive rapid cycles of DNA synthesis and mitosis independently of overall cell growth.

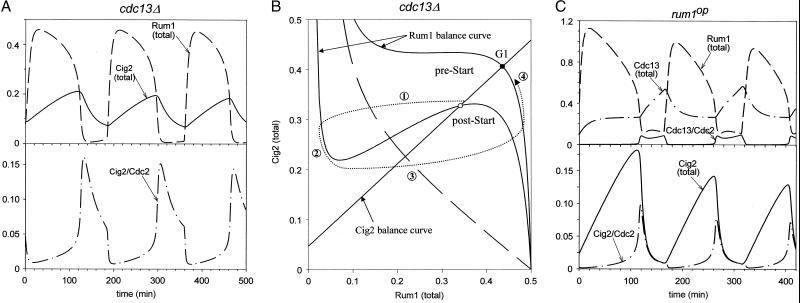
In Fig. 3A we simulate endoreplication cycles in cdc13Δ. In this case, the interactions between Rum1 and Cig2 generate size-controlled oscillations of SPF, but cells never enter mitosis because MPF (Cdc13/Cdc2) is missing. The portrait in Fig. 3B shows how this cycle works. In G₁ phase, when cells are small, the Cig2 (total) and Rum1 (total) balance curves intersect in a unique stable steady state with lots of Rum1 and total Cig2, but little Cig2-dependent kinase activity because most of the cyclin molecules are tied up in inactive trimers. However, as the cell grows, the rate of Rum1 phosphorylation by Cig2-dependent kinase increases and the Rum1 balance curve drops. Eventually the G₁ steady state loses stability, Rum1 is degraded, and Cig2/Cdc2 dimers are unmasked, driving the cell into S phase (① in Fig. 3B). Then Cig2 level drops ② because, as we assume, Rum1 was shielding Cig2 from proteolysis (notice that, although MPF = 0, UbE2 retains a basal activity of V_6′). The subsequent drop in Cig2-mediated phosphorylation of Rum1 allows Rum1 to make a comeback ③. As Rum1 accumulates, Cig2 is stabilized and reaccumulates ④. As described in the footnote to Table 1, we assume that doubling the DNA content causes an increase in the phosphatase that opposes SPF in the phosphorylation of Rum1, which is equivalent to reducing the effective activity of SPF and is modeled by dividing k_p by 2. This brings the Rum1 balance curve back to the pre-Start position, and the system arrests at the G₁ checkpoint. Cell size must increase by another factor of two before Start is executed again. (During endoreplication, cells do not divide but their DNA-to-mass ratio oscillates over a 2-fold range.)

Figure 3.

(A) Endoreplication cycles in cdc13Δ. Simulations with parameters as in Table 1, except k₁ = 0 (therefore, G2K = PG2 = G2R = PG2R = 0). Because cells never divide, k_p gets smaller by a factor of two each cycle of DNA replication, and cell mass must increase by a factor of two to compensate. (B) Phase portrait for the periodic execution of Start without intervening mitoses. This time we select from Fig. 1 only those steps involved in the synthesis, degradation and interactions of Cig2 and Rum1 (Eqs. A8 and A9 of the Appendix), and plot their balance curves (solid lines) in the phase plane. The dashed curve shows how the activity of Cig2/Cdc2 is quenched as Rum1 accumulates. In pre-Start, the balance curves intersect in a unique stable steady state corresponding to a G₁ checkpoint (•). In post-Start, due to cell growth, the steady state (○) has become unstable by a Hopf bifurcation. Instead of going to a G₂ state, the trajectory (dotted curve) carries the cell back to G₁, as described in the text. (C) Endoreplication cycles in rum1^OP. Simulations with parameters as in Table 1, except k₃ = 0.375 and Cig1 = 0.07. During endoreplication cycles, Cig1 can accumulate because it is not destroyed at anaphase, as normally it would be (31).

In the model, if we overexpress cig2 in a cdc13Δ cell (k₁ = 0, k₅ > 0.0075 min⁻¹—i.e., rate of Cig2 synthesis greater than four times the basal rate), the system settles on a stable steady state with high Cig2-dependent kinase activity and little Rum1 (simulation not shown). These mutant cells arrest in G₂ phase, as recently observed (P. Russell, personal communication).

Fig. 3C illustrates the other case, rum1^OP, in which fission yeast cells undergo multiple rounds of DNA replication. As before, there is a G₁ steady state with lots of Rum1, which is destabilized by growth. In this case, however, because the cell contains excess Rum1, it must grow larger before it can eliminate the G₁ steady state. After Start, Rum1 is degraded, Cig2-dependent kinase activity rises, and the cell enters S phase. But even when Rum1 degradation is large (post-Start), the level of Rum1 remains high enough to squash Cdc13-dependent kinase activity; hence the cell does not enter mitosis. There is enough SPF activity to trigger DNA synthesis but not enough MPF activity to trigger mitosis.

Other simulations (data not shown) confirm the observations of Martin-Castellanos et al. (19) that the Rum1-insensitive, Cig1-dependent kinase is essential for endoreplication in rum1^OP mutants. On the other hand, Cig1 is not essential for endoreplication in cdc13Δ (see Fig. 3A, for which Cig1 = 0), as observed by Fisher and Nurse (15).

We have simulated a variety of other mutants and find the model in close agreement with experiments. For instance, increasing the stability of Rum1 (experimentally by mutating some of its Cdc2-specific phosphorylation sites and theoretically by decreasing k_p) lengthens G₁ phase and allows Rum1 to accumulate to a much higher level (18). Notably, the cig1Δ cig2Δ double mutant shows nearly wild-type cell cycles, demonstrating that a single B-type cyclin (Cdc13) can drive the complete fission yeast division cycle (2, 15), and the time-course of Cdc13/Cdc2 activity through this simulated cycle (data not shown) supports the “two level model” of CDK activity these authors proposed.

Critique of Assumptions and Tests of the Model

The cell cycle of wild-type fission yeast is regulated by a size-dependent checkpoint in G₂ phase, as proved by many elegant experimental papers (for reviews, see refs. 27 and 32), and recently described in detail by a mathematical model (6) of a consensus molecular mechanism. In wee1⁻ mutants, which lack the G₂ control mechanism, the cell cycle is regulated by a size-dependent checkpoint in G₁ phase (Start). We propose that Start control in S. pombe is driven by antagonistic interactions between Cdc13 and Rum1. As illustrated in Fig. 1, we assume that Rum1 binds to Cdc13/Cdc2 dimers, inhibiting their kinase activity and rendering the Cdc13 subunit more susceptible to proteolysis. On the other hand, Cdc13/Cdc2 phosphorylates Rum1, leading to Rum1’s rapid proteolysis. Therefore, Rum1 and Cdc13/Cdc2 cannot coexist. Before Start, Rum1 wins and Cdc13-dependent kinase activity is repressed. After Start, Rum1 is destroyed and Cdc13/Cdc2 predominates. The G₁/S and metaphase/anaphase transitions of the cell cycle can be thought of as transitions between these two alternative stable steady states. Nasmyth (4) has proposed a similar idea for control of the budding yeast cell cycle.

There are many ways to build a model of Start control in fission yeast; why do we make these particular assumptions? Of fundamental importance is the role of Rum1 during endoreplication cycles. Rum1 might play only an indirect role, inhibiting Cdc13, so that rum1^OP is functionally equivalent to cdc13Δ. We are skeptical of indirect models for several reasons. First, cdc13Δ rum1Δ cells do not endoreplicate efficiently (J. Hayles and P. Nurse, personal communication), so it appears that Rum1 plays some role in endoreplication cycles besides inhibiting Cdc13. Second, Cdc13-dependent kinase activity can be detected in rum1^OP cells (21), suggesting that there is a phase of the endoreplication cycle when Rum1 is reduced and Cdc13 is reappearing, but not enough to drive cells into mitosis (see Fig. 3C). Third, if Rum1 is not involved in endoreplication cycles, what is? Another plausible candidate is Cdc10, which could be involved with Cig1 and Cig2 in a positive feedback loop at the G₁/S transition, as proposed for Start control in budding yeast (33). However, recent evidence (ref. 34; B. Baum and P. Nurse, personal communication) indicates that Cdc10 is activated in M phase and stays on throughout G₁ and S, so activation of Cdc10 at the G₁/S transition is unlikely to play a crucial role in endoreplication cycles.

Alternatively, Rum1 might be directly involved in endoreplication cycles, presumably by interaction with Cig2, as we have assumed in Fig. 1. Direct models are appealing because exactly the same trigger mechanism for the G₁/S transition is operative in normal and endoreplication cycles. When the G₁ steady state is lost, Rum1 starts to fall and Cdc13 to rise. But then, in rum1^OP, the cell is redirected back to G₁. Why? In early G₂, after Rum1 falls, Cdc13 is rising (which prevents Rum1 from reappearing) but Cig2 is falling (which allows Rum1 to reappear). Which signal wins? In the normal cycle, Cdc13 wins, Rum1 stays low, and the cell proceeds from early G₂ to late G₂. But in rum1^OP, because some of the rising Cdc13-dependent kinase remains inhibited by excess Rum1, the Cig2 signal wins: Rum1 reappears, Cdc13 is lost, and the cell switches from early G₂ back to G₁. In this battle it is relevant that Rum1 binds more strongly to Cdc13/Cdc2 than to Cig2/Cdc2 (k₇ ≫ k₈ in Table 1) (19, 21, 22), which tips the scales in favor of Cig2 in rum1^OP. Our mathematical simulations demonstrate that this intuitive explanation actually works. Furthermore, in our experience, the model is robust: to get endoreplication in rum1^OP does not require careful balancing of the rate constants; it comes about quite naturally, once the mechanism is wired together properly.

Observation of Rum1 fluctuations in a rum1^OP strain would provide strong support for the direct model, but testing this prediction must await development of methods to synchronize cultures of endoreplicating cells.

Our model makes several other predictions that can be tested experimentally. (i) wee1⁻ cdc13^OP: if cdc13 is overexpressed, the G₁ checkpoint should become cryptic and cell should die like wee1⁻ rum1Δ. (ii) cdc10^ts mutants blocked at the G₁ checkpoint: expression of cdc13 from a plasmid should push cells to the G₂ steady state, skipping S phase and causing a mitotic catastrophe (9). (iii) Successive deletion of Cdc2-specific phosphorylation sites of Rum1: cells should execute Start at increasingly larger size, if size control operates at the point of Rum1 phosphorylation by SPF.

Crucial to our proposed mechanism of endoreplication cycles is the assumption that Cig2 is stable in Cig2/Cdc2/Rum1 trimers. For this reason, Cig2 subunits accumulate during G₁ phase when Rum1 is present, and are lost after cells pass Start, when Rum1 disappears. If this hypothesis is correct, then Cig2 level just before Start should be higher in rum1^OP strains and smaller in rum1Δ strains. If the assumption is incorrect, there is a back-up hypothesis: that Cig2 synthesis is inhibited (perhaps indirectly) by Cig2/Cdc2. Then, as Rum1 falls and Cig2-dependent kinase activity rises, the rate constant for Cig2 synthesis (k₅) would decrease, causing Cig2 level to fall. Inactivation of the Cdc10 transcription factor after S phase (34) could be just such a signal. If neither the rate of Cig2 degradation nor its rate of synthesis depends on Rum1 binding to Cig2/Cdc2, then our model of endoreplication cycles is not feasible.

For our model to work it is most important that, as Rum1 disappears after Start, Cdc13 should increase and Cig2 should decrease. To capture this idea, we have assumed that Rum1 binding has opposite effects on the cyclins: stabilizing Cig2 and destabilizing Cdc13. We have given some indirect experimental evidence for these assumptions, but we emphasize here that, from a theoretical perspective, the effect of Rum1 binding on Cdc13 stability depends on the state of its ubiquitin-mediated proteolytic pathway. If UbE is “off” during G₁ phase, as in our model, then Rum1 binding must destabilize Cdc13, to keep its level low during G₁. However, if UbE is “on” during G₁ phase, as suggested for budding yeast (35) and fission yeast (P. Nurse, personal communication), then Rum1 binding must stabilize Cdc13 during G₁, just like Cig2. What is essential to our model is the portrait in Fig. 2B, which indicates that a pool of Cdc13 collects in inactive Cdc13/Cdc2/Rum1 trimers at the G₁ steady state.

Whether or not the particular mechanism in Fig. 1 survives future experimental tests, the underlying enterprise of mathematical modeling will remain unimpeached. The process of model building and analysis is not itself an hypothesis subject to falsification, but rather a tool for exploring molecular mechanisms. Constructing the correct mechanism for a complex biochemical control system like the cell cycle is akin to assembling a jigsaw puzzle. We have used the computer as a table to lay out all the pieces we know of the Start puzzle in fission yeast. Obviously, some pieces are missing and we have had to fill in the gaps with hypothetical interactions. But we believe the basic features of the overall picture are becoming clear. Future work will probably show that we have some of the pieces in upside-down, but, in the meantime, we hope this proposed solution will serve as a serious working hypothesis for cell cycle control in S. pombe.

Appendix

To exploit the power of phase plane analysis, we must reduce the full set of 13 differential equations (DEs) in Table 1 to just two DEs for the interactions of Rum1 and Cdc13/Cdc2 in G₁ phase of the cell cycle in wee1⁻ cells. First, we ignore the contributions of Cig1 and Cig2 to CDK activity. Next, because we are interested in G₁ control rather than G₂ control, we ignore tyrosine phosphorylation of Cdc2 and activation of the ubiquitin pathway for cyclin degradation. Making these simplifications, we are left with just three DEs:

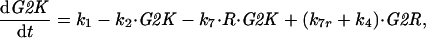A1

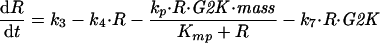A2

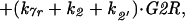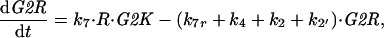A3

with mass treated as a parameter that increases slowly as the cell grows. Finally, we assume that association and dissociation of trimers are fast reactions, so that trimer concentration, G2R, can be calculated from the equilibrium condition

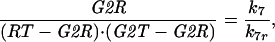A4

where we have introduced two new variables: G2T = [total Cdc13] = G2K + G2R, and RT = [total Rum1] = R + G2R. Using the quadratic equation to solve Eq. A4 for G2R, we are able to write G2R = F(RT, G2T):

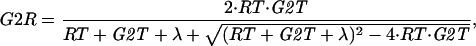A5

where λ = k_7r/k₇ = equilibrium dissociation constant for Cdc13/Cdc2/Rum1 trimers. Now we can rewrite Eqs. A1 and A2 as

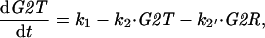A6

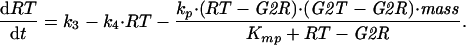A7

Because G2R = F(RT, G2T), these equations form a closed set of nonlinear DEs in the variables G2T and RT. This pair of DEs is easy to study by phase plane methods, using commercially available software like phaseplane (36).

The Cdc13 balance curve is the locus of points (RT, G2T) where Cdc13 synthesis be exactly balanced by Cdc13 degradation: k₁ = k₂⋅G2T + k_2′·F(RT,G2T). This condition defines G2T as a function of RT. We cannot solve the equation explicitly, but the phaseplane program can solve it numerically and plot the relation between RT and G2T: this curve is just the Cdc13 balance curve in Fig. 2B. The Rum1 balance curve has a more complex shape, with local extrema, because its defining equation is more complicated.

By similar arguments, we can describe cdc13Δ cells by a pair of nonlinear DEs for G1T = [total Cig2] = G1K + G1R, and RT = [total Rum1] = R + G1R:

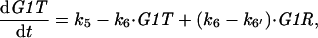A8

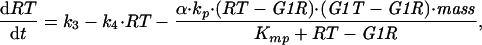A9

where G1R = F(RT, G1R), given by Eq. A5 with λ = k_8r/k₈ = equilibrium dissociation constant for Cig2/Cdc2/Rum1 trimers. Eqs. A8 and A9 are used to construct the phase plane portraits in Fig. 3B.