Desynchronization of cells on the developmental path triggers the formation of spiral waves of cAMP during Dictyostelium aggregation

Abstract

Whereas it is relatively easy to account for the formation of concentric (target) waves of cAMP in the course of Dictyostelium discoideum aggregation after starvation, the origin of spiral waves remains obscure. We investigate a physiologically plausible mechanism for the spontaneous formation of spiral waves of cAMP in D. discoideum. The scenario relies on the developmental path associated with the continuous changes in the activity of enzymes such as adenylate cyclase and phosphodiesterase observed during the hours that follow starvation. These changes bring the cells successively from a nonexcitable state to an excitable state in which they relay suprathreshold cAMP pulses, and then to autonomous oscillations of cAMP, before the system returns to an excitable state. By analyzing a model for cAMP signaling based on receptor desensitization, we show that the desynchronization of cells on this developmental path triggers the formation of fully developed spirals of cAMP. Developmental paths that do not correspond to the sequence of dynamic transitions no relay-relay-oscillations-relay are less able or fail to give rise to the formation of spirals.

The aggregation of Dictyostelium discoideum amoebae after starvation provides one of the best examples of spatiotemporal pattern formation at the supracellular level. This transition from a unicellular to a multicellular stage of the life cycle occurs by a chemotactic response to cyclic AMP (cAMP) signals emitted by aggregation centers in a periodic manner (1–3). Amoebae are capable of relaying the signals emitted periodically by a center located in their vicinity. This excitable response to periodic signals explains the wavelike nature of aggregation over territories whose dimensions can reach up to 1 cm: within each aggregation territory, the amoebae move toward a center in concentric or spiral waves with a periodicity of the order of 5 to 10 min (4–6). Waves of cellular movement correlate with waves of cAMP (7); the latter present a striking similarity to waves observed in oscillatory chemical systems such as the Belousov–Zhabotinsky reaction (8).

As shown by computer simulations using a model for cAMP relay and oscillations based on receptor desensitization proposed by Martiel and Goldbeter (9, 10), concentric waves can readily be explained by assuming the existence of a pacemaker generating periodic pulses of cAMP in the midst of a field of excitable cells. It is much more difficult to explain the origin of spontaneously occurring spiral waves of cAMP. A common artifice to obtain spirals, also used for Dictyostelium (11–14), is to break concentric or planar waves; as the medium is excitable, spirals develop at the extremities of the broken wave. More recently, Pálsson and Cox (15) have used the above-mentioned model (9) to show that the random generation of cAMP pulses after the passage of a wave can give rise to the formation of spirals. Levine et al. (16) also considered the random generation of cAMP pulses in a hybrid model including cAMP production and cell movement and showed that the development of spirals was favored by the feedback exerted by cAMP signals on the excitability of the system. Incorporation of the variation of cell density due to chemotaxis was also shown (17) to favor, in the presence of a pacemaker, the spontaneous formation of spiral waves.

Here we propose a physiologically plausible scenario, only based on cellular properties, for the onset of spiral waves of cAMP at the early stages of D. discoideum aggregation. We take into account the ontogenesis of the cAMP signaling system by allowing it to evolve on the developmental path (18, 19) that brings this system successively from a nonexcitable state to a state in which it displays the relay property, and from such an excitable state into the domain of sustained oscillations of cAMP, before the system becomes excitable again. The transitions between the different modes of dynamic behavior are brought about by continuous changes in biochemical parameters such as the activity of adenylate cyclase and phosphodiesterase in the hours after starvation. Our results indicate that spiral waves of cAMP naturally originate from the desynchronization of cells on the developmental path.

Model for cAMP Signaling Based on Receptor Desensitization

In the model for cAMP oscillations in Dictyostelium based on the reversible desensitization of the cAMP receptor (9, 10), extracellular cAMP binds to the receptor, which exists in two states (20), one of which is active (R) and the other desensitized (D). Only the complex formed by cAMP with the receptor in the R state is capable of activating adenylate cyclase, the enzyme synthesizing cAMP. A positive feedback loop arises from the transport of intracellular cAMP into the extracellular medium where it binds to the cAMP receptor and is hydrolyzed by phosphodiesterase. This model accounts for the oscillatory synthesis of the cAMP signal, with a periodicity of 5 to 10 min (21), and for the accompanying, periodic alternation of the receptor between the phosphorylated (D) and dephosphorylated (R) states (22). The model predicts that the interval between two cAMP peaks—and, consequently, the period of the oscillations—is primarily set by the time required for resensitization of the cAMP receptor.

The model for cAMP signaling is governed by the following system of three differential equations giving the time evolution of the total fraction of active cAMP receptor (ρ_T) and the normalized concentrations of intracellular (β) and extracellular (γ) cAMP (9):

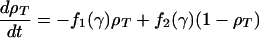1a

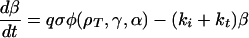1b

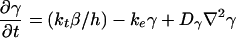1c

with

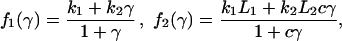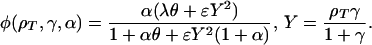2

As considered by Tyson and Murray (11), we have incorporated into Eq. 1c the diffusion of cAMP into the extracellular medium. In this study, we disregard the chemotactic movement of cells, to better focus on the biochemical and developmental aspects of the mechanism of spiral formation.

Developmental Path for the cAMP Signaling System

Besides accounting for relay of suprathreshold cAMP pulses and for autonomous oscillations of cAMP, the model also provides an explanation for the sequence of developmental transitions no relay-relay-oscillations-relay observed during the hours that follow starvation (23). Although the actual developmental path takes place in a parameter space of higher dimensions, the theoretical analysis shows that the continuous increase in the activities of adenylate cyclase and phosphodiesterase after starvation (24–26) suffices to account for these developmental transitions (18, 19). In this view, aggregation centers would be those cells that would be the first to reach the domain of sustained, autonomous oscillations of cAMP as a result of a progressive rise in the activities of adenylate cyclase and phosphodiesterase. Such a phenomenon provides a prototype for the ontogenesis of biological rhythms, by showing how continuous changes in biochemical parameters—associated here with the synthesis of enzymes or receptors—can lead to the onset of autonomous oscillations once a critical value of a control parameter is exceeded (10).

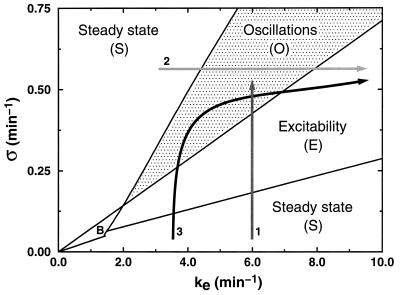
We have established the diagram showing the different modes of dynamic behavior of the cAMP signaling system as a function of the two main parameters of the model governed by Eqs. 1a–1c, namely the maximum activity (σ) of adenylate cyclase and the rate constant of extracellular phosphodiesterase (k_e). Domains S, E, and O in Fig. 1 correspond, respectively, to the regions in which the cAMP signaling system reaches a nonexcitable stable steady state, an excitable steady state, or autonomous oscillations of cAMP. Excitability is determined here as the capability of the system to propagate without attenuation a wave of cAMP initiated by a suprathreshold cAMP pulse applied at the center of the spatially distributed system.

Figure 1.

Stability diagram showing the different modes of dynamic behavior of the cAMP signaling system in the adenylate cyclase (σ)-phosphodiesterase (k_e) parameter space. The different regions are those of a stable, nonexcitable steady state (S), excitability (E) (defined here as the capability of sustaining without attenuation the propagation of a wave of cAMP upon a suprathreshold elevation of extracellular cAMP), sustained autonomous oscillations of cAMP (O), and bistability (B), which denotes the coexistence of two stable steady states (the latter behavior, for which there exists no experimental support so far, is not considered here). The arrows refer to possible developmental paths followed by the signaling system in this parameter space as a result of variation in enzyme activities during the hours that follow starvation. As shown in the text, only path 3 gives rise to the formation of stable, fully developed spirals of cAMP. The diagram has been established by linear stability analysis and numerical integration of Eqs. 1a–1c for the parameter values listed in the last column of table 2 in ref. 9, except the values of k₁, k_-1, k₂, k_-2, which have been multiplied by a factor of 2.5 to obtain waves with a period of the order of 5 min in Fig. 6. For path 2, σ = 0.6 min⁻¹.

Of the three distinct developmental paths considered in Fig. 1, only path 3 accounts for the observed sequence of transitions no relay-relay-oscillations-relay. This path corresponds to the progressive increase in the activity of the two enzymes observed during the hours that follow starvation (24–26). We shall show that the nature of the variation in σ and k_e markedly affects the formation of cAMP waves. Developmental path 3 will be compared with paths 1 and 2 for which k_e or σ remain constant, respectively; as is clear from Fig. 1, the latter two paths correspond to different sequences of dynamical transitions.

Onset of Spiral Waves of cAMP

We now determine the spatiotemporal evolution of cAMP in a two-dimensional medium represented by a spatial grid of typically 100 × 100 points corresponding to a 1-cm² area covered by a layer of cells; the results remain qualitatively unchanged when considering a finer spatial grid. The elements of the grid (100 μm × 100 μm) correspond to groups of about 10 cells; this represents a density of the order of 10⁵ cells/cm², which is above the critical cell density of 2.5 × 10⁴ cells/cm² found for relay (27). Thus, the present simulations are based on the physiologically plausible assumption (see Discussion) that groups of about 10 cells in each “patch” of the grid behave synchronously with respect to their development.

In contrast to others (15, 16) we do not subject the system to any kind of random or periodic pulsing of cAMP. Searching for physiologically plausible conditions giving rise to the spontaneous formation of spiral waves, we first attempted to incorporate a random spatial distribution of parameters such as σ or/and k_e but always failed to generate stable spirals in such conditions. We then included a homogeneous temporal variation in these parameters corresponding to the synchronous evolution of all cells along the developmental paths 1, 2, or 3 considered in Fig. 1. Again stable spirals were never generated in such a way.

Key to the formation of stable spirals is the desynchronization of cells on the developmental path. Up to 10⁵ cells can aggregate around a center; it is inevitable that these cells at any moment do not possess exactly the same amounts of enzymes and do not start their development after starvation in the same initial conditions, if only because they are caught by starvation at different stages of the cell cycle (29–31). Such a heterogeneity due to cell cycle phase distribution was previously invoked to account for the asynchrony in development of the relaying competence (27) and onset of cAMP oscillations (30) in Dictyostelium cells. To characterize this biochemical heterogeneity, we shall consider that at the beginning of starvation cells are distributed along the developmental path. As each point of the path corresponds to a particular time, this is equivalent to considering a distribution of (positive) starting times (t_s) for cells evolving along the same developmental path. This will ensure that some cells will be more advanced than others on this path: the larger t_s, the more advanced the cells in their development.

The probability of the starting time will be taken as a decreasing exponential:

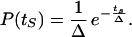3

Parameter Δ measures the desynchronization of cells on the developmental path. The larger Δ, the more heterogeneous the distribution of cells on this path; conversely, when Δ = 0, all cells evolve synchronously. Integration of Eq. 3 shows that 90% (99%) of cells will have a value of t_s between 0 and 2.3 (4.6) Δ. The exponential distribution was retained to ensure that a small percentage of cells is more advanced than the others on the path, so that a minute fraction will reach first the oscillatory domain. Similar results are obtained when using distributions other than exponential, e.g., uniform over a prescribed time interval.

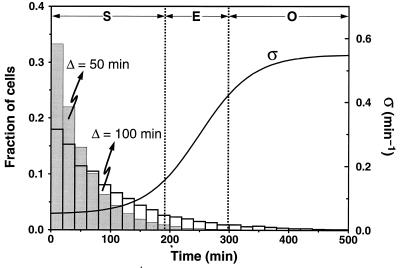
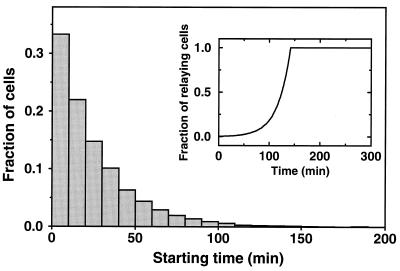
Shown in Fig. 2 are the distributions of starting times along the developmental path 1 (see Fig. 1) for Δ = 50 min (gray histogram) and 100 min (blank histogram), respectively. The solid curve in Fig. 2 shows the variation of parameter σ as a function of time (k_e remains constant along this path). As σ increases, the cAMP signaling system crosses successively the domains (separated by the dotted vertical lines) of nonexcitable steady states (S), excitable states (E), and autonomous oscillatory behavior (O).

Figure 2.

Developmental path 1 (see Fig. 1) and distribution of starting times on this path. The solid line gives the time evolution of parameter σ (in min⁻¹) according to the equation σ(t) = 0.3 + 0.25 tanh [(t − 250)/90] where time t is expressed in min. A similar sigmoidal evolution can be obtained by using a logistic equation for σ(t). The increase in σ brings the signaling system successively through the regions of nonexcitability (S), excitability (E), and autonomous oscillations (O) defined in Fig. 1. The histograms show the distribution of starting times grouped in 20-min intervals, generated according to Eq. 3 for Δ = 50 min (gray bars) or 100 min (empty bars). The starting time for a particular cell is given by the abscissa of the point on the curve σ(t) at which this cell begins its progression on this curve.

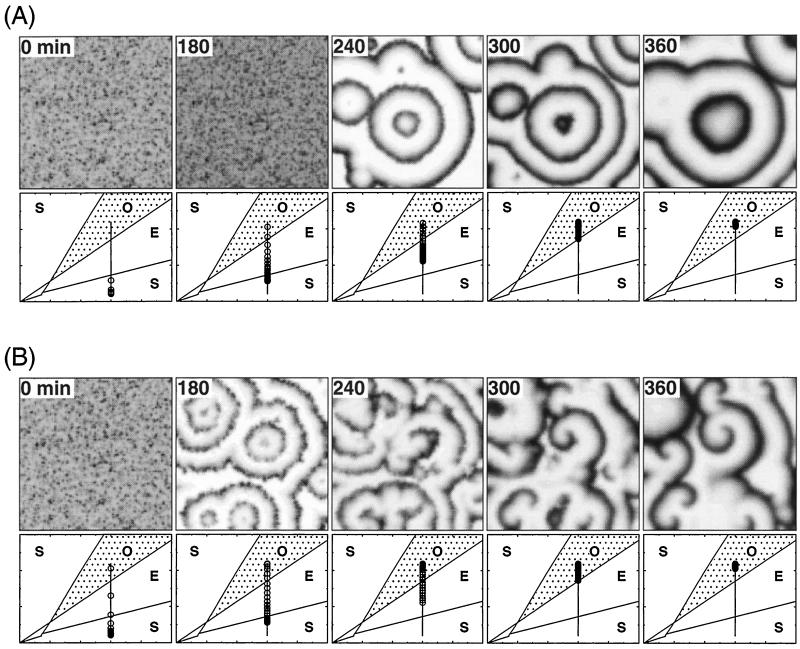
To study the spatiotemporal evolution of the signaling system we consider a spatially random distribution of the values of parameter σ at which this parameter starts to increase on the developmental path; this heterogeneous spatial distribution of σ follows from the probability distribution of the starting times given by Eq. 3. In Fig. 3, we show the spatiotemporal evolution obtained for Δ = 50 min (A) and 100 min (B). In each case, the upper row shows the concentration of extracellular cAMP (γ) at the different times indicated in minutes in the upper left corner of the panels; the lower row gives the distribution of cells on the developmental path at the corresponding times (each circle represents 5% of the total number of cells considered). For Δ = 50 min, almost all cells are initially in the nonexcitable state (see also Fig. 2); concentric (target) waves of cAMP are seen to develop after about 4 hr. No spiral is observed in these conditions.

Figure 3.

Developmental paths and wavelike patterns of cAMP. Shown is the two-dimensional spatial distribution of cAMP (Upper) at indicated times (in min) resulting from the progression of cells along the developmental path 1 (Lower) shown in Fig. 2, for a desynchronization factor Δ = 50 min (A) and 100 min (B). For the cell distribution along the developmental path, each circle represents a 5% fraction of the total amount of cells considered. Parameter values are as in Fig. 1; the diffusion coefficient of cAMP, D_γ, is taken equal to 1.5 × 10⁻⁴ cm²/min (28). The area of 1 cm² is represented as a grid of 100 × 100 points. The spatiotemporal evolution of the system is obtained by integrating Eqs. 1a–1c by means of an explicit Euler method with finite differences for the spatial term in Eq. 1c; the time step used was 10⁻² min, and the precision of the integration was checked by halving this step. For each point of the grid a starting time on the developmental path is chosen according to the probability distribution shown in Fig. 2; the resulting desynchronization of cells on the developmental path creates a spatial heterogeneity in the parameter(s) that vary on this path.

In contrast, for Δ = 100 min, the desynchronization of cells is stronger so that a significant amount of cells rapidly reaches the oscillatory domain and initiates concentric patterns while at that time the other cells are still either in the excitable or nonexcitable state (see Fig. 3B at 180 min). Because of the heterogeneity in the oscillation frequency between emerging pacemakers and in the refractory period among regions of excitable (and nonexcitable) cells, concentric wavefronts are distorted and sometimes break. The loose ends of the broken fronts curl around to form spiral waves (see Fig. 3B at 300 min). These spirals, however, fail to fully develop so as to occupy the whole field, in contrast to those to be described below for path 3. Moreover, bulk oscillations occur in the regions not occupied by spirals, the reason being that for path 1 all cells end in the oscillatory domain.

To determine whether the passage through a domain of excitability before the entry into the oscillatory domain influences the type of wavelike pattern observed, we tested the developmental path 2 of Fig. 1, in which k_e (but not σ) increases. The results (not shown) indicate that only bulk oscillations without any waves occur in these conditions.

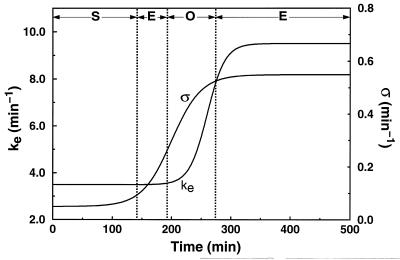
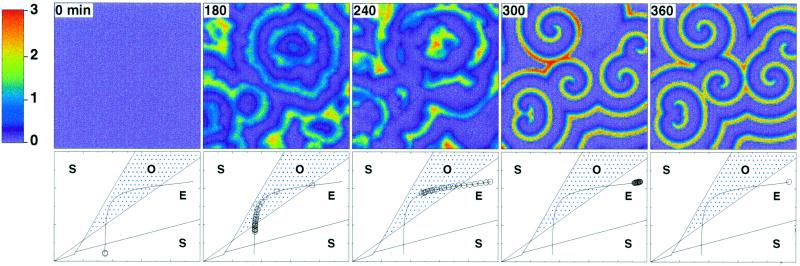
We now turn to path 3 of Fig. 1, which combines an increase in both σ and k_e. This path brings the system across regions S, E, O, E successively. Shown in Fig. 4 is the time evolution of the two parameters. The distribution of starting times obtained here for Δ = 25 min (spirals also are obtained for larger values of the desynchronization factor Δ; see Discussion) is given in Fig. 5. The temporal sequence of spatial cAMP patterns associated with this evolution of the two biochemical parameters is shown in Fig. 6 (Upper), together with the distribution of cells along the developmental path at the times considered (Lower). After some 150 min, concentric waves form, but they are disturbed (see Fig. 6 at 180 min) and later break (see Fig. 6 at 240 min), again as a result of the heterogeneity both in pacemaker frequency and refractory period. In contrast with the case of path 1 illustrated in Fig. 3, spirals take over the whole field (see Fig. 6 at 360 min) as the majority of cells return into an excitable state. The parameters having reached their asymptotic values, which now correspond to a situation in which all cells are excitable, these stable spirals are maintained, with a period close to 5 min.

Figure 4.

Developmental path 3 (see Fig. 1). The solid lines give the time evolution of parameter σ (in min⁻¹) according to the equation σ(t) = 0.3 + 0.25 tanh [(t − 200)/50] and of parameter k_e (in min⁻¹) according to the equation k_e(t) = 6.5 + 3 tanh [(t − 260)/30], where time t is expressed in min. These sigmoidal evolutions, which also could be obtained by using logistic equations, are chosen so as to yield a delay in the rise of k_e respective to the rise in σ, as observed in the experiments (26). The combined increase in σ and k_e corresponds to the developmental path 3 shown in Fig. 1; it brings the signaling system successively through the regions of nonexcitability (S), excitability (E), autonomous oscillations (O), and again excitability (E).

Figure 5.

Distribution of starting times grouped in 10-min intervals, generated according to Eq. 3 for Δ = 25 min. (Inset) Time evolution of the fraction of cells capable of relaying a suprathreshold pulse of cAMP. This curve, to be compared with the experimental curve (see Fig. 1 in ref. 27), is obtained by calculating the cumulated number of cells entering domain E on path 3 (see Figs. 1 and 4), for the distribution of starting times shown in the present figure.

Figure 6.

Fully developed spiral waves of cAMP triggered by the desynchronized progression of cells along the developmental path. Shown is the two-dimensional spatial distribution of cAMP (Upper) at indicated times (in min) resulting from the evolution of cells along the developmental path 3 in Fig. 1 (Lower), associated with the time evolution of σ and k_e prescribed in Fig. 4. The distribution of starting times is given in Fig. 5. Here again each circle represents a 5% fraction of the total amount of cells considered. Parameter values are as in Fig. 3; the desynchronization factor Δ is equal to 25 min. The color scale indicates the level of the normalized concentration of extracellular cAMP, γ.

Discussion

We have presented a developmentally based scenario for the onset of spiral waves of cAMP in the course of D. discoideum aggregation. The mechanism relies on the desynchronized evolution of cells on a developmental path that corresponds to continuous changes in enzyme activities after starvation, which bring about transitions between distinct modes of cAMP signaling. We have compared three different types of developmental paths and showed that only one of these, which corresponds to the observed increase in adenylate cyclase and phosphodiesterase, allows the formation of stable, fully developed spiral waves. These spirals form spontaneously without any kind of external perturbation (e.g., random firing of cAMP pulses) or unnatural intervention (breaking up waves). Our results indicate that of key importance for the triggering of spiral waves is the creation of defects in concentric waves, due to the combined effects of the temporal evolution of the biochemical parameters and of the desynchronization of these biochemical changes among different cells, which allows the simultaneous presence in the medium of nonexcitable, excitable, and oscillating cells. An additional requirement is that cells should follow the appropriate developmental path crossing successively the nonexcitable, excitable, and oscillatory states and return finally to an excitable state, as observed in the experiments.

The comparison of Figs. 3 and 6 suggests that the formation of fully developed spirals is favored by the eventual return of the signaling system to an excitable state. Another contributing factor is the desynchronization of cells measured by parameter Δ (see Fig. 3). In Fig. 6, spirals can be obtained even with a relatively small value of Δ = 25 min; stronger desynchronizations would favor the creation of a larger number of smaller spirals. For this value of Δ, the time required for all cells to go from the nonexcitable to the excitable state is of the order of 4.6 Δ, i.e., about 120 min (see Fig. 5 Inset). This value matches the observed time required for the acquisition of the relaying competence in aggregating Dictyostelium cells (27). It should be compared with the duration of the cell cycle, which is about 8 hr in axenic conditions (29) and shorter, of the order of 4 hr, when cells are grown in a bacterial medium (32). In contrast, the larger values of Δ, of the order of 100 min, yielding less developed spirals in Fig. 3 for the developmental path 1, would yield a much larger value, of the order of the cell cycle length, i.e., 8 hr, for the time required for development of the relaying competence in the whole cell population. The choice of a value Δ = 25 min in Figs. 5 and 6 also holds with another set of experimental results. Indeed Fig. 5 indicates that it takes about 1 hr for 90% of the cells to enter the autonomous oscillatory domain; this agrees with the observation that there is a cell-cycle-dependent 1-hr delay between cells that are the fastest and the slowest to produce cAMP oscillations (30).

The above discussion raises the question as to whether there exists an optimal range for cell desynchronization in regard to the formation of spirals. If the formation of large spirals appears to be favored from an evolutionary point of view, because they result in larger cell aggregates, smaller values of Δ should prove more effective. However, spirals fail to develop from concentric waves when desynchronization is too low, because no defects appear in these conditions. The balance between these two antagonistic effects points to the existence of an optimal range of Δ values.

The above scenario for the onset of spirals includes the effect of the inhibitor of phosphodiesterase considered by Pálsson and Cox (15), when considering that this inhibitor yields a lower effective value of k_e early after starvation. Further addition of the inhibitor would correspond to bending the path 3, which more efficiently produces spirals, toward the left initially; results similar to those shown in Fig. 6 are obtained in these conditions. In a mutant lacking the phosphodiesterase inhibitor, a large number of small concentric waves rather than spirals are observed and appear later (E. Pálsson and E. C. Cox, personal communication). In the model, accordingly, numerical simulations indicate that concentric waves are favored over spirals and form later when path 3 is shifted to the right, as a result of the absence of the inhibitor.

As indicated above, our results have been obtained for a cell density such that about 10 cells occupy one element of the spatial grid. Implicit in our description is the assumption that cells in this group behave as being synchronous in their development after starvation. Such a local synchronization could result from the fact that small groups of cells close to each other are almost certainly clonally related recently and therefore have undergone their last division at more or less the same time. Moreover, the short-range action of a differentiation-inducing factor secreted by starving cells favors the synchrony of development in their neighborhood (33).

Preliminary simulations with a finer spatial grid, which allows us to consider the evolution of single cells at the expense of increased computer time, yield similar results as to the effect of desynchronization on the onset of spiral waves. However, it is more difficult first to generate waves and, in a second time, to break them to obtain spirals if all cells are desynchronized. Small clumps of coordinated cells, desynchronized with respect to other such clumps, are more prone to overcome the leveling by diffusion of the spatial inhomogeneities that initiate waves and later nucleate the defects needed for spiral formation. A finer spatial grid further allows us to address the effect of cell density if each element of such a grid contains several cells (considered as synchronous) and the chemical reaction terms in the kinetic equation (Eq. 1c) for extracellular cAMP are multiplied by a factor related to the ratio of intracellular to extracellular volumes. In agreement with experimental observations (34), numerical simulations indicate that increasing cell density favors the formation of spirals.

Many studies of the formation of spiral patterns in chemical systems (35–37) have focused on the role of spatial heterogeneities (including obstacles) in breaking wavefronts so that their loose ends may curl into spirals. The mechanism outlined here for the breaking of wavefronts and subsequent formation of spirals in Dictyostelium cells is different in that it combines spatial heterogeneity with the temporal evolution of dynamical properties of the medium.

The present analysis brings to light the possible role played by the desynchronization of the biochemical changes induced after starvation in triggering the formation of spiral waves of cAMP. The model predicts that better synchronization of cells, e.g., through temperature shift (27, 38), release from nocodazole block (30), or dilution of stationary phase cells into growth medium (29), should favor the appearance of concentric waves over spirals. Desynchronization may be but one important factor for the emergence of spiral patterns in Dictyostelium, together with other contributing factors, including cell movement. Our results show how the concept of developmental path, which accounts for the sequential transitions in dynamic behavior of the cAMP signaling system in the course of time, ties in with the selection of a spatial pattern in the form of spirals of cAMP.