Detecting immigration by using multilocus genotypes

Abstract

Immigration is an important force shaping the social structure, evolution, and genetics of populations. A statistical method is presented that uses multilocus genotypes to identify individuals who are immigrants, or have recent immigrant ancestry. The method is appropriate for use with allozymes, microsatellites, or restriction fragment length polymorphisms (RFLPs) and assumes linkage equilibrium among loci. Potential applications include studies of dispersal among natural populations of animals and plants, human evolutionary studies, and typing zoo animals of unknown origin (for use in captive breeding programs). The method is illustrated by analyzing RFLP genotypes in samples of humans from Australian, Japanese, New Guinean, and Senegalese populations. The test has power to detect immigrant ancestors, for these data, up to two generations in the past even though the overall differentiation of allele frequencies among populations is low.

Classical theory in population genetics has focused on the long term effects of immigration on allele frequency distributions in semi-isolated populations, concentrating on the stationary distribution resulting from a balance between forces of immigration, genetic drift, and mutation (1–4). Less theory exists addressing the effect of recent immigration among populations with low levels of genetic differentiation. A theory describing the effects of immigration on the genetic composition of individuals in populations that are not at genetic equilibrium is needed to interpret much of the data being generated using current genetic techniques.

In this paper we consider the multilocus genotypes that result when individuals are immigrants, or have recent immigrant ancestry. We propose a test that allows recent immigrants to be identified on the basis of their multilocus genotypes; the test has considerable power for detecting immigrant individuals even when the overall level of genetic differentiation among populations is low. Molecular genetic techniques that allow multilocus genotypes to be described from single individuals are relatively new, and much of the information contained in these types of data is not fully exploited by estimators of long term gene flow that are currently available (5–7). We provide an example of an application of the method to restriction fragment length polymorphism (RFLP) genotypes from human populations; the method may also be applied to analyze multilocus allozyme and microsatellite data.

Theory

A collection of I discrete populations of a diploid species exchange immigrants, with random mating among individuals within populations. Consider a set of l loci in linkage equilibrium, and let k_j be the number of alleles at the jth locus. Let x = {x_hji} be a matrix of the allele frequencies in each population, where x_hji is the frequency of the hth allele (h = 1, 2, … , k_j) at the jth locus (j = 1, 2, … , l) in the ith population (i = 1, 2, … , I). A set of n = {n₁, n₂, … , n_I} chromosomes are sampled from the I populations, where n_i is the number sampled from the ith population. Let X = {X_ijm} be the matrix of genotypes among the sampled individuals, where X_ijm is the genotype at the jth locus of the mth individual sampled from the ith population.

The population allele frequencies are generally unknown, and we therefore derive the probability density of allele frequencies in each population by using a Bayesian approach. The tests presented in this paper make use of the allele frequency distributions to calculate genotype probabilities. It is assumed that the total number of alleles at the jth locus in each population is identically k_j. The set of alleles observed in the collection of populations as a whole is used as an estimate of k_j. Without additional information, we initially assign an equal probability density to the frequencies of the alleles at the jth locus in the ith population. The prior probability density of allele frequencies (i.e., before sampling) is then (8)

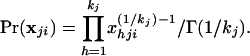1

The posterior probability density of the allele frequencies at the jth locus, conditioned on the alleles observed in a sample from population i, is now determined. Let the vector n_ji = {n_1ji, … , n_kjji}, where n_hji is the observed number of copies of the hth allele at the jth locus in a sample from the ith population. The posterior probability density of allele frequencies is then

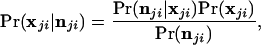2

where

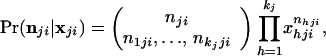3

and we define n_ji = Σ_h=1^k_j n_hji. The marginal distribution of n_ji (conditional on n_ji) is

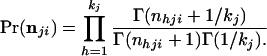4

Eq. 2 then simplifies to

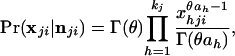5

where θ = n_ji + 1 and

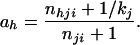6

Eq. 5 is a Dirichlet probability density function (8) with parameters θ and a_h, where h = 1, 2, … , k_j.

Genotype Probabilities

If individual m is born to nonimmigrant parents in population i, the probability that the individual has genotype X_ijm at the jth locus, assuming random mating, is

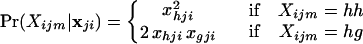7

for all h = 1, 2, … , k_j and g = 1, 2, … , k_j where g ≠ h. The actual allele frequencies in population i are unknown and we therefore consider the probability of the genotype for individual m, conditional on the sample of alleles from the ith population, denoted as Pr(X_ijm|n_ji). The genotype of individual m is created by sampling two alleles at random from population i. Since the allele frequencies are not known we use the Dirichlet density of Eq. 5 to describe the probability density of allele frequencies and integrate over all possible allele frequencies

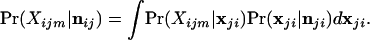8

The marginal probability of the observed genotype, obtained in this way, is equal to the probability of sampling two alleles from a compound multinomial-Dirichlet distribution (7)

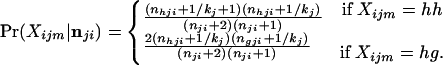9

This is the posterior probability that the genotype X_ijm is observed for the jth locus when the individual is a nonimmigrant from population i. If the allele frequencies are independent among loci (i.e., there is no linkage disequilibrium), the genotype probabilities at other loci are calculated similarly. The probability of the multilocus genotype X_im = {X_i1m, … , X_ilm} of individual m is then a product over the probabilities of the observed allelic configurations for each locus

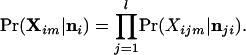10

We now consider situations in which one parent is a resident of population i, and the other is an immigrant born to nonimmigrant parents in population i′. In this case, one allele copy is of immigrant origin. There is generally no prior information regarding the source of an individual’s alleles (chromosomes), and each copy at a locus is therefore equally likely to have been derived from the immigrant source. If we consider the genotype of individual m, born in population i, and denote an immigrant allele from population i′ using a prime symbol, the probability of the mixed genotype X_(i,i′)jm at the jth locus is

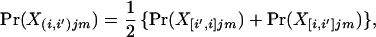11

where parentheses in the subscripts indicate that the alleles making up the genotype are averaged with respect to possible source populations, and brackets indicate that the alleles making up the genotype are labeled according to their source population. If an individual has alleles h and g at a particular locus, for example, these possibilities are X_[i,i′]jm = hg′ and X_[i′,i]jm = h′g, where h′ indicates that allele h is derived from population i′ and h indicates that it is derived from population i. Conditional on the allele frequencies, the probabilities of the genotypes, labeled according to source population, are

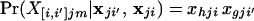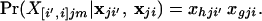12

Sampling a single allele for each population from a multinomial-Dirichlet density with the appropriate population parameters, we obtain

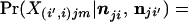13

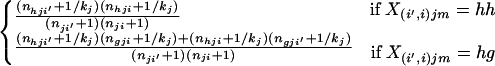for all h = 1, 2, … , k_j and g = 1, 2, … , k_j where g ≠ h. This is the posterior probability that the genotype X_(i′,i)jm is observed for the jth locus when the individual is of mixed ancestry from populations i and i′. The probability of the multilocus genotype X_(i′,i)m = {X_(i′,i)1m, … , X_(i′,i)lm} is then

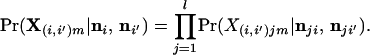14

Identifying Immigrant Genotypes

In this section, we describe a test for detecting individuals born in a population other than the one from which they are sampled; these individuals are first-generation immigrants. Consider an individual m randomly sampled from population i. The probability of the observed multilocus genotype for the individual, given that the individual was born in population i and has no recent immigrant ancestry, is calculated using Eq. 10 above as Pr(X_im|n_i). If individual m was instead born in population i′ to parents with no recent immigrant ancestry and subsequently immigrated to population i, then the probability of observing the multilocus genotype of the individual is calculated using Eq. 10 above as Pr(X_im|n_i′). The relative probability that the individual was born to parents with no recent immigrant ancestry in population i, rather than population i′, is therefore given by the ratio of the probabilities

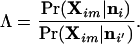15

In practice, we take logarithms and use the equivalent form

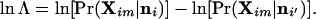16

Positive values of ln Λ indicate that the null hypothesis (that the individual is not an immigrant) is favored, while negative values indicate that the alternative hypothesis (that the individual is an immigrant) is favored. A value of ln Λ = ln(10) = 2.30, for example, indicates that individual m is 10 times more likely to have arisen in population i, while a value of ln Λ = −2.30 indicates the individual is 10 times less likely to have arisen in i than i′. The distribution of the statistic Λ under the null hypothesis (that the individual is not an immigrant) was examined using Monte Carlo simulation (see below).

We now describe a test for detecting an individual with a single parent that is an immigrant, or is descended from an immigrant. In this case, one allele copy at each locus is of possible immigrant origin and the other is of local origin. For l independent loci, the probability of observing the genotype of individual m, given that the individual was born in population i and has an immigrant parent from population i′, is calculated using Eq. 14 as Pr(X_(i′,i)m|n_i, n_i′).

The individual might instead have an ancestor d generations in the past that was an immigrant. The probability of the observed genotype X_(i′,i)jm at the jth locus under this hypothesis is

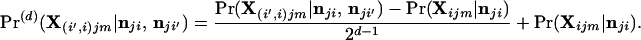17

For l independent loci, the posterior probability of observing the genotype of individual m, given that this individual has an immigrant ancestor d generations removed from population i′, is

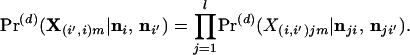18

The relative probability that individual m, born in population i, did not have an immigrant ancestor from population i′ at generation d in the past is

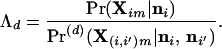19

We again use logarithms to calculate this statistic as ln Λ_d. The analysis can be extended to consider individuals of mixed parentage over several generations, but the number of possible outcomes makes an exhaustive analysis difficult. In certain cases, when fewer ancestral immigration patterns are possible, based on prior information, the method outlined above might be extended to decide among the possible alternatives.

Critical Region and Power of Tests

The critical (rejection) region for the test statistic calculated using the methods described in the preceding sections contains all values of the statistic such that Λ < C, where C is chosen to satisfy Pr(Λ < C) = α under the null hypothesis. For a specified value of C, the value of α is given by

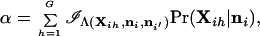20

where

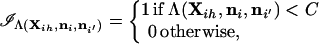21

and the sum is over the total number of possible genotype configurations G = ∏_j=1^l(k_j + 1)k_j/2. A Monte Carlo estimator of α is

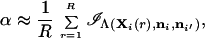22

where X_i(r) is the rth simulated genotype with R genotypes simulated in total from the posterior probability distribution Pr(X_ih|n_i). The random variables X_i(r) can be generated using the following procedure: for the jth locus, generate the first allele by assigning to allele type h the probability

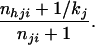23

If the first allele is of type h, generate the second allele by assigning to allele type h the probability

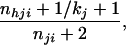24

or to allele type g ≠ h the probability

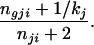25

It is also possible to determine C by generating a set of genotypes as outlined above and considering the value of the test statistic that falls below 1 − α percent of the values for the simulated genotypes (see Fig. 1). The power of the test to reject the null hypothesis when it is false, for a specified critical region α, is

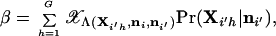26

where

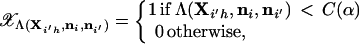27

where C(α) is the value of C that specifies the critical region with probability α determined using Eq. 20. A Monte Carlo estimator of the power β is

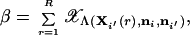28

where X_i′(r) is the rth simulated genotype, with R genotypes simulated in total from the posterior probability distribution Pr(X_i′h|n_i′). The power of the test is illustrated graphically as the overlap between the distributions of the statistic generated by simulating genotypes under the null and alternative hypotheses (see Fig. 2).

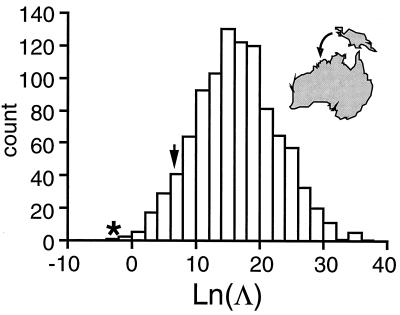
Figure 1.

Illustration of Monte Carlo method for examining significance of test statistic ln Λ for comparison of Australian (sample) and New Guinean (potential source) populations. Histogram of 1,000 values of the ln-probability difference generated by simulating genotypes given the allele counts observed for the Australian (sample) population. A total of 72 markers, for which the individual Australian 1 has been typed, were used to generate the distribution. See Eqs. 23–25. The critical region for the test statistic (α = 0.05) is that portion of the distribution to the left of the arrow. The posterior probability ratio (ln Λ = −2.76) for the individual Australian 1 is indicated by an asterisk.

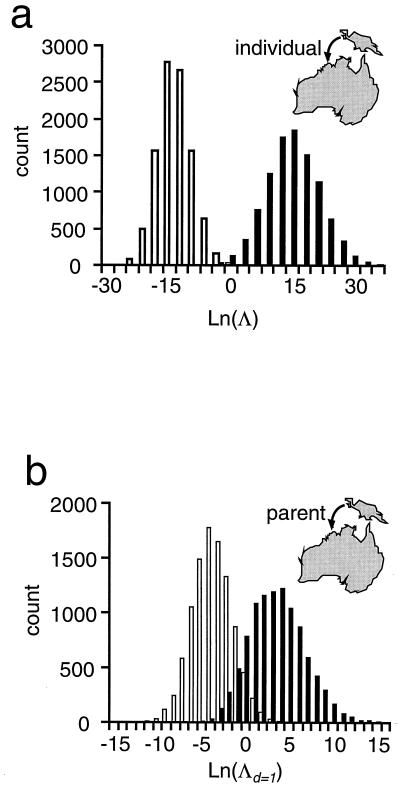
Figure 2.

Histograms indicating the power of the immigration tests for two cases. (a) The hypothesis that an Australian individual is an immigrant (d = 0) from New Guinea is considered. The shaded columns represent the distribution of ln Λ generated given the alleles observed for the Australian sample, while the unshaded columns represent the distribution of ln Λ generated given the alleles observed for the New Guinean sample. (b) The hypothesis that one parent of an Australian individual was an immigrant (d = 1) from New Guinea is considered. The shaded columns represent the distribution of ln Λ generated given the alleles observed for the Australian sample, while the unshaded columns represent the distribution of ln Λ generated given the alleles observed for the Australian and New Guinean samples and assuming that the individual received one allele at each locus from each population.

Application

We have applied our method to a set of 12 individuals from each of four human populations. We chose to compare two population samples with quite low genetic differentiation (9) and two population samples with quite high genetic differentiation from a set of population samples studied previously (10). The samples with low differentiation are from an Australian population and a New Guinean population (F_ST distance = 0.056). The samples with high differentiation are from a Japanese population and a Senegalese population (F_ST distance = 0.232). The Australian sample was collected from a coastal region of Australia, and the New Guinea sample from the highland region of New Guinea. The Japanese sample consists of individuals born in Japan and was collected in the San Francisco Bay Area (11). The Senegalese sample consists of Niokolonke individuals of the Mandenka population collected in southeastern Senegal (10). These 48 individuals have been typed at approximately 50 loci (12) by using RFLPs. The physical locations of the loci suggest that most are unlinked. Multiple restriction enzymes were used to type several of the loci so that the total number of genetic markers was approximately 75. The procedures employed in the sampling and the genetic analysis are described in detail elsewhere (11).

The power of the test to detect immigrants depends on the extent of differentiation between the populations compared (Table 1) as well as the number of loci examined and the number of individuals sampled (unpublished observations). A test of the hypothesis that an individual is an immigrant has high power in all the population comparisons. A test of the hypothesis that an individual has an immigrant parent has lower power for a comparison of individuals from the Australian and New Guinean samples than for a comparison of individuals from the Japanese and Senegalese samples. The test has power to detect an immigrant ancestor through the grandparent generation for a comparison of individuals from Japan and Senegal.

Table 1.

Power of posterior probability ratio tests for recent immigration, with α = 0.05

Sample population	Potential source	Power at d
		0	1	2	3	4
Australian	New Guinean	1.00	0.83	0.37	0.17	0.09
New Guinean	Australia	1.00	0.94	0.60	0.25	0.14
Senegalese	Japanese	1.00	1.00	0.78	0.37	0.16
Japanese	Senegalese	1.00	1.00	0.76	0.41	0.20

If d = 0, the individual under consideration immigrated from source population; d = 1, one parent of the individual immigrated; if d = 2, one grandparent of the individual immigrated; if d = 3, one great-grandparent of the individual immigrated; if d = 4, one great-great-grandparent of the individual immigrated from source population. 

The distribution of the statistic under Monte Carlo simulation (Fig. 2) illustrates the power of the tests. In Fig. 2a, individuals sampled in Australia are postulated to have immigrated from New Guinea. There is little overlap between the distribution of the test statistic generated by Monte Carlo simulation under the null hypothesis that an individual was born in the Australian population (at right of Fig. 2a) and that under the alternative hypothesis that an individual is an immigrant from the New Guinea population (at left of Fig. 2a). In Fig. 2b, individuals in the Australian sample have a single parent that is an immigrant from New Guinea under the alternative hypothesis. In this case there is more overlap between the distributions generated under the null and alternative hypotheses, indicating that the test has reduced power by comparison with the test for detecting first-generation immigrants (i.e., Fig. 2a).

We applied the test to predict whether individuals sampled in Australia have New Guinean ancestry, and vice versa, and whether individuals sampled in Japan have African ancestry, and vice versa. A total of four individuals from the complete set of 48 comparisons produced significant test statistics at some level of ancestry (Table 2). Three of the four individuals (Australia 1, Australia 2, and Australia 3) who appeared to be immigrants, or descended from immigrants, were drawn from the Australian population, which appears likely to have experienced recent exchanges of immigrants (11). In the case of three individuals (Australia 1, Australia 3, and Japanese 1) it appears possible that an ancestor two or more generations removed was an immigrant, whereas in the case of one individual (Australia 2) it appears most probable that the individual is a first-generation immigrant. Given these results, one might consider excluding individual Australia 1, for example, from the Australian population sample for evolutionary studies, as it is quite probable that this individual has recent immigrant ancestry.

Table 2.

Power of the posterior probability ratio test to detect immigrant ancestry: Four individuals with posterior probability ratios indicating possible immigration (α < 0.05)

Individual	Potential source	No. of markers	Value	Hypothetical immigrant ancestor
				Individual (d = 0)	Parent (d = 1)	Grandparent (d = 2)	Great-grandparent (d = 3)
AUS1	NGN	76	ln Λ	−2.76	−2.89	−1.65	−0.89
			α	0.000	0.009	0.022	0.037
			Power	1.000	0.821	0.347	0.197
AUS2	NGN	73	ln Λ	4.48	0.87	−0.37	−0.11
			α	0.032	0.179	0.244	0.288
			Power	1.000	0.828	0.332	0.136
AUS3	NGN	82	ln Λ	5.23	−0.50	−0.90	−0.56
			α	0.032	0.049	0.064	0.092
			Power	1.000	0.862	0.375	0.149
JPN1	SEN	69	ln Λ	17.80	1.52	−1.26	−1.10
			α	0.021	0.014	0.029	0.045
			Power	1.000	0.999	0.771	0.431

Twelve individuals from each of four populations were included. Australians (AUS) were considered as possible immigrants, or descendants of immigrants, from New Guinea (NGN), and vice versa. Japanese (JPN) were considered as possible immigrants, or descendants of immigrants, from the Senegalese (SEN) population, and vice versa. Values of ln Λ or ln Λ_d are given in the first row for each individual. Values in the second row are significance levels (α values) approximated using the Monte Carlo approach (1,000 iterations per test). Values in the third row are the power of the test for this individual (α < 0.05). 

Discussion

The test for detecting recent immigration developed in this paper provides information relevant to a wide range of problems in population biology and human genetics. In the area of human genetics, for example, the method may be used to identify individuals whose genomes are not typical of the populations in which they currently live, or of their ethnic group. This may be helpful in genetic counselling. In the area of evolutionary biology, it is often important to identify immigrant individuals to study their behavior and interactions with resident individuals. It may also be important to quantify the amount of recent immigration in populations that are not at genetic equilibrium. In the field of conservation genetics, this test may be useful for identifying the population of origin for zoo animals whose history is poorly known to implement successful captive breeding programs.

At least three potentially misleading results may arise when applying the method considered here. First, the failure to reject the hypothesis that an individual was an immigrant, or descended from immigrants, may simply reflect the fact that the appropriate populations for comparison were not included in the analysis. Second, an individual might incorrectly appear to have originated in a particular population other than the one from which it was sampled. This might be due to similarities in allele frequencies, due to long-term gene flow, between that population and a third population from which the individual actually originated, but which was not included in the sample of populations. Third, the fact that many pairwise comparisons between populations are performed for each of a large number of individuals means that some individuals will appear to be immigrants purely by chance. This can be corrected for by using smaller values for α.

The analyses of human populations presented in this paper show that, even with a sample of only 60 independent loci, the method we have proposed has power to detect immigrant ancestry up to two generations in the past. This is despite our conservative correction for uncertainties of allele frequencies. A larger number of loci will increase the power and could allow a single immigrant great-grandparent (out of 8 total), or a single immigrant great-great-grandparent (out of 16 total), to be identified. The precise number of loci needed to obtain a given level of power depends on the degree of genetic differentiation between populations; with greater differentiation, fewer loci are needed to obtain the same level of power. Computer simulations should prove useful in exploring the statistical performance of the method more generally.

Program availability.

A program written in the C computer language for performing the calculations described in this paper is available by anonymous ftp from mw511.biol.berkeley.edu in directory /pub, or on the World-Wide Web at site http://mw511.biol.berkeley.edu/homepage.html.

ABBREVIATION

RFLP

restriction fragment length polymorphism