Incorrect nucleotide insertion at the active site of a G:A mismatch catalyzed by DNA polymerase β

Abstract

Based on a recent ternary complex crystal structure of human DNA polymerase β with a G:A mismatch in the active site, we carried out a theoretical investigation of the catalytic mechanism of incorrect nucleotide incorporation using molecular dynamics simulation, quantum mechanics, combined quantum mechanics, and molecular mechanics methods. A two-stage mechanism is proposed with a nonreactive active-site structural rearrangement prechemistry step occurring before the nucleotidyl transfer reaction. The free energy required for formation of the prechemistry state is found to be the major factor contributing to the decrease in the rate of incorrect nucleotide incorporation compared with correct insertion and therefore to fidelity enhancement. Hence, the transition state and reaction barrier for phosphodiester bond formation after the prechemistry state are similar to that for correct insertion reaction. Key residues that provide electrostatic stabilization of the transition state are identified.

Insertion fidelity of DNA polymerases plays a central role in the replication and repair of DNA (1). DNA polymerase β (pol β) is the simplest eukaryotic DNA polymerase. It catalyzes the template-directed nucleotidyl transfer reaction during the repair of “simple” base lesions with moderate fidelity, producing approximately one error per 3,000 nucleotides synthesized during base excision DNA repair (2). There is great interest in how pol β achieves such fidelity without an intrinsic proofreading exonuclease. This interest is stimulated by a wealth of kinetic and site-directed mutagenesis studies available for pol β (2, 3).

A recent structural study of the precatalytic complex [pol β, DNA template, primer and a nonreactive deoxynucleoside triphosphate (dNTP) analogue, 2′-deoxy-adenosine-5′-(α,β)-methylene triphosphate (dAMPCPP)] provided for the first time a ternary complex structure with an active-site G:A mismatch (4). The two Mn²⁺ ions in the active site were found to be octahedrally coordinated. The primer O3′ group was found to be replaced by a water molecule, relative to its position in an earlier structure of a ternary complex with a matched (i.e., Watson–Crick) base pair (5).

All families of DNA polymerases are believed to catalyze the nucleotidyl transfer reaction through a universal two-metal-ion mechanism (6). Reaction pathways for correct nucleotide incorporation have been extensively investigated by using various models. However, the reaction pathway for incorrect insertion is still unknown. Earlier studies had found that the rate of catalytic reaction for the correct base pair is a crucial factor in achieving high fidelity in DNA synthesis (7). The incorrect nucleotide insertion reaction catalyzed by DNA polymerases exhibiting modest to high fidelity is much slower than for the correct insertion (8, 9).

A variety of computational techniques have been used in this study, including classic molecular dynamics simulation and quantum mechanics to set up the reactive system, as well as the combined quantum mechanics and molecular mechanics method (QM/MM) for the nucleotidyl transfer reaction. The QM:MM version of the ONIOM method developed by the Morokuma group was used, with electronic coupling between QM and MM regions implemented through an electronic embedding approach (10, 11), similar to normal QM/MM implementations.

Results and Discussions

“Two-State” Mechanism.

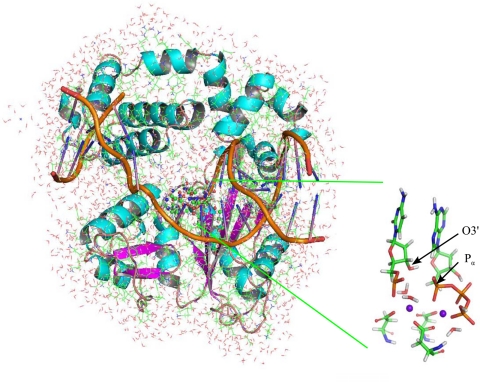
Two states, a “ground state” and a “prechemistry state,” have been identified from molecular dynamics simulations. The ground state represents the most stable conformation of the mismatch ternary complex and was derived from the x-ray crystal structure (Fig. 1). However, the arrangement of reactive atoms in this state is unfavorable and does not provide a clear pathway for the nucleotidyl transfer reaction. Formation of P–O bond between O3′ and the dNTP P^α is energetically unlikely (as indicated from our QM/MM calculations below). Therefore, we propose a two-stage reaction mechanism, in which a local structural change occurs in the active site: the primer terminal O3′ replaces one of the water molecules bound to the catalytic Mg ion (Mg_cat²⁺), with the result being an active site similar to that found in our study of correct insertion (12). This reorganized prechemistry state can then follow the correct insertion reaction pathway that involves proton transfer and phosphodiester bond formation at O3′. We obtained the prechemistry state by constrained molecular dynamics on the equilibrated ground state structure that led to the dissociation of an O_wat–Mg_cat²⁺ coordination and formation of an O3′–Mg_cat²⁺ coordination. Once formed, this prechemistry state was found to be stable after 5 ns of unconstrained molecular dynamics simulation.

Fig. 1.

The equilibrated ground state structure based on the x-ray crystal data (Batra 2007). (Inset) Stick diagram of the essential region treated by quantum mechanics.

Obtaining an estimate of the relative free energy and the free energy barrier between ground state and prechemistry state is problematic when using a molecular mechanical force field because the breaking and forming of metal-oxygen coordination cannot be properly described. Yet, one approach to accomplish this goal is through stepwise free energy calculation with the QM/MM/molecular dynamics implementations, such as QM/MM-FE (free energy) (13) and QM/MM-MFEP (minimum free energy path) (14). However, such calculations would be highly time-consuming. As an alternative, we carried out a series of managed quantum mechanics calculations using a cluster model of the active site to obtain estimates of the energy differences/barrier between the two states. Cluster models have been used in previous theoretical studies of DNA polymerases (15, 16). Our cluster model was constructed from the crystal structure, and during the geometry optimization and potential energy scans, the model closely resembles the active-site structure. Using the O3′–Mg²⁺ distance as the reaction coordinate, we successfully obtained the potential-energy profile for the necessary active-site structural reorganization (coordinated water molecule replaced by primer O3′). A potential barrier of 14.1 kcal/mol was required for the transformation, and the transition state (TS) was found at O3′–Mg²⁺ = 2.8 Å, which is close to a heptacoordinated Mg structure. The cluster prechemistry state was found to be a local minimum located 4.4 kcal/mol higher than the cluster ground state. Although further structural relaxation allows further stabilization by 2.7 kcal/mol with the changes of hydrogen-bonding network, the potential-energy path connecting the prechemistry state and ground state is more appropriately used for the estimation of the energies associated with the Mg²⁺ coordination change. Whereas the estimate of the barrier and relative energies of the two states was reasonable and not overall limiting, the actual values may depend upon, on the one hand, how the cluster is defined and, on the other hand, the effect of the dynamical molecular lattice in the real system. [Details of the cluster calculations are provided in supporting information (SI) Fig. S1.] Although further investigation of the rearrangement of the ground state is warranted, our molecular dynamics simulations and quantum mechanics calculations suggest the existence of a local prechemistry state and a viable transformation pathway.

Nucleotidyl Transfer Reaction Mechanism.

The unconstrained minimized structures for both ground state and prechemistry state using the amber ff99 force field (17) were further optimized at the ONIOM(B3LYP/6-31G*:Amber) level of theory. A comparison of key active-site distances between optimized structures and the crystal structure is presented in SI Computational Methods. We also investigated the interactions between the crucial primer O3′ and the surrounding environment. For the ground state structure, O3′ forms a hydrogen bond with O5′ on the incoming nucleotide triphosphate, whereas for the prechemistry state, a hydrogen bond between O3′ and OD2 of Asp-256 is more stable by 0.4 kcal/mol. The latter arrangement is similar to our previous study of correct insertion (12) but to a lesser extent energetically. For the correct insertion case, the Asp-256 interaction is ≈4 kcal/mol more stable than the O5′ interaction (12).

While attempting a “direct” reaction from the ground state initial structure, we were unable to predefine a deprotonation pathway for the primer terminal O3′–hydrogen. When we attempted to enforce direct O3′–P^α bond formation without prior proton transfer, the energy continued to rise and at O3′–P^α = 2.0 Å, 47 kcal/mol above the ground state. The H3′–O3′ bond was still present. (Details of the calculations are provided in Fig. S2.) Therefore, we ruled the direct pathway for O3′–P^α bond formation as an unlikely nucleotidyl transfer reaction mechanism.

From the prechemistry state initial minimized structure, we were able to successfully carry out the reaction in a manner similar to our previous study in correct insertion (12). Moreover, we were able to identify the TS for the proton transfer from O3′ to OD2 of Asp-256 with a barrier of 6.0 kcal/mol. The product of the proton transfer is a local minimum 3.4 kcal/mol higher than the initial prechemistry state [for correct insertion, this intermediate is 3.5 kcal/mol higher than the initial state (12)]. An illustration of the potential-energy profile for proton transfer is presented in Fig. S3. The structure of the proton transfer product features a weakened OD1(Asp-256)–Mg_cat²⁺ interaction with the O–Mg²⁺ distance increasing from 2.07 to 2.94 Å (Fig. S4). The interaction between Asp-256 and Mg_cat²⁺ recovers during the formation of the O3′–P^α bond and thereby contributes to the stabilization of the TS.

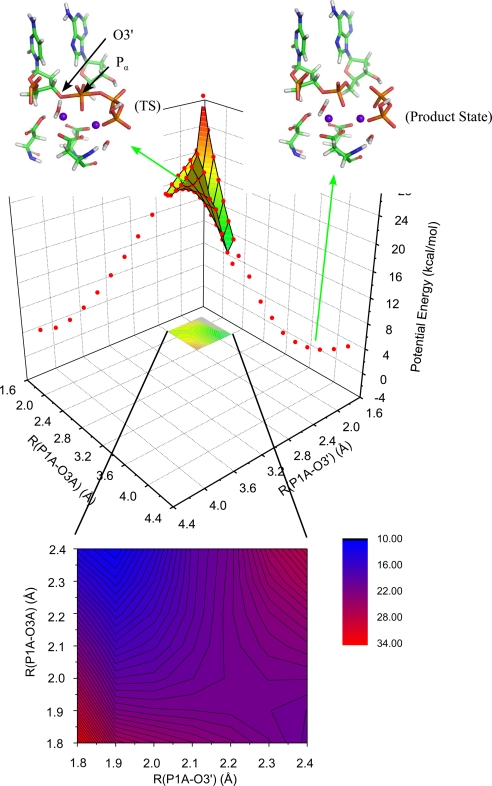
A two-dimensional adiabatic potential-energy surface, as a function of the distances associated with the bond-forming and bond-breaking process, was obtained at the ONIOM(B3LYP/6-31G*:Amber) level of theory (Fig. 2). Overall, despite the differences in the mismatched DNA, the results are similar to our prior study for correct insertion. The distance between the primer O3′ and P^α of dATP (R_O3′-P1A) describes the nucleophilic attack process; that between P^α and α–β bridging oxygen (R_P1A-O3A) describes the bond-breaking process. The TS is identified at R_O3′-P1A = 2.25 Å and R_P1A-O3A = 1.95 Å (2.2 and 1.9 Å, respectively, in correct insertion) with energy E(TS) = 20.7 kcal/mol relative to the prechemistry initial state [21.5 kcal/mol in A:dTTP correct insertion (12)] and 17.3 kcal/mol relative to the deprotonated intermediate state [18.0 kcal/mol in correct insertion (12)]. The reaction proceeds with an associative mechanism, similar to the correct insertion case. The reaction proceeds first by the formation of the O3′–P^α bond, then is followed by the P^α–O3A bond-breaking. An intact scaffold comprised of both metal ions, Asp-190, Asp-192, and the triphosphate is crucial throughout the development of the TS.

Fig. 2.

The essential reaction pathway between the deprotonated prechemistry state and the product state (phosphodiester bond formed).

Although the phosphodiester bond formation is the rate-determining step, in a multistep reaction, the overall rate, as well as the apparent free energy of activation, depends on the relative free energy of the intermediate states (ΔG₀) relative to the ground state, ΔG* = ΔG₀ + ΔG*_TS. The calculated apparent activation energy for correct insertion (A:dTTP; 21.5 kcal/mol) is ≈4.7 kcal/mol higher than the approximate experimental value of 16.8 kcal/mol [using k_pol of 3.2 s⁻¹ (7)]. A higher level of theory or inclusion of entropic effects might have an effect. From our calculations, we find that there is only a small difference in activation energies from the prechemistry state for incorrect insertion and A:dTTP correct insertion (12). For misinsertion in the G:A mismatch, however, the higher apparent (overall) activation energy is mainly due to the additional energy difference between the ground state and the prechemistry state, which is estimated to be ≈3.8 kcal/mol [based on k_pol(G:dCTP)/k_pol(G:dATP) = 12.5/0.019 = 660] (18).

As the reaction proceeds toward the product state, the O3′–Mg_cat²⁺ distance increases. When the reaction reaches a stable product state with R_O3′-P1A = 1.66 Å, R_P1A-O3A = 3.4 Å, there is an energy change of −0.4 kcal/mol relative to prechemistry initial state, which is significantly more positive than the value of −5.2 kcal/mol we obtained in A:dTTP correct insertion. A recent study on fidelity of Dpo4 suggested that pyrophosphorolysis occurring immediately after misincorporation (reverse reaction) can contribute to enhanced fidelity of the DNA polymerase (19). Our calculations support such a possibility because the G:A mismatch and pyrophosphate complex has an energy higher than the ground state of the complex, and because the release of pyrophosphate and Mg_bind²⁺ may be limited by the “closed”-to-“open” conformational change that must take place for the next enzymatic cycle.

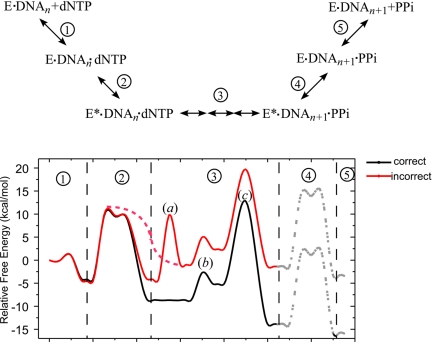
Comments on Free Energy Profiles, Fidelity, and Checkpoints.

Many kinetic models have been proposed for the DNA polymerases (20–22). It is now believed that, for DNA polymerase β, after binding DNA, there is a fast dNTP initial binding step before the pol β undergoes a conformational change from the open to the closed form; nucleotide insertion is the rate-determining step; pyrophosphate is released as or after pol β undergoes a closed-to-open conformational change. A free energy profile can be estimated by using information such as the initial binding constant, the rate of conformation change (step 2), and our calculated and estimated energy differences (Fig. 3). A stopped-flow fluorescence analysis (23) suggested that the conformational change step (k₂ ≈ 64.4 s⁻¹) is faster than the nucleotide insertion step [k_pol is 12.5 s⁻¹ for G:dCTP and 0.019 s⁻¹ for G:dATP (18)]. Kinetics analysis for T7 DNA polymerase also suggested a faster conformational step, in which k₂ (≈660 s⁻¹) is approximately twice as faster as k_pol (≈360 s⁻¹) (21). Using TS theory, a free energy barrier of 15.0 kcal/mol for pol β can be obtained for conformational change, 16.1 kcal/mol for G:dCTP correct insertion, and 19.8 kcal/mol for G:dATP incorrect insertion. The kinetics analysis of T7 DNA polymerase also suggested that there is only a small difference in the dNTP initial binding constant (K_d,1, region 1 of Fig. 3) between correct (G:dCTP) and incorrect (G:dGTP) insertion (28 vs. 200 μM, corresponding to 1.16 kcal/mol difference in binding free energy), significantly less than the difference reflected in K_d [G:C vs. G:A is ≈270:1.9 (8), corresponding to 2.94 kcal/mol difference in binding free energy]. Accordingly, in our schematic free energy profile (Fig. 3), the binding free energy of correct insertion comes from both dNTP initial binding and the conformational change from the open to the closed form, whereas for incorrect insertion, there is little gain from the conformational change. The computational studies of Schlick's group (24) suggested possible difference conformational change pathway for correct and incorrect insertion. Although the free energy barrier for the open-to-closed conformational change may not differ significantly between correct and incorrect insertion, the closed-to-open conformational change in step 2 of Fig. 3 may have a lower barrier for incorrect insertion. A faster reverse closed-to-open conformational change, however, may provide a basis for checking the misinsertion. From our finding described here, incorrect insertion will undergo an extra step to reach the prechemistry state that occurs subsequent to subdomain closing before the nucleotidyl transfer reaction can occur, making the overall chemical step slower than correct insertion [for k_pol, G:dCTP vs. G:dATP is ≈12.5:0.019 (18)]. The fidelity is defined as (eff_incorrect + eff_correct)/eff_incorrect, where efficiency (eff) for incorrect or correct insertion is given by k_pol/K_d in pre-steady-state or single-turnover analysis and k_cat/K_m in steady-state analysis. The efficiency differences between correct and incorrect insertion can be seen from the energy difference of the chemical TS relative to the reference state (DNA:pol β binary complex and dNTP). For incorrect insertion, the reaction energy released is less compared with correct insertion. The energy barrier for reverse pyrophosphorolysis reaction immediately after incorrect insertion is also lower than that in correct insertion, which may provide a way for removing incorrectly inserted dNTP as suggested in the study of Dpo4 (19).

Fig. 3.

Schematic representation of the free energy profile. Steps: 1, initial binding of dNTP; 2, open-to-closed conformational change; 3a, O3′ replacing water in Mg_cat²⁺ coordination (for misincorporation only); 3b, proton transfer from O3′ to Asp-256; 3c, phosphodiester bond formation; 4, closed-to-open conformational change; 5, release of pyrophosphate and Mg ions. The dashed lines represent possible transition pathways and barriers.

Residue Contributions to Rate of Misinsertion and Insertion Fidelity.

To examine the roles of different residues in catalysis and therefore the role in fidelity, we applied an energy decomposition analysis that is based on electrostatic interactions. The electrostatic interaction between the atoms directly involved in the reaction (the quantum atoms) and the remaining atoms of the system is a key factor that regulates the reaction rate. That is, the lowering of the activation barrier by the enzyme can be attributed to a stabilization of the TS via electrostatic interactions of the quantum-described active site with the environment. With the current study, we are able to estimate the effects of each residue on the rate of the central nucleotidyl transfer reaction. We are not yet able to, however, estimate the contributions to the free energy difference between ground state and prechemistry state. Therefore, the residue electrostatics contributions we computed represent partial contributions to the change in the observed k_pol.

For the current calculations, the total electrostatic interaction of a given residue with the QM atoms is approximated as E_elec(QM/MM) = Σ(Q_αQ_β/R_αβ), where Q_α are the fitted partial charges for the QM atoms using the ESP method (25) taken from the QM calculation. (Q_β is the partial charge of the MM atom; R_αβ is the distance between two atoms.) Such approximations have been successfully applied previously (26, 27).

The electrostatic contributions to the stabilization of the TS for each residue during the nucleotidyl transfer reaction are similar for both correct insertion (12) and incorrect insertion, with few exceptions. A comparison with the earlier study of A:dTTP correct insertion is presented in Table S1. These results can also be compared with experimental mutagenesis studies: mutagenesis information for G:dATP misinsertion is available for N294A, N294Q, E295A, R183A, K280A, R149A (8), R283A (28), and Y271A (29). The first four mutants were found to reduce the misinsertion rate k_pol by 29- to 80-fold; the next four mutants only reduce k_pol by 1.0- to 2.7-fold. In our calculations, we found that some of the rate change can be at least partially explained by the electrostatic stabilizing effect on the TS, such as for S180A, R183A, and S188A. Because the electrostatic stabilizing effect of the TS is similar between correct and incorrect insertion, these mutants have a similar effect on the rate of correct insertion and therefore do not change fidelity significantly. However, the residue contribution analysis for some mutants—such as N294A or E295A, which suggest more complicated roles of the residues—is not in accord with the mutagenesis studies. These two mutants likely play a similar role for the chemical reaction in both the correct and incorrect insertion cases because the fidelity is affected by <3-fold (8). Our residue electrostatic contribution analysis found that Tyr-271 destabilizes the TS by 0.64 kcal/mol; the Y271A mutant, however, is found to reduce both the binding free energy (lower K_d) and reaction rate (k_pol), including a reduction in G:A fidelity by 5,800-fold (29). For this case, the difference likely depends on structural effects, rather than a simple electrostatic effect.

Conclusion

In the present study, the G:dATP misinsertion reaction catalyzed by human DNA pol β is investigated by using a combination of computational methods. A two-state mechanism is proposed that may serve as a general mechanism for either misinsertion or misextension. The dislocation of the O3′ group is commonly found in mismatched DNA pol β structures (30, 31). The prechemistry state is identified as a local stable state, which can be accessed via a local structural change at the active site. The association of the O3′ with Mg_cat²⁺ is a major requirement leading to the lowest energy barrier during the reaction. The fact that incorrect insertion reveals a similar TS and reaction barrier once the O3′ is properly positioned again emphasizes the importance of the reaction scaffold (triphosphate, Asp-190, Asp-192, and two Mg ions) for the formation of phosphodiester bond. The immediate product state is less stable in G:dATP incorrect insertion vs. A:dTTP correct insertion. However, we must reach this conclusion with a couple of caveats. First, we have calculated the energy surface rather than the free energy surface. Second, a larger basis set would need to be used to draw a secure quantitative conclusion.

A general energy profile was obtained combining our calculated results and other experimental information. This profile reveals that two features—the O3′ displacement and the higher energy product state—distinguish incorrect insertion from correct insertion (12), and these features also account for fidelity in the mismatched case. Amino acid side chain effects on fidelity, including alternations of metal ions, can also be discussed in context of the current profile; the effects on the binding free energy, the relative free energy difference between the ground state and prechemistry state, and the relative energy of TS all contribute to fidelity.

Computational Methods

A recent x-ray crystal structure of the ternary (gapped DNA-dNTP analog-pol β) G:A mismatch complex (4) was used to construct the initial structures for theoretical calculations (Fig. 1). This structure, which has two Mn ions in the catalytic and dNTP-binding sites, provides the current best description of the stable active-site mismatched ternary complex structure before the phosphodiester bond formation. As a prelude to the theoretical study, the dNTP analog, dAMPCPP, was changed to the corresponding 2′-deoxyribo-adenosine triphosphate (dATP) molecule by replacing the α-β bridging carbon with oxygen, and all Mn ions were replaced by Mg ions. Hydrogen atoms were added to the model using the LEaP program of the Amber 9 package (32, 33). Protonation states on all residues of pol β were based on estimated pK_a values from the PropKa program at pH of 7 (http://propka.chem.uiowa.edu/). H(dATP)³⁻ has a pK_a value of 6.47 (34), which suggests a significant fraction of dATP exists as H(dATP)³⁻. Previous studies also suggested that the protonated form is required to stabilize the product state (12). A proton transfer process, together with the deprotonation of the primer 3′-hydroxyl group, is consistent with the deuterium isotope studies that two proton transfers occur for nucleotidyl transfer reactions catalyzed by RNA and DNA polymerases (35). The proton was assigned to a free oxygen atom on the γ-phosphate. A total of 7 Mg and 13 Na ions were included to maintain electrical neutrality of the total system. All of the crystal water molecules were preserved. The system was then solvated in a box of solvent with 22663 water molecules. The Amber ff99 force field (17) was used for DNA, the base group of dATP and protein; the TIP3P model (36) was used for water molecules. Partial atomic charges for dATP molecule (Table S2) were taken from the ESP charges of our previous QM/MM calculations on the correct insertion system (12). Long-range interactions were treated using the particle mesh Ewald (PME) method (37, 38).

The x-ray crystal-like structure underwent a 5.5-ns molecular dynamics simulation. A snapshot structure after 2.7 ns was taken and annealed to 100 K before geometry minimization to obtain the ground state of the ternary complex with G:A mismatch. Another snapshot after 3.0 ns underwent constrained molecular dynamics to adjust the active-site structure to be similar to that with matched base pair (5). The adjusted structure was then stabilized by a 5.3 ns molecular dynamics simulation. A snapshot was taken after 1.4 ns and annealed to 100 K followed by geometry minimization to obtain the initial structure for the prechemistry state. All simulations and minimizations were performed using the SANDER module of the Amber 9 package (33). Details of the simulations are described in SI Computational Methods.

To study the energetics associated with the transformation from the ground state to the prechemistry state, we carried out QM calculations on a model cluster constructed from the x-ray crystal structure. Three protons were assigned to neutralize the system, one at Asp-256 to mimic Arg-254, and two on the triphosphate to mimic Arg-149 and Arg-183. The QM calculations were carried out at the B3LYP/6-311G** level of theory. The minimized structure remains structurally similar to the x-ray crystal structure. Potential-energy profiles for the transformation from the ground state to the prechemistry state were obtained by using the O3′-Mg_cat²⁺ distance as reaction coordinate.

A hybrid QM/MM potential using the ONIOM(MO:MM) method was applied in the calculations for both ground state and prechemistry states. The quantum region includes parts of Asp-190, Asp-192, Asp-256, primer terminal nucleotide, dTTP, two Mg ions, and several water molecules, which brings the total charge of the quantum system to −2 (the total system remains neutral). The complete DNA, protein and waters 12 Å from the QM atoms were retained. The ground state initial structure includes 58 quantum atoms, 6 link atoms for a total of 13585 atoms. The prechemistry state includes 55 quantum atoms (one less water) and 6 link atoms for a total of 13630 atoms. A detailed description of the systems can be found in SI Computational Methods. MM atoms within 8 Å from the QM atoms were allowed to move during the geometry optimization. The quantum region was treated using density functional theory with the B3LYP exchange-correlation functional (39, 40) and 6-31G* basis set in Gaussian 03 (41). The remainder of the system was treated using the Amber ff99 force field (17). The calculations were performed using the ONIOM module as implemented in Gaussian 03 (41). Electrostatic interactions between the QM and MM regions were included using the ONIOM electronic embedding method.

Multiple one- and two-dimensional adiabatic potential-energy surfaces were calculated for selected reaction coordinates that can be used to describe the various bond-forming and bond-breaking processes. Settings for the potential-energy surface scan and convergence criteria are described in SI Computational Methods.