Tail End of the S6 Segment

Abstract

The permeation pathway in voltage-gated potassium channels has narrow constrictions at both the extracellular and intracellular ends. These constrictions might limit the flux of cations from one side of the membrane to the other. The extracellular constriction is the selectivity filter, whereas the intracellular bundle crossing is proposed to act as the activation gate that opens in response to a depolarization. This four-helix bundle crossing is composed of S6 transmembrane segments, one contributed by each subunit. Here, we explore the cytoplasmic extension of the S6 transmembrane segment of Shaker potassium channels, just downstream from the bundle crossing. We substituted cysteine for each residue from N482 to T489 and determined the amplitudes of single channel currents and maximum open probability (P _o,max) at depolarized voltages using nonstationary noise analysis. One mutant, F484C, significantly reduces P _o,max, whereas Y483C, F484C, and most notably Y485C, reduce single channel conductance (γ). Mutations of residue Y485 have no effect on the Rb⁺/K⁺ selectivity, suggesting a local effect on γ rather than an allosteric effect on the selectivity filter. Y485 mutations also reduce pore block by tetrabutylammonium, apparently by increasing the energy barrier for blocker movement through the open activation gate. Replacing Rb⁺ ions for K⁺ ions reduces the amplitude of single channel currents and makes γ insensitive to mutations of Y485. These results suggest that Rb⁺ ions increase an extracellular energy barrier, presumably at the selectivity filter, thus making it rate limiting for flux of permeant ions. These results indicate that S6_T residues have an influence on the conformation of the open activation gate, reflected in both the stability of the open state and the energy barriers it presents to ions.

INTRODUCTION

The transmembrane permeation pathway (pore) in potassium channels is formed at the convergence of four radially oriented subunits. Transected along the axis of the pore, this pathway has a central water-filled cavity with restrictions at its extracellular and intracellular ends (Doyle et al., 1998). The extracellular restriction is the selectivity filter (Hille, 2001) that endows potassium channels with the power to discriminate strongly between monovalent cations as similar as K⁺ and Na⁺. The water-filled central cavity is the binding site for some cationic pore blockers (Zhou et al., 2001a). Finally, the intracellular restriction is believed to be a movable gate that can be opened and closed by relevant stimuli, such as intracellular binding of ligands or changes of membrane potential (Yellen, 1998; Perozo et al., 1999; Del Camino and Yellen, 2001).

In voltage-gated potassium channels, in which each subunit has six transmembrane segments (S1–S6), the selectivity filter is formed from the extracellular loops between S5 and S6; the central cavity is lined mainly by the hydrophobic S6 transmembrane segments; and the cytoplasmic activation gate is the site where the four helical S6 segments converge in a right-handed bundle crossing (Liu et al., 1997; Holmgren et al., 1998; Del Camino et al., 2000; Del Camino and Yellen, 2001). Membrane potential is sensed primarily by the positively charged S4 segments, which move when the membrane potential changes (Bezanilla, 2000). These movements are transmitted to the activation gate, causing it to open or close (Sigworth, 1994; Yellen, 1998; Bezanilla, 2000; Horn, 2000).

Movement of ions is markedly different through the selectivity filter versus the open activation gate. Whereas large monovalent and multivalent ions, including small peptides and anions, can traverse the open activation gate (Liu et al., 1997; Zhou et al., 2001a), only a highly restricted subset of small, monovalent cations can cross the selectivity filter of voltage-gated potassium channels (Heginbotham and MacKinnon, 1993; Heginbotham et al., 1994). Furthermore, the narrow selectivity filter typically contains at least two K⁺ ions at a time in a single-file arrangement (Doyle et al., 1998; Morais-Cabral et al., 2001; Zhou et al., 2001b). This suggests that the selectivity filter is the primary obstacle to flux of permeant ions, like K⁺ and Rb⁺.

We ask here whether the cytoplasmic extension of the S6 segment below the bundle crossing can influence movement of K⁺ ions. To this end, we introduced cysteines into each of eight consecutive residues in this region of Shaker potassium channels. We assayed effects of the individual mutations on permeation using nonstationary noise analysis, pore block, and biionic selectivity between K⁺ and Rb⁺. The results show that this cytoplasmic region affects the movement of both permeant and impermeant ions through the open activation gate.

MATERIALS AND METHODS

DNA Clones and Site-directed Mutagenesis

The wild-type background we use for mutations is Shaker H4 containing four modifications: deletion of residues 6–46 to remove N-type inactivation, T449V to inhibit C-type inactivation, and C301S and C308S to reduce sensitivity of the wild-type channel to cysteine modification (Holmgren et al., 1996). To increase the expression level, we introduced the Kozak consensus sequence (5′-GCCACCATGG; Kozak, 1991) before the coding region by site-directed mutagenesis. Based on this background, we constructed eight cysteine mutants (N482C, Y483C, F484C, Y485C, H486C, R487C, E488C, and T489C). Mutagenesis was done with QuickChange^TM site-directed mutagenesis kits from Stratagene. All of the cDNA clones were sequenced to verify each mutation. We used a standard calcium phosphate method to transiently transfect tsA201 and HEK293 cells. The culture dishes were coated with poly-l-ornithine (Sigma-Aldrich) to facilitate the formation of outside-out patches.

Electrophysiology

Standard patch-clamp recording methods were used to record ionic currents from outside-out patches with an Axopatch 200B amplifier (Axon Instruments, Inc.). For nonstationary noise analysis of K⁺ currents, the pipette contained (mM): 105 KF, 35 KCl, 10 EGTA, 10 HEPES, pH 7.4, and the bath contained (mM): 150 NaCl, 2 KCl, 1.5 CaCl₂, 1 MgCl₂, 10 HEPES, pH 7.4. To estimate single channel Rb⁺ currents, we replaced all of the K⁺ in both bath and pipette solutions with Rb⁺. To examine block by tetrabutylammonium (TBA),* we incorporated TBA in the pipette solution. The bath and pipette solutions were the same as for noise analysis. The Rb⁺-substituted solutions were also used to examine the effects of Rb⁺ on TBA block. To estimate Rb⁺/K⁺ selectivity we measured reversal potentials in outside-out patches. For these experiments, the pipette solution contained (Rb⁺ _i): 105 RbF, 35 RbCl, 10 EGTA, 10 HEPES, pH 7.4, and the bath solution contained (K⁺ _o or Rb⁺ _o): 140 KCl or RbCl, 1 CaCl₂, 10 HEPES, pH 7.4.

All of the experiments were done at room temperature. Liquid junction potentials between the bath and the pipette solution were corrected. Electrode resistance was in the range of 1–2 MΩ. The voltage error due to series resistance was <3 mV after compensation. The currents were low-pass filtered at 5–10 kHz and acquired with a DigiData 1200B digitizer using Clampex 8.0 (Axon Instruments, Inc.). For nonstationary noise experiments, the outside-out patch currents were filtered at 10 kHz and sampled at 200 kHz. Capacitance and leakage currents were subtracted by the use of a P/−8 correction protocol from a −120 mV holding potential.

Data Analysis

Data were analyzed using pCLAMP (Axon Instruments, Inc.), ORIGIN 6.1 (OriginLab), and Fortran (Compaq). Throughout the paper, error bars represent the standard error of the mean.

G-V relationship

The voltage dependence of conductance (G) was estimated from an isochronal measurement of the amplitude of outward tail currents at a fixed voltage, set between −60 and −90 mV for different mutants. The G-V relationships were fitted to the Boltzmann equation:

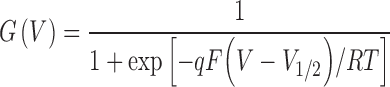where G(V) is normalized conductance, V _1/2 is the half-activation voltage, q is the charge, and RT/F is 25 mV at room temperature.

Nonstationary noise analysis.

Estimation of the single channel current amplitude (i) at 0 mV, the number of channels (N), and the maximal probability of a channel being in the open state (P _o,max) in a patch of membrane was done by nonstationary noise analysis (Sigworth, 1980). The mean current (I) and variance (σ²) were calculated from 55–60 current traces, measured during step depolarizations delivered at a rate of 0.5 Hz. In most patches the variance was calculated from differences between successive traces (Heinemann and Conti, 1992). The mean-variance relationships were fitted to the equation:

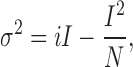(1)

where i and N are free parameters with estimates^{^} i and^{^}N. P _o,max is then:

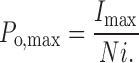Permeability ratio.

Under biionic conditions, we measured the change in reversal potential (ΔV _rev) from the solution K⁺ _o/Rb⁺ _i to solution Rb⁺ _o/Rb⁺ _i. The Rb⁺/K⁺ permeability ratio can be expressed as

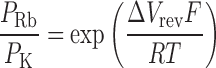(Hille, 2001).

Blockade by TBA.

The kinetics of intracellular TBA block were determined from outside-out patches using the time course of current reduction during a depolarizing voltage step. The dissociation rate constant k _off in the presence of different concentrations of TBA ([TBA]) is calculated as:

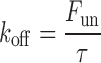where τ is the time constant of the current relaxation, and F _un is the equilibrium fraction of unblocked current, estimated from the ratio of steady-state to peak current. The association rate constant k _on was calculated as:

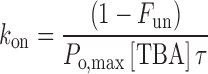where P _o,max is the maximum open probability at 0 mV estimated from noise analysis. We define the apparent blocking rate k′_on = [TBA]k _on. K _d, the dissociation constant for block, is the ratio of k _off to k _on. The K _d values in Table III are means of estimates at all TBA concentrations.

TABLE III.

TBA Block

	i	P o,max	k on	k off	K d
	pA		s−1M−1 (× 106)	s−1	μM
WT	1.16 ± 0.08 (n = 5)	0.85 ± 0.03	1.91	29.5	15.4
Y485C	0.63 ± 0.04 (n = 5)	0.78 ± 0.02	1.14	22.3	19.6
Y485S	0.66 ± 0.07 (n = 3)	0.71 ± 0.05	1.00	20.9	20.9
Y485A	0.55 ± 0.03 (n = 3)	0.52 ± 0.04	0.56	19.4	34.7
WT/Rb+	0.31 ± 0.02 (n = 3)	0.83 ± 0.01	1.72	51.1	29.7
Y485A/Rb+	0.28 ± 0.01 (n = 4)	0.79 ± 0.01	0.46	32.4	70.9

RESULTS

The four hydrophobic S6 segments of Shaker line a major portion of the permeation pathway and are believed to form the activation gate where they cross at their cytoplasmic ends, in the vicinity of residue 476 (Liu et al., 1997; Del Camino et al., 2000; Del Camino and Yellen, 2001). We mutated eight residues (N482–T489) downstream from the S6 segment to examine the role of this region on permeation. For convenience, we refer to these eight residues as the tail of the S6 segment or the S6_T region. S6_T residues were substituted individually by cysteines in a Shaker construct lacking the cytoplasmic inactivation ball and containing the T449V mutation that impairs C-type inactivation. We used this construct as the wild-type background for our mutations, and measured currents from outside-out patches.

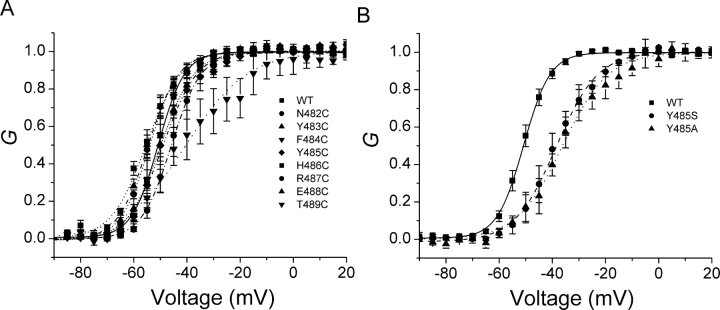
Fig. 1 shows potassium currents in response to families of depolarizations for the wild-type channel and each cysteine mutant. Other than small differences in activation kinetics, the macroscopic currents from these S6_T mutants are rather comparable to those of wild-type channels. This is further substantiated by normalized conductance-voltage (G-V) curves for these constructs, based on isochronal measurements of tail current amplitudes (Fig. 2 A; Table I).

Figure 1.

Ionic currents of WT and cysteine mutants. The currents were activated in response to depolarizing voltage steps from −100 to 40 mV in 5-mV steps. The holding potential was −120 mV. We plot here the currents at every 10-mV interval.

Figure 2.

Normalized G-V curves. The G values were obtained from the tail currents at −60 mV. The smooth lines are fits to a Boltzmann function, with fitting parameters summarized in Table I. A shows all cysteine mutants, and B shows two other mutants of residue Y485.

TABLE I.

Effects of Mutations on the G-V Relationships

	G-V
	V 0.5	q
	mV	e0
WT	−50.0 ± 1.2	5.2 ± 0.3 (n = 4)
N482C	−44.6 ± 2.4	5.2 ± 0.4 (n = 4)
Y483C	−54.4 ± 2.8	4.6 ± 0.2 (n = 5)
F484C	−36.6 ± 5.3	2.3 ± 0.7 (n = 4)
Y485C	−48.8 ± 1.1	4.1 ± 0.5 (n = 4)
H486C	−55.9 ± 1.2	4.3 ± 0.6 (n = 5)
R487C	−54.0 ± 1.0	4.7 ± 0.4 (n = 3)
E488C	−50.0 ± 3.1	4.8 ± 0.6 (n = 4)
T489C	−50.7 ± 2.2	5.8 ± 0.3 (n = 4)

Estimated parameters from fits of G-V curves to single Boltzmann functions for K⁺ currents in outside-out patches (Fig. 2).

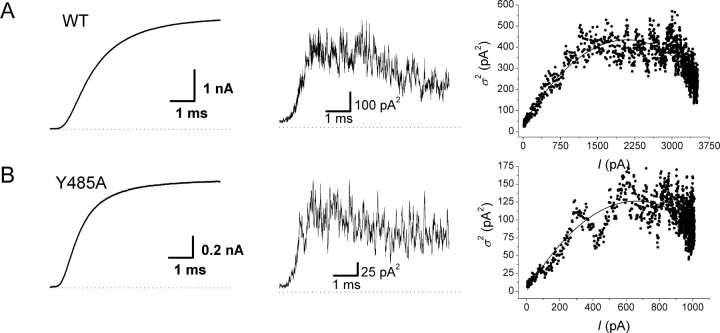
Some of the mutants, most notably F484C and Y485C, consistently had smaller macroscopic currents than others. In separate experiments using whole cell recording, we also noted that the amplitudes of the ionic currents, relative to gating currents, were small for these two mutants (unpublished data). We therefore suspected that their relatively small ionic currents were due to a decrease in either single channel conductance (γ) or peak open probability (P _o,max). To distinguish these two alternatives, we did nonstationary noise analysis (Sigworth, 1980) on the wild-type and all eight cysteine mutants, measuring K⁺ currents in outside-out patches.

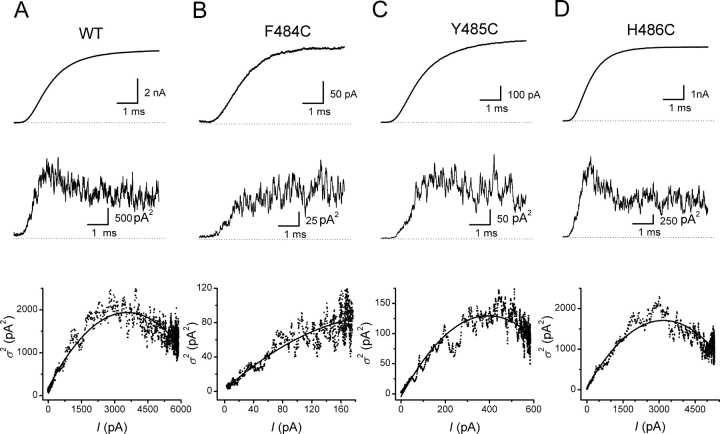
Fig. 3 shows an example of these experiments on the wild-type and three of the mutants, F484C, Y485C, and H486C. These mutants were selected for display because F484C has the largest effect on P _o,max and Y485C has the largest effect on γ, whereas H486C has little effect on either. The top panels show the typical sigmoidal activation kinetics for the mean currents from ∼60 depolarizations to 0 mV. The middle traces show the average variance of the individual current traces around the mean value. The variance is minimal at the beginning of the records before the channels begin to open. In all cases, except for F484C, the variance reaches a maximal value before the mean current has reached its plateau. This observation is shown more clearly in the bottom panels that plot the variance against the mean current for these patches. Theoretically, the parabolic relationship between variance and mean reaches its peak when the open probability equals 0.5 (Sigworth, 1980), which is not achieved for F484C. In the patch shown for F484C, P _o,max was 0.38. Fits of the parabolic relationship between the variance and mean current also produce an estimate of the single channel current (i) at 0 mV for each patch.

Figure 3.

Nonstationary noise analysis. Data from wild-type and three mutants. (Top) Mean current for 55–60 depolarizations to 0 mV from a holding potential of −120 mV. (Middle) Time course of average variance. (Bottom) Variance-mean relationships fit by Eq. 1 with results in Table II.

Table II summarizes the data for these experiments. Three consecutive mutants (Y483C, F484C, and Y485C) show significant decreases in the single channel current, whereas only F484C decreases P _o,max significantly. The amplitude of the macroscopic current depends on the product of i and P _o,max. In accordance with the relatively small ionic currents in patches expressing F484C, the smallest value of iP _o,max is observed for F484C (Table II), due to decreases in both i and P _o,max. The value of iP _o,max for Y485C is also quite small, due almost entirely to a decreased value for single channel current.

TABLE II.

Noise Analysis

	i	P o,max	iP o,max
	pA
WT	1.16 ± 0.08	0.85 ± 0.03	0.99 ± 0.09 (n = 5)
N482C	1.18 ± 0.05	0.77 ± 0.03	0.91 ± 0.04 (n = 5)
Y483C	0.89 ± 0.061	0.77 ± 0.02	0.68 ± 0.05 (n = 5)1
F484C	0.80 ± 0.041	0.38 ± 0.021	0.30 ± 0.01 (n = 6)1
Y485C	0.63 ± 0.041	0.78 ± 0.02	0.49 ± 0.04 (n = 5)1
H486C	1.23 ± 0.06	0.86 ± 0.01	1.05 ± 0.04 (n = 5)
R487C	1.06 ± 0.02	0.86 ± 0.02	0.91 ± 0.04 (n = 4)
E488C	1.13 ± 0.09	0.84 ± 0.03	0.95 ± 0.10 (n = 5)
T489C	0.90 ± 0.08	0.84 ± 0.02	0.76 ± 0.08 (n = 4)

¹Significant difference from wild-type at the P < 0.05 level (t test).

The low value of P _o,max for F484C at 0 mV either represents a true maximum, or else may be an underestimate if the voltage-dependent open probability for this mutant has not reached its maximum value by 0 mV. However, parameters of fitted G-V curves for K⁺ currents in the same patches used for noise measurements (Fig. 2 A; Table I) indicate that the P _o,max of F484C is underestimated by no more than ∼4% at 0 mV.

Because of the difficulty controlling the expression level of Shaker in transfected cells, we were unable to verify the reductions in i using single channel recording. The most likely artifact of noise measurements that might produce an apparent reduction in i would be a decrease in mean open time by S6_T mutations. Low-pass filtering of brief openings could prevent the signal-processed currents from reaching their full amplitudes (Yellen, 1984). To test this possibility, we digitally over-filtered the currents we used for our noise measurements to see if this would decrease the estimates of i. The data were originally analogue-filtered at 10 kHz by the patch clamp amplifier and sampled at 200 kHz. After additionally filtering these currents with a digital, 5-kHz low-pass Gaussian filter, which leaves the original currents filtered at 4.5 kHz (Colquhoun and Sigworth, 1995), there was no change in the estimates of i in either wild-type (n = 5), Y485C (n = 5), or Y485A (n = 3; P > 0.05, paired t test for each construct). Therefore, the estimated reductions of i are inconsistent with an artifact due to an effect of mutations on gating.

The effect of Y485C on single channel current, a 46% reduction, raises a question about how this reduction can be achieved when the rate-limiting step in movement of K⁺ ions through an open channel is usually thought to be controlled by the selectivity filter near the extracellular end of the permeation pathway (Doyle et al., 1998). The idea that the selectivity filter is rate limiting is supported by the fact that large cysteine reagents, even anionic species, are capable of diffusing into an open channel from the cytoplasmic side of the bundle crossing and modifying cysteines introduced into the middle of the S6 segment (Liu et al., 1997), but these reagents cannot cross the selectivity filter. Moreover, the rates of modification of some of these cysteines (Liu et al., 1997; Del Camino et al., 2000) are close to those reported for modification of free thiols in solution (Stauffer and Karlin, 1994). These results suggest that the open activation gate is not a significant barrier to movement of permeant ions through the channel.

How then does Y485C reduce single channel conductance? We consider two alternatives. The first is that the mutation has an allosteric effect on the selectivity filter, perhaps transmitted through the S6 segment. Long-range structural interactions between these two regions of the KcsA potassium channel have been reported (Perozo et al., 2001). The second is that the mutation has local consequences on the movement of K⁺ ions in the vicinity of the bundle crossing.

First, we consider the possibility of an allosteric effect on the selectivity filter. If mutations of Y485 alter the conformation of the selectivity filter enough to affect the energetics of K⁺ ion movement, then they might also be expected to alter the selectivity of the pore. To investigate this possibility, we measured the Rb⁺/K⁺ selectivity for wild-type channels and three mutants of Y485. Using an intracellular solution with Rb⁺ as the predominant cation, we measured the change in reversal potential when the extracellular solution was switched between high [Rb⁺] and high [K⁺]. The calculated permeability ratios for Rb⁺/K⁺ were 0.78 ± 0.02 (n = 3), 0.78 ± 0.01 (n = 4), 0.76 ± 0.01 (n = 5), and 0.76 ± 0.01 (n = 3), for wild-type, Y485A, Y485C, and Y485S, respectively. The effects of the mutations were not significant (P > 0.05, t test), arguing against the possibility that they affect the selectivity filter. However, all three mutations significantly reduce the amplitude of the single channel current (Table III), especially Y485A that causes a 53% reduction. The mutations Y485A and Y485S also reduced P _o,max at 0 mV (Table III), an effect not explained by depolarizing shifts of the G-V relationships (Fig. 2 B).

If mutations of Y485 reduce γ locally, rather than at the selectivity filter, this might occur either by increasing the energy barrier for K⁺ ions to pass through the bundle crossing or by a change of K⁺ occupancy within the permeation pathway. To explore these possibilities, we examined the movements of another cation, namely the cationic pore blocker TBA. TBA blocks by entering the open channel from the cytoplasmic side of the membrane (French and Shoukimas, 1981) and binding within the central cavity of the pore (Zhou et al., 2001a). It cannot pass through the more extracellular selectivity filter. We tested whether the rate constants for TBA movement through the open bundle crossing, or its binding affinity within the pore, were affected by mutations of Y485. Rate constants for entering (k _on) and leaving (k _off) the channel were estimated from the kinetics of block, taking advantage of the fact that only the open channel can be blocked (Armstrong, 1971). The estimates of k _on were corrected for the effects of mutations of Y485 on the open probability, most notably for Y485A (Table III).1

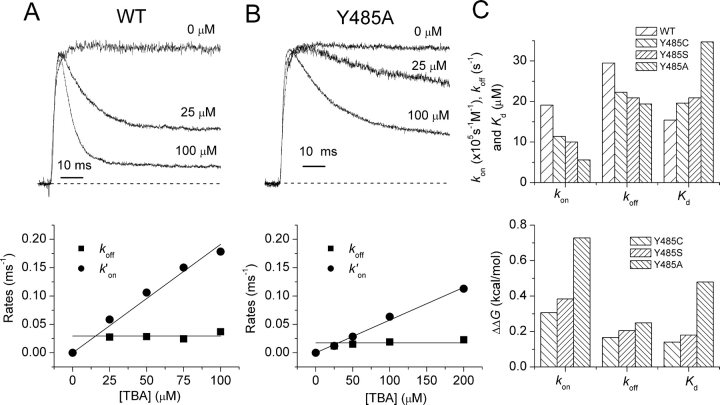
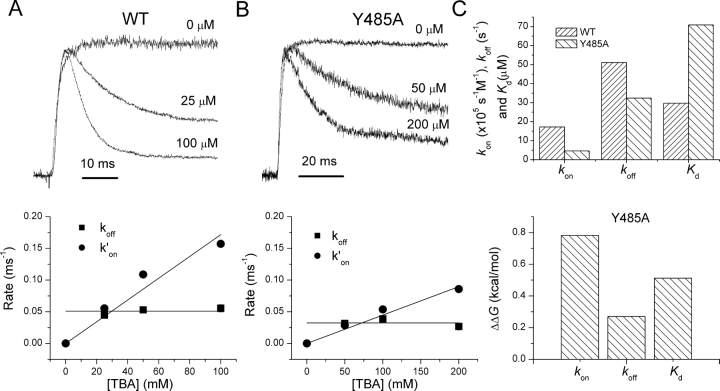
Fig. 4, A and B, shows K⁺ currents in outside-out patches for wild-type and Y485A channels, respectively, in response to voltage steps to 0 mV. Normalized time-dependent relaxations at indicated TBA concentrations ([TBA]) are also shown. Clearly, TBA is a more potent blocker of wild-type than Y485A channels, as seen from both the kinetics and the steady-state block. The kinetics of TBA block are well fit by single exponential relaxations. The time constants of these relaxations were used along with the relative levels of peak and steady-state currents to determine the blocking and unblocking rates shown in the lower panels of Fig. 4, A and B. The linear dependence of the blocking rate k ^′ _on on [TBA], and the insensitivity of the unblocking rate constant k _off to [TBA] indicate the adequacy of a simple model in which a single molecule of TBA blocks the pore.

Figure 4.

TBA block. Data for wild-type (A) and Y485A (B) shown. Left panels show normalized currents for intracellular [TBA] = 0, 25, and 100 mM. Right panels show estimates of k′_on and k _off plotted against [TBA]. The slope of linear fits of k′_on versus [TBA] were used in the estimates of the rate constant k _on. C shows estimates of rate constants and K _d (top) and of ΔΔG ₀ (bottom) calculated for differences from wild-type channels. These values were derived from the natural logarithm of the ratio of rate constants for mutant and wild-type channels. Data for all mutants in Table III.

The dissociation constants for TBA block are larger for all three mutants of Y485 than for wild-type channels, indicating a decreased affinity for TBA binding (Fig. 4 C and Table III). In addition, both k _on and k _off are reduced for all of these mutants, indicating moderately higher energy barriers for entering and exiting the central cavity of the pore (Fig. 4 C).

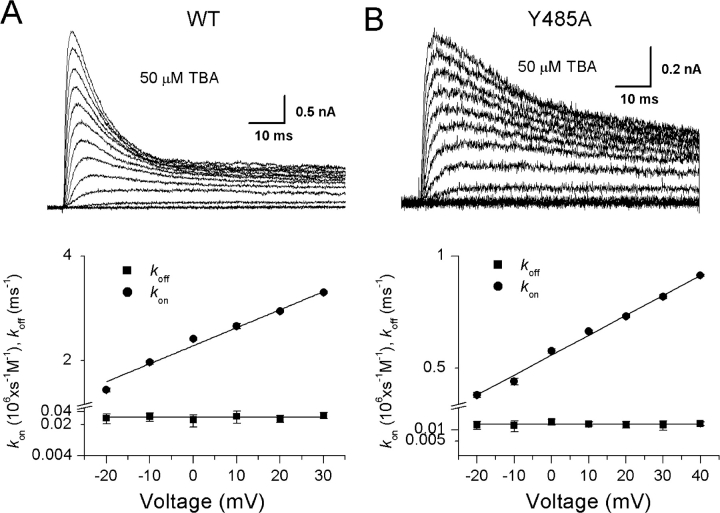
We further examined the possibility that the position of the TBA binding site within the membrane electric field is affected by the Y485A mutation. Fig. 5 shows the effect of membrane potential on TBA block for both wild-type and Y485A channels. The currents shown were elicited by a series of voltage steps from −80 to 40 mV in the constant presence of 50 mM internal TBA. The values of k _on and k _off were estimated from the kinetics and magnitude of steady-state block at each voltage, and their estimates are plotted on semilogarithmic axes against membrane potential in the bottom panels of Fig. 5. Although the kinetics of the block are quite different for wild-type and mutant channels, the estimates of k _on and k _off were independent of [TBA] (unpublished data), a manipulation that also affects kinetics; this result supports the reliability of this method of estimation.

Figure 5.

Voltage dependence of TBA block for wild-type (A; n = 3–5) and Y485A (B; n = 3–5) channels. Currents from depolarizations between −80 and 40 mV in the presence of 50 mM intracellular TBA. Estimates of k _on and k _off are plotted against membrane potential in the bottom panels. The exponential increase in k _on was fit by Eq. 2, with parameters k _on(0) = 2.22/0.54 s⁻¹mM⁻¹ and d = 0.30/0.31 for WT/Y485A channels, respectively. k _off was 0.03/0.014 ms⁻¹, respectively, for WT/Y485A channels.

The plots in the bottom panels of Fig. 5 reveal a striking asymmetry in the effect of voltage on the individual rate constants. Although k _on increases monotonically with depolarization, k _off is unaffected. The data for k _on were fit by the following relationship,

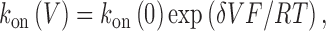(2)

where δ is the voltage dependence of k _on. Because k _off is voltage-independent, δ formally represents the fractional distance of the TBA binding site within the electric field, although some of the voltage dependence may be due to coupled movement between TBA and K⁺ ions within the permeation pathway (French and Shoukimas, 1981; Guo and Lu, 2001; Thompson and Begenisich, 2001). The estimates of δ are 0.30 and 0.31 for wild-type and Y485A, respectively, implying that the mutation has little effect on the electric field in the vicinity of the TBA binding site.

The effect of the Y485A mutation of TBA block suggests that local changes below the bundle crossing, rather than allosteric changes at the selectivity filter, affect the pore's conductance to K⁺, as well as the movement and binding of TBA. A local effect of mutations of Y485 on permeation seems a reasonable possibility, considering that the sidechain of Y485 is predicted to point toward the central axis of the pore, based on a homology alignment of the S6 segment with the inner helix of KcsA (Zhou et al., 2001a). However, the mutations of Y483 and F484, which are not predicted to face the pore axis, also significantly reduce single channel conductance.

How, then, do these S6_T mutations reduce single channel conductance locally if the selectivity filter is rate limiting for ion flux? Perhaps the premise is wrong. The selectivity filter may be so exquisitely tuned for K⁺ ions (Doyle et al., 1998; Morais-Cabral et al., 2001) that the energy barriers for K⁺ movement are low enough to be comparable to those near the open activation gate. In this case, a mutation that raises energy barriers near the bundle crossing might significantly affect current flow. As a test of this idea, we examined the effect of the Y485A mutation on currents carried by poorly permeant Rb⁺ ions. We assume that the lower single channel current amplitude of Rb⁺ (Heginbotham and MacKinnon, 1993) is due primarily to increased energy barriers for Rb⁺ movement at the selectivity filter (Morais-Cabral et al., 2001); moreover, the open activation gate and central cavity of the pore are likely to be rather nonselective among small monovalent cations (Roux and MacKinnon, 1999). Therefore, the selectivity filter is expected to be more rate limiting along the permeation pathway for Rb⁺ flux than for K⁺ flux. Consequently, we predict that if S6_T mutations have a local effect on permeation near the bundle crossing, then Rb⁺ currents will be less sensitive to the S6_T mutations that reduce K⁺ currents. We tested this prediction in Y485A, because this mutant has the largest effect on single channel currents of K⁺ ions (Table III).

In accordance with our prediction, when Y485 is mutated to alanine, the single channel current for Rb⁺ measured by noise analysis is not reduced significantly (Fig. 6 and Table III; P > 0.05, t test), in contrast to the 53% reduction seen for K⁺ currents. This difference between K⁺ and Rb⁺ cannot be explained by Rb⁺ ions making the permeation pathway somehow insensitive to the Y485A mutation, because this mutation has a similar effect on TBA block for K⁺ and Rb⁺ currents, raising the K _d for block while decreasing both k _on and k _off (Fig. 7 and Table III). Therefore, although Y485A has local effects on TBA movement regardless of the permeant ion, the consequences on Rb⁺ movement through the open activation gate are swamped out by reduced Rb⁺ permeability at the selectivity filter.

Figure 6.

Nonstationary noise measurements of Rb⁺ currents in WT (above) and Y485A (below) channels. Plots as in Fig. 3. See Table III for parameter estimates.

Figure 7.

TBA block of Rb⁺ currents in WT (A) and Y485A (B). Plots as in Fig. 4 with estimates in Table III.

DISCUSSION

The bundle crossing of the four S6 segments of voltage-gated potassium channels subserves at least two functions. First, it is the location of the activation gate (Liu et al., 1997; Holmgren et al., 1998; Del Camino et al., 2000; Del Camino and Yellen, 2001). Furthermore, it is a narrow portal that separates the water-filled central cavity of the permeation pathway from the intracellular solution. This constriction, therefore, might affect permeation when the channel is open. We are unaware of data that address the latter speculation directly. However, we show here that cysteine mutations of three S6_T residues below the bundle crossing moderately reduce single channel conductance, γ. The sidechain of one of these residues, Y485, is predicted to face inward into the permeation pathway, by homology alignment with KcsA (Zhou et al., 2001a). However, it has been proposed that the S6 segments of Shaker potassium channels, unlike KcsA, have a kink at the approximate level of residue V474; this would tend to move the four Y485 residues dramatically away from the central axis of the pore (Del Camino et al., 2000). It therefore remains an open question whether the three cysteine mutants that affect γ, Y483C, F484C, and Y485C, are involved in short-range or long-range interactions with ions that traverse the bundle crossing. Alternatively, the mutations may produce upstream allosteric consequences that affect ion movement through the pore.

We have argued that the reductions of γ are due to local effects (i.e., near the activation gate) of S6_T residues on permeation because of two results. First, S6_T mutations have unmeasurable consequences on the permeability ratios for Rb⁺/K⁺, tending to rule out a significant role of these mutations on the selectivity filter. Second, the same mutations affect energetics of TBA block, suggestive of an increase in an energy barrier for this monovalent cation to cross the open activation gate. The cysteine mutant with the largest effect on γ, a 46% reduction, is Y485C. Of the eight S6_T residues we examined, Y485 is the only one absolutely conserved in voltage-gated potassium channels (Liu et al., 1997). To further explore Y485's influence on the permeation pathway, we made two other mutants, Y485S and Y485A, both of which also reduce γ, most notably Y485A that produces a 57% reduction.

What are the relative roles of the selectivity filter and the open activation gate in limiting cation flux? Clearly, the selectivity of the channel is determined primarily by the selectivity filter, because diverse ions, including multivalent cations and anions, can enter the central cavity of the channel from the intracellular aspect of the channel (Liu et al., 1997; Del Camino et al., 2000); but only the members of a very small set of monovalent cations are capable of crossing the selectivity filter unless it is disrupted by mutation (Heginbotham et al., 1994).

Can an increased energy barrier for cation movement near the open activation gate account for the reduction of γ? The energy barrier for entry of TBA, represented in the blocking rate constant k _on, is increased by 0.71 kcal/mol by the Y485A mutation (Fig. 4 C and Table III). If we assume that the single channel current at 0 mV is dominated by unidirectional efflux, because the outward driving force on K⁺ ions is ∼105 mV at this voltage, then the reduction of γ by mutation Y485A can be used to roughly estimate the change in an activation energy barrier for K⁺ flux. The increase in ΔΔG is RTln(γ_WT/γ_Y485A) = 0.43 kcal/mol. Thus, the movements of both TBA and K⁺ are affected by the Y485A mutation. The greater effect of Y485A on the energy barrier for TBA entry is consistent with the fact that the selectivity filter only partially limits K⁺ flux, whereas it absolutely prevents TBA from exiting the channel into the extracellular solution. These results suggest that both the selectivity filter and the open activation gate contribute significant energy barriers to K⁺ flux in the Y485A mutant. The relative contribution of each is impossible to quantify from these data, however, because of the complexities of permeation in channels capable of holding more than one ion at a time in a single-file pore (Hille and Schwarz, 1978; Eisenman and Horn, 1983; Begenisich, 1992). It is well established that Shaker, like other potassium channels, is a multiion pore under normal ionic conditions (Heginbotham and MacKinnon, 1993; Pérez-Cornejo and Begenisich, 1994; Stampe and Begenisich, 1996; Harris et al., 1998).

The effect of the Y485A mutation is dramatically different when K⁺ ions are substituted by Rb⁺. Using energetic approximations again, ΔΔG for permeant ion flux is increased by 0.77 kcal/mol by this substitution in wild-type channels, presumably by limiting flux through the selectivity filter. In the presence of this higher energy barrier at the selectivity filter, the effect of the Y485A mutation is insignificant (ΔΔG ∼ 0.06 kcal/mol; Table III). Thus, Rb⁺ flux is rate limited by the selectivity filter, even in the presence of the Y485A mutation. Interestingly, Y485A causes almost the same increase in the energy barrier for TBA entry in K⁺ and Rb⁺ solutions (0.71 vs. 0.76 kcal/mol, respectively; Table III and Fig. 7).

Our results show that in the presence of certain S6_T mutations, the permeation pathway presents significant energy barriers at each end. This could have implications for the selectivity of the channel among permeant cations, because the selectivity filter is much more selective than the open activation gate. In a simple permeation model, for example, if a nonselective barrier is placed in series with a selective barrier, the order of selectivities for different permeant ions is not changed; however, the magnitudes of selectivities tend to be reduced by the nonselective barrier (Eisenman and Horn, 1983). The Y485A mutation did not cause a measurable increase in Rb⁺/K⁺ permeability, however. This could be due to the fact that the permeation model used to make the above prediction was too simplistic, a two-barrier one-site pore capable of holding at most one ion at a time. Another possibility is that the difference between the permeability of Rb⁺ and K⁺ is so small that a change in P _Rb/P _K, caused by Y485A, is too difficult to detect. A preliminary experiment suggests that this is the case. P _Cs/P _K was increased from 0.100 ± 0.005 (n = 3) to 0.134 ± 0.004 (n = 3) by the Y485A mutation (unpublished data). We interpret this small reduction in selectivity as due to an increase in a nonselective energy barrier, rather than an allosteric effect of Y485A on the selectivity filter, although these alternative possibilities cannot be distinguished from our data.

S6_T mutations affect not only single channel conductance and pore block. Some mutations of F484 and Y485 also reduce open probability at depolarized voltages. Because these results were obtained at 0 mV, where activation gates are maximally open, the decreases in P _o,max reflect a nonvoltage-dependent destabilization of the open state. Interestingly, this closed-open equilibrium at a depolarized voltage is sensitive to the species of permeant ion; P _o,max is decreased by the Y485A mutation for K⁺, but not for Rb⁺ currents (Table III). Stabilization of the open state by Rb⁺ ions was first reported by Swenson and Armstrong (1981). Together with recent results from crystallographic studies of ion occupancy of KcsA channels (Morais-Cabral et al., 2001; Zhou et al., 2001b), our results suggest that Rb⁺ ions affect not only ion movement, but also the conformation of the selectivity filter, and that this effect is responsible for changes in the closed-open equilibrium at depolarized voltages. Although P _o,max can be modulated by both permeant ion and S6_T mutations, the identity of the “gate” underlying the closed-open equilibrium at depolarized voltages is an open question. The most likely candidates are the activation gate itself and the selectivity filter. It is possible, for example, that S6_T mutations have long-range consequences on the conformation of the selectivity filter, albeit without a significant effect on selectivity.

In conclusion, mutations of three S6_T residues, Y483, F484, and Y485, reduce single channel conductance, apparently by raising an energy barrier to permeant ion flux near the open activation gate. The mechanism underlying this phenomenon is unknown. The opening of the S6 bundle crossing appears to involve a physical widening (Perozo et al., 1999; Del Camino and Yellen, 2001; Eaholtz and Zagotta, 2001), which may be affected by these mutations. This speculation is supported by the fact that peak open probability is decreased by some mutations of F484 and Y485. We hypothesize, therefore, that S6_T residues have an influence on the conformation of the open activation gate, reflected in both the stability of the open state and the energy barriers it presents to ions.