Analytical reconstruction of 4D dynamic cardiac SPECT with noise-reduction and non-uniform attenuation compensation

Abstract

Background

This study focuses on quantitative reconstruction of dynamic cardiac SPECT.

Material and methods

The Karhunen-Loeve (KL) transform is first applied to gated frames or sinogram data to de-correlate the dynamic information along the time direction. Then the Poisson noise is treated by a penalized weighted least-squares minimization, followed by an analytical inversion of the treated sinograms with attenuation compensation via the Novikov formula. The reconstruction is completed by inverse KL transform.

Results

Dynamic or gated cardiac sinograms were simulated from the NCAT phantom mimicking the human torso, and their reconstructions by the presented method showed significant improvement over the conventional methods of frame-by-frame reconstruction.

Conclusion

This analytical reconstruction of dynamic SPECT is consistent and efficient with a good potential for practical use.

1. Introduction

Dynamic cardiac SPECT (single photon emission computed tomography) images have been widely used to visualize cardiac motion and other functions. There are many factors degrading the image quality, such as noise and attenuation. The Poisson noise in the projection frame sequences is much higher than that in static studies because the number of counts per frame is much lowered. Conventionally, the dynamic cardiac SPECT is reconstructed by filtering each projection frame with frequency domain filter and then backprojecting the filtered data one-by-one, i.e., by the well-known filtered backprojection (FBP) procedure. Thus the inter-frame correlation was not considered and the attenuation was neglected at all.

Research efforts have been devoted to iterative image reconstruction which models the Poisson noise and compensates for the non-uniform attenuation for a penalized maximum likelihood (pML) solution, where the intra- and inter-frame correlations are considered in the penalty. Wernick et al. employed it to seek a penalized weighted least-squares (PWLS) estimate of the entire sequence in the Karhune-Loève (KL) domain for a fast reconstruction of dynamic PET (positron emission tomography) [1]. Narayanan et al. extended this framework to gated SPECT and showed that it is almost equally effective as iterative reconstruction but much faster in computation [2]. These KL-domain methods both enable de-noising and accelerating frame-by-frame reconstruction.

Based on our previous work on dynamic cardiac SPECT [3], we propose an analytical method for quantitative reconstruction. In this study, the KL transform was used to extract the inter-frame correlation and the noise, which is completely uncorrelated, was separated and restored in higher KL components. Then a PWLS strategy was used to smooth the noise. Reconstruction was carried out by Novikov’s inverse formula in the KL domain. The approach can be further improved by discarding higher components, which are dominated mainly by noise, for further reduction of noise and computation.

2. Method

In our previous work [3], we presented a KL domain spatio-temporal noise smoothing. In this paper, we further extend the approach to fully 4D quantitative reconstruction with addition of nonuniform attenuation compensation in the KL domain. The spatio-temporal noise smoothing will be refined by using a PWLS criterion in the KL domain. Different components will be smoothed according to their eigenvalues. Thus the higher components, which are dominated mainly by noise, will be smoothed more.

2.1. KL Transform of Gated Sinogram Sequence

KL transform is used for signal de-correlation. The ordered principal components maximize the data variance and provide a unique means for noise reduction and feature extraction. The forward KL transform for temporal frames is defined as:

$$\text{KL\hspace{0.17em}transform}:\stackrel{⌣}{Y}=M·{\lambda }_{i,j}^{\mathit{time}}$$ (1)

where ${\lambda }_{i,j}^{\mathit{time}}$ is the gated projection data. M is the eigenvectors of time covariance matrix, which can be obtained by estimation of all the dynamic frames [1, 3]. In the KL domain, the components are independent and remain the same form as in the spatial domain. Since the KL transform is a linear operation, many deduced algorithms in the spatial domain would be still applicable in the KL domain.

2.2. PWLS Noise Smoothing in KL Domain

The PWLS cost function is defined as:

$$\mathrm{\Phi }(p)=\frac{1}{2}{(Y-p)}^T{\mathrm{\Sigma }}^{-1}(Y-p)+\beta Q(p)$$ (2)

in which Y is a vector of measured projection, p represents the ideal sinograms, and Σ is the diagonal variance matrix of Y. The adjustable parameter β is introduced for the regularizing penalty term Q(p) to control the degree of smoothness. Minimizing Φ(p) means a tradeoff between the smoothness and a weighted agreement with the measurements, where the smoothing parameter β controls that tradeoff. In this study, we use a quadratic penalty:

$$Q(p)=\frac{1}{2}{(p-\mu )}^T{W}^{-1}(p-\mu )$$ (3)

where μ = E(p), and the matrix W ⁻¹, known as the regularization operator, determines the nature of the smoothing.

In the KL domain, the proposed KL-PWLS smoothing method is based on the separability assumption that the regularization operator is chosen to be separable into two components of:

$$W^{-1}={[K_t\otimes W^{2D}]}^{-1}$$ (4)

Eq.(2) can then be greatly simplified into K independent functions in the KL domain[2, 4]:

$$\begin{array}{ll}\begin{array}{l}{\mathrm{\Phi }}_l({\stackrel{⌣}{p}}_l)=\frac{1}{2}{({\stackrel{⌣}{y}}_l-{\stackrel{⌣}{p}}_l)}^T{\stackrel{⌣}{\mathrm{\Sigma }}}_l^{-1}({\stackrel{⌣}{y}}_l-{\stackrel{⌣}{p}}_l)\\ +\frac{1}{2}(\beta /d_l){({\stackrel{⌣}{p}}_l-{\stackrel{⌣}{\mu }}_l)}^T{[W^{2D}]}^{-1}({\stackrel{⌣}{p}}_l-{\stackrel{⌣}{\mu }}_l)\end{array}\hfill & l=1,\mathrm{...},K\hfill \end{array}$$ (5)

where p̆_l, y̆_l, and μ̆_l are the l-th KL components of p, y and μ, see Eq.(1). Notation Σ̆ is the diagonal variance matrix of y̆_l, and d_l is the eigenvalue associated with the l-th vector.

The method for estimating Σ and determining the penalty term is described in our previous work [4].

Eq.(5) shows that in the KL domain, β/d_l is used as smoothing parameter, thus the KL components with small eigenvalues would be smoothed more.

2.3. Quantitative Reconstruction Based on Novikov’s Inverse Formula in KL domain

An inversion algorithm for the attenuated Radon transform in parallel-beam geometry was derived by Novikov and its detailed description is given in [5, 6]. In the following, we present our KL domain Novikov inverse formula.

Let (x, y) be the stationary coordinate in image domain and (t, θ) be the rotation coordinate in sinogram space. The KL domain Novikov inverse formula can be expressed as:

$${\phi (\overrightarrow{r})=\frac{1}{4\pi }\mathit{div}\underset{0}{\overset{2\pi }{\int }}\overrightarrow{j}[exp\left({[D\mu ]}_{\theta }(s,t)\right)\stackrel{\sim }{q}(t,\theta )]|}_{\begin{array}{l}s=\overrightarrow{r}•\overrightarrow{j}\\ t=\overrightarrow{r}•\overrightarrow{k}\end{array}}d\theta$$ (6)

where j⃗ = (cosθ, sin θ), k⃗ = (−sinθ, cosθ), div is the divergence operation, φ(r⃗) is the reconstructed image frame from its corresponding sinogram data frame p̆(t,θ) in the KL domain and

$$\stackrel{\sim }{q}(t,\theta )=e^{-h_1}\{cos(h_2){\stackrel{\sim }{q}}_1(t,\theta )+sin(h_2){\stackrel{\sim }{q}}_2(t,\theta )\}$$

$${\stackrel{\sim }{q}}_1(t,\theta )=Hcos(h_2)e^{h_1}\stackrel{⌣}{p}(t,\theta )$$ (7)

$${\stackrel{\sim }{q}}_2(t,\theta )=Hsin(h_2)e^{h_1}\stackrel{⌣}{p}(t,\theta )$$ (8)

with h₁ = ½ [Rμ](t,θ), h₂ = [Hh₁](t,θ), and the operators H, D, and R are defined as follows:

$$[Hg](s)=\frac{1}{\pi }\underset{-\infty }{\overset{+\infty }{\int }}\frac{g(\tau )}{s-\tau }d\tau$$ (9)

$${[D\mu ]}_{\theta }(s,t)=\underset{t}{\overset{\infty }{\int }}{\mu }_{\theta }(s,\tau )d\tau$$ (10)

$$[R\mu ](s,\theta )=\underset{-\infty }{\overset{\infty }{\int }}{\mu }_{\theta }(s,t)dt$$ (11)

The above KL domain quantitative reconstruction is performed frame-by-frame for each principal component, and the result is ${\mathrm{\Phi }}_{m,n}=({\phi }_{m,n}^1,{\phi }_{m,n}^2,\cdots {\phi }_{m,n}^l,{\phi }_{m,n}^{l+1},\cdots ,{\phi }_{m,n}^K)$ for each image pixel (m, n). Since the higher-order components with smaller eigenvalues may have little information and could be discarded for both noise reduction and computing efficiency, the resulted first l reconstructed frames from the lower-order components are

$${{\mathrm{\Phi }}_{m,n}}^{\prime }=({\phi }_{m,n}^1,{\phi }_{m,n}^2,\cdots {\phi }_{m,n}^l).$$

An inverse KL transform on these reconstructed l frames will generate the dynamic image sequence of

$${\widehat{f}}_{m,n}^{\mathit{time}}=M^T{{\mathrm{\Phi }}_{m,n}}^{\prime }.$$ (12)

2.4. Procedure Summary

The presented quantitative reconstruction for gated SPECT in KL domain with noise reduction and attenuation compensation is summarized as follow:

1. Apply the KL transform on the dynamic data along the time axis.

2. Implement the KL-PWLS noise smoothing according to Eq.(5), where the higher components can be discarded for further reduction of noise and computation time.

3. Reconstruct the KL components one-by-one based on the KL domain Novikov’s inverse formula (6)–(11).

4. Apply the inverse KL transform on the reconstructed KL components for the dynamic image sequence.

3. Results

The 4D mathematical torso phantom (gNCAT) with defects inside the myocardium was used to show the feasibility of presented solution. A dynamic sequence consisted of 16-interval gated activity distributions each of 128 cubic size was generated in which the radiotracer distribution changes with time, simulating the dynamic ground truth. The comparison of the presented KL-PWLS-Novikov approach with frame by frame FBP and OSEM is shown in Fig. 1.

Fig. 1.

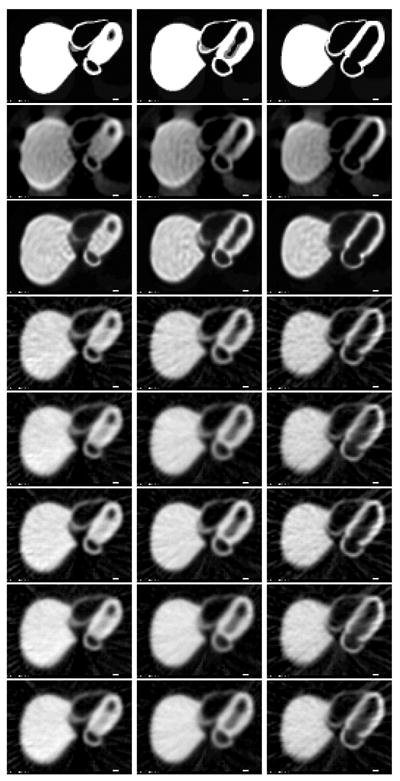
Temporal behavior of dynamic cardiac SPECT images reconstructed by different approaches for the gNCAT phantom. From left to right – a transverse slice from temporal frame 3, 10 and 16. From top to bottom – activity phantom, reconstructed image by FBP, OSEM (with 5 iterations for each frame and a subset size of 8), KL-PWLS-Novikov from all components with β =100, β =300, and KL-PWLS-Novikov from the first 2, 4 and 6 KL components with β =300.

The standard FBP and OSEM reconstruction on the 16 dynamic frames were pre-filtered by a Butterworth filter with order 5 and cutoff frequency 0.4. With the same PC configuration (1.5GHz, 1.0GB), it took 15 seconds for FBP and 66 seconds for OSEM reconstruction. The FBP showed a density variation on a uniformly-distributed source region because it does not compensate for the attenuation. For the OSEM, some image density variation on a uniformly-distributed region was also seen because of its non-uniform convergence behavior across the field-of-view (FOV). The presented KL-PWLS-Novikov took 32 seconds on reconstructing all the components. By discarding the higher components, the computation time would reduce significantly over OSEM, even over FBP.

4. Conclusion

In this paper, we presented an analytical approach to quantitative dynamic SPECT reconstruction with simultaneous noise reduction and non-uniform attenuation compensation. The temporal correlation among the dynamic frames was considered by the KL transform. In the KL domain, a PWLS noise smoothing was carried out on each KL component according to its eigenvalue, i.e., adaptive to its signal-to-noise ratio [4], and the components with smaller eigenvalues could be discarded for further reduction of noise and computing time. Novikov’s inverse formula was adapted to reconstruct the smoothed KL components with compensation for the non-uniform attenuation. Then the dynamic image sequence was obtained by the inverse KL transform.

The presented method has some advantages over the conventional FBP approach for the quantitative capacity of attenuation compensation and noise reduction. Compared to the well-known OSEM, the presented approach shows a good performance on computational efficiency and a more consistent performance on resolution uniformity across the FOV.

The presented approach assumed all the voxels obey the nearly-same tendency of time activity curve (TAC). This may add in some edge blurring in the inversion results. It could be mitigated by clustering the voxels into subgroups and applying a different KL transform on each subgroup, which is currently under investigation.