On the evaluation and optimization of protein X-ray structures for pKa calculations

Abstract

The calculation of the physical properties of a protein from its X-ray structure is of importance in virtually every aspect of modern biology. Although computational algorithms have been developed for calculating everything from the dynamics of a protein to its binding specificity, only limited information is available on the ability of these methods to give accurate results when used with a particular X-ray structure. We examine the ability of a pKa calculation algorithm to predict the proton-donating residue in the catalytic mechanism of hen egg white lysozyme. We examine the correlation between the ability of the pKa calculation method to obtain the correct result and the overall characteristics of 41 X-ray structures such as crystallization conditions, resolution, and the output of structure validation software. We furthermore examine the ability of energy minimizations (EM), molecular dynamics (MD) simulations, and structure-perturbation methods to optimize the X-ray structures such that these give correct results with the pKa calculation algorithm. We propose a set of criteria for identifying the proton donor in a catalytic mechanism, and demonstrate that the application of these criteria give highly accurate prediction results when using unmodified X-ray structures. More specifically, we are able to successfully identify the proton donor in 85% of the X-ray structures when excluding structures with crystal contacts near the active site. Neither the use of the overall characteristics of the X-ray structures nor the optimization of the structure by EM, MD, or other methods improves the results of the pKa calculation algorithm. We discuss these results and their implications for the design of structure-based energy calculation algorithms in general.

Obtaining the X-ray structure of a protein has become a standard requirement in modern biology, not too unlike identifying the location of its gene on the chromosome and setting up an efficient expression system. Once available, the X-ray structure provides a wealth of information on how to interpret past experiments and how to design new experiments that will provide information on the function of the protein. The X-ray structure by itself, however, does not reveal much information regarding the physical characteristics of the protein. Extensive calculations are needed to determine the substrate or ligand specificity, the stability, the dynamics, and the electrostatic features of the protein, and it is often not possible to know whether the results of such calculations are trustworthy. With the vast number of protein X-ray structures being solved in various structural genomics projects (Heinemann et al. 2000; Yokoyama et al. 2000; Stevens et al. 2001), it is becoming more and more important to have access to fast and reliable algorithms that can tell us something about the physical characteristics of a protein from its X-ray structure. Presently algorithms are available for predicting everything from the pKa values of a protein (Bashford and Karplus 1990; Yang et al. 1993; Antosiewicz et al. 1994, 1996; Demchuk and Wade 1996; Alexov and Gunner 1997; Sham et al. 1997, 1998; Alexov and Gunner 1999; Mehler and Guarnieri 1999; Nielsen and Vriend 2001) to its large-scale motions (Amadei et al. 1993; de Groot et al. 1997, 1999) and binding characteristics (Goodsell et al. 1996; Kramer et al. 1999). However, although most of these algorithms give a good correlation with experimental data for a subset of existing protein structures (Kramer et al. 1997, 1999; Mehler and Guarnieri 1999; Gabdoulline and Wade 2001; Nielsen and Vriend 2001; Guerois et al. 2002), it is not trivial to know when an algorithm gives a reliable result when used with a novel X-ray structure. This is mainly due to the high sensitivity to the details of the protein structure displayed by many structure-based algorithms that calculate energies inside proteins. It is well known, for example, that small molecule docking programs are highly dependent on having the “correct” structure of the protein/receptor (Claussen et al. 2001). In addition, the results of molecular dynamics (MD) simulations (Braxenthaler et al. 1997) and electrostatic calculations (Nielsen et al. 1999; Nielsen and Vriend 2001) are known to be sensitive to structural details.

When calculating a property of a protein from its X-ray structure, which is dependent on structural details, it is therefore essential to know whether the structure is capable of giving accurate results with the algorithm in question. Information on the usefulness of the X-ray structure can often be inferred from a visual inspection of the structure. For example, if a ligand is present in the active site, then it is likely that the structure is well suited for drug design and docking studies, whereas an extended or open structure, as seen for example for some of the protein kinases (Cox et al. 1994), indicates that the structure is poorly suited for studies of the active form of the enzyme.

Even much smaller changes in the structure of a protein are also likely to have a profound effect on the results of structure-based energy calculations, as illustrated by the large differences in the calculated pKa values of the hen egg white lysozyme (HEWL) active-site residues resulting from a 180° change in the χ² angle of HEWL Asn 46 (Nielsen et al. 1999). Here we examine the sensitivity of a pKa calculation algorithm to the structural differences among 41 HEWL wild-type X-ray structures. This analysis provides us with information on the reliability of pKa calculations when used with a given X-ray structure. Because the desolvation energies and the electrostatic interaction energies that are calculated by the pKa calculation algorithm are essential components of most structure-based energy calculations, the conclusions that we present here are applicable to other types of structure-based energy calculation methods.

We investigate whether it is possible to select a more reliable subset of HEWL structures for pKa calculations by using properties of the X-ray structure such as the resolution, the crystallization conditions, and the output of structure validation software. We also investigate whether it is possible to standardize the HEWL structures by a computational protocol so that all give the correct result with the pKa calculation algorithm. Finally, we discuss the implications of the present results for the design and application of protein structure-based energy calculations in general.

pKa calculation algorithms

pKa calculation algorithms are used mainly in studies of enzyme mechanisms (Raquet et al. 1997; Lamotte-Brasseur et al. 2000; Morikis et al. 2001b) and in the study of protein stability (Yang and Honig 1993, 1994; Lambeir et al. 2000; Morikis et al. 2001a). In the study of enzyme mechanisms, these algorithms aid by identifying the residues that are likely to be proton donors and proton acceptors, and in protein stability studies they are capable of predicting the origins of the pH-dependence of protein stability. Most pKa calculation algorithms rely on finite-difference solvers of the Poisson-Boltzmann equation (FDPB-solvers) to provide the electrostatic energies of a protein structure, although several alternative approaches to pKa calculations exist (Sham et al. 1997; Mehler and Guarnieri 1999; Sandberg and Edholm 1999). In the present paper we deal exclusively with an FDPB-based pKa calculation algorithm.

The major differences between FDPB-based pKa calculation algorithms lie in the way that they model protein flexibility. The treatment of the protein flexibility can be divided roughly into two classes: explicit treatment and implicit treatment. Methods that treat the flexibility of the protein explicitly employ MD simulations (Zhou and Vijayakumar 1997; van Vlijmen et al. 1998; Gorfe et al. 2002), proton optimization (Alexov and Gunner 1997), or rotamer optimization techniques (Alexov and Gunner 1999). Methods with implicit treatment of protein flexibility typically adjust the dielectric constant for the entire protein (Antosiewicz et al. 1994; Karshikoff 1995; Antosiewicz et al. 1996) to achieve better correlation with experimental results, although algorithms that use a residue-dependent value of the protein dielectric constant have also been developed (Demchuk and Wade 1996; Nielsen and Vriend 2001).

Generally, the methods that use an implicit description of the protein flexibility have been more successful in obtaining a good overall correlation with experimental data, whereas the methods that optimize the hydrogen-bond network have proven superior in calculating active-site pKa values (Nielsen and Vriend 2001), presumably because the details of the hydrogen-bond network are very important in active sites. It has also been reported that structural averaging (van Vlijmen et al. 1998; Gorfe et al. 2002) can improve the correlation between experimental and calculated pKa values, although the improvements in some cases seem to be insignificant (Koumanov et al. 2001). Attempts at incorporating pKa calculations in MD algorithms have also been made (Baptista et al. 1997), but presently these algorithms have not proven to give a significant improvement in the accuracy of the calculated pKa values.

Calibrating pKa calculation methods

The accuracy of a pKa calculation result is evaluated by calculating the RMSD between the calculated and experimentally determined pKa values for all protein titratable groups that titrate within 5–6 pH units of physiological pH. Consequently, pKa calculation algorithms have been calibrated to give low RMSD values for a set of well-behaved model proteins with experimentally measured pKa values. However, most titratable groups are situated on the surface of proteins, and a significant fraction of surface groups are involved in crystal contacts (Carugo and Argos 1997; Valdar and Thornton 2001). Because crystal contacts perturb the details of the local structure, and restrict the mobility, they can induce the formation of salt bridges and charged hydrogen bonds in the crystal that are present only transiently in solution. The calibration of pKa calculation methods that use an implicit description of protein dynamics on a large unfiltered set of titratable residues is therefore bound to introduce a bias in the pKa calculation methods, such that the pKa values of surface residues are calculated correctly even though the conformations of these are different from the conformations that they occupy in solution (Nielsen and Vriend 2001).

It is tempting to speculate that this is a significant part of the reason why many pKa calculation methods give the best results with a relatively high protein dielectric constant (Antosiewicz et al. 1994; Demchuk and Wade 1996), which essentially smears out the effect of the surrounding protein environment. It is therefore our belief that more accurate pKa calculation methods can be constructed by calibrating pKa calculation methods on a set of experimentally measured pKa values which does not contain any titratable groups that are influenced by crystal contacts.

In the present study we chose to focus exclusively on the calculated pKa values for the two key active-site residues of HEWL. We did so because one of the most important uses for pKa calculation algorithms is to identify the proton donor from a set of titratable residues in the active site of an enzyme (Raquet et al. 1997; Lamotte-Brasseur et al. 1999, 2000), and the pKa values of surface residues are not essential when answering such a question.

Identifying the proton donor in a catalytic mechanism

Many enzymes have bell-shaped pH activity profiles, and this naturally leads to the assumption that catalysis at low pH is limited by the protonation of an active-site residue, and similarly that catalysis at high pH is limited by the deprotonation of another active-site residue. Enzymatic pH activity profiles can generally be decomposed into a pH-k_cat profile and a pH-K_m profile. From the pH-k_cat profile, one can extract the pKa values of the active-site groups when the substrate is bound, whereas the pH-k_cat/pH-K_m profile will give the pKa values of these two groups in the apo-form of the enzyme (Kyte 1995). Here we will assume that the same two groups are responsible for the shapes of both the pH-k_cat profile and the pH-k_cat/pH-K_m profile, and, furthermore, that these two groups are the catalytic nucleophile (the group that limits activity at low pH) and the proton donor (the group that limits activity at high pH) in the catalytic mechanism. It is not obvious that this is the case for most enzymes because experimental data on the subject are very scarce. However, for Bacillus circulans xylanase, convincing experimental data (McIntosh et al. 1996; Joshi et al. 2001) have been presented that justify the assumption that the catalytic nucleophile and the proton donor are indeed the residues that govern the shape of the pH-k_cat/pH-K_m profile. Because the catalytic mechanism of the xylanases is identical to that of HEWL, and because it is well known that the proton donor in HEWL (Glu 35) indeed has an elevated pKa value in the apo-form of the enzyme (Demchuk and Wade 1996), we will identify the proton donor in the HEWL catalytic mechanism by examining pKa values calculated from apo-crystal structures of HEWL.

Ideally, one should identify the proton donor in a catalytic mechanism as the residue which has a pKa value identical to the pKa value for the proton donor determined from kinetic data. Unfortunately, pKa calculation methods are not yet accurate enough to match kinetically measured pKa values directly, and a better strategy is therefore to identify the proton donor as the acidic group in the active site predicted to have the highest pKa value. In many cases, the choice is between two or three acidic residues, such as is the case for lysozyme and most other glycosyl hydrolases (Davies and Henrissat 1995), and in the present work we propose a set of criteria that, to the best of our judgement, enables us to confidently identify the proton donor in a catalytic mechanism from calculated pKa values for two acidic residues.

We require that the proton donor has a pKa value of at least 5.0, and that the difference between the pKa value of the proton donor and that of the other acid is at least 1.5 units, with the proton donor having the higher pKa value of the two. In the following we refer to these criteria as the “local identification criteria” or local ID criteria.

Hen egg white lysozyme

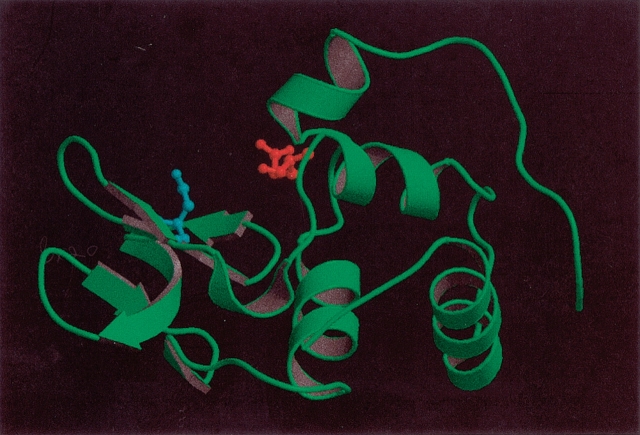
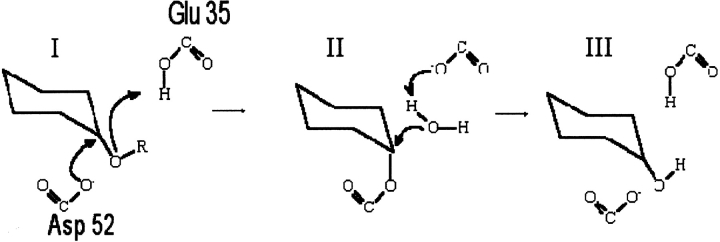
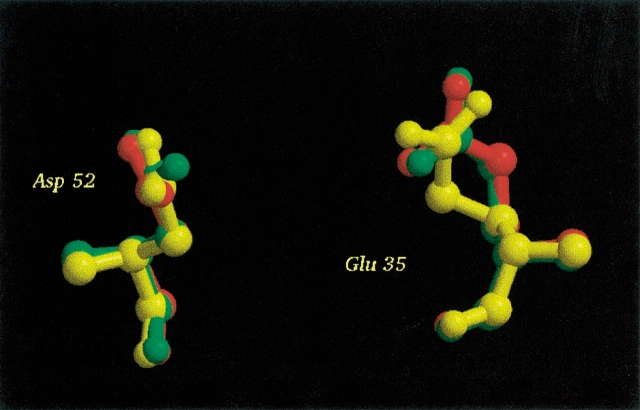
HEWL is a 129-residue enzyme which serves as one of the paradigms for investigating the effect of crystallization conditions. The PDB contains more than 100 structures of wild-type HEWL, and HEWL thus provides an excellent model system for studying the effect of structural variation on the results of pKa calculation methods. HEWL is a monomeric single-domain enzyme, which consists of an all-α region and a β-rich region. The active site is situated in a cleft between the two regions, and the two key active-site residues are Glu 35 and Asp 52 (Fig. 1 ▶). HEWL is a retaining glycosyl hydrolase (Family 22 in the CaZy database http://afmb.cnrs-mrs.fr/CAZY/; Coutinho and Henrissat 1999), and recently it was elegantly proven that hydrolysis proceeds via a covalent enzyme-substrate intermediate (Vocadlo et al. 2001) with Glu 35 being the proton donor and Asp 52 the nucleophile in the catalytic mechanism. The initial step of the catalytic mechanism (Fig. 2 ▶) is the donation of a proton by Glu 35 to the glycosidic oxygen of the substrate. Subsequently, Asp 52 performs a nucleophilic attack on the anomeric carbon atom of the substrate, thus forming a covalent bond with the substrate. In the final step, the covalent enzyme-substrate intermediate is hydrolyzed by a water molecule, and the initial protonation states are regenerated.

Figure 1.

Hen egg white lysozyme (PDB Id: 7LYZ). The active-site residues Glu 35 and Asp 52 are shown in red and cyan, respectively. The figure was prepared with the MOLSCRIPT (Kraulis 1998) and Raster3D (Merrit and Bacon 1997) programs.

Figure 2.

The general catalytic mechanism for retaining glycosyl hydrolases. (I) Protonation of the glycosidic oxygen by the proton donor (Glu 35) and attack on the glucose C1 by the nucleophile (Asp 52). Departure of the reducing end of the substrate. (II) Activation of a water molecule, cleavage of C1-Asp 52 covalent bond. (III) Regeneration of the initial protonation states.

Objective

Our main interest with pKa calculation methods is to be able to confidently and correctly identify the proton-donating residue in the catalytic mechanism given a single X-ray structure or a range of X-ray structures of an enzyme. A prerequisite for being able to do this is a pKa calculation algorithm that gives the correct result when used with the correct solution-like structure of the enzyme. In the following we illustrate that the WHAT IF pKa calculation routines (Nielsen and Vriend 2001) indeed constitute such a method, and we analyze our ability to correctly identify Glu 35 as the proton donor in HEWL using 41 wild-type X-ray structures of the enzyme. We furthermore evaluate protocols for determining the fitness of an X-ray structure for pKa calculations and continue to examine methods for preparing and optimizing X-ray structures for pKa calculations.

Results

We examined the ability of a protein pKa calculation algorithm to identify the proton donor in the catalytic mechanism of HEWL. Initially we evaluated the feasibility of identifying the proton donor using a large number of unmodified X-ray structures. We then continued to investigate the possibility of using crystallization criteria, the resolution of the X-ray structure, and structure validation software to select a better subset of HEWL X-ray structures, and we examined the reasons for correctly and incorrectly calculated pKa values using three representative HEWL structures as an example. Next we explored several ways of “correcting” HEWL X-ray structure coordinates to improve the correlation with experimental data, and finally we discuss the implications for protein structure-based energy calculations in the light of the results presented here.

Calculating pKa values for 41 HEWL X-ray structures

pKa values were calculated for all residues of 41 HEWL wild-type X-ray structures to identify the proton donor in the catalytic mechanism (Table 1). None of the structures contain any inhibitors or substrate molecules in the active site, and the structures therefore present a set of X-ray structures that could be obtained for the apo-form of any given enzyme. RMSD values for Cα positions between 2LZT and the rest of the structures are low (maximum RMSD, 1.62; mean value, 0.66), thus demonstrating that the structures are indeed very similar as measured by Cα-RMSD values.

Table 1.

pKa calculations of HEWL wild-type X-ray structures

Structure	Resolution	Space group	Structural rmsd. Cα/all atomsa	Overall pKa rmsdb	pKa E35	pKa D52	Residue identified by local ID criteriac	Comments
Exp.	–		–		6.20	3.68	Glu 35	Experimental
193L	1.33 Å	P 43 21 2	0.65/1.29	1.00	5.45	4.25	–	Microgravity, NaCl
1AKI	1.5 Å	P 21 21 21	0.50/1.18	1.01	5.06	2.93	Glu 35	pH 4.5
1BGI	1.7 Å	P 21 21 21	0.50/0.93	1.09	5.46	2.18	Glu 35	High temperature, Cl−
1F0W	1.9 Å	P 21 21 21	0.54/1.15	1.09	5.78	3.79	Glu 35	pH 6.5
1F10	1.7 Å	P 21 21 21	0.64/1.30	0.71	5.26	3.81	–	pH 6.5 low humidity
1HEL	1.7 Å	P 43 21 2	0.64/1.12	1.62	5.14	6.01	–
1HSX	1.9 Å	P 21 21 21	0.53/1.11	0.96	5.61	3.83	Glu 35	pH 9.5
1HSW	2.0 Å	P 21 21 21	0.59/1.20	0.87	5.60	2.03	Glu 35	pH 9.5, low humidity
1LKR-A	1.6 Å	P 1 21 1	1.57/1.83	0.92	5.14	3.64	–	Iodinated
1LKR-B	1.6 Å	P 1 21 1	1.62/1.86	1.12	5.70	1.92	Glu 35	Iodinated
1LMA	1.75 Å	P 1 21 1	0.49/1.12	1.47	5.59	1.77	Glu 35	Iodide, low humidity
1LSA	1.7 Å	P 43 21 2	0.79/1.42	1.44	4.82	6.57	Asp 52	120 K
1LSB	1.7 Å	P 43 21 2	0.78/1.50	1.29	6.43	3.80	Glu 35	180 K
1LSC	1.7 Å	P 43 21 2	0.67/1.36	1.15	6.80	4.80	Glu 35	250 K
1LSD	1.7 Å	P 43 21 2	0.66/1.26	0.74	6.06	4.09	Glu 35	280 K
1LSE	1.7 Å	P 43 21 2	0.64/1.36	1.28	6.61	4.30	Glu 35	295 K
1LSF	1.7 Å	P 43 21 2	0.78/1.47	1.20	6.98	4.33	Glu 35	95 K
1LYS-A	1.72 Å	P 21	0.64/1.50	1.16	5.44	1.72	Glu 35	313 K
1LYS-B	1.72 Å	P 21	0.70/1.54	1.12	5.70	1.92	Glu 35	313 K
1LYZ	2.0 Å	P 43 21 2	0.71/1.25	1.45	5.96	5.53	–
1LZA	1.6 Å	P 43 21 2	0.66/1.30	0.95	5.73	3.70	Glu 35
1LZT	1.97 Å	P 1	0.38/0.88	1.54	5.32	3.70	Glu 35
1QTK	2.03 Å	P 43 21 2	0.66/1.28	1.15	5.84	4.19	Glu 35	55 bar
1UCO-A	2.0 Å	P 21	0.46/1.28	0.91	5.48	3.70	Glu 35
1UCO-B	2.0 Å	P 21	0.68/1.45	1.12	5.70	1.92	Glu 35
2LYM	2.0 Å	P 43 21 2	0.64/1.30	0.83	5.66	3.95	Glu 35
2LYZ	2.0 Å	P 43 21 2	0.65/1.21	1.24	5.35	3.88	–
2LZT	2 Å	P 1	—/—	1.12	5.70	1.91	Glu 35	Nitrate
3LYM	2.0 Å	P 43 21 2	0.63/1.25	1.03	5.63	3.93	Glu 35	1.3 M NaCl, high pressure
3LYT	2.5 Å	P 21	0.86/1.95	1.26	7.28	5.17	Glu 35
3LYZ	2.0 Å	P 43 21 2	0.65/1.21	0.97	4.82	4.63	–
3LZT	0.92 Å	P 1	0.35/0.67	1.15	5.55	3.42	Glu 35	low temperature
4LYM	2.1 Å	P 43 21 2	0.71/1.26	1.13	5.49	4.09	–	low humidity
4LYT	2.5 Å	P 21	0.56/1.36	2.03	4.29	5.61	–
4LZT	0.95 Å	P 1	0.15/0.43	1.07	5.34	1.78	Glu 35	Nitrate
5LYM	1.8 Å	P 21	0.42/1.36	0.82	5.38	3.30	Glu 35	Nitrate
5LYT	1.9 Å	P 43 21 2	0.76/1.35	1.08	5.93	4.02	Glu 35
5LYZ	2.0 Å	P 43 21 2	0.68/1.24	1.40	4.49	6.26	Asp 52
6LYT	1.9 Å	P 43 21 2	0.64/1.28	0.98	5.50	4.01	–
6LYZ	2.0 Å	P 43 21 2	0.65/1.22	1.49	5.87	3.95	Glu 35
7LYZ	2.5 Å	P 1	0.55/1.10	0.61	5.34	2.97	Glu 35
Avg. pKa	–	–	–	1.14	5.62	3.74	Glu 35
Avg. Titration curve	–	–	–		5.60	3.80	Glu 35

^a Structural rmsds are measured relative to the 2LZT structure.

^bBetween calculated and experimentally measured pKa values.

^c The local ID method identifies either Glu 35 or Asp 52 as the proton donor if the following two criteria are fulfilled: 1. The residue has a pKa value higher than 5.0; 2. pKa(residue)-pKa(other candidate) ≧1.5. These two criteria were chosen arbitrarily, but they represent situations where the authors according to their own judgement could identify the proton donor with reasonable certainty from a set of experimentally measured pKa values.

In terms of pKa calculations, the differences between the 41 structures become more evident. For 29 of the 41 structures (70.7%), Glu 35 is successfully identified as the proton donor using the local ID criteria. For three structures (6LYT, 4LYM, and 2LYZ), the pKa values of Glu 35 and Asp 52 almost fall within the local ID criteria (these structures miss the criteria by 0.01, 0.10, and 0.03 pH units, respectively), and Asp 52 is identified as the proton donor in only two structures (1LSA and 5LYZ). In one additional structure (1HEL), Asp 52 has a higher pKa value than Glu 35.

Resolution

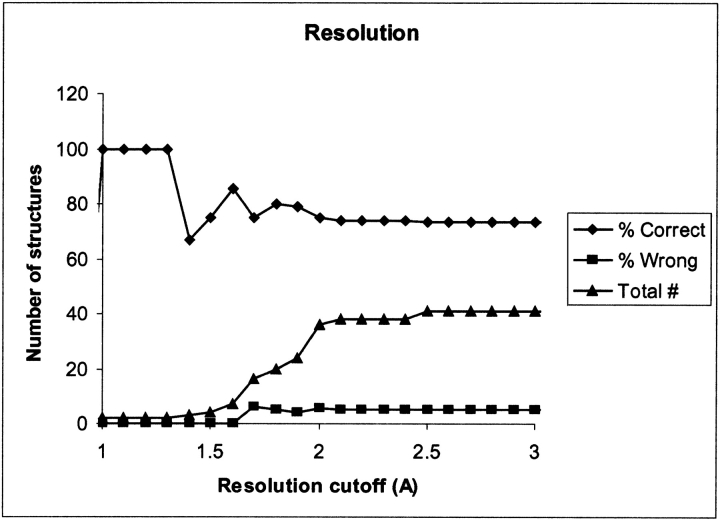
Low resolution can be responsible for incorrect positioning of atoms in X-ray structures, and we therefore expect a correlation between the resolution of the X-ray structure used for the pKa calculation and the accuracy of the pKa calculation results. Figure 3 ▶ shows the correlation between the percentage of structures for which the local ID criteria correctly identify Glu 35 and the cutoff for the resolution of the structures. For the set of X-ray structures presented here, there is no strong evidence of a correlation between the resolution and the quality of the pKa calculation, although the two structures with a resolution less than 1 Å both give a correct result.

Figure 3.

Percentage of structures where the pKa calculations correctly identify Glu 35 as the proton donor (♦) or identify Asp 52 (▪) as judged by the local ID method. (▴) The total number of structures within the cutoff. Only structures that have a resolution that is equal to or less than the cutoff value (x-axis) are considered.

Crystallization conditions

The present data set of 41 structures have been solved from crystals grown under a wide range of conditions. One might expect that the less biologically relevant crystallization conditions, the worse the pKa calculation result. From the data in Table 1 this does not seem to be the case. A good example of the relative insensitivity to crystallization conditions comes from comparing the results obtained with the structures 1AKI, 1F0W, and 1HSX. These structures are solved at pH 4.5, 6.5, and 9.5, respectively, and because the pKa value of Glu 35 is 6.20, one might expect the HEWL structure to change at basic pH values so that the charged form of Glu 35 would be stabilized. The calculated pKa value for Glu 35 in the three structures is 5.06, 5.78, and 5.61, respectively, and from the pKa calculations there is thus no indication of a structural rearrangement to better solvate the negative charge on Glu 35 in 1HSX. This is in agreement with the findings of Biswal et al. (2000), who examined 20 different HEWL structures and found only very small changes due to changes in pH.

Similarly there is no correlation between the temperature and the pKa calculation results, as evidenced by comparing the results for 1LSA, 1LSB, 1LSC, 1LSD, 1LSE, and 1LYS.

Space groups

The present set of HEWL structures are crystallized in five different space groups: P 43 21 2: 20 structures, P 21 21 21: 6 structures, P 1 21 1: 3 structures, P 21: 7 structures, and P 1: 5 structures. Only structures in the P 43 21 2 space group give rise to the identification of Asp 52 as the proton donor, and additionally seven more structures in this space group give pKa values that are inconclusive (i.e., neither Glu 35 nor Asp 52 can be identified according to the local ID criteria). In the four other space groups (21 of the 41 structures), only three structures give an inconclusive result, and in all remaining cases, Glu 35 is identified as the proton donor. In all but one of the P 43 21 2 structures, Asn 44 forms a crystal contact with either Arg 45 or Arg 68 from a symmetry-related molecule. Asn 44 forms a hydrogen-bond with Asp 52 in several structures, and is thus of critical importance for the protonation state of the active-site residues, as will be illustrated later.

Structure validation tools

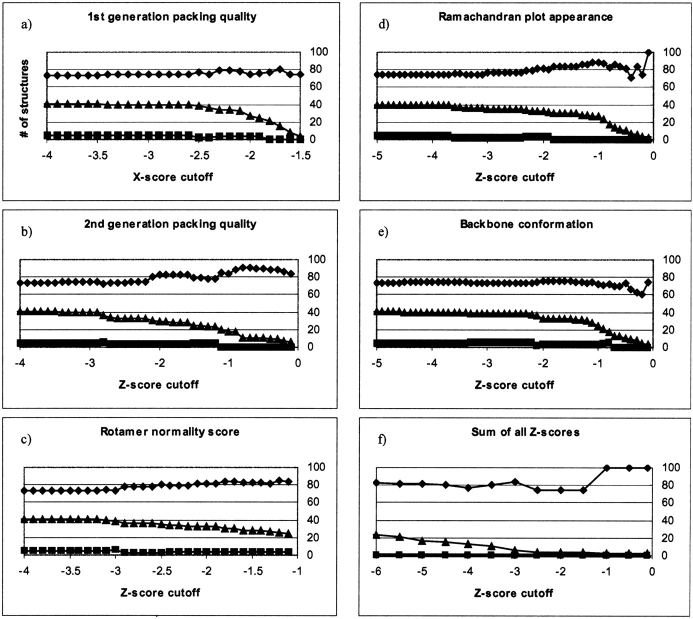
It is possible to get a correct prediction of the catalytic proton donor for almost three-quarters of the unmodified HEWL X-ray structures, and although this number seems encouraging it also means that for one-quarter of all crystal structures, we are likely to get an inconclusive (or even wrong) answer when we apply a structure-based energy calculation method to an X-ray structure. Wrong and inconclusive answers do not present a major obstacle in themselves; the real problem is that it is not possible to distinguish “bad” from good results based only on the resolution and the crystallization conditions of the X-ray structure. Several tools have been constructed for the validation of protein X-ray structures. The more well known of these tools are WHAT_CHECK (Hooft et al. 1996b) and PROCHECK (Laskowski et al. 1993). We used WHAT_CHECK with all of the 41 HEWL X-structures, and analyzed the correlation of WHAT_CHECK Z-scores with the ability of the local ID criteria to correctly identify the proton donor in the catalytic mechanism. Figure 4 ▶ shows the percentage of correct and wrong predictions by the local ID criteria versus the Z-score cutoff. Only structures with WHAT_CHECK Z-scores above or equal to the cutoff were included in the analysis using the local ID criteria. Figure 4 ▶ shows a weak correlation between increasing Z-score and the percentage of structures that give correct results, but the significance of this correlation is too low to warrant any conclusions as to whether Z-scores are able to discriminate between “good” and “bad” structures for pKa calculations.

Figure 4.

Correlation between WHAT_CHECK Z-score cutoffs for structures and the percentage of these structures that give correct results (♦) or wrong results (▪) when the local ID criteria are used to identify the proton donor. (▴) The total number of structures that fulfill the cutoff criteria. (a) 1st generation packing quality, (b) 2nd generation packing quality, (c) Rotamer normality score, (d) Ramachandran plot appearance, (e) Backbone conformation score, (f) the sum of all Z-scores.

Structural differences that give rise to differences in pKa values

Because there seems to be no correlation between the global properties of an X-ray structure and the accuracy of the pKa calculation for active-site residues, it is of interest to find the structural differences between X-ray structures that are responsible for the differences in the calculated pKa values. Here we examine the differences between three HEWL structures (2LZT, 4LYT, and 7LYZ) which represent cases with a very good prediction, a bad prediction, and an average prediction, respectively, for the pKa values of the two active-site acids. Visual comparison of the three structures reveals very few differences, and from the superpositioning of Glu 35 and Asp 52 (Fig. 5 ▶) it is not straightforward to rationalize the large difference in the calculated pKa values of the active-site residues for these three structures. Table 2 shows the calculated contributions to the pKa shifts for Glu 35 and Asp 52, and it is clearly seen that the main differences among the three structures lies in the interaction with other titratable groups in the case of Glu 35, and in both the interactions with other titratable groups and in the interaction with the nontitratable charges (the so-called background interaction energy) in the case of Asp 52.

Figure 5.

Glu 35 and Asp 52 from 2LZT (red), 4LYT (green), and 7LYZ (yellow). Only very small differences between the positions of these two side chains are observed for these three structures. The figure was prepared with the MOLSCRIPT (Kraulis 1998) and Raster3D (Merrit and Bacon 1997) programs.

Table 2.

Decomposition of the pKa calculated pKa shifts for Glu 35 and Asp 52 in 2LZT, 4LYT, and 7LYZ

PDB ID	Glu 35 ΔpKa	Glu 35 ΔpKadesolv	Glu 35 ΔpKabackgr	Glu 35 ΔpKacharge	Asp 52 ΔpKa	Asp 52 ΔpKadesolv	Asp 52 ΔpKabackgr	Asp 52 ΔpKacharge
2LZT	1.30	1.58	−0.44	0.16	−2.1	1.54	−2.8	−0.8
4LYT	−0.16	1.56	−0.7	−1.01	1.6	1.47	0.00	0.15
7LYZ	0.93	1.66	−0.72	−0.01	−0.9	1.72	−2.19	−0.47

ΔpKa is the change in pKa value as compared to the pKa value for the model compound.

If we remove the interactions between the Glu 35–Asp 52 pair and all other titratable groups (Table 3), it is seen that the influence of all other titratable groups on the pKa values of Glu 35 and Asp 52 is not responsible for the high pKa of Asp 52 in 4LYT. The effect of removing all titratable groups is similar in all three structures: the pKa value of Glu 35 is raised slightly, and the pKa value of Asp 52 is lowered. Thus the structural effects that are responsible for the large differences in pKa values between the three structures are to be found in the interactions that determine the background interaction energy of Asp 52.

Table 3.

The effect on the calculated pKa values of Glu 35 and Asp 52 if the interactions with all other titratable groups in the enzyme are ignored

	2LZT		4LYT		7LYZ
Interactions removed	pKa E35	pKa D52	pKa E35	pKa D52	pKa E35	pKa D52
None	5.58	1.89	4.29	5.61	5.34	2.97
All except interaction Glu 35-Asp 52 interaction	6.25	2.71	5.21	5.49	6.12	3.54

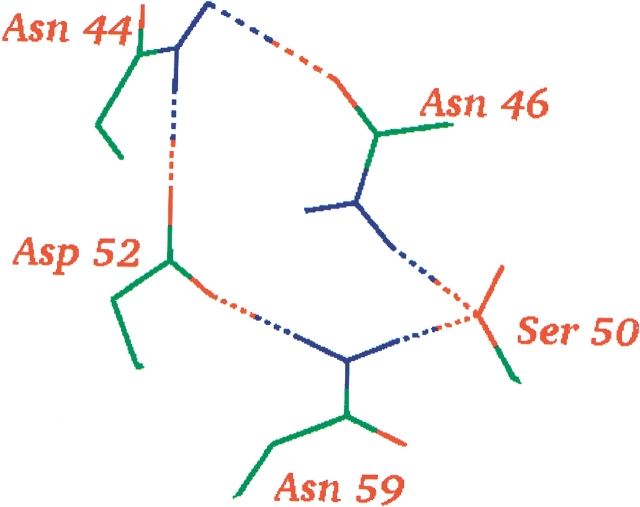
Table 4 shows the residues that contribute the most to the background interaction energy for Asp 52 in the three structures. Mainly five groups are responsible for the large differences in background interaction energy of Asp 52, namely Asn 44, Asn 46, Thr 51, Gln 57, and Asn 59. The sum of the contributions from all other groups is insignificant compared to the contribution from the five residues, as seen from the sums of the interaction energies presented in Table 4. To explain why these five residues play such an important role in determining the background interaction energy, it is instructive to examine the environment of Asp 52. Asp 52 in 2LZT is involved in a circular hydrogen-bond network consisting of Asp 52 – Asn 44 – Asn 46 – Ser 50 – Asn 59 – (Asp 52; Fig. 6 ▶). In 7LYZ, another circular hydrogen-bond network is formed between Asn 59 – Asp 52 – Asn 46 – Ser 50 – (Asn 59), and in this structure Asp 52 thus also participates in two hydrogen-bond networks. In 4LYT, the residues surrounding Asp 52 occupy slightly different positions, and Asp 52 participates in only one hydrogen bond (with Asn 59). Differences in the hydrogen-bonding pattern are therefore the underlying reason for the large differences in the background interaction energies, but to explain in detail why these differences arise we must consider both the neutral and the charged states of Asp 52 in its environment: when the pKa calculation algorithm must choose where to place the proton, it places it where it is most favorable from a hydrogen-bond energetic point of view. In 2LZT, the proton is placed on the Oδ that forms the hydrogen bond with Asn 59; in 4LYT and 7LYZ, the proton is placed on the other Oδ. This immediately explains why there is such a large difference between the contribution of Asn 59 to E_backgr in 2LZT and the contribution in 4LYT and 7LYZ, because only in 2LZT does the proton on Asp 52 make a strong unfavorable interaction with Asn 59. The details of the hydrogen-bond network also explain why there is such a difference in E_backgr between Asp 52 in 2LZT and 7LYZ, and Asp 52 in 4LYT. Because Asp 52 participates in only one hydrogen bond in 4LYT, there is no extra energy cost of adding a proton to this residue (ΔpKa_backgr = 0.0). In both 2LZT and 7LYZ however, Asp 52 participates in two good hydrogen bonds, and the protonation of Asp 52 therefore results in a significant energy penalty (2LZT: ΔpKa_backgr = −2.8, 7LYZ: ΔpKa_backgr = −2.2)

Table 4.

Residues that give big differences in the background interaction energy of Asp 52 (in kT/e)

Residue	ΔEbackgr (2LZT)	ΔEbackgr (4LYT)	ΔEbackgr (7LYZ)
Asn 44	−0.296	0.018	−0.452
Asn 46	−1.848	−1.143	−2.561
Thr 51	−0.492	−0.353	−0.860
Gln 57	0.298	−0.003	−0.182
Asn 59	−3.861	0.372	−0.652
Sum	−6.199	−1.109	−4.707
Sum all diffs	−6.473	−1.667	−5.380

The row labeled “Sum” lists the sum of the changes in the background interaction energy when removing the five residues listed in the table. The row labeled “Sum all diffs” is the sum of all the differences in the background interaction energy for all residues in HEWL.

In 2LZT, the proton is put on the Asp 52 oxygen that hydrogen bonds with Asn 46. In 4LYT and in 7LYZ, the proton is placed on the other oxygen, and consequently the effect of removing the contribution of Asn 59 is smaller by almost an order of magnitude in these two structures than it is in 2LZT.

Figure 6.

The circular hydrogen-bond network around Asp 52 in 2LZT. Only side chains and their hydrogen bonds are shown. The notation used in the text for this hydrogen-bond network is Asp 52 – Asn 44 – Asn 46 – Ser 50 – Asn 59 – (Asp 52). Figure prepared with WHAT IF (Vriend 1990).

Crystal contacts

We suspected that the differences in hydrogen-bond network around Asp 52 might be due to crystal-induced effects, because 4LYT crystallizes in a different space group than 2LZT and 7LYZ. Neither in 2LZT nor in 4LYT are the residues around Asp 52 involved in crystal contacts (incomplete unit cell information in 7LYZ made it impossible to analyze the crystal contacts for this structure), and we were therefore not able to pinpoint the reason for the differences in the hydrogen-bond network. We speculate that the poor resolution of 4LYT provides an explanation for the alternative placement of the side chains around Asp 52.

The solution structure of HEWL

The fact that 2LZT and 7LYZ give good results with the WHAT IF pKa calculation package for the two active-site residues does not necessarily mean that these two structures provide a more accurate description of the environment of Glu 35 and Asp 52 than does 4LYT. It is possible that 2LZT and 7LYZ give good results merely because many pKa calculation packages (including the one we use here) were calibrated on a set of X-ray structures that includes 2LZT. This would provide an example of “getting the right result for the wrong reason”, and in order to exclude this possibility it is important to verify that the hydrogen-bond network around Asp 52 is formed in solution in the same way as it is in the two crystal structures 2LZT and 7LYZ. The PDB contains a single NMR structure of HEWL (PDBID: 1E8L; Schwalbe et al. 2001) which contains 50 models. Considering the resolution of NMR structures, we find Asn 44, Asn 46, and Asn 59 to be within hydrogen-bonding distance of Asp 52. Further evidence for the donation of hydrogen bonds to both Oδs of Asp 52 comes from an X-ray structure of HEWL D52S (Hadfield et al. 1994). The X-ray structure (PDBID: 1LSY) shows clear differences in the position of residues 44 and 46 when Asp 52 is mutated to serine, thus indicating that these residues are dependent on the Asp 52 side chain for proper orientation.

Calculating pKa values from the average titration curves of the 50 structures in 1E8L gives pKa values of 9.00 and 4.50 for Glu 35 and Asp 52, respectively. Although Glu 35 thus would be identified by the local ID criteria by using the NMR ensemble, it is clear that the pKa values of the two active-site residues are quite different from the experimentally measured values, and we therefore conclude that NMR structures should be used with caution for pKa calculations.

Calculating the pKa values of Glu 35 and Asp 52 correctly is thus highly dependent on having the correct hydrogen-bond network around Asp 52 in 2LZT, 4LYT, and 7LYZ. The generality of this conclusion is confirmed by examining the number of hydrogen bonds to Asp 52 for all of the structures in Table 1. In only six of the structures where both Asp 52 Oδs accept hydrogen bonds is Glu 35 not identified, and in four of these cases, a change in one of the pKa values of less than 0.10 units would have allowed identification of Glu 35 according to the local ID criteria. Glu 35 is identified in several structures where Asp 52 accepts only a single hydrogen bond. In these cases the environment provides several interactions that favor a negative charge on Asp 52, although the interactions cannot be described as hydrogen-bonds, because the angular criteria and distance criteria that normally define hydrogen bonds are not fulfilled.

Optimizing X-ray structures

We investigate the effect of using EMs, MD simulations, and CONCOORD (de Groot et al. 1997) analysis to optimize each of the 41 HEWL X-ray structures. EM, MD, and CONCOORD analyses were performed as described in Materials and Methods, and pKa values were computed for the final EM structure, for the average structure and for the minimized average structure for both the short MD simulations (200 psec) and the CONCOORD analysis. After the first 100 psec of each simulation, snapshot structures were recorded every 10 psec from the long MD simulations and used directly for pKa calculations. The final pKa values from the snapshot calculations were arrived at either by taking the average of the calculated pKa values for each frame or by averaging the titration curve for each group over all snapshots and determining the pKa value from this average titration curve (van Vlijmen et al. 1998).

Table 5 shows the results from the MD simulation protocols when the 41 X-ray structures were submitted to the above analyses. It is seen that none of the optimization methods are able to improve the frequency with which Glu 35 is identified as the proton donor. Instead, all methods used here make the predictions more incorrect, with the MD-based methods being worst of all.

Table 5.

Effect of EM, MD, and CONCOORD analyses

Method	Average RMSD	Correct	Wrong	Avg. pKa Glu 35 (std. dev.)	Avg. pKa Asp 52 (std. dev.)	Avg. titr. Glu 35	Avg. titr. Asp 52
X-ray struct. ɛ = 8	1.10	30	2	5.61 (0.40)	3.70 (0.91)	5.70	3.80
X-ray struct. ɛ = 4	1.49	28	5	6.32 (0.79)	4.47 (1.34)	6.40	4.40
X-ray struct. ɛ = 16	0.66	1	0	4.78 (0.25)	3.66 (0.59)	4.90	3.70
EM	1.01	19	0	5.42 (0.30)	4.13 (1.03)	5.50	4.20
Avg. MD	1.09	0	0	2.86 (0.78)	3.21 (0.49)	2.90	3.30
Avg. MD + EM	1.13	0	0	2.69 (0.74)	3.20 (0.49)	2.70	3.30
Avg. CC	0.94	13	0	5.28 (0.31)	4.02 (0.72)	5.40	4.20
Avg. CC + EM	0.97	12	1	5.24 (0.36)	4.04 (0.82)	5.30	4.20
89 snapshots (2LZT)	0.96	0	0	3.60 (0.64)	2.88 (0.68)	3.70	2.90
89 snapshots (5LYZ)	1.18	2	1	2.82 (0.89)	2.27 (1.01)	2.90	2.30

Average RMSD, average between calculated and experimentally measured pKa values for all groups; Correct, number of the original 41 X-ray structures where Glu 35 was identified as the proton donor after EM, MD, or CC analysis, using the local ID criteria; Wrong, number of the original 41 X-ray structures where Asp 52 was identified as the proton donor after EM, MD, or CC analysis, using the local ID criteria; EM, final structure of a steepest descent energy minimization; MD, average structure of the last 100ps of a 200ps molecular dynamics simulation; MD + EM, energy minimized (steepest descent) structure of the MD structures; CC, Average structure of 2000 CONCOORD structures; CC + EM, Energy minimized (steepest descends) of the CC structures.

A small improvement in the average overall RMSD is seen when using the final structures of the EM, MD simulation, and the average structures from the CONCOORD analysis, thus proving that the structures produced by these methods are able to more accurately describe the environment of the average titratable group.

Neither when using the average structure from an MD simulation nor when using the energy minimized average structure for MD simulations does the overall RMSD of the calculations improve. Similarly, a significant decrease is seen in the accuracy of the predictions for Glu 35 and Asp 52, with both residues predicted to have a pKa value below 5.

Setting the initial protonation states

The MD simulation methods used in Table 5 were performed with all titratable groups in their standard ionization state at pH 7.0. To examine whether the charges on Glu 35 and Asp 52 force HEWL to adopt a conformation in the simulations that favors negative charges on both these residues, we performed three additional MD simulations where we protonated either Glu 35 or Asp 52 or both residues. We note that HEWL contains only one histidine residue and that this His is more than 15 Å removed from the active-site residues, and the MD simulations with alternative protonation states can therefore be carried out without adjusting any other protonation states.

If the pKa values calculated from the snapshots of these MD simulations correspond to the protonation states used in the simulations, it means that the HEWL structure adjusts to stabilize the protonation state imposed by the set-up for the MD simulation. Table 6 shows that this is indeed the case. Protonating either Glu 35 or Asp 52 leads to a strong shift in the calculated pKa value for the protonated residue compared to the pKa value calculated from the trajectory where both groups are in their unprotonated form.

Table 6.

Effect of changing protonation states in molecular dynamics simulations

Protonation state	Avg. RMSD	Avg. pKa GLU 35 (std. dev.)	Avg. pKa ASP 52 (std. dev.)	pKa GLU 35 avg. titr. curv.	pKa ASP 52 avg. titr. curv.
35 Glu-, 52 Asp-	0.95	3.60 (0.64)	2.88 (0.68)	3.70	2.90
35 GluH, 52 Asp-	0.86	5.29 (0.47)	3.37 (0.50)	5.40	3.40
35 Glu-, 52 AspH	1.19	2.84 (0.59)	4.90 (0.57)	2.90	5.00
35 GluH, 52 AspH	0.94	4.75 (0.88)	4.86 (0.85)	4.70	5.00

Avg. RMSD: The average RMSD between calculated and experimentally measured pKa values for all groups.

Similarly, protonating both groups leads to an elevated pKa for both groups, thus illustrating that MD simulations change the protein structure to stabilize the protonation state used in the MD simulations. This is in agreement with the results of Wlodek et al. (1997), who found the calculated pKa value of the N-terminus of BPTI to be dependent on the protonation state used in the MD simulation.

The protonation states used in the MD simulations thus determine the HEWL active-site pKa values that are calculated from the trajectory. More importantly, however, a comparison of the calculated pKa values for the HEWL X-ray structures crystallized at different pH values with the results of the simulations in Table 6 reveals that the two HEWL X-ray structures at pH 9.5 (1HSX and 1HSW) give significantly different results from the MD simulation with both Glu 35 and Asp 52 in their deprotonated form. Because the experimental pKa values of both Glu 35 and Asp 52 are significantly lower than 9.5 (Glu 35 pKa =6.20, Asp 52 pKa =3.68), this strongly suggests that the structural changes that occur in the Glu 35 −, Asp 52 − simulation are artefacts of the MD simulation, and not an accurate description of the actual structural changes that occur upon deprotonation of Glu 35 and Asp 52. Consequently, incorporating protonation and deprotonation reactions in MD simulations therefore cannot be expected to lead to structures that are more accurate for pKa calculations. Similarly, coupling pKa calculations and MD simulations is not likely to give any improvement in the realism of the MD simulation or in the accuracy of the calculated pKa values, as long as MD simulations are not capable of reproducing the structural changes (or lack of structural changes) that occur upon deprotonation of a residue.

Discussion

The calculation of pKa values for active-site residues in enzymes is of importance in the study of enzyme mechanisms. In the present study, we investigated the best strategy for identifying the proton donor in the catalytic mechanism of an enzyme using pKa calculations on a set of X-ray structures. The results show that the best strategy is to use the unmodified X-ray structures directly for pKa calculations and identify the proton donor as the residue that fulfills the local ID criteria in the majority of the structures. We find that an improvement in the results can be achieved by excluding structures that make crystal contacts near the active-site residues. Excluding the HEWL structures from the P43 21 2 space group improves the prediction accuracy from 29/41 (70.7%) to 18/21 (85.7%), and eliminates the only two structures that identify Asp 52 as the proton donor.

The resolution of the X-ray structures, the crystallization conditions, and the quality of the X-ray structures did not show any significant correlation with the ability to correctly identify the proton donor, and none of these criteria should therefore be used to select a more trustworthy subset of X-ray structures. It should be noted, however, that the two high-resolution structures that we examined both gave the correct prediction, and we therefore cannot exclude the possibility that high-resolution structures will give more accurate results than low-resolution structures. We would indeed expect this to be true, but the present data do not warrant such a conclusion.

The use of energy minimizations, molecular dynamics simulations, and CONCOORD analysis marginally improves the overall agreement with experimental pKa values, but significantly degrades the ability to correctly identify the proton donor in HEWL. In our hands, MD simulations are particularly ill-suited for producing both average and snapshot structures for pKa calculations, because the calculated pKa values are highly dependent on the protonation state used in the MD simulation. Furthermore, it is evident that the structure produced by the MD simulations for a particular protonation state of Glu 35 and Asp 52 (Table 6) is different from the X-ray structure solved at a pH value where these two residues populate the same protonation state (Table 1), as seen by the large differences in the calculated pKa values. Here we have shown this to be the case only for a particular MD simulation package and for a particular MD simulation setup, but we expect similar results for other MD simulation packages, because the GROMACS standard force field and the simulation protocol used here do not differ significantly from other MD force fields and MD protocols. These conclusions are in contrast to the those reported by Van Vlijmen et al. (1998) and Gorfe et al. (2002), who argued that the use of MD improves the accuracy of pKa calculations, but our conclusions agree well with the observations of Koumanov et al. (2001) and Wlodek et al. (1997). We note that Van Vlijmen et al. (1998) and Gorfe et al. (2002) focused on the overall RMSD between experimental and calculated pKa values, and we believe that this is the main reason that they arrived at the conclusion opposite of ours. In our opinion, pKa calculations are interesting mostly for the very low number of active-site groups and buried groups that have highly shifted pKa values. The overall RMSD between calculated and experimentally measured pKa values is dominated by the contribution from surface-group pKa values that typically are almost unperturbed by the protein environment, and observing changes in the overall RMSD will therefore give a misleading picture of the effect of MD simulations and other protein structure improvement tools if one is primarily interested in the pKa values of functionally important groups.

The results presented here rely on the assumption that the WHAT IF pKa calculation method (Nielsen and Vriend 2001) will give the correct result when used with the “correct” structure. We define the correct structure as the structure of HEWL which is predominant in solution at the temperature and at the concentration that was used in the NMR experiments for determining the experimental pKa values. We have carefully examined the crystal contacts made in each crystal, and only for structures in the P 43 21 2 space group do we find crystal contacts in the vicinity of the two active acids. Because we thus examine only the pKa values of the two active-site acids Glu 35 and Asp 52, and because we get much worse results with the structure in the P 43 21 2, we are confident that the structures of the HEWL active site is a good representation of the solution structure of the active site, and consequently that the WHAT IF pKa calculation package calculates correct pKa values when used with the correct solution-like structure. This is furthermore corroborated by comparing the X-ray structures of HEWL to the NMR structure of the enzyme. Specifically it is important that the critical hydrogen-bond network around Asp 52 is formed in the NMR structure, as mentioned earlier. We have furthermore assumed that the WHAT IF pKa calculation routines are not biased by the choice of protein dielectric constant towards giving good results with only a certain subset of X-ray structures. We did this by recalculating all pKa values for the structures in Table 1 with a dielectric constant of both 4 and 16 and found that the correlations between the “correctness” of the results and the resolution, WHAT_CHECK scores, and crystallization conditions did not improve. The conclusions that we arrive at here are therefore not biased by our choice of dielectric constant. We were able to identify Glu 35 in only one of the 41 structures when using a dielectric constant of 16 but we observed a large drop in the overall RMSD, thus illustrating that a high dielectric constant will give poor pKa values for active-site residues, but accurate pKa values for surface residues. Using a dielectric constant of 4 gives a higher overall RMSD, and only a slightly worse performance for the active-site residues (Table 5).

In summary, we have proposed a set of criteria for identifying the proton donor from two candidate acidic residues in an enzyme. We have applied these criteria with the WHAT IF pKa calculation routines (Nielsen and Vriend 2001) to a set of 41 HEWL X-ray structures and showed that we successfully identify the correct residue in 85% of the structures if we exclude structures with crystal contacts near the active site. We furthermore find that EM, MD, and CONCOORD analyses are not currently capable of successfully optimizing protein X-ray structures for pKa calculations, and given the generality of the energies calculated in pKa calculation algorithms, we expect this conclusion to be true also for other structure-based energy calculation methods such as drug docking algorithms, protein design algorithms, and protein structure analysis tools.

In the light of this we consider it essential that the development and optimization of protein structure-based energy calculation methods are concerned not only with the construction of the algorithm for a few test cases, but also with the development of a specific protocol for preparing protein structures for the algorithm in question. Such protein preparation protocols should take into account the sensitivity of the algorithm in question, the source of the protein structure (NMR, X-ray, or homology model), and the desired level of detail of the results. Preferably the protein preparation protocol should be an integrated part of the energy-calculation procedure such that the X-ray structure is optimized simultaneously with the calculation of the desired energetic quantity. We note that the pKa calculation method developed by Alexov and Gunner (1999) presents an example of such a method. Unfortunately this method has not been benchmarked, and we are therefore unable to comment on the prediction accuracy of the method. Work on integrating structure optimization tools with structure-based energy calculation methods is on-going in our lab.

Materials and methods

Selection of X-ray structures

The PDB was searched for structures which had a 100% sequence identity to the HEWL sequence in 2LZT. All structures that contained a significant number of ions or cofactors were excluded, and we arrived at a set of 64 wild-type HEWL structures. From this set we manually selected 41 structures that cover a wide range of crystallization conditions and resolutions.

pKa calculations

pKa calculations were carried out with the WHAT IF (Vriend 1990) pKa calculation routines as described (Nielsen and Vriend 2001), with the exception that the protein dielectric constant was set to 8 for all titratable groups. The WHAT IF pKa calculation routines perform a global optimization of the hydrogen-bond network for every single protonation state needed in FDPB-based pKa calculations. We employ the hydrogen-bond optimization algorithm developed by Hooft et al. (1996a) to produce the optimal hydrogen-bond network for every protonation state. The algorithm by Hooft et al. (1996a) does not change heavy atom positions, except in the cases where a better hydrogen-bond network can be produced by flipping the χ2, χ2, or χ3 angles of His, Asn, and Gln, respectively. The WHAT IF pKa calculation routines employ DelPhi II (Nicholls and Honig 1991) for solving the Poisson-Boltzmann equation and use the OPLS forcefield as source of charges and radii (Jorgensen and Tirado-Rives 1988).

Retrieval of WHAT_CHECK scores

WHAT_CHECK (Hooft et al. 1996b) scores were retrieved from the compilation of WHAT_CHECK reports on all PDB files, which can be accessed at http://www.cmbi.kun.nl/pdbreport/. The Z-scores reported for “Users of a structure” were used.

Energy minimizations and molecular dynamics simulations

The GROMACS (Lindahl et al. 2001) molecular dynamics package (version 3.0) was used for all energy minimizations (EMs) and molecular dynamics (MD) simulations. The standard GROMACS force field was used in all calculations.

All EMs and MD simulations were performed in a box of water with a minimum distance between the edge of the box and the protein of 5 Å.

EMs were carried out with a steepest descents algorithm until the largest force was less than 2000 kJ mol⁻¹ nm⁻¹.

Two types of MD simulations were carried out: 200 psec (short) simulations and 1 nsec (long) simulations. Both simulations were preceded by steepest descents minimization as described above and by a 0.5 psec MD simulation where all protein atoms were kept fixed. The MD simulations were carried out with a Berendsen temperature coupling (Berendsen et al. 1984) to a bath at 300K. The MD stepsize was 2 fs, and a 10 Å cut-off was used for coulombic interactions which were calculated with a dielectric constant of one. All remaining MD parameters were set as described at http://www.gromacs.org/documentation/reference_3.0/online/getting_started.html#full.

Average structures

Average structures of the short MD simulations were calculated as the average position of all protein heavy atoms during the last 100 psec of the run using the program g_covar of the Gromacs 3.0 package.

Minimized average structures

Minimized average structures were produced by performing a steepest descents energy minimization of the average structures obtained from the short MD runs. The energy minimization was carried out until the largest force was smaller than 2000 kJ mol⁻¹ nm⁻¹.

Snapshot structures

The first 100 psec of the long MD simulations were discarded, and snapshot structures were taken every 10 psec. Each frame was used directly for pKa calculations. The final pKa value for each residue in the trajectory was calculated in two ways: (1) by calculating the average pKa value from all the individual snapshot pKa values, and (2) by calculating the average titration curve from all snapshots and thereafter calculating a pKa value from the average titration curve.

CONCOORD analysis

Coordinate sets were produced by the CONCOORD method (de Groot et al. 1997). Two thousand structures were generated. The average structure of the 2000 structures was calculated by the g_covar program of the GROMACS package.

The energy minimized structure of the average structure was calculated by performing a steepest descents energy minimization as described above.

Abbreviations

• HEWL, hen egg white lysozyme

• RMSD, root mean square difference

• PDB, Protein Data Bank