Fluorescence tomographic imaging in turbid media using early-arriving photons and Laplace transforms

Abstract

We present a multichannel tomographic technique to detect fluorescent objects embedded in thick (6.4 cm) tissue-like turbid media using early-arriving photons. The experiments use picosecond laser pulses and a streak camera with single photon counting capability to provide short time resolution and high signal-to-noise ratio. The tomographic algorithm is based on the Laplace transform of an analytical diffusion approximation of the photon migration process and provides excellent agreement between the actual positions of the fluorescent objects and the experimental estimates. Submillimeter localization accuracy and 4- to 5-mm resolution are demonstrated. Moreover, objects can be accurately localized when fluorescence background is present. The results show the feasibility of using early-arriving photons to image fluorescent objects embedded in a turbid medium and its potential in clinical applications such as breast tumor detection.

Biomedical optical imaging has been explored as an important noninvasive diagnostic technique for detecting of tissue abnormalities (1). At long visible wavelengths and in the near infrared, light can penetrate deeply into biological tissue with minimum absorption. However, light traversing biological tissue undergoes multiple elastic scattering events. The objective of time-resolved photon migration studies is to reduce or eliminate the resulting turbidity, which obscures small embedded lesions. Two main approaches have been followed. The first exploits the use of diffusive photons (2–4). These photons are well modeled by diffusion theory, which can be used to obtain information about the turbid medium the photons traverse. Another advantage of this method is the large signal level. However, spatial resolution is poor due to the broad spatial distribution of the diffusive photons inside the turbid medium. The second approach uses a forward scattering “transillumination” geometry and uses time (5, 6) or coherence (7) gating to exploit the earliest-arriving photons, which undergo little or no scattering and traverse the medium in nearly straight-line paths. As a result, high spatial resolution can be obtained. However, because of the large extent of scattering in biological tissues, the amount of these earliest-arriving photons is very small. Thus, this concept works best in relatively thin samples.

Recently, attention has been directed to the intermediate regime, which may provide the best trade-off between signal-to-noise (S/N) level and spatial resolution. In this regime, photons undergo many small angle scattering changes but are not fully randomized. Few-millimeter resolution has been achieved in reasonably thick samples (2–4 cm) by using the early-arriving photons (up to tens of picoseconds) (8, 9). In addition, extraction of spatial information can be improved by use of theory to model these early-arriving photons (10).

Most photon migration schemes use differences in absorption/scattering between the embedded object and the surrounding medium for contrast. Alternatively, Boas et al. (11), working in the frequency domain, explored the use of fluorescence to provide contrast, thus significantly reducing excitation background. Fluorescence spectroscopy studies have suggested that endogenous tissue fluorophores may provide useful diagnostic information (for example see ref. 12). Moreover, selective uptake of many exogenous dyes has been demonstrated in neoplastic lesions (for example see ref. 13). The use of fluorescence labeled anti-tumor antibodies also has been suggested (14). Such agents would serve as fluorescent markers with high quantum yields to detect embedded lesions in the breast, brain, or perhaps other organs. However, the use of fluorescence has been limited by the concern that the long fluorescent lifetime, typically of the order of a few nanoseconds, inevitably obscures the desired temporal resolution.

Recently, we demonstrated that the long fluorescence lifetime does not affect temporal resolution, provided that the very early part of the observed signal is used to extract the information (15, 16). This is because the rising edge of the fluorescence decay curve is determined by the electronic transition time, which is on the order of 10⁻¹³ s. Therefore, by using the early part of the fluorescence signal, accurate spatial information about a fluorescent object embedded in turbid media can be obtained. In this paper, we apply this concept to thick (6.4 cm) tissue-like phantom samples to detect embedded objects using a tomographic scheme.

MATERIALS AND METHODS

The experiments were performed in a cylindrical glass beaker 6.4 cm in diameter. In preparing the phantom samples, 60 ml of 1 μm diameter 2.5% polystyrene bead stock solution (PolySciences) was mixed in 200 ml of water as the scattering medium, with black ink added for absorption. This mixture was designed to match the optical parameters of human breast tissue [typical ranges of optical parameters of (compressed) human breast tissue are μ′_s = 7–12 cm⁻¹ and μ_a = 0.02–0.03 cm⁻¹, see ref. 9]. Using Mie theory (17), we calculated that in the wavelength range from 750 to 800 nm the scattering coefficient, μ_s, of the medium varies from 144 to 160 cm⁻¹ (thus the diameter of the beaker is equal to about 1,000 scattering mean free paths); and the anisotropy coefficient, g, is between 0.954 and 0.959. Thus, the reduced scattering coefficient, μ′_s, defined as μ_s(1 − g), varies between 6.88 and 6.96 cm⁻¹. Black ink was added to provide an absorption coefficient, μ_a, of 0.05 cm⁻¹. The embedded fluorescent objects were glass cells filled with HITCI iodide dye (Exciton, Dayton, OH) dissolved in methanol. For simplicity, no attempt was made to simulate the turbidity of the fluorescent objects by adding scatterers. Due to their small size compared with that of the medium, this would be a very small effect.

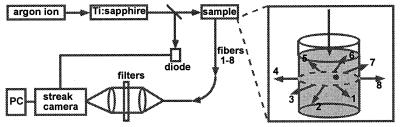
The schematic diagram of the experimental apparatus is depicted in Fig. 1. All experiments used ≈2-ps laser pulses [Coherent (Santa Clara, CA) Mira 900 mode-locked Ti:sapphire laser pumped by Coherent Innova 400 argon ion laser] for excitation and a streak camera system [Hamamatsu (Middlesex, NJ) C5680 with M5675 synchroscan unit] for detection. The excitation wavelength was 752 nm, the repetition rate was 76 MHz, and the average power incident on the sample was either 100 or 600 mW. A small portion of the excitation light was deflected by a quartz plate to a fast photodiode (Hamamatsu C1808–02) as an optical triggering signal. Eight coherent fiber bundles (Sumitomo Electric, Torrance, CA) were used to collect the fluorescence light and transmit it to the entrance slit of the streak camera. Each fiber bundle was 500 μm in diameter and consisted of 10,000 single-mode silica fibers. This allowed maximum optical throughput with minimum temporal dispersion. Two 752-nm holographic notch filters (Kaiser Optical Systems, Ann Arbor, MI) were used to remove the excitation light (total extinction at the laser wavelength ≈10⁻¹²). Fluorescence from 760 to 800 nm was detected. The streak camera was operated in the single photon counting mode, and the system was shot-noise limited. The overall temporal resolution was about 10 ps.

Figure 1.

Schematic diagram of experimental apparatus and sample geometry.

The excitation beam impinged on the sample from the top of the beaker. The distal ends of the eight detection fiber bundles were evenly positioned around the circumference of the beaker in the horizontal plane containing the embedded fluorescent object(s). The depth of this plane was 1.5 cm below the top surface. The proximal ends of the fiber bundles were arranged in a line and imaged onto the streak camera input slit. The streak camera was used as both a time- and spatially resolved multichannel detector. Signals from different fiber bundles appeared at different horizontal locations on the charged-coupled device array of the streak camera, and the temporal information was displayed vertically. Both the time delay and the intensity transmission of the eight channels were calibrated.

Experimental Results.

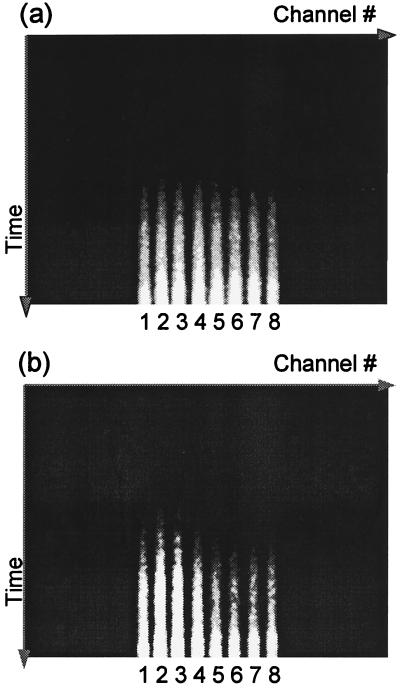
In the first experiment, a 1-mm fluorescent object (65 μM HITCI) was embedded in the phantom. Fig. 2 shows typical streak camera results measured under the conditions of 600-mW laser power and 1-min data accumulation time. The full temporal window is about 1.5 ns, which is significantly shorter than the signal duration. In the experiment, the time delay was adjusted so that the very early-arriving fluorescence photons were measured. In Fig. 2a, the fluorescent object was positioned at the center of the beaker, and therefore the eight collection channels receive roughly the same amount of signal. In Fig. 2b, the object was displaced 1 mm from the center and, as expected, one fiber receives the signal earlier than the others. This preliminary data demonstrates that the prototype tomographic system is able to detect a deeply embedded object, and that the system is very sensitive to the location of the object.

Figure 2.

Typical streak camera output in phantom experiments. (a) Embedded fluorescent object close to the center of the beaker. (b) Object 1 mm away from the center. Time increases from top to bottom, and detection channels 1 through 8 are displayed from left to right. The light regions are signals.

Tomographic Analysis.

Above we showed that the early-arriving photon technique is very sensitive to the position of the embedded fluorescent object. However, accurate extraction of the spatial information requires applying a theoretical model in an inverse manner. Such a model should take into account the photon migration terms of both excitation (input) and emission (output) photons, denoted as PMI and PMO, respectively, as well as the fluorescence decay term, F. Assuming the fluorescent object to be a point source, the observed signal is the convolution of the three terms mentioned above,

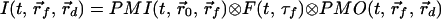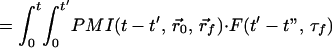1

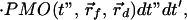where r⃗₀, r⃗_f, and r⃗_d are the positions of the incident beam, the embedded object and the detection fiber, respectively, and τ_f is the fluorescence lifetime. It can be shown that to a good approximation, the effect of boundaries on the photon migration process also enters as a convolution in the time domain; therefore, each photon migration term (PMI or PMO) under given boundary conditions can be written as a convolution of photon migration in an infinite medium (PMI_inf or PMO_inf) and an extra boundary condition term (BC) (18, 19). That is,

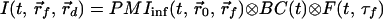1`

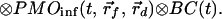Considering the convolution theorem (20), Eq. 1′ can be analyzed using Laplace transformation:

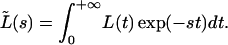2

Thus, Eq. 1′ becomes:

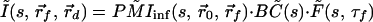3

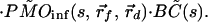Note that in Eq. 3 the photon migration excitation step and fluorescence decay term, as well as the boundary condition terms, are common for all of the collection channels, and they appear as multiplicative factors in the Laplace transform domain. In addition, the Laplace transformation naturally introduces a weighing factor, exp(−st), which emphasizes the early part of the signal. This is advantageous in extracting accurate spatial information with high resolution. Using the diffusion approximation,

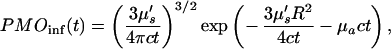4

Eq. 3 becomes (21):

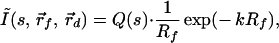5

where R_f = |r⃗_d − r⃗_f|, k = 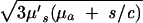and Q(s) includes the terms that are common to all channels. For a given value of s, Q(s) is a numerical constant independent of the positions of the detection channels. Thus, Eq. 5 can be inverted easily to determine the position of the embedded object using standard nonlinear fitting techniques, such as the Leverberg–Marquardt method (22).

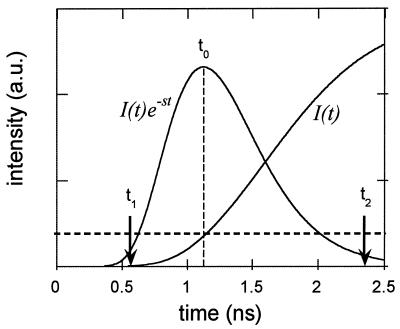
Generally speaking, the Laplace transform analysis can be evaluated at any values of s. However, as implied earlier, different s values emphasize different parts of the time-resolved curve. Thus, analyses with different values of s possess different capabilities for extracting spatial information. This is demonstrated in Fig. 3. Here we plot the time-resolved fluorescence signal, I(t), calculated numerically using Eq. 1, when the fluorescent object is at the center of the beaker. Also plotted is the curve I(t)exp(−st), with s equal to 4 ns⁻¹. The choice of s value is a trade-off between resolution (better at earlier times) and S/N (better at later times). The optimum occurs when I(t)exp(−st) peaks at the earliest time, t₀, at which I(t) has adequate S/N. In the following analysis, representative S/N values of 30 (zero background data) and 5 (1:10 background data) were chosen to determined the s values. More detailed discussion about experimental conditions, data S/N, and localization accuracy will be found in ref. 19. In addition, due to experimental limitations, only a narrow range of values of s can be used. On the one hand, the noise level and the limited dynamic range of the detector strongly affect the very early part of the curves, t < t₁, where the signal is small. Thus, s has to be smaller than some critical value, s₁, to avoid introducing a large error in the Laplace transform integration. On the other hand, because of the limited window size of the streak camera, ≈1.5 ns, the later part of the curve, t > t₂, is truncated. As a result, s has to be greater than a second critical value, s₂. This leads to a second criterion for choosing the optimal s value, i.e.,

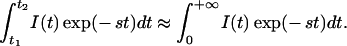Following these two criteria, we can determine the optimal s value based on the S/N in phantom experiments. It should be emphasized that the selection of optimal s value ultimately is determined by the S/N of the experiments. We then can Laplace-transform the eight-channel data at the optimal s value, from which the position of the fluorescent object can be tomographically determined using Eq. 5.

Figure 3.

Determination of the optimal s value, based on a diffusion theory calculation of the signal level. The adequate S/N level, determined by the experimental conditions and desired imaging resolution, is schematically represented by the horizontal dashed line.

Eq. 5 can be extended easily to multiple fluorescent objects. For example, in the case of two embedded objects, a and b, the analog of Eq. 5 is:

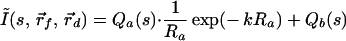6

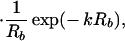where R_a,b = |r⃗_d − r⃗_a,b|. In the following, we use Eq. 5 or 6 to extract the location(s) of embedded fluorescent object(s).

Localizing and Resolving Embedded Fluorescent Objects.

Experiments were performed to study localization and resolution using early-arriving photons and the Laplace transform analysis. The embedded fluorescent objects were two 1-mm diameter glass cells containing 65 μM HITCI. In these experiments, the objects were always positioned in the plane of the collection fibers. However, the analysis can be adapted easily to three-dimensional experiments.

The experimental procedure was the following: (i) One fluorescent object was positioned at the center of the beaker. It was then displaced toward fiber bundle no. 2 in 1-mm steps along the direction θ = π/2, until it was 5 mm away from the center. (The angle is defined in such a way that the angle for the ith channel, θ_i = i π/4.) (ii) A second object was then added at a location 5 mm from the center in the direction θ = 5π/4. The first object was then moved back toward the center in 1-mm steps. (iii) Once the first object reached the center, the second was moved 2.5 mm closer to the center. The first object was then moved outward again along θ = π/2 in 1-mm steps. (iv) Finally, the first object was removed, and the second was moved outward from the center along θ = 5π/4 in 2.5-mm steps. For each combination of object positions, time-resolved fluorescence data was collected. The laser power was 600 mW, and the data accumulation time was 1 min.

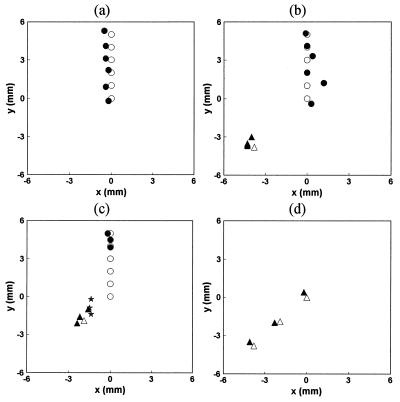
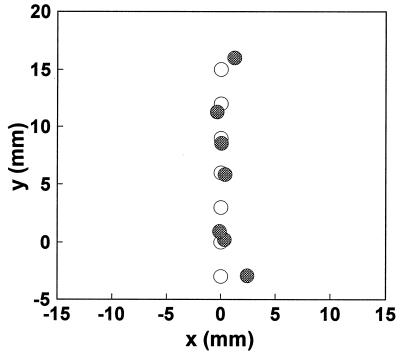
From the measured curves, the Laplace transform for each of the eight channels was calculated. To extract the spatial information, the two-object tomographic algorithm, Eq. 6 was always used. In the present case, the known values of μ′_s and μ_a were used. An s value of 6 ns⁻¹ was chosen, providing a good trade-off between S/N and temporal resolution (roughly 1/s). The fitting code assumed two objects to be present and predicted either two objects at two different locations or two objects collapsed to the same location (i.e., the concentration for the second object was computed to be close to zero). The calculation time was on the order of second using a PowerPC computer. The fitting results for the above experimental procedures (i) through (iv) are shown in Fig. 4 a–d), together with the actual positions of the fluorescent objects. Here, the circles and triangles denote the positions of objects 1 and 2, respectively, with the open and solid symbols indicating the actual and estimated positions, respectively. In Fig. 4a, the fitting code correctly predicts that only one object was present, and the average error was about 0.3 mm between the experimental estimates and the actual positions of the object. Similarly, in Fig. 4b, the locations of both objects were correctly predicted. However, in Fig. 4c, at the first three positions, the fitting algorithm predicted only one object present with its position (denoted by a star) close to the “center of gravity” of the two objects. In other words, the system could not resolve the two objects. However, as the two objects were moved farther apart, the fitting code once again was able to recognize the presence of two objects and predict their positions. Not surprisingly, in Fig. 4d the experimental estimate was again about 0.3 mm from the actual position.

Figure 4.

Comparison of experimentally estimated object positions with the actual positions. The open symbols are the actual positions of the objects, and the filled symbols are the experimental estimates. The stars denote the collapsed positions when the algorithm cannot resolve the two objects.

In summary, at the current S/N level we can localize an object with an uncertainty of about 0.3 mm, and we can resolve two objects if they are separated by 4–5 mm.

Background Fluorescence.

So far we have considered the case in which all of the fluorescence arises from the embedded objects. However, in practical applications fluorescence arises from the surrounding medium as well, and this reduces contrast. Because of the large volume of the surrounding medium, even a small amount of background fluorophore can have a tremendous impact on the data analysis.

Generally speaking, the difficulties introduced by the background fluorescence can be approached as two sub-problems. The first issue is how to subtract this background signal. In principle, this can be done if there is an accurate theoretical model available. On the other hand, several scenarios may be proposed to subtract the background experimentally. One is to rely on a symmetric laser source-detector geometry and a uniform background fluorophore distribution, so that the background signals are identical among all the detection channels, and thus will cancel after subtracting one channel from the other. A more practical approach is to introduce a second fluorescence agent that does not selectively accumulate inside the target, so that the background fluorescence can be measured with this reference. Moreover, considering that selective accumulation of the contrast agent inside the tumor may be delayed, background subtraction may be done by making two measurements at different times, depending on the pharmacodynamics/pharmacokinetics of the contrast agent. Lastly, it is possible that a combination of theoretical modeling and experimental subtraction will be the best approach. All of these will be carefully studied in later stages of this research.

The second part of the problem is to understand how the noise associated with the background fluorescence signal affects the actual signal from the embedded objects, once a suitable means has been determined to subtract the background. To address this point, we performed an experiment using the apparatus and phantom medium described above. A single, 5-mm diameter glass cell containing 0.65 μM HITCI was placed inside the beaker, and more HITCI was added to the medium so that the background concentration was 0.065 μM (10:1 contrast ratio). The volume of the dye cell was 0.15 ml, whereas the volume of the scattering medium was 150 ml. Therefore, there was roughly 100 times more fluorophore in the background than inside the object. To remove the background signal, fluorescence emission was collected with and without the embedded object present, and subtraction then was performed between the two to yield the signal from the embedded object plus the background noise. The object was moved inside the medium in 3-mm steps. The laser power was 100 mW, and the data collection time was 1 min. In these experiments the background signal was observed to be about 50 times stronger than the object signal. As a result of the large background, the object signal measured was noisier than that measured in the zero background experiments.

After background subtraction, the Laplace transform-based inverse algorithm, Eq. 5, was used to extract the position of the embedded object. Because the noise level was higher here, the smaller value of s = 3 ns⁻¹ was used. The predicted positions of the object are shown in Fig. 5, together with the actual positions. The average uncertainty was about 1.5 mm.

Figure 5.

Localization result at 10:1 contrast ratio. The open symbols are the actual positions of the objects, and the filled symbols are the experimental estimates.

DISCUSSION

We have developed a tomographic technique using early-arriving photons for detecting of fluorescent objects embedded in turbid media with optical properties similar to those of human breast tissue and under the conditions of 100–600 mW near-infrared incident power and 1-min data acquisition time. Most importantly, we have shown that the method can resolve two separate objects, as well as to localize a single object, which demonstrates in an elementary way the imaging capability of our approach. In addition, we have addressed the practical issue of detecting a fluorescent object in the presence of background fluorescence.

To extract spatial information, we developed a tomographic algorithm based on the Laplace transform of the well known diffusion approximation to the photon migration process. The Laplace transformation naturally introduces a favorable weighing factor, facilitating the best trade-off between signal level and spatial resolution. Moreover, the above algorithm does not require a priori knowledge of the number of embedded objects to be detected. The maximum number of embedded objects is, in principle, only limited by the number of collection channels. The present experiment used eight channels, but there is no reason a much large number of detection channels could not be used. However, some potential difficulties that might arise when dealing with a large number of objects include longer calculation time and larger localization uncertainty, due to the need to include more free parameters in the fitting code. In addition, we note that in the model developed here the fluorescent objects are assumed to be points, Eq. 1, and therefore size information cannot be extracted.

In analyzing the above data, μ′_s and μ_a were known, and the object positions were the only unknowns. However, the tissue optical properties need not be known, and the analysis then can be carried out with an extra fitting parameter, k. It is also possible with this method to extract μ_s′ and μ_a explicitly. To do this, the use of two or more s values is required. Here, because the functional form of Q(s) may not be known (especially the boundary condition terms), a ratio can be used to cancel the common terms. For example, in the case of a single object, by taking the ratio between a pair of detection channels (1 and 2), Eq. 5 becomes:

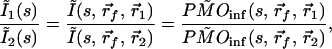7

where r⃗₁ and r⃗₂ are the positions of the two detection fibers. Note that the Q(s) terms completely cancel. Using the diffusion approximation, we have

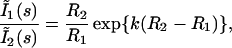8

where R_1,2 = |r⃗_1,2 − r⃗_f|. Because k = 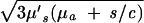, μ′_s and μ_a can be determined by using two or more values of s.

With two embedded objects, a and b, the ratio between two channels, 1 and 2, can be written,

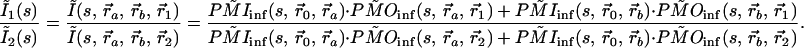9

Note that the common terms, F and BC, still cancel. Because the photon migration excitation process can be modeled in the same way as emission, the inversion of Eq. 9 is not complicated. However, the ratio method requires more spatial detection channels, because information is used in pairs.

O’Leary et al. (23) have reported a frequency domain experiment (at 50 and 200 MHz) to localize a fluorescent object embedded in a turbid medium. This is mathematically equivalent to taking the Fourier transform of the time domain signals. There is a strong mathematical similarity between the Laplace and Fourier transforms, and as the Fourier transform also obeys the convolution theorem, an equation similar to Eq. 6 also could be used. However, in the present study we chose the Laplace transform rather than the Fourier transform for the following reasons. (i) Physically, the Laplace transform selects a well defined temporal window in the time domain, as described in Fig. 3. In contrast, the Fourier transform selects a particular frequency component, which is not necessary localized at a given portion of the time domain signals. Thus, the Laplace transform analysis is able to emphasize the early part of the signal in a straightforward manner. (ii) Our time domain data are truncated at ≈1.5 ns. Such truncation is equivalent to a temporal step function, which leads to errors in all of the frequency components. As a result, the Fourier transform of our time domain data exhibits strong oscillation as a function of frequency, due to the nature of the Fourier transform operation. On the other hand, as discussed above, the truncation error can be minimized in the Laplace transform analysis for s values of interest, i.e., those that tend to emphasize the very early part of the time-resolved signals.

Although Eq. 5 was derived using the diffusion approximation solution, the Laplace transform method is not restricted to the use of this equation. For example, the path integral solution (10), which is known to describe the early-arriving photons more accurately than the diffusion approximation can be readily incorporated into this analysis (note, however, that even in the diffusion approximation, photon paths are more well defined at earlier times). Despite the lack of a simple analytical solution similar to Eq. 5, computer fitting techniques easily should be able to extract the spatial information, owing to the fact that the excitation and fluorescence decay terms have been canceled.

Finally, we note that the current experimental system can be improved by including more spatially resolved collection channels, and optimizing various optical components in the system. These modifications should lead to an overall increase in signal by a factor of 25–50 (18), which will allow us to work with correspondingly lower laser powers and shorter data accumulation time. With these improved values, this technique has the potential to be used in clinical applications such as breast tumor detection, where selective exogenous agents such as those used in photodynamic therapy or fluorescence-labeled anti-tumor antibodies can be introduced as fluorescent markers for neoplasia.

CONCLUSIONS

This paper has presented a multichannel tomographic technique to localize and resolve fluorescent objects embedded in turbid media with tissue optical properties using early-arriving photons. We demonstrated that early-arriving fluorescence photons from a deeply embedded fluorescent object can be measured with good S/N. A tomographic algorithm was developed based on an analytic description of the photon migration process. Excellent agreement was obtained between the actual positions of the fluorescent objects and the experimental estimates. The results demonstrate the feasibility of using early-arriving photons to image fluorescent objects embedded in a turbid medium with biologically relevant parameters.

ABBREVIATIONS

S/N

signal-to-noise

PM

photon migration