Abstract
The inhibitory effects of inorganic phosphate (Pi) on isometric force in striated muscle suggest that in the ATPase reaction Pi release is coupled to force generation. Whether Pi release and the power stroke are synchronous events or force is generated by an isomerization of the quaternary complex of actomyosin and ATPase products (AM.ADP.Pi) prior to the following release of Pi is still controversial. Examination of the dependence of isometric force on [Pi] in rabbit fast (psoas; 5-15 °C) and slow (soleus; 15-20 °C) myofibrils was used to test the two-step hypothesis of force generation and Pi release. Hyperbolic fits of force-[Pi] relations obtained in fast and slow myofibrils at 15 °C produced an apparent asymptote as [Pi]∞ of 0.07 and 0.44 maximal isometric force (i.e. force in the absence of Pi) in psoas and soleus myofibrils, respectively, with an apparent Kd of 4.3 mm in both. In each muscle type, the force-[Pi] relation was independent of temperature. However, 2,3-butanedione 2-monoxime (BDM) decreased the apparent asymptote of force in both muscle types, as expected from its inhibition of the force-generating isomerization. These data lend strong support to models of cross-bridge action in which force is produced by an isomerization of the AM.ADP.Pi complex immediately preceding the Pi release step.
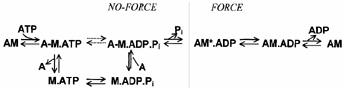
Energy transduction in muscle contraction results from the coupling between MgATP hydrolysis and the cyclic interaction between myosin heads (‘cross-bridges’) and actin. The process occurs in discrete steps with product release associated with a structural change in the actomyosin complex (‘power stroke’) producing one or more force-generating transitions. The power stroke produces force, shortening and external work (for a review see Goldman, 1987; Brenner, 1990; Geeves & Holmes, 1999; Gordon et al. 2000). Studies on isolated proteins and on demembranated fibres have identified a reaction pathway for the cross-bridge ATPase cycle that is now generally accepted:
In this scheme, nucleotide occupancy of the myosin-active site modulates the binding affinity of myosin for actin, defining two general categories of cross-bridges: ‘strongly binding states’ (AM, AM.ADP) and ‘weakly binding states’ (A-M.ATP, A-M.ADP.Pi; the line between A and M indicates that cross-bridges spend most of their time in the detached form). Although the mechanism of chemomechanical coupling is unknown, the exoergonic release of inorganic phosphate (Pi) is thought to power the working stroke (for a review see Cooke, 1997). The evidence supporting this assignment is that an increased [Pi] strongly depresses maximal isometric force (Brandt et al. 1982; Cooke & Pate, 1985; Kawai et al. 1987; Pate & Cooke, 1989a) while the rate of force development (Millar & Homsher, 1990; Walker et al. 1992) and of force decay from rigor (Hibberd et al. 1985) increase. The reduction of the free energy of hydrolysis of MgATP at elevated [Pi] shifts cross-bridges from force-producing states (AM*.ADP) to low or non-force-producing states (A-M.ADP.Pi) in rapid equilibrium with detached states (Eisenberg et al. 1980; Cooke & Pate, 1985). In fast skeletal muscle, Pi release is not the rate-limiting step of the overall cross-bridge cycle (Cooke, 1997), but this is less certain in slow skeletal muscle (Millar & Homsher, 1992). Moreover, transient kinetic analysis of the effects of sudden increases in Pi on the kinetics of force production suggested the idea of a two-step mechanism for Pi release, with a force-generating isomerization of AM.ADP.Pi state preceding the release of Pi and the formation of the strongly binding AM*.ADP state (reviewed by Morris & Homsher, 1998).
The evidence for a two-step model for Pi dissociation and force generation are: saturation kinetics of the [Pi] dependence of the rate of rigor decay (Goldman et al. 1984; Hibberd et al. 1985) or active force decay (Dantzig et al. 1992; Walker et al. 1992) induced by photolysis of caged-Pi; the rate of force increase following the sudden reduction of pressure in the presence of Pi (Fortune et al. 1991, 1994); a Pi-dependent intermediate rate derived from sinusoidal analysis of active muscle in the presence of Pi (Kawai & Halvorson, 1991). Unfortunately, in psoas muscle fibres the kinetics of Pi-jumps at 15-20 °C in the [Pi] range expected to saturate the process is very fast (100-200 s−1; Dantzig et al. 1992) and close to the time resolution of those studies. Similar experiments performed in slow muscle fibres, where the rate of Pi-transients is much slower than in fast muscle, produced inconclusive results because the effect of Pi on isometric force is smaller and Pi release steps are not kinetically different from the rate-limiting steps of the pathway (Millar & Homsher, 1992). Also, if available data from measurements of Pi-transients suggest that Pi release from AM*.ADP.Pi follows a force-generation isomerization, it is frequently said in the literature that the power stroke occurs after the release of Pi and recent ‘swinging lever arm’ models of cross-bridge action (mainly based on structural and molecular genetics data on slow myosins) identify Pi release as the event which ‘prompts’ the power stroke (Houdusse & Sweeney, 2001; Spudich, 2001).
If force generation and Pi release are synchronous (as in Scheme 1), the steady-state dependence of isometric force on [Pi] will decline hyperbolically with a zero asymptote of force. However, if force is produced by an isomerization of A-M.ADP.Pi (non-force generating) to AM*.ADP.Pi (force generating) from which Pi is released (forming a force-exerting AM*.ADP state), the force-[Pi] plot will approach an asymptote significantly different from zero as [Pi]→∞ (see Gordon et al. 2000 for discussion of this point). Unfortunately, previous studies of the force-[Pi] relation in skinned fibres were of insufficient resolution to assess this point because diffusional [Pi] gradients can arise within fibres, distorting the results. Recently, the diffusional limitations of skinned fibres were circumvented by using single myofibrils (Bartoo et al. 1993; Friedman & Goldman, 1996; Colomo et al. 1997; Barman et al. 1998; Tesi et al. 1999). Because myofibrils (1-3 μm diameter) rapidly equilibrate with the bathing medium (< 1 ms), control of the solution inside the myofilament lattice is possible and rapid changes in the perfusing solution can be made to examine the kinetics of mechanical events induced by solution change (Tesi et al. 2000). Myofibrils can be isolated from different muscle types and are thus the ideal preparation for comparative studies.
Scheme 1.
Below, the effect of [Pi] on maximal isometric force was studied in single myofibrils or thin bundles of myofibrils (< 3 μm diameter) from rabbit fast (psoas) and slow (soleus) muscle in the temperature range 5-20 °C. Hyperbolic fits to the force-[Pi] relations gave asymptotes of force significantly different from zero in both muscle types, indicating that at infinite [Pi] a significant fraction of AM*.ADP.Pi cross-bridges remained in force-generating states (i.e. force generation precedes Pi release itself). Further, 2,3-butanedione 2-monoxime (BDM), which is thought to shift the equilibrium between AM.ADP.Pi and AM*.ADP.Pi towards the non-force-generating form (Herrmann et al. 1992; McKillop et al. 1994; Regnier et al. 1995) additively decreased the asymptote of the force-[Pi] relation. The results of this steady-state study support the hypothesis that force in striated muscle is generated in an isomerization of the AM.ADP.Pi state immediately preceding the Pi release step itself. Preliminary results of this study have been reported (Piroddi et al. 2001).
METHODS
Myofibrils
Single myofibrils or thin bundles of 2-4 myofibrils were prepared from rabbit fast and slow skeletal muscle by homogenization of glycerinated rabbit psoas or soleus muscle, as previously described (Tesi et al. 1999, 2000). Rabbits were killed by intravenous administration of pentobarbitone (120 mg kg−1) through the marginal ear vein. All the procedures were conducted in accordance with the official regulations of the European Community Council on use of laboratory animals (directive 86/609/EEC) and the study was approved by the Ethical Committee for Animal Experiments of the University of Florence.
Apparatus for force measurement and rapid solution change
Methods used to record isometric force from single striated muscle myofibrils and to make rapid solution changes were as previously described (Colomo et al. 1997, 1998; Tesi et al. 2000). In these experiments the compliance of the force transducers was 1-3 nm nN−1 and their frequency response was linear to 5 kHz. Myofibril shortening associated with force-probe compliance was kept ≤ 3 % of initial length.
Myofibrils were maximally activated and relaxed by rapid translation between two continuous streams (each 150 μm wide) of relaxing (pCa 8.0) and activating (pCa 4.5) solutions of variable composition. The solutions flowed by gravity from a double-barrelled glass pipette placed at 90 deg to the axis of the preparation (at 0.5 mm distance). The gravity-driven flow of each solution was ≈120 μl min−1, flowing past the myofibril at 2 cm s−1. Solution changes occurred with a time constant of 2 ms and were complete in 10 ms. During experiments, myofibrils were subjected to several activation-relaxation cycles by switching the position of the perfusion pipette. To compare maximal isometric force in two experimental conditions, some myofibrils were sequentially activated using a 3- to 4-channel perfusing system loaded with relaxing solution and two or three different activating solutions (e.g. different [Pi]). Effects of changes of the activating solution were observed from the change in force triggered by the sudden change in position of the perfusing system (‘Pi-jump’ protocol). The 3- to 4-channel perfusing system was produced by replacing double-barrelled glass pipettes with fused silica chromatography columns (guard column IP-deact., 250 μm internal diameter; Restek, USA), glued side-by-side with each channel directly connected to a solution reservoir.
Isometric force was maintained over 4-5 activation cycles without significant decline in mechanical performance (< 10 % decrease in isometric force). Experiments were performed at 5 and 15 °C in rabbit psoas myofibrils and at 15 and 20 °C in rabbit soleus myofibrils.
In some experiments, release-re-stretch protocols applied to myofibrils during the contraction plateau were used to measure the rate of tension redevelopment, kTR (Brenner, 1988).
Solutions: composition and reduction of contaminant Pi
All solutions were made as described by Brandt et al. (1998) and contained 5 mm MgATP, 1 mm free magnesium, pH 7.0 and a final ionic strength of 200 mm. Solutions of different composition (e.g. pCa or [Pi]) were made by solving the multiple equilibria for metals and ligands using the following apparent association constants (log values at pH 7.00): CaEGTA 6.3, MgEGTA 1.6, CaATP 3.7, MgATP 4.1. Although continuous solution flow minimizes alterations in the concentration of MgATP and its hydrolysis products within the myofibril, these measurements have been made in the presence of a MgATP regenerating system: creatine phosphate (CP, 10 mm) and creatine kinase (CPK, 200 units ml−1). As previously observed (Tesi et al. 1999), the presence of this re-phosphorylating system reduces the run-down of preparations.
The Pi contamination in experimental solutions was estimated spectrophotometrically (Baginski et al. 1967) using samples collected before the addition of CPK, whose presence interfered with the colorimetric assay. Standard solutions contained 170 ± 30 μM (n = 17) contaminating Pi from spontaneous breakdown of MgATP and CP (Tesi et al. 2000). These solutions are referred to as ‘nominal Pi’ solutions.
Contaminant Pi was reduced by passing experimental solutions through a column containing the enzyme purine nucleoside phosphorylase (PNP), immobilized on activated sepharose-4B beads, with substrate 7-methylguanosine (Brune et al. 1994). The [Pi] in the column eluate was < 5 μM. When used, these solutions are referred to as ‘Pi -free’ solutions.
Contractions recorded from myofibrils perfused with Pi-free solutions were used as a reference. Test contractions at a given [Pi] were obtained using solutions first scavenged for Pi to which known amounts of Pi were added (‘test solutions’).
Nucleoside phosphorylase (‘bacterial’), 7-methylguanosine, ATP, ADP and BDM, were purchased from Sigma Chemical Co., and CP/CPK was from Roche Diagnostics Co. All results are given as means ± s.e.m.
Cross-bridge scheme
Cross-bridge schemes like Scheme 1, in which force generation coincides (and/or follows) Pi release, predict steady-state relations between isometric force and [Pi] whose limit for [Pi]→∞ is zero. Their general form is:
| (1) |
where A and Kd are constants, the last one corresponding to the [Pi] giving half-maximal effect and Ntot is the total number of cross-bridges present. The subscript ‘app’ indicates a constant or a parameter measured experimentally which can be a combination of different fundamental constants.
Force- [Pi] curves with an asymptote of force significantly different from zero are predicted only by cross-bridge schemes in which force is generated in a transition prior to Pi release. The steady-state effect of [Pi] on force was analysed using a simplified four-state cross-bridge (CB) scheme (Scheme 3) based on the six-state model proposed by Regnier et al. (1995).
Scheme 3.
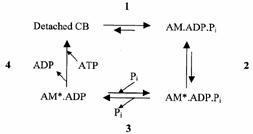
This model assumes that force is generated by an isomerization of the AM.ADP.Pi state (Step 2) immediately preceding the Pi release step (Step 3). A calcium-sensitive transition (Step 1) before force generation is included in order to account for the [Ca2+] dependence of kTR. The rate-limiting step of the cycle is assumed to be associated with ADP release (pooled together with ATP binding and cross-bridge dissociation in Step 4). This model predicts a sigmoidal force-log[Pi] relation (if steps are strain dependent) and, on a linear scale, a hyperbolic relation between force and [Pi] with a force asymptote at infinite [Pi] significantly different from zero.
Force was assumed to be proportional to the sum of cross-bridge fractions in the AM*.ADP.Pi and AM*.ADP states (each yielding identical forces) and was computed assuming that [Pi] only affects k-3 [Pi], the reversal of Pi release. Steady-state force as a function of [Pi] is given by:
| (2) |
When eqn (2) is derived from steady-state calculations of fractional occupancy of force-generating states in Scheme 3 with the assumption that Step 4 is the rate-limiting step of the cross-bridge cycle (i.e. k+4 is small), relative force as a function of [Pi] (relforce, force[Pi] /force[Pi],free) can be approximated by:
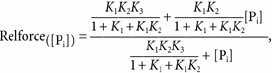 |
(3) |
where:
| (4) |
| (5) |
As K1 values can be estimated from the measured rate of force development, the equilibrium constants K2 and K3 for force generation and Pi release steps can be obtained from the hyperbolic fitting of force-[Pi] relations according to Scheme 3.
RESULTS
Effect of [Pi] on force in maximally activated rabbit fast skeletal myofibrils at 5 and 15 °C
Two different protocols were used to study the effect of [Pi] on maximal isometric force. In one case, we compared maximal isometric force obtained in two or more contraction-relaxation cycles in Pi-free control conditions ([Pi] < 5 μM; see Methods) to those in the presence of 0.2-70 mm [Pi] (test conditions; Fig. 1A and B). In the second case, the effect of [Pi] was measured from the amplitude of a Pi-jump (see Methods) in Pi-free conditions to different final ligand concentrations (Fig. 1C). The myofilament [Pi] was assumed to be equal to that of the perfusing solution because the small preparation diameter (1-3 μm) and the continuous flow of solutions prevent formation of diffusional gradients. Most experiments used the Pi-jump protocol because ‘run-down’ was minimized. The rate of isometric force generation was obtained from the time course of force rise after rapid activation (kactiv; Tesi et al. 2000) and/or from the time course of force redevelopment following a release-re-stretch protocol (kTR; Brenner, 1988). Though kTR is a more reproducible measure of the rate of force development, the release-re-stretch manoeuvre used for kTR measurement could not be used with [Pi] in experimental solutions higher than 5 mm as the tension at the end of the re-stretch was almost as large as the steady-state force. Unless otherwise stated, the apparent rate of force generation was estimated as kTR below 5 mm [Pi] and as kactiv in all the other conditions. In both cases experimental tracings were fitted as monoexponential processes.
Figure 1. Effects of Pi addition in myofibrils from rabbit fast and slow skeletal muscle.

Left, psoas muscle myofibrils (A-C); right, soleus muscle myofibrils (D-F). A, psoas myofibril 15 °C: maximal isometric force in the presence of 5 mm Pi is 0.49 of the value in control Pi-free conditions. In Pi-free and 5 mm Pi conditions, kactiv was 6.0 s−1 and 11 s−1, respectively. B, psoas myofibril at 5 °C: kactiv was slowed down considerably (1.5 s−1); 5 mm Pi dropped force to 0.48 of the Pi-free value and increased kactiv to 4.3 s−1. C, psoas myofibril at 5 °C subjected to a ‘Pi-jump’ protocol from Pi-free to 5 mm Pi (arrows mark the time of the solution change associated with the change in [Pi] from Pi-free to 5 mm and reverse). Isometric force dropped to 0.35 of Pi-free value. kactiv in Pi-free conditions: 1.4 s−1; kPi(+), 25.7 s−1; kPi(-), 1.7 s−1. D, soleus myofibril at 20 °C: 5 mm Pi dropped force to 0.74 of Pi-free value; kactiv in Pi-free and 5 mm Pi were 3.3 s−1 and 3.4 s−1, respectively. E, soleus myofibril at 15 °C: force is decreased to 0.82 of Pi-free value; kactiv, in both Pi-free and 5 mm Pi was 1.7 s−1. F, soleus myofibril at 15 °C subjected to a ‘Pi -jump’ protocol from Pi -free to 50 mm Pi. Isometric force dropped to 0.50 of Pi-free value. kactiv in Pi-free conditions was 1.9 s−1; kPi(+), 6.3 s−1; kPi(-), 1.7 s−1.
Maximal isometric force per cross-sectional area and kTR in Pi-free conditions (Table 1) averaged respectively 356 ± 62 mN mm−2 and 6.6 ± 1.5 s−1 (n = 29) at 15 °C and 265 ± 14 mN mm−2 and 1.9 ± 0.1 s−1 (n = 36) at 5 °C. As previously reported (Brandt et al. 1982; Cooke & Pate, 1985; Millar & Homsher, 1990; Walker et al. 1992), Pi addition to control solution strongly reduced steady-state force generated by psoas myofibrils at both 5 and 15 °C (Fig. 2A) and increased kTR (Table 1). At 5 °C, compared with Pi-free conditions, 5 mm Pi dropped force by about 50 % and increased kTR by three times (6.4 ± 2.4 s−1, n = 7). As previously reported (Tesi et al. 2000), the kinetics of the drop in force induced by a sudden increase in [Pi] (kPi(+); Fig. 1C, downward arrow) was about three times faster than kTR at the same final [Pi] (see Table 1) while the kinetics of the force increase induced by a sudden decrease in [Pi] (kPi(-); Fig. 1C, upward arrow) was not significantly different from kTR at the same final [Pi]. The relative force data were fitted to hyperbolic relations and the maximal effect of [Pi] on isometric force ([Pi]→∞) was estimated by the apparent asymptote (Asymptoteapp) of the relation while the Pi sensitivity of isometric force by the [Pi] at which force depression is half-maximal (Kd,app). At 5 °C, Asymptoteapp and Kd,app were 0.05 ± 0.02 and 4.15 ± 0.50 mm, respectively. In the temperature range tested, the Asymptoteapp or Kd,app of the force-[Pi] relations of fast muscle myofibrils were not different (respectively 0.07 ± 0.02 and 4.33 ± 0.36 mm at 15 °C). At both 5 and 15 °C, the extrapolated Asymptoteapp is low but significantly different from zero (P < 0.0001).
Table 1.
Effect of [Pi] on contractile properties of fast (psoas) and slow (soleus) muscle myofibrils and results of the hyperbolic fitting of force-[Pi] relations at different temperatures
| Psoas myofibrils | Soleus myofibrils | ||||
|---|---|---|---|---|---|
| 5°C | 15°C | 15°C | 20°C | ||
| Tension (mN mm−2) | Pi-free | 265 ± 14 (n = 36) | 356 ± 62 (n = 29) | 220 ± 30 (n = 36) | 310 ± 40 (n = 28) |
| kTR (s−1) | Pi-free | 1.9 ± 0.1 (n = 36) | 6.6 ± 1.5 (n = 29) | 2.0 ± 0.1 (n = 36) | 3.2 ± 0.2 (n = 28) |
| 5mM Pi | 6.4 ± 2.4 (n = 7) | 10.0 ± 2.1 (n = 5) | 2.1 ± 0.3 (n = 5) | 3.0 ± 0.4 (n = 5) | |
| kPi(+) (s−1) | 5 mM Pi | 18.2 ± 2.0 (n = 13) | — | 3.2 ± 0.7 (n = 6) | 11.3 ± 0.7 (n = 12) |
| Force- [Pi] curve | Kd,app (mM) | 4.15 ± 0.50 | 4.33 ± 0.36 | 4.37 ± 1.85 | 4.80 ± 1.70 |
| Asymptoteapp | 0.05 ± 0.02 | 0.07 ± 0.02 | 0.44 ± 0.06 | 0.46 ± 0.04 | |
Values of tension, kTR and kPi(+) are means ±s.e.m. obtained in psoas and soleus myofibrils. Hyperbolic fitting of experimental force-[Pi] data: Kd,app and Asymptoteapp obtained from [Pi] giving half the maximal effect and extrapolated value of relative tension for [Pi]→∞, respectively. Asymptoteapp: P < 0.0001 in psoas an soleus myofibrils at the different temperatures tested. Control Pi-free: [Pi] < 5 μM.
Figure 2. Force- [Pi] relations in fast and slow skeletal muscle at different temperature.
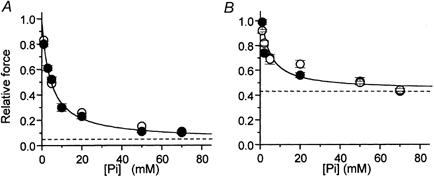
Maximal isometric force obtained in the presence of different [Pi] normalized over control force in Pi-free conditions. A, force-[Pi] relation of psoas myofibrils at 5 °C (•) and 15 °C (○). B, force-[Pi] relation of soleus myofibrils at 15 °C (•) and 20 °C (○). Continuous lines: hyperbolic fittings of force-[Pi] relations obtained at 15 °C in both muscle types; dashed lines: asymptotes of force-[Pi] relations. Results of hyperbolic fittings are reported in Table 1.
Effect of [Pi] on force in maximally activated rabbit slow skeletal myofibrils at 15 and 20 °C
The effect of [Pi] on maximal isometric force in soleus myofibrils at 15 and 20 °C was studied using the procedure described above (Fig. 1D-F). In Pi-free conditions, maximal isometric force and kTR (Table 1) were respectively 310 ± 40 mN mm−2 and 3.2 ± 0.2 s−1 (n = 28) at 20 °C and 220 ± 30 mN mm−2 and 2.0 ± 0.1 s−1 (n = 36) at 15 °C. At both temperatures, isometric force in rabbit soleus myofibrils decreased less with [Pi] than in psoas myofibrils (Fig. 2B). Moreover, the rate of force generation was not significantly affected by [Pi], in the range tested. As in psoas myofibrils, the kinetics of the drop in force induced by a jump increase in [Pi] at 20 °C (kPi(+)) was about three times faster than kTR (Table 1). As already observed by Millar & Homsher (1992), in soleus muscle the difference between kTR and kPi(+) values tended to disappear on lowering the temperature to 15 °C (Table 1). At both temperatures, kPi(-) was very close to kTR. The hyperbolic fit of the force-[Pi] relation at 15 °C gave an asymptote which was about six times that observed in psoas myofibrils (Asymptoteapp = 0.44 ± 0.06). On the other hand, the value of Kd,app estimated for slow myofibrils was very close to that obtained in psoas myofibrils at the same temperature (4.37 ± 1.85 mm). Again, in the 15-20 °C range, temperature did not affect the shape of the force-[Pi] relation (Asymptoteapp = 0.46 ± 0.04; Kd,app = 4.80 ± 1.70 mm; 20 °C).
The results of force-[Pi] experiments in both fast and slow myofibrils show the presence of a force asymptote significantly different from zero at infinite [Pi], supporting the hypothesis that force generation precedes Pi release.
Effect of [BDM] on isometric force and on force inhibition by [Pi] in maximally activated rabbit fast and slow skeletal myofibrils
If a two-step model for Pi release and force generation (Scheme 3) is correct, the Asymptoteapp of the force-[Pi] relation will be determined by the fraction of cross-bridges in force-generating states at infinite [Pi], which is set by the equilibrium constant of the force-generating step (K2, Scheme 3). In soleus muscle, because the extrapolated value for isometric force at infinite [Pi] is almost 0.5, the equilibrium constant K2 for the force-generating isomerization is about 1. BDM is thought to decrease the value of this equilibrium, probably by decreasing the forward rate (k+2) of the force-generating isomerization, with little effect on ATP binding or hydrolysis steps (pooled in Step 4 in Scheme 3; Herrmann et al. 1992; McKillop et al. 1994). If this is the case, Scheme 3 predicts that the Asymptoteapp will be reduced by the addition of BDM. Because BDM depresses force more as temperature is reduced (Fryer et al. 1988; Horiuti et al. 1988), the effect of BDM on psoas and soleus myofibrils was tested at the lowest temperature used for experiments on the Pi effect in the same preparation (5 °C and 15 °C, respectively).
As seen in Fig. 3, both fast (A) and slow (B) skeletal muscle myofibrils promptly responded to BDM application. The extent of force depression by BDM was very dose-dependent. In both myofibril types, the relations between [BDM] and relative force were fitted to hyperbolae from which Kd,app for force depression in psoas and soleus myofibrils were estimated as 3.3 ± 2.8 mm and 6.9 ± 4.5 mm. Though other determinants associated with the muscle type cannot be excluded, the large difference in the amplitude of the maximal effect of BDM in fast and slow myofibrils (100 % in psoas myofibrils at 5 °C and 40 % in soleus myofibrils at 15 °C) is expected from the strong temperature dependence of the BDM effect. In both myofibril types, the kinetics of the BDM-jumps were very close to the kinetics of force generation. This shows that BDM interaction and its force inhibition are fast.
Figure 3. Effect of BDM on maximal isometric force in rabbit psoas (5 °C) and soleus (15 °C) myofibrils.
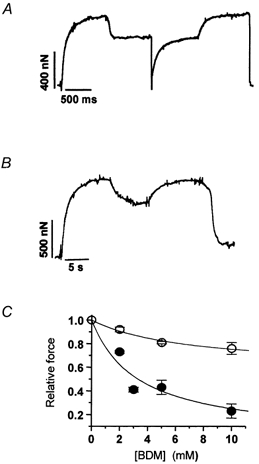
A, experimental tracing from a psoas myofibril subjected to exposure to 2 mm BDM by rapid solution change at the plateau of an isometric contraction. Relative force in the presence of 2 mm BDM: 0.71; kTR in control conditions and in the presence of 2 mm BDM: 2.3 s−1 and 1.6 s−1, respectively. Force transients following application and removal of BDM: rates of force decrease and increase were 1.9 s−1 and 1.8 s−1, respectively. B, experimental tracing from a soleus myofibril subjected to 10 mm BDM. Relative force in the presence of 10 mm BDM: 0.74; kactiv in control conditions 0.8 s−1. Force transients following application and removal of BDM: rates of force decrease and increase were 0.8 s−1 and 0.7 s−1, respectively. C, relation between [BDM] and maximal isometric force in rabbit psoas (5 °C, •) and soleus myofibrils (15 °C, ○). Hyperbolic fit of each data set (continuous lines) gave half-maximal effect of force depression in fast and slow myofibrils at [BDM] of 3.3 ± 2.8 mm and 6.9 ± 4.5 mm, respectively.
The influence of BDM on the inhibition of isometric force by Pi in maximally activated psoas and soleus myofibrils at 5 and 15 °C is shown in Fig. 4. Results were obtained with a multilpe-jump protocol performed during a single activation-relaxation cycle, using a four-channel perfusion pipette. Myofibrils (Fig. 4A and B) were first activated in control conditions (Pi-free, no BDM). After reaching a stable plateau, they were submitted first to an increase in [Pi] producing a sudden drop in force and then exposed to a solution containing both Pi and BDM (2 and 10 mm in psoas or soleus myofibrils, respectively), leading to a further decrease in force. The jumps were then sequentially reversed. In some experiments, kTR was measured in the different conditions showing that BDM depresses the rate of force generation in both muscle types (by 20 % and 14 %, in fast and slow myofibrils, respectively). Usually, only one activation-relaxation cycle was performed, as the multilpe-jump protocol induced a strong run-down of force (especially in slow myofibrils). As already shown (McKillop et al. 1994), the effect of BDM and Pi on force was additive: in psoas myofibrils subjected to multilpe-jump experiments, 1 mm Pi and 2 mm BDM applied alone decreased force to 0.76 ± 0.02 (n = 5) and to 0.74 ± 0.02 (n = 5), respectively. When applied together, force dropped to 0.47 ± 0.04. Similar results were obtained in soleus myofibrils where 50 mm Pi alone decreased the relative force to 0.51 ± 0.01 (n = 10), 10 mm BDM decreased it to 0.74 ± 0.05 (n = 11) and 50 mm Pi and 10 mm BDM together decreased it to 0.34 ± 0.02 (n = 6). In both fast and slow myofibrils, the affinity of the myofibril for Pi was increased by BDM (Fig. 4C and D). In psoas myofibrils (5 °C) 2 mm BDM decreased Kd,app to 0.77 ± 0.07 mm; in soleus myofibrils (15 °C) 10 mm BDM decreased Kd,app to 1.27 ± 0.01 mm. In soleus myofibrils, the presence of a high asymptote of the force-[Pi] relation permitted the quantification of the effect of BDM on this parameter. As shown in Fig. 4D, 10 mm BDM decreased the Asymptoteapp of the force-[Pi] relation by about 30 %, as expected from its additive inhibitory effect on isometric force. Interestingly, also under these condition, the Asymptoteapp of the force-[Pi] relation of soleus myofibrils remained significantly different from zero (0.32 ± 0.01).
Figure 4. Influence of BDM on the inhibition of isometric force by Pi in maximally activated psoas and soleus myofibrils.
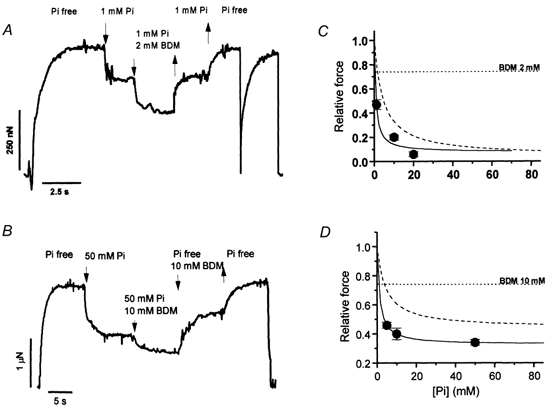
A, experimental tracing from a multiple-jump protocol (1 mm Pi, 2 mm BDM) on a psoas myofibril (5 °C). 1 mm Pi-jump: relative force = 0.75 of maximal Pi-free value; 1 mm Pi + 2 mm BDM jump: relative force = 0.49. kTR of force development or redevelopment in control conditions: 1.9 s−1 and 2.3 s−1, respectively. B, experimental tracing from a multiple-jump protocol (50 mm Pi, 10 mm BDM) on a soleus myofibril (15 °C). 50 mm Pi-jump: relative force = 0.51; 50 mm Pi + 10 mm BDM: relative force = 0.38. kTR of force development in control conditions: 1.5 s−1. C, force-[Pi] curve obtained in psoas myofibrils at 5 °C in the presence of 2 mm BDM. Continuous line: hyperbolic fitting of experimental points (Kd,app = 0.77 ± 0.07 mm; Asymptoteapp = 0.08 ± 0.07). Dashed line: hyperbolic fit of the force-[Pi] relation (no BDM) at the same temperature from Fig. 2A. Dotted line: mean effect of 2 mm BDM alone at the same temperature (relative force: 0.74 ± 0.02, n = 5). D, force-[Pi] curve obtained in soleus myofibrils at 15 °C in the presence of 10 mm BDM. Continuous line: hyperbolic fit of experimental points (Kd,app = 1.27 ± 0.01 mm; Asymptoteapp = 0.32 ± 0.01). Dashed line: hyperbolic fit of the force-[Pi] relation (no BDM) at the same temperature from Fig. 2B. Dotted line: mean effect of 10 mm BDM alone at the same temperature (0.74 ± 0.05, n = 11).
DISCUSSION
These experiments showed that in both fast and slow skeletal muscle myofibrils, force depression induced by Pi approaches an asymptotic value as [Pi]→∞ which is significantly different from zero. The results are inconsistent with a cross-bridge power stroke in which force is produced only during or subsequent to the release of Pi. The data support the hypothesis that force is produced in a cross-bridge isomerization prior to Pi release.
Comparison with previous results in skinned fibres from fast and slow muscle
There is a good agreement between the results obtained here for the force-[Pi] relation in psoas and soleus myofibrils and previous observations in skinned fibres from the same muscles (Fig. 5). In fast muscle myofibrils (Fig. 5A), the effect of Pi on isometric force was larger than previously reported in fibre preparations. This comparison is complicated by the variability of force produced in skinned fibres. This variability stems from differences in Pi contamination and Pi gradients inside fibres of variable size and ATPase activity. Interestingly, the data that are closer to myofibrillar data are those obtained with fibre preparations of reduced size (split fibres; Pate et al. 1998; •) and/or in the presence of an enzymatic Pi-scavenging system to reduce contamination in control conditions (Pate et al. 1998; Millar & Homsher, 1990; ○). As previously observed (Tesi et al. 2000), the large effect of Pi in our experiments is predicted from the inverse correlation between the amplitude of force depression by Pi and the diameter of the preparation (Stienen et al. 1990; Kentish, 1986) and from the use of ‘Pi-Mop’ systems (Pate et al. 1998). Pi contamination of controls has a strong effect on the shape of the force-[Pi] curve in the sub-millimolar [Pi] range, and on the maximal depression of force by Pi. This is especially true in psoas fibres at 15 °C, which have a very fast ATPase activity and high basal Pi contamination (500-700 μM; Dantzig et al. 1992), producing significant force inhibition (about 30 %; Pate et al. 1998, Tesi et al. 2000; see also Fig. 6B). Only when starting from essentially ‘Pi-free’ conditions and reduced diffusional barriers can the entire range of the force-[Pi] relation be resolved. Allowing for the difference in Pi contamination (i.e. fibre data in Fig. 5A scaled by about 30 %), the maximal effect of Pi observed in the fast psoas myofibrils is close to but still larger than that in skinned fibres. This comparison of myofibril and fibre force-[Pi] relations has to be taken with some caveat, as important differences from group to group in Pi gradients within skinned preparations can be present under the same experimental conditions.
Figure 5. Depression of isometric force by [Pi] in myofibrils and skinned fibres from fast and slow muscle.
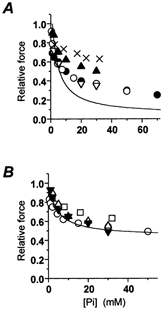
A, force-[Pi] relation obtained in psoas myofibrils at 15 °C (continuous line; same relation as in Fig. 2A) and data previously obtained in skinned fibres from the same muscle at 15 °C. •, Pate et al. 1998; ○, Millar & Homsher, 1990; ▿, Wahr et al. 1997; ▴, Potma et al. 1995; ×, Zhao et al. 1996. B, force-[Pi] relation obtained in soleus myofibrils at 20 °C (continuous line; same relation as in Fig. 2B) and data previously obtained in skinned fibres from the same muscle at 15-20 °C. ▾, Potma et al. (1995); ○, Millar & Homsher (1992); ▵, Wahr et al. (1997); □, Wang & Kawai (1997).
Figure 6. Simulations with Scheme 3 of force-[Pi] curves and underlying distributions of cross-bridges in force-generating states in fast and slow myofibrils.
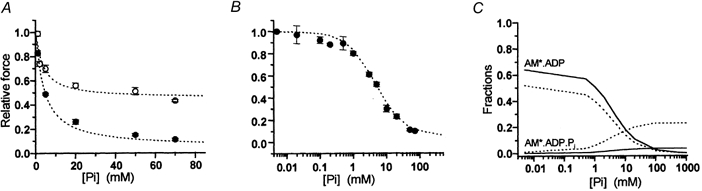
A, simulations (lines) of experimental force-[Pi] data (points) obtained in psoas (•) and soleus (○) myofibrils at 15 °C. B, simulation of experimental force-log[Pi] data obtained in psoas myofibrils at 5 °C. C, fractions of cross-bridges in the two states AM*.ADP and AM*.ADP.Pi of Scheme 3 associated with force generation as a function of [Pi]. Continuous line: psoas myofibrils; dotted line: soleus.
In soleus myofibrils (Fig. 5B), the correspondence between our data and previous reports in larger preparation is very good. This is probably because in slow muscle ATPase at room temperature is 10 times lower than in fast fibres (Potma et al. 1995, He et al. 1998), reducing the influence of Pi gradients during contraction and the resultant scatter of data.
The depression of force by Pi we observe in myofibrils is thus reliable and reveals a major difference in the maximal amplitude of the depressant effect of Pi in psoas and soleus muscles. This effect might be caused by the different MHC (myosin heavy chain) isoform expressed in the two muscle types. SDS gel electrophoresis of myofibrils isolated from the fast and slow muscles (results not shown) showed that while psoas myofibrils only expressed MHC-II isoforms (mostly MHC-2X), soleus myofibrils only expressed MHC-I isoform (MHCβ-slow). This is consistent with recent estimates of myosin isoform composition obtained in the same muscles (Tikunov et al. 2001). Myosin heavy chain isoform composition could modulate the kinetic and steady-state properties of cross-bridge action (Bottinelli & Reggiani, 2000) and the responsiveness to Pi.
Simulations of force-[Pi] relation of fast and slow skeletal muscle
The force-[Pi] relation obtained in both fast and slow myofibril types (Fig. 2A and B) could be equally well fitted by exponential or hyperbolic relations. The choice of the fitting function is determined by analytical expression of the mechanism. An exponential relation (i.e. force declining linearly with log[Pi]) is expected if force generation is directly coupled to a strain-dependent Pi release step, as in the Pate & Cooke model (1989b). A hyperbolic relation (i.e. S-shaped force decline on a log plot) is expected if the force generation event occurs in a step immediately preceding Pi release (Scheme 3). In the first case, there is only one force-generating state (AM*.ADP) while in the second both the isomerized AM*.ADP.Pi and AM*.ADP states sustain force (in both cases the fraction of the cross-bridges in AM rigor-like state is very low). Compelling evidence for a two-step mechanism for Pi release and force generation came from the saturation kinetics exhibited by the [Pi] dependence of the rate of: (i) force decline induced by a sudden increase in [Pi] by photorelease of caged-Pi (Dantzig et al. 1992); (ii) force increase caused by a sudden decrease in pressure (Fortune et al. 1991); (iii) the 2πb component of force transients caused by sinusoidal length changes (Kawai & Halvorson, 1991). Above, we assume a two-step model for Pi release and force generation (Scheme 2) and use the steady-state modulation of isometric force by [Pi] to test the model and the rates of Pi transients and kTR (Table 1), obtained in fast and slow myofibril and fibre studies, to isolate specific rate constants.
Scheme 2.

Results of the hyperbolic fitting of force-[Pi] relations in myofibrils (Table 1) showed that the affinity of Pi for binding to the AM*.ADP state is similar in fast and slow muscle (Kd,app about 4.5 mm) and independent of temperature. Kd,app estimates in fast and slow myofibrils are similar to those obtained from skinned psoas and soleus muscle fibres (see Wilson et al. 1995; Wahr et al. 1997; Wang & Kawai, 1997) and to 18O estimations of Pi incorporation during contraction (Bowater & Sleep, 1988). On the other hand, the apparent asymptote of the force-[Pi] relation (i.e. the amount of residual force at infinite [Pi]) was insensitive to temperature but very different in the two muscle types: i.e. it was seven-fold greater in soleus than in psoas myofibrils (0.44 and 0.07, respectively; Fig. 2; Table 1). The existence of a force asymptote significantly different from zero in the force-[Pi] relation is not consistent with coincident force generation and Pi release (eqn (1)). This is because at infinite [Pi] all the cross-bridges would exist in non-force-generating states and force would be zero. The two-step mechanism assumed in Scheme 3 permits the existence of a significant fraction of cross-bridges in the force-generating AM*.ADP.Pi state also at infinite [Pi]. The size of this fraction is given by the Asymptoteapp and will depend mainly on the value of the equilibrium constant of the force isomerization step (K2). When Pi-force curves experimentally determined in fast and slow myofibrils are simulated by the simplified steady-state treatment of Scheme 3 (eqns (3–5)), the equilibrium constants for the two steps associated with force generation and Pi release (K2, K3) can be estimated from the parameters of hyperbolic fitting, with an additional estimate for K1 (the calcium-controlled step) derived from kTR measurements (Table 2). Figure 6A and B shows the good agreement between experimental force-[Pi] curves of fast and slow myofibrils and the results of the simulation of our data with Scheme 3.
Table 2.
Equilibrium and individual rate constants derived from the simulation of force-[Pi] curve in fast and slow myofibrils by the model illustrated in Scheme 3
| Psoas | Soleus | ||
|---|---|---|---|
| 5°C | 15°C | 15°C | |
| K2 | 0.05 | 0.09 | 0.92 |
| K3 (mM) | 110 | 64 | 10 |
| k+1 | 5 | 20 | 6 |
| k−1 | 1 | 5 | 1 |
| k+2 | 8 | 20 | 3 |
| k-2 | 180 | 250 | 3.3 |
| k+3 | 500 | 1000 | 40 |
| k-3 (M−1 s−1) | 0.5 ± 104 | 1.5 ± 104 | 0.4 ± 104 |
| k+4 | 1 | 3 | 1 |
Equilibrium constants for Steps 2 and 3 of Scheme 3 (abbreviated as K2, K3) as derived from hyperbolic fitting of experimental force-[Pi] curves of fast and slow myofibrils at the different temperatures (see Methods, eqns (4–5)). Forward and backward rate constants for all the transitions assumed by the cross-bridge model of Scheme 3 (abbreviated as k+x and k-x and expressed s−1, when not otherwise stated) were assigned based on kTR and kPi(+) measurements in myofibrils (this study and Tesi et al. 2000) or in skinned fibres from psoas (Millar & Homsher, 1990; Dantzig et al. 1992; Zhao & Kawai, 1994; Regnier et al. 1995) and soleus muscle (Millar & Homsher, 1992; Wahr et al. 1997; Wang & Kawai, 1997), in similar experimental conditions. Simulation of soleus myofibrils at 20°C not shown.
On the basis of these estimations of the equilibrium constants and of kPi and kTR measurements in myofibrils (this study; Tesi et al. 2000) and in skinned fibres in similar conditions, rates for individual cross-bridge transitions were readily found (Table 2), yielding excellent agreement with estimations of the associated Pi release rates obtained in skinned fibres from fast and slow muscle by different approaches (Millar & Homsher, 1990, 1992; Fortune et al. 1991; Kawai & Halvorson, 1991; Dantzig et al. 1992; Zhao & Kawai, 1994). The set of rates we used for the different steps accounts also for the observation of kTR not being accelerated by an increased release of Pi in slow muscles (Millar & Homsher, 1992) as ADP release from AM*.ADP, which limits the cross-bridge cycle (and is the main determinant of k+4 in Scheme 3), has about the same rate as the forward rate of the force-generating isomerization. In this case, simulations of kTR with Scheme 3 show little dependence on the [Pi] and may even show a slight slowing of kTR.
Within the model we used, the observed difference in Asymptoteapp of the force-[Pi] relation of psoas and soleus myofibrils (15 °C) is matched by a ten times increase (from 0.09 to 0.92) of the equilibrium constant for the force-generating isomerization K2, and is then associated with a different shift of cross-bridge fractions in the two force-generating states at different [Pi]. As shown in Fig. 6C, in both muscle types, the population of ‘strong’ force-generating AM*.ADP cross-bridges, responsible for 98-100 % of the total developed force in Pi-free conditions, decreases almost to zero as [Pi] approaches an infinite value. This decrease is paralleled by an increase in the fraction of the force-generating AM*.ADP.Pi state, which in soleus muscle at high [Pi] is important and much larger than that in psoas muscle. A two-step model for Pi release and force generation predicts a deviation from linearity of the force-log[Pi] curve in the range of high (more than 50 mm) and low (less than 200 μM) [Pi]. While the first condition is problematic to study because of the ionic strength constraint on the polymerization state of contractile proteins, the use of myofibrils (in association with the Pi-Mop system) made possible the resolution of the S-shaped force-log[Pi] curve in the low [Pi] range. Figure 6B shows that the simulation with Scheme 3 of the force-log[Pi] relation of psoas myofibrils at 5 °C was excellent. An S-shaped force-log[Pi] relation was anticipated by previous studies in fast and slow muscle (Millar & Homsher, 1992; Araujo & Walker, 1996) but uncertainty about the [Pi] within the fibre lattice precluded rigorous conclusions. In the only other study of the steady-state effect of [Pi] on force which approaches the resolution of myofibril studies, Pate & Cooke (1998) obtained a force-log[Pi] curve in psoas fibres that was very close to what we observed in myofibrils. Although they favoured a one-step model for Pi release and force generation, the simulation of their binding isotherm led them to suggest that force could be produced by more than one AM.ADP state and/or by states located before Pi release, sustaining force in the quaternary form AM*.ADP.Pi. A sigmoidal force-log[Pi] relation is also expected if AM*ADP.Pi does not contribute to force but more than one AM*.ADP force-exerting state is assumed. We excluded this possibility because the analytical treatment of cross-bridge pathway locating force-generating transitions after Pi release or in the Pi release step itself invariantly predicts a zero asymptote of force at infinite [Pi] (see eqn (1)).
In summary, while we cannot rule out more complicated mechanism, Scheme 3 is the simplest cross-bridge pathway accounting for the observed force-[Pi] relations in myofibrils.
What is the nature of the working stroke and how is the free energy of Pi release coupled to it? Dantzig et al. (1992) speculated in a discussion on this point that force is produced by an isomerization of the complex of actomyosin and ATPase products, but that Pi release stabilized the isomerization. Recently, Geeves & Holmes (1999) pointed out that structural studies indicate that myosin exists as a ‘closed’ (with ATP or ADP.Pi bound in the nucleotide and phosphate pocket) and an ‘open’ molecule in which Pi does not bind and is free to escape as the molecule undergoes the transition between closed and open state. They also described a three-step binding process of actin to myosin in which, after collision (electrostatic interactions) and isomerization (hydrophobic surfaces interaction, possibly corresponding to weak-strong transition in Scheme 3), molecular reorganization of the actomyosin complex and tight binding are triggered by switch-2 movement which opens the ‘back door’ of the Pi tube, permitting Pi release. According to Geeves & Holmes, the transition has an equilibrium constant < 1 prior to Pi release and >> 1 after Pi release. This step, fast in solution, is probably very strain-sensitive so that in the isometric case, the complete opening of the Pi pocket is prevented by the lack of motion and the state is trapped between fully open and fully closed, i.e. between a state with a finite Kd for Pi (which can enter and exit freely the pocket) or a state in which Pi is non-exchangeable (as strain closes the pocket again with Pi in it). Thus the force-generating state is one in which the cross-bridge oscillates between the open and closed state. Note that the equilibrium constant for Step 2 that we derived in our model for fast muscle is 0.09 and 0.05 (similar to the value of 0.2 deduced from caged-Pi studies; Dantzig et al. 1992). The energy source for this transition is probably thermal and the release of Pi, whose equilibrium is far to the right, is what actually couples and pulls the reaction to the right.
Effect of BDM and temperature on the force-[Pi] relation
As shown in Fig. 2 and Table 1, temperature had no significant effect on estimations of Kd,app and Asymptoteapp of the force-[Pi] curves in psoas and soleus myofibrils. This result agrees with previous studies reporting minor effects of temperature on the amplitude of force inhibition by [Pi] in both fast (Ranatunga, 1999; Chinn et al. 2000; Coupland et al. 2001) and slow (Millar & Homsher, 1992; 15-20 °C range) muscle fibres.
BDM is a non-competitive inhibitor of actomyosin ATPase (Herrmann et al. 1992), which implies that BDM exerts its effects by binding to sites outside the ADP and Pi binding sites. The effect of BDM on the force-[Pi] curve of myofibrils (Fig. 3) is consistent with previous skinned fibre studies, reporting a temperature-dependent, non-competitive and completely reversible inhibition by millimolar concentrations of BDM of force production in both fast (McKillop et al. 1994; Zhao & Kawai, 1994) and slow (Fryer et al. 1988) muscle types. Effects of BDM were additive to those of Pi (McKillop et al. 1994). In both fast and slow muscles, force-[Pi] curves in the presence of BDM exhibited the same hyperbolic dependence on [Pi] as controls (Fig. 4), but both Asymptoteapp and Kd,app were reduced. In soleus myofibrils at 15 °C, the clear resolution of the Asymptoteapp of the force-[Pi] curve in the presence of BDM (10 mm) made it possible to simulate the effect of BDM on the equilibrium constant for Pi release and force generation steps, assuming the two-step model of Scheme 3 (eqn (3)). Both K2 and K3 were found to be significantly reduced (K2 = 0.55; K3 = 4 mm). The reduction of K2 is in agreement with solution (Herrmann et al. 1992) and fibre studies (McKillop et al. 1994; Zhao & Kawai, 1994; Regnier et al. 1995), which suggested that the inhibitory effect of BDM is produced by a concentration-dependent reduction of the equilibrium constant of the force-generating isomerization, most likely by a decrease of k+2. In soleus myofibrils, a good fit of the effect of BDM on force was obtained by decreasing k+2 from 3 to 1.8 s−1 and leaving k-2 unchanged. Assuming an instantaneous decrease of the forward rate of the force-generating isomerization, the model predicts force transients of rate close to kTR, as observed (Fig. 4). Reductions in the value of k+2 as opposed to an increase of k-2 were chosen as only by this it is possible to account for the observed reduction of force, kTR and kPi in the presence of BDM (Regnier et al. 1995). The reduction of K3 (related to the observed decrease of Kd,app) in soleus myofibrils in the presence of BDM can be explained by an increase in the value of the second-order rate constant for Pi binding to the AM*.ADP complex (k-3) from 0.4 × 104 to 1 × 104m−1 s−1. The possibility of a minor effect of BDM on the Pi release step was also suggested by McKillop et al. (1994) in their simulation of pressure-induced tension transients in the presence of BDM and Pi.
Acknowledgments
We are grateful to Dr Earl Homsher (UCLA) for reading and making valuable suggestions on the manuscript and for help with model calculations. We also thank Dr Neil Millar for the gift of the software kfit/ksim, Dr M. A. Pellegrino for SDS gel electrophoresis analysis of myofibrils used, Dr Jacopo Chini for enzyme immobilization and help with the Pi-scavenging protocol, and Mr Alessandro Aiazzi, Mr Mario Dolfi and Mr Adrio Vannucchi for technical assistance. This work was supported by Università degli studi di Firenze (60 %). The financial support of the EU is also acknowledged (HPRN-CT-2000-00091).
REFERENCES
- Araujo A, Walker JW. Phosphate release and force generation in cardiac myocytes investigated with caged phosphate and caged calcium. Biophysical Journal. 1996;70:2316–2326. doi: 10.1016/S0006-3495(96)79797-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baginski ES, Foa PP, Zak B. Determination of phosphate: study of labile organic phosphate interference. Clinica Chimica Acta. 1967;15:155–158. [Google Scholar]
- Barman T, Brune M, Lionne C, Piroddi N, Poggesi C, Stehle R, Tesi C, Travers F, Webb M. ATPase and shortening rates in frog fast skeletal myofibrils by time-resolved measurements of protein-bound and free Pi. Biophysical Journal. 1998;74:3120–3130. doi: 10.1016/S0006-3495(98)78018-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartoo ML, Popov VI, Fearn LA, Pollack GH. Active tension generation in isolated skeletal myofibrils. Journal of Muscle Research and Cell Motility. 1993;14:498–510. doi: 10.1007/BF00297212. [DOI] [PubMed] [Google Scholar]
- Bottinelli R, Reggiani C. Human skeletal muscle fibres: molecular and functional diversity. Progress in Biophysics and Molecular Biology. 2000;73:195–262. doi: 10.1016/s0079-6107(00)00006-7. [DOI] [PubMed] [Google Scholar]
- Bowater R, Sleep J. Demembranated muscle fibres catalyse a more rapid exchange between phosphate and adenosine triphosphate than actomyosin subfragment 1. Biochemistry. 1988;27:5314–5323. doi: 10.1021/bi00414a055. [DOI] [PubMed] [Google Scholar]
- Brandt PW, Colomo F, Piroddi N, Poggesi C, Tesi C. Force regulation by Ca2+ in skinned cardiac myocytes of frog. Biophysical Journal. 1998;74:1994–2004. doi: 10.1016/S0006-3495(98)77906-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brandt PW, Cox RN, Kawai M, Robinson T. Effect of cross-bridge kinetics on apparent Ca2+ sensitivity. Journal of General Physiology. 1982;79:997–1016. doi: 10.1085/jgp.79.6.997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brenner B. Effect of Ca2+ on cross-bridge turnover kinetics in skinned single rabbit psoas fibres: implications for regulation of muscle contraction. Proceedings of the National Academy of Sciences of the USA. 1988;83:3265–3269. doi: 10.1073/pnas.85.9.3265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brenner B. Muscle mechanics and biochemical kinetics. In: Squire JM, editor. Molecular Mechanism in Muscular Contraction. London: McMillan Press; 1990. pp. 77–149. [Google Scholar]
- Brune M, Hunter JL, Corrie JET, Webb MR. Direct, real time measurements of rapid inorganic phosphate release using a novel fluorescent probe and its application to actomyosin subfragment 1 ATPase. Biochemistry. 1994;33:8262–8271. doi: 10.1021/bi00193a013. [DOI] [PubMed] [Google Scholar]
- Chinn MK, Myburgh KH, Pham T, Franks-Skiba K, Cooke R. The effect of polyethylene glycol on the mechanics and ATPase activity of active muscle fibres. Biophysical Journal. 2000;78:927–939. doi: 10.1016/S0006-3495(00)76650-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colomo F, Nencini S, Piroddi N, Poggesi C, Tesi C. Calcium dependence of the apparent rate of force generation in single myofibrils from striated muscle activated by rapid solution changes. Advances in Experimental Medical Biology. 1998;453:373–382. doi: 10.1007/978-1-4684-6039-1_42. [DOI] [PubMed] [Google Scholar]
- Colomo F, Piroddi N, Poggesi C, Te Kronnie G, Tesi C. Active and passive forces of isolated myofibrils from cardiac and fast skeletal muscle of the frog. Journal of Physiology. 1997;500:535–548. doi: 10.1113/jphysiol.1997.sp022039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooke R. Actomyosin interactions in striated muscle. Physiological Review. 1997;77:671–697. doi: 10.1152/physrev.1997.77.3.671. [DOI] [PubMed] [Google Scholar]
- Cooke R, Pate E. The effects of ADP and phosphate on the contraction of muscle fibres. Biophysical Journal. 1985;48:789–798. doi: 10.1016/S0006-3495(85)83837-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coupland ME, Puchert E, Ranatunga KW. Temperature dependence of active tension in mammalian (rabbit psoas) muscle fibres: effect of inorganic phosphate. Journal of Physiology. 2001;536:879–891. doi: 10.1111/j.1469-7793.2001.00879.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dantzig JA, Goldman YE, Millar NC, Lacktis W, Homsher E. Reversal of the cross-bridge force-generating transition by photogeneration of phosphate in rabbit psoas muscle fibres. Journal of Physiology. 1992;451:247–278. doi: 10.1113/jphysiol.1992.sp019163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eisenberg E, Hill TL, Chen Y. Cross-bridge model of muscle contraction. Biophysical Journal. 1980;29:195–227. doi: 10.1016/S0006-3495(80)85126-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fortune NS, GeeveS MA, Ranatunga KW. Tension responses to rapid pressure release in glycerinated rabbit muscle fibres. Proceedings of the National Academy of Sciences of the USA. 1991;88:7323–7327. doi: 10.1073/pnas.88.16.7323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fortune NS, Geeves MA, Ranatunga KW. Contractile activation and force generation in skinned rabbit muscle fibres: effect of hydrostatic pressure. Journal of Physiology. 1994;474:283–290. doi: 10.1113/jphysiol.1994.sp020021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman AL, Goldman YE. Force and force transients in bundles of 1–3 myofibrils from rabbit psoas muscle. Biophysical Journal. 1996;71:2774–2785. doi: 10.1016/S0006-3495(96)79470-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fryer MW, Neering IR, Stephenson DG. Effect of 2,3-butanedione monoxime on the contractile activation properties of fast- and slow-twitch rat muscle fibres. Journal of Physiology. 1988;407:53–75. doi: 10.1113/jphysiol.1988.sp017403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geeves MA, Holmes KC. Structural mechanism of muscle contraction. Annual Review of Biochemistry. 1999;68:687–728. doi: 10.1146/annurev.biochem.68.1.687. [DOI] [PubMed] [Google Scholar]
- Goldman YE. Kinetics of the actomyosin ATPase in muscle fibres. Annual Review of Physiology. 1987;49:637–654. doi: 10.1146/annurev.ph.49.030187.003225. [DOI] [PubMed] [Google Scholar]
- Goldman YE, Hibberd M, Trentham DR. Relaxation of rabbit psoas muscle fibres from rigor by photochemical generation of adenosine-5′-triphosphate. Journal of Physiology. 1984;35:577–604. doi: 10.1113/jphysiol.1984.sp015394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon AM, Homsher E, Regnier M. Regulation of contraction in striated muscle. Physiologica Review. 2000;80:853–924. doi: 10.1152/physrev.2000.80.2.853. [DOI] [PubMed] [Google Scholar]
- He Z, Stienen GJ, Barends JP, Ferenczi MA. Rate of phosphate release after photoliberation of adenosine 5′-triphosphate in slow and fast skeletal muscle fibres. Biophysical Journal. 1998;75:2389–2401. doi: 10.1016/s0006-3495(98)77683-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrmann C, Wray J, Travers F, Barman T. Effect of 2,3-butanedione monoxime on myosin and myofibrillar ATPases. An example of uncompetitive inhibitor. Biochemistry. 1992;31:12227–12232. doi: 10.1021/bi00163a036. [DOI] [PubMed] [Google Scholar]
- Hibberd MG, Dantzig JA, Trentham DR, Goldman YE. Phosphate release and force generation in skeletal muscle fibres. Science. 1985;228:1317–1319. doi: 10.1126/science.3159090. [DOI] [PubMed] [Google Scholar]
- Horiuti K, Higuchi H, Umazume Y, Konishi M, Okazaki O, Kurihara S. Mechanism of action of 2,3-butanedione 2-monoxime on contraction of frog skeletal muscle fibres. Journal of Muscle Research and Cell Motility. 1988;9:156–164. doi: 10.1007/BF01773737. [DOI] [PubMed] [Google Scholar]
- Houdusse A, Sweeney HL. Myosin motors: missing structures and hidden springs. Current Opinion in Structural Biology. 2001;11:182–194. doi: 10.1016/s0959-440x(00)00188-3. [DOI] [PubMed] [Google Scholar]
- Kawai M, Gúth K, Winnikes K, Haist C, Rúegg JC. The effect of inorganic phosphate on the ATP hydrolysis rate and the tension transients in chemically skinned rabbit psoas fibres. Pflügers Archiv. 1987;408:1–9. doi: 10.1007/BF00581833. [DOI] [PubMed] [Google Scholar]
- Kawai M, Halvorson HR. Two step mechanism of phosphate release and the mechanism of force generation in chemically skinned fibres of rabbit psoas muscle. Biophysical Journal. 1991;59:329–342. doi: 10.1016/S0006-3495(91)82227-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kentish JC. The effects of inorganic phosphate and creatine phosphate on force production in skinned muscles from rat ventricle. Journal of Physiology. 1986;37:585–604. doi: 10.1113/jphysiol.1986.sp015952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKillop DFA, Fortune NS, Ranatunga KW, Geeves MA. The influence of 2,3-butanedione 2-monoxime (BDM) on the interaction between actin and myosin in solution and in skinned muscle fibres. Journal of Muscle Research and Cell Motility. 1994;15:309–318. doi: 10.1007/BF00123483. [DOI] [PubMed] [Google Scholar]
- Millar NC, Homsher E. The effect of phosphate and calcium on force generation in glycerinated rabbit skeletal muscle fibres. Journal of Biological Chemistry. 1990;265:20 234–20 240. [PubMed] [Google Scholar]
- Millar NC, Homsher E. Kinetics of force generation and phosphate release in skinned rabbit soleus muscle fibres. American Journal of Physiology. 1992;262:C1239–1245. doi: 10.1152/ajpcell.1992.262.5.C1239. [DOI] [PubMed] [Google Scholar]
- Morris C, Homsher E. The use of caged compounds. In: Sugi H, editor. Current Methods in Muscle Physiology: Advantages, Problems, and Limitations. Oxford: Oxford University Press; 1998. pp. 71–89. [Google Scholar]
- Pate E, Cooke R. Addition of phosphate to active muscle fibres probes actomyosin states within the powerstroke. Pflügers Archiv. 1989a;414:73–81. doi: 10.1007/BF00585629. [DOI] [PubMed] [Google Scholar]
- Pate E, Cooke R. A model of cross-bridge action: the effects of ATP, ADP and Pi. Journal of Muscle Research and Cell Motility. 1989b;10:181–196. doi: 10.1007/BF01739809. [DOI] [PubMed] [Google Scholar]
- Pate E, Franks-Skiba K, Cooke R. Depletion of phosphate in active muscle fibres probes actomyosin states within the powerstroke. Biophysical Journal. 1998;74:369–380. doi: 10.1016/S0006-3495(98)77794-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piroddi N, Colomo F, Poggesi C, Tesi C. Force depression by inorganic phosphate in single myofibrils from fast and slow striated muscle. Biophysical Journal. 2001;80:510a. doi: 10.1016/S0006-3495(00)76845-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Potma EJ, Van Graas IA, Stienen GJ. Influence of inorganic phosphate and pH on ATP utilisation in fast and slow skeletal muscle fibres. Biophysical Journal. 1995;69:2580–2589. doi: 10.1016/S0006-3495(95)80129-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranatunga KW. Effects of inorganic phosphate on endothermic force generation in muscle. Proceeding of the Royal Society of London B. 1999;266:1381–1385. doi: 10.1098/rspb.1999.0791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Regnier M, Morris C, Homsher E. Regulation of cross-bridge transition from a weakly to strongly bound state in skinned rabbit muscle fibres. American Journal of Physiology. 1995;38:C1532–1539. doi: 10.1152/ajpcell.1995.269.6.C1532. [DOI] [PubMed] [Google Scholar]
- Spudich JA. The myosin swinging cross-bridge model. Nature Reviews Molecular Cell Biology. 2001;2:387–392. doi: 10.1038/35073086. [DOI] [PubMed] [Google Scholar]
- Stienen GJM, Roosemalen MCM, Wilson MGA, Elzinga G. Depression of force by phosphate in skinned muscle fibres of the frog. American Journal of Physiology. 1990;259:C349–357. doi: 10.1152/ajpcell.1990.259.2.C349. [DOI] [PubMed] [Google Scholar]
- Tesi C, Colomo F, Nencini S, Piroddi N, Poggesi C. Modulation by substrate concentration of maximal shortening velocity and isometric force in single myofibrils from frog and rabbit fast skeletal muscle. Journal of Physiology. 1999;516:847–853. doi: 10.1111/j.1469-7793.1999.0847u.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tesi C, Colomo F, Nencini S, Piroddi N, Poggesi C. The effect of inorganic phosphate on force generation in single myofibrils from rabbit skeletal muscle. Biophysical Journal. 2000;78:3081–3092. doi: 10.1016/S0006-3495(00)76845-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tikunov BA, Sweeney HL, Rome LC. Quantitative electrophoretic analysis of myosin heavy chains in single muscle fibers. Journal of Applied Physiology. 2001;90:1927–1935. doi: 10.1152/jappl.2001.90.5.1927. [DOI] [PubMed] [Google Scholar]
- Wahr PA, Cantor HC, Metzger JM. Nucleotide-dependent contractile properties of Ca2+-activated fast and slow skeletal muscle fibres. Biophysical Journal. 1997;72:822–834. doi: 10.1016/s0006-3495(97)78716-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker JW, Lu Z, Moss RL. Effects of Ca2+ on the kinetics of phosphate release in skeletal muscle. Journal of Biological Chemistry. 1992;267:2459–2466. [PubMed] [Google Scholar]
- Wang G, Kawai M. Force generation and phosphate release steps in skinned rabbit soleus slow-twitch muscle fibres. Biophysical Journal. 1997;73:878–894. doi: 10.1016/S0006-3495(97)78121-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson GJ, Shull SE, Cooke R. Inhibition of muscle force by vanadate. Biophysical Journal. 1995;68:216–226. doi: 10.1016/S0006-3495(95)80177-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y, Gangadhara Swamy PM, Humphries KA, Kawai M. The effect of partial extraction of troponin C on the elementary steps of the cross-bridge cycle in rabbit psoas muscle fibres. Biophysical Journal. 1996;71:2759–2773. doi: 10.1016/S0006-3495(96)79469-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y, Kawai M. BDM affects nucleotide binding and force generation steps of the cross-bridge cycle in rabbit psoas muscle fibres. American Journal of Physiology. 1994;266:C437–447. doi: 10.1152/ajpcell.1994.266.2.C437. [DOI] [PubMed] [Google Scholar]


