On the reaction mechanism of l-lactate oxidase: Quantitative structure-activity analysis of the reaction with para-substituted l-mandelates

Abstract

The rate constants for reduction of the flavoenzyme, l-lactate oxidase, and a mutant (in which alanine 95 is replaced by glycine), by a series of para-substituted mandelates, in both the 2-¹H- and 2-²H- forms, have been measured by rapid reaction spectrophotometry. In all cases, significant isotope effects (¹H/²H = 3–7) on the rate constants of flavin reduction were found, indicating that flavin reduction is a direct measure of α-C-H bond breakage. The rate constants show only a small influence of the electronic characteristics of the substituents, but show a good correlation when combined with some substituent volume parameters. A surprisingly good correlation is found with the molecular mass of the substrate. The results are compatible with any mechanism in which there is little development of charge in the transition state. This could be a transfer of hydride to the flavin N(5) position or a synchronous mechanism in which the α-C-H is formally abstracted as a H⁺ while the resulting charge is simultaneously neutralized by another event.

l-Lactate oxidase is a newly studied member of the family of FMN-containing enzymes that catalyze the oxidation of α-hydroxyacids, comprising glycolate oxidase (EC 1.1.3.1), l-lactate oxidase, l-lactate monooxygenase (EC 1.13.12.4), flavocytochrome b₂ (EC 1.1.2.3), long-chain α-hydroxyacid oxidase (EC 1.1.3.15), and l-mandelate dehydrogenase. A considerable amount of mechanistic work has been carried out with l-lactate monooxygenase and with flavocytochrome b₂ (for reviews, see refs. 1 and 2), which has been interpreted as supporting a carbanion mechanism, in which the substrate α-proton is abstracted by an active site base and the electrons from the resulting substrate carbanion are transferred to the flavin. The crystal structures of two of the family members, glycolate oxidase (3) and flavocytochrome b₂ (4), have been solved and show an arrangement of conserved protein residues surrounding the FMN prosthetic group and substrate that are consistent with such a carbanion mechanism. In these structures, the substrate is positioned on the si-face of the flavin with the carboxylate in ionic interaction with arginine residues and stabilized by H-bond interaction with a tyrosine residue (5). A conserved histidine residue is located so that the α-carbon of the substrate would be positioned between the flavin N(5) and the histidine N1. The histidine residue therefore has been envisaged as the active site base responsible for abstracting the proton from the α-position of the substrate, with concomitant attack of the highly nucleophilic carbanion on flavin N(5).

While the crystal structures of only two of the family members are available so far, the amino acid sequences of all the enzymes are known: glycolate oxidase (6, 7), flavocytochrome b₂ (8), lactate monooxygenase (9), lactate oxidase (10), long chain α-hydroxyacid oxidase (11), and mandelate dehydrogenase (12, 13). All enzymes of the group show considerable homology, and all have the strictly conserved set of active site residues described above.

It is beyond the scope of this paper to describe in detail the experimental evidence in support of the “carbanion” mechanism, but much of the same type of evidence had suggested that the reaction mechanism of d-amino acid oxidase was similar to that of the α-hydroxyacid-oxidizing enzymes, consistent with the similarity in chemical properties of the substrates and the type of reaction catalyzed. However, the recent x-ray structural determination of d-amino acid oxidase was inconsistent with removal of hydrogen from the α-position of the substrate as a proton, since there was no protein residue in the vicinity of the flavin to act as a base. The structure of the active site suggested that in this case there was little alternative to direct hydride transfer from substrate in the reduction of the enzyme flavin (14). This conclusion has been corroborated in recent work with d-amino acid oxidase from the yeast Trigonopsis variabilis involving reaction of the enzyme flavin with a series of substituted d-phenylglycine substrates (15).

While the crystal structures of glycolate oxidase and flavocytochrome b₂ are consistent with the operation of a carbanion mechanism, the recent results with d-amino acid oxidases caused us to seek more evidence with enzymes of the α-hydroxyacid oxidation family that would help to discriminate between a hydride transfer mechanism and one involving abstraction of the α-proton by an active site base and subsequent reduction of the flavin from the substrate carbanion. An attractive approach would be to examine the effect of para-substituents with l-mandelate substrates, since the slope of a linear free energy relationship between enzyme activity and the electronic characteristics of the substituents would be expected to be opposite for the two mechanisms. Such a linear free energy correlation study has been reported with the l-mandelate dehydrogenase of Rhodotorula graminis, employing a series of m- and p- substituted mandelates, and interpreted in support of a carbanion mechanism (16). In this study, however, the reaction constant, ρ, was small in value (0.36 ± 0.07), and the experimental parameter considered, k_cat, is not neccesarily a measurement of the breakage of the C-H bond of the substrate. An attempt to measure directly the reduction of the flavin in l-lactate monooxygenase was made impractical because of the strong inhibition of this enzyme by d-α-hydroxyacids, necessitating the use of enantiomerically pure l-mandelates. However, our recent work with the mechanistically related l-lactate oxidase from Aerococcus viridans (10) showed that this enzyme was not inhibited by the d-forms of substrates, permitting the use of racemic substrates for mechanistic studies. In this paper we have studied the reduction of l-lactate oxidase and an active site mutant, A95G, which has enhanced activity with bulky substrates (17), with a number of p-substituted mandelates, both as the α-¹H- and α-²H-forms.

MATERIALS AND METHODS

Enzymes.

Wild-type lactate oxidase from A. viridans was a gift from Hideo Misaki (Asahi Chemical Industries, Tokyo), and crude preparations of A95G lactate oxidase were from Toshio Kokubo (CIBA–Geigy). Further purification of the mutant enzyme was based on the method described previously (17). Enzyme concentration was estimated using an ɛ₄₅₇ = 11.0 × 10³ M⁻¹ cm⁻¹ (10).

Substituted Mandelic Acids.

Mandelic acid was from Aldrich; (d,l)-α-²H-mandelic acid (mp 116°) was prepared by exchange in ²H₂O (18); (d,l)-p-OH-mandelic acid was from Fluka; (d,l)-p-OCH₃-mandelic acid, synthesis, (l)-p-OCH₃-mandelic acid (mp 104°, [α]_D = +160°, resolution with S-(−)-1-phenylethylamine in ethanol in analogy to ref. 19); (d,l)-p-CH₃-mandelic acid, synthesis (20), (l)-p-CH₃-mandelic acid (mp 134°, [α]_D = +152°, resolution with S-(−)-1-phenylethylamine); (d,l)-p-F-mandelic acid, synthesis, (20), (l)-p-F-mandelic acid (mp 153–156°, [α]_D = +133°, resolution with S-(−)-1-phenylethylamine); (d,l)-p-Cl-mandelic acid was from Janssen; (l)-p-Cl-mandelic acid [mp 121°, [α]_D = +136°; resolution with S-(−)-1-phenylethylamine (19)]; (d,l)-p-CF₃-mandelic acid, synthesis (21), (l)-p-CF₃-mandelic acid [mp 146°, [α]_D = +133°, resolution with (+)-ephedrine in ethanol (22)]; (d,l)-p-NO₂-mandelic acid, synthesis (22), (l)-p-NO₂-mandelic acid [mp 95°, [α]_D = +85°, resolution with (+)-ephedrine (22)]; 2-²H-p-substituted mandelic acids were prepared using the H297N mutant of mandelate racemase (23) and were a gift from John A. Gerlt (University of Illinois).

Methods.

Standard buffer was 10 mM imidazole adjusted to pH 7.0 with HCl in the presence of 100 mM KCl. For the preparation of stock solutions of p-substituted mandelates, the solid free acid was dissolved in water and adjusted to pH 7.0. The instruments and the methods used for rapid reaction studies were as described previously (10, 17). Protocatechuate dioxygenase (10–50 nM) and protocatechuate (100 μM) were added to solutions to ensure anaerobiosis. In all stopped flow experiments, multiple reaction traces, typically 4 or more, were recorded at several different wavelengths for each set of conditions used. The values obtained varied by less than 5%; the rate constants reported throughout are the average values. Regression analyses were carried out using the mystat program (Systat, Evanston, IL).

RESULTS AND DISCUSSION

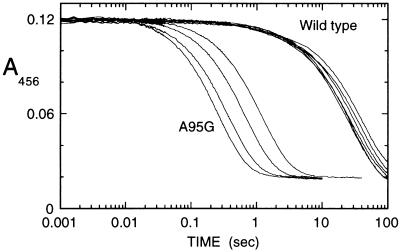
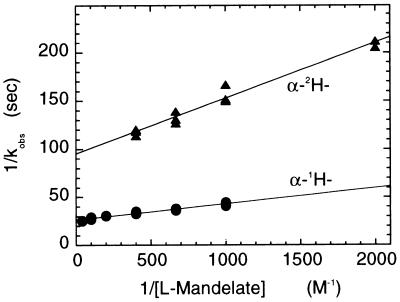
Stopped flow traces of the anaerobic reductive half-reaction of wild-type and A95G lactate oxidases with various concentrations of l-mandelate at pH 7.0 and 25°C are shown in Fig. 1. These traces are analyzed accurately as single exponential reactions, whose observed first order rate constants are dependent on the substrate concentration. No absorbance changes were detected at any wavelength greater than 530 nm. This fact combined with the single exponential decay of absorbance in the 400–500 nm region shows that neither wild-type nor A95G lactate oxidase has any observable interaction with product during the reductive half-reaction, i.e., that product dissociation is probably faster than reduction of the enzyme flavin (10, 17). Double reciprocal plots between the observed rate constant (k_obs) and the concentration of l-mandelate (Fig. 2) determine the reduction rate constant (k_red) from the reciprocal of the y-axis intercept and the apparent K_d of substrate binding from the slope/intercept (24). These values are listed in Table 1. Consistent with previous results with other bulky substrates (17), the A95G enzyme is considerably more reactive with l-mandelate than is the wild-type enzyme. (It should be noted that errors occurred in the calculation of the k_cat values of l-mandelate and l-α-hydroxy-β-methyl valerate for A95G reported in ref. 17; the correct values are 6.6 and 12 s⁻¹, respectively, and the corresponding K_m values are 5.7 and 70 mM.) With either enzyme form, the reduction is uninfluenced by the presence of the d-isomer, the k_obs value being determined simply by the concentration of the l-isomer (results not shown). With l-²H-mandelate the same overall kinetic behavior, the same value for the K_d of substrate binding, and a decreased value of k_red consistent with a primary deuterium isotope effect ca. 5 is observed. The product of the oxidation of mandelate was identified as phenylglyoxylic acid by its characteristic absorption spectrum.

Figure 1.

Stopped flow traces of the reduction of A95G and wild-type lactate oxidase with l-mandelate. Equal volumes of argon-equilibrated enzyme solution (12 μM final concentration) were mixed with argon-equilibrated l-mandelate solutions of different concentration, and reduction of the flavin monitored at 456 nm. Conditions were pH 7.0 at 25°C. The traces with wild-type enzyme, curves from right to left, were obtained with l-mandelate concentrations of 1, 1.5, 2.5, 5, 10, and 25 mM. The traces with A95G enzyme, curves right to left, were obtained with l-mandelate concentrations of 1, 2, 5, and 10 mM.

Figure 2.

Determination of the reduction rate constants (k_red) and dissociation constant (K_d) for reaction of wild-type lactate oxidase with α-¹H-l-mandelate and α-²H-dl-mandelate. Reaction traces such as those of Fig. 1 are strictly single exponential in character, yielding at each concentration a pseudo-first order rate constant, k_obs. The reciprocal of k_obs is here plotted vs. reciprocal of the l-mandelate concentration, to yield values of 1/k_red from the y-intercept and K_d from the slope/intercept (24). The data shown are for α-¹H-l-mandelate (•) and α-²H-dl-mandelate (▴), with the concentration of the latter expressed as the l-form.

Table 1.

Reduction rate constants (k_red) and dissociation constants (K_d) for reaction of lactate oxidases with α-¹H- and α-²H-para-substituted mandelates at 25°C and pH 7

Mandelate derivative	Wild-type lactate oxidase					A95G lactate oxidase
	kred, sec−1		Kd, mM		R-value	kred, sec−1		Kd, mM		R-value
	α-1H-	(α-2H-)	α-1H-	(α-2H-)		α-1H-	(α-2H-)	α-1H-	(α-2H-)
DL- OH-	0.009		2.03		0.9856	0.29		16.2		0.9996
		(ND)		(ND)			(ND)		(ND)
L- CH3O-	0.055		0.83		0.9939	1.61		4.0		0.9993
		(0.009)		(0.98)	0.9854		(0.38)		(5.8)	0.9998
L- CH3-	0.048		0.34		0.9721	3.17		3.9		0.9998
		(0.007)		(0.34)	0.8226		(0.60)		(3.5)	0.9994
L- H-	0.038		0.64		0.9747	5.88		6.3		0.9999
DL- H-		(0.010)		(0.61)	0.9888		(1.52)		(4.3)	0.9995
L- F-	0.037		0.36		0.9558	1.85		3.6		0.9998
		(ND)		(ND)			(ND)		(ND)
L- Cl-	0.023		0.23		0.8972	0.98		1.3		0.9962
		(0.003)		(0.12)	0.5882		(0.18)		(1.8)	0.9978
L- CF3-	0.018		0.51		0.9064	0.20		3.1		0.9943
		(0.003)		(0.37)	0.9883		(0.05)		(5.6)	0.9987
L- NO2-	0.017		0.34		0.9785	0.21		3.2		0.9977
		(ND)		(ND)			(ND)		(ND)

ND, no data. 

For linear free energy relationship studies, a series of p-substituted l-mandelate analogues, including both the α-¹H- and α-²H-forms, were reacted with A95G and wild-type enzymes under the same conditions as with unsubstituted mandelate. In all cases the same pattern of absorbance traces as in Fig. 1 was observed (data not shown). Table 1 summarizes reduction rate constants (k_red) and apparent dissociation constants of this series of p-substituted mandelates. In all cases the k_red values for the mutant enzyme were 10- to 150-fold larger and the K_d values were 5- to 12-fold larger than those for wild-type enzyme. All mandelate derivatives tested showed deuterium isotope effects on k_red between 3 and 7, when the α-¹H and α-²H-derivatives were used (Table 1), indicating that in all cases the step involving removal of the α-hydrogen is at least partially and probably largely rate-limiting. There was no significant difference in the K_d values between α-¹H- and α-²H mandelates.

For the interpretation of linear free energy relationships, the certitude that the observed step corresponds to the chemical event being considered is a cardinal issue. In our case, the analysis of the kinetic data was fully consistent with the observed reduction of the oxidized enzyme flavin being directly coupled with the step in which the substrate α-C-H bond is broken. This results from the magnitude of the isotope effect observed within the series of p-substituted mandelates, which is clearly a primary one, and from the fact that there is no significant difference of K_d for α-¹H- and α-²H-mandelates. This is consistent with the same mechanism of C-H bond rupture being operative within the series of mandelates studied. Based on this, an interpretation of the data was attempted.

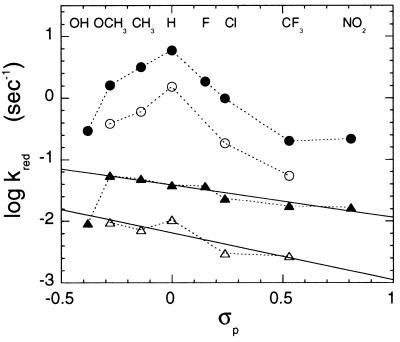
Hammett plots of reduction rate constants for both wild-type and A95G enzymes are shown in Fig. 3. With the exception of p-hydroxy and p-nitro mandelates, wild-type enzyme shows an approximately linear relation to the Hammett σ substituent parameter, with a similar negative slope (the Hammett ρ value) of −0.6 for both protio- and deuterocompounds. Hydroxy- and nitro-substituents are good hydrogen bond partners, and are frequently observed to disturb the Hammett relation (15, 16, 26, 27). We have therefore not used the data for these compounds in the subsequent regression analyses of Fig. 4 and Table 2. The negative Hammett ρ value for wild-type enzyme shown in Fig. 3, even though small, would appear to be inconsistent with the formation of a discrete carbanion in the transition state, since the resultant negative charge should be reflected by a positive Hammett ρ value. The mutant enzyme, on the other hand, displays the tent-shaped relationship shown in Fig. 3, with both positive and negative Hammett ρ components.

Figure 3.

Hammett plots of the reduction rate constants of A95G (circles) and wild-type (triangles) lactate oxidase by α-¹H- (solid symbols) or α-²H- (open symbols) forms of p-substituted l-mandelates. The derivatives used were dl-hydroxy-, l-methoxy-, l-methyl-, l- and dl- H-, l-fluoro-, l-chloro-, l-trifluoromethyl- and l-nitro-mandelates. The σ-parameters of p-substituted functional groups were taken from ref. 25.

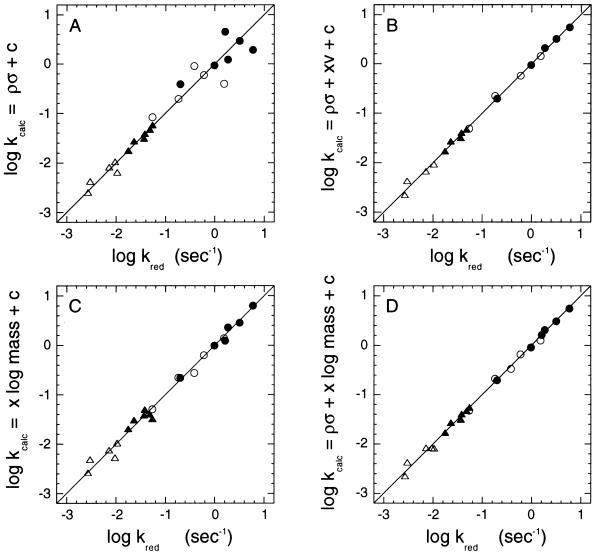
Figure 4.

Multiple regression analyses of the data of Fig. 2 and Table 1, omitting the data points for hydroxy- and nitro-mandelates. Symbols are as in Fig. 3. See text for details, and Table 2 for numerical details of the regression analyses.

Table 2.

Bivariate and multiple regression analyses of reduction rate constants of wild-type and A95G lactate oxidase with a series of α-¹H- and α-²H-mandelates

Variable	Hammett ρ	Coefficient of other component (x)	Constant (c)	R2	F	P	n
σ	log k(H,wild)= −0.633 (±0.082) σ		−1.418 (±0.023)	0.936	58.938	0.002	6
	log k(D,wild) = −0.763 (±0.243) σ		−2.194 (±0.072)	0.766	9.830	0.052	5
	log k(H,A95G) = −1.311 (±0.574) σ		+0.282 (±0.159)	0.566	5.221	0.084	6
	log k(D,A95G) = −1.283 (±0.648) σ		−0.404 (±0.191)	0.567	3.923	1.142	5
σ + π	log k(H,wild) = −0.566 (±0.133) σ	−0.060 (±0.088) π	−1.403 (±0.033)	0.945	25.718	0.013	6
	log k(D,wild) = −0.400 (±0.376) σ	−0.308 (±0.255) π	−2.100 (±0.102)	0.865	6.398	0.135	5
	log k(H,A95G) = −1.064 (±0.975) σ	−0.220 (±0.648) π	+0.337 (±0.243)	0.582	2.091	0.270	6
	log k(D,A95G) = −0.919 (±1.277) σ	−0.309 (±0.866) π	−0.310 (±0.348)	0.593	1.455	0.407	5
σ + Es	log k(H,wild) = −0.609 (±0.123) σ	+0.012 (±0.042) Es	−1.408 (±0.042)	0.938	22.784	0.015	6
	log k(D,wild) = −0.560 (±0.371) σ	+0.103 (±0.133) Es	−2.102 (±0.142)	0.820	4.553	0.180	5
	log k(H,A95G) = −0.598 (±0.586) σ	+0.382 (±0.203) Es	+0.581 (±0.201)	0.801	6.053	0.088	6
	log k(D,A95G) = −0.446 (±0.754) σ	+0.422 (±0.270) Es	−0.026 (±0.288)	0.805	4.136	0.195	5
σ + ν	log k(H,wild) = −0.632 (±0.187) σ	−0.042 (±0.140) ν	−1.395 (±0.058)	0.921	11.615	0.079	5
	log k(D,wild) = −0.477 (±0.509) σ	−0.402 (±0.399) ν	−2.029 (±0.179)	0.862	3.111	0.372	5
	log k(H,A95G) = −1.332 (±0.119) σ	−0.810 (±0.089) ν	+0.738 (±0.037)	0.997	308.291	0.003	5
	log k(D,A95G) = −1.001 (±0.285) σ	−1.029 (±0.224) ν	+0.155 (±0.100)	0.991	54.295	0.096	5
log mass	log k(H,wild) =	−2.414 (±1.232) log mass	+3.963 (±2.775)	0.490	3.837	0.122	6
	log k(D,wild) =	−3.767 (±1.573) log mass	+6.248 (±3.548)	0.657	5.736	0.096	5
	log k(H,A95G) =	−9.091 (±0.675) log mass	+20.635 (±1.520)	0.978	181.352	0.001	6
	log k(D,A95G) =	−8.980 (±0.806) log mass	+19.757 (±1.818)	0.976	124.082	0.002	5
σ + log mass	log k(H,wild) = −0.584 (±0.119) σ	−0.393 (±0.626) log mass	−0.538 (±1.402)	0.944	25.199	0.013	6
	log k(D,wild) = −0.526 (±0.336) σ	−1.822 (±1.789) log mass	+1.898 (±4.020)	0.846	5.493	0.154	5
	log k(H,A95G) = −0.316 (±0.070) σ	−7.998 (±0.371) log mass	+18.195 (±0.831)	0.997	537.413	0.001	6
	log k(D,A95G) = −0.223 (±0.203) σ	−8.156 (±1.081) log mass	+17.915 (±2.492)	0.985	66.968	0.015	5

The data with p-hydroxymandelate and p-nitromandelate have been excluded from the analyses. H and D, α-¹H- and α-²H-mandelates; R, correlation constant; F, ratio of regression sum of squares explained by the equation for log k_calc to residual sum of squares not explained by the equation; P, significance value; n, number of compounds used in the analysis. The Taft steric (Es) and hydrophobic (π) factors used were from ref. 25 and Charton ν values from ref. 29. 

In Fig. 4, the various k_red values obtained with wild-type and mutant enzymes, employing ¹H- and ²H-mandelates are plotted vs. the k_red values calculated from correlation analyses, where for each set, log k_calc = σρ + constant (c), or log k_calc = x log mass + c, or log k_calc = σρ + x (other component) + c, where x is the coefficient of the other component. The numerical values of each analysis and statistical reliability factors are given in Table 2. Fig. 4A reproduces the data of Fig. 3 in this new format. It is seen that the data for wild-type enzyme (open and solid triangles) fit reasonably to a simple Hammett relationship, but that the results with the mutant enzyme (open and solid circles) deviate wildly. Two-parameter correlations of Hammett σρ and Taft steric (Es) factors or σρ and hydrophobic (π) factors do not result in any better correlation (see numerical values in Table 2). While van der Waals radii and Taft E_s factors do not improve significantly the quality of the correlations, the substituent volume-related factor ν introduced by Charton (29) gives a good correlation (Fig. 4B and Table 2). Intriguingly, a good correlation was found with the simple logarithm of the molecular weight of the molecule as shown in Fig. 4C. The two parameter fit, using both σ and log mass, shows the best correlation (Fig. 4D). The conclusion from this analysis is that the reaction leading to reduction of the enzyme flavin shows only a small dependence on electronic effects, as reflected by the Hammett σρ-parameter, and an important influence from steric/mass- dependent factors of the substrate.

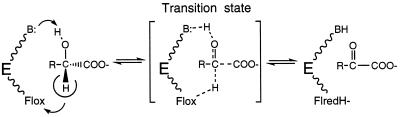
The value of k_red, which is a direct measure of substrate α-C-H bond breakage, is clearly related to factors directly or indirectly linked to the volume (steric factors) and/or the mass of the substrate. The dependence on mass number could indicate that vibrations involving the p-substituted phenyl ring are very important in the approach to the transition state. It should be kept in mind that during substrate dehydrogenation and independent of the mechanism (hydride or carbanion type), reorientation of substituents will be important as the tetrahedral substrate converts to the more planar transition state (e.g., Scheme SI):

Scheme I.

The interpretation of the remarkable correlation of k_red with the substrate mass is not straightforward, since to our knowledge such an effect is unprecedented. It should be emphasized that the correlation is with the molecular weight of the mandelate molecule, not with the mass or volume of the p-substituent. Quite trivially, it should be pointed out that the molecular volume is dependent, albeit not linearly, on the mass of the molecule. Thus, two possibilities arise. First, the correlation could be simply coincidental, a case that cannot be dismissed in view of the limited range of substrate variation accessible for enzymatic studies. Second, and more likely, α-C-H bond breakage could be coupled to vibrations of the p-substituent in the approach to the transition state, which, in turn, will be dependent on its mass. We are currently pursuing this intriguing possibility by studying the IR-vibrations of substituted mandelates and by normal mode calculations. Initial AM1 vibrational analysis indicates that a large number of normal modes involve significant movement of both the α-H and the p-substituent.

The increase in the rates of k_red observed with A95G and with substrates having a bulky α-substituent such as mandelate, when compared with wild-type enzyme, might have the same molecular origins. We have modeled a three-dimensional structure of lactate oxidase by adapting its sequence to the known structures of either glycolate oxidase (3, 5) or b₂ (4) using the Swiss-Model protein modeling server (30). The active center topography shows that the -CH₃ group of A95 is located adjacent to flavin N(5) and just below the flavin plane with which it is in contact, and is within 3–4 Å from the C(2) center of the substrate. Since transfer of redox equivalents occurs between the latter center and the flavin N(5) it is readily understandable that the -CH₃ group in question will affect the approach of the substrate and the subsequent reaction. Conversely, the space resulting from removal of the methyl group of A95 will allow for greater steric freedom and efficient catalysis of substrates with large α-substituents.

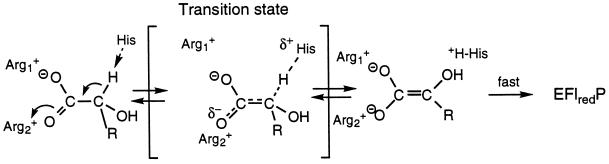
To reiterate, the present results are not compatible with a carbanion mechanism in its classical formulation, i.e., one in which a substantial negative charge occurs during the transition state, e.g., as in the case of plasma amine oxidase, where a Hammett ρ value of +1.5 was found (26). The present results are clearly compatible with any mechanism in which breakage of the substrate α-C-H bond is coupled with a second event that neutralizes the charge that develops. A hydride mechanism, in which abstraction of the α-C-OH proton is coupled with transfer of the α-C-H as a hydride to the flavin N(5), is an obvious possibility (cf. Scheme SI). A “carbanion” mechanism, in which the negative charge is delocalized to the carboxylate moiety, is an alternative that should also be considered (31). It should be noted that all members of the α-hydroxyacid dehydrogenation family contain a second conserved arginine residue, R289 in flavocytochrome b2, R164 in glycolate oxidase, R187 in lactate monooxygenase, and R181 in lactate oxidase, which has only recently received attention as a possible active site residue in glycolate oxidase (5). In this enzyme the distances between the side chain nitrogens of the arginine in question and the carboxylate oxygens of a bound inhibitor were 3.0 and 3.2 Å. Modeling of the structures of lactate monooxygenase and lactate oxidase show similar distances to the carboxyl oxygens of substrate.

The conserved presence of these two arginine residues suggests that they may serve to neutralize the carboxylate-localized negative charge of the initial “carbanion,” as shown in Scheme SII:

Scheme II.

In this formulation, it should be noted that there is no change in net charge of the enzyme reaction center in progressing from the enzyme–substrate complex through the transition state to the intermediate. This may be accomplished either by a strengthening of the arginine–carboxylate interaction(s) in the transition state over the reactants or by actual proton transfer from an arginine to the developing endiolate species.

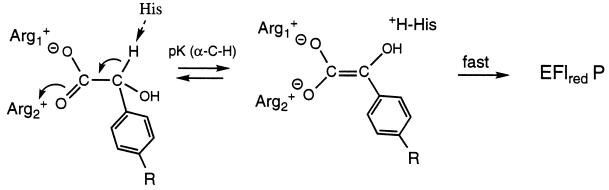
It might be expected that the electronic nature of the substituent R of the mandelate substrate would affect the reduction rate constant in the same fashion as with the classical Hammett effects on ionization of substituted benzoic acids, since the pK_a of the α-C-H moiety should show similar substituent effects, and since the concentration of the intermediate will be expected to affect the subsequent rate of flavin reduction (Scheme SIII).

Scheme III.

However, this expectation is not necessarily true, as the value of k_red is determined by the rate-limiting step in the mechanism sequence. Provided that the intermediate in Scheme SIII reacts with the enzyme flavin much faster than it is formed, and substituent-induced effects are exerted also on the reverse reaction (k₄ in the model below), the value of k_red can be insulated from the equilibrium defining the pK_a of the intermediate. This was shown by modeling the reaction by numerical simulation:

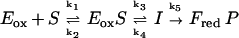Using the following values of rate constants as examples; k₁ = 10⁵ M⁻¹⋅s⁻¹, k₂ = 100 s⁻¹, k₃ = 2 s⁻¹, k₅ = 100 s⁻¹, and giving E_ox S and I the absorbance properties of oxidized flavin, essentially identical reduction curves were obtained with values of k₄ = 0, 2, or 5 s⁻¹. The simulated traces fitted perfectly to single exponentials (equivalent to our experimental k_obs values) and double reciprocal plots of k_obs⁻¹ vs. [S]⁻¹ yield a y intercept value of 0.5 sec (=1/k₃) and slope/intercept equal to 10⁻³ M (k₂/k₁). These results are completely analogous to our experimental results such as those shown in Fig. 2. Thus, in terms of Scheme SIII, there could be considerable variation in the value of pK_a of the intermediate, (reflected by the ratio k₃/k₄), without any significant effect on the value of k_red. This is a further argument that interpretation of the slopes of Hammett plots in terms of mechanism must be made with caution, especially when the slopes are small. In the past two decades, a wealth of experiments have been described, also by us, which have been interpreted as supporting the carbanion mechanism (1, 2). Clearly the issue is not solved, and also different concepts, such as “hydride”- and “carbanion”-chemistry being possible at the same active center (28, 32) should be considered seriously. In fact, a rotation of some 40° around the substrate C(1)-C(2) axis would move the α-substituent to allow for the attack of the active site histidine (His 265 in lactate oxidase) onto the α-C-H (“carbanion” mechanism) or, alternatively, onto the α-C-OH (initiation of hydride transfer).