Genetic Expectations of Quantitative Trait Loci Main and Interaction Effects Obtained With the Triple Testcross Design and Their Relevance for the Analysis of Heterosis

Abstract

Interpretation of experimental results from quantitative trait loci (QTL) mapping studies on the predominant type of gene action can be severely affected by the choice of statistical model, experimental design, and provision of epistasis. In this study, we derive quantitative genetic expectations of (i) QTL effects obtained from one-dimensional genome scans with the triple testcross (TTC) design and (ii) pairwise interactions between marker loci using two-way analyses of variance (ANOVA) under the F₂- and the F_∞-metric model. The theoretical results show that genetic expectations of QTL effects estimated with the TTC design are complex, comprising both main and epistatic effects, and that genetic expectations of two-way marker interactions are not straightforward extensions of effects estimated in one-dimensional scans. We also demonstrate that the TTC design can partially overcome the limitations of the design III in separating QTL main effects and their epistatic interactions in the analysis of heterosis and that dominance × additive epistatic interactions of individual QTL with the genetic background can be estimated with a one-dimensional genome scan. Furthermore, we present genetic expectations of variance components for the analysis of TTC progeny tested in a split-plot design, assuming digenic epistasis and arbitrary linkage.

ESTIMATION of the type of gene action at loci underlying quantitative traits has been a major research focus of quantitative genetics. When defining gene action at single loci we generally distinguish between additive gene action and deviations from additivity due to intralocus allelic interactions, such as dominance and overdominance. With more than one locus, the genotype can also be affected by interlocus interactions, i.e., epistasis. New insights from molecular studies have demonstrated the importance of epistatic interactions in the inheritance of complex traits for a broad spectrum of organisms (Schadt et al. 2003; Brem et al. 2005). However, the majority of epistatic effects are assumed to be small while available genetic models and experimental designs suffer from limited power of detection. Therefore, new strategies need to be devised for the detection and estimation of epistatic quantitative trait loci (QTL) effects.

Many models have been developed to distinguish between different types of gene action and to estimate the magnitude of genetic effects. Anderson and Kempthorne (1954) and Gamble (1962) proposed the estimation of additive, dominance, and epistatic effects from first-moment statistics, i.e., generation means. These parameters reflect sums of gene effects over all loci and, consequently, positive and negative effects at individual loci may cancel each other. Cockerham (1954) proposed a general model for estimating the type of gene action from second-moment statistics. He developed a set of orthogonal contrasts to partition the genetic variance into additive, dominance, and epistatic components. For populations derived from a cross between two inbred lines, simpler models such as the F₂- and the F_∞-metric model have been described (see Van Der Veen 1959). In the presence of epistasis, the choice of metric becomes crucial and depends on the genetic material under study and the experimental design employed for estimating genetic effects. A detailed comparison of the statistical properties and genetic expectations of the F₂- and the F_∞-metric model has been given by Kao and Zeng (2002) and Yang (2004). With an F₂ population, the F₂ metric is to be preferred because genetic effects under the F₂-metric model are orthogonal and thus, in contrast to the F_∞-metric model, unbiased estimates of genetic effects can be obtained irrespective of the presence of epistasis (Alvarez-Castro and Calborg 2007). Furthermore, the genetic variance can be partitioned into eight independent components and genetic covariances are absent, if only first-order interactions are present. Melchinger et al. (2007) gave further arguments for the superiority of the F₂ metric for the analysis of heterosis with the North Carolina Experiment III (design III), originally devised by Comstock and Robinson (1952).

In addition to different genetic models, different experimental designs have been proposed for estimating the type of gene action from second-moment statistics. However, as pointed out by Kearsey and Jinks (1968), many designs have serious limitations with respect to unbiased estimation of genetic effects. Frequently, absence of epistasis is assumed but a valid test of this assumption is not provided. Furthermore, the different components of variance are estimated with varying precision and power and linkage disequilibrium between loci is not accounted for. The design III partially overcomes these limitations. The experimental units are produced from backcross matings of F₂ plants to the two parental lines from which the F₂ was derived. Additive and dominance components of variance can be estimated with nearly equal precision under the assumption of diploidy, biallelic and equal gene frequencies, and absence of linkage and epistasis. Thus, an estimate of the average degree of dominance can be obtained from the ratio of the dominance and additive variance components. Cockerham and Zeng (1996) extended Comstock and Robinson's analysis of variance (ANOVA) to include linkage and two-locus epistasis for F₂ and F₃ progenies and developed orthogonal contrasts for marker-aided mapping of QTL using single-marker ANOVA. Melchinger et al. (2007) demonstrated the exceptional features of the design III for the identification of QTL contributing to heterosis. They defined a new type of heterotic gene effect, denoted as augmented dominance effect d_i*, which equals the net contribution of QTL i to midparent heterosis (MPH). It comprises the dominance effect d minus half the sum of additive × additive (aa) epistatic interactions with the genetic background. The novelty of their approach is that QTL significantly contributing to MPH are identified and both dominance and epistasis are accounted for.

An elegant extension of the design III proposed by Kearsey and Jinks (1968), named the triple testcross (TTC) design, provides a test of significance for the presence of epistasis. In the TTC design, testcrosses are produced not only with the two parental lines but also with the F₁ derived from them. For every progeny from a segregating population, e.g., F₂ plant or recombinant inbred line (RIL), three sets of data can be created: (i) the average parental testcross performance, (ii) the difference between the parental testcross performances, and (iii) the deviation of testcross progenies with the F₁ from the mean of the parental testcrosses. Making use of the advances of marker technology, Kearsey et al. (2003) and Frascaroli et al. (2007) presented experimental results from QTL analyses based on the TTC design with data from Arabidopsis and maize, respectively, but genetic expectations of QTL effects estimated with their respective models were not given and the connection to the analysis of heterosis was not made.

In this study, we give genetic expectations of QTL effects estimated with the TTC design in the presence of epistasis. We show that with the TTC design dominance × additive epistatic interactions of individual QTL with the genetic background can be estimated with one-dimensional genome scans. We also demonstrate that the limitation of the design III in the analysis of heterosis to separate QTL main effects and their epistatic interactions with all other QTL can partially be overcome with the TTC design. Objectives of this study were to (1) extend the theory given by Melchinger et al. (2007) to derive quantitative genetic expectations of QTL effects obtained from one-dimensional genome scans with the TTC design using composite-interval mapping (CIM), (2) give quantitative genetic expectations of pairwise interactions between marker loci using two-way ANOVA, (3) derive genetic expectations of variance components of the ANOVA for the TTC progeny tested in a split-plot design for digenic epistasis and arbitrary linkage, and (4) relate our results to the analysis of MPH. Application of our theory to experimental data has been published by Kusterer et al. (2007).

THEORY

Experimental design:

Let us assume a random population of RILs derived from the cross between two homozygous lines P1 and P2. Further, we assume that the RILs are backcrossed to their parental lines and the F₁ derived from them, yielding testcross progenies H_t of RIL p (p = 1, …, n) with testers P1 (t = 1), P2 (t = 2), and F₁ (t = 3). The parental line exhibiting superior average testcross performance is denoted as P2.

To obtain maximum precision of progeny means in subsequent QTL analyses we suggest that the testcross progeny H_t are evaluated in a split-plot design with n main plots, each main plot comprising all three testcrosses of the pth RIL. The model for the phenotypic trait values Y_tpk can be written as

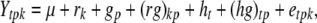with r_k being the effect of the kth replication (k = 1, …, r), g_p the genetic effect of the pth RIL, (rg)_kp the main plot error term, h_t the effect of the tth tester, (hg)_tp the interaction between tester t and RIL p, and e_tpk the subplot error term. While testers are considered fixed, all other effects are assumed random. Following Kearsey and Jinks (1968), three linear transformations Z_s (s = 1, 2, 3) on the performance data are generated with Z_1pk = (Y_1pk + Y_2pk)/2 and Z_2pk = Y_1pk − Y_2pk, and Z_3pk = (Y_1pk + Y_2pk − 2Y_3pk). Thus, Z_spk denotes the phenotypic value of transformation Z_s for RIL p grown in the kth block and Z_sp the mean over replicates of Z_s for RIL p. Note that Z₁ and Z₃ are not orthogonal. Thus, partitioning of the genetic variance in the ANOVA is given for the linear transformation 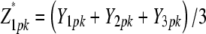instead of Z_1pk.

Following Melchinger et al. (2007) the genetic constitution of parameters in the expected mean squares of the ANOVA of the TTC design (Table 1) is derived below. Let P1 and P2 differ at loci set Q = {1, …, q} affecting the quantitative trait of interest and let v_i be an indicator variable for the genotype at locus i taking values 0 for homozygous P1 or 2 for homozygous P2. We define the additive effect a_i and the dominance effect d_i at QTL i in accordance with the definition of Falconer and Mackay (1996, p. 109), except that a_i is negative when the trait-increasing allele is contributed by P1. Epistatic effects between loci i and j are denoted aa_ij for additive × additive, ad_ij for additive at locus i and dominance at locus j, da_ij for dominance at locus i and additive at locus j, and dd_ij for dominance × dominance. The sum of additive × additive epistatic effects over all pairs of QTL is denoted [aa] and aa epistatic interactions of QTL i with the entire genetic background are denoted [aa_i·]. The same notation is followed for ad, da, and dd epistatic effects. To allow extensions to multiple loci we express linkage between loci i and j with the linkage value 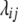(Schnell 1961), which can be calculated from the recombination frequency r_ij as 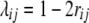. Linkage disequilibrium between loci i and j in the gametic array of progeny derived from cross P1 × P2 is given by the linkage disequilibrium parameter D_ij (Falconer and Mackay 1996, p. 18). For RILs derived without random mating prior to selfing, D_ij can be calculated as 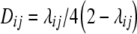. General derivations of expectations and variances for the TTC design based on the theory presented by Melchinger et al. (2007) are given in the appendix.

TABLE 1.

Analysis of variance on linear transformations 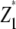, Z₂, and Z₃ calculated from testcross performance of recombinant inbred lines (RIL) evaluated in a split-plot design with n main plots each comprising testcrosses of the pth RIL with testers P1 (t = 1) and P2 (t = 2) and their F₁ (t = 3)

Source of variation	d.f.a	Expected mean squareb
Main plots
Replication	r − 1
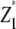	n − 1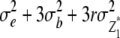
Main plot error	(n − 1)(r − 1)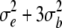
Subplots
Z2	1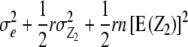
RIL × Z2	n − 1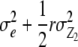
Z3	1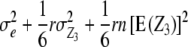
RIL × Z3	n − 1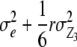
Subplot error	2n(r − 1)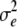

^ar, number of replicates; n, number of RILs.

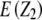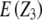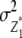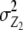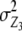^b and refer to expectations of Z₂ and Z₃, respectively; , , and refer to the progeny variance arising from interactions with testers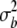; and and 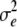are error variances of the whole-plot and subplot errors, respectively.

Assuming digenic epistasis and with Q_i denoting the loci set Q excluding element i we obtain

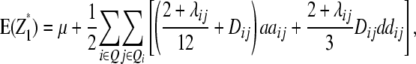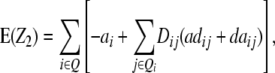and

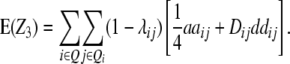As follows from the ANOVA (Table 1), the presence of epistasis can be tested with the linear transformation Z₃, the null hypothesis being H₀: 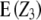= 0. In the absence of linkage ( 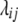= D_ij = 0), 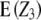simplifies to 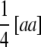, the sum of additive × additive epistatic effects over all pairs of QTL. Our results on 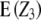are in agreement with the results of Kearsey and Jinks (1968), who developed a test of significance for the net contribution of aa effects in the TTC design performed with testcrosses of F₂ plants. As mentioned by these authors, if aa_ij effects have different signs and cancel in the composite effect 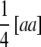, then the null hypothesis will be accepted even though strong epistasis may be present.

Assuming digenic epistasis but arbitrary linkage, genetic expectations of the variance components for the TTC are as follows:

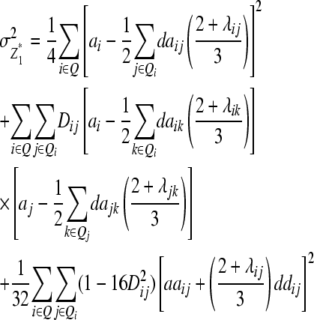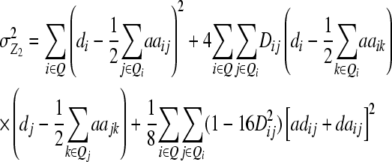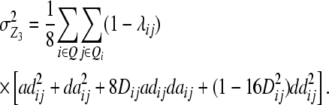We note that with the TTC design partitioning of the genetic variance on the basis of linear transformations 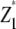, Z₂, and Z₃ differs from the design III. The progeny variance among RILs in the TTC design is reduced compared with the design III ( 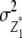< 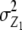). Both variance components comprise the same genetic effects, but the influence of da and dd epistatic effects is decreased by the factor 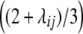, i.e., by two-thirds for unlinked loci. The variance component from interaction of RILs with the two parental testers (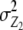) is identical for the TTC design and the design III. The genetic variance component arising from Z₃ is a complex function of different epistatic effects. In the absence of linkage, rejection of the null hypothesis H₀: 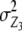= 0 provides evidence for epistasis of type ad and/or da.

As can be seen from Table 1, the proposed split-plot design in which each of n main plots comprises three subplots, i.e., the three testcrosses of the pth RIL, is advantageous compared with a randomized complete block design (RCB). The standard error of progeny means Z₂ and Z₃ is calculated from the subplot error, which is expected to be smaller than the error variance of the RCB. Competition effects between the three different testcross progenies are not expected due to equal inbreeding coefficients (F = 0.5). Compared with the design employed by Frascaroli et al. (2007), who assigned testers to t main plots and progenies from the same tester to subplots, this design has the advantage that the test for epistasis summed over all loci (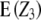) becomes more powerful due to more degrees of freedom of the main plot error ((n − 1)(r − 1) > (t − 1)(r − 1)). In addition, the subplot error variance should be decreased due to the small number of subplots per main plot resulting in higher precision of progeny means Z₂ and Z₃.

QTL analysis with the TTC design:

Melchinger et al. (2007) derived quantitative genetic expectations of QTL effects obtained with the design III and RILs. Using CIM and assuming digenic epistasis they demonstrated that in one-dimensional genome scans on Z₁ and Z₂ the contrast of the two (unobservable) homozygous genotype classes at QTL i equals the augmented additive (a_i*) and dominance (d_i*) effects:

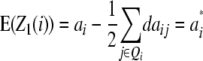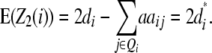They concluded that the sum of QTL effects equals genotypic expectations for the parental difference (PD) and MPH. Thus,

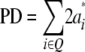and

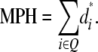For the identification of QTL affecting the PD or MPH it is favorable that in a_i* and d_i* main effects and epistatic interactions of QTL i with the genetic background are confounded. However, the dissection of augmented QTL effects into their components is desirable when the relative contribution of the individual effects is of interest, i.e., the additive effect a_i at QTL i and [da_i·] epistasis contributing to the PD and the dominance effect d_i at QTL i and [aa_i·] epistasis contributing to MPH.

The contribution of the additive effect a_i at QTL i and its [da_i·] epistatic interactions can be estimated from one-dimensional genome scans with H₃ and the linear transformation Z₃. Following Melchinger et al. (2007), with CIM, i.e., estimating the QTL position and including cofactors in the model, we obtain the following quantitative genetic expectations of QTL effects at QTL i:

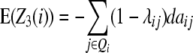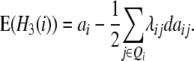Thus, with the TTC design, genome scans on H₃ and Z₃ can be adopted for estimating to what extent the individual effects a_i and [da_i·] contribute to the augmented additive effect a_i* in the absence of linkage.

On the basis of one-dimensional genome scans, the TTC design does not provide a solution to the dissection of the augmented dominance effect d_i* into its components, i.e., the dominance effect of QTL i and [aa_i·]. However, as commonly practiced in QTL analyses, digenic epistasis can be estimated by two-way ANOVA on the basis of interactions of two-locus combinations of marker genotypes. In the following, we derive quantitative genetic expectations of contrasts for two-locus marker genotypes with linear transformations Z_s of the TTC design. We assume two QTL i and j and two marker loci m₁ and m₂, each with genotype classes v (v_i = 0, 2; v_j = 0, 2; 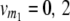; 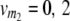), and define the vector 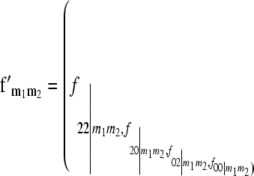with 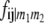referring to the conditional probability of the QTL genotype v_iv_j (v_iv_j = 22, 20, 02, 00) given marker genotype 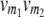( 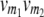= 22, 20, 02, 00). Following the parameterization of gamete frequencies given by Schnell (1961), the four-locus genotype frequencies of RILs 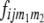can be expressed by using six two-locus 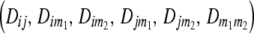and one four-locus linkage disequilibrium parameter as

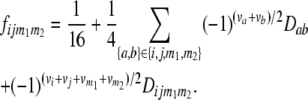Following Melchinger et al. (2007), conditional expectations of linear functions Z_s (Z_s = Z₁, Z₁*, Z₂, Z₃) and testcross progenies H_t (t = 1, 2, 3) are obtained by

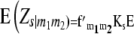and

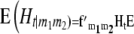with the matrices 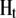and 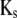denoting the coefficients of genetic effects given the genotype of the parental RIL, the tester t, and for 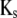the linear transformation s (for details see the appendix). 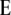denotes the vector of genetic effects defined according to the F₂ metric. From this, we obtain the expectations of the interaction between markers m₁ and m₂ for linear functions Z_s and testcross progenies H_t as

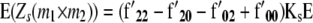and

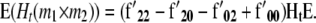For arbitrary linkage between all four loci (i, j, m₁, m₂) calculations of conditional QTL genotype frequencies become rather unwieldy. Therefore, we exemplify our derivations for the special case in which marker loci m₁ and m₂ are unlinked (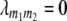) and QTL i is linked to marker m₁ and QTL j to marker m₂ (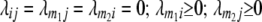). Conditional probabilities of QTL genotypes at loci i and j are given in Table 2. Summation over QTL i and j yields genotypic expectations for interactions between marker pairs with linear transformations Z_s calculated from the TTC design,

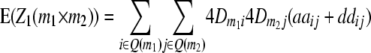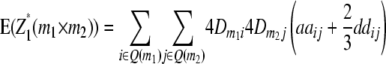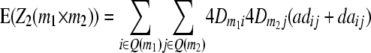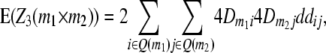where Q(m₁) denotes all loci in set Q in linkage disequilibrium with marker m₁.

TABLE 2.

Frequencies (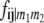) of the four possible QTL genotypes of recombinant inbred line (RIL) parents at QTL i and j conditional on the marker genotype v (v = 0, 2) at marker loci m₁and m₂ calculated using the two-locus linkage disequilibrium parameters 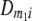and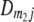

Genotype at QTL		Genotype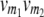
i	j	22	20	02	00
2	2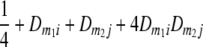
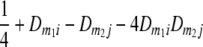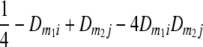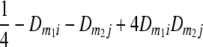2	0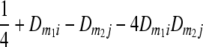
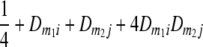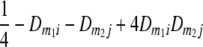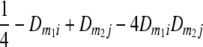0	2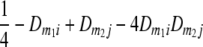
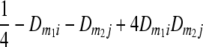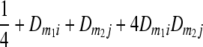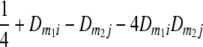0	0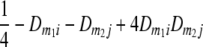

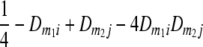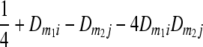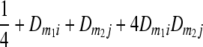For the dissection of heterotic-effect d_i* into its components, estimates of aa epistatic interactions of QTL i with other QTL in the genome are of particular interest and can be obtained from two-way ANOVAs of marker interactions with H₃. The genotypic expectation for interactions between marker pairs with testcross progenies H₃ is given by

With cofactors in the model and assuming (i) that QTL linked to markers m₁ and m₂ interact only with each other and not with other QTL and (ii) 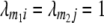, then the genotypic expectations of interactions between markers simplify to

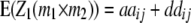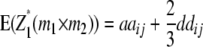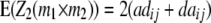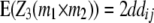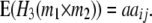While augmented additive and dominance effects are estimated in one-dimensional scans of Z₁ and Z₂, respectively, estimates of two-way marker interactions on Z₁ and Z₁* yield a confounded estimate of aa and dd interactions, and Z₂ captures ad and da epistasis. A first estimate of genetic background interactions contributing to d_i* at QTL i can be obtained with two-way marker interactions on H₃. Unbiased estimates of dd epistasis can be obtained with two-way ANOVAs on Z₃.

It becomes obvious that genetic expectations of two-way marker interactions obtained with the TTC design are not straightforward extensions of effects estimated with the same linear transformation in one-dimensional scans. Note that this is also true under the F_∞ model employed by Kearsey et al. (2003) and Frascaroli et al. (2007) and for the separate analysis of backcross progenies as performed by Stuber et al. (1992). A summary of genetic expectations of QTL effects estimated from one-dimensional genome scans and two-way ANOVAs of marker interactions on (i) the three possible testcrosses (H₁, H₂, H₃), (ii) the RIL lines (H₄), and (iii) the linear transformations Z_s are given in Table 3 for both the F₂- and the F_∞-metric models. Genetic expectations of QTL effects comprising epistatic effects but no main effects are identical for the two models. Genetic expectations of QTL effects obtained with one-dimensional genome scans on Z₁ and Z₂ differ, because under the F_∞ metric estimates of QTL main effects are confounded with epistasis. Following Yang (2004), genetic expectations for the F_∞-metric model are obtained by substituting a_i and d_i of the F₂ model with 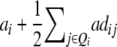and 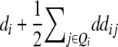, respectively. As evident from Table 3, additional complexity is introduced by the use of the F_∞ metric. In the general case of populations with arbitrary gene frequencies the NOIA model devised by Alvarez-Castro and Calborg (2007) could be used for transforming the QTL effects determined in such a population to the genetic effects defined under the F₂ or the F_∞ metric.

TABLE 3.

Genetic expectations of QTL effects obtained with the triple testcross (TTC) design and estimated from one-dimensional genome scans 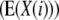and two-way ANOVAs of marker interactions 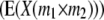between unlinked marker loci m₁ and m₂ (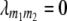) on the three possible testcrosses (H₁, H₂, H₃), the RIL lines (H₄), and the linear transformations Z_s under the F₂- and F_∞-metric models

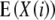
Progeny	F2 metric	F∞ metric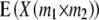
H1	ai + di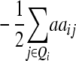	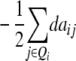ai + di	+ + +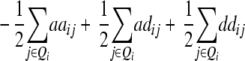
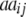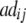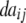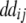
H2	ai − di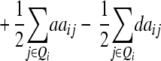	ai − di	− − +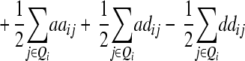
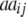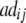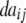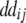
H3	ai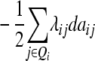	ai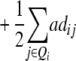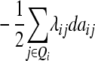
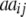H4	2ai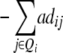	2ai	4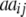
Z1	ai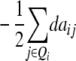	ai	+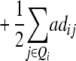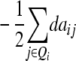
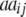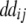
Z1*	ai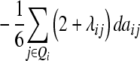	ai	+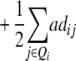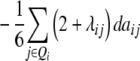
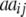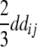
Z2	2di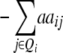	2di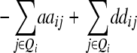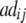	2 + 2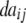
Z3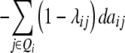
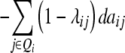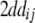Z4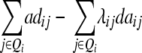

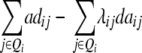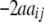DISCUSSION

Genetic expectations of QTL effects:

In this study, genetic expectations of QTL effects are estimated with the TTC design. Accounting for all types of digenic epistasis and arbitrary linkage, genetic expectations are given for one-dimensional genome scans and two-way marker ANOVAs under both the F₂- and the F_∞-metric models. These theoretical results contribute significantly to the interpretation of QTL mapping experiments estimating the type of gene action with the TTC design and the design III. The advantages of these two designs have been widely recognized but, to date, genetic expectations of QTL effects have been given for the design III using only single-marker ANOVA (Cockerham and Zeng 1996) and one-dimensional genome scans with CIM (Melchinger et al. 2007).

When making inferences on the predominant type of gene action, profound knowledge on the genetic expectations of QTL effects is crucial, as was demonstrated by Cockerham and Zeng (1996) with a reanalysis of data from Stuber et al. (1992). Stuber et al. (1992) estimated the type of gene action in a marker-aided design III experiment with F₃ lines of maize. They performed the QTL analysis separately for the testcrosses with each parent (i.e., on H₁ and H₂) and detected that overdominance but not epistasis plays a major role in the inheritance of grain yield. Accounting for epistasis and performing a joint analysis of both testcrosses, Cockerham and Zeng (1996) found mostly QTL with dominant and epistatic gene action. Similarly divergent results were found for experimental studies on rice grain yield. Xiao et al. (1995) found dominance to be the most important type of gene action. When accounting for epistasis in the genetic model, Li et al. (2001) and Luo et al. (2001) detected strong evidence for overdominance and epistasis. Thus, interpretation of experimental results from QTL mapping studies on the predominant type of gene action can be severely affected by the choice of statistical model and the provision of epistasis. As evident from Table 3, genetic expectations of QTL effects estimated with the TTC design and the design III are complex and comprise both main and epistatic effects. This fact has been widely neglected in the literature. The theoretical results presented here assist in the interpretation of experimental results obtained with two of the major designs employed in the analysis of gene action and heterosis. We therefore believe that reanalysis of previously collected data sets with the statistical methods presented here as well as the joint analysis of similar data sets with a special focus on epistasis will be rewarding. The general quantitative genetic theory given in the appendix allows derivation of genetic expectations of QTL effects for experiments where production of testcross progenies was performed with double-haploid lines or F₂ or F₃ populations.

Analysis of heterosis with the TTC design:

Melchinger et al. (2007) demonstrated that in the analysis of the genetic causes of heterosis we need to identify genomic regions that harbor augmented dominance effects d_i* instead of identifying QTL with maximum dominance d_i and dd interactions that control F₁ performance. With the design III, the confounding of QTL effects with epistatic background variation is desirable for the identification of heterotic QTL. However, it is also a limitation because partitioning of augmented QTL effects a_i* and d_i* into their main and epistatic components is not possible. By adding the F₁ as a third tester, this limitation can partially be overcome. The contribution of [da_i·] epistatic interactions of QTL i with the genetic background to the augmented additive effect a_i* can be estimated with genome scans on Z₃ and two-way marker interactions with H₃ can be used to estimate aa interactions of individual QTL with the genetic background. Because the search for interactions may be restricted to those QTL with significant augmented dominance effects (d_i*), the problem of multiple testing is alleviated. However, two-way marker interactions will provide only a rough estimate of the contributions of [aa_i·] epistasis to d_i* due to limited power of detection. Furthermore, QTL with a significant positive dominance effect d_i and positive [aa_i·] epistasis may remain undetected in a genomewide scan with Z₂ if the two effects cancel each other, resulting in nonsignificant d_i* effects. We are currently in the process of developing new experimental designs that allow separate estimation of d_i and [aa_i·] components contributing to d_i* and, consequently, MPH in one-dimensional genome scans.

Detection of epistatic interactions:

The development of statistical tools and powerful experimental designs for an efficient identification of genetic interactions is a major challenge in the analysis of quantitative traits. As a result of limited statistical power, detection of significant epistatic QTL interactions has proved difficult in marker-aided studies on complex traits, such as yield, even with dense marker coverage and large populations (e.g., Schön et al. 2004; Mihaljevic et al. 2005). On the contrary, the presence of significant epistasis has been demonstrated when clearly defined genes were investigated and efficient molecular tools were at hand. Doebley et al. (1995) demonstrated dependency of QTL effects on genetic background for plant and inflorescence architecture in maize and teosinte. Epistatic interactions of QTL and expression QTL (eQTL) involved in regulation of flowering in Arabidopsis were reported by Keurentjes et al. (2007). Kroymann and Mitchell-Olds (2005) cloned two QTL for growth rate in Arabidopsis exhibiting significant epistasis with the genetic background. The authors pointed out that the two QTL would not have been detected with classical QTL analysis approaches and that we are likely to introduce an ascertainment bias because QTL with significant epistatic interaction effects might not be representative of the majority of QTL with small effects contributing to gene networks.

In this study, we have developed a one-dimensional genome scan for epistatic interactions of type dominance × additive. QTL detected with CIM on the linear transformation Z₃ exhibit significant [da_i·] epistasis with the genetic background. With this method, statistical power of detection is increased compared with statistical tests for epistasis based on interactions of all possible marker pairs, because the number of significance tests is greatly reduced and thus safeguarding against a high false discovery rate becomes less rigorous. Employing diallel crosses of three homozygous parents, Jannink and Jansen (2001) proposed a one-dimensional search for significant background interactions of QTL. With simulated data, they reported a twofold increase in power with the proposed one-dimensional search compared with standard two-dimensional searches. Blanc et al. (2006) employed a similar method in an experimental study with multiparental crosses of maize and found substantial evidence for QTL × genetic-background interactions, especially for grain yield. With both methods the partitioning of epistasis into its components is not feasible. Nevertheless, with the increasing availability of QTL mapping populations derived from multiline crosses these methods are a valuable contribution to the identification of QTL with significant interactions with the genetic background.

In addition to genetic interactions of type dominance × additive [da_i·], interactions of type additive × dominance [ad_i·] can be detected in the absence of linkage with a one-dimensional genome scan on the linear transformation Z₄ = 2H₃ − H₄ if, in addition to the testcrosses of the RILs, their line per se performance (H₄) is tested, as was done by Frascaroli et al. (2007) and Kusterer et al. (2007) (see the appendix and Table 3). Epistatic interactions of type [ad_i·] or [da_i·] of QTL i may not play a major role in elite breeding material, because when summed over the entire genetic background, they are likely to cancel each other due to opposite signs of individual interactions. However, so far we have not been able to verify this hypothesis in QTL analyses. Many experimental studies demonstrated only minor importance of significant ad or da epistasis on the basis of two-way ANOVAs of marker interactions (e.g., Hua et al. 2003) but it has been difficult to distinguish between true and false negatives due to the limitations of statistical tests. With the variance component 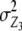, the TTC design provides a significance test for the presence of ad and da epistasis. With the one-dimensional genome scan on Z₃ and Z₄ (if data on per se performance of RILs are available) and reasonable sample sizes we can achieve sufficient power to estimate the magnitude of [ad_i·] or [da_i·] interactions of individual QTL as well as the hypothesis [ad_i·] = [da_i·]. Once QTL are identified to interact with the genetic background, two-way marker ANOVAs on Z₂ can be performed to obtain individual estimates of QTL interactions between these QTL and other QTL in the genome .

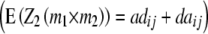In conclusion, we are still at the beginning of understanding the complex interactions of individual genes and gene networks even with extensive genomic tools at hand. Knowledge about genetic expectations of QTL effects in the presence of epistasis will facilitate the assessment of gene action and function and will help elucidate the quantitative genetic basis of heterosis. As pointed out by Jannink and Jansen (2001), marker-assisted transfer of single genes affecting quantitative traits may be a fruitless endeavor if alleles show strong epistasis and fail to interact with the target genome in the same way as with the donor genome. On the other hand, with a more profound understanding of gene interactions, breeders may be empowered to utilize new alleles from nonadapted genetic resources or genetic engineering that exhibit favorable epistasis with the genetic background. In combination with newly developed statistical methods, such as Bayesian approaches (Xu and Jia 2007), multiple-interval mapping (Kao et al. 1999), or two-stage analyses (Brem et al. 2005), powerful experimental designs can significantly increase the efficiency of experiments analyzing phenotypic data on agronomic traits such as yield. Furthermore, the same experimental designs can be used for molecular studies on the quantitative genetics of transcription, protein, or metabolite data. We believe that the analysis of gene interactions will be of increasing importance in future molecular and quantitative genetics research and that the theoretical results from this study provide improved analytical tools for the interpretation of a wide range of experimental data.

APPENDIX: GENERAL DERIVATION OF EXPECTATIONS, VARIANCES, AND COVARIANCES OF LINEAR TRANSFORMATIONS Z_S FOR THE TTC DESIGN

Following Melchinger et al.'s (2007) expectations, variances and covariances of linear transformations Z_s (Z_s = Z₁, Z₁*, Z₂, Z₃, Z₄) are given by

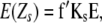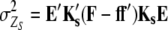and

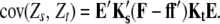Assuming digenic epistasis 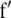denotes the frequencies of the four possible genotypes at two QTL i and j, F denotes a diagonal matrix with these frequencies on the diagonal, and E denotes the vector of genetic effects 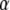_AD; i.e., .

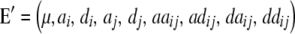Elements of the matrix H_t denote the coefficients of genetic effects 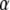_AD in the conditional genotypic expectation of testcross progeny H_t of a RIL with genotype v_iv_j (v_iv_j = 22, 20, 02, 00) at QTL i and j for testcross performance (t = 1, 2, 3) with tester P1 (t = 1), P2 (t = 2), or F₁ (t = 3) or per se performance (t = 4). Assuming digenic epistasis, elements of H_t are given in Table A1. The matrices K_s are obtained for the TTC design by calculating

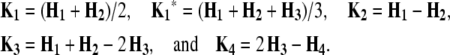TABLE A1.

Coefficients in 4 × 9 matrix H_t (t = 1, 2, 3, 4) for the conditional expectation of the genotypic value of testcross progeny H_t of a RIL with genotype v_iv_j (v_iv_j = 22, 20, 02, 00) at QTL i and j for testcross performance (t = 1, 2, 3) with tester P1 (t = 1), P2 (t = 2), or F₁ (t = 3) or per se performance (t = 4)

	Genetic parameter
RIL genotype vivj	μ	ai	1/2di	aj	1/2dj	aaij	1/2adij	1/2daij	1/4ddij
H1 (testcrosses with P1)
22	1	0	1	0	1	0	0	0	1
20	1	0	1	−1	−1	0	0	−1	−1
02	1	−1	−1	0	1	0	−1	0	−1
00	1	−1	−1	−1	−1	1	1	1	1
H2 (testcrosses with P2)
22	1	1	−1	1	−1	1	−1	−1	1
20	1	1	−1	0	1	0	1	0	−1
02	1	0	1	1	−1	0	0	1	−1
00	1	0	1	0	1	0	0	0	1
H3 (testcrosses with F1)
22	1	1/2	0	1/2	0	(1 + λ)/4	−λ/2	−λ/2	λ
20	1	1/2	0	−1/2	0	−(1 + λ)/4	λ/2	−λ/2	−λ
02	1	−1/2	0	1/2	0	−(1 + λ)/4	−λ/2	λ/2	−λ
00	1	−1/2	0	−1/2	0	(1 + λ)/4	λ/2	λ/2	λ
H4 (per se performance)
22	1	1	−1	1	−1	1	−1	−1	1
20	1	1	−1	−1	−1	−1	−1	1	1
02	1	−1	−1	1	−1	−1	1	−1	1
00	1	−1	−1	−1	−1	1	1	1	1