Exploring Population Genetic Models With Recombination Using Efficient Forward-Time Simulations

Abstract

We present an exact forward-in-time algorithm that can efficiently simulate the evolution of a finite population under the Wright–Fisher model. We used simulations based on this algorithm to verify the accuracy of the ancestral recombination graph approximation by comparing it to the exact Wright–Fisher scenario. We find that the recombination graph is generally a very good approximation for models with complete outcrossing, whereas, for models with self-fertilization, the approximation becomes slightly inexact for some combinations of selfing and recombination parameters.

COALESCENT theory provides a continuous-time approximation for the history of small samples in large populations and coalescent simulation is a widely used tool in population genetics. Under this framework, the genealogy of a sample of DNA sequences is modeled backward in time and neutral mutations are superposed on this genealogy to generate sequence polymorphism data (Kingman 1982; Hudson 1983; Rosenberg and Nordborg 2002). Forward simulations, in contrast, model the evolution of all the sequences in a population exactly, forward in time and generation by generation. Because coalescent simulations consider only those chromosomes that carry material ancestral to the sample, and, by making a continuous-time approximation skip uninteresting generations whose events do not affect the sample, they are computationally much more efficient than forward simulation programs. However, despite their inefficiency, forward simulations are necessary if we wish to simulate data sets under complex and realistic biological scenarios (e.g., natural selection at multiple linked loci) that are difficult to model accurately using the coalescent. Given the dramatic growth in the power of computing, forward-time simulations are currently feasible for large genomic regions (e.g., megabase scale) and many simulation packages have been developed recently (e.g., Balloux 2001; Hey 2004; Hoggart et al. 2005; Peng and Kimmel 2005; Dudek et al. 2006; Guillaume and Rougemont 2006; Sanford et al. 2007) and have also found important applications (e.g., Balloux and Goudet 2002; Pineda-Krch and Redfield 2005; Peng and Kimmel 2007). Here, we present an exact forward-in-time algorithm that can efficiently simulate the evolution of a finite population undergoing mutations, recombination, and natural selection at multiple linked loci. In contrast to existing forward-time simulators that consider the population genealogy generation by generation, our forward algorithm uses the genealogical information for multiple generations at a time, and on the basis of this information, simulates only those chromosomes in the next generation that can potentially contribute to the future population. We show that such a forward–backward scheme combined with other optimizations can lead to substantial improvements in run-time efficiency. We use our simulation program to evaluate coalescent models with recombination by comparing them to the exact Wright–Fisher model.

SIMULATION ALGORITHM

Our algorithm is implemented in the C++ programming language and we simulate data sets under the Wright–Fisher model assumptions. Individuals in a population are assumed to be diploid, the population size is assumed constant (this assumption can readily be relaxed), and generations are always nonoverlapping. Chromosomes within the population are represented by sorted arrays of integers that correspond to the locations of their mutations in base pairs. In this representation, a location is considered polymorphic if it occurs in some but not all of the chromosomes. Over time, the chromosome arrays undergo changes due to recombination (i.e., are partially replaced by parts of other arrays) and mutation (i.e., new integer locations get inserted). They also increase or decrease in the number of copies due to genetic drift. At any given time, we keep track of chromosomes belonging only to the current and previous generations and keep reusing these arrays. We use a pseudo infinite-sites model for mutations (i.e., where the number of sites is finite but new mutations can appear only at nonpolymorphic locations) and a finite-sites model for recombination and remove locations that are no longer polymorphic, at regular intervals. The total number of new mutations added to a chromosome in any particular generation is modeled as a Poisson random variable with mean equal to the per-generation per-sequence mutation rate u. Meiotic recombination is modeled as a single crossing-over event and the probability that a recombination event occurs in any particular generation is equal to 1 − e^−r, where r denotes the per-generation per-sequence rate of recombination.Our forward algorithm proceeds by simulating the population in the next generation as a function of (i) the population in the previous generation and (ii) the simulated genealogy for the next k generations. We use the simulated genealogy to tell us which of the chromosomes in the next generation can contribute material to the future population that exists after k generations from now. Only those chromosomes are explicitly simulated in the next generation since all the other chromosomes are destined to disappear. We outline all the steps in our simulation program below:

1. Let gen(0) represent the current generation, gen(1) represent the generation being simulated, and gen(2), gen(3), gen(4), … , etc., represent subsequent generations. Before creating the individuals of gen(1), we generate the future genealogical information of the population for k generations [i.e., information required for creating gen(2) to gen(k + 1)]. This involves simulating the ancestry of the chromosomes in the next k generations and determining whether or not they will undergo recombination in any particular generation. Using this information, we can see that two key events are possible:

   1. All the descendants of a chromosome belonging to gen(1) may be lost by gen(k + 1) without any of their homologs having undergone recombination.
   2. A chromosome or its homolog may recombine in gen(2), but both of them can lose all their descendants by gen(k + 1) without any of their homologs having undergone any subsequent recombination [i.e., from gen(3) to gen(k + 1)]. Chromosomes that belong to categories a or b, cannot potentially leave any trace in the future population that exists at gen(k + 1). Therefore, it is not necessary to explicitly simulate such chromosomes in gen(1).

2. Chromosomes of gen(1) are created by randomly sampling chromosomes from gen(0) and determining whether or not they undergo recombination. When a chromosome of gen(0) gets chosen the first time and does not recombine, we simply exchange the pointers to the arrays between gen(1) and gen(0) to create a new chromosome of gen(1). If it gets picked again or if it undergoes recombination, we create a new chromosome by copying parts of the relevant arrays into the arrays of gen(1) using the memcpy() function. The only exception to this occurs when a recombination is the last event involving a particular individual. In this case, we first exchange the pointers to the arrays for one of the homologs (provided it has not been picked already) and explicitly copy only part of the other array using memcpy(). After creating all the chromosomes of gen(1), we generate new mutation locations for each chromosome and insert them into the sorted arrays using a binary search and the memove() function.

3. Using the future genealogical information, create only those chromosomes in gen(1) that can potentially contribute to the population that exists at gen(k + 1). Assume that the other arrays are empty. [Note that the main idea in step 2, when creating a new generation, was to reuse the arrays from the previous generation as much as possible and avoid copying. If we eliminate some of the nonancestral chromosomes from any generation (see appendix a), the fraction of chromosomes for which explicit array copying is necessary decreases substantially.]

4. Update the future genealogy by one more generation. Repeat step 3. Remove nonpolymorphic locations from the population at regular intervals.

5. Simulate the whole population during the last k + 2 generations of the simulation (i.e., if the simulation is run for l generations, we explicitly simulate all the chromosomes from generations l − k − 1 to l) as well as during the last k + 2 generations up to the generation during which nonpolymorphic locations get removed from the population (i.e., if fixed mutations get removed every n generations, then we explicitly simulate all the chromosomes from generations n − k − 1 to n, 2n − k − 1 to 2n, 3n − k − 1 to 3n, … , etc.). [Note that this last step is essential because at the end of the simulation as well as during the generation at which nonpolymorphic locations get removed, we require all the chromosomes present in the population (for example, to determine which chromosomal locations are nonpolymorphic) and not just the ones that can contribute to the future population.]

The parameter k has to be chosen optimally for this algorithm to work most effectively. There is a trade-off between the computational effort spent to look forward for k generations and the effort saved by the elimination of nonancestral chromosomes from the next generation. In terms of run-time complexity, creating a new generation mainly involves array copy operations that take linear [i.e., O(N)] time in terms of the number of mutations [binary search takes O(ln(N)) time while exchanging the pointers takes constant time] accumulated in the array. In contrast, looking forward for a few generations takes only constant time and is independent of the number of mutations carried.

The expected proportion of individuals in categories a or b first increases as the depth of the look-ahead (i.e., k) increases but eventually becomes nearly constant. So, increasing k beyond a certain range will not be desirable. The expected proportion decreases as the per-generation per-sequence recombination rate increases, and therefore this strategy becomes less effective for high values of r. Table 1 shows the expectation of the fraction of chromosomes in category a as a function of k and r for a population with 500 diploid individuals and evolving under the standard neutral model (also see appendix a). In all the simulations presented here, we use a fixed value of k = 8 and remove nonpolymorphic locations after every N generations, where N denotes the size of the population (appendix b shows some run-time comparisons for different values of the look-ahead parameter).

TABLE 1.

The fraction of chromosomes in class a as a function of k and r

ka	rb	Fraction in class ac	2Nd
2	0.000000	0.531224	1000
2	0.105361	0.464082	1000
2	0.287682	0.381282	1000
4	0.000000	0.687642	1000
4	0.105361	0.565018	1000
4	0.287682	0.435589	1000
8	0.000000	0.810645	1000
8	0.105361	0.609490	1000
8	0.287682	0.447974	1000

^aNumber of generations of look-ahead under the standard neutral model.

^bPer-generation per-sequence recombination rate.

^cAverage fraction of chromosomes in class a as determined from 10 million simulations. Chromosomes in class a cannot potentially leave any trace in the future population that exists after k generations.

^dTotal number of chromosomes in the diploid population.

For models with natural selection, we simulate the evolution of selected and neutral sites separately. We first generate the future genealogical information by simulating the ancestry of all the chromosomes in the population considering only the selected sites. If the number of sites under selection remains small, this information can be generated quickly. Then, using this information, we simulate the evolution of the remaining (neutral) sites according to the algorithm described earlier. Note that as the proportion of sites under selection increases, the look-ahead strategy becomes relatively less effective.

Random number generation:

Random numbers are generated using the Mersenne Twister algorithm (Matsumoto and Nishimura 1998). The external files mtrand.cpp and mtrand.h are used along with our program to enable random number generation. mtrand.cpp is a fast and high-quality random number generator whose period length is a large prime number that is one less than a power of 2.

Comparison with other forward simulation programs:

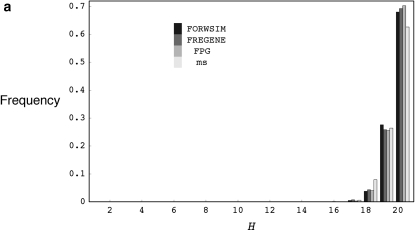
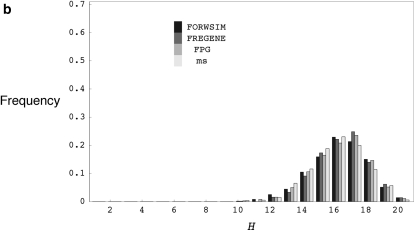
We first compare the approximate running time of our simulation program (FORWSIM) with two other currently available forward-time simulation programs for the standard neutral model. These comparisons demonstrate that our look-ahead strategy combined with other standard optimizations can result in large gains in run-time efficiency (Table 2a, appendix c shows some run-time comparisons for models with natural selection at multiple sites). The comparisons also confirmed that, for all the programs tested, the means and distributions of some simple summary statistics are in agreement with coalescent simulations (Table 2b, Figure 1).

TABLE 2.

Approximate run times for forward simulation programs and average value of summary statistics for forward and coalescent simulation programs

				Timee
2Na	Generations	ub	rc	FORWSIMd	FREGENEf	FPGg	msh	Len (Mb)
a. Approximate run times for forward simulation programs
100	1,000	0.01	0.01	0.03	0.06	1.61	0.006	0.05
100	1,000	0.10	0.10	0.04	0.08	2.09	0.006	0.05
100	1,000	0.25	0.25	0.05	0.11	2.89	0.0075	0.05
1,000	10,000	0.01	0.01	1.74	4.71	265.06	0.006	0.05
1,000	10,000	0.10	0.10	2.85	18.50	450.90	0.035	1.00
1,000	10,000	0.25	0.25	6.51	43.79	1136.29	0.367	1.00
10,000	100,000	0.01	0.01	281.42	2241.59	45868.58	0.023	1.00
10,000	100,000	0.10	0.10	1153.41	13620.02	—	8.701	10.00
10,000	100,000	0.25	0.25	4470.48	34825.89	—	40.663	50.00

				FORWSIM		FREGENE		FPG		msh
2N	Generations	u	r	E[S]i	E[H]j	E[S]	E[H]	E[S]	E[H]	E[S]	E[H]
b. Average value of summary statistics for forward and coalescent simulation programs
1,000	10,000	0.01	0.01	71.250	16.066	69.637	16.242	71.551	16.078	71.016	15.916
1,000	10,000	0.10	0.10	708.614	19.612	704.071	19.635	708.089	19.656	706.603	19.538

^aTotal number of chromosomes under the standard neutral Wright–Fisher model with constant population size and with uniform mutation and recombination rates.

^bPer-generation per-sequence mutation rate.

^cPer-generation per-sequence recombination rate.

^dFORWSIM is our C++ program freely available at http://people.cornell.edu/pages/bp85.

^eTime taken in seconds for a single run on a 2.2 Ghz 64-bit AMD processor machine with 8 GB of RAM.

^fFREGENE is a C++ program freely available at http://www.ebi.ac.uk/projects/BARGEN/download/FREGEN/fregeneweb.html.

^gFPG is a C program freely available at http://lifesci.rutgers.edu/∼heylab/ProgramsandData/Programs/FPG/FPG_Documentation.htm#FilesinthisPackage. For FPG, the number of chromosome segments was always fixed at 500.

^hms is a C program that simulates data sets under the coalescent framework and is freely available at http://home.uchicago.edu/∼rhudson1/source.html. ms was run with population crossing-over rate ρ = 4Nr and population mutation rate θ = 4Nu and sample size of 20. (For details about ms, see Hudson 2002.)

ⁱTotal number of SNPs for a sample size of 20 chromosomes. Average values are based on 1000 simulations.

^jNumber of distinct haplotypes. Average values are based on a sample of 20 chromosomes and 1000 simulations.

Figure 1.—

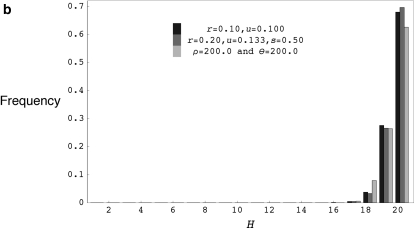
(a) The distribution of the number of distinct haplotypes H for coalescent simulations with ρ = 200.0 and θ = 200.0 and forward simulations with r = 0.100, u = 0.100, and 2N = 1000, using FORWSIM, FREGENE, and FPG. (b) The distribution of the number of distinct haplotypes H for coalescent simulations with ρ = 20.0 and θ = 20.0, and forward simulations with r = 0.010, u = 0.010, and 2N = 1000, using FORWSIM, FREGENE, and FPG. H values are for samples of 20 chromosomes and forward simulation programs were run for 20N generations.

IS THE ANCESTRAL RECOMBINATION GRAPH A GOOD APPROXIMATION TO THE EXACT SCENARIO?

Under the coalescent framework, the genealogy of a sample of sequences with recombination can be approximated by a graph called the ancestral recombination graph (ARG) (e.g., see Hudson 1983; Griffiths and Marjoram 1996). If s denotes the probability of self-fertilization and F = s/(2 − s), the genealogy of a sample for partial selfing (i.e., 0 < s < 1) can be approximated by an outcrossing version of the ARG with a rate of coalescence that is 1 + F times faster and a rate of recombination that is 1 − s times slower (see Nordborg 2000). The recombination graph makes two main assumptions:

1. It assumes that the lineages we follow backward in time recombine only with nonancestral lineages. This follows because we are tracing the ancestry of small samples in large populations and therefore the number of lineages ancestral to the sample remains small compared to the total population size.

2. It also assumes that in a large population all the recombination events are independent of one another. We use forward simulations of the exact Wright–Fisher model with and without self-fertilization and compare the expected decay of pairwise linkage disequilibrium (LD) to values generated with equivalent coalescent simulations and verify the accuracy of these approximations.

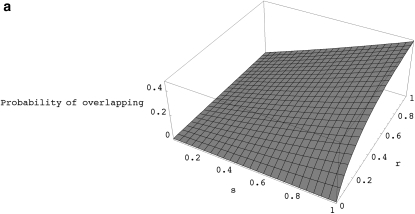
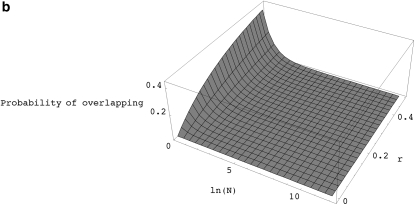
When the recombination rate is high, the number of ancestral lineages in the recombination graph can become very large and so it is not obvious whether the first approximation will be accurate in finite populations. When there is partial selfing, going backward in time, a pair of lineages resulting from a single recombination event can spend a significant amount of time together within the same ancestors before they find different parents or coalesce. Thus, it can be shown that there is a significant probability that such lineages may recombine again (i.e., overlapping recombinations) before they find different ancestors (see appendix d, Figure 2a). This clearly violates the assumption that all recombination events happen independently of one another. For models without selfing, the probability of such overlapping recombination events is expected to be much smaller as long as the population size is reasonably large (see appendix d, Figure 2b).

Figure 2.—

(a) The probability of overlapping recombination events as a function of the recombination rate (r) and the probability of self-fertilization (s) for a population with N = 1000 diploid individuals. (b) The probability of overlapping recombination events as a function of recombination rate (r) and population size (N) for models without self-fertilization (i.e., s = 0).

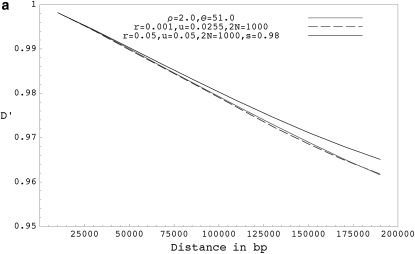
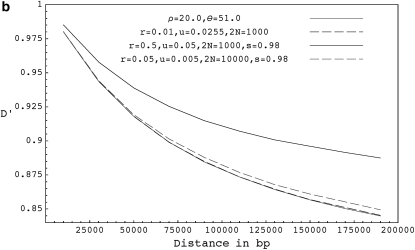
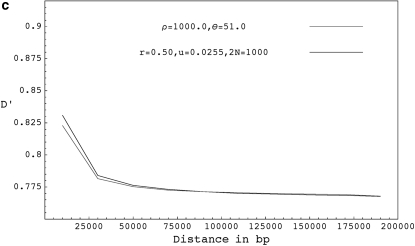
Figure 3 shows the expected decay of the absolute value of pairwise D′ (the normalized measure of LD that takes values between −1 and 1) for forward-time simulations with selfing, forward-time simulations without selfing, and coalescent simulations with equivalent parameters. When simulating using the coalescent, we assume that recombination happens only with nonancestral chromosomes, which ignores the chance of recombination events between ancestral lineages. When r is high, the expected value of D′ is slightly higher in forward simulations without selfing than in comparable coalescent simulations presumably because the number of ancestral lineages is large and recombinations with ancestral lineages are not rare. Because recombination events with ancestral lineages will be associated with some coalescence, we reach the most recent common ancestor slightly sooner in the exact case than in the ARG. Nevertheless, for models with only outcrossing, we see from results in Figures 1, 3, and from Table 2, that the expectations and distributions under the coalescent with recombination are close to the expectations under the exact scenario even for higher values of r. We also compared the frequencies of some triplet based LD patterns (Padhukasahasram et al. 2004, 2006) at different distances and reached similar conclusions (results not shown here). For models with selfing, the ARG remains a close approximation to reality as long as either r or s remains small (Figures 3 and 4, Table 3). When r and s are both very high, the ARG approximation breaks down due to overlapping recombination events and expected value of D′ is significantly higher in forward simulations compared to the equivalent coalescent model.

Figure 3.—

(a) The expected decay of pairwise D′ for coalescent simulations with ρ = 2.0 and θ = 51.0 (shaded curve), forward simulations with r = 0.001, u = 0.0255, and 2N = 1000 (solid dashed curve), and forward simulations with selfing for r = 0.05, u = 0.05, 2N = 1000, and s = 0.98 (solid curve). (b) The expected decay of pairwise D′ for coalescent simulations with ρ = 20.0 and θ = 51.0 (shaded curve), forward simulations with r = 0.01, u = 0.0255, and 2N = 1000 (solid dashed curve), forward simulations with r = 0.5, u = 0.05, 2N = 1000, and s = 0.98 ( solid curve), and forward simulations with r = 0.05, u = 0.005, 2N = 10,000, and s = 0.98 (shaded dashed curve). (c) The expected decay of pairwise D′ for coalescent simulations with ρ = 1000.0 and θ = 51.0 (shaded curve), and forward simulations with r = 0.50, u = 0.0255, and 2N = 1000 (solid curve). D′ values shown are based on a sample size of 20 chromosomes collected from the final populations and are averaged over 10,000 runs. Forward simulations were run for 40N generations.

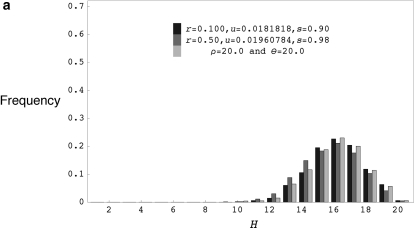
Figure 4.—

(a) The distribution of the number of distinct haplotypes H for coalescent simulations with ρ = 20.0 and θ = 20.0, forward simulations with r = 0.100, u = 0.0181818, s = 0.90, and 2N = 1000 and forward simulations with r = 0.50, u = 0.01960784, s = 0.98, and 2N = 1000. (b) The distribution of the number of distinct haplotypes H for coalescent simulations with ρ = 200.0 and θ = 200.0, forward simulations with r = 0.200, u = 0.1333333, s = 0.50, and 2N = 1000 and forward simulations with r = 0.10, u = 0.10, and 2N = 1000. H values are for samples of 20 chromosomes drawn from the final population and forward simulation programs were run for 40N generations for models with selfing and 20N generations for models without selfing.

TABLE 3.

Average value of summary statistics for forward simulations with and without selfing

					FORWSIMe		msf
2Na	Generations	ub	rc	sd	E[S]g	E[H]h	E[S]	E[H]
1,000	10,000	0.0100	0.0100	0.00	71.250	16.066	71.016	15.916
1,000	20,000	0.0182	0.1000	0.90	70.687	15.968	71.016	15.916
1,000	20,000	0.0196	0.5000	0.98	70.804	15.586	71.016	15.916
1,000	10,000	0.1000	0.1000	0.00	708.614	19.612	706.603	19.538
1,000	20,000	0.1333	0.2000	0.50	711.662	19.563	706.603	19.538

^aTotal number of chromosomes under the standard neutral Wright–Fisher model with constant population size and uniform mutation and recombination rates.

^bPer-generation per-sequence mutation rate.

^cPer-generation per-sequence recombination rate.

^dProbability of selfing.

^eFORWSIM is our forward simulation program written in C++ and is freely available at http://people.cornell.edu/pages/bp85.

^fms is a C program that simulates data sets under the coalescent framework and is freely available at http://home.uchicago.edu/∼rhudson1/source.html. ms was run with the population crossing-over rate ρ = 4Nr and population mutation rate θ = 4Nu.

^gTotal number of SNPs for a sample size of 20 chromosomes. Average values are based on 1000 simulations.

^hNumber of distinct haplotypes. Average values are based on a sample of 20 chromosomes and 1000 simulations.

SUMMARY

We have presented an exact forward-in-time algorithm that can efficiently simulate the evolution of a finite population under the Wright–Fisher model of evolution. Comparisons with other currently available forward-in-time simulators show that our C++ program is able to simulate data sets quickly and all the tested programs appear to function correctly. Further refinements to our algorithm are possible to improve its efficiency. For example, instead of using a constant depth of look-ahead, we may change the depth during the run. Note that toward the later stages of a simulation, when the amount of polymorphism in the population becomes high, a deeper look-ahead might prove to be more advantageous. Also, it may be possible to determine other categories of chromosomes (apart from those in classes a or b) that cannot potentially leave any trace in the future population that exists after k generations. Alternately, instead of using the look-ahead strategy described before, we may explicitly construct chromosomes for a small number of generations in terms of the chromosomes of gen(1) by generating the recombination breakpoints of the future (this may be useful when r is very high). Doing this will allow us to eliminate all the chromosomes that are nonancestral to the population that exists at gen(k + 1) but will require greater computational effort than the former look-ahead strategy. Finally, we anticipate that a parallel implementation of this algorithm that can simultaneously utilize a large number of computer processors (which can all access the same memory), can make forward-time simulations practical for very large populations.

We checked the accuracy of the ancestral recombination graph approximation by comparing the expected decay of pairwise linkage disequilibrium in forward and coalescent simulations. Our results indicate that the standard coalescent with recombination will be a close approximation to the exact scenario for completely outcrossing populations with 2N = 1000 chromosomes or more, even for higher values of r. The ARG is also a good approximation for models with selfing as long as either the selfing rate (s) or recombination rate (r) remains small. When s and r are both very high, the scaled ARG for partial self-fertilization becomes slightly inexact due to substantial probability of overlapping recombination events. Therefore, for such parameter ranges, it is best to simulate data sets using exact Wright–Fisher simulations (or alternately modify existing coalescent simulation programs to allow for overlapping recombination events).

APPENDIX A: CALCULATIONS

Let gen(0) represent the current generation, gen(1) represent the generation being simulated and gen(2), gen(3), gen(4), …, etc., represent subsequent generations. Let 2N denote the total number of chromosomes in the population and k denote the number of generations of look-ahead. Assuming random mating as follows: v(m), the probability that m chromosomes do not get chosen for the next generation is (1 − m/2N)^2N: q(m), the probability that a chromosome is chosen exactly m times is ^2NC_m(1/2N)^m(1 − 1/2N)^2N−m.

Assuming n copies of a chromosome in the current generation, the probability that exactly m copies get chosen in the next generation is s(n, m) = ^2NC_m(n/2N)^m(1 − n/2N)^2N−m.

The chance that a chromosome does not recombine in any given generation is approximately e^−r.

Assuming n copies of a chromosome in the current generation, the chance that none of the copies of the chromosome that get picked in the next generation, recombine, can be approximated as

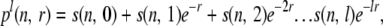(A1)

where l denotes the maximum number of copies that can be picked in the next generation.

For k = 1 and r > 0, a chromosome can be lost if it does not get picked in gen(2). Therefore, the chance that a chromosome is lost without its homolog having undergone recombination is

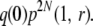For k = 2 and r > 0, a chromosome can be lost if it does not get picked in gen(2) or gets picked 1 to 2N − 1 times in gen(2) but none of those copies get picked in gen(3). Therefore, the probability that all the copies of a chromosome are lost without any of their homologs having undergone any recombination is nearly

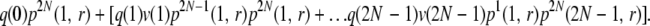(A2)

Note that if a chromosome gets picked m times in the next generation, then its homolog can get picked at most 2N − m times and therefore we have to choose l appropriately in the terms in Equation A2. We assume that if there are x copies of a chromosome in any given generation, then there are also x homologs, when calculating the probability that none of those homologs will recombine. There is a small chance that some of the copies of a chromosome will be homologs of one another in the next generation. Therefore, the probability given by Equation A2 is not exact.

In general, when N is large, a is small and r > 0, the chance P(a) that all the descendants of a chromosome from gen(1) are lost at gen(a + 2) but not before that, without any of their homologs having undergone recombination is nearly 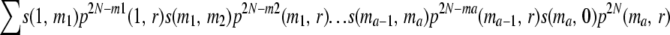, where m₁, m₂, … , m_a can all vary from 1 to 2N − 1. Therefore, for k > 0, the total probability T(k) that all the copies of a chromosome are lost by gen(k + 1), without any of their homologs having undergone any recombination is nearly

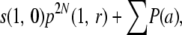(A3)

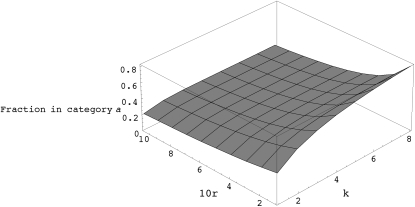
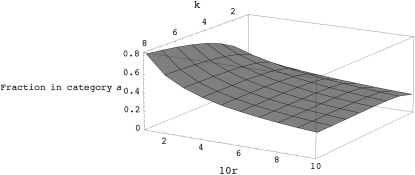
where a varies from 0 to k − 1. Table A1 shows the approximate probability given by (A3) as a function of k and r. Figures A1 and A2 show different views of this likelihood surface.

Figure A1.—

The fraction of chromosomes in category a as a function of recombination rate (r) and number of generations of look-ahead (k).

Figure A2.—

The fraction of chromosomes in category a as a function of recombination rate (r) and number of generations of look-ahead (k).

For r = 0, T(k) is exactly equal to

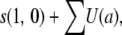(A4)

where a varies from 0 to k− 1 and U(a) = 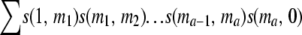, where m₁, m₂, …, m_a all vary from 1 to 2N − 1.

TABLE A1.

Approximate probability that a chromosome is in class a as calculated from Equation A3

ka	rb	Fraction in class ac	Fraction in class ad	2Ne
2	0.000000	0.531224	0.531224	1000
2	0.105361	0.464134	0.464082	1000
2	0.287682	0.381373	0.381282	1000
4	0.000000	0.687639	0.687642	1000
4	0.105361	0.565068	0.565018	1000
4	0.287682	0.435686	0.435589	1000
8	0.000000	0.810644	0.810645	1000
8	0.105361	0.609553	0.609490	1000
8	0.287682	0.448077	0.447974	1000

^aNumber of generations of look-ahead under the standard neutral model.

^bPer-generation per-sequence recombination rate.

^cApproximate probability that a chromosome is in class a as calculated from Equation A3.

^dProbability that a chromosome is in class a as calculated from 10 million simulations.

^eTotal number of chromosomes in the diploid population.

APPENDIX B

TABLE B1.

FORWSIM running times for different values of the look-ahead parameter

					Timed
2Na	Gen	Length (Mb)	ub	rc	No look-ahead	ke= 2	k = 8	k = 12
10,000	100,000	1.0	0.01	0.01	381.35	210.73	170.28	198.59
10,000	100,000	20.0	0.10	0.10	2593.21	1082.32	771.02	786.98
10,000	100,000	50.0	0.25	0.05	6482.35	2329.72	1187.71	1151.42
10,000	100,000	50.0	0.25	0.25	7521.44	3546.32	2700.23	3006.86
20,000	200,000	20.0	0.01	0.01	2368.04	1192.49	915.21	1141.35
20,000	200,000	50.0	0.10	0.10	9505.73	3573.17	2192.54	2315.15

^aTotal number of chromosomes in the diploid population.

^bPer-generation per-sequence mutation rate.

^cPer-generation per-sequence recombination rate.

^dTime taken in seconds on a machine with two 2.66 GHz dual-core Intel Xeon processors and 8 GB of RAM.

^eNumber of generations of look-ahead under the standard neutral model.

APPENDIX C

TABLE C1.

Approximate run-times for models with positive selection at multiple sites

						Timef
2Na	Generations	ub	rc	hd	se	NEWSELg	FPGh
1,000	10,000	0.01	0.01	0.50	0.01	4.78	82.06
1,000	10,000	0.10	0.10	0.50	0.01	5.70	174.91

^aTotal number of chromosomes under the standard Wright–Fisher model with constant population size and uniform mutation and recombination rates.

^bPer-generation per-sequence mutation rate.

^cPer-generation per-sequence recombination rate.

^dDominance. A value of 0.5 denotes incomplete dominance in heterozygotes.

^eStrength of selection per sequence.

^fApproximate time taken for a single run on a machine with two 2.66 GHz dual-core Intel Xeon processors and 8 GB of RAM.

^gNEWSEL is our C++ program freely available at http://people.cornell.edu/pages/bp85. We ran our simulation program under a simple model where 40 known sites are subject to positive selection and fitness effects are additive.

^hFPG is a C program freely available at http://lifesci.rutgers.edu/∼heylab/ProgramsandData/Programs/FPG/FPG_Documentation.htm#FilesinthisPackage. FPG was run for roughly comparable parameters for the same model.

APPENDIX D

Let N be the total number of individuals in the population and s be the selfing probability and r be the per-generation per-sequence recombination rate. For a given chromosome, the chance of no recombination events in any given generation can be approximated by e^−r. We first calculate the probability that, going backwards in time, a pair of lineages resulting from a recombination event will eventually find two different ancestors.

The probability that it finds different ancestors in the first generation is (1 − s)(1 − 1/N) (i.e., not created by selfing and choose different ancestors).

The probability that it finds different ancestors in the second generation is (s/2 + (1 − s)/(2N))(1 − s)(1 − 1/N) [i.e., probability of selfing but choosing different chromosomes in the same ancestor in the first generation (i.e., s/2) or not created by selfing but picking different chromosomes within the same parent in the first generation (i.e., (1 − s)/2N) and then not created by selfing and choosing different ancestors in the second generation].

The probability that it finds different ancestors in the second generation without further recombination is (s/2 + (1 − s)/(2N))(1 − s)(1 − 1/N)e^−2r.

In general, the probability that a pair finds different ancestors in the nth generation but not before that is: (s/2 + (1 − s)/(2N))ⁿ⁻¹(1 − s)(1 − 1/N) and the probability that this happens without subsequent recombinations is (s/2 + (1 − s)/(2N))ⁿ⁻¹(1 − s)(1 − 1/N)e^−(2n−2)r.

Thus, the total probability that a recombination event will eventually split lineages into two separate ancestors is (summing up to n = infinity) 2(1 − s)(1 − 1/N)/(2 − (s + (1 − s)/(N))). Now, the total probability that this happens without any subsequent recombination events is (summing appropriate terms up to n = infinity) 2(1 − s)(1 − 1/N)/(2 − (s + (1 − s)/(N))e^−2r). Therefore, the probability of overlapping recombination events, given that after a recombination event the pair of lineages will find different ancestors is (s + (1 − s)/(N))(1 − e^−2r)/(2 − (s + (1 − s)/(N))e^−2r). Figure 2a shows this probability as a function of s and r.

Similarly, for models without self-fertilization, going backward in time, the probability that a pair of lineages finds different ancestors in the first generation is (1 − 1/N). The probability of finding different ancestors in the second generation is (1 − 1/N)/2N (i.e., pick different chromosomes in the same parent in the first generation (i.e., 1/2N) and pick different parents in the second generation, etc.). The probability of finding different ancestors in the second generation without subsequent recombination is (1 − 1/N)e^−2r/2N.

In general, the probability that a pair of lineages finds different ancestors in the nth generation is (1 − 1/N)/(2N)ⁿ⁻¹and the probability that this happens without subsequent recombinations is

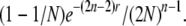The total probability that after a recombination event, a pair of lineages will eventually find two separate ancestors is (summing appropriate terms up to infinity) 2N − 2/(2N − 1) and the total probability that this happens without any subsequent recombination is 2N − 2/(2N − e^−2r). Therefore, the probability of overlapping recombination events, given that a pair of lineages will eventually find two different individuals is: (1 − e^−2r)/(2N − e^−2r). Figure 2b shows this probability as a function of N and r.