Prediction of protein domain boundaries from sequence alone

Abstract

We present here a simple approach to identify domain boundaries in proteins of an unknown three-dimensional structure. Our method is based on the hypothesis that a high-side chain entropy of a region in a protein chain must be compensated by a high-residue interaction energy within the region, which could correlate with a well-structured part of the globule, that is, with a domain unit. For protein domains, this means that the domain boundary is conditioned by amino acid residues with a small value of side chain entropy, which correlates with the side chain size. On the one hand, relatively high Ala and Gly content on the domain boundary results in high conformational entropy of the backbone chain between the domains. On the other hand, the presence of Pro residues leads to the formation of hinges for a relative orientation of domains. The method was applied to 646 proteins with two contiguous domains extracted from the SCOP database with a success rate of 63%. We also report the prediction of domain boundaries for CASP5 targets obtained with the same method.

The knowledge of protein domain boundaries is of paramount importance for comparative sequence analysis and three-dimensional structure prediction methods. Domains are generally regarded as compact, semi-independent units (Richardson 1981) that could fold autonomously (Wetlaufer 1973).

Several methods have been developed to identify domains in globular proteins starting from atomic coordinates. All of these methods are based on a simple geometrical model stating that a domain has relatively more contacts within itself than with residues in the remainder of the structure (Busetta and Barrans 1984; Kikuchi et al. 1988; Islam et al. 1995; Siddiqui and Barton 1995; Berezovsky et al. 1999). With the current rapid growth in the number of sequences with unknown structures, it is very important not only to accurately define protein structural domains, but to predict domain boundaries on the basis of amino-acid sequence alone.

Recently, several methods for predicting domain boundaries from amino acid sequence have been proposed on the basis of a multiple sequence alignment (Park and Teichmann 1988; Sonnhammer and Kahn 1994^; Adams et al. 1996^; Gracy and Argos 1998^; Guan and Du 1998^; Gouzy et al. 1999; George and Heringa 2002) and on statistically derived distributions of domain lengths (Wheelan et al. 2000). However, these methods can only be successful at identifying domains if the sequence has detectable similarity to other sequence fragments in databases or when the length of the unknown domains does not substantially deviate from the average of known protein structures.

In this work, we describe a new method to predict domain boundary from protein sequence alone using a simple physical approach based on the fact that the protein unique three-dimensional structure is a result of the balance between the gain of attractive native interactions and the loss of conformational entropy, that is, that the topology of the chain determines how much the chain entropy is lost as native interactions are formed. Conformational entropy is often subdivided into backbone and side chain entropies, although the side chain size and nature is expected to impose steric constraints on the backbone. A large contribution to the loss of conformational entropy upon folding is due to side chains that are restricted in the folded protein. On the basis of this idea, we assume that a high side chain entropy of a region in a protein chain must be compensated by a high interaction energy within the region, which could correlate with a well-structured part of the globule, that is, with a domain unit. This means that the domain boundary is conditioned by amino acid residues with a small value of side chain entropy, which correlates with the side chain size. On the one hand, relatively high Ala and Gly content on the domain boundary results in a high conformational entropy of the backbone chain between the domains. On the other hand, the presence of Pro residues leads to the formation of hinges for a relative orientation of domains. Considering here the conformational entropy as the number of degrees of freedom on the angles φ, ψ, and χ for each amino acid along the chain, our method for domain boundary prediction relies on finding the minima in a latent entropy profile. This offers a possibility of identifying domain boundaries in proteins without prior knowledge of their tertiary structure, opening the road to useful applications both in sequence analysis and structure prediction.

Results and discussion

We tested our method using the SCOP database (Murzin et al. 1995) and also applied it to the target sequences for CASP5 (http://PredictionCenter.llnl.gov/casp5/targets/). Calculations and analysis were performed for 646 two-domain proteins. The results and the characteristic entropy profiles for 366 proteins from 29 groups consisting of 44 superfamilies are presented in Table 1. The size of individual domains varies widely. We do not take into account the minima corresponding to small putative domains, shorter than 50 residues, so that the domain lengths in our dataset vary from 50 to 679 residues.

Table 1.

Results of domain boundary prediction for 29 groups consisting of 44 superfamilies

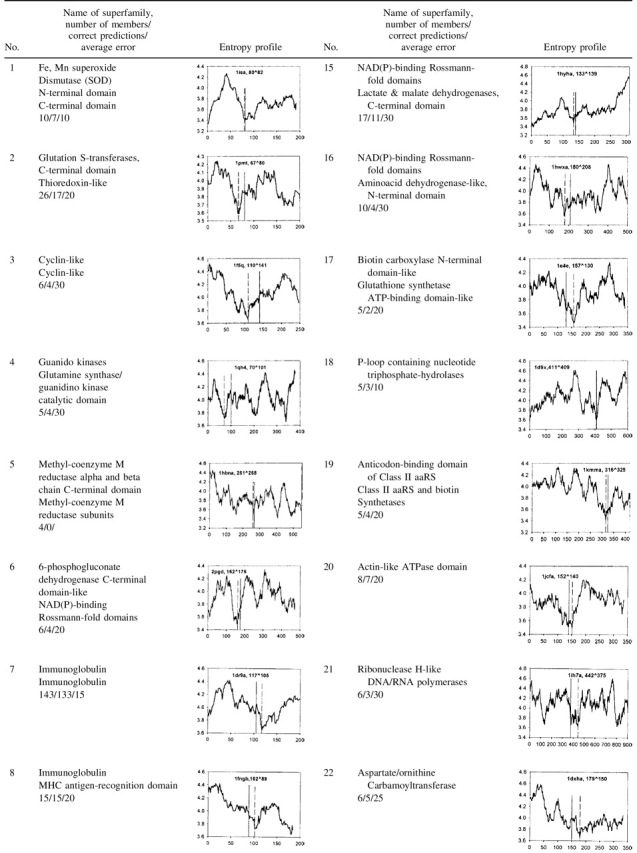
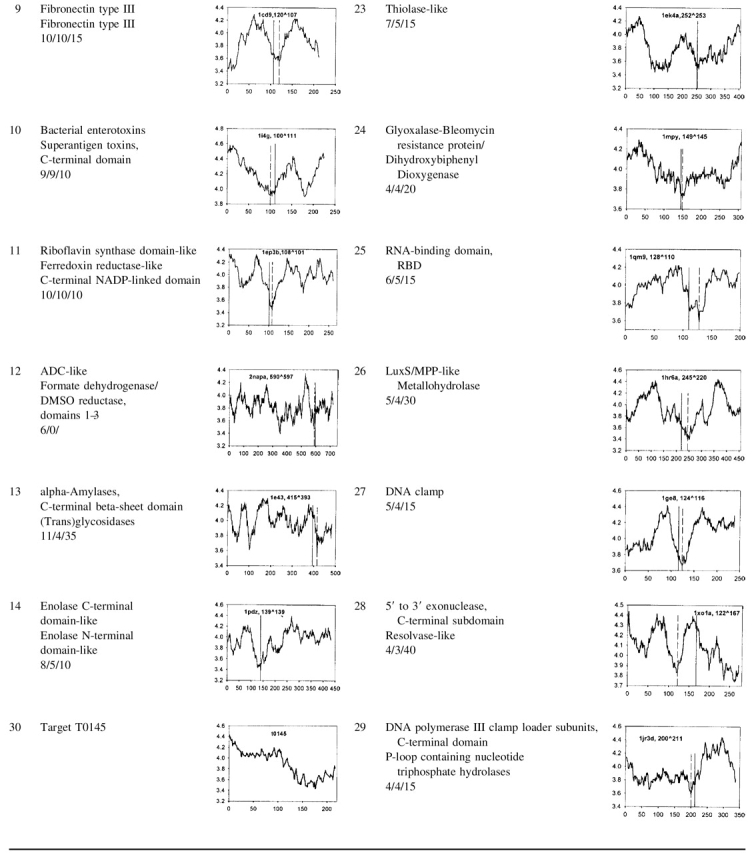
The name of the SCOP superfamily, the number of proteins in the group, the number of correct predictions (cases in which the entropy minimum falls within 40 residues from the domain boundary), and the average error (average distance between the deepest minimum in each of the proteins and the corresponding domain boundary) are shown in the second column. The latent entropy profile is in the third column together with the PDB code (Bernstein et al. 1977) of the selected group member. The predicted domain boundary corresponds to the deepest minimum in the plot (the first number after the PDB code and vertical broken line in the plot), the experimental one (the second number and vertical line) is defined according to the SCOP.

We predict the domain boundary for two-domain proteins to be located at the position where the latent entropy profile has its deepest minimum. This minimum is conditioned by amino acid residues with a small value of number of degrees of freedom on the angles φ, ψ, and χ (Table 3), which correlates with the side chain size. Therefore, the relative high content of small residues (except proline) results in a high conformational entropy of the backbone chain between the domains. A prediction is considered as successful when the predicted domain boundary falls within the window ± 40 residues of the domain boundary assigned by SCOP.

Table 3.

Number of degrees of freedom for the angles ϕ, ψ, and χ for each amino acid

aa	A	E	Q	D	N	L	G	K	S	V	R	T	P	I	M	F	Y	C	W	H
n	2	5	5	4	4	4	3a	6	4	3	6	4	1	4	5	4	5	4	4	4

(aa) The name of the residue shown in one letter code, (n) the number of degrees of freedom.

^a The set of conformations for the main chain of Glycine is larger than that of other residues, which is taken into account by assigning three rather than two degrees of freedom for Glycine.

We observed that when the domain boundary does not coincide with the deepest minima, it very often matches the position of the other minima in the plot. This could be exploited to improve our method in the future, but at present, we consider these cases as failures when evaluating the accuracy of the method. In general, several other minima are sometimes observed in the plot, and they might contain information about ordered structural segments.

As can be seen from Table 1, the accuracy of the predictions is different for different superfamilies. The quality of the predictions is very good when the protein length is <450 residues. In these cases, the position of domain boundaries correlates well with the position of the deepest minima in the plots (see Table 1, Nos. 1–3, 7–11, 20, 22, 24–27, and 29). Its value varies from 3.4 (the average number of degrees of freedom for the angles φ, ψ, and χ) to 3.9 in different groups suggesting that a global optimum threshold does not exist. If there are several equally deep minima in the profile, one should use additional information from the entropy profile with a smaller window size, 9 or 5 residues to choose one of them (Table 1, No. 23).

It can be seen from Table 1 that domain boundaries for some groups including proteins longer than 450 residues are difficult to predict (see Table 1, Nos. 5, 12, 13, 16, and 21). Usually in these cases, the profile contains additional minima. For large proteins, this method will provide valuable information about a potential sequence position of domain limits that could be complemented with additional information for further localization of domain boundaries.

Studies of the distribution of 20 amino acid residues within the domain boundary region including 81 residues (40 from each side from the boundary) for 366 proteins from the 29 groups consisting of 44 superfamiles have indicated a preference for amino acid residues with a small side chain entropy value in comparison with the distribution of the residues for all 366 protein lengths. This confirms the hypothesis that domain boundaries are conditioned by such a type of amino acid residues.

The problem of separating protein structure into their constituent domains becomes more complex as the number of domains increases. Usually, the accuracy of the prediction is quite good if single-domain proteins are included in the test set (Islam et al. 1995; Siddiqui and Barton 1995). The correct assignment for two-domain proteins varies from 50% to 70% of accuracy (Islam et al. 1995; Siddiqui and Barton 1995; Jones et al. 1998; Wheelan et al. 2000; George and Heringa 2002).

In our case, the accuracy of the method depends on the group. Using 280 two-domain proteins not selected into groups (see Materials and Methods) and considering the resolution of our method to be ± 40 residues (the window size), the predictions are accurate in 63% of cases, random in 47%, and the Z score is 5. In the case of 29 groups, the prediction is accurate in 80%, random in 56%, and the Z score is 11.

Table 2 presents the result of the prediction of domain boundaries for 21 CASP5 targets longer than 150 residues and nonhomologous to proteins of known three-dimensional structures. This blind test is the most suitable for assessing the accuracy of the new method and will allow potential users to verify the quality of our results on an unbiased test set.

Table 2.

Results of domain boundary predictions for CASP5 targets

No.	Target	Result	No.	Target	Result	No.	Target	Result
1	T0129	111 (95)	8	T0158	73 (180)	15	T0173	158
2	T0134	92	9	T0159	232 (151)	16	T0174	235 (356)
3	T0145	130	10	T0161	74	17	T0177	107
4	T0146	200	11	T0162	202 (70,125)	18	T0179	86 (177)
5	T0147	115	12	T0165	197	19	T0186	267 (63)
6	T0148	70	13	T0171	107	20	T0187	349 (193)
7	T0149	115	14	T0172	105 (227)	21	T0194	125

The Result column shows the sequence position of the predicted domain boundary. In some cases another minimum is very close (or equal) to the deepest one and its position is shown in parenthesis.

We plan to extend our method to the prediction of domain boundaries in multidomain proteins by analyzing the correlation between the position of other minima and the boundaries of domain units.

The entropy parameter (the number of degrees of freedom on the angles χ) correlates with the side chain entropy. In fact, the value of the average entropy parameter calculated as a summation of the individual number of the entropy parameter over its complete sequence and normalized by the protein length correlates with the average side chain entropy |gn considered by Galzitskaya et al. (2000).

The average entropy parameter for proteins in our database falls in a defined region (from 3.6 to 4) as has been demonstrated by Galzitskaya et al. (2000). Proteins with a high entropy parameter (>4) usually belong to DNA-binding proteins or bind some additional agents. In general, one of the domains has larger conformational entropy than the other, by, on average, 0.1–0.2 units (Table 1, Nos. 1, 7, 8, 19, 20, 22, 24, and 29). The need to balance the conformational entropy with the energy of interactions is one of the general conditions to achieve the functional active form of a protein, and it is possible that the domain organization is necessary for proteins to compensate for the large conformational entropy of one of the domains and to enhance the stability of the whole protein (see profile No. 30 in Table 1).

We would like to underline here that there are many domain prediction algorithms using information from multiple sequence alignments or statistical analysis. However, there are no prediction algorithms relying only on protein sequence such as the one described here that, although very simple, provides valuable and reasonable information about protein domain organization and can be useful for sequence analysis and structure prediction.

Materials and methods

Database of two-domain proteins

We inspected the SCOP database 1.59 release (Murzin et al. 1995) and found 974 domain proteins with sequence identity values <80%. Domains are often composed by a single-chain continuous segment (Islam et al. 1995; Jones et al. 1998), therefore, we removed all structures in which split domains were present (140 proteins). Then, we restricted our database to two-domain proteins and removed protein structures with one domain shorter than 50 residues. At this stage, the data set consisted of 646 structures. We selected them into groups consisting of 44 superfamilies and considered only those that included more than three structures (29 groups containing 366 two-domain proteins). The domain boundaries were assigned according to SCOP.

Calculation of the entropy profile

The latent entropy profile is calculated as follows. First, the number of degrees of freedom for the angles φ, ψ, and χ is determined for each residue (Table 3); then, the propensities for the residues inside the window are averaged and assigned to the central residue of the window. Therefore, the influence of residues along the sequence flanking each window is included in our calculation. The value of the average entropy parameter (the average number of degrees of freedom on the angles φ, ψ, and χ) for every position of the polypeptide chain provides the latent entropy profile whose minima are predicted to correlate to domain boundaries (only the deepest minimum should be considered for two-domain proteins). We used a sliding window of 41 residues. This value was selected for two reasons. First, a domain should contain a hydrophobic core and should be larger than 40 residues. Second, this window size has been found to be the best compromise between a good resolution of the plot and a tolerable level of noise.

Estimation of accuracy of the method

The probability p_i to guess the domain boundary by chance in our method is the relation between two lengths, double length of the window size (80 residues) and the protein length decreased by 50 residues from each end. In the case when the reduced length is <80 residues, the probability p_i is equal to 1. Therefore, the Z-score is (M-<M>)/σ, in which M is the number of correctly predicted domain boundaries by our method and <M> is the average number of expected successful random predictions in our method that is equal to the summation of probabilities p_i, in which i changes from 1 to the considered number of the proteins. σ is the standard deviation.