Skip to main content
PMC home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2003 May;12(5):914–922. doi: 10.1110/ps.0228703

Comparison of 13CαH and 15NH backbone dynamics in protein GB1

Djaudat Idiyatullin 1, Irina Nesmelova 1, Vladimir A Daragan 1, Kevin H Mayo 1
PMCID: PMC2323862  PMID: 12717014

Abstract

This study presents a site-resolved experimental view of backbone CαH and NH internal motions in the 56-residue immunoglobulin-binding domain of streptococcal protein G, GB1. Using 13CαH and 15NH NMR relaxation data [T1, T2, and NOE] acquired at three resonance frequencies (1H frequencies of 500, 600, and 800 MHz), spectral density functions were calculated as F(ω) = 2ωJ(ω) to provide a model-independent way to visualize and analyze internal motional correlation time distributions for backbone groups in GB1. Line broadening in F(ω) curves indicates the presence of nanosecond time scale internal motions (0.8 to 5 nsec) for all CαH and NH groups. Deconvolution of F(ω) curves effectively separates overall tumbling and internal motional correlation time distributions to yield more accurate order parameters than determined by using standard model free approaches. Compared to NH groups, CαH internal motions are more broadly distributed on the nanosecond time scale, and larger CαH order parameters are related to correlated bond rotations for CαH fluctuations. Motional parameters for NH groups are more structurally correlated, with NH order parameters, for example, being larger for residues in more structured regions of β-sheet and helix and generally smaller for residues in the loop and turns. This is most likely related to the observation that NH order parameters are correlated to hydrogen bonding. This study contributes to the general understanding of protein dynamics and exemplifies an alternative and easier way to analyze NMR relaxation data.

Keywords: NMR, relaxation, spectral density, correlation times

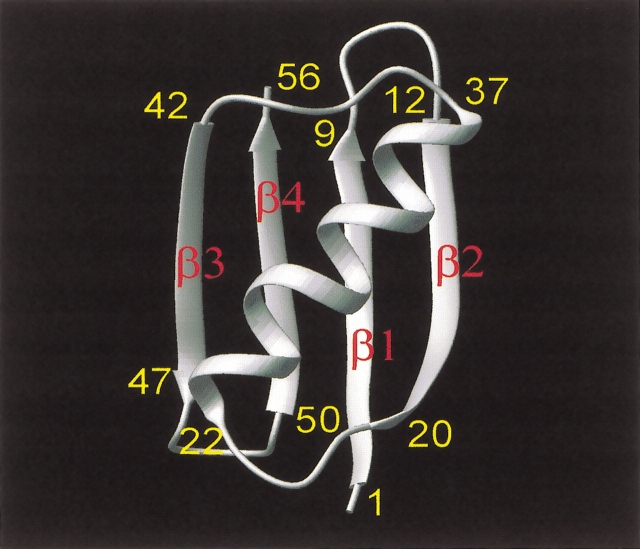
The 56 residue immunoglobulin-binding domain of streptococcal protein G (GB1) is an ideal model system with which to investigate protein dynamics by using NMR relaxation. It is a small, yet highly stable (Alexander et al. 1992) (Tm of 87 °C at pH 5.4), well-structured protein (Gronenborn et al. 1991) that is folded as a four-stranded β-sheet (residues 2–8, 13–20, 42–46, and 51–56), on top of which lies an α-helix running from residues 22 to 37 (Fig. 1 ▶). GB1 already has been extensively studied in terms of its thermodynamic stability. Over the predenaturation temperature range between 5 and 30°C, the calorimetrically determined free energy of unfolding for GB1 (Alexander et al. 1992) varies little and, on raising the temperature further, falls gradually to zero by 87°C. In this regard, GB1 behaves thermodynamically like a larger protein and, therefore, may be considered representative of any number of proteins.

Figure 1.

Figure 1.

Open in a new tab

Overall fold for GB1. The overall fold of GB1 is illustrated as given by Gronenborn et al. (1991).

NMR relaxation provides the only way to derive site-specific dynamics information through the protein sequence. Using multifield measurements of relaxation parameters T1, T2, and NOEs, one can obtain many motional parameters related to various bond rotations. Although 15N NMR relaxation has become a standard tool for studying protein dynamics, the picture remains incomplete without knowledge of the internal motions of various CH bonds. Backbone CαH bond motions reflect correlations of φ and ψ dihedral angles and the influence of side-chain χ1 rotations (Daragan and Mayo 1996a,b; Daragan et al. 1997; Ramirez et al. 1998; Idiyatullin et al. 2000). As with NH groups, information on CH internal motions can be derived from analysis of NMR relaxation data. Despite the importance of 13C NMR relaxation studies of proteins, there are few research groups where such measurements are being performed (Daragan et al. 1997; Kemple et al. 1997; A.L. Lee et al. 1997; L.K. Lee et al. 1997; Carr et al. 1998; Hall and Tang 1998; Lee et al. 1998; Yang et al. 1998; Guenneugues et al. 1999; Huang et al. 1999; Walsh et al. 2001). One of the reasons for this is the influence of 13C-13C interactions in uniformly 13C-enriched proteins, which increases line broadening and introduces undesirable contributions to relaxation parameters from 13C -13C dipolar interactions. Nevertheless, these problems can be reduced significantly by using random fractionally 13C-enriched protein.

Once NMR relaxation parameters have been acquired, most researchers analyze their data using the Lipari-Szabo (1982a,b) “model free” approach. The major limitation with using this method for analysis is that it is only valid for isotropic overall tumbling with internal rotational jumps between n equivalent states. In actual proteins, a multitude of internal motional correlation times are required to fully describe various bond rotational fluctuations and correlated motions. A novel method was recently developed to avoid many of the problems associated with the standard model free approaches (Idiyatullin et al. 2001). This new approach yields a motional correlation time distribution without assuming the nature of the molecular motions or the number of motional modes, that is, Lorentzians, involved in the dynamics processes. Here, we have used 13C and 15N NMR relaxation data and this new model free approach to examine 13CαH and 15NH internal motional modes in protein GB1.

Results

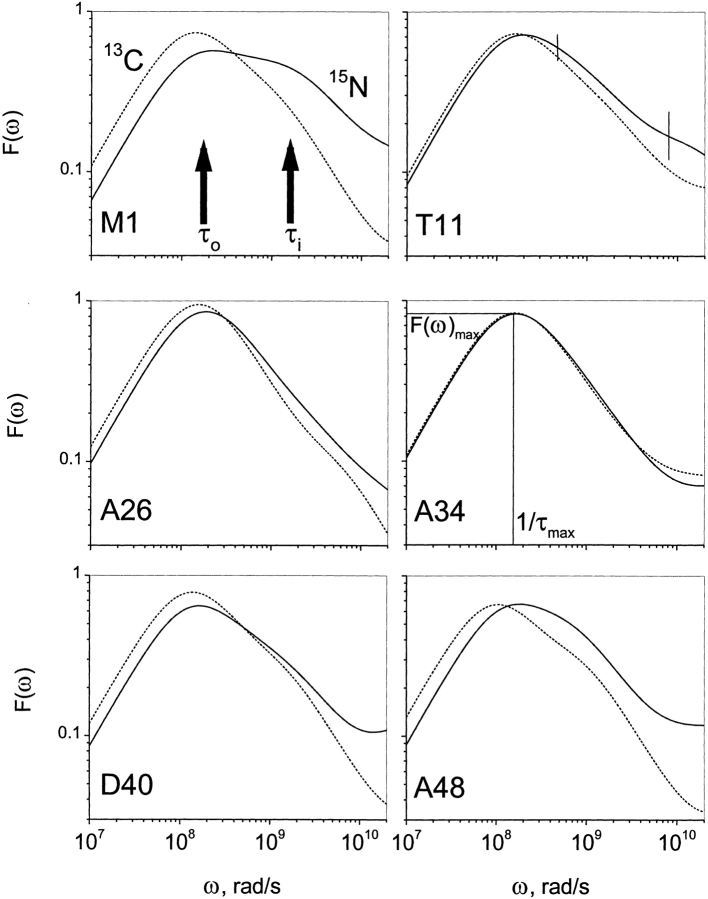
13CαH and 15NH relaxation data were acquired at three frequencies (1H frequencies of 500, 600, and 800 MHz). These results are exemplified in Figure 2 ▶ with 13C and 15N NMR relaxation data (T1, T2, and {1H}-13C NOE) at 500 and 800 MHz. Using these relaxation data, F(ω) curves were calculated and motional correlation time distributions are plotted in Figure 3 ▶ for residues M1, T11, A26, A34, D40, and A48 in protein GB1. Similarly appearing curves were obtained for all 13CαH and 15NH groups of residues throughout the protein. Two observations common to these distributions can be made: (1) F(ω) curves for 13CαH are generally shifted to lower frequency compared to those for 15NH. This is primarily due to increased viscosity of the 13C-enriched protein in D2O, which results in somewhat slower overall tumbling motions. (2) The maximum of F(ω), F(ω)max, for 13CαH is usually greater than for 15NH. As will be discussed below, this results partly from a shift of the 13CαH internal motional correlation time distribution closer to that of overall tumbling and partly from correlated bond rotations that influence 13CαH fluctuations more than they do those of 15NH.

Figure 2.

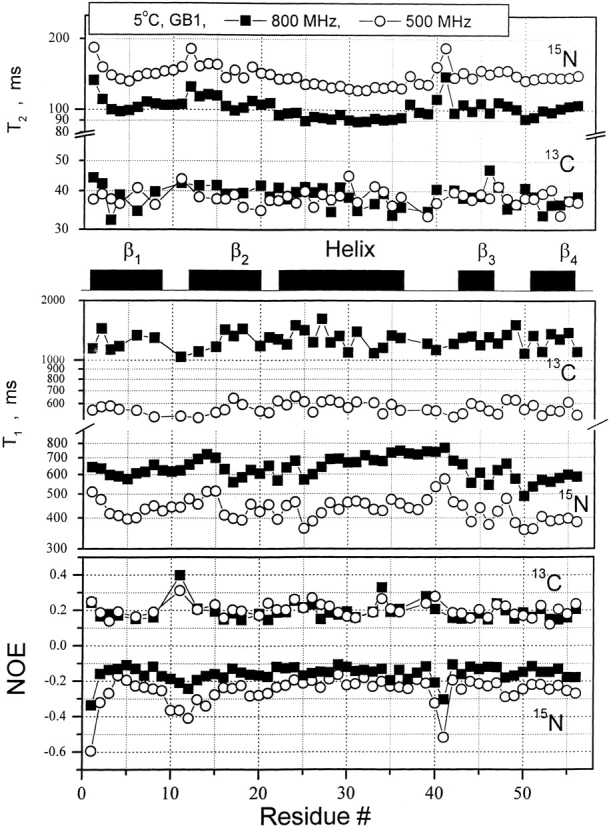
Figure 2.

Open in a new tab

R1, R2, and NOE data for protein GB1. 13C and 15N NMR relaxation data [T1, T2, {1H}- 15N NOE, and {1H}-13C NOE] on random fractionally 13C-enriched protein GB1 and from a separate sample, uniformly 15N-enriched protein GB1 are plotted versus the GB1 residue number for data acquired at 1H spectrometer frequencies of 500 MHz (open circles) and 800 MHz (filled squares). Secondary structure elements for the protein are given between panels. The temperature for all measurements was 5°C.

Figure 3.

Figure 3.

Open in a new tab

Plots of F(ω) for six residues in GB1. Because ω is inversely related to the correlation time, F(ω) gives the distribution of motional correlation times for CH and NH fluctuations over the nanosecond to picosecond range. F(ω) motional correlation time distributions are exemplified with six CH and NH groups: M1 (β-strand 1), T11 (turn 1), A26 (α-helix), A34 (α-helix), D40 (loop), and A48 (turn 2) through the structure of GB1. Solid lines give F(ω) curves for 15NH, whereas dotted lines give F(ω) curves for 13CαH. F(ω) curves were truncated at 100 psec because internal motions occurring on the picosecond time scale are not accurately defined.

F(ω)max, labeled in the panel for residue A34, is the maximum height of the F(ω) curve, and 1/τmax is the corresponding value for the inverse correlation time read from the ω frequency axis. For well-separated overall tumbling and internal motional correlation times, F(ω)max and τmax would be equivalent to the well-known Lipari-Szabo order parameter, S2, and overall tumbling correlation time, τo, respectively. By visualizing spectral density functions using the F(ω) approach, it is obvious that this is not the case. This is most evident in the F(ω) curve for the NH of M1 (Fig. 3 ▶), which clearly shows overlapping peaks from at least two motional correlation time distributions on the nanosecond time scale, one for overall tumbling and the other(s) for internal motions. The centers of these distributions are roughly indicated by vertical arrows marked τo and τi, respectively. In most other F(ω) curves, shoulders are evident at higher frequency. In these cases, S2 < F(ω)max and τo > τmax.

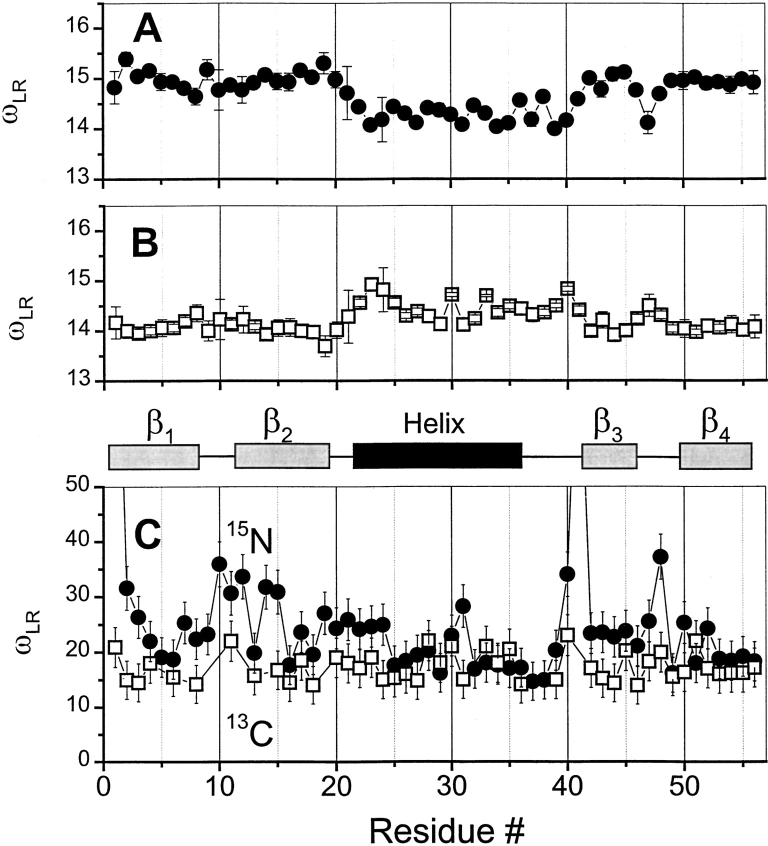
Contributions from multiple Lorentzians was assessed and semiquantified by taking the line width of F(ω) curves at half-height, 1/2 F(ω)max, a value that has been termed ωLR (Idiyatullin et al. 2001). A single Lorentzian resulting from overall tumbling of a spherical molecule has an ωLR value of 13.93. GB1, however, is ellipsoid in shape with a D||/Dz ratio of 1.8. Because of this, ωLR depends on the orientation of a particular Cα-H and N—H vector within the molecular frame of GB1. Using the program TENSOR II (Daragan and Mayo 1997) and the coordinates for GB1 averaged over 60 NMR-derived structures from the PDB database [accession code: GB1], values of ωLR for Cα-H and N—H vectors in GB1 have been calculated and found to fall generally in the range from about 14 to 15 (Fig. 4A ▶, B). Some vectors are oriented more parallel to the long axis of the molecule, yielding smaller values of ωLR, whereas others are oriented more perpendicular to this axis, resulting in larger values of ωLR. Experimentally determined values for ωLR are plotted versus residue number in Figure 4C ▶. In most cases, the observed ωLR is larger than expected for overall tumbling alone, indicating that the shape of the molecule plays a minor role in this broadening phenomenon. Moreover, the magnitudes of ωLR demonstrate that there are significant contributions to F(ω) from internal motions occurring on the nanosecond time scale.

Figure 4.

Figure 4.

Open in a new tab

ωRL plotted versus residue number from GB1. Calculated values for ωRL are plotted for CH (A) and NH (B) vectors in GB1 and for experimentally determined values of ωRL for 13CαH (open squares) and for 15NH (filled circles) (C). Values of ωRL for C—H and N—H vectors in GB1 were calculated using the program TENSOR II (Daragan and Mayo 1997) and the coordinates for GB1 averaged over 60 NMR-derived structures from the PDB (accession code GB1). Experimentally determined values for ωRL are plotted for 5°C. For calculated values of ωRL, the scale is more expanded to illustrate the effect through the sequence. Secondary structure elements in GB1 are shown between panels.

Due to the presence of multiple motional modes, the Lipari-Szabo model (Lipari and Szabo 1982a,b) cannot be used to analyze these data. Moreover, even use of the Clore et al. (1990) model, which is limited to three Lorentzians, is questionable because the number of motional modes composing these distributions is unknown. One of the advantages of using the F(ω) approach is that, without concern for the number of Lorentzians involved in internal motional processes, F(ω) curves can be deconvoluted into two main components, Fo(ω) for overall tumbling and Fi(ω) for the distribution of correlation times associated with internal motions. The deconvolution procedure is described in the Materials and Methods section. Deconvolution of F(ω) allows one to derive more accurate values for the order parameter, S2, and overall tumbling correlation time, τo, because Fo(ω) is essentially devoid of contributions from nanosecond time scale internal motions. τo values, derived as 1/ω at Fo(ω)max (data not shown), are generally larger for 13CαH groups than for 15NH groups. This results from increased viscosity due to D2O in the 13C-enriched protein sample and H2O in the 15N-enriched protein sample. The residue-averaged τo value for 13CαH is 8.2 ns, whereas the residue-averaged τo value for 15NH is 6.4 ns. This difference can be explained by hydrodynamic effects because the ratio of these τo values is essentially the same as that for the viscosities for D2O and H2O.

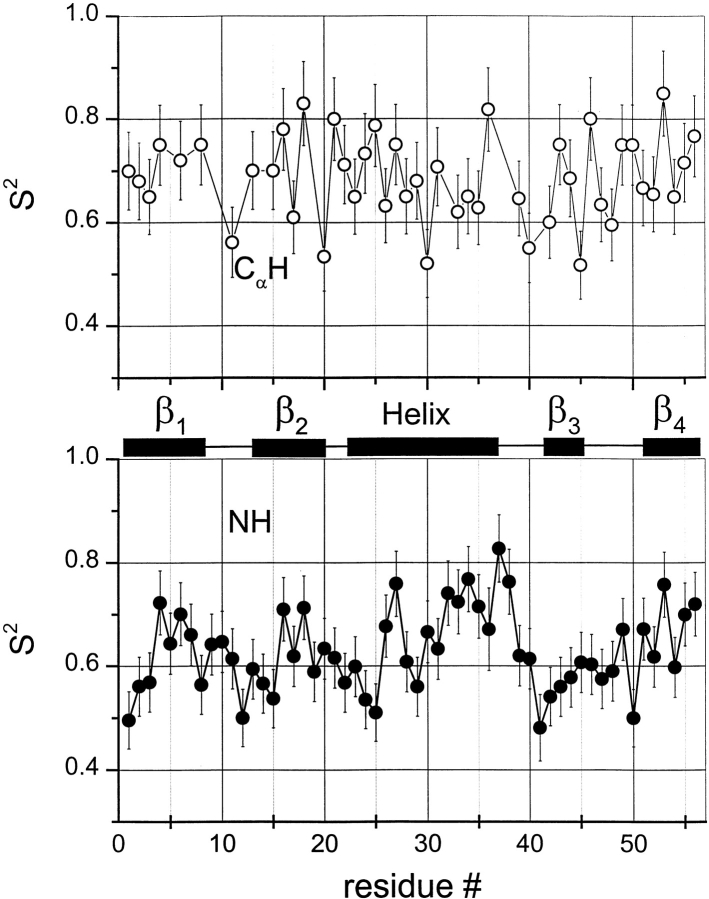
S2CH and S2NH values, plotted in Figure 5 ▶, fall approximately between 0.5 and 0.8. S2NH values appear to be more structurally correlated, with generally lower values being observed for residues located at the N-terminus, the C-terminal part of the helix, and within turns 1 and 2 and the loop. This may have been anticipated because a computational analysis on peptide dynamics using the “internally restricted correlated rotation” (IRCR) model (Daragan and Mayo 1996b) indicates that S2NH is more sensitive to structural differences than is S2CH. Moreover, analysis of these data indicates that S2NH is correlated to hydrogen bonding. In GB1, NHs of 36 out of 56 residues are involved in hydrogen bonds. An average of these S2NH values is 0.76 ± 0.04, whereas the average S2NH for all other nonhydrogen bonded NHs, aside from those of the N- and C-terminal residues, is 0.62 ± 0.05. Even when omitting turn and loop residues from the calculation, this difference remains. Another observation is that S2CH values, for any given residue, tend to be larger than S2NH values. As will be discussed later, the reason for this is related to more complicated CαH bond motions involving correlated φ, ψ, χ (side-chain) bond rotations.

Figure 5.

Figure 5.

Open in a new tab

13CαH and 15NH order parameters versus residue number. Order parameters were obtained using the F(ω) deconvolution approach as described in the Materials and Methods section. Open circles are for 13CαH and filled circles are for 15NH. Secondary structure elements in GB1 are shown between panels.

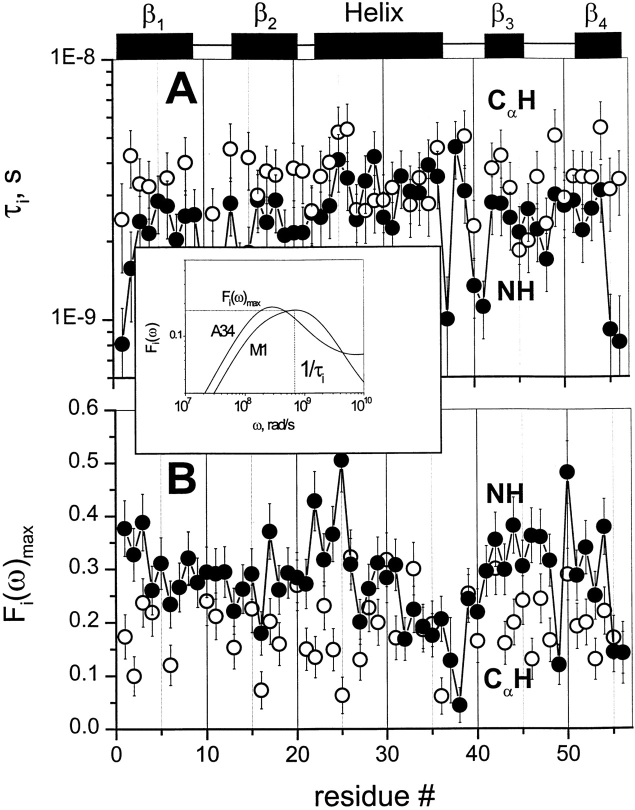
Two parameters are key to discussing the Fi(ω) component: Fi(ω)max, which represents a weighted sum of correlation coefficients for internal motions, and τiR, the value of 1/ω read at Fi(ω)max. Although Fi(ω) curves represent a rather broad distribution of internal motional correlation times over about two orders in magnitude, analysis and comparison of these nanosecond time scale motions is simplified by using τiR. These internal motional parameters for 13CαH (open circles) and 15NH (filled squares) groups are plotted in Figure 6A and B ▶. Fi(ω)max values indicate that nanosecond time scale internal motions contribute significantly to the spectral density function, somewhat more so for NH than for CαH. For both CαH and NH groups, τiR values fall close to each other, lying between 1 and 5 ns. On average, however, τiR is somewhat larger for CαH than for NH, indicating that CαH internal motions on the nanosecond time scale are slower and/or are involved in more concerted types of motion.

Figure 6.

Figure 6.

Open in a new tab

Fi(ω)max and τiR values plotted versus the residue number. τiR (A) and Fi(ω)max (B) values are plotted for 13CαH (open circles) and 15NH (filled squares) versus the GB1 residue number. τiR represents the inverse of the frequency ω at Fi(ω)max. Secondary structure elements in GB1 are shown between panels. The insert exemplifies the function Fi(ω) for 15NH for two residues M1 and A34 that results from deconvolution of F(ω) into Fo(ω) and Fi(ω).

Discussion

This 13C and 15N NMR relaxation study has presented a comprehensive, site-resolved experimental view of backbone CαH and NH internal motions in protein GB1. The three primary results of the study are: (1) nanosecond time scale internal motions are observed for all backbone NH and CαH groups; (2) CαH internal motions are slower on the nanosecond time scale than are NH internal motions, possibly reflecting the influence of correlated bond rotations; and (3) NH order parameters are correlated to the presence of hydrogen bonding and better reflect structural differences in the protein.

Although a number of 15N NMR relaxation-based studies on protein dynamics have reported the presence of nanosecond time scale internal motions for a few residues (e.g., Clore et al. 1991; Barchi et al. 1994; Mandel et al. 1996; Coles et al. 1999; Berglund et al. 2000; Hidehito et al. 2000; Seewald et al. 2000; Zajicek et al. 2000; Baber et al. 2001; Canet et al. 2001), most protein dynamics studies do not, or perhaps cannot, accurately derive internal motional correlation times, primarily due to the paucity of NMR relaxation data and limitations of the motional model(s) used. In fact, two of these dynamics investigations (Barchi et al. 1994; Seewald et al. 2000) were performed on the same protein GB1, and nanosecond time scale internal motions were reported for only a handful of NHs, and even these were different in each study. Moreover, when internal motions are analyzed, discussion is limited most often to the picosecond time scale. However, even on an 800-MHz NMR spectrometer, the accessible frequency range is limited to about 160 psec and picosecond time scale internal motions (less than about 100 psec) cannot be accurately determined when overall tumbling is much slower than this limiting value, and order parameters are not at their lower limit as for fast internal rotations of methyl groups in side chains (Daragan and Mayo 1996a, 1997, 1998).

Given the present findings with protein GB1, it is plausible that all groups in all proteins undergo nanosecond time scale internal motions. This proposal is consistent with the concept forwarded by Frauenfelder et al. (1991) that there exists a hierarchy of internal motions in proteins. This hierarchy ranges from picoseconds to nanoseconds to microseconds to milliseconds and slower. NMR relaxation studies, which are most sensitive to motions occurring on the nanosecond to picosecond time scales, on small GXG tripeptides devoid of folded structure revealed that internal motions for backbone CαH and NH groups fall in the 70- to 100-psec range (Mikhailov et al. 1999), whereas in protein GB1, internal motions for backbone groups fall in the subnanosecond to 5-nsec range, as well as in the picosecond range. Internal motions on the picosecond time scale were mostly omitted from this discussion primarily because these faster time scale motions are least accurately determined as mentioned above. Nevertheless, because spectral density functions for GB1 trail into the picosecond range, it is most probable that picosecond time scale internal motions (less than about 100 psec) contribute about 10% or less to the spectral density function. In any event, because of the prevalence of nanosecond time scale internal motions, caution should be exercised by investigators who only use the Lipari-Szabo model free approach to analyze NMR relaxation data. When overall tumbling and internal motions occur on the same time scale, multiple Lorentzians overlap, and this leads to overestimated order parameters and underestimated overall tumbling correlation times when using the Lipari-Szabo approach or any approach that uses fewer Lorentzians than the number of motional modes present. Using the F(ω) approach avoids this problem.

On the nanosecond time scale, motional fluctuations for CαHs are slower than they are for NHs. Slower internal motions for backbone CHs suggest more complicated, concerted types of motions. This interpretation is supported by results on partially folded peptides where NH backbone motions could be described by motions about a single bond, that is, the Cα-N φ-bond, whereas CαH motions could only be explained fully by considering concerted φ, ψ, and χ bond rotations (Ramirez et al. 1998; Idiyatullin et al. 2000). Furthermore, this idea is consistent with the observed larger order parameters for CαHs compared to those for NHs. The average value for S2 in β-sheet segments is 0.7 for 13CαH and 0.6 for 15NH, whereas the average value for S2 for the helix is 0.65 for 13CαH as well as for 15NH. Although most protein dynamics studies interpret S2 values in terms of restricted motional amplitudes, angular variance is only one contribution to the order parameter. Another is the presence of correlated bond rotations, which can have a significant influence on S2 (Daragan and Mayo 1996b, 1997). When considering both motional amplitudes and correlated motions, order parameters for CαH and NH backbone bond motions can be expressed (Daragan and Mayo 1997) as:

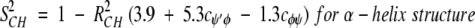graphic file with name M1.gif (1a)
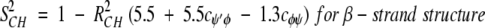graphic file with name M2.gif (1b)
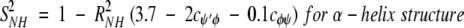graphic file with name M3.gif (1c)
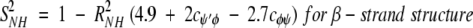graphic file with name M4.gif (1d)

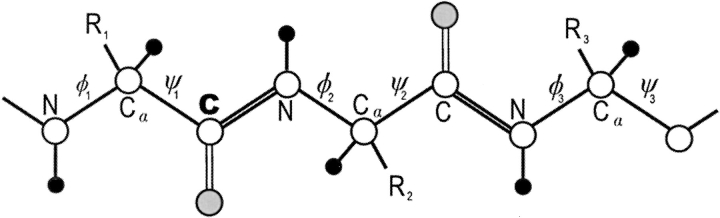
cφψ is the rotational correlation coefficient for ψi and φi backbone rotations; and cψ′φ is the rotational correlation coefficient for ψi−1 and φi backbone rotations, and R2 is the average squared amplitude of φ and ψ rotations [R2 = σφσψ]. For a short peptide segment, ψi and φi bonds are illustrated in Figure 7 ▶. Notice that order parameters defined in this way (equation 1a–d) are structure dependent. For model peptides conformed in α-helix and β-strand (extended) structures, Daragan and Mayo (1996b) have estimated typical ranges for cψ′φ and cφψ correlation coefficients:

Figure 7.

Figure 7.

Open in a new tab

Sketch of peptide backbone. A tripeptide backbone is illustrated to show φ and ψ backbone dihedral angles as discussed in the text.

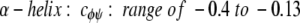graphic file with name M5.gif (2a)
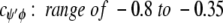graphic file with name M6.gif (2b)
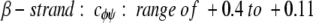graphic file with name M7.gif (2c)
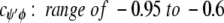graphic file with name M8.gif (2d)

Molecular dynamics calculations on protein GB1 (E. Ermakova, I. Nesmelova, V.A. Daragan, D. Idiyatullin, and K.H. Mayo, unpubl.) show that for most residues, cφψ is closer to zero, whereas cψ′φ is largely negative. In any event, the question here is how do these correlation coefficients affect the order parameter. For 15NH motions, correlated backbone motions will always act to minimize S2NH because cψ′φ is always negative. On the other hand, for 13CαH motions, cφψ is negative and cψ′φ acts to increase S2. Because it is reasonable to assume that R2CH has about the same value as R2NH (Daragan and Mayo 1997), the observation that S2CH is greater than S2NH, especially for β-sheet residues, supports the proposition that CαH fluctuations are related to correlated bond rotations.

Materials and methods

Protein production

The 56-residue protein GB1 was produced as a recombinant protein as described by Barchi et al. (1994). Escherichia coli containing the expression system for GB1 were grown on M9 minimal media containing glucose as the carbon source, 20% of which was uniformly 13C-enriched glucose. The 13C-enriched protein was purified by HPLC using a linear acetonitrile/water gradient, and purity was checked by MALDI-TOF mass spectrometry and analytical HPLC on a C18 Bondclone (Phenomenex) column. For NMR measurements, freeze-dried samples were dissolved in D2O in 20 mM potassium phosphate. Protein concentration, determined from the dry weight of freeze-dried samples, was 10 mg/mL. The pH was adjusted to pH 5.25 by adding microliter quantities of NaOD or DCl.

NMR relaxation experiments

With 13C- and 15N-enriched GB1, spin-lattice (T1), rotating frame spin-lattice (T1ρ) relaxation times and heteronuclear NOEs were measured at three Larmor precession frequencies (1H frequencies of 500, 600, and 800 MHz) on Varian Inova 500, 600, and 800 NMR spectrometers equipped with triple-resonance probes. The temperature was held at 5°C, with calibration being performed by using the chemical shifts of resonances from methanol.

13C and 15N T1 and T1ρ relaxation times were measured by using the HSQCSE pulse sequence (Yamazaki et al. 1994; Farrow et al. 1995), which employs pulsed field gradients for the coherence transfer pathway whereby magnetization passes from 1H to 13C (or 15N) and back again to 1H for observation. To attenuate crosscorrelation between dipolar and chemical-shift anisotropy mechanisms during the relaxation period, an even number of 180° 1H pulses with alternating phase were applied every 5 msec (Kay et al. 1992; Palmer III et al. 1992). Spectra were recorded by using seven different relaxation delays with values from 10 msec up to 2Ti, where Ti is the respective relaxation time. For all T1 and T1ρ experiments, the recycle period was 1.7 sec, and all relaxation curves followed single exponential decay. To prevent 13C-13C scalar and dipolar coupling effects on relaxation parameters (Yamazaki et al. 1994), GB1 was randomly 13C-enriched to only 20%. In this case, residual effects on T1 values from neighboring 13C groups was less than 5% and negligible for 13C-{1H}NOEs. This was estimated by comparing relaxation parameters measured using 100% 13C-enriched GB1 and 20% 13C-enriched GB1. For T1ρ relaxation experiments, the carrier for 13C was set at 59 ppm and the frequency of the field lock was 2.6 kHz.

Steady-state {1H }-13C and {1H }-15N NOEs were determined from two spectra recorded with proton broadband irradiation and in the absence of proton saturation (Yamazaki et al. 1994; Farrow et al. 1995). Saturation was achieved by application of 120° 1H pulses applied every 5 msec (Markley et al. 1971) during repetition times of 3 sec.

All experiments were repeated two times for T1 and T1ρ and four times for NOEs. Average values are reported.

Relaxation data analysis

Because relaxation measurements were performed at high frequency where the influence of chemical shift anisotropy and chemical exchange terms are significant, the square dependence of these terms on the value of the magnetic field was used during the minimization procedure described below. The CSA constants used were −25 ppm for 13C (Peng and Wagner 1994) and −170 ppm for 15N (Tjandra et al. 1996). Moreover, the length of the amide HN bond used in 15N relaxation studies is the subject of an ongoing debate (Korzhnev et al. 2001). Because this work does not propose to solve the problem of NH bond vibrational corrections, a traditional value of 1.02 Å for the length of the N—H bond was used (Kay et al. 1989), which is widely employed by other authors in field.

We have recently developed an approach to analyzing NMR relaxation data, which yields a correlation time distribution for molecular motion without assuming the nature of the molecular motions or the number of motional modes, that is, Lorentzians (Idiyatullin et al. 2001). We introduced the function F(ω), which is related to the spectral density function as:

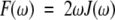graphic file with name M9.gif (3)

Although the function ωJ(ω) is almost equivalent to the imaginary part of the dielectric spectrum as described by Debye (1929) and has been used for many years in various branches of science, we are not aware that it has ever been used to interpret NMR relaxation data as is being done here.

F(ω) can be represented as the sum of the peaks corresponding to the motional modes, and the spectral density function J(ω) can be expressed as a sum of Lorentzians:

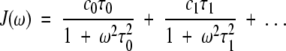graphic file with name M10.gif (4)

If motional correlation times are well separated, positions of peak maxima on the frequency axis, ω, are equal to the inverse of the correlation times 1/τi and the peak maxima are equal to the weighting coefficients ci in equation 4. Although values for ci and τi for i > 2 cannot be determined accurately, F(ω) can be fairly accurately described for any number of Lorentzians. This is due to the fact that during minimization F(ω) remains stable, even though mutual switching of ci and τi values prevents determination of their specific values. For J(0) = c0τ0 + c1τ1, for example, various combinations of c0, τ0, c1, and τ1 give the same value of J(0). In this regard, J(0) can be determined more accurately than can the individual terms in J(0). The same can be stated for F(ω), that is, many combinations of ci and τi give the same value of F(ω) over a wide range of frequencies. These properties of F(ω) allow the function to be used easily in the interpretation of NMR relaxation data where there are a large number of motional modes.

The largest peak in a F(ω) curve corresponds to low-frequency motions associated with overall tumbling, and any other peaks or shoulders on the higher frequency side result from the presence of a distribution of internal motional correlation times on the nanosecond and picosecond time scales. The highest frequency peak, that is, picosecond time scale, cannot be determined accurately because the accessible spectrometer frequency range is limited, with a 900-MHz spectrometer, for example, to correlation times in the frequency range up to 2π(900 + 225) MHz = 7 GHz (ωH + ωC), corresponding to a correlation time of 140 psec. The height of the major peak, F(ω)max, is equal to c0 in equation 4 when there is no nanosecond time scale internal motions. For molecules tumbling isotropically, the coefficient c0 can be interpreted as the squared order parameter. However, when nanosecond time scale internal motions are present, Lorentzians for overall tumbling and internal motions overlap and lead to the inequality:

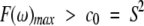graphic file with name M11.gif (5)

When τo and τi are not well-separated, the presence of nanosecond time scale internal motions may be reflected in the half-height line width, ωLR, of the major peak of F(ω). In effect, ωLR = ωR/ωL, where ωR and ωL are the high- and low-frequency positions taken at the half-height of F(ω), that is, F(ωR) = F(ωL) = 0.5F(ω)max. If the spectral density function can be described by a single Lorentzian, then ωLR = 13.93.

Using 13C and 15N relaxation data, F(ω) curves, which are independent of any motional model, were determined over the frequency range 0 < ω <6.28 × 109 rad/sec by using the Monte Carlo minimization protocol described previously by Idiyatullin et al. (2001) using the program FRELAN (www.nmr-relaxation.com) developed in our lab. Because ω is inversely related to the correlation time, these plots, in fact, give the distribution of motional correlation times over the nanosecond to picosecond range. These distributions are truncated at about 100 psec because of inaccuracies in determining F(ω) at shorter correlation times, tbat is, higher frequencies, where actual experimental data are lacking. Three main parameters define F(ω): F(ω)max, τmax, and ωLR, where τmax is the inverse of the frequency ω at F(ω)max. With well-separated correlation time distributions for overall tumbling and internal motion, τmax will be close to the value of the correlation time for overall tumbling, τ0. However, if internal motions have correlation times close to τ0, the value τmax will be less than the value of τ0.

To obtain parameters related to overall tumbling and internal motion, F(ω) was deconvoluted into two parts:

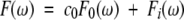graphic file with name M12.gif (6)

where the weighting coefficient, c0, can be interpreted as the squared order parameter, S2, and F0(ω) contains overall tumbling correlation times:

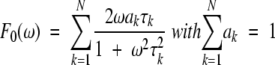graphic file with name M13.gif (7)

and Fi(ω) contains correlation times for internal motions:

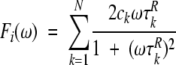graphic file with name M14.gif (8)

To simplify the deconvolution procedure, it was assumed that F0(ω) can be described by a single Lorentzian because correlation times in equation 7 are narrowly distributed. In this case, one needs to determine x = τo (x > τmax) to minimize Fi(ω) for all ω < ωmax under the condition:

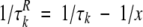graphic file with name M15.gif (9)

By doing this, correlation times which are close to τo become accentuated and maxima associated with overall tumbling and internal motions become better separated. By deriving Fi(ω) in this way, the internal motional correlation time distribution can be visualized and the associated parameters Fi(ω)max and τi can be used as general terms to describe internal motions for N—H and C—H vectors.

To calculate F(ω), one needs to determine the coefficients ci and correlation times τi for i = 0, 1, . . ., N, with N being as large as possible for any given set of experimental data. For example, with three relaxation parameters (e.g., T1, T2, and NOE) acquired at three magnetic field strengths, nine fitting parameters, that is, five Lorentzians, can be determined by taking into account that Σci = 1. Although it is practically impossible to obtain reliable values for ci and τi for N > 2, linear combinations and other functions of ci and τi over a given frequency range are very stable and can be determined accurately (LeMaster 1999; Idiyatullin et al. 2001). This is basically the key to obtaining the function F(ω) from experiment.

One way to calculate F(ω) is to use the Monte Carlo procedure and a simple step-by-step algorithm outlined below:

  1. Randomly take five values of the internal motional correlation time τi and amplitudes ci. To cover a range of possible errors and to account for the influence of rotational anisotropy, t2 should be about 50 to 70% larger than the estimated overall correlation time τo for a given protein molecule. To estimate τo, the empirical equation can be used (Daragan and Mayo 1997):

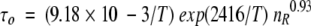
    graphic file with name M16.gif (10)

    where nR is the number of residues, and T is the temperature in Kelvin.

  2. Using minimization program, find appropriate values ci and τi that best fit the experimental data, that is, minimize the sum of the nine terms:

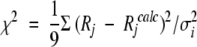
    graphic file with name M17.gif (11)

    Rj are experimental parameters; Rjcalc are calculated parameters, and σj are the experimental errors in determining Rj. If χ2 < 1, then store the set of ci and τi. If χ2 > 1, then repeat steps 1 and 2. By repeating this process n times, one obtains n sets of ci and τi.

  3. For each k-th set of ci and τi, calculate F(ω)k. The probability Pk of finding the k-th set of ci and τi is (Andrec et al. 1999):

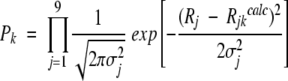
    graphic file with name M18.gif (12)

    Rjkcalc are calculated parameters for the k-th set.

  4. 5n-weighted Lorentzians can now be used to describe F(ω). The average value of F(ω) and the standard deviation Δ(ω) of F(ω) can be calculated as:

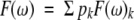
    graphic file with name M19.gif (13a)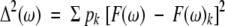
    graphic file with name M20.gif (13b)

    with pk = Pk/Σ Pk.

Acknowledgments

This work was supported by a research grant from the National Institutes of Health (NIH, GM-58005) and benefited from use of the high field NMR facility at the University of Minnesota. NMR instrumentation was provided with funds from the NSF (BIR-961477), the University of Minnesota Medical School, and the Minnesota Medical Foundation. We also thank Judy Haseman for preparing 13C-and 15N-enriched samples of protein GB1.

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.

Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.0228703.

References

  1. Alexander, P., Fahnestock, S., Lee, T., Orban, J., and Bryan, P. 1992. Thermodynamic analysis of the folding of the Streptococcal protein G IgG-binding domains B1 and B2: Why small proteins tend to have high denaturation temperatures. Biochemistry 31 3597–3603. [DOI] [PubMed] [Google Scholar]
  2. Andrec, M., Montelione, G.T., and Levy, R.M. 1999. Estimation of dynamics parameters from NMR relaxation data using the Lipari-Szabo model free approach and Bayesian statistical methods. J. Magn. Reson. 139 408–421. [DOI] [PubMed] [Google Scholar]
  3. Baber, J.L., Szabo, A., and Tjandra, N. 2001. Analysis of slow interdomain motion of macromolecules using NMR relaxation data. J. Am. Chem. Soc. 123 3953–3959. [DOI] [PubMed] [Google Scholar]
  4. Barchi, J.J., Grasberger, B., Gronenborn, A.M., and Clore, G.M. 1994. Investigation of the backbone dynamics of the IgG-binding domain of streptococcal protein G by heteronuclear two-dimensional 1H-15N NMR spectroscopy. Protein Sci. 3 15–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Berglund, H., Olerenshaw, D., Sankar, A., Federwisch, M., McDonald, N.Q., and Driscoll, P.C. 2000. The three-dimensional solution structure and dynamic properties of the human FADD death domain. J. Mol. Biol. 302 171–188. [DOI] [PubMed] [Google Scholar]
  6. Canet, D., Barthe, P., Mutzenhardt, P., and Roumestand, C. 2001. A comprehensive analysis of multifield 15N relaxation parameters in proteins: determination of 15N chemical shift anisotropies. J. Am. Chem. Soc. 123 4567–4576. [DOI] [PubMed] [Google Scholar]
  7. Carr, P.A., Fearing, D.A., and Palmer III, A.G. 1998. 3D accordion spectroscopy for measuring 15N and 13CO relaxation rates in poorly resolved NMR spectra. J. Magn. Reson. 32 25–33. [DOI] [PubMed] [Google Scholar]
  8. Clore, G.M., Szabo, A., Bax, A., Kay, L.E., Driscoll, P.C., and Gronenborn, A.M. 1990. Deviations from the simple two-parameter model free approach to the interpretation of 15N NMR relaxation of proteins. J. Am. Chem. Soc. 112 4989–4991. [Google Scholar]
  9. Clore, G.M., Driscoll, P.C., Wingfield, P.T., and Gronenborn, A.M. 1991. Analysis of the backbone dynamics of interleukin-1β using two-dimensional inverse detected heteronuclear 15N-1H NMR spectroscopy. Biochemistry 29 7387–7401. [DOI] [PubMed] [Google Scholar]
  10. Coles, M., Diercks, T., Muehlenweg, B., Bartsch, S., Zoelzer, V., Tschesche, H., and Kessler, H. 1999. The solution structure and dynamics of human neutrophil gelatinase-associated lipocalin. J. Mol. Biol. 289 139–157. [DOI] [PubMed] [Google Scholar]
  11. Daragan, V.A. and Mayo, K.H. 1996a. A novel model-free analysis of 13C NMR relaxation of alanine methyl side-chain motions in peptides, J. Mag. Reson. 110 164–175. [Google Scholar]
  12. ———. 1996b. Analysis of internally restricted correlated rotations in peptides and proteins using 13C and 15N NMR relaxation data. J. Phys. Chem. 100 8378–8388. [Google Scholar]
  13. ———. 1997. Motional model analyses of protein and peptide dynamics using 13C and 15N NMR relaxation. Prog. NMR Spectrosc. 32 63–105. [Google Scholar]
  14. ———. 1998. A simple approach to analyzing protein side-chain dynamics from 13C-NMR relaxation data. J. Magn. Reson. 130 329–334. [DOI] [PubMed] [Google Scholar]
  15. Daragan, V.A., Ilyina, E., Fields, C.G., Fields, G.B., and Mayo, KH. 1997. Backbone and side-chain dynamics of residues in a partially folded β-sheet peptide from PF4. Protein Sci. 6 355–363. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Debye, P. 1929. Polar molecules. Chemical Catalogue Co., New York.
  17. Farrow, N.A., Zhang, O., Szabo, A., Torchia, D.A., and Kay, L.E. 1995. Spectral density function mapping using 15N relaxation data exclusively. J. Biomol. NMR 6 153–162. [DOI] [PubMed] [Google Scholar]
  18. Frauenfelder, H., Sligar, S.G., and Wolynes PG. 1991. The energy landscape and motions of proteins. Science 254 1598–1603. [DOI] [PubMed] [Google Scholar]
  19. Gronenborn, A.M., Filpula, D.R., Essig, N.Z., Achari, A., Whitlow,.M., Wingfield, P.T., and Clore, G.M. 1991. A novel, highly stable fold of the immunoglobulin binding domain of streptococcal protein G. Science 253 657–660. [DOI] [PubMed] [Google Scholar]
  20. Guenneugues, M., Gilquin, B., Wolff, N., Menez, A., and Zinn-Justin, S. 1999. Internal motion time scales of a small, highly stable and disulfide-rich protein: A 15N, 13C NMR and molecular dynamics study. J. Biomol. NMR 14 47–66. [DOI] [PubMed] [Google Scholar]
  21. Hall, K.B. and Tang, C. 1998. 13C relaxation and dynamics of the purine bases in the iron responsive element RNA hairpin. Biochemistry 37 9323–9332. [DOI] [PubMed] [Google Scholar]
  22. Hidehito, T., Hung, F., Li, M., Bredt, D.S., and Zhang, M. 2000. Solution structure and backbone dynamics of the second PDZ domain of postsynaptic density-95. J. Mol. Biol. 295 225–237. [DOI] [PubMed] [Google Scholar]
  23. Huang, K., Ghose, R., Flanagan, J.M., and Prestegard, J.H. 1999. Backbone dynamics of the N-terminal domain in E. coli DnaJ determined by 15N- and 13CO-relaxation measurements. Biochemistry 38 10567–10577. [DOI] [PubMed] [Google Scholar]
  24. Idiyatullin, D., Krushelnitsky, A., Nesmelova, I., Blanco, F., Daragan, V.A., Serrano, L., and Mayo, K.H. 2000. Internal motional amplitudes and correlated bond rotations in an α-helical peptide derived from 13C and 15N NMR relaxation. Protein Sci. 9 2118–2127. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Idiyatullin, D., Daragan, V.A., and Mayo, K.H. 2001. A new approach to visualizing spectral density functions and deriving motional correlation time distributions: Applications to an α-helix-forming peptide and to well-folded protein. J. Magn. Reson. 152 132–148. [DOI] [PubMed] [Google Scholar]
  26. Kay, L.E., Torchia, D.A., and Bax, A. 1989. Backbone dynamics of proteins as studied by 15N inverse detected heteronuclear NMR spectroscopy: Application to staphylococcal nuclease. Biochemistry 28 8972– 8979. [DOI] [PubMed] [Google Scholar]
  27. Kay, L.E., Nicholson, L.K., Delaglio, F., Bax, A., and Torchia, D.A. 1992. Pulse sequences for removal of the effect of cross correlation between dipolar and chemical-shift anisotropy relaxation mechanisms on the measurement of heteronuclear T1 and T2 values in proteins. J. Magn. Reson. 97 359–375. [Google Scholar]
  28. Kemple, M.D., Buckley, P., Yuan, P., and Prendergast, F.G. 1997. Main chain and side chain dynamics of peptides in liquid solution from 13C NMR: Melittin as a model peptide. Biochemistry 36 1678–1688. [DOI] [PubMed] [Google Scholar]
  29. Korzhnev, D.M., Billeter, M., Arseniev, A.S., and Orekhov, V.Y. 2001. NMR studies of Brownian tumbling and internal motions in proteins. Prog. Nucleic Magn. Reson. Spectrosc. 38 197–266. [Google Scholar]
  30. Lee, A.L., Urbauer, J.L., and Wand, A.J. 1997. Improved labeling strategy for 13C relaxation measurements of methyl groups in proteins. J. Biomol. NMR 9 437–440. [DOI] [PubMed] [Google Scholar]
  31. Lee, C.S., Kumar, T.K., Lian, L.Y., Cheng, J.W., and Yu, C. 1998. Main-chain dynamics of cardiotoxin II from Taiwan cobra (Naja naja atra) as studied by carbon-13 NMR at natural abundance: Delineation of the role of functionally important residues. Biochemistry 37 155–164. [DOI] [PubMed] [Google Scholar]
  32. Lee, L.K., Rance, M., Chazin, W.J., and Palmer III, A.G. 1997. Rotational diffusion anisotropy of proteins from simultaneous analysis of 15N and 13C α nuclear spin relaxation. J. Biomol. NMR 9 287–298. [DOI] [PubMed] [Google Scholar]
  33. LeMaster, D.M. 1999. NMR relaxation order parameter analysis of the dynamics of protein side chains. J. Am. Chem. Soc. 121 1726–1742. [Google Scholar]
  34. Lipari, G. and Szabo, A. 1982a. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. I. Theory and range of validity. J. Am. Chem. Soc. 104 4546–4559. [Google Scholar]
  35. ———. 1982b. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. II. Analysis of experimental results. J. Am. Chem. Soc. 104 4559–4570. [Google Scholar]
  36. Mandel, A.M., Akke, M., and Palmer, A.G. 1996. Dynamics of ribonuclease H: Temperature dependence of motions on multiple timescales. Biochemistry 35 16009–16023. [DOI] [PubMed] [Google Scholar]
  37. Markley, J.L., Horsley, W.J., and Klein, M.P. 1971. Spin-lattice relaxation measurement in slowly relaxing complex spectra. J. Chem. Phys. 53 3604–3605. [Google Scholar]
  38. Mikhailov, D.V., Washington, L., Voloshin, A.M., Daragan, V.A., and Mayo, K.H. 1999. Angular variances for internal bond rotations of side-chains in GXG-based tripeptides derived from 13C-NMR relaxation measurements. Biopolymers 49 373–383. [DOI] [PubMed] [Google Scholar]
  39. Palmer III, A.G., Skelton, N.J., Chazin, W.J., Wright, P.E., and Rance, M. 1992. Suppression of the effect of cross-correlation between dipolar and anisotropic chemical-shift relaxation mechanisms in the measurement of spin-spin relaxation rates. Mol. Phys. 75 699–711. [Google Scholar]
  40. Peng, J.W. and Wagner, G. 1994. Investigation of protein motions via relaxation measurements. Methods Enzymol. 239 563–596. [DOI] [PubMed] [Google Scholar]
  41. Ramirez-Alvarado, M., Daragan, V.A., Serrano, L., and Mayo, K.H. 1998. Motional dynamics of residues in a β-hairpin peptide measured by 13C-NMR relaxation. Protein Sci. 7 720–729. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Seewald, M.J., Pichumani, K., Stowell, C., Tibbals, B.V., Regan, L., and Stone, M.J. 2000. Role of backbone conformational heat capacity in protein stability: Temperature dependent dynamics of the B1 domain of Streptococcal protein G. Protein Sci. 9 1177–1193. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Tjandra, N., Szabo, A., and Bax, A. 1996. Protein backbone dynamics and 15N chemical shift anisotropy from quantitative measurement of relaxation interference effect. J. Am. Chem. Soc. 118 6986–6991. [Google Scholar]
  44. Walsh, S.T., Lee, A.L., DeGrado, W.F., and Wand, A.J. 2001. Dynamics of a de novo designed three-helix bundle protein studied by 15N, 13C, and 2H NMR relaxation methods. Biochemistry 40 9560–9569. [DOI] [PubMed] [Google Scholar]
  45. Yamazaki, T., Muhandiram, R., and Kay, L.E. 1994. NMR Experiments for the measurement of carbon relaxation properties in highly enriched, uniformly 13C, 15N-labeled proteins: Application to 13Cα carbons. J. Am. Chem. Soc. 116 8260–8278. [Google Scholar]
  46. Yang, D., Mittermaier, A., Mok, Y.K., and Kay, L.E. 1998. A study of protein side-chain dynamics from new 2H auto-correlation and 13C cross-correlation NMR experiments: Application to the N-terminal SH3 domain from drk. J. Mol. Biol. 276 939–954. [DOI] [PubMed] [Google Scholar]
  47. Zajicek, J., Chang, Y., and Castellino, F.J. 2000. The effects of ligand binding on the backbone dynamics of the kringle 1 domain of human plasminogen. J. Mol. Biol. 301 333–347. [DOI] [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES