A neural-network based method for prediction of γ-turns in proteins from multiple sequence alignment

Abstract

In the present study, an attempt has been made to develop a method for predicting γ-turns in proteins. First, we have implemented the commonly used statistical and machine-learning techniques in the field of protein structure prediction, for the prediction of γ-turns. All the methods have been trained and tested on a set of 320 nonhomologous protein chains by a fivefold cross-validation technique. It has been observed that the performance of all methods is very poor, having a Matthew’s Correlation Coefficient (MCC) ≤ 0.06. Second, predicted secondary structure obtained from PSIPRED is used in γ-turn prediction. It has been found that machine-learning methods outperform statistical methods and achieve an MCC of 0.11 when secondary structure information is used. The performance of γ-turn prediction is further improved when multiple sequence alignment is used as the input instead of a single sequence. Based on this study, we have developed a method, GammaPred, for γ-turn prediction (MCC = 0.17). The GammaPred is a neural-network-based method, which predicts γ-turns in two steps. In the first step, a sequence-to-structure network is used to predict the γ-turns from multiple alignment of protein sequence. In the second step, it uses a structure-to-structure network in which input consists of predicted γ-turns obtained from the first step and predicted secondary structure obtained from PSIPRED. (A Web server based on GammaPred is available at http://www.imtech.res.in/raghava/gammapred/.)

The prediction of secondary structure is an intermediate step in structure prediction. Helices and strands are the most common stabilizing secondary structures, but proteins cannot attain globularity in the absence of turns, which provide a directional change for the polypeptide chain. Therefore, the prediction of tight turns in proteins is as important as helix and strand prediction. The tight turns are classified as δ-turns, γ-turns, β-turns, α-turns, and π-turns, depending on the number of residues involved in forming the turn (Chou 2000). The β-turns are the most commonly found turns in proteins. In the past, several methods were developed for predicting β-turns in proteins (Shepherd et al. 1999; Kaur and Raghava 2002a,b).

The γ-turn is the second most characterized and commonly found turn, after the β-turn. A γ-turn is defined as a three-residue turn with a hydrogen bond between the carbonyl oxygen of residue i and the hydrogen of the amide group of residue i + 2. There are two types of γ-turns: inverse and classic (Bystrov et al. 1969). In the past, a systematic and careful search for γ-turns in proteins was carried out, but not a single γ-turn prediction method has been developed so far (Alkorta et al. 1996). We therefore believe that it will be worthwhile to develop a prediction method for γ-turns.

In this study, we have applied several techniques for γ-turn prediction that are used commonly in secondary structure or β-turn prediction. Besides the commonly used techniques, we have also used a new machine-learning technique called the Weka classifier. The methods used in the present study can be divided into two categories, statistical and machine-learning techniques. The statistical methods include the Sequence Coupled Model and the GOR method (Garnier et al. 1978; Gibrat et al. 1987; Chou 1997a,b; Chou and Blinn 1997). The machine-learning techniques include the neural network (using the SNNSv4.2 package; Zell and Mamier 1997) and Weka3.2 (Witten and Frank 1999).

Initially, we implemented all these methods as they were used in the literature. But we found that the performance of all these methods is nearly the same and very poor. We studied the effect of predicted secondary structure and multiple sequence alignment information obtained from PSIPRED (Jones 1999; Kaur and Raghava 2002b, 2003). Based on our observations, we developed a method called GammaPred, for γ-turn prediction (MCC = 0.17). GammaPred is a neural-network-based method that uses two steps. In the first step, a sequence-to-structure network is used to predict the γ-turns from multiple alignment of the protein sequence. In the second step, GammaPred uses a structure-to structure network, in which the input is the predicted γ-turns obtained from the first step and the predicted secondary structure.

Results

The performance of various methods is shown in Table 1. All the methods have been trained and tested using fivefold cross-validation. The prediction performance measures have been averaged over five sets and are expressed as the mean ± standard deviation. The input in all the methods is a single amino acid sequence. In the case of statistical methods, parameters/propensities have been calculated for turns and non-turns separately (as described in Materials and Methods). In the case of Weka, three algorithms have been used. The neural network has been trained using a back-propagation algorithm. As shown in Table 1, the performance of all methods is very poor (MCC ≤ 0.06) and is comparable except for the Weka J48 classifier, in which MCC is only 0.02. The performance of all methods in terms of Q_pred (the probability of correct prediction) is significantly lower than the Q_obs (the coverage of γ-turns).

Table 1.

Results of γ-turn prediction methods, when single sequence was used as input

Method	Qtotal	Qpred	Qobs	MCC
Sequence coupled model	66.3 ± 0.8	2.8 ± 0.4	50.1 ± 2.4	0.05 ± 0.01
	(57.8 ± 1.9)	(5.9 ± 0.6)	(43.2 ± 2.4)	(0.08 ± 0.01)
GOR	62.1 ± 2.0	4.7 ± 0.4	55.4 ± 2.3	0.06 ± 0.01
	(75.5 ± 1.4)	(6.1 ± 0.6)	(45.5 ± 2.1)	(0.09 ± 0.01)
SNNS (std. back-propagation)	56.1 ± 4.0	4.3 ± 0.4	59.4 ± 6.7	0.06 ± 0.01
	(57.4 ± 2.5)	(5.4 ± 0.6)	(73.1 ± 5.2)	(0.11 ± 0.01)
Weka (logistic regression)	61.7 ± 1.8	4.7 ± 0.5	56.2 ± 2.0	0.06 ± 0.01
	(61.9 ± 0.8)	(5.7 ± 0.7)	(69.4 ± 2.3)	(0.11 ± 0.01)
Weka (naive Bayes)	66.5 ± 1.5	4.8 ± 0.6	49.5 ± 4.7	0.06 ± 0.01
	(56.8 ± 2.2)	(5.3 ± 0.5)	(72.1 ± 1.6)	(0.10 ± 0.01)
Weka (J48 classifier)	89.6 ± 0.5	4.3 ± 1.1	10.4 ± 2.2	0.02 ± 0.01
	(91.1 ± 0.4)	(6.4 ± 0.7)	(13.1 ± 1.4)	(0.05 ± 0.01)

The performance is averaged over five test sets.

Values in parentheses correspond to the performance of γ-turn prediction methods, when secondary structure information obtained from PSIPRED was also used.

Effect of secondary structure on γ-turn prediction

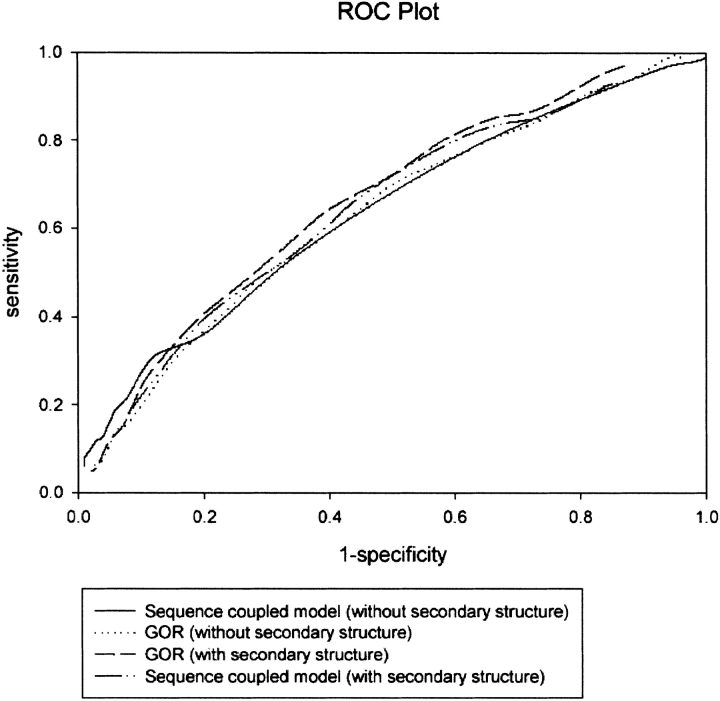
To further improve the performance, the secondary structure predicted by PSIPRED has been used to filter the γ-turn prediction in the case of statistical methods. In the case of machine-learning methods, predicted secondary structure information along with the predicted γ-turns (obtained from the first step) have been used as the input for a structure-to-structure network and Weka classifiers. The performance of all the methods, after incorporating secondary structure information, has been shown in Table 1. However, the performance of all the methods increases significantly, but its magnitude is much higher in the case of machine-learning methods (MCC increases from 0.06 to 0.11) in comparison to statistical methods (MCC increases from 0.06 to 0.08/0.09). The prediction performance of statistical methods with and without secondary structure information is also compared objectively by using a single performance metric, the ROC. It is clear from the ROC plot (Fig. 1 ▶) that without secondary structure, both GOR and the Sequence Coupled Model perform equally, as the ROC value of both the methods is equal to 0.62. When secondary structure information is used in prediction, the GOR method slightly outperforms the Sequence Coupled Model. Its ROC value equal to 0.65 is indicative of its better performance and is in agreement with its higher MCC value as compared to that of the Sequence Coupled Model, which has ROC = 0.63.

Figure 1.

ROC curves for statistical methods with and without secondary structure.

Information from multiple alignment

The comparative results of neural networks and Weka classifiers are shown in Table 2. The prediction accuracy is increased from 56.1% to 76.6% when the network 5(21)-25-1 is trained on multiple alignment matrices. The prediction accuracies are 62.7%, 59.0%, and 92.5% for the Weka classifiers logistic regression, naive Bayes, and J48, respectively. Moreover, the improvement is more significant in the case of the neural network in comparison to Weka classifiers.

Table 2.

Performance of SNNS and Weka classifiers using multiple alignment and secondary structure information

	Multiple alignment				Multiple alignment and secondary structure
		Weka classifiers				Weka classifiers
	SNNS (first network)	Logistic regression	Naive Bayes	J48 classifier	SNNS (second network)	Logistic regression	Naive Bayes	J48 classifier
Qtotal	76.6 ± 1.8	62.7 ± 1.8	59.0 ± 1.9	92.5 ± 0.2	74.0 ± 1.8	62.6 ± 1.8	57.4 ± 0.9	92.6 ± 0.2
					(72.0 ± 2.0)	(62.8 ± 1.8)	(57.3 ± 1.3)	(92.3 ± 0.4)
Qpred	5.1 ± 0.7	5.5 ± 0.7	5.1 ± 0.4	5.0 ± 1.1	6.3 ± 0.7	5.6 ± 0.7	5.0 ± 0.4	5.0 ± 1.2
					(6.0 ± 0.7)	(5.4 ± 0.7)	(4.8 ± 1.0)	(5.1 ± 1.3)
Qobs	58.6 ± 2.3	63.9 ± 3.0	65.3 ± 1.8	7.2 ± 0.9	83.2 ± 2.8	65.1 ± 2.9	65.4 ± 1.8	7.2 ± 0.9
					(80.0 ± 2.4)	(65.1 ± 2.0)	(65.4 ± 2.0)	(7.4 ± 0.8)
MCC	0.12 ± 0.01	0.10 ± 0.01	0.09 ± 0.01	0.02 ± 0.01	0.17 ± 0.01	0.12 ± 0.01	0.11 ± 0.01	0.03 ± 0.01
					(0.16 ± 0.01)	(0.12 ± 0.01)	(0.11 ± 0.01)	(0.03 ± 0.01)

Values in parentheses correspond to the prediction results obtained by excluding the proteins that were used to develop the PSIPRED method.

Multiple alignment and secondary structure information

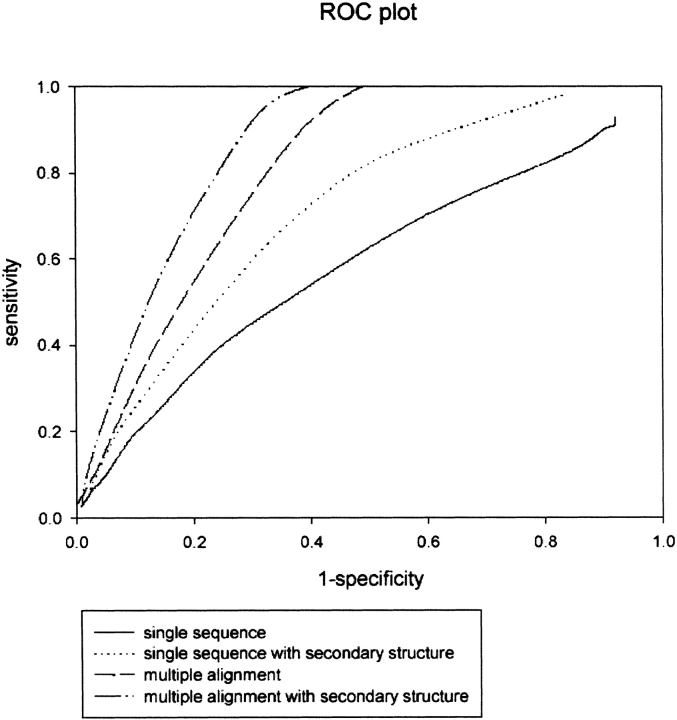
We combined the information obtained from secondary structure and multiple alignments to study the combined effect on machine-learning-based methods. There has been tremendous improvement in the performance of methods, as shown in Table 2. The neural-network method achieved an MCC value of 0.17, which is much higher than the MCC value of 0.06 in the absence of secondary structure and multiple alignments information. As shown in Figure 2 ▶, the ROC is also improved significantly. The corresponding areas under the ROC curves are: single sequence, 0.61; single sequence with secondary structure, 0.65; multiple alignment, 0.69; and multiple alignment with secondary structure, 0.73. These ROC values reflect the better discrimination of the network system, consisting of a first network trained on multiple alignment profiles and a second filtering network trained on the output of the first network and secondary structure in comparison to three other network systems. The results are consistent with threshold-dependent measures.

Figure 2.

ROC curves for four different neural-network systems.

PSIPRED cross-validation

Although our data set is nonhomologous, it contains some of the protein chains used to train PSIPRED. As a consequence, we have cross-validated the results of SNNS and Weka classifiers by removing those proteins from our data set that were used to develop PSIPRED. The results are given in Table 2. It is clear that the difference in prediction results is very small or almost negligible.

GammaPred server

Based on our study, we have developed a Web server that allows the user to predict γ-turns in proteins over the Web. The Web server is available free for academic or nonprofit users. Users can enter a primary amino acid sequence in fasta or plain text format. The output consists of predicted secondary structure and γ-turn or non-γ-turn residues. (A sample of prediction output is shown as Supplemental Material.)

Discussion

Today there exist prediction methods that can predict helices and strands from the amino acid sequence and even β-turns, but not γ-turns. Compared with β-turns, γ-turns are little investigated. This is because of the lower occurrence of γ-turns in proteins. In the past, studies of γ-turns were carried out, but not a single prediction method has been developed so far. It will be useful to develop a method for identifying γ-turn residues within a protein sequence.

In this work, the prediction method for γ-turn prediction has been developed in a systematic way. To establish baseline performance, the existing statistical methods such as GOR and the Sequence Coupled Model have been implemented in the first stage of prediction of γ-turns using a fivefold cross-validation technique. Both the methods perform equally. In the second stage, the machine-learning methods such as neural network and Weka classifiers have been used to further improve the prediction performance. Surprisingly, it is found that both the statistical methods as well as machine-learning methods have the same performance level on single sequences. When secondary structure information is incorporated, the machine-learning methods outperform statistical methods. Moreover, the neural-network prediction results are comparable to the Weka logistic regression classifier. One important point that can be noticed is that Q_pred, the probability of correct prediction, is significantly low in all the methods.

Because there does not exist any γ-turn prediction method, there are no values with which to compare the results obtained in this study. But given that the β-turn prediction study is similar to this study, the results obtained from this study can be compared with methods of β-turn prediction. The overall results with single sequences as well as with secondary structure are comparatively poorer than β-turn prediction methods BTPRED (Shepherd et al. 1999) and BetaTPred2 (Kaur and Raghava 2003; http://www.imtech.res.in/raghava/betatpred2/). This is owing to the fact that the data set used in this study is definitely more unbalanced than the data sets used in the β-turn prediction study. The present data set has a ratio of ~30:1 of non-γ-turn and γ-turn residues. The fact that γ-turns are very few resulted in poor Q_pred and MCC values in all the prediction results. Moreover, a γ-turn consists of three residues and thus is much more flexible than a β-turn. In the BetaTPred2 study, an MCC of 0.43 is reported for β-turn prediction (Kaur and Raghava 2003).

It is known that secondary structure prediction performance improves drastically when information from multiple sequence alignments is used. From this study, it is clear that a combination of a machine-learning algorithm and evolutionary information contained in multiple sequence alignment has improved the performance of γ-turn prediction. MCC is dramatically increased from 0.06 with a single sequence to 0.12. Moreover, when secondary structure is used, the neural network and Weka classifiers have final MCCs of 0.17 and 0.12, respectively. Because Weka classifiers have not been used in protein secondary structure prediction before, it will also be interesting to see the performance of this new type of learning machine. Comparing the results of neural network and Weka classifiers results in favor of the neural network. However, it should also be noted that much more time is spent in optimizing the networks and compensating for unbalanced data sets as compared with Weka classifiers.

In summary, we found that prediction performance is not very high for γ-turn prediction even by using a neural-network method and other machine-learning algorithms. This is because the number of γ-turns present in the data set is low. This work is an attempt toward using and optimizing machine-learning methods for the prediction of γ-turns in proteins. It can also be concluded that machine-learning methods perform poorly when the available data are sparse or ill-defined. However, further improvement in γ-turn prediction performance is possible with further extension or growth of the sequence database of proteins and if more effort is put into optimizing the training set.

Materials and methods

The data set

In this study, 320 nonhomologous protein chains were used in which no two chains have >25% sequence identity (Guruprasad and Rajkumar 2000). The structure of these proteins is determined by X-ray crystallography at 2.0 Å resolution or better. The PROMOTIF program has been used to assign γ-turns in proteins (Hutchinson and Thornton 1996). Each chain contains one minimum γ-turn.

The extracted γ-turn residues have been assigned different secondary structure states by DSSP (Kabsch and Sander 1983). It has been found that the maximum number of γ-turn residues have a C state followed by an S state and a T state in their nomenclature (see Electronic Supplemental Material).

Fivefold cross-validation

In this study, a fivefold cross-validation technique has been used, in which the data set is randomly divided into five subsets, each containing an equal number of proteins (Kaur and Raghava 2003). Each set is an unbalanced set that retains the naturally occurring proportion of γ-turns and non-γ-turns. The methods have been trained on four sets, and the performance is measured on the remaining fifth set. This process is repeated five times so that each set is tested. The average performance has been calculated for all methods on all sets. The strategy has been changed slightly in case of SNNS to avoid overtraining of the neural network. In SNNS we have used one set for validation also, so the training data consist of three sets instead of four.

Methods used for γ-turn prediction

Statistical method

Sequence Coupled Model

Chou (1997b) proposed a residue-coupled model based on a first-order Markov chain to predict β-turns in proteins. The same approach has been used here for γ-turn prediction. Given a tripeptide, its attribute to the γ-turn set S⁺ or the non-γ-turn set S⁻ is expressed, respectively, by an attribute function ψ (ψ⁺ for a γ-turn and ψ⁻ for a non-γ-turn), which can be defined as:

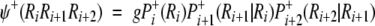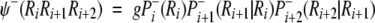where g = 10⁴ is the amplifying factor used to move the data to a range easier to handle, P_i⁺(R_i) is the probability of amino acid R_i occurring at subsite i in the γ-turn tripeptide set S⁺. P_i⁺(R_i) is independent of the other subsites because R_i is located at the first position of the three-subsite sequence. P_{i + 1}⁺(R_{i + 1} | R_i) is the probability of amino acid R_{i + 1} occurring at the subsite (i + 1) given that R_i has occurred at position i, and so forth. The probabilities have been calculated for turns and non-turns for all the five training sets (see Electronic Supplemental Material). The discriminant function can be calculated from the following equation:

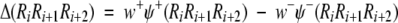where w⁺ and w⁻ are the weight factors for the probabilities derived from the γ-turn and non-γ-turn training data sets, respectively. Thus, a γ-turn is predicted if Δ > 0. In the present study, the weight factors w⁺ and w⁻ have been set to unity, that is, w⁺ = w⁻ = 1.

GOR

The GOR method calculates the probability of a given amino acid in a given secondary structure element based on information theory. The bridge to this probability is a function called the information: I(S, R) = log P(S | R)/P(S), where P(S) is the probability of state S in the database and P(S | R) is the conditional probability of a conformation S knowing that a residue R is present. Furthermore, P(S | R) = P(S, R)/P(R), where P(S, R) is the probability of the joint event, residue R in conformation S, and P(R) is the probability of observing a residue R.

The directional information values for window size five have been calculated for each of the 20 amino acids from a training data set consisting of γ-turn and non-γ-turn sequences by using the following equation (see Electronic Supplemental Material). For window size 5, we have:

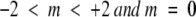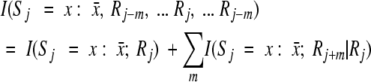Machine-learning methods

Neural Network Method (SNNS)

In the present study, two feed-forward back-propagation neural networks with a single hidden layer have been used. The window size and the number of hidden units have been optimized. In this study two networks have been used: (1) sequence to structure and (2) structure to structure. In both networks, the input window of size five and a single hidden layer (hidden units 25) have been used. The neural-network method has been developed using SNNS version 4.2 from Stuttgart University (Zell and Mamier 1997). The training is carried out using error-back-propagation with a sum of square error function (SSE; Rumelhart et al. 1986).

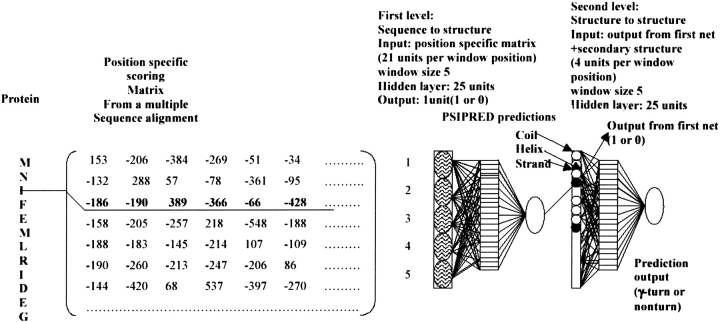
The input to the first network is either a single sequence or multiple alignment profiles. Patterns are presented as windows of five residues in which a prediction is made for the central residue. The binary encoding scheme has been used in the case where a single sequence is used as input, whereas a “position-specific scoring matrix generated by PSI-BLAST” has been used as input in the case of multiple sequence alignment (Kaur and Raghava 2003). The prediction obtained from the first net and the secondary structure obtained from PSIPRED were used as input to the second net (structure-to-structure) net. Four input units in the second net encode each residue, where one unit codes for output from the first net and the remaining three units are the reliability indices of three secondary structure states—helix, strand, and coil (Fig. 3 ▶).

Figure 3.

(Left) The neural-network system used for γ-turn prediction; it consists of two networks: a first-level sequence-to-structure network and a second-level structure-to-structure network. (Middle) Basic cell containing 20 + 1 units to code residues at that position in the window; here, window size = 5. (Right) Hidden layer containing 25 units. In the second-level network, four units encode each residue. Closed circles indicate prediction obtained from first network; open circles indicate secondary structure state (helix, strand, and coil) predicted by PSIPRED.

Weka-3.2-based methods

The machine-learning package Weka 3.2 is a collection of machine-learning algorithms for solving real world data mining problems (Witten and Frank 1999). Here, we have used the following three algorithms of Weka: (1) logistic regression, which is a variation of ordinary regression and particularly useful when the observed outcome is restricted to two values (Hosmer and Lemeshow 1989); (2) a naive Bayes algorithm, which implements Bayesian classification based on Bayes’ theorem of conditional probability (Domingos and Pazzani 1997); and (3) a J48 classifier based on the C4.5 algorithm proposed by Quinlan (1993), which generates a classification-decision tree for the given data set by recursive partitioning of data. As data in this study are highly unbalanced (many more non-turns than γ-turns), we have used Weka’s cost-sensitive classification option in which the data sets have been weighted according to the distribution of γ-turns and non-γ-turns and penalties have been assigned to each class (γ-turn/non-γ-turn) in the cost matrix. The penalties have been optimized by learning the classifier several times.

Multiple sequence alignment and secondary structure

PSIPRED uses PSI-BLAST to detect distant homologs of a query sequence and generate a position-specific scoring matrix as part of the prediction process (Jones 1999). These intermediate PSI-BLAST-generated position-specific scoring matrices are used as input in our methods in the case in which multiple sequence alignment is used. The matrix has 21 × M elements, where M is the length of the target sequence and each element represents the frequency of occurrence of each of the 20 amino acids at one position in the alignment (Altschul et al. 1997). The predicted secondary structure from PSIPRED is used to filter the γ-turn prediction in the case of statistical methods and input for the structure-to-structure network and Weka classifiers.

Filtering the prediction

Because the prediction is performed for each residue separately, prediction includes several unusually short γ-turns of one or two residues. To exclude such unrealistic turns, we have applied a simple filtering rule, the “state-flipping” rule as described in the work of Shepherd et al. (1999).

Performance measures

Threshold-dependent measures

Four parameters have been used in the present work to measure the performance of γ-turn prediction methods as described by Shepherd et al. (1999) for β-turn prediction. These four parameters can be derived from the four scalar quantities: p (the number of correctly classified γ-turn residues), n (the number of correctly classified non-γ-turn residues), o (the number of non-γ-turn residues incorrectly classified as γ-turn residues), and u (the number of γ-turn residues incorrectly classified as non-γ-turn residues). Another way to visualize and arrange these four quantities is to use a contingency or confusion matrix C:

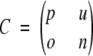The four parameters that can be derived from these four quantities are: (1) Q_total (or prediction accuracy) is the percentage of correctly classified residues; (2) Matthew’s correlation coefficient (MCC), accounts for both over- and underpredictions; (3) Q_pred is the percentage of correctly predicted γ-turns (or probability of correct prediction); and (4) Q_obs is the percentage of observed γ-turns that are correctly predicted (or percent coverage). The parameters can be calculated by the following equations:

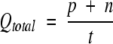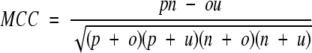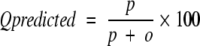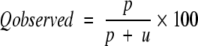where t = p + n + o + u is the total number of residues.

Threshold-independent measures

One problem with the threshold-dependent measures is that they measure the performance on a given threshold. They fail to use all the information provided by a method. The Receiver Operating Characteristic (ROC) is a threshold-independent measure that was developed as a signal-processing technique. For a prediction method, an ROC plot is obtained by plotting all sensitivity values (true positive fraction) on the y-axis against their equivalent (1-specificity) values (false-positive fraction) for all available thresholds on the x-axis. The area under the ROC curve is taken as an important index because it provides a single measure of overall accuracy that is not dependent on a particular threshold (Deleo 1993). It measures discrimination, the ability of a method to correctly classify γ-turn and non-γ-turn residues. Sensitivity (Sn) and specificity (Sp) are defined as:

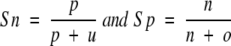Electronic supplemental material

The supplementary information consists of: 1) PDB codes protein chains; 2) composition of residues in γ and non-γ turns; and 3) secondary structure composition of γ-turn residues in terms of DSSP 8 states. It also includes probabilities and different types of γ turns.