Conformational states of the switch I region of Ha-ras-p21 in hinge residue mutants studied by fluorescence lifetime and fluorescence anisotropy measurements

Abstract

The hinge residues (Val29 and Ile36) of the switch I region (also known as the effector loop) of the Ha-ras-p21 protein have been mutated to glycines to accelerate the conformational changes typical for the effector loop. In this work, we have studied the influence of the combined mutations on the steady-state structure of the switch I region of the protein in both the inactive GDP-bound conformation as in the active GTP-bound conformation. Here, we use the fluorescence properties of the single tryptophan residue in the Y32W mutant of Ha-ras-p21. This mutant has already been used extensively as a reference form of the protein. Reducing the size of the side chains of the hinge residues not only accelerates the conformational changes but also affects the steady-state structures of the effector loop as indicated by the changes in the fluorescence properties. A thorough analysis of the fluorescence changes (quantum yield, lifetimes, etc.) proves that these changes are from a reshuffling between the rotamer populations of Trp. The population reshuffling is caused by the overall structural rearrangement along the switch I region. The effects are clearly more pronounced in the inactive GDP-bound conformation than in the active GTP-bound conformation. The effect of both mutations seems to be additive in the GDP-bound state, but cooperative in the GTP-bound state.

Ha-ras-p21 is a small protein (189 residues) that belongs to the extended group of guanine nucleotide-binding proteins (G-proteins or GNBPs; Bourne et al. 1990^{, 1991}). The membrane-bound Ha-ras-p21 functions as a molecular switch that controls growing, proliferation, and differentiation processes of the cell. The ras-genes were identified as protooncogenes because of the high occurrence of point mutations of these genes in human tumors (Barbacid 1987). The Ha-ras-p21 binds guanine nucleotides complexed with magnesium ions. These magnesium ions contribute to the tight binding of nucleotides. The physiological state of the protein (and thereby also the position of the molecular switch) depends on the nature of the bound nucleotide. In the active form, the protein has GTP bound, and upon hydrolysis of GTP and the release of the γ-phosphate, the protein changes to the inactive state. After the hydrolysis, the GDP remains bound to the protein. Exchanging the GDP for GTP allows the protein to switch back to the active state (Wittinghofer and Pai 1991). The structural differences between the GTP-bound and GDP-bound conformations are mainly confined to two segments, the so-called “switch regions.” These regions show an increased flexibility in X-ray structures and in nuclear magnetic resonance (NMR) and electron paramagnetic resonance (EPR) experiments (Farrar et al. 1997; Ito et al. 1997). Both switches are connected to the γ-phosphate of GTP with hydrogen bonds. In this way, the conformational change can best be described as a loaded-spring mechanism. After hydrolysis of the GTP and release of the γ-phosphate, the switch regions can relax into the GDP-specific conformation. This mechanism is likely universal for the conformational change in the GNBPs (Vetter and Wittinghofer 2001).

Both hydrolysis and nucleotide exchange processes determine the conformational state of the protein and are controlled by external proteins: the GTPase activating proteins (GAPs) in the case of the hydrolysis and the guanine exchange factors (GEFs) and guanine nucleotide release proteins (GNRPs) in the case of the nucleotide exchange (McCormick 1994). For detailed reviews on the structures of G-proteins and their interactions with GAPs, GEFs, and effectors, see Sprang (1997) and Vetter and Wittinghofer (2001).

Our main interest focuses on the study of the dynamics of conformational transitions that occur in this protein. The biological relevance of the system as well as the small size of Ha-ras-p21 make it a perfect model system to study the mechanisms of conformational transitions in GTP-activated proteins. The G-domain of the Ras-protein with 166 residues is considered as the minimal signaling unit where most other GNBPs are seen as variations on this canonical structure (Vetter and Wittinghofer 2001). In our previous research, we studied the conformational transition using computational methods, for example, molecular dynamics (MD) and targeted molecular dynamics (TMD) in order to find possible hinges and levers of the transition as well as to find a possible pathway for the activation and deactivation of the molecule (Schlitter et al. 1994; Díaz et al. 1995). In this way, it became clear that the conformational transition between both states of the protein is not a single process but rather a succession of different micro transitions. It is possible to determine the residues that may constitute energy barriers for a certain micro transition and then design mutants that may affect the transition state of that particular micro transition in a stabilizing or destabilizing way. According to the calculated TMD pathway, the effector loop (switch I region, residues 30–38) plays a key role in the transition by transmitting the recognition signal from the P-loop, which interacts with the phosphate chain of the nucleotide, to the switch II region. Two residues (V29 and I36) were identified as the main hinges in the movements of the effector loop (Díaz et al. 1997a). They show important dihedral transitions during the conformational changes. We expected, therefore, that their substitution by glycines would lower the activation energy of the micro transitions and would speed up the overall conformational transition. In a previous paper (Kuppens et al. 1999), these mutants were experimentally constructed and studied. Therefore, we used a fluorescent mutant of Ha-ras-p21 (Y32W) that contains a tryptophan as a fluorescent label in the effector loop. Beryllium trifluoride is an analog of the ground state of the γ-phosphate in GTP, so it binds to the Ha-ras-p21 GDP complex and activates it by forming an analog of the Ha-ras-p21 GTP complex. The fluorescence properties of the W32 in the GTP-bound form and in the (GDP-BeF₃⁻)-bound form are identical (Díaz et al. 1997b). As predicted, the rate constant of the conformational change appeared to be ~100 times higher in both mutants when compared with the wild type. But we also got some indications of structural rearrangements in the binding site caused by the introduced mutations. These indications are supported by the results of Spoerner et al. (2001), who investigated the conformation of the effector loop in the active state using ³¹P-NMR spectroscopy. The ³¹P-NMR experiments on the GTP-bound p21 reported the existence of (at least) two conformational states with a strongly temperature-dependent interconversion (Geyer et al. 1996). The so-called state 2 corresponds to the structure found in the complex with the effectors and is the actual active conformation of Ha-ras-p21. State 1, however, may represent either a single conformation or a mixture of conformational substates in fast exchange on the NMR time scale. In the spectrum of the highly flexible V29G/I36G variant, only state 1 gets populated supporting the idea that state 1 is not a well-defined arrangement of atoms fixed in space. They conclude that the higher flexibility of the loop disturbs the fast equilibrium of conformational substates of the effector loop in the active state (Spoerner et al. 2001).

In this study, we take a deeper look into the structural and conformational consequences that are correlated with the mutants we have described previously. We also constructed the mutant containing both mutations at the hinges of the effector loop to check if the hinges act in an independent or rather in a cooperative way.

Results

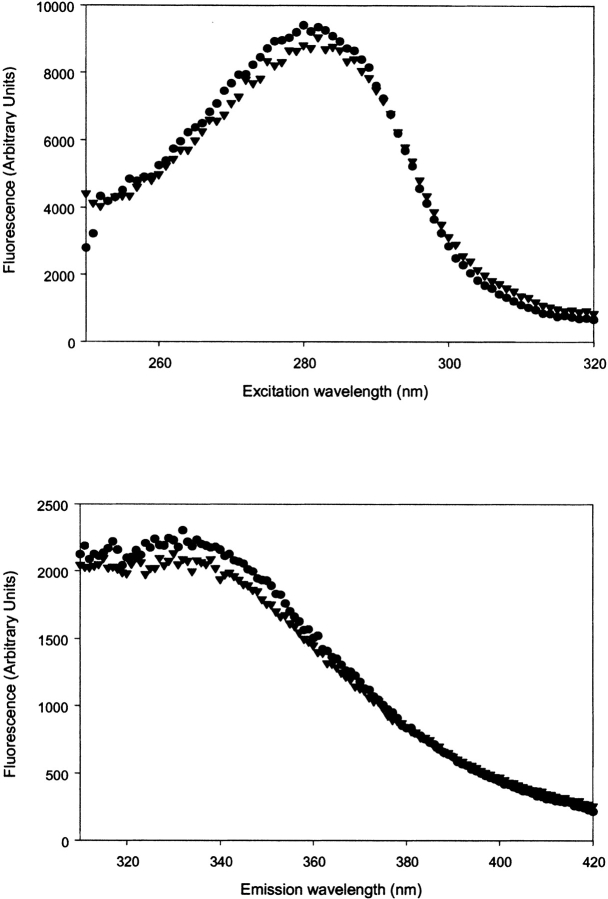
The GDP-bound state and the GTP (or GDP-BeF₃⁻)-bound state can be distinguished using the difference in fluorescence of Trp32 of the Y32W mutant of Ha-ras-p21. In the Y32W mutant, this difference is ~60% (Díaz et al. 1997b). In both double mutants (V29G-Y32W and Y32W-I36G), the drop in fluorescence intensity is reduced to 30% and lower (Kuppens et al. 1999). In the triple mutant (V29G-Y32W-I36G) of Ha-ras-p21 containing both mutated hinge residues and the fluorescent Trp, we could not see a significant difference in fluorescence intensity of the GDP-bound state in the presence and absence of BeF₃⁻. The excitation and emission spectra for the triple mutant are shown in Figure 1 ▶.

Figure 1.

(Top) Fluorescence excitation (emission wavelength 343 nm) and (bottom) fluorescence emission (excitation wavelength 280 nm) spectra of Ha-ras-p21 (V29G-Y32W-I36G). Spectra with GDP (circles) and GDP-BeF₃⁻ (triangles) bound to p21 (5μM) are displayed.

Fluorescence lifetime measurements were performed on all relevant mutants (V29G-Y32W, Y32W-I36G, V29G-Y32W-I36G, and Y32W as reference) in the GDP-bound and the GTP-bound state using phase fluorimetry. To prevent possible hydrolysis of the GTP in the GTP-bound conformation, we made use of the nonhydrolysable analog GTPγS. In previous studies, we used the fluorescence lifetime measurements to obtain the tryptophan fluorescence characteristics of the single tryptophan in the Y32W mutant of the protein in the different conformational states (Díaz et al. 1997b). It appeared that the time dependence of the tryptophan fluorescence emission can be described by a sum of three exponentials, that is, there are three distinct lifetimes, each of which is characterized by a corresponding amplitude. It also appeared that the fluorescence lifetimes of the tryptophan are approximately the same in the different states; the only differences arise from the amplitude fractions where we noticed the difference between the GDP state and the GTP state. The multiexponential fluorescence decay can be a result of the presence of different quenching residues in the close neighborhood of the Trp residue. The relevant quenchers in proteins are the disulfide bridge, the amino-acid side chains of protonated histidine, cysteine and tyrosine, and the carbonyl carbon of the peptide bond (Chen et al. 1996; Chen and Barkley 1998; Sillen et al. 2000). In the case of Ha-ras-p21, there are no disulfide bridges present at all, and in the close neighborhood of the single Trp residue, none of the other mentioned quenchers is present either. Therefore, the different fluorescence lifetimes can be explained as originating from different conformations of tryptophan with different distances between the atom CE3 of tryptophan and the carbonyl atom of the peptide bond (Sillen et al. 2000). This means that the origin of the different lifetimes comes from the existence of different rotamer conformations (or microconformations) of the tryptophan and that the nature of these rotamer conformations is not changed toward the backbone of the loop after the conformational change. What happens is a change in the probability of populating a possible rotamer state because of a change in the environment surrounding the loop (Sillen et al. 2000). Because of the high solvent exposure of the loop region containing the tryptophan residue and the relatively low restriction in the side-chain movement, the residue can easily populate the multiple rotamer conformations. Because the tryptophan fluorescence properties are different in the different conformations of the protein, we can deduce some structural information about the effector loop that contains the tryptophan residue. Differences in the fluorescence lifetimes and amplitudes that occur when we compare the different mutants with each other will most probably be the effect of structural rearrangements at the level of the effector loop that are caused by the corresponding mutations (i.e., V29G, I36G, or both).

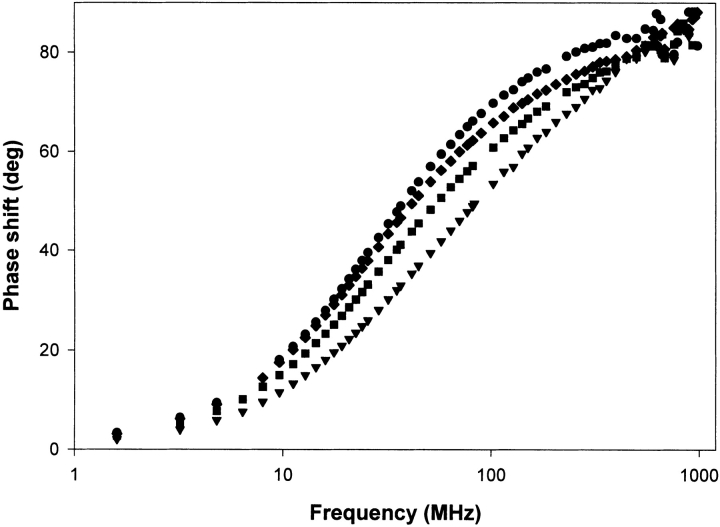
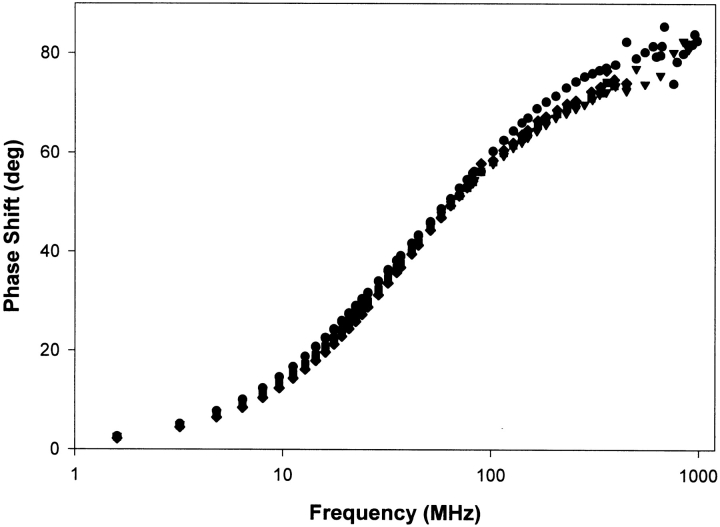
The phase measurements of the fluorescence lifetimes of Trp32 in the different mutants of p21 in the GDP-bound state are displayed in Figure 2 ▶. The analysis of these measurements with Globals Unlimited results in the corresponding fluorescence lifetimes displayed in Table 1. The phase measurements clearly indicate major differences for the different mutants. For all mutants, we see the three intrinsic fluorescence lifetimes and corresponding amplitude fractions as previously described in Díaz et al. (1997b). The differences in the time-resolved fluorescence of the different mutants are apparent on the level of the amplitude fractions. Table 1 shows that the three lifetimes are approximately identical for all mutants again indicating that the rotamer conformations of Trp are unaffected. On the other hand, we see a shift in the amplitude fractions, that is, the amplitude of the short lifetime (a₁) grows from 12% in the Y32W reference mutant to 40% in the triple mutant (V29G-Y32W-I36G); the amplitude of the second lifetime (a₂) grows from 18% in the reference mutant to 44% in the triple mutant; and the amplitude of the longest lifetime (a₃) drops from 70% in the reference mutant to 16% in the triple mutant. These amplitude shifts are quite similar (especially concerning a₂ and a₃) to the amplitude shifts in the Y32W mutant when we compare the GDP-bound structure with the GTP-bound structure. To study the same fluorescence properties in the GTP-bound structures of the different mutants of p21, we replaced the GDP by the nonhydrolysable GTPγS. The phase measurements of the fluorescence lifetimes of Trp32 in the different mutants of p21 in the GTPγS bound state are displayed in Figure 3 ▶, the corresponding fluorescence lifetimes are shown in Table 2. When we compare the fluorescence lifetimes and amplitude fractions of the different mutants in their GTPγS bound conformation, we see that the differences are not as pronounced as in the GDP-bound conformation. The fluorescence properties of the different mutants in the GTP bound conformation obviously do not show the extended differences as seen for the GDP-bound conformation. Table 2 shows us that the amplitude fraction a₃ of the longest lifetime is not altered, whereas this fraction had the largest difference in the GDP conformation. Only a rather limited rearrangement between the amplitude fractions of both shorter lifetimes is noticeable.

Figure 2.

Phase measurements of the fluorescence lifetimes of the different mutants of Ha-ras-p21 in the GDP bound state: Y32W (circles), V29G-Y32W (diamonds), Y32W-I36G (squares), and V29G-Y32W-I36G (triangles).

Table 1.

Tryptophan fluorescence lifetimes, relative amplitudes, and amplitude-averaged lifetimes of the different mutants of Ha-ras-p21 in the GDP-bound state

	a1	τ1 (ns)	a2	τ2 (ns)	a3	τ3 (ns)	χ2
p21 Y32W	0.12 ± 0.04	0.63 ± 0.30	0.18 ± 0.03	2.88 ± 0.73	0.70 ± 0.04	5.77 ± 0.25	1.13
p21 V29G-Y32W	0.22 ± 0.02	0.62 ± 0.08	0.27 ± 0.02	2.62 ± 0.29	0.51 ± 0.05	6.08 ± 0.11	1.10
p21 Y32W-I36G	0.29 ± 0.02	0.74 ± 0.06	0.36 ± 0.02	2.60 ± 0.21	0.35 ± 0.03	5.75 ± 0.15	1.11
p21 V29G-Y32W-I36G	0.40 ± 0.06	0.88 ± 0.10	0.44 ± 0.04	2.43 ± 0.27	0.16 ± 0.03	5.69 ± 0.33	2.39

Figure 3.

Phase measurements of the fluorescence lifetimes of the different mutants of Ha-ras-p21 in the GTP bound state: Y32W (circles), V29G-Y32W (diamonds), Y32W-I36G (squares), and V29G-Y32W-I36G (triangles).

Table 2.

Tryptophan fluorescence lifetimes, relative amplitudes, and amplitude-averaged lifetimes of Ha-ras-p21 in the GTPγS-bound state

	a1	τ1 (ns)	a2	τ2 (ns)	a3	τ3 (ns)	χ2
p21 Y32W	0.20 ± 0.02	0.47 ± 0.06	0.57 ± 0.02	2.59 ± 0.16	0.23 ± 0.02	5.60 ± 0.19	1.39
p21 V29G-Y32W	0.30 ± 0.02	0.57 ± 0.08	0.51 ± 0.08	2.76 ± 0.27	0.19 ± 0.06	5.52 ± 0.44	1.58
p21 Y32W-I36G	0.28 ± 0.04	0.51 ± 0.07	0.50 ± 0.06	2.65 ± 0.19	0.22 ± 0.04	5.49 ± 0.23	1.43
p21 V29G-Y32W-I36G	0.35 ± 0.02	0.50 ± 0.05	0.42 ± 0.02	2.48 ± 0.13	0.23 ± 0.02	6.04 ± 0.20	1.70

Because the conformational changes and differences between the different mutants are clearly accompanied by fluorescence changes, we can get a more detailed interpretation of the observed changes by analyzing the quantum yields and the average lifetimes.

Because by definition Q/τ = k_r, we assume that Q/τ = k_r and that changes in this factor, for example, upon a mutation, are reflecting changes in the radiative rate constants or in static quenching, which indeed reduces Q without influencing k_r. A reduction of τ is generally considered as a signal of dynamic quenching, but can be the result of a shortening of individual lifetimes (with constant amplitudes), which we identify as pure dynamic quenching, or to an increase in the amplitudes of short lifetimes, which we consider as population reshuffling. All these factors lead to changes in the quantum yield and can be combined into a set of factors as follows (Sillen and Engelborghs 1998; Sillen et al. 1999):

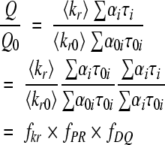Where subscript 0 refers to the reference state, for example, the wild-type protein, and where f_kr represents the change in the average radiative rate constant k_r, f_PR represents population reshuffling, and f_DQ represents pure dynamic quenching. It should be noted that static quenching also influences f_kr and heterogeneous static quenching (i.e., different for each life time component) also influences f_PR next to f_kr. It is clear these factors have to be analyzed with caution because of the complicating effect of static quenching. This factorization gives us the possibility to analyze in greater detail the quenching behavior and fluorescence differences between the different variants of the Ha-ras-p21 protein.

Table 3 displays the fluorescence quantum yields of the different mutants of Ha-ras-p21. In combination with the average fluorescence lifetimes the average radiative k_r and nonradiative k_nr rate constants are calculated. In all cases, we see a drop in the average radiative rate constant upon the introduction of the hinge residue mutations. There is no apparent difference in the average radiative rate constant when we compare the GTP-bound conformation with the GDP-bound conformation.

Table 3.

Average lifetimes, quantum yields, radiative and nonradiative rate constants of the Ha-ras-p21 variants

	τavg (ns)	Q	〈kr〉 (ns−1)	〈knr〉 (ns−1)
p21 Y32W (GDP)	4.7	0.241	0.051	0.16
p21 V29G-Y32W (GDP)	3.9	0.154	0.039	0.22
p21 Y32W-I36G (GDP)	3.2	0.126	0.039	0.27
p21 V29G-Y32W-I36G (GDP)	2.3	0.098	0.043	0.39
p21 Y32W (GTP)	2.9	0.139	0.048	0.30
p21 V29G-Y32W (GTP)	2.6	0.102	0.039	0.35
p21 Y32W-I36G (GTP)	2.7	0.107	0.040	0.33
p21 V29G-Y32W-I36G (GTP)	2.6	0.100	0.038	0.35

Table 4 gives a detailed overview of the quenching analysis of the discussed variants of Ha-ras-p21. Comparison between the GDP-bound conformation and the GTP-bound conformation for the Y32W reference mutant and the two single-hinge residue mutants indicates that the difference in fluorescence properties is mainly caused by population reshuffling. In the triple mutant, with both hinges mutated, the proportion of the quantum yields equals one, which was to be expected because of the earlier observed absence of any difference in fluorescence intensity between the two conformations (Fig. 1 ▶). The effect of a mutated hinge residue can be studied in a similar way by making a quenching analysis of these mutants using the Y32W variant as reference state. Here, we notice both f_PR and f_kr are different from one, indicating multiple causes for the changed fluorescence properties upon introduction of the mutations. The errors on the ratios f_DQ and f_PR are estimated to be ~10%, on the basis of the errors on the τ’s and the α’s, respectively. In these error calculations, the weight factors (α’s in the case of f_DQ and τ’s in the case of f_PR) are considered to be constants.

Table 4.

Relative changes in quantum yields and the quenching factors (fkr, fPR, and fDQ) that contribute to possible differences in the fluorescence properties

GTP-bound conformations of the different variants of Ha-ras-p21 with the GDP-bound conformations as reference
	Q/Q0	fkr	fPR	fDQ
p21 Y32W	0.58	0.94	0.66	0.94
p21 V29G-Y32W	0.66	1.00	0.68	0.98
p21 Y32W-I36G	0.85	1.03	0.86	0.96
p21 V29G-Y32W-I36G	1.02	0.88	1.15	0.99

GDP-bound conformations of the double and triple mutants of Ha-ras-p21 against the GDP-bound conformation of the Y32W reference mutant
	Q/Q0	fkr	fPR	fDQ
p21 V29G-Y32W	0.64	0.76	0.82	1.01
p21 Y32W-I36G	0.52	0.76	0.69	0.99
p21 V29G-Y32W-I36G	0.41	0.84	0.52	0.94

GTP-bound conformations of the double and triple mutants of Ha-ras-p21 against the GTP-bound conformation of the Y32W reference mutant
	Q/Q0	fkr	fPR	fDQ
p21 V29G-Y32W	0.73	0.81	0.87	1.03
p21 Y32W-I36G	0.77	0.83	0.91	1.02
p21 V29G-Y32W-I36G	0.72	0.79	0.88	1.02

Another method used to look at the mobility of the fluorophore-containing structure is by using time-resolved fluorescence anisotropy decay measurements. In this situation, there is a multiexponential anisotropy decay caused by the global rotation of the whole protein and by the local mobility of the Trp residue, caused both by the movement of the Trp-containing loop structure and the movement of the residue itself. Table 5 displays the fluorescence anisotropy decay parameters of the different mutants in the GDP-bound structure. In the case of the wild-type protein data, we had to apply the associative type of fitting. Each particular lifetime is associated with a specific anisotropy decay. The shortest lifetime (τ₁), however, is too short and too small in population to contribute to the measured anisotropy decay. The middle lifetime (τ₂) is actually long enough to see the anisotropy decay but is also very low populated (18%). Together with the low value for α, this makes that we were not able to resolve a significant value for φ₁. The anisotropy parameters obtained for the longest lifetime (τ₃), which is highly populated (70%), give the most significant results for the wild-type protein. All other mutants were fitted in the regular nonassociative way with global anisotropy decay parameters and gave satisfactory results. The r₀ values are the initial anisotropy values, with a theoretical maximum of 0,4 when the absorption and emission dipoles of the fluorescent group are colinear. In the case of tryptopan, the value is usually lower because of a mixture of the ¹L_a and ¹L_b transitions (Valeur and Weber 1977; Ruggiero et al. 1990). We attribute the long rotational correlation time φ₂ to the rotational motion of the whole protein, which is expected to be around 25 ns. The value of φ₂ is much larger than the fluorescence lifetime and therefore the accuracy of this parameter is rather limited resulting in relatively high errors. The interesting information about the mobility of the loop structure is given by the parameters α and φ₁, with φ₁ the correlation time for the internal motion and α the amount of depolarization that occurs as a result of internal motion of the fluorophore. This amount is related to the angle over which the fluorophore can move. We can see a clear evolution in these parameters upon increasing flexibility between the different hinge residue mutants in the GDP-bound state. The increase in α from 0,11 in Y32W (τ₃) to 0,40 in the triple mutant shows us the increasing importance of the internal mobility in the measured fluorescence depolarization. With this parameter, the angle over which the fluorophore can move is calculated resulting in angles of around 16 degrees for the Y32W mutant to 31 degrees for the double-hinge residue mutant (Table 5). Both the single-hinge residue mutants are showing values lying in between these. The correlation time φ₁ of internal mobility decreases significantly in the double-hinge mutant supporting the much higher mobility and higher speed of movement of the fluorophore in this mutant.

Table 5.

Fluorescence anisotropy decay parameters of the GDP-bound state of the different Ha-ras-p21 hinge residue variants

	r0	α	φ1 (ns)	φ2 (ns)	β
p21 Y32W (τ2)	0.23 ± 0.06	0.07 ± 0.04	*	28.1 ± 4.4	13°
p21 Y32W (τ3)	0.29 ± 0.06	0.11 ± 0.03	0.62 ± 0.17	22.6 ± 5.5	16°
p21 V29G-Y32W	0.15 ± 0.07	0.20 ± 0.07	0.77 ± 0.18	20.6 ± 7.2	21°
p21 Y32W-I36G	0.23 ± 0.05	0.18 ± 0.04	0.54 ± 0.11	28.3 ± 6.1	20°
p21 V29G-Y32W-I36G	0.21 ± 0.03	0.40 ± 0.07	0.34 ± 0.07	16.7 ± 8.2	31°

* No significant value obtained: error much larger than obtained parameter

Discussion

The small difference in overall fluorescence intensity of the GDP- and GTP-bound state of the triple mutant made kinetic experiments (using a stopped flow instrument) to study the conformational change from the GDP to the (GDP-BeF₃⁻)-bound state impossible, but it gave us a further indication on the structural rearrangements occurring in the binding site as a result of the multiple point mutations. The fact that the drop in the fluorescence signal from 60% in the Y32W-reference reduced to 30% and less in both double mutants was the first indication of structural rearrangements in the binding site. In these cases, the kinetic experiments were still possible and therefore our research at that point was not focused toward the phenomenon we are studying in this paper. All the measured and calculated fluorescence parameters of the triple mutant in the GDP-bound state are identical to those of the Y32W-reference protein in the GTP-bound complex. The most straightforward interpretation of this would be to conclude that the triple mutant protein, although in the GDP-bound complex, is frozen in the GTP conformation. In this case, the affinity for BeF₃⁻ would be at least as high as in the case of the wild-type protein if not even higher. This is, however, very unlikely as the double mutants (V29G-Y32W and Y32W-I36G) already show a marked decrease of affinity for BeF₃⁻ (Kuppens et al. 1999).

In this study, we wanted to characterize the structural rearrangements in the direct neighborhood of the Trp32 by a comparison of the different time-resolved fluorescence properties of the so-called “switch I mutants” (Kuppens et al. 1999) in their distinct conformations (active and inactive). The measurements of the different mutants in the inactive GDP-bound conformation clearly show a major influence of the point mutation(s) on the fluorescence properties and therefore also on the structure and position of the switch I region. The differences appear largely in the amplitude fractions while the three distinct lifetimes stay practically constant. The amplitude of the longest lifetime (a3) drops from 70% in the reference mutant (Y32W) to 16% in the triple mutant. Both shorter lifetimes are compensating this with a raise of their amplitude fractions from, respectively, 12% to 40% for the shortest lifetime (τ1) and from 18% to 44% for the middle lifetime (τ2). These large differences can only be explained by structural rearrangements that place the fluorescent Trp32 in a different environment in the different mutants.

In this discussion, however, it is of crucial importance to keep in mind that we are talking about a highly flexible loop structure (both in GDP- and GTP-bound states). Talking about the position of this loop can give the impression that this is a fixed and localized conformational state. As mentioned in the introduction, the high dynamic mobility (even in the wild-type state) was already extensively proven by X-ray, NMR, and EPR studies. In this way, the position of the loop becomes an averaged parameter of a broad range of closely related conformations in a fast equilibrium. This implies the possibility that with the introduction of one or more mutations, this equilibrium is altered, the average position can be altered, or the range of conformations can be broadened (e.g., as in a Gaussian distribution where the base is broadened and the curve is flattened) and the time scale of the transition can be altered as well.

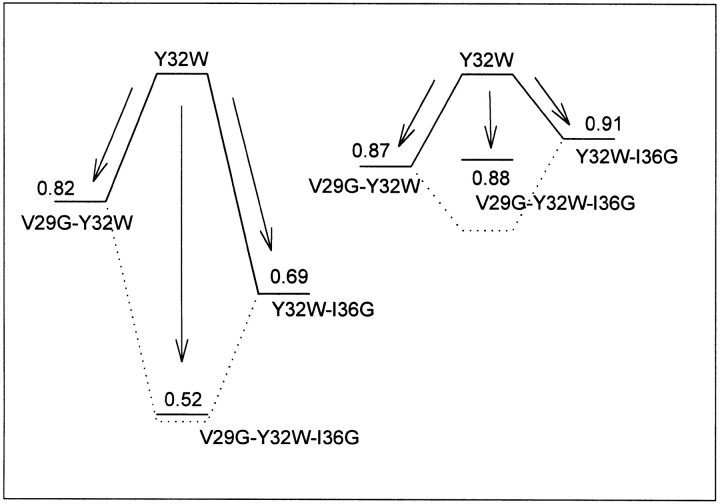
We have factorized the changes in quantum yield and average lifetime as three factors: f_kr, f_DQ, and f_PR. We notice that in the GDP-bound state, the effect of the hinge residue mutations on the conformational parameter f_PR (indicating the extent of population reshuffling in the tryptophan rotamers) is clearly additive (Fig. 4 ▶; Table 4). This implies that the already flexible structure is made even more flexible by replacing the hinges with small Gly residues. In the single-hinge residue mutants, we only increase the flexibility at one end of the loop (respectively, the side of V29 or the side of I36). In the double-hinge mutant, the restriction of movement is deleted from both sides giving the loop a very high degree of freedom probably resulting in an extremely broadened range of possible conformational substates.

Figure 4.

Visual representation of the f_PR factors (quantifying the extend of population reshuffling) between the different hinge residue mutants and the Y32W reference protein. The GDP-bound structures (left side) and the GTP-bound structures (right side) are placed on the same scale to point out the explicit difference between both cases. The dotted line shows the hypothetical value of f_PR when the two single hinge residue mutants show cumulative effects on the population reshuffling.

On the other hand, when we look at the fluorescence properties of Trp32 in the active GTPγS-bound conformation, we do not see major differences between the different mutants. The effect on f_PR is rather limited, and almost identical for all mutants. The effect seems to be slightly higher for the V29G-hinge residue mutant. The additivity of the influence in the double-hinge mutant is also lost (Fig. 4 ▶). We can explain this phenomenon by taking a closer look at the structure of the loop. In the GTP-bound conformation, the loop is attached with hydrogen bridges to the γ-phosphate of the GTP ligand. A main role is played by the conserved residue Thr-35, which not only forms a highly stabilizing hydrogen bridge with the γ-phosphate of GTP but also contributes via its side-chain hydroxyl in the coordination of the important Mg²⁺-ion and via the methyl group that packs against the effector loop and is responsible for a reduction in the flexibility of the loop. The fixation at the position of residue 35 not only explains the much smaller effect of the hinge residue mutations in the GTP-bound conformation, but also explains the higher effect for the V29G mutation, as the loop gets divided in two parts with the Trp residue positioned on the side of residue 29. The locking of the loop through the bridge between Thr35 and the phosphate also explains the loss of additivity (or presence of cooperativity) in the double-hinge mutant.

Nevertheless, the loop still displays a high flexibility (but likely not as extended as for the GDP-bound state) in its wild-type state. The introduction of the hinge residue mutations does not affect the fluorescence parameters to the extent they did in the GDP-bound state. Nevertheless, their introduction increases the flexibility with a certain amount resulting in a shifted equilibrium of the conformational substates as also supported by the results of Spoerner et al. (2001).

This hypothesis is further supported by the results of the quenching analysis displayed in Table 4. The difference between the GTP-bound conformation and the GDP-bound conformation is displayed solely in the population reshuffling (f_PR), which is correlated to a conformational difference between the “average” position of the loop in both states. The difference disappears with increasing flexibility. More information concerning the influence of the mutations can be gathered when we compare the quenching factors of the mutants with the wild type. Both in the GDP- and GTP-bound states, the differences in fluorescence properties are displayed in a combination of differences in f_kr and f_PR. The difference in radiative rate constant (k_r) is of the same order of magnitude for all mutants in both states. More interesting is the population reshuffling phenomenon in the hinge residue mutants because this population reshuffling in the case of p21 is always correlated to conformational changes. We see in the GTP-bound state a rather limited population reshuffling happening that has the same order of magnitude for all mutants. In the GDP-bound state, the population reshuffling is of greater magnitude in all cases and it increases with higher flexibility of the effector loop all of which support the higher-stated hypothesis and confirm the crucial role of residue Thr35 in the structure and functionality of the Ha-ras-p21 protein.

The anisotropy measurements are in qualitative agreement with the expected increasing flexibility upon introduction of more Gly residues. The increased contribution of the correlation time for internal mobility and accordingly, the calculated average angle over which the fluorophore rotates, clearly point in this direction. The conclusion is that fluorescence spectroscopy can reveal different kinds of dynamical behavior of proteins. Rotamer populations reflect heterogeneity or dynamics on a time scale much slower than nanoseconds, while the fluorescence anisotropy decay reflects local dynamical flexibility of the fluorophore and the segment containing the Trp residue in the nanosecond timescale.

Materials and methods

Analytical-grade beryllium sulfate and potassium fluoride from Merck & Co. were used to prepare the stock solution of beryllium fluoride; all other chemicals employed were analytical grade or better.

The beryllium fluoride stock solution was prepared in buffer A (64 mM Tris, 50 mM HCl, 1 mM NaN₃, 1 mM dithioerytrol [DTE]), containing 1 mM MgCl₂, 0.75 M KF, and 0.25 M BeSO₄. The pH was later adjusted to 7.2. The effective concentration of beryllium trifluoride was calculated using the effective complexing constants of the beryllium fluoride system at a given final concentration of the Be²⁺ and F⁻ ions (Mesmer and Baes 1969), the beryllium fluoride concentration of the stock turned out to be 176 mM.

The mutants (V29G-Y32W, Y32W-I36G, and V29G-Y32W-I36G) were constructed by long-range PCR (Cheng et al. 1994) of the ptac-ras plasmid (Tucker et al. 1986) containing the Y32W mutation, which was kindly provided by Prof. Dr. A. Wittinghofer. Escherichia coli cells of the WK6 line (Δ(lac-proAB) galE straA nal^r [F′ lacI^q lacZΔM15 pro AB⁺]; Zell and Fritz 1987) were transformed with the obtained plasmids. The mutant proteins were purified as described previously (Díaz et al. 1997b), their purity was checked by SDS-PAGE (Laëmmli 1970) and their activity was tested by measuring their ability to bind GDP.

Steady-state fluorescence measurements were performed on a Fluorolog 1691 spectrofluorimeter (Spex Industries). The excitation wavelength was 280 nm, the emission wavelength 343 nm both with slit apertures of 2 mm, giving a dispersion of 7.2 and 3.6 nm/mm, respectively, for the excitation and emission monochromators.

Fluorescence quantum yields were determined relative to tryptophan in water according to the method of Parker and Rees (1960) using a quantum yield for tryptophan in water of 0.14 (Chen 1967).

Fluorescence lifetimes were measured using multifrequency-phase fluorimetry between 1.6 Mhz and 1 Ghz (Vos et al. 1997; Sillen et al. 2000). An excitation wavelength of 295 nm was used to measure exclusively the tryptophan fluorescence, while the emission wavelength was set at 330 nm using an Oriel filter. N-acetyl-L-tryptophanamide in water was used as reference. Analysis of the data was done with global analysis using the software of Globals Unlimited (University of Illinois).

The time-resolved fluorescence anisotropy decay was measured using the same multifrequency-phase fluorimeter. The anisotropy decay parameters are obtained by analyzing the experimental data using the following formulas:

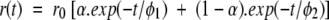with

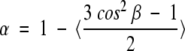Here is r(t), the time-dependent anisotropy value and r₀, the initial anisotropy, equal to 0.4 if the emission dipole is colinear with the absorption dipole. α is the amount of depolarization that occurs from internal motion of the fluorophore and is directly related to the range of angles (β) over which the fluorophore can move. φ₁ and φ₂ are respectively the correlation times of internal motion and the rotation of the whole protein.

Abbreviations

• GDP, 5′-guanosine diphosphate

• GTP, 5′-guanosine triphosphate

• GNBP, guanine nucleotide binding protein

• NMR, nuclear magnetic resonance

• EPR, electron paramagnetic resonance

• GAP, GTPase activating protein

• GEF, guanine exchange factor

• GNRP, guanine nucleotide release protein

• MD, molecular dynamics

• TMD, targeted molecular dynamics

• SDS-PAGE, sodium dodecyl sulphate polyacryl amide gel electrophoresis