Reliable prediction of T-cell epitopes using neural networks with novel sequence representations

Abstract

In this paper we describe an improved neural network method to predict T-cell class I epitopes. A novel input representation has been developed consisting of a combination of sparse encoding, Blosum encoding, and input derived from hidden Markov models. We demonstrate that the combination of several neural networks derived using different sequence-encoding schemes has a performance superior to neural networks derived using a single sequence-encoding scheme. The new method is shown to have a performance that is substantially higher than that of other methods. By use of mutual information calculations we show that peptides that bind to the HLA A*0204 complex display signal of higher order sequence correlations. Neural networks are ideally suited to integrate such higher order correlations when predicting the binding affinity. It is this feature combined with the use of several neural networks derived from different and novel sequence-encoding schemes and the ability of the neural network to be trained on data consisting of continuous binding affinities that gives the new method an improved performance. The difference in predictive performance between the neural network methods and that of the matrix-driven methods is found to be most significant for peptides that bind strongly to the HLA molecule, confirming that the signal of higher order sequence correlation is most strongly present in high-binding peptides. Finally, we use the method to predict T-cell epitopes for the genome of hepatitis C virus and discuss possible applications of the prediction method to guide the process of rational vaccine design.

The hallmark of the immune system is its ability to recognize and distinguish between self and nonself (potential pathogen). T cells do this by recognizing peptides that are bound to major histocompatibility complex (MHC) receptors. A number of methods for predicting the binding of peptides to MHC molecules have been developed (for review, see Schirle et al. 2001) since the first motif methods were presented (Rothbard and Taylor 1988; Sette et al. 1989). The discovery of allele specific motifs (Falk et al. 1991) lead to the development of more accurate algorithms (Pamer et al. 1991; Rötzschke et al. 1991). In the simpler prediction tools it is assumed that the amino acids at each position along the peptide sequence contribute with a given binding energy, which can be independently added up to yield the overall binding energy of the peptide (Parker et al. 1994; Meister et al. 1995; Stryhn et al. 1996). Similar types of approaches are used by the EpiMatrix method (Schafer et al. 1998), the BIMAS method (Parker et al. 1994), and the SYFPEITHI method (Rammensee et al. 1999). These predictions, however, fail to recognize correlated effects where the binding affinity of a given amino acid at one position is influenced by amino acids at other positions in the peptide. Two adjacent amino acids may, for example, compete for the space in a pocket in the MHC molecule. Artificial neural networks (ANN) are ideally suited to take such correlations into account and neural network methods for predicting whether or not a peptide binds MHC molecules have earlier been developed (Brusic et al. 1994; S. Buus, S.L. Lauemøller, P. Worning, C. Kesmir, T. Frimurer, S. Corbet, A. Fomsgaard, J. Hilden, A. Holm, and S. Brunak, in prep.). Brusic et al. (1994). use a conventional sparse (orthogonal) encoding of the 20 amino acid alphabet as well as 6 and 9 letter reduced alphabets. The conventional sparse encoding of the amino acids ignores their chemical similarities. Here we use a combination of several sequence encoding strategies to take these similarities into account, explicitly. The different encoding schemes are defined in terms of Blosum matrices and hidden Markov models, in addition to the conventional sparse encoding.

More detailed predictions of peptide binding have been made by dividing binding affinities into classes of affinity ranges, and by inverting the networks it was found that the different classes are associated with different binding sequence motifs (Adams and Koziol 1995). Neural networks have also been trained to predict MHC binding using different affinity thresholds (Gulukota et al. 1997). Mamitsuka (1998) trained the transition and emission probabilities of a fully connected hidden Markov model using a steepest descent algorithm so as to minimize the differences between the predicted and target probabilities for each peptide. Using this method he obtained better results than using neural networks or hidden Markov models. We had earlier developed matrix methods (Lauemøller et al. 2001) and ANNs, which are special in that they are trained to predict quantitative (continuous) values for binding affinities between peptides and the human MHC molecule HLA-A2 (S. Buus, S.L. Lauemøller, P. Worning, C. Kesmir, T. Frimurer, S. Corbet, A. Fomsgaard, J. Hilden, A. Holm, and S. Brunak, in prep.). Buus et al. have demonstrated that neural networks trained to perform quantitative predictions of peptide MHC binding are superior to conventional classification neural networks trained to predict binding versus nonbinding.

In this paper we describe an improved method that extends the neural network approach (described by S. Buus, S.L. Lauemøller, P. Worning, C. Kesmir, T. Frimurer, S. Corbet, A. Fomsgaard, J. Hilden, A. Holm, and S. Brunak, in prep.).using a combination of several neural networks defined using a number of different sequence encoding strategies including a hidden Markov model encoding to achieve a more accurate prediction of the peptide/MHC binding affinity.

Materials and methods

Data

Two sets of data were used to derive the prediction method. One set was used to train and test the neural networks, and consists of 528 nine-mer amino acids peptides for which the binding affinity to the HLA class I molecule A*0204 has been measured by the method described by Buus et al. (1995). The data set consists of 76 peptides with a binding affinity stronger than 50 nM, 144 with a binding affinity stronger than 500 nM, 159 with a binding affinity between 500 and 50,000 nM, and 225 peptides with a binding affinity weaker than 50,000 nM. This data set is hereafter referred to as the Buus data set. The second data set was used to train the hidden Markov model. This data set was constructed from sequences downloaded from the Syfpeithi database (Rammensee et al. 1995, 1999). All sequences from the database were downloaded and clustered into the nine super-types (A1, A2, A3, A24, B7, B27, B44, B58, and B62) and 3 outlier types (A29, B8, and B46) described by Sette and Sidney (1999). The sequences in the A2 super-type cluster were aligned manually and trimmed into 211 unique 9-amino-acid long peptides. This data set is hereafter referred to as the Rammensee data set.

Hidden Markov models and neural network training

Both neural networks and hidden Markov models were constructed to derive an optimal prediction scheme for HLA-A2 peptide binding.

Hidden Markov models

A hidden Markov model was generated for the HLA-A2 type based on the sequences in the Rammensee data set. The model was constructed using the hmmbuild command from the Hmmer package (Eddy 1998) using the following command “hmmbuild-F–fast–pam BLOSUM62-gapmax 0.7 hmmerfile fastafile.” Here fastafile is an input file containing the sequences in the Rammensee data set in FASTA format, and hmmerfile is the output file generated by the hmmer program.

An epitope similarity score S for the 9-amino-acid long peptide is calculated as

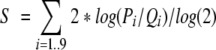where P_i is the probability for finding a given amino acid on position i in the hidden Markov model and Q_i is the probability for finding the amino acid in the Swiss Prot database (Bairoch and Apweiler 2000). These probabilities can be calculated from the output from the hmmbuild program as described in the manual.

Neural networks

Encoding of the peptide amino acid sequence.

Several types and combinations of sequence encodings were used in the neural network training. The first is the conventional sparse encoding where each amino acid is encoded as a 20-digit binary number (a single 1 and 19 zeros). The second is the Blosum50 encoding in which the amino acids are encoded as the Blosum50 score for replacing the amino acid with each of the 20 amino acids (Henikoff and Henikoff 1992). Other Blosum encoding schemes were tried and we found that all encodings with Blosum matrices corresponding to a clustering threshold in the range 30–70% gave comparable performance. In the following we will use the Blosum50 matrix when we refer to Blosum sequence encoding. A last encoding scheme is defined in terms of a hidden Markov model. The details of this encoding are described later in section 3.3. The sparse versus the Blosum sequence-encoding scheme constitutes two different approaches to represent sequence information to the neural network. In the sparse encoding the neural network is given very precise information about the sequence that corresponds to a given training example. One can say that the network learns a lot about something very specific. The neural network learns that a specific series of amino acids correspond to a certain binding affinity value. In the Blosum encoding scheme, on the other hand, the network is given more general and less precise information about a sequence. The Blosum matrix contains prior knowledge about which amino acids are similar and dissimilar to each other. The Blosum encoding for leucine has, for instance, positive encoding values at input neurons corresponding to isoleucine, methionine, phenylalanine, and valine and negative encoding values at input neurons corresponding to, for instance, asparagine and aspartic acid. This encoding helps the network to generalize; that is, when a positive example with a leucine at a given position is presented to the network, the parameters in the neural network corresponding to the above similar and dissimilar amino acids are also adjusted in a way so that the network appears to have seen positive examples with isoleucine, methionine, phenylalanine, and valine and negative examples with asparagine and aspartic acid at that specific amino acid position. This ability to generalize the input data is of course highly beneficial for neural network training when the number of training data is limited. The use of Blosum sequence encoding might, on the other hand, even in situations where data are not a limiting factor, be an important aid to guide the neural network training, simply because the Blosum matrix encodes a subtle evolutional and chemical relationship between the 20 amino acids (Thorne et al. 1996).

Neural network training.

The neural network training is performed in a manner similar to that described by S. Buus, S.L. Lauemøller, P. Worning, C. Kesmir, T. Frimurer, S. Corbet, A. Fomsgaard, J. Hilden, A. Holm, and S. Brunak, in prep.), especially with respect to the tranformation applied to the measured binding affinities before doing the network training, and the procedure used for the balanced training of the neural network.

We develop the method with optimal predictive performance in a two-step procedure. In the first round the method is optimized on a subset of 428 of the 528 peptides in the Buus data set, and its performance is evaluated on an independent evaluation set of the remaining 100 peptides. In this manner we minimize the risk of over-fitting. In the second round the method is retrained on the full set of data using the parameter settings obtained in the first round.

The test and training of the neural networks is performed using a fivefold cross-validation by splitting the 428 peptides into five sets of training and test data. The splitting is performed such that all test and training sets have approximately the same distribution of high, low, and nonbinding peptides. The training data are used to perform feed-forward and back-propagation and the test data, to define the stopping criteria for the network training as described by Baldi and Brunak (2001).

The performance of the neural networks is measured using the Pearson correlation coefficient on the test set (Press et al. 1989).

The neural network architecture used is a conventional feed-forward network (Baldi and Brunak 2001) with an input layer with 180 neurons, one hidden layer with 2–10 neurons, and a single neuron output layer. The 180 neurons in the input layer encode the 9 amino acids in the peptide sequence with each amino acid represented by 20 neurons. The back-propagation procedure was used to update the weights in the network.

We transform the measured binding affinities as described by S. Buus, S.L. Lauemøller, P. Worning, C. Kesmir, T. Frimurer, S. Corbet, A. Fomsgaard, J. Hilden, A. Holm, and S. Brunak, in prep. to place the output values used in the training and testing of the neural networks on a scale between 0 and 1. The transformation is defined as 1-log(a)/log(50,000), where a is the measured binding affinity. In this transformation high binding peptides, with a measured affinity stronger than 50 nM, are assigned an output value above 0.638, intermediate binding peptides, with an affinity stronger than 500 nM, an output value above 0.426, and peptides, with an affinity weaker than 500 nM, an output value below 0.426. Peptides that have an affinity weaker than 50,000 nM are assigned an output value of 0.0.

Because the distribution of binding affinities for the peptides in the training and test sets is highly nonuniform, with a great over-representation of low and nonbinder peptides, it is important that the network training is done in a balanced manner. This is done by partitioning the training data into a number of N subsets (bins) such that the ith bin contains peptides with a transformed binding affinity between (i − 1)/N and i/N. In balanced training, data from each bin are presented to the neural network with equal frequency.

For each of the five training and test sets, a series of network trainings were performed each with a different number of hidden neurons (2, 3, 4, 6, 8, and 10) and a different number of bins (1, 2, 3, 4, and 5) in balancing of the training. For each series, a single network with the highest test performance was finally selected.

Results

Mutual information

One important difference between linear prediction methods like first order hidden Markov models and nonlinear prediction methods like neural networks with hidden layers is their capability to integrate higher order sequence correlation into the prediction score. A measure of the degree of higher order sequence correlations in a set of aligned amino acid sequences can be obtained by calculating the mutual information matrix. For the case of peptide nine-mers, this is a 9 × 9 matrix where each matrix element is calculated using the formula

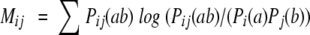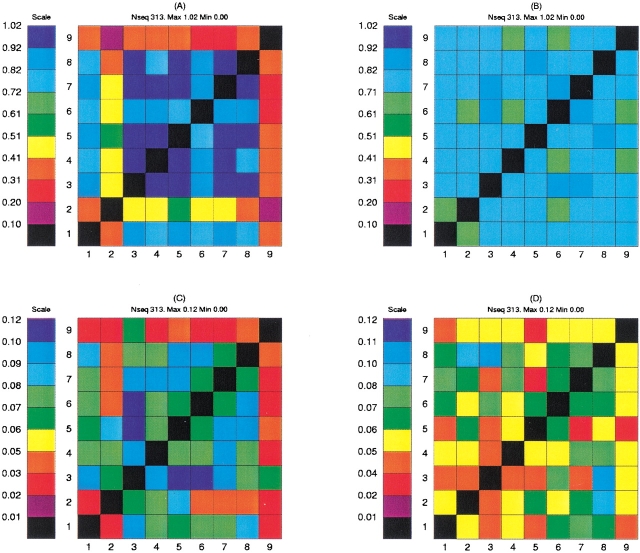
Here the summation is over the 20 letters in the conventional amino acid alphabet and i, j refers to positions in the peptide. P_ij(ab) is the probability of mutually finding the amino acid a at position i and amino acid b at position j. P_i(a) is the probability of finding the amino acid a at position i irrespective of the content at the other positions, and likewise for P_j(b). A positive value in the mutual information matrix indicates that prior knowledge of the amino acid content at position i will provide information about the amino acid content at position j. The statistical reliability of a mutual information calculation relies crucially on the size of the corresponding data set. In the mutual information calculation one seeks to estimate 400 amino acid pair frequencies at each position in the matrix. Such estimates are naturally associated with large uncertainties when dealing with small data sets. In Figure 1A,B ▶ we show the mutual information matrix calculated for two different sets of nine-mer alignments. The first data set was constructed so as to obtain the largest possible positive set, by combining peptides from the Rammensee data set with the peptides from the Buus data set that have a measured binding affinity stronger than 500 nM. This set contains 313 unique sequences. The second data set was constructed as a negative set by extracting 313 unique random peptides from the Mycobaterium tuberculosis genome. The mutual information content is calculated using the conventional 20 amino acid alphabet. The figure demonstrates a signal of mutual information between the seven nonanchor residue positions (1, 3, 4, 5, 6, 7, and 8) in the data set defined by peptides that bind to the HLA molecule. It is worth remarking that the mutual information content between any of the two anchor positions (2 and 9) and all other amino acids is substantially lower than the mutual information content between any two nonanchor positions. The significance of the mutual information content calculations can be improved by applying a suitable reduced sequence alphabet in the calculations (Brusic et al. 1994). In Figure 1C,D ▶ we show the mutual information matrices for the two data sets described above, calculated using a reduced 6-letter alphabet derived from the side-chain surface area defined as A = “GAS”, B = “CTDV”, C = “P”, D = “NLIQMEH”, E = “KFRY” and F = “W”. Here the syntax A = “GAS” means that amino acids G, A, and S all are encoded by the letter A. The matrices in Figure 1C,D ▶ display a similar behavior to the plots in Figure 1A,B ▶, however, with the difference that the signal of mutual information in the data set derived from low and nonbinding peptides has been substantially decreased compared to that of the data set defined by HLA-A2 binding peptides.

Figure 1.

Mutual information matrices calculated for two different data sets. (A,C) The mutual information matrix calculated for a data set consisting of 313 peptides derived from the Rammensee data set combined with peptides from the Buus data set with a binding affinity stronger than 500 nM. (B,D) The mutual information matrix calculated for a set of 313 random peptides extracted from the Mycobaterium tuberculosis genome. In the upper row the mutual information plot is calculated using the conventional 20-letter amino acid alphabet. In the lower row the calculation is repeated using the six-letter amino acid alphabet defined in the text.

Combination of more than one neural network prediction

We combine the output from the two networks trained using sparse and Blosum sequence encoding, respectively, in a simple manner, as a weighted sum of the two. To select the weight that corresponds to the optimal performance, we plot the sensitivity/PPV as well as the relative operating characteristic (ROC) curves (Sweet 1988) for a series of weighted sum combinations of the two network outputs. The sensitivity is defined as the ratio TP:AP. Here TP (true positives) is the number of data points for which both the predicted score is above a given prediction threshold value and the measured binding affinity is above a given classification threshold value. AP (actual positives) is the total number of data points that have a measured binding affinity above the affinity threshold value. The PPV is defined as TP:PP. Here PP (predicted positives) is the total number of predictions with a score above the prediction threshold value. The PPV is a measure of the reliability of the prediction method. The ROC curves are closely related to the sensitivity/PPV curves. However, with the important difference that one of the axes in the ROC curve is the false-positive proportion FP:AN (actual negatives) and not the true positive to predicted postive ratio (the PPV). The area under the ROC curve (A_roc) provides an estimate of the accuracy of the prediction method. A random method will have a value of A_roc = 0.5. A_roc > 0.8 indicates that the method has moderate accuracy and A_roc = 1 that the prediction method is perfect (Sweet 1988). In a sensitivity/PPV plot, the curve for the perfect method is the one where the area under the curve is unity. The curves are estimated using the Bootstrap method (Press et al. 1989). N data sets were constructed by randomly drawing M data points with replacement from the original data set of M peptides. For each of the N data sets a sensitivity/PPV curve and a ROC curve was calculated and the curves displayed in Figure 2 ▶ are derived from the mean of these N sensitivity/PPV and ROC curve realizations.

Figure 2.

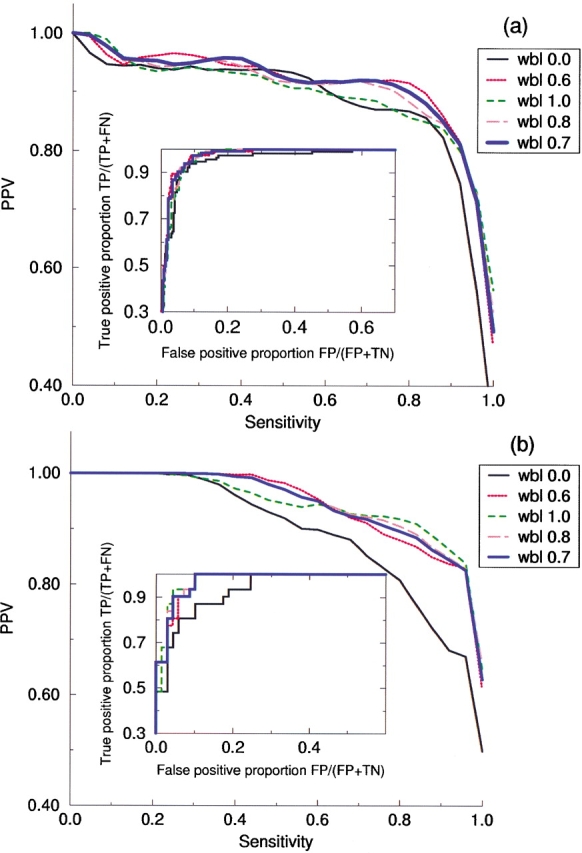
(A) Sensitivity/PPV plot calculated using a classification binding affinity of 500 nM for a series of linear combinations of the two neural network methods corresponding to Blosum50 and sparse sequence encoding, respectively. The curves were calculated by use of the Bootstrap method (Press et al. 1989) using 500 data set realizations. (A) 428 peptides in the test/train data set; (B) 100 peptides in the evaluation set. In (A) we determine the optimal performance to be the thick blue curve, corresponding to a combination of the two neural network methods with 70% weight on the Blosum50 encoded prediction and 30% weight on the sparse encoded prediction. This set of weights also results in close to optimal performance in lower graph. Inserts to the graphs show the corresponding ROC curves.

It is important to stress that we shall use the sensitivity/PPV curves in a comparative analysis of the prediction performance of different prediction methods, and not to derive specific relationships between prediction score thresholds and prediction reliability. We are aware that the later analysis would be problematic, when the data set used to derive the sensitivity/PPV curve has characteristics very different from that of the background distribution. In our situation the background distribution of data is peptides selected at random in protein sequences and this data set clearly has a distribution of binding affinities very different from the data set used in the analysis in this work.

In Figure 2 ▶ the sensitivity/PPV curves for the 428 peptides in the train and test set and the 100 peptides in the evaluation set are shown for a measured binding affinity threshold value equal to 0.426, corresponding to a binding affinity of 500 nM. In the insert to the figures the corresponding ROC curves are shown. From the figure it is clear that both the sparse and the Blosum encoded neural networks have a performance that is inferior to any combination of the two. In Figure 2A ▶ the optimal combination is found to have a weight on the Blosum encoded network close to 0.7 and a weight on the sparse encoded network close to 0.3. This set of weights for the combination of the two neural network predictions is also, in Figure 2B ▶, seen to improve to the prediction accuracy for the 100 peptides in the evaluation set. This is, however, less obvious, due to the small number of binding peptides in the evaluation set. The evaluation set contains 31 peptides with binding affinity stronger than 500 nM.

The Pearson correlation coefficient between the predicted and the measured binding affinities for the sparse encoded, the Blosum encoded, and the combined neural network method on the peptides in the train/test set is found to be 0.849, 0.887, and 0.895, respectively. For the peptides in the evaluation set the corresponding values are found to be 0.866, 0.926, and 0.928, respectively.

The neural network training and testing is next repeated using the full data set in a fivefold cross-validation. The combined method, hereafter referred to as comb-I, is defined using the weights on the Blosum and the sparse encoded neural networks, respectively, estimated above.

Integration of data from the Rammensee database in the neural network training

In Figure 3B ▶ we show the performance of the hidden Markov model evaluated on the 528 peptides in the Buus data set. The plot displays a reasonable correlation between the hidden Markov model score and the measured binding affinity. This correlation demonstrates that the sequences in the Rammensee data set contain valuable information and that the neural network training could benefit from an integration of the Rammensee sequence data into the training data set. It is, however, not obvious how such an integration should be done. The Rammensee data are binary in nature. They describe that a given peptide does bind to the HLA molecule but not the strength of the binding. The data in the Buus data set, on the other hand, are continuous in that each peptide is associated with a binding affinity. It turns out that a fruitful procedure for integrating the Rammensee data into the neural network training is to use the output scores generated by the hidden Markov model as additional input to the neural network. The hidden Markov model is trained on the peptides in the Rammensee data set. The model is nine residues long, and the scores used as input to the neural network are the nine scores obtained when aligning a nine-mer peptide to the model. Two neural networks, each with 189 input neurons (180 for sequence encoding and 9 to encode the scores from the hidden Markov model), are next trained in a fivefold manner as described above using the hidden Markov model scores combined with the sparse or Blosum sequence encoding in the input layer, respectively. In the final combined method, the prediction value is calculated as the simple average with equal weight of the sparse and blosum encoded neural network predictions.

Figure 3.

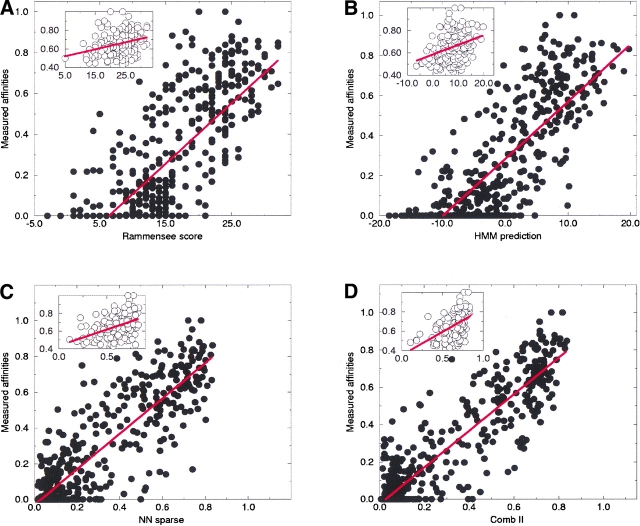
Scatter plot of the predicted score versus the measured binding affinity for the 528 peptides in the Buus data set. The figure shows the performance for four different prediction methods. The insert to each figure shows an enlargement of the part of the plot that corresponds to a binding affinity stronger than 500 nM. (A) Rammensee matrix method, (B) Hidden Markov Model trained on sequences in the Rammensee data set, (C) Neural Network trained with sparse sequence encoding, and (D) Comb-II neural network method. The straight line fit to the data in (C) and (D) have slope and intercept of 0.989, −0.029 and 0.979, −0.027, respectively.

This method is hereafter referred to as comb-II and is the one used in the hepatitis C virus (HCV) genome predictions described below.

Neural network methods compared to hidden Markov model methods and the matrix method by Rammensee

In Table 1, we give the test performance measured in terms of the Pearson correlation coefficient for the 528 peptides in the Buus data set for six different prediction methods: One method is the matrix method by Rammensee (1999), the second the hidden Markov model trained on the Rammensee data set, and the other four are neural networks methods trained using sparse and Blosum sequence encoding, the linear combination of the two, and the linear combination including input from the hidden Markov model. For the matrix method by Rammensee and the hidden Markov method we calculate the Pearson correlation between the raw output scores and the logarithmically transformed measured binding affinities, although this might not be what optimally relates the prediction score to the measured binding affinity.

Table 1.

Comparison of prediction methods

Method	Pearson (all)	Pearson (500 nM)	Pearson (50 nM)
Rammensee	0.761 ± 0.016	0.296 ± 0.073	0.066 ± 0.116
HMM	0.804 ± 0.014	0.332 ± 0.061	0.142 ± 0.096
NN_Sparse	0.877 ± 0.011	0.438 ± 0.065	0.345 ± 0.090
NN_B150	0.899 ± 0.010	0.498 ± 0.064	0.382 ± 0.099
Comb-I	0.906 ± 0.009	0.508 ± 0.063	0.392 ± 0.092
Comb-II	0.912 ± 0.009	0.508 ± 0.054	0.420 ± 0.080

The Pearson correlation coefficient between the predicted score and the measured binding affinity for the 528 peptides in the Buus data set. The six methods in the table are: Rammensee = Score matrix method by H.G. Rammensee; HMM = hidden Markov model trained on sequence data in the Rammensee data set; NN_Sparse = neural network with sparse sequence encoding; NN_BL50 = neural network with Blosum50 sequence encoding; Comb-I = combination of neural network trained using sparse and Blosum50 sequence encoding, respectively; and Comb-II = combination of neural network trained using sparse, Blosum50 and hidden Markov model sequence encoding, respectively. The numbers given in the table are calculated using the Bootstrap method (Press et al. 1989) with 500 data set realizations. The correlation values are estimated as average values over the 500 data set realizations and the error bars the associated standard deviations.

The numbers given in Table 1 are calculated using the bootstrap method with 500 data set realizations. The correlation values are estimated as average values over the 500 data set realization and the error-bars as the associated standard deviations. From the results shown it is clear that the neural network methods have a higher predictive performance compared to both the method by Rammensee and the hidden Markov model. The difference in predictive performance between the neural network and the Rammensee and the hidden Markov model methods is most significant for data sets defined by peptides with a binding affinity stronger than 50 nM, thus indicating that the signal of higher order sequence correlation is most strongly present in peptides that bind strongly to the HLA-A2 molecule. The same conclusion can be drawn from the data displayed in Figure 3 ▶. Here the test performance for the 528 peptides is shown as a scatter plot of the prediction score versus the measured binding affinity for four of the six methods above. Again it is clear that the neural network methods, in general, and the combined methods, in particular, have a higher predictive performance than both the Rammensee and the hidden Markov model methods. The least square straight line fit to the data shown in Figure 3C,D ▶ also validates the quality and accuracy of the neural network predictions. In the two plots the straight line fits have a slope and intercept of 0.989, −0.029 and 0.979, −0.027, respectively, thus demonstrating the strength of the neural network trained on quantitative date in providing a direct relationship between the neural network output and the measured binding affinity.

In Figure 4 ▶ we show the sensitivity/PPV curves calculated for the data in the 528 peptide-set using the four different neural network methods as well as the method by Rammensee and the hidden Markov model method. All curves are estimated using the bootstrap method described above. The upper graph shows the sensitivity/PPV curves for the six methods calculated for a classification threshold corresponding to 500 nM, and the lower graph the sensitivity/PPV curves for a clasification threshold corresponding to 50 nM. In the insert to the graphs is shown the corresponding ROC curves for the six methods. In the labels to the curves in the insert we give the estimated ROC areas (Sweet 1988). In both graphs it is clear that the combined neural methods have a performance superior to that of the other four methods. All four neural network methods and, in particular, the two combined methods have a performance that is substantially higher than that of the Rammensee method. The ranking of the six methods obtained using the ROC area method is identical to the ranking estimated using the Pearson correlation measure given in Table 1. Using a Student’s t test to compare the mean error of prediction (predicted binding affinity-measured binding affinity) between the comb-II method and the two neural network methods trained with a single sequence encoding, we find that the P values are less than 10⁻⁴ and 0.005 for sparse and Blosum sequence encoding, respectively. The individual schemes for ranking the different methods thus all confirm that the combination of several neural network methods trained with different sequence representation has a performance superior to any neural network trained with a single sequence representation. Figure 4 ▶ further demonstrates that the integration of the data from the Rammensee database in the training of the neural networks, in terms of the hidden Markov model input data, increases the reliability of the combined neural network method substantially. For an affinity threshold of 500 nM the plot shows that at a PPV of 0.975 the combined neural network method comb-II has a sensitivity of 0.54, where the combined neural network method comb-I, which does not include hidden Markov model (HMM) data, has a sensitivity of only 0.22. In Figure 4A ▶, the largest sensitivity gap between the combined neural method comb-II and the method of Rammensee is found at a PPV equal to 0.7, corresponding to a difference of 0.38 in sensitivity or a difference in the number of true positive predictions of 29 of a total of the 76 high binding peptides in the data set. In Figure 4B ▶, the largest sensitivity gap between the two methods is found at a PPV equal to 0.88, corresponding to a difference of 0.37 in sensitivity or a difference in the number of true positive predictions of 54 of a total of the 144 intermediate binding peptides in the data set.

Figure 4.

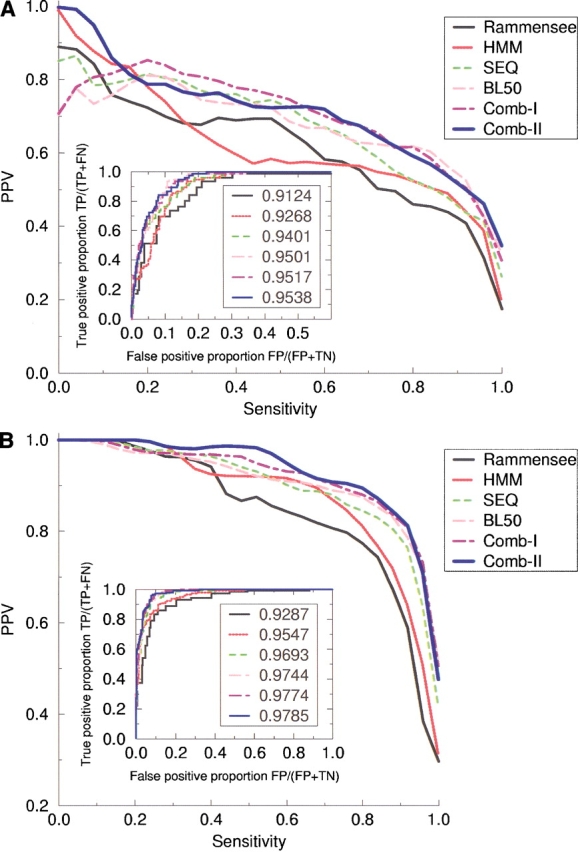
Sensitivity/PPV curves calculated from the 528-peptide data set. Six methods are shown in the graphs: Rammensee, Matrix method by Rammensee (Rammensee et al. 1999); HMM, hidden Markov Model trained on data from the Rammensee database; SEQ, neural network with sparse sequence encoding; BL50, neural network with Blosum50 sequence encoding; Comb-I, combination of neural network trained with sparse and Blosum50 sequence encoding, respectively; and Comb-II, combination of neural network with sparse, Blosum50 and hidden Markov model sequence encoding. (A) The curves for a classification affinity threshold of 50 nM. (B) The curves corresponding to a classifcation affinity threshold of 500 nM. The sensitivity/PPV curves were calculated as described in Figure 2 ▶ using 528 data set realizations. The insert to the graphs shows the ROC curves defined in the text. The value given with the label to each of the curves in the insert is the area under the ROC curve.

Both the method by Rammensee and the hidden Markov model are linear methods derived from binary affinity data. Neural networks can, on the other hand, both train on data with continuous binding affinities and, if it contains a hidden layer, include higher order sequence correlations in the output score. To estimate the importance of the ability of the neural network to train on continuous data and the importance of integration of higher order sequence correlations in the prediction score, we transformed the Buus data set into binary data by assigning peptides with a measured binding affinity stronger than 500 nM, an output value of 0.9, and all other peptides a value of 0.1. In a fivefold cross-validation of a neural network using sparse sequence encoding the test performance on the 528 peptides in the Buus data set was found to be 0.838 ± 0.013 and 0.856 ± 0.013 for networks trained without and with a hidden layer. These numbers should be compared to the 0.877 ± 0.011 obtained for a neural network with a hidden layer trained and tested in a similar manner using continuous affinity data. The result confirms the importance of both training the prediction method on data with continuous binding affinities and ability of the neural network method to integrate higher order sequence correlation in the prediction score.

HCV genome predictions

We use the prediction method (comb-II) to predict the location of T-cell epitopes in the genome of hepatitis C virus (HCV) (GenBank entry, NC 001433). The genome was downloaded from GenBank (Benson et al. 2002).

The HCV genome is relativly small. It contains 9,413 bp, and a coding region that translates into a number of 3,002 nine-mer peptides. Using the comb-II method to predict the binding affinity for all possible nine-mers in the genome, we find a number of 54 strong binding peptides (affinity stronger than 50 nM) and 177 intermediate binding peptides (affinity stronger than 500 nM). A detailed analysis of the location of the predicted epitopes in the HCV genomes demonstrates that the genome contains regions of high epitope concentration, as well as large regions where epitopes basically are absent. Most striking is the total absence of both strong and intermediate binding peptides in the amino-terminal part of the structural E2 domain of the genome. This domain contains the hypervariable sequence region located in the amino-terminal of E2, and one could speculate that the absence of epitopes in the region might be related to viral escape from the host immune system by means of sequence mutations (Cooper et al. 1999). Furthermore we observe that epitopes are most abundant in the nonstructural domain NS2 and in the carboxy-terminal of the structural E2 domain.

Discussion

We describe a novel method for predicting the binding affinity of peptides to the HLA-A2 molecule. The method is a combination of a series of neural networks that as input take a peptide sequence as well as the scores of the sequence to a HMM trained to recognize HLA-A2 binding peptides. The method combines two types of neural network predictions. In half the networks the amino acid sequence is encoded using a classic orthogonal sparse encoding and in the other half of the networks the amino acids are encoded as their Blosum50 scores to the 20 different amino acids. We show that a combined approach, where the final prediction is calculated as a linear combination of the two network predictions leads to an improved performance over simpler neural network approaches. We also show that the use of the Blosum50 matrix to encode the peptide sequence leads to an increased performance over the classic orthogonal sparse encoding. The Blosum sequence encoding is beneficial for the neural network training especially in situations where data are limited. The Blosum encoding helps the neural network to generalize, so that the parameters in the network corresponding to similar and dissimilar amino acids are adjusted simultaneously for each sequence example.

A detailed comparison of the derived neural network method to that of linear methods such as the matrix method by Rammensee and the first order hidden Markov model has been carried out. The predictive performance was measured in terms of both the Pearson correlation coefficient and in terms of sensitivity/PPV and ROC curve plots. For all measures it was demonstrated that the neural network methods, in general, and the combined neural network method, in particular, have a predictive performance superior to that of the linear methods.

Analysis of the mutual information in peptides that bind HLA-A2 revealed correlations between the amino acids located between the anchor positions. Neural networks with hidden units can take such correlations into account, but simpler methods such as neural networks without hidden units, matrix methods, and first order hidden Markov models cannot. It is this ability to integrate higher order sequence correlations into the prediction score combined with the use of several neural networks derived from different sequence encoding schemes and the fact that neural networks can be trained on data with continuous binding affinities that gives the present method an edge to the other methods in the comparison.

By calculating the mutual information we show that there exist correlations between different positions in peptides that can bind HLA-A2. Previous studies have shown that the sequence information contained in a motif correlates with the predictive power that can be obtained (Gorodkin et al. 1999). Here we show that the extra predictive power obtained using neural networks can be attributed to the mutual information between positions in a motif. Other published strategies capable of dealing with higher order sequence correlations rely on neural networks (Brusic et al. 1994; S. Buus, S.L. Lauemøller, P. Worning, C. Kesmir, T. Frimurer, S. Corbet, A. Fomsgaard, J. Hilden, A. Holm, and S. Brunak, in prep.) and decision trees (Savoie et al. 1999). Another approach is taken by Mamitsuka (1998), who trains a fully connected hidden Markov model. In this approach different paths through the hidden Markov model corresponding to the different sequence motifs can handle higher order sequence correlations. Three-dimensional models have also been used to predict MHC-peptide binding (Altuvia et al. 1995). This approach may give information that is complementary to what can be obtained from the sequence alone and one possible way to improve the predictive accuracy could be to combine predictions based on sequence with predictions based on structure.

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.