Improved amino acid flexibility parameters

Abstract

Protein molecules exhibit varying degrees of flexibility throughout their three-dimensional structures, with some segments showing little mobility while others may be so disordered as to be unresolvable by techniques such as X-ray crystallography. Atomic displacement parameters, or B-factors, from X-ray crystallographic studies give an experimentally determined indication of the degree of mobility in a protein structure. To provide better estimators of amino acid flexibility, we have examined B-factors from a large set of high-resolution crystal structures. Because of the differences among structures, it is necessary to normalize the B-factors. However, many proteins have segments of unusually high mobility, which must be accounted for before normalization can be performed. Accordingly, a median-based method from quality control studies was used to identify outliers. After removal of outliers from, and normalization of, each protein chain, the B-factors were collected for each amino acid in the set. It was found that the distribution of normalized B-factors followed a Gumbel, or extreme value distribution, and the location parameter, or mode, of this distribution was used as an estimator of flexibility for the amino acid. These new parameters have a higher correlation with experimentally determined B-factors than parameters from earlier methods.

The flexibility inherent in protein molecules is being accorded greater recognition as more studies reveal the importance of local or even global disorder for the proper functioning of a protein (Wright and Dyson 1999; Bright et al. 2001; Dunker et al. 2001; Namba 2001). A flexible structure may allow a protein to bind to many partners (Dunker et al. 2001), or the energetic consequences of structural rearrangement on binding may couple low affinity with high specificity (Schulz 1979; Dunker et al. 1998). Being able to identify regions of proteins or entire molecules that are disordered will prove invaluable to efforts to annotate the functions of the vast number of new proteins being identified by the genome sequencing projects.

Both the major methods for the determination of protein structures give information on the motions of atoms in a protein (Peng and Wagner 1994; Trueblood et al. 1996), so experimentally determined structural data provides a means to investigate protein flexibility. X-ray crystallographic studies have produced a large number of high-resolution protein structures in which the atomic displacement factors (Trueblood et al. 1996), also known as the B- or temperature factors, give information on the mobility of each of the atoms in the structure. This B-factor reflects the degree of thermal motion and static disorder of an atom in a protein crystal structure (Drenth 1994). Early efforts to predict protein flexibility (Karplus and Schulz 1985; Vihinen et al. 1994) also made use of B-factors from a set of protein structures.

Other uses of B-factors have included studying active sites and binding pockets (Carugo and Argos 1998), delineating protein regions (Carugo and Argos 1998), testing for errors in protein structures (Stroud and Fauman 1995), correlating side-chain mobility with conformation (Carugo and Argos 1997a), investigating crystal packing contacts (Carugo and Argos 1997b), analyzing (Altman et al. 1994) or predicting (Romero et al. 1997, 1998) disordered regions in proteins, evaluating the occupancy of water molecules in crystal structures (Carugo 1999), considering protein thermal stability (Vihinen 1987; Parthasarathy and Murthy 2000), and finding breaking points in helices (Carugo 2001).

For complex molecules like proteins, B-factors can be highly variable within a single structure as a result of the effects of local packing and the structural environment of the atom. The distributions of these B-factors are highly irregular when viewed protein by protein, probably because of a combination of the relatively small number of residues in a protein chain, differences in the refinement methods used (Tonrud 1996), and the degree of care taken to determine accurate B-factor values (Stroud and Fauman 1995). Because of these considerations, the B-factors in a protein must be normalized before comparisons among different protein chains can be made (Karplus and Schulz 1985; Vihinen et al. 1994; Carugo and Argos 1997a,b , 1998).

If B-factors are considered over the length of a protein chain, it becomes clear that there are segments in many proteins that are undergoing movements on a much larger scale than the rest of the protein. Early work (Karplus and Schulz 1985; Vihinen et al. 1994) suggested that the N and C termini of proteins were the most flexible regions, yet frequently it is interior segments that are the most flexible. Before normalization of the B-factors, it is necessary to detect and remove such highly mobile segments as, otherwise, they will influence the normalization process.

Following previous work (Karplus and Schulz 1985; Vihinen et al. 1994), we have examined the C^α B-factors of a nonredundant set of structures (Hobohm et al. 1992) from the Protein Data Bank (Berman et al. 2001), but with a much larger data set. We have used more robust statistical methods, taken from the quality control literature (Iglewicz and Hoaglin 1993) to detect outliers in the B-factor distribution of a protein. Such outliers are the amino acids undergoing motion on a different scale when compared with the rest of the protein.

The set of normalized B-factors, produced after removal of these outliers, was analyzed for each amino acid. It was found that the B-factors of an amino acid followed an extreme value or Gumbel distribution. An estimator of the flexibility of the amino acid was taken from the location parameter, or modal value, of this distribution. These estimators were shown to be better correlated with experimentally determined B-factors than those from the earlier methods of Karplus and Schulz (1985) and Vihinen et al. (1994).

Results

A set of nonidentical protein chains (at the 25% sequence identity level) was taken from the PDB-Select database (Hobohm et al. 1992). After applying certain quality constraints (see Materials and Methods), a subset of 290 protein chains was identified for further study (Table 1). These chains were further divided into 10 groups containing 261 chains with each of the chains being omitted from one of the groups. Only the B-factors of the C^α atoms were used in this work as results from the other backbone atoms, or an average of the backbone atoms gave similar results. A total of 67,552 amino acids were included in this study and the counts of each amino acid in the set are given in Table 2. A second, or test, set of 196 nonidentical chains, which were also not homologous to the first set, was taken from the April 2002 version of PDB-Select (supplemental Tables 1 and 2).

Table 1.

High-resolution protein chains and randomly assigned sample exclusion number

1191		0	1bfd		3	1hal		6	1nox		6	1tsp		2	2kin B		2
1531		4	1bfg		0	1hfc		1	1npl	A	8	luae		0	2mcm		7
1ali	A	0	1bft	A	0	1hgx	A	8	1npk		9	1unk	A	8	2nac	A	8
1a28	B	1	1bgp		5	1ida	A	3	1nul	B	3	1uxy		5	2pgd		8
1a2p	A	9	1bkf		3	1idk		9	1nwp	A	1	1vca	A	2	2phy		2
1a2y	A	3	1bkr	A	8	1ido		8	1onr	A	7	1vhh		9	2pia		1
1a34	A	4	1brt		7	1ifc		5	1opd		7	1vjs		7	2pii		1
1a68		0	1btn		9	1iib	A	0	1opy		2	1vls		1	2plc		4
1a7t	A	9	1bvl		1	1ixh		4	1oyc		9	1vps	A	3	2por		2
1a8e		2	1c52		4	1jdw		0	1pda		9	1vsd		2	2pth		6
1a9s		8	1cem		6	1jfr	A	3	1pdo		6	1vwl	B	2	2rn2		5
1aac		7	1ceo		1	1jhg	A	8	1pgs		5	1wab		8	2rsp	B	7
1aba		6	1cex		2	1jpc		4	1phe		2	1wba		1	2sak		6
1ad2		9	1cfb		0	1kid		3	1phn	A	1	1whi		7	2scp	A	7
1ado	A	7	1chd		8	1knb		0	1php		1	1who		8	2sic	I	1
1afw	A	6	1chm	A	3	1kpt	A	7	1pii		9	1wht	B	8	2sil		3
1agj	A	5	1clc		6	1kuh		4	1plc		1	lxgs	A	2	2spc	A	2
1agq	D	0	1cnv		0	1kvu		8	1pmi		6	1xnb		5	2tgi		7
1ah7		7	1cpc	B	9	1lam		5	1pne		4	1xso	A	6	2tys	A	4
1aj2		4	1cse	E	4	1lbu		0	1pnk	A	4	1xyz	A	3	2vhb	B	2
1ak1		1	1csh		8	1lcl		6	1poa		3	1yai	C	3	2wea		4
1ako		4	1ctj		8	1lis		4	1poc		4	1yas	A	0	3chy		3
1akz		9	1cyd	A	5	1lit		3	1pot		0	lycc		5	3cox		6
1al3		5	1dad		1	1lki		2	1ppn		7	1yer		0	3cyr		6
1alo		3	1dkz	A	6	1lkk	A	0	1pud		1	1ytb	A	0	3daa	A	6
1alv	A	1	1dor	A	7	1lmb	3	4	1qba		8	1yve	I	8	3grs		0
1amm		8	1dos	A	5	1lml		7	1qnf		9	1zin		6	3lzt		2
1amp		3	1dun		2	1lt5	D	9	1ra9		9	256b	A	9	3pcg	M	7
1amx		7	1dup	A	4	1lts	A	9	1rcf		9	2a0b		7	3pte		6
1aoc	A	7	1dxy		5	1luc	B	1	1rec		8	2abk		5	3sdh	A	2
1aoh	A	0	1ecp	A	5	1mai		3	1reg	Y	5	2acy		8	3seb		8
1aop		0	1ede		2	1mbd		3	1rge	A	7	2arc	A	7	3tss		8
1aoq	A	5	1edg		5	1mka	A	0	1rie		4	2ayh		8	3vub		6
1aoz	A	5	1edt		0	1mml		5	1rmg		1	2bop	A	1	4pga	A	3
1apy	B	6	1ezm		3	1mol	A	8	1rro		7	2cba		7	5csm	A	1
1aq0	A	9	1fdr		4	1mpg	A	6	1rsy		2	2ccy	A	4	5hpg	A	3
1aq6	A	1	1fds		5	1mrj		9	1rva	A	8	2chs	A	9	5p21		9
1aqb		0	1fna		5	1mrp		1	1sbp		0	2ctc		3	6gsv	A	2
1arb		4	1fua		6	1msc		1	1sfp		0	2dri		9	7ahl	A	3
1arv		5	1fur	A	1	1mty	G	7	1sft	B	2	2end		4	7rsa		4
1atl	A	3	1fvk	A	1	1mty	B	6	1slu	A	7	2fha		5
1atz	B	0	1fwc	A	5	1mty	D	8	1sra		3	2fiv	A	2
1avm	A	4	1gai		9	1mug	A	3	1svb	A	4	2gdm		6
1awd		7	1gd1	O	6	1mzm		9	1svp		4	2hbg		9
1axn		5	1gdo	A	1	1nar		2	1tca		9	2hft		6
1ayl		3	1gif	A	7	1nba	B	0	1thv		2	2hmz	A	2
1bal		4	1gky		8	1nbc	A	2	1thx		6	2hpd	A	6
1bbp	A	4	1gnd		6	1nci	A	5	1tib		1	2hts		7
1bdo		1	1gsa		2	1nif		8	1tml		5	2ilb		0
1beb	A	9	1guq	A	9	1nls		5	1trk	A	3	2kin	A	2

Table 2.

Counts of amino acids, outliers, and terminal residues not in the electron density

				Outlier runs				No density
Amino acid	Count	Outliers	% Outliers	Length	N-term	C-term	All	N-term	C-term
A	5845	224	3.8	1	61	58	380	20	15
C	908	20	2.2	2	47	45	237	15	16
D	4110	264	6.4	3	20	21	139	7	10
E	3934	255	6.5	4	11	10	91	8	8
F	2688	31	1.2	5	9	6	56	10	3
G	5405	312	5.8	6	4	1	31	2	4
H	1578	61	3.9	7	1	1	23	5	3
I	3713	62	1.7	8	–	1	15	6	4
K	3954	232	5.9	9	–	–	9	2	3
L	5556	129	2.3	10	–	1	10	3	1
M	1400	67	4.8	11	1	–	6	1	–
N	3233	196	6.1	12	–	–	2	1	1
P	3171	140	4.4	13	1	–	5	1	1
Q	2530	138	5.5	14	–	–	1	1	2
R	3044	133	4.4	16	–	–	1	2	3
S	4142	275	6.6	17	–	–	–	1	1
T	4041	184	4.6	18	–	–	1	1	–
V	4739	100	2.1	19	–	–	1	–	1
W	1023	13	1.3	20–49	–	1	2	4	1
Y	2538	43	1.7	≥50	–	1	1	2	1
Totals	67552	2879	4.3		155	146	1011	92	78

Plots of the C^α B-factors of a protein chain by amino acid showed that many proteins had regions of unusually high flexibility (e.g., 1FNA; Dickinson et al. 1994; Fig. 1A ▶) where it appears that these regions are undergoing motions different from those in the rest of the chain. To normalize and then compare the B-factors of these protein chains with those from other chains, these residues need to be removed before the normalization process can be applied. A standard approach to identifying outliers is to define an outlier as being three standard deviations or more from the mean, often called having a Z-score (Z = [x − μ]/σ) of ≥3. Following this approach, the five residues above the upper dotted line in Figure 1A ▶ would be removed. However, this leaves several residues with unusually high B-factors when compared with the majority of residues in this protein. When a median based approach, as described in the Materials and Methods section, is applied, all the residues in the highly flexible loop of 1FNA are marked as outliers at an M_i value of 3.5 (the lower dotted line in Fig. 1A ▶).

Figure 1.

Raw and normalized B-factors for 1FNA (Dickinson et al. 1994). (A) The experimentally observed B-factors for 1FNA with the Z = 3.0 (upper) and M = 3.5 (lower) cut-off lines indicated. (B) Normalized B-factors after outliers at Z ≥ 3.0 removed (gray circles), and after outliers at M ≥ 3.5 removed (triangles). The lack of variation in the normalized B-factors can be seen if outliers are not removed properly.

The effect of including residues with unusually high B-factors on the normalization of B-factors of a chain can be seen in Figure 1B ▶. In all cases, the B-factors were normalized to zero mean and unit variance based on the mean and standard deviation of the B-factors, with either outliers detected by a Z score ≥3 excluded, or outliers detected by an M score ≥3.5 excluded. In the case where outliers detected by being three standard deviations from the mean were removed, the remaining normalized B-factors show much smaller variation than when outliers were removed by the median based method.

With Z-score–based outlier detection, the flexible loops in 1FNA centered on residues 27 and 42 have normalized B-factors that are less than one standard deviation from the mean. However, for the median based method of detecting outliers, these flexible loops have normalized B-factors that are more than two standard deviations from the mean. The resulting lack of variability in the normalized B-factors, when outliers are not properly removed, substantially affects comparisons among different chains. Consequently, the median-based method for detecting outliers was used before the protein chains in the data set were normalized.

Previous studies on B-factors have omitted the first three and last three residues in the chain (Karplus and Schulz 1985; Vihinen et al. 1994) and recursively reduced isolated high values until no isolated high value remained (Vihinen et al. 1994). Frequently, though, for residues visible in the electron density, terminal residues are not the most flexible in the protein and highly flexible residues occur in groups. For the 290 protein-chain set studied here, an investigation of the occurrence of outliers (where a B-factor had an M_i value ≥3.5) was undertaken. A total of 2879 outliers were detected and Table 2 presents the results of this study.

Of the 290 chains, approximately half had a flexible N terminus (155) and almost as many chains had a flexible C terminus (146). Only 29% (84) of the chains had both termini flexible while 75% (217) of chains had at least one flexible terminus. A total of 359 and 385 amino acids were in flexible N and C termini, respectively, as determined by the outlier criterion. These represent 12.5% and 13.4%, respectively, of the total of detected outliers. Thus, over 74% of the detected outliers, and 70% of the outlier runs, are not in the termini of the protein chains. Approximately 70% of the flexible N or C termini were of one or two residues in length. Values were very similar in the “test” set of 196 protein chains (supplemental Table 2).

Only 24, or ~8%, of the chains had no outliers. In the 266 chains containing outliers, the outliers were distributed in a total of 1011 runs of varying lengths (Table 2). Approximately 61% of the outlier runs were of lengths of one or two residues. The longest run of outliers was 53 residues at the C terminus of 1FUR, a single-chain protein with three domains. This outlier run corresponded to the third domain of 1FUR, which is markedly more mobile than the rest of the protein. A total of 19 chains had outlier runs of >10 residues, with 1PUD having two outlier runs of 11 residues. Nearly 56% of the residues in outliers were in runs of >3 residues in length, which accounted for ~25% of the outlier runs. Excluding 1FUR, the longest outlier run was 21 in the 290-chain set and 14 in the 196 chain set.

The above results apply to residues that were visible in the electron density and so had B-factors assigned. However, in many instances, terminal residues may not be seen in the electron density. By aligning the amino acids in the SEQRES records of the PDB files with the amino acids given in the ATOM records, an analysis of terminal residues not present in the electron density was undertaken. In the 290-chain set, 92 chains had missing N-terminal density and 78 had missing C-terminal density, with 132 chains having at least one terminus with missing density (Table 2). In the 196 chain “test” set the values were 89, 57, and 115, respectively, a slightly higher proportion (Supplemental Table 2). Although the number of terminal residues not seen in the electron density could be very large, approximately two thirds of the cases consisted of five or fewer residues and only 14% to 15% of cases had >10 residues.

After removal of the outliers and normalization of the B-factors for each chain, the normalized B-factors were collated by amino acid across all the chains. For each amino acid, the normalized B-factors were counted into bins of 0.2 normalized units. Plots of the distribution of the bin counts showed that the B-factors followed an extreme value, or Gumbel, distribution (Fig. 2 ▶) and not a normal distribution. Accordingly, a Gumbel distribution was fit to the bin counts (Fig. 2 ▶) and the location and scale parameters for the distribution were recorded (Tables 3, 4). Both normal and log-normal (after transforming the normalized B-factor values to be positive) distributions were also fit to the normalized B-factor counts. Compared to the Gumbel distribution, the normal and log normal gave inferior fits to the data, though the log normal was superior to the normal distribution.

Figure 2.

Plots of the normalized B-factors for each amino acid, counted in bins of 0.2 normalized units, with the Y axis giving the percentage of the B-factors in each bin. The best fit to the Gumbel distribution and the parameters of the fit (λ–location, δ–scale) for each amino acid are shown. Axes scales are the same in all plots.

Table 3.

Location parameters of the fit of the B-factors to a Gumbel distribution

	Whole data set			Two rigid neighbors			One rigid and one flexible neighbor			Two flexible neighbors
Amino acid	290	Mean	Std dev	290	Mean	Std dev	290	Mean	Std dev	290	Mean	Std dev
A	−0.605	−0.605	0.005	−0.792	−0.792	0.008	−0.609	−0.609	0.006	−0.387	−0.387	0.008
C	−0.693	−0.692	0.008	−0.823	−0.823	0.016	−0.718	−0.718	0.008	−0.594	−0.593	0.024
D	−0.279	−0.279	0.005	−0.584	−0.584	0.014	−0.285	−0.285	0.007	0.072	0.072	0.016
E	−0.160	−0.160	0.009	−0.480	−0.480	0.019	−0.168	−0.168	0.009	0.189	0.189	0.017
F	−0.719	−0.719	0.003	−0.934	−0.934	0.011	−0.737	−0.737	0.008	−0.552	−0.552	0.006
G	−0.537	−0.537	0.009	−0.760	−0.760	0.012	−0.588	−0.588	0.008	−0.241	−0.241	0.010
H	−0.662	−0.662	0.009	−0.870	−0.870	0.015	−0.634	−0.634	0.015	−0.486	−0.485	0.016
I	−0.682	−0.682	0.003	−0.889	−0.889	0.011	−0.693	−0.693	0.005	−0.538	−0.538	0.006
K	−0.043	−0.043	0.005	−0.243	−0.243	0.011	−0.065	−0.065	0.005	0.176	0.176	0.008
L	−0.631	−0.631	0.004	−0.865	−0.865	0.011	−0.642	−0.642	0.003	−0.422	−0.422	0.008
M	−0.626	−0.626	0.010	−0.826	−0.826	0.022	−0.646	−0.646	0.013	−0.486	−0.485	0.013
N	−0.381	−0.381	0.006	−0.578	−0.577	0.014	−0.399	−0.398	0.004	−0.185	−0.185	0.018
P	−0.271	−0.271	0.005	−0.397	−0.396	0.013	−0.315	−0.315	0.009	−0.120	−0.120	0.014
Q	−0.369	−0.368	0.008	−0.563	−0.563	0.017	−0.362	−0.362	0.010	−0.159	−0.158	0.024
R	−0.448	−0.448	0.006	−0.639	−0.638	0.016	−0.412	−0.412	0.009	−0.315	−0.314	0.014
S	−0.423	−0.424	0.009	−0.642	−0.641	0.012	−0.411	−0.412	0.012	−0.231	−0.231	0.016
T	−0.525	−0.525	0.007	−0.707	−0.707	0.017	−0.507	−0.506	0.008	−0.390	−0.390	0.012
V	−0.669	−0.669	0.004	−0.847	−0.847	0.008	−0.673	−0.673	0.005	−0.501	−0.501	0.008
W	−0.727	−0.727	0.009	−0.886	−0.886	0.019	−0.755	−0.754	0.013	−0.614	−0.614	0.009
Y	−0.721	−0.721	0.005	−0.904	−0.904	0.007	−0.761	−0.761	0.007	−0.503	−0.503	0.008
DS+	−0.623	−0.623	0.016	−0.780	−0.772	0.046	−0.693	−0.693	0.016	−0.496	−0.494	0.042
DS−	−0.737	−0.737	0.008	−0.832	−0.821	0.036	−0.735	−0.735	0.010	−0.684	−0.683	0.022
All	−0.520	−0.520	0.001	−0.725	−0.725	0.003	−0.528	−0.527	0.001	−0.332	−0.333	0.003

DS+ and DS− are cysteine residues forming and not forming disulphide bridges, respectively.

“Mean” and “Std dev” were calculated from 10 samples, each omitting a different 10% of the chains.

Table 4.

Scale parameters of the fit of the B-factors to a Gumbel distribution

	Whole data set			Two rigid neighbors			One rigid and one flexible neighbor			Two flexible neighbors
Amino acid	290	Mean	Std dev	290	Mean	Std dev	290	Mean	Std dev	290	Mean	Std dev
A	0.718	0.717	0.004	0.556	0.556	0.009	0.704	0.704	0.005	0.847	0.847	0.009
C	0.668	0.668	0.010	0.607	0.607	0.014	0.671	0.671	0.010	0.671	0.670	0.015
D	0.921	0.921	0.006	0.726	0.726	0.011	0.889	0.889	0.007	1.055	1.055	0.014
E	0.963	0.963	0.005	0.806	0.805	0.014	0.912	0.911	0.005	1.110	1.110	0.016
F	0.599	0.599	0.004	0.465	0.465	0.010	0.582	0.582	0.005	0.653	0.653	0.011
G	0.843	0.843	0.005	0.651	0.651	0.006	0.811	0.811	0.009	0.967	0.967	0.007
H	0.754	0.754	0.010	0.598	0.597	0.009	0.734	0.734	0.010	0.894	0.894	0.014
I	0.632	0.632	0.004	0.510	0.510	0.009	0.617	0.617	0.004	0.685	0.686	0.008
K	0.912	0.912	0.006	0.863	0.863	0.007	0.862	0.862	0.008	1.016	1.016	0.009
L	0.681	0.681	0.003	0.504	0.504	0.009	0.650	0.650	0.007	0.788	0.788	0.005
M	0.685	0.685	0.006	0.575	0.575	0.014	0.641	0.641	0.010	0.740	0.740	0.013
N	0.851	0.851	0.008	0.736	0.735	0.011	0.848	0.848	0.009	0.901	0.901	0.017
P	0.850	0.850	0.004	0.753	0.752	0.006	0.866	0.866	0.008	0.857	0.857	0.009
Q	0.849	0.849	0.007	0.730	0.729	0.007	0.817	0.817	0.008	1.007	1.007	0.015
R	0.814	0.814	0.006	0.676	0.676	0.011	0.807	0.807	0.006	0.942	0.942	0.010
S	0.841	0.840	0.008	0.698	0.698	0.014	0.847	0.846	0.008	0.915	0.914	0.010
T	0.758	0.758	0.004	0.648	0.648	0.008	0.742	0.742	0.006	0.861	0.862	0.015
V	0.619	0.619	0.002	0.503	0.503	0.006	0.603	0.603	0.003	0.707	0.707	0.009
W	0.627	0.626	0.011	0.578	0.577	0.024	0.609	0.609	0.013	0.656	0.656	0.011
Y	0.615	0.615	0.004	0.460	0.461	0.008	0.567	0.567	0.005	0.740	0.741	0.009
DS+	0.712	0.713	0.020	0.709	0.701	0.065	0.666	0.666	0.022	0.723	0.722	0.018
DS−	0.635	0.635	0.011	0.576	0.585	0.023	0.673	0.674	0.016	0.599	0.598	0.021
All	0.779	0.779	0.002	0.646	0.646	0.004	0.760	0.760	0.002	0.871	0.871	0.003

See notes to Table 3.

In the study of Wampler (1997), B-factors of lysozyme structures were modeled by a mixture of up to six Gaussian distributions. To estimate the probability distributions of mixtures of Gaussians on a significantly larger dataset and compare them to our model, we first analyzed the autocorrelation function averaged over all 290 proteins from our dataset (Fig. 3 ▶). An almost identical function was obtained when all proteins were connected into one long series of normalized B-factors. With the restriction that this analysis ignores tertiary interactions among the residues, only B-factors up to 4–6 residues apart show significant correlation, while residues seven or more locations away from each other may, on average, be considered uncorrelated.

Figure 3.

The average autocorrelation function, over lags, or residue separations of 0 to 20, of the B-factors in a chain for the entire dataset. For residue separations of 1 to 7, the coefficients were 0.78, 0.61, 0.46, 0.34, 0.23, 0.15, and 0.09, respectively.

Assuming statistical independence of B-factors separated by seven or more residues, we performed a density estimation of the hypothesized models using the maximum-likelihood approach. The results for mixtures of k Gaussian distributions and for one Gumbel distribution are presented in Table 5 and compared with the observed distribution in Figure 4 ▶. From Figure 4 ▶, it is clear that the Gumbel distribution provides a more natural fit to the data. Combining more normal distributions, that is, setting k > 2, gives slightly improved numerical fits, but is difficult to justify because an arbitrary number of Gaussian distributions can fit well to any given data.

Table 5.

Estimated parameters of the mixture of up to six Gaussian functions and the Gumbel distribution using a maximum-likelihood approach with the computed log-likelihood values

Mixture of k Gaussian distributions
k	Estimated parameters	Log-likelihood
1	w = 1	−13,018
	μ = 0.24
	σ = 1.67
2	w = (0.86, 0.14)	−10,818
	μ = (−0.18, 2.77)
	σ = (0.80, 2.92)
3	w = (0.69, 0.27, 0.04)	−10,396
	μ = (−0.45, 1.29, 5.31)
	σ = (0.58, 0.98, 4.19)
4	w = (0.57, 0.32, 0.09, 0.02)	−10,296
	μ = (−0.61, 0.73, 3.05, 9.11)
	σ = (0.49, 0.71, 1.46, 7.46)
5	w = (0.48, 0.34, 0.14, 0.03, 0.01)	−10,239
	μ = (−0.73, 0.33, 1.85, 4.86, 12.29)
	σ = (0.41, 0.50, 0.78, 1.69, 8.22)
6	w = (0.39, 0.33, 0.18, 0.07, 0.02, 0.01)	−10,229
	μ = (−0.85, 0.02, 1.11, 2.68, 5.65, 14.35)
	σ = (0.36, 0.39, 0.53, 0.87, 2.08, 9.61)

Gumbel distribution
Estimated parameters	Log-likelihood
λ = −0.52; δ = 0.93	−10,723

Figure 4.

The distribution of the B-factors, as observed (black); as modeled by a mixture of three Gaussian functions (green; maximum-likelihood estimates, w = [0.04, 0.27, 0.69]; μ = [5.31, 1.29, −0.45]; σ = [4.19, 0.98, 0.58]); and as modeled by two Gumbel distributions, one with λ = −0.52; δ = 0.93 (red, maximum-likelihood estimate) and another with λ = −0.52; δ = 0.78 (blue, least-squares fit). The observed distribution was smoothed and the area under the curve was normalized to 1.

In Figure 4 ▶, we also compare our maximum-likelihood and least-squares estimates of the Gumbel distribution with the observed distribution of B-factors. The maximum-likelihood estimate gives an improved numerical fit but it is visibly worse than the least-squares fit in the left tail and around the mean while it compensates in the right tail. However, after convergence of crystallographic refinement, higher B-factors are more likely to contain errors because of the influence of static disorder. The high B-factor tail may also include values that should have been treated as outliers, but were just below the cutoff that was used. For those reasons, we further used only the least-squares estimate of the Gumbel distribution in this study.

From the location parameter (or modal value) of the fitted Gumbel distribution, an estimate of the flexibility of each amino acid was obtained. Amino acids that generally have lower B-factors will have lower location parameters. The order of the amino acids by ascending location parameter was W Y F C I V H L M A G T R S N Q D P E K. Based on these location parameters, the amino acids were divided into two groups of 10 with W Y F C I V H L M A being defined as rigid amino acids and G T R S N Q D P E K being defined as flexible amino acids.

Following the approach of Karplus and Schulz (1985) and Vihinen et al. (1994), the amino acids were then divided into three groups depending on the classification of their neighboring residues as either rigid or flexible. Three groups of amino acids, those with two rigid neighbors, those with two flexible neighbors, and those with one flexible and one rigid neighbor, were created. These groups were collated by amino acid, counted into bins and fit to a Gumbel distribution as described above. Location and scale parameters for each amino acid in each group are given in Tables 3 and 4, respectively.

To test whether the estimates were sensitive to the choice of chains being analyzed, the entire process was repeated 10 times with a different 10% of the protein chains excluded from the data set. Thus, for each amino acid in each group, 10 location and scale parameters of the fit to the Gumbel distribution were obtained. The mean and standard deviation of these parameters are given in Tables 3 and 4. It can be seen that there was very little influence on the fits to the Gumbel distribution by the removal of 10% of the data set and that the parameters are stable to changes in the data set from which they were derived.

A comparison of the Gumbel distribution derived parameters with those of Karplus and Schulz (1985) and Vihinen et al. (1994) was performed in two ways. Firstly, plots of the parameters for the whole data set and the three different neighbor groups were created (Fig. 5 ▶). To allow the comparison to be made more easily, the parameters of Karplus and Schulz (1985) and Vihinen et al. (1994) were rescaled, as described in Materials and Methods. As Karplus and Schulz (1985) did not publish their parameters for the whole data set but only for the neighbor groupings, these parameters had to be recalculated. Because of inconsistencies in the list of PDB files they published, these data could not be reproduced exactly. However, the average difference between the original and recalculated neighbor groups was 0.003, and only four parameters showed differences >0.01, with the maximum difference being 0.026 for leucine with two rigid neighbors.

Figure 5.

Comparison of the parameters developed here (G) with those of Vihinen et al. (1994; V) and those of Karplus and Schulz (1985; KS). The parameters by each method are shown for two flexible neighbors (red circles), one flexible and one rigid neighbor (green squares), two rigid neighbors (blue triangles), and for the complete data set (magenta diamonds).

Noticeable features of this comparison are that the parameters derived from the entire data set, without regard to the neighbors, are close to those for one flexible and one rigid neighbor for all methods. The parameters derived in this work show a clear consistency across the neighbor groupings with a similar pattern of flexibility parameters across the amino acids. Most noticeable in the parameters of Vihinen et al. (1994) are the absence of any overlap among the neighbor groupings and the very limited range of values for amino acids with two rigid neighbors. In the Vihinen et al. (1994) parameter set, any amino acid with two flexible neighbors is more flexible than the most flexible amino acid with one or two rigid neighbors. This is not the case in the two other parameter sets. Inconsistency in parameter values is the main characteristic of the Karplus and Schulz (1985) data set. For example, an amino acid with one flexible and one rigid neighbor may be more rigid than when it has two rigid neighbors (Cys) or more flexible than when it has two flexible neighbors (Asp).

A second test of the parameters was to determine correlation coefficients of flexibility values, calculated from a weighted sliding window, for each of the parameter sets with the experimental B-factors. This was performed as described in Materials and Methods for odd-sized windows varying from 1 to 13 in length for both the 290 and 196 chain sets. The mean of these correlation coefficients, for each window size, over the 290 and 196 protein chain sets is given in Figure 6 ▶. In all cases, the parameters derived in this work give a better correlation with the experimental data. Apart from a window size of one, the parameters of Vihinen et al. (1994) were superior to those of Karplus and Schulz (1985) for the 290 chain set but their values overlapped in the 196 chain set. The 196 chain “test” set, which predominately consisted of more recently solved structures, gave slightly higher mean correlation coefficients for all parameter sets.

Figure 6.

Means, over the 290 (solid lines) and 196 (dashed lines) protein chain sets, of the correlation coefficients of the flexibility parameters, in sliding windows of lengths 1 to 13, with the experimental B-factors. (Circles) The parameters developed here, (triangles) those of Vihinen et al. (1994), and (squares) those of Karplus and Schulz (1985).

For all three parameter sets, a window size of 9 gave the best correlation, and windows of 7 and 11 gave the next best correlations. Correlation coefficients varied over a wide range, with the highest values being >0.7 and lowest values being <−0.3 for all the parameter sets. The mean correlation coefficients for a window of size 9 were 0.34, 0.31, and 0.30 in the 290 chain set and 0.37, 0.33, and 0.33 in the 196 chain set, for the parameters developed here, those of Vihinen et al. (1994) and those of Karplus and Schulz (1985), respectively.

Discussion

The flexibility inherent in the structures of proteins has gained prominence recently with the realization that many proteins are intrinsically disordered in solution or have regions that are substantially disordered (Wright and Dyson 1999; Bright et al. 2001; Dunker et al. 2001). As one of the indicators of mobility in protein structures is the X-ray crystallographic B-factor, we have re-examined the distributions of B-factors in proteins to attempt to improve amino acid flexibility parameters.

Extending the earlier approaches of Karplus and Schulz (1985) and Vihinen et al. (1994), we selected a much larger set of high resolution, nonidentical protein structures to provide a data bank of experimentally determined amino acid B-factors. Efforts were made to identify the unusually flexible regions in the proteins and to fit a probability distribution to the range of B-factors observed for each amino acid in the data set.

Although proteins generally show a pattern of relatively rigid secondary structural elements and relatively flexible loops, some local regions undergo motions on a different scale when compared with other parts of the protein. Earlier studies concentrated on the N and C termini as the main highly flexible regions (Karplus and Schulz 1985; Vihinen et al. 1994), however, our data indicated that most of the regions with unusually high B-factors were not at the termini of chains. To proceed with a comparative study of protein B-factors, it was necessary to identify and remove these regions from the main study.

Attempting to identify outliers in a sample based on the number (often three) of standard deviations a point is from the mean can be problematical when the mean and standard deviation must be calculated from the sample (Iglewicz and Hoaglin 1993). This is because the outliers to be identified contribute disproportionately to the mean and standard deviation. Depending on the sample size, there is an upper limit to the number of standard deviations a point can be from the mean of a sample (Shiffler 1988). For these reasons, median-based approaches are superior for the identification of outliers (Shiffler 1988; Iglewicz and Hoaglin 1993).

Accordingly, a robust median-based statistic (see Materials and Methods) that is widely used in quality control studies (Iglewicz and Hoaglin 1993) was used to identify outliers in the B-factors of each protein chain. A cut-off value to decide an outlier is somewhat arbitrary and a value of 3.5 was chosen, following the recommendation of Iglewicz and Hoaglin (1993) based on a simulation study.

Only half, approximately, of the chains had a flexible N or C terminus as determined by the M score, although 75% had at least one terminus flexible. The lengths of these terminal flexible regions were usually <3 amino acids assumed in earlier studies (Karplus and Schulz 1985; Vihinen et al. 1994). Most of the outliers and most of the runs of outliers, however, were not at the termini, demonstrating the need for a more detailed approach to identifying outliers than omitting a small number of terminal residues.

Flexibility at the termini of protein chains can also lead to the terminal amino acids not being seen in the electron density. In the two sets of protein chains used here, approximately half of the chains had at least one terminus containing residues not visible in the electron density. In most cases, the number of residues not visible at a chain terminus was small, consistent with the results seen for B-factor outliers. While chain termini are considerable sources of flexibility (over 80% of the chains studied here had either residues missing in the electron density or B-factor outliers in at least one terminus), in general, these regions are short and flexibility in the rest of the chain must be considered to identify unusually mobile residues.

If outliers were not identified properly, then any subsequent normalization of the B-factors would result in mobile regions, such as loops, in a protein having very low normalized B-factors, as was shown for 1FNA (Fig. 1 ▶). Consequently, comparative studies across a set of proteins would be affected. Of the amino acids, the aromatic residues and Ile had the lowest percentage occurrence in outliers while Asn, Asp, Glu, Lys, and Ser had the highest occurrence.

Instead of simply using the mean of the normalized B-factors (Karplus and Schulz 1985; Vihinen et al. 1994) as the estimator of an amino acid’s flexibility, the distribution of the normalized B-factors for each amino acid was examined. It was clear that the distribution was not symmetric and did not follow a normal distribution, so an arithmetic average would not be a good estimator of the most probable value for an amino acid. An extreme value, or Gumbel, distribution (Castillo 1988) of the type widely used in database searching (Altschul et al. 1990) was found to be the best model of the observed distribution. This may be rationalized as the experimental B-factor provides an estimate of the extent of mobility of an atom in a protein.

By fitting the Gumbel distribution to the normalized B-factors, a more accurate estimate of the parameters of the distribution would be obtained. The location parameter, or mode, of the fitted Gumbel distribution was used as the estimator of each amino acid’s flexibility. Similarly to earlier work (Karplus and Schulz 1985; Vihinen et al. 1994), the amino acids were divided into two groups, “rigid” and “flexible”, based on the location parameter. It was decided to divide the amino acids into two equal groups of 10, rather than use the location parameter from fitting to the entire data set as a division. Gly and Thr have location parameters close to, but slightly lower than, that of the entire data set but were classified as flexible here. In the study of Vihinen et al. (1994) Thr is classified as rigid, although it is just below the average value, while it is flexible in the Karplus and Schulz (1985) data set.

Based on these definitions of the amino acids, flexibility parameters were developed for each amino acid depending on the nature of its immediate neighbors. An interesting observation of this study was that when cysteine residues were analyzed by whether or not they were in a disulphide bridge, it was noted that cysteine residues forming a disulphide bridge were more flexible than those that did not. Thus, although a disulphide bridge stabilizes a protein structure as a whole, the effect of joining two backbone segments, both subject to thermal motion, appears to increase the local mobility of both the cysteine residues.

The parameters developed in this work show a consistency of pattern across the amino acids and neighbor groupings, with the more flexible amino acids, even when they have two rigid neighbors, being more flexible than some of the more rigid amino acids with two flexible neighbors. The inconsistency of the parameters developed by Karplus and Schulz (1985) is most likely because of the very small data set (31 proteins) that they were able to use. The complete separation of the parameter groups and the lack of variation within the two-rigid-neighbor group in the parameters of Vihinen et al. (1994) are difficult to explain.

When the parameter sets were tested against the experimentally determined B-factors using a weighted, sliding window, the parameters developed here consistently outperformed the other parameter sets. Although the correlation coefficients were not particularly high, with a maximum of 0.34 in the 290 chain set and 0.37 in the 196 chain set, this is to be expected when a single number is being used to estimate a parameter, which can take a range of values following a probability distribution. For all parameter sets, a window of 9 gave the best correlation. This is consistent with the autocorrelation study of the B-factors within a chain, which showed limited correlation at a residue separation larger than four.

In this work, we have developed a new set of amino acid based parameters for estimating the flexibility within a protein chain that has superior performance to earlier efforts. To develop these parameters, we used robust statistical techniques to identify outliers, amino acids with unusually high mobility, in the B-factor distribution of a protein chain. This study revealed that the majority of highly mobile segments in proteins are not at the chain termini, and if these segments are not accounted for, and outliers properly removed, comparisons among protein chains will be hampered. We also showed that B-factors follow an extreme value distribution and used the location parameter, or modal value, of this distribution as the estimator of an amino acid’s flexibility. These parameters and the method of identifying highly flexible segments (or outliers) will prove useful in studies of disordered proteins and mobile segments in proteins, in protein-protein interaction studies, and as a simple predictor of flexibility from an amino acid sequence.

Although flexibility indices measured by amino acid location parameters of the corresponding Gumbel distributions show an improved fit to the protein chain flexibility, a generalization of this method will be our future interest. This research will comprise representing flexibility indices by both the location and scale parameters of a Gumbel distribution and incorporating them into a probabilistic framework. Such an approach would allow us to account for different degrees of flexibility (measured by the B-factor values) and use the analysis toward further elucidation of biological phenomena.

Materials and methods

Selection of protein chains

A total of 290 protein chains (Table 1) were taken from the August 1998, 25% sequence identity threshold, nonredundant list of PDB-Select (Hobohm et al. 1992). Chains were selected if they had a resolution ≤2Å, an R-factor ≤20%, a chain length ≥80 residues, no missing backbone or side chain atoms and contained no nonstandard residues as listed by PDB-Select. Three protein chains that met these criteria (2BBK L and H; 1CEW I) were excluded because of the abnormally small amount of variation in their B-factors, and the B-factors given for chain 1AMM were multiplied by 8π² to put them on the same scale as those of the other protein chains. All of the protein chains were randomly allocated to one of 10 equally sized groups as indicated in Table 1. Ten new sets of protein chains, each containing 90% of the total, were formed by excluding the protein chains assigned to each of the groups in turn. These smaller sets were used to provide a measure of the variability in the parameters calculated below.

A further 196 chains (at the 25% sequence identity threshold) were taken from the April 2002 version of PDB-Select (Supplemental Table 1). These chains were selected using the same criteria given above and omitted chains in the original data set and those which were connected to them by the network of homologous relationships listed in PDB-Select. Over 86% of these chains were deposited after the creation date of the list used for the first set of chains. This provided an independent set of more recently solved protein chains to test the parameters developed here.

Detection of outliers

A median-based method to detect outliers (Iglewicz and Hoaglin 1993) was used. First, the median of the C^α B-factors in a chain was determined and then the median of absolute displacements (MAD) from the median was determined. An M value for each B-factor was calculated as follows:

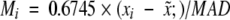where x_i is the B-factor of the ith residue, x̃; is the median of the B-factors, MAD is as described above, and multiplication by 0.6745 is used because the expected value of MAD is 0.6745σ for large sample sizes (Iglewicz and Hoaglin 1993). An M_i value of 3.5 was used to define an outlier.

Normalization of B-factors

After removal of the outliers, the mean (μ_noout) and standard deviation (σ_noout) of the remaining C^α B-factors in the chain were determined and a normalized B-factor was calculated as B_norm,i = (B_i-μ_noout)/σ_noout. Thus, the normalized B-factors (excluding those designated as outliers) have zero mean and unit variance. The normalization technique used in earlier work (Karplus and Schulz 1985; Vihinen et al. 1994) was (after removal of the 3 N- and 3 C-terminal residues) B_norm = (B + D_p)/〈B〉_p + D_p) where 〈B〉_p is the average of the B-factors in the chain, the average B_norm is 1 and D_p was chosen so that the root mean square deviation of the B_norm values would be 0.3. This is equivalent to setting B_norm = 0.3(B − 〈B〉_p)/σ_p + 1. For comparative purposes, the parameters of Karplus and Schulz (1985) and Vihinen et al. (1994) were adjusted to be on the same scale as the parameters calculated here by using the formula (parameter − 1)/0.3.

Determination of parameters

Normalized C^α B-factors were collected for each amino acid in the data set and counted in bins of 0.2 normalized units. For cysteine residues separate counts were also made for residues forming (DS+) or not forming (DS−) disulphide bridges. The residue counts were fitted to a Gumbel or extreme value distribution (Castillo 1988; Altschul and Erickson 1988) using SigmaPlot (SPSS Inc.). For a Gumbel distribution, the cumulative distribution function is G(x) = exp (−exp [−{x-λ}/δ]), with λ and δ being the location and scale parameters, respectively (Castillo 1988). The probability density function is g(x) = exp(−[x-λ]/δ)exp (−exp [−{x-λ}/δ])/δ and the mode, median, and mean of a Gumbel distribution are: λ, λ+0.3665δ, and λ+0.5777δ, respectively (Castillo 1988). After the fitting process, the residues with the lowest 10 location parameters were deemed rigid amino acids and the remaining 10 were deemed flexible.

A similar counting and fitting procedure was performed with the original data set divided into three groups depending on whether the two neighboring amino acids were both classified as rigid, or whether both were classified as flexible, or whether one was classified as flexible and the other as rigid. This entire procedure was repeated for each of the 10 data subsets that omitted a different 10% of the protein chains.

Autocorrelation and maximum-likelihood estimators

By considering the normalized C^α B-factors as a discrete-time series, the autocorrelation function was calculated for each chain and the overall autocorrelation function was obtained as a simple average of individual autocorrelation functions over all proteins. The lag (or residue separation) k autocorrelation was calculated as

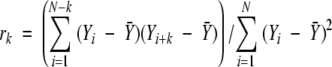(Box et al. 1994) which is equivalent to the normalized autocovariance as used in signal processing (Hayes 1996).

The probability density function of a mixture of k Gaussian distributions is given by

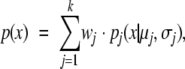where x is a 1D random variable and each p_j a Gaussian distribution with mean μ_j and standard deviation σ_j. Coefficients w_j are positive and sum to one. Parameters of a mixture of Gaussian distributions were estimated using an expectation-maximization algorithm (McLachlan and Peel 2000) with 100 random starts and suitably chosen convergence parameters. Only every tenth residue was included in the analysis in order to avoid correlated examples. After repeating the procedure 10 times for different choices of examples, the variance of the estimate was small and the overall estimate was obtained by simple averaging. The location and mode of the Gumbel distribution were also estimated using a maximum-likelihood estimator (Evans et al. 1993) with the same number of random starts and convergence parameters.

Calculation of flexibility in a running window and correlation with B-factors

The amino acid flexibility parameters calculated here, along with those of Karplus and Schulz (1985) and Vihinen et al. (1994), were applied to each of the protein chains in a running window to obtain a flexibility value for each amino acid in the context of its protein chain. A flexibility parameter was assigned to each amino acid in the protein chain on the basis of the classification of its neighbors as rigid or flexible. Then, a hat-shaped window (Claverie and Daulmerie 1991) was used to weight the contribution of each amino acid in the window to the final flexibility value of the amino acid. Windows with odd lengths of 1 to 13 were used. For a window of length 5 centered at residue i, residues i − 2 and i + 2 had weights of ⅓, residues i − 1 and i + 1 had weights of 2/3, and residue i had a weight of 1. In the case of a window of length 7, the weights were ¼, ½, ¾, 1, ¾, ½, ¼ for residues i − 3 to i + 3, respectively, and so on for other window sizes. The flexibility value for each amino acid was the sum of the products of the window weight and the flexibility parameter for each residue in the window. Correlation coefficients for the window-based flexibility values with the B-factors for each protein chain were calculated for all window sizes and for all three parameter sets. The average and standard deviations of the correlation coefficients over the 290 and 196 protein chain sets were determined.

Electronic supplemental material

A Microsoft Word document contains tables: (1) the 196 protein chains in the “test” set and (2) the counts of amino acids, outliers, and terminal residues not in the electron density for this set.