Abstract
The conformational equilibrium between 310- and α-helical structure has been studied via high-resolution NMR spectroscopy by Millhauser and coworkers using the MW peptide Ac-AMAAKAWAAKA AAARA-NH2. Their 750-MHz nuclear Overhauser effect spectroscopy (NOESY) spectra were interpreted to reflect appreciable populations of 310-helix throughout the peptide, with the greatest contribution at the N and C termini. The presence of simultaneous αN(i,i + 2) and αN(i,i + 4) NOE cross-peaks was proposed to represent conformational averaging between 310- and α-helical structures. In this study, we describe 25-nsec molecular dynamics simulations of the MW peptide at 298 K, using both an 8 Å and a 10 Å force-shifted nonbonded cutoff. The ensemble averages of both simulations are in reasonable agreement with the experimental helical content from circular dichroism (CD), the 3JHNα coupling constants, and the 57 observed NOEs. Analysis of the structures from both simulations revealed very little formation of contiguous i → i + 3 hydrogen bonds (310-helix); however, there was a large population of bifurcated i → i + 3 and i → i + 4 α-helical hydrogen bonds. In addition, both simulations contained considerable populations of π-helix (i → i + 5 hydrogen bonds). Individual turns formed over residues 1–9, which we predict contribute to the intensities of the experimentally observed αN(i,i + 2) NOEs. Here we show how sampling of both folded and unfolded structures can provide a structural framework for deconvolution of the conformational contributions to experimental ensemble averages.
Keywords: Molecular dynamics, π-helix, 310-helix, force-shifted cutoff, conformational ensemble, helix-coil transition
The 310-helix is the fourth most common type of secondary structure in proteins after α-helices, β-sheets, and reverse turns (Barlow and Thornton 1988). Approximately 15%–20% of all helices in protein structures are 310-helices, which are commonly found as N- or C-terminal extensions to an α-helix (Barlow and Thornton 1988). 310-Helices in proteins are typically only three to five residues long compared with a mean of 10–12 residues for α-helices (Richardson and Richardson 1988). Their formation can be introduced by cα-q-disubstituted amino acids, such as α-aminoisobutyric acid (AIB; Karle and Balaram 1990). Such peptides crystallize into pure 310-, pure α-, or mixed 310/α-helices depending on their length and relative AIB content, and these authors concluded that a six-residue helical peptide with only L amino acids is equally likely to form 310- and α-helix (Karle and Balaram 1990).
310-Helices have been proposed to be intermediates in the folding/unfolding of α-helices (Millhauser 1995). The rationale for this suggestion is that there is a lower entropic penalty for the necessary loop closure for the formation of i → i + 3 versus i → i + 4 hydrogen bonds. Helix-coil theory has been modified to include the 310-helix, indicating that 310-helix should be populated in the helix-coil transition (Sheinerman and Brooks 1995; Rohl and Doig 1996). These modified helix-coil theories also predict that 310-helical segments will be short. There is also experimental evidence from solution electron spin resonance (ESR) spectroscopy that the population of 310-helix in an α-helical peptide demonstrates length dependence, with longer peptides favoring the α-helical conformation (Fiori et al. 1993), which is also predicted by the modified helix-coil theories (Sheinerman and Brooks 1995; Rohl and Doig 1996). For L amino acids, there is not a disallowed region between the α-helical (φ = −57°, ξ = −47°) and 310-helical (φ = −49°, ξ = −27°) conformations, allowing for free interconversion between the two. However, in AIB peptides, the steric interactions from the two methyl groups on the α-carbon result in the 310-helix geometry being favored energetically over the α-helix (Zhang and Hermans 1994). Previous short simulations have addressed the α/310-helix equilibrium in both AIB-rich peptides (Zhang and Hermans 1994) and alanine-based peptides (Tirado-Rives et al. 1993). The results of these studies indicate that the 310-helical conformation is not favored in L amino acids, although 310-helical intermediates have been observed in transitions between α-helical and nonhelical states (Daggett and Levitt 1992).
Millhauser and coworkers (1997) have investigated the α/310-helix equilibrium in an alanine-based peptide with NMR spectroscopy. The MW peptide was designed to reduce signal overlap for high-field NMR (Ac-AMAAKA WAAKAAAARA-NH2). This peptide is a variant of the 3K peptide (Marquesee et al. 1989), which has been the subject of many ESR and fourier transform infrared (FTIR) studies (Todd and Millhauser 1991; Fiori et al. 1993, 1994; Miick et al. 1993, Smythe et al. 1995). The NOESY spectra of the MW peptide were acquired at 750 MHz (pH 5.0, 274 K) and revealed 57 NOEs and 3JHNα coupling constants for 13 of the 16 residues (Millhauser et al. 1997). From the circular dichroism (CD) spectra, the peptide is expected to be ∼48% helical at 274 K and 25% helical at 298 K (Millhauser et al. 1997). The MW peptide displays both of the standard benchmark NOEs used to distinguish 310-helix [αN(i, i + 2)] and α-helix [αN(i, i + 4)]. Many helical peptides reflect both connectivities simultaneously (Osterhout et al. 1989; Bradley et al. 1990; Merutka et al. 1993) and structural interpretation of these NOEs can be ambiguous. Isolated turns are an expected component of random coil structure and may also contribute to the intensity of αN(i, i + 2) NOEs (Chandrasekhar et al. 1991).
Molecular dynamics (MD) trajectories that sample both helical and nonhelical conformations can be useful in interpreting the structural basis for ensemble averaged observables like the αN(i, i + 2) NOESY cross-peaks. Conformational ensembles of small peptides can be calculated with distance-restrained MD simulations and/or simulated annealing with distance and torsional restraints taken from NMR spectra (Gratias et al. 1998). Often the lack of experimental distance restraints limits the usefulness of these calculated structures for interpreting structurally ambiguous cross-peaks. Another approach is to perform unrestrained MD simulations that can sample a variety of conformational states and compare them with experiment. Here we take the latter approach and describe 25-nsec, room temperature molecular dynamics simulations of the MW peptide starting as an α-helix, using two different nonbonded cutoffs (8 Å and 10 Å). In addition, we describe the mechanisms of transitions between helical and nonhelical conformers and the importance of 310- and π-helix in this process.
Results
α-Helical content and comparison with circular dichroism data
The helical content during the simulation of the MW peptide was calculated based on two different properties: (1) repeating (φξ) helical structure and (2) the percentage of intact i → i + 4 hydrogen bonds (O . . . HN distance ≤2.6 Å; Fig. 1 ▶). In the dihedral definition, three or more consecutive residues had to be in the helical region of conformational space (−100° ≤ φ ≤ −30° and −80° ≤ ξ ≤ −5°; Daggett et al. 1991; Daggett and Levitt 1992). This definition is very broad; the ideal values of α-helix (φ = −57°, ξ = −47°), 310-helix (φ = −49°, ξ = −27°), and π-helix (φ = −57°, ξ = −70°) all fall into this region. For comparison, the β-region is defined as (−170° ≤ φ ≤ −50° and 80° ≤ ξ ≤ 170° ).
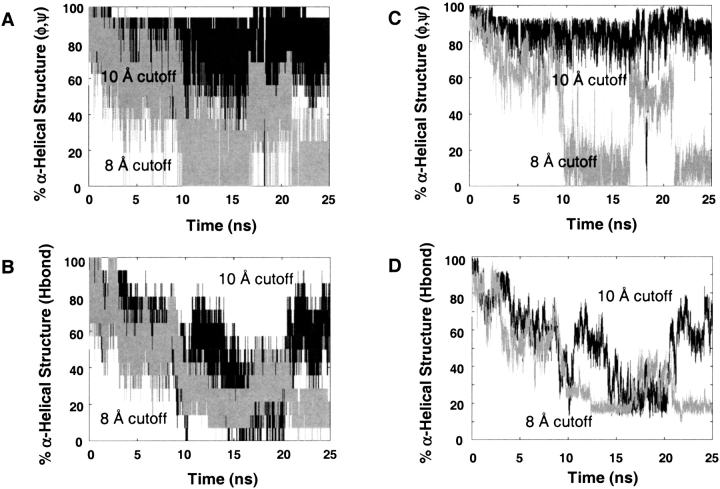
Figure 1.
Percentage of α-helical structure for the 8 Å and 10 Å cutoff simulations. A and C were calculated using repeating helical (φξ) angles, and B and D were calculated as a percentage of native (i → i + 4) hydrogen bonds. The plots in panels C and D have been smoothed.
The peptide unfolded and refolded over the course of the 8 Å cutoff trajectory and sampled nonhelical conformations. In contrast, the peptide remained very helical with the 10 Å cutoff using the dihedral metric. Both definitions of helical structure give similar curve shapes, but the absolute values and fluctuations differed over time (Fig. 1 ▶). Using the 10 Å cutoff, the peptide had a higher helix content using the (φξ) definition, but the α-helix content using the hydrogen bond definition was similar to that of the 8 Å trajectory.
Our calculated helix contents cannot be compared quantitatively with experiment because of the uncertainties in structural properties that contribute to the helical CD signal and the complications from absorbance of Trp (Chakrabartty et al. 1993). Nevertheless, we can estimate the helix contents from the CD spectra of the peptide, using the method of Chakrabartty et al. (−40,000[1–2.5/n] deg cm2/dmole and 0 deg cm2/dmole is used to represent 100% and 0% helix, respectively, where n is the number of residues in the peptide; 1993). Using this approach, we estimate the peptide to be ∼48% helical at 274 K (the NMR spectra were acquired at 274 K) and 24% at the simulation temperature of 298 K. For the 8 Å cutoff, the helical content was 41% ± 23% for the (φξ) definition, 38% ± 21% by the hydrogen bond distance definition, and 27% ± 18% if the hydrogen bonds were also required to be within 45° of linearity. Such alignment has been suggested to be important to CD signals (Gans et al. 1991). For the 10 Å cutoff, the helical content was 85% ± 14% for the (φξ) definition, 53% ± 17% by the hydrogen bond distance definition, and 36% ± 19% with the angular constraint added. The helix content, as measured by i → i + 4 hydrogen bonds, is close to the experimental value (24% at 298 K) for both the 8 Å (27%) and 10 Å (36%) cutoff simulations.
Comparison with high-resolution NMR data
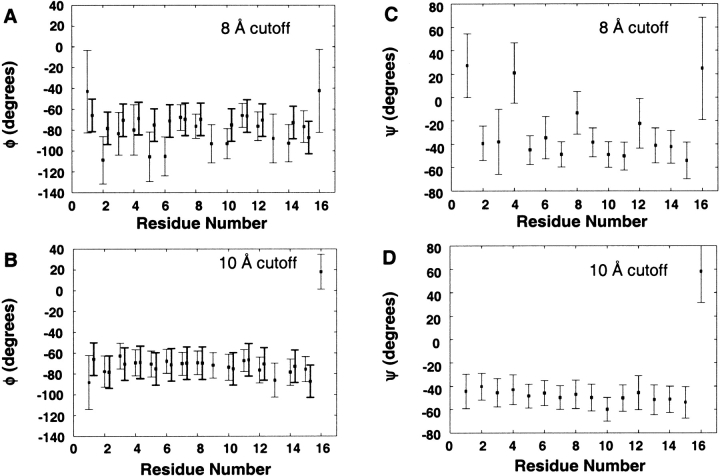
Experimental 3JHNα scalar coupling constants (Millhauser et al. 1997) were used to calculate the average φ dihedral angles using the Karplus relationship (3JHNα = 6.4 cos2 θ − 1.4 cos θ + 1.9, where θ = │φ − 60│; Karplus 1959). A conservative estimate for the uncertainty of converting 3JHNα to φ using this relationship is at least 0.7 Hz (Karplus 1959; Wüthrich 1986). The experimental uncertainty in the magnitude of 3JHNα constants for the MW peptide is also in the range of 0.5 Hz (Millhauser et al. 1996), and the fluctuations in calculated 3JHNα constants are of the same order of magnitude. The 1- to 25-nsec ensemble-averaged (φξ) dihedral angles are presented with their fluctuations in Figure 2 ▶, along with the experimental values for comparison. The (φξ) angles of the peptide in the 10 Å trajectory fluctuated much less compared with the 8 Å trajectory, as would be expected for a predominantly helical ensemble. The φ angles explored in both simulations were in the range of the experimentally derived values with the exception of Ala 6 (Fig. 2 ▶). Averaging over this same time period, the r−6 weighted distances calculated for the 57 experimental NOEs were in good agreement (≤5 Å) with experiment for both the 8 Å and 10 Å trajectories with only a few minor violations, all of which are within the cutoff if the standard deviation in the distance is considered (Fig. 3 ▶). Because the NMR spectra were acquired at 274 K, the level of agreement between simulation and experiment is acceptable given that the peptide is known by CD to sample more nonhelical conformations at this temperature.
Figure 2.
Average dihedral (φξ) angles (averaged from 1–25 nsec) for both the 8 Å and 10 Å cutoff simulations. Experimental 3JHNα coupling constants were converted to <φ> using the Karplus relation and are shown in bold for comparison. The error bars on the experimental values reflect a variation of 1 Hz.
Figure 3.
Summary of the experimentally observed NOEs and corresponding distances from the simulations. The distances between protons were calculated as an ensemble average over the simulation by using weighted averages, (≤rw>) = ≤r−6>−1/6) where rw is the weighted distance and r is the actual distance between the two hydrogens of interest. The calculated NOE weighted distances (averaged over 1–25 nsec) are shown for the 8 Å cutoff simulation (top) and the 10 Å cutoff simulation (bottom).
Calculation of Zimm-Bragg helix-coil parameters
In Zimm-Bragg helix-coil theory (Zimm and Bragg 1959), the propagation parameter s is the equilibrium constant between an existing helical segment and the addition of a new i → i + 4 hydrogen bond. During an MD simulation, we can estimate this equilibrium constant by considering waiting times, τ, for the hcc → hhc and hhc → hhh (propagation) and the hhc → hcc and hhh → hhc transitions as an average over time (Daggett et al. 1991; Daggett and Levitt 1992), where h indicates that a residue is in the helical region of (φξ) space and c means that it is not. The waiting times reflect the populations of the different conformations, and the ratio of the average waiting times is used to calculate the equilibrium constant between the two populations.
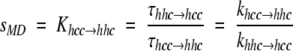 |
The average waiting times to add a helical residue (e.g., hhc → hhh) were faster using the 10 than the 8 Å cutoff (0.4 versus 3.4 psec), whereas the τhhh → hhc values were similar (6.6 versus 7.1 psec). These differences are due to the heightened stability of the helix using the longer cutoff (more details provided following). The peptide rarely left the helical basin of (φϕ) space, so that excursions to "coil" were very minor.
Our average values of sMD for Khcc → hhc and Khhc → hhh for the alanine residues were 1.5 and 2.0, respectively, using the 8 Å cutoff and 5.4 and 15.9 using 10 Å. Typical experimental values for s in alanine-based peptides like the one investigated here are in the range of 1.5 to 2.0 (Marqusee et al. 1989; Lyu et al. 1990; Rohl et al. 1992), although the lysine residues used to solubilize these peptides appear to contribute to the higher value compared with a value of ∼1 obtained using other background host peptides (Scheraga et al. 2002). The calculated sMD values for the 8 Å trajectory are within the experimentally determined range of values, whereas they are too large for the 10 Å trajectory. With our values of sMD and the average helical contents (θ), we can estimate the macroscopic nucleation parameter, σ, from equation 3b of Zimm and Bragg (1959):
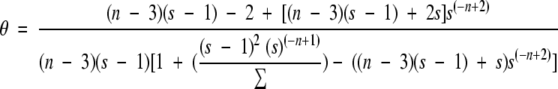 |
Using the hydrogen bond definition of α-helical content, the calculated macroscopic σ was 1.8 × 10−4 and 5.8 × 10−13 using the 8 Å and 10 Å cutoffs, respectively. For the 8 Å trajectory, the values for σ are within the range typically assumed by experimentalists (1 × 10−3 to 1 × 10−5; Marqusee et al. 1989; Lyu et al. 1990; Rohl et al. 1992; Scheraga et al. 2002).
Structural transitions and peptide hydrogen bonding
The local region of conformational space occupied by each residue is shown for α-helical (cyan) and β-structure (red) as a function of time in Figure 4 ▶. There were many conformational transitions throughout the 8 Å cutoff simulation and fewer using the 10 Å cutoff. The most significant loss of α-helical structure occurred from 9.8 to 16.5 nsec and again after 21 nsec using an 8 Å cutoff. These transitions involved numerous residues in the center of the sequence. In addition, large deviations from the helical state occurred near the N terminus: Ala 1, Ala 3, and Ala 4 sampled extended and β-regions of conformational space, which led to the formation of transient β-turns throughout the trajectory (Table 1).
Figure 4.
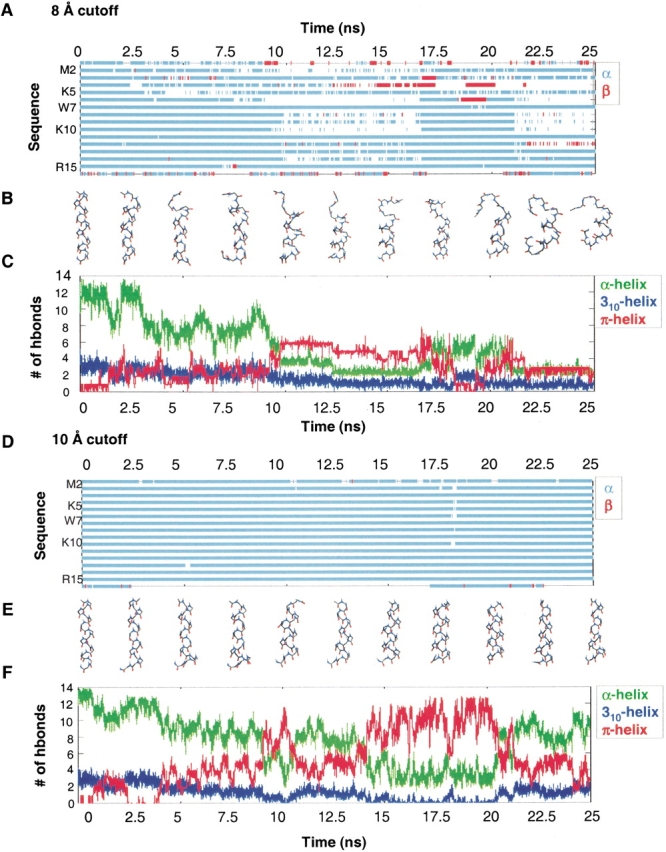
Conformational behavior of the MW peptide. (A) Structural transitions for the 8 Å cutoff simulation shown as a (φξ) conformational space plot for each residue of the peptide. Local α-helical and β-conformations are shown in cyan and in red, respectively, and are based on the corresponding (φξ) regions defined in the text. (B) Representative structures are shown every 2.5 nsec for the 8 Å cutoff simulation. (C) Number of α-, 310-, and π-helical hydrogen bonds (O . . . H distance ≤2.6 Å) for the 8 Å cutoff simulation. (D) Structural transitions for the 10 Å cutoff simulation, as described earlier. (E) Representative structures from the 10 Å cutoff simulation. (F) Number of α-, 310-, and π-helical hydrogen bonds for the 10 Å cutoff simulation.
Table 1.
Percentage of simulation time in which turns were formeda
| Turn residuesb | 8 Å Type I turna (%) | 8 Å Type II turna (%) | 8 Å Most populatedc (nsec) | 10 Å Type I turna (%) | 10 Å Type II turna (%) | 10 Å Most populated (nsec) |
| 1–4 | 60.8 | 35.6 | 1–9 | 88.9 | 26.8 | 1–5, 10–25 |
| αN(2,4) | ||||||
| 2–5 | 58.0 | 36.7 | 10–20 | 10.9 | 14.7 | 16–22 |
| 3–6 | 3.8 | 5.9 | 16–18 | 0.3 | 9.6 | 16–20 |
| 4–7 | 13.3 | 19.4 | 5–10, 17–24 | 0.7 | 5.9 | 1–5 |
| αN(5,7) | ||||||
| 5–8 | 13.5 | 11.6 | 10–17 | 0.1 | 1.5 | 16–20 |
| 6–9 | 0.7 | 1.7 | 4–8 | 0.2 | 1.0 | 16–17 |
| αN(7,9) | ||||||
| 7–10 | 0.7 | 1.3 | 18–20 | 0 | 0 | |
| 8–11 | 0.1 | 0.1 | 20–25 | 0 | 0 | |
| 9–12 | 0 | 0 | 0 | 0 | ||
| 10–13 | 0 | 0 | 0 | 0 | ||
| 11–14 | 0 | 0 | 0 | 0 | ||
| 12–15 | 0 | 0 | 0 | 0 | ||
| 13–16 | 0 | 0 | 0 | 0 |
a The percentage of total simulation time (0–25 nsec) in which specific turns formed. Turn formation was calculated based on the distance separating i and i + 3 Cα atoms, d, and the angle θ formed by the vector connecting the i and i + 1 Cα atoms, Ri, i+1, and that for the i + 2 and i + 3 atoms, Ri+2, i+3 (Kuntz 1972). Using this approach, type I hairpin turns have d ≤ 5.5 Å and θ ≤ 135°. Typically, type I β-turns are defined by the (φξ) angles for the i + 1 and i + 2 residue in the turn: i + 1(φ = 60°, ξ = −30°), i + 2(φ = −90°, ξ = 0°). Type II hairpin turns have either d ≤ 5.5 Å and 135° > θ ≥ 120° or 5.5 Å ≤ d ≤ 6.5 Å and 135° ≥ θ. Type II β-turns are typically defined by i + 1(φ = −60°, ξ = 120°), i + 2(φ = 80°, ξ = 0°).
b Residues involved in turn formation. Turns that may contribute to experimental αN(i, i + 2) NOE cross-peaks are shown.
c The time that the most populated turn was continuously intact.
The total number of 310-, α-, and π-hydrogen bonds over time are shown in Figure 4 ▶. For both simulations, the structures from 0 to 10 nsec were primarily α-helical, and the greatest population of π-helical conformers was from 10 to 20 nsec. Both simulations exhibited major transitions from α → π and π → α, indicating that this transition is reversible on the 25-nsec timescale. The structures from 10 to 20 nsec contained a mixture of 310-, α-, and π-hydrogen bonds, as well as turns (Fig. 4 ▶).
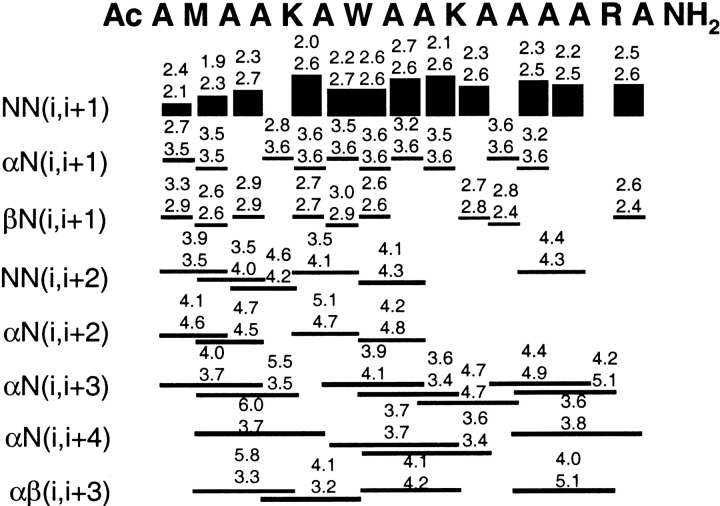
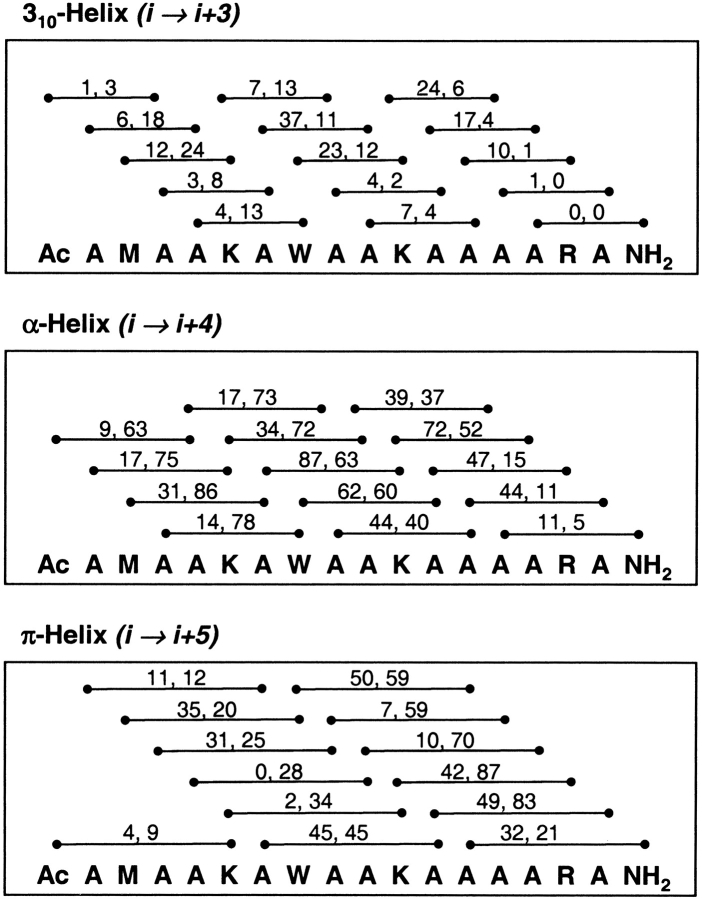
Figure 5 ▶ displays the percentage of total simulation time that hydrogen bonds were satisfied (O . . . H distance ≤2.6 Å) for every possible 310, α-, and π-hydrogen bond in the sequence in both simulations. For the 8 Å cutoff, 310-hydrogen bonding had the lowest population with 1.6 ± 1.5 hydrogen bonds, or 16% of the hydrogen bonds made by the peptide. This was followed by π-hydrogen bonding (3.2 ± 1.5, or 30% of the hydrogen bonds) and α-helical hydrogen bonding (5.4 ± 1.9 or 41%). For the 10 Å cutoff, 310-hydrogen bonding had the lowest population with 1.3 ± 1.5 hydrogen bonds, or 16% of the total hydrogen bonds made. This was followed by π- (5.5 ± 1.5, or 40% of the hydrogen bonds) and α-helical hydrogen bonding (7.4 ± 1.9 or 53%). Thus, both the 8 Å and 10 Å simulations had a lower population of 310- than π-helix.
Figure 5.
Diagram of possible 310-, α-, and π-hydrogen bonds for the MW peptide. Above each possible hydrogen bond is the percentage of simulation time (averaged over 1–25 nsec) that it was intact (O . . . HN distance ≤2.6 Å) during the 8 Å (on the left) and 10 Å (on the right) cutoff simulation. Each hydrogen bond reflects the percentage of the time that it satisfies the distance criterion, regardless of bifurcation with other peptide donors/acceptors. Using a more stringent hydrogen bonding definition including both distance (O . . . HN distance ≤2.6 Å) and angular cutoffs (O . . . H-N angle within 45° of linearity) significantly lowered the calculated population of i → i + 3 hydrogen bonds observed per structure. When the angular constraint was applied, for the 8 Å cutoff simulation the average number of i → i + 3 hydrogen bonds decreased from 1.6 (using the distance criterion alone) to <0.1 hydrogen bonds per structure. For the 10 Å cutoff simulation, the average number of i → i + 3 hydrogen bonds decreased from 1.3 (using the distance criterion alone) to <0.1 hydrogen bonds per structure. This large difference is because the distribution of 310-hydrogen bond angles (O . . . HN) was broader, with the average bond angle falling in the range of 50°–60° from linearity. Because the average 310-hydrogen bond angle was larger than the 45° angular cutoff criteria, applying the angular cutoff for 310-hydrogen bonding discards an unacceptable number of energetically important 310-hydrogen bonds. Both the π- and α-hydrogen bond angles were much more linear on average.
Most of the occurrences of 310-helix were isolated, with only one i → i + 3 hydrogen bond in the peptide. The largest number of 310-hydrogen bonds at any given time was 8, and this was observed in <0.01% of the structures. The vast majority of the i → i + 3 hydrogen bonds were bifurcated with adjacent (i → i + 4) α-helical hydrogen bonds. The formation of isolated and sequential 310/α-bifurcated hydrogen bonds occurred throughout the sequence. All of the contiguous 310-hydrogen bonded structures contained bifurcated hydrogen bonds.
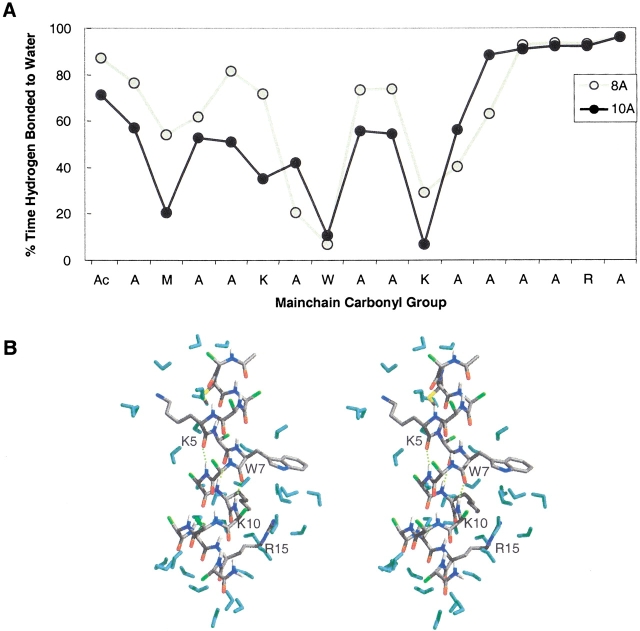
The peptide bonds not only formed intramolecular hydrogen bonds, but they also interacted with solvent (Fig. 6 ▶), particularly when they were not involved in bifurcated hydrogen bonds. In general, the main chain carbonyl groups of the large and bulky residues interacted less with solvent than did the alanines. In the final snapshot from the 10 Å simulation, various forms of side chain shielding of the main chain are illustrated (Fig. 6B ▶). In the case of Lys 5, its side chain projects into solution, whereas the much smaller Ala 8 and 9 appear to keep water at bay. Solvation of the Trp 7 side chain diverts waters from its main chain. The side chain of Arg 15 does not shield its own carbonyl, but by laying down on the helix, it helps to shield residues upstream.
Figure 6.
Peptide interactions with water. (A) Percentage of time that main chain carbonyl groups formed hydrogen bonds with water. Hydrogen bonds were based on a 2.6 Å distance cutoff and 45° angular cutoff. (B) Stereoview of the 10-nsec snapshot from the 10 Å cutoff simulation showing different mechanisms of side chain shielding of the peptide bond from water.
Mechanism of the α → π transition
For both the 8 Å and 10 Å cutoff simulations, the total number of main chain hydrogen bonds was roughly constant throughout the α → π transition, although the number of hydrophobic contacts (nonpolar carbon distances ≤5.4 Å) increased by ∼5–10. This finding indicates that interactions between hydrophobic side chains contribute to the formation of the π-helix. The side chains that became more buried on π-helix formation were similar in the two simulations: Met3, Trp 7, Ala 8, Lys 10, Ala 1l, Ala 13, Arg 15, and Ala 16.
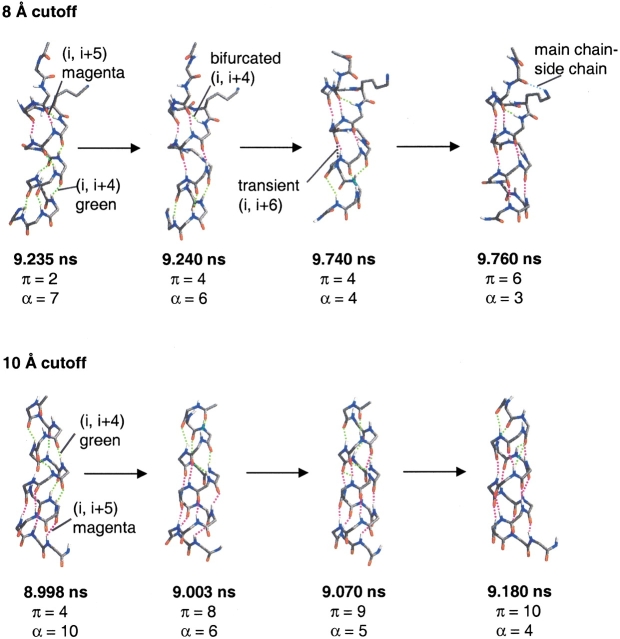
For the 8 Å cutoff simulation, the most dramatic transition between α- and π-helix occurred from 9.2 to 9.7 nsec (Fig. 7 ▶). The structure at 9.235 nsec had two π (i → i + 5) hydrogen bonds and a turn comprising residues 3–6. From 9.235 to 9.24 nsec, two α-helical hydrogen bonds (Ala 6/Lys 10 and Trp 7/Ala 11) broke and reformed as π-hydrogen bonds (Ala 6/Ala 11 and Trp 7/Ala 12). From 9.24 to 9.74 nsec, the structures remained fairly stable with four π-hydrogen bonds and transient bifurcated i → i + 6 hydrogen bonds. Then, two α-helical hydrogen bonds (Lys 10/Ala 14 and Ala 11/Arg 15) broke and reformed as π-hydrogen bonds (Lys 10/Arg 15 and Ala 11/Ala 16). The bifurcation of both 310- and π-hydrogen bonds with α-helical hydrogen bonds was important for the formation and stability of the mixed α/π ensemble.
Figure 7.
Four representative structures during the α → π transition show the propagation of π-helical hydrogen bonds for the 8 Å and 10 Å cutoff simulations. π-Helical hydrogen bonds are shown in magenta and α-helical hydrogen bonds are shown in green. The main chain–side chain hydrogen bond between Ala 1 and Lys 5 is shown in blue for the 8 Å cutoff simulation. The number of hydrogen bonds is given below each structure.
For the 10 Å cutoff simulation, the most dramatic transition between α- and π-helix occurred from 8.9 to 9.1 nsec (Fig. 7 ▶). The 8 Å cutoff simulation initially formed π-helix at the N terminus and propagated toward the C terminus, whereas the opposite was true for the 10 Å cutoff. In both simulations, when there were contiguous π-helix hydrogen bonds, the average π-helix (φξ) angles (−76°, −52°) of the intervening residues were in agreement with the average angles found in the Protein Data Bank (−76°, −41°; Weaver 2000; Fodje and Al-Karadaghi 2002). We note that these are different from the old theoretical π-helix (φξ) angles (−57°, −70°; Low and Grenville-Wells 1953; Ramachandran and Sasisekharan 1968). In addition to π-helical conformations, there were also a number of Schellman-like conformations (Schellman 1980; Gunasekaran et al. 1998) over the C-terminal residues 11–16. These structures formed hydrogen bonds between residues 11 and 16 and 12 to 15, and residue 16 was in the αL-conformation. These Schellman-like conformations were transient.
Importance of main chain–side chain hydrogen bonding
In the 8 Å cutoff simulation, a hydrogen bond between the N-terminal cap, Ace, and Lys 5 was the dominant main chain–side chain (mc–sc) hydrogen bond. This hydrogen bond was intact before (9.053–9.057 nsec), during (9.265–9.267, 9.376–9.393, 9.478–9.634 nsec), and after (9.801–9.829, 9.846–9.856 nsec) the α → π transition (9.235–9.760 nsec) shown in Figure 7 ▶. This interaction played a significant role in stabilizing the formation of π-helical structure, as well as assisting in the formation of the first two π-hydrogen bonds by restricting the conformational space available to the chain. After these π-hydrogen bonds formed, the Ace/Lys 5 interaction facilitated the dihedral transition of Ala 1 out of the β-region, resulting in the formation of the next two π-hydrogen bonds (Fig. 7 ▶).
In a similar manner, a hydrogen bond between Ace and Trp 7 stabilized a structural transition from mixed α/π-helix into α-helix and turn structures around 18.5 nsec in the 8 Å cutoff simulation. This hydrogen bond stabilized the structures both before (17.979–17.98 nsec) and after (18.562–18.582 nsec) the transition. In addition, this interaction stabilized the turns over residues 4–7 and residues 5–8. Similar interactions and transitions were observed using the 10 Å cutoff (Fig. 7 ▶).
The effect of changing the nonbonded cutoff on energetics
Up to this point we have focused on the peptide’s structural properties. Although these two simulations are in reasonable agreement with the CD and NMR data, the 10 Å cutoff simulation is in poor agreement with the calculated Zimm-Bragg helix-coil parameters, and it shows slower helix-coil transitions than the 8 Å cutoff. We have investigated the effects of changing the cutoff on the energetics, particularly because a priori one would expect the longer cutoff range of 10 Å to be in better agreement with experiment.
For the entire system, the average protein–protein, protein–water, and water–water energies were compared for the first nanosecond of the 8 Å and 10 Å cutoff simulations (Table 2), because during this time period the two trajectories were the most similar with respect to peptide conformation. The greatest relative changes in energy going from an 8 Å to a 10 Å cutoff were the protein–protein and the protein–water van der Waals interactions (Table 2), which both contribute to slower transitions in the 10 Å cutoff simulation. The reason for this is that the repulsive van der Waals term is scaled as a function of cutoff distance to compensate for the attractive interactions lost on truncation (Levitt et al. 1997). Values of 0.84 and 0.92 are used for 8 Å and 10 Å, respectively. In this way, sterically hindered transitions between conformational states are discouraged less with the 8 Å cutoff.
Table 2.
Average nonbonded interaction energies
| Interaction typesa | 〈∑ijUij〉 8 Å (kcal/mole) | 〈∑ijUij〉 10 Å (kcal/mole) |
| P..P (vdw) | −40.0 | −73.1 |
| P..P (els) | −75.0 | −85.6 |
| P..W (vdw) | −5.1 | −58.4 |
| P..W (els) | −293.1 | −348.6 |
| W..W (vdw) | 2870.3 | 3682.8 |
| W..W (els) | −15888.3 | −23310.3 |
| Total (vdw) | 2825.4 | 3551.5 |
| Total (els) | −16256.0 | −23544.5 |
a Van der Waals (vdw) and electrostatic (els) contributions to the potential energy of protein–protein (P..P), protein–water (P..W), and water–water (W..W) interactions, and the total potential energy of the system.
A unique feature of our force-shifted potential is that hydrogen bond energies are invariant of cutoff within the cutoff range (Levitt et al. 1995). The potential energy pairwise sum of all atoms involved in protein–protein and protein–water hydrogen bonds change <5% between an 8 Å and a 10 Å cutoff. This was also true for the water–water hydrogen bond energies. The pairwise sum of nonpolar peptide–water contacts showed significantly larger shifts (∼20%–30%) in interaction energy between an 8 Å and a 10 Å cutoff. Spatial decomposition of these pairwise sums showed, in general, that, although the additional 2 Å spherical shell adds many interactions to the sum, they comprise a small percentage of the total pairwise sum compared with the shifted short (0–4 Å) and medium-range (4–6 Å) interactions. The shifts in the short-range repulsive van der Waals interactions were the most significant contributions to the slower transitions in the 10 Å cutoff simulation.
Discussion
Recent temperature-jump experiments have shown that the kinetics of helix formation tend to be single exponential or multiphasic with a fast phase of τ = 10–20 nsec, which is thought to represent helix propagation and fraying, and a slower phase (τ = 130–300 nsec), which appears to represent helix nucleation (Williams et al. 1996; Gilmanshin et al. 1997; Thompson et al. 1997; Huang et al. 2001a,b, 2002; Werner et al. 2002). The bulk of the experimental studies show an increase in the relaxation rate with temperature indicative of an activation barrier for folding and unfolding. However, some recent simulation studies (Hummer et al. 2000, 2001) have indicated that helix formation kinetics can be modeled as a diffusive conformational search within the coil state with no barrier for the transition to the helical state. Such a process predicts a departure from single-exponential to nonexponential or stretched-exponential relaxation kinetics in temperature-jump experiments, which is rare but has been reported in some experimental studies (Sabelko et al 1999; Leeson et al. 2000; Huang et al. 2002). However, Ferguson and Fersht (2003) recently pointed out that these stretched-exponential kinetics occur on a timescale that poses problems for the instrumentation. If this is the case, such results could be artifacts, and they note that nonexponential kinetics have disappeared when they have removed all artifacts. They also point out that the kinetic data can be fit within experimental error to a series of sequential or parallel exponentials.
Alternatively, rather than barrierless folding, such kinetics, if free from artifact, could be due to heterogeneity of the nonhelical/coil state. In this regard, our results for both simulations indicate that π-helical intermediates may contribute to the roughness of the free energy landscape of helical peptides. Nevertheless, even though our molecular dynamics simulations are fairly long compared with other simulation studies, the 25-nsec simulation period is an insufficient amount of time for crossover from the coil to the helical state. Consequently, we focus on structural properties of the helix → coil process.
Although our 8 Å and 10 Å cutoff simulations were similar overall with respect to their ability to model the NMR results, the peptide sampled many fewer nonhelical conformations using the longer cutoff. This leads to disparities between the s and σ parameters associated with helix-coil theory. The values determined from the 8 Å simulation, however, are in good agreement with experiment. Using the 10 Å cutoff, the peptide appears to be artificially stabilized in the helical state at this timescale. It is possible, however, that this is nothing more than a sampling problem and that the simulations would converge with increasing simulation time, and, in fact, the two simulations are similar if other properties are considered (such as hydrogen bonds). We note that the proper timescale and amplitude of motion was obtained in simulations of barstar using the 10 Å cutoff as assessed by comparison with the results of NMR relaxation experiments (Wong and Daggett 1998). The differences observed here are mainly due to shifts in short-range interactions, rather than the effects of long-range electrostatic interactions. For the purposes of seeing interesting conformational behavior on a reasonable timescale by MD, the 8 Å cutoff simulations are preferred for this system. However, the longer time required for equilibration and the effect on the barrier to conformational transitions for our methods using a 10 Å cutoff may in fact be correct. Future studies will involve the calibration of our van der Waals’ screening term to reproduce timescales being determined by fast IR measurements on labeled peptides (W. DeGrado and F. Gai, pers. comm.). In addition, we note that unfolding times from MD simulations of the engrailed homeodomain are in good agreement with temperature-jump experiments (Mayor et al. 2003).
Nonetheless, it is important to remember that force fields are empirically derived, contain many interrelated terms, and are parameterized with specific characteristics in mind. In this way, increasing a cutoff does not always result in the naïve, expected effect. Furthermore, we show that shorter cutoffs can not only be adequate, but can be better than a longer cutoff. The relative interplay of force-field terms and the many ways in which nonbonded interactions can be truncated make generalizations like those popularized by Schreiber and Steinhauser (1992a,b), who assert that simulations using short cutoffs are unstable and ultimately wrong, unsound. Although this may have been true for their force field and methods, we have repeated their work and do not obtain the same results with our force field and protocols (D.A.C. Beck, in prep.).
Turns versus contiguous 310-helix: Interpretation of αN (i,i + 2) connectivities
A low population of i → i + 3 hydrogen bonds (<20%) was observed throughout the 8 Å cutoff simulation. No one of the structures contained two contiguous unbifurcated i → i + 3 hydrogen bonds. Instead, the i → i + 3 hydrogen bonds were bifurcated or merely turns. In the latter part of the simulation (after 10 nsec), prolonged turn formation was only observed for residues 1–4, 2–5, and 5–8. Simultaneous turn formation separated by several residues was more common than contiguous turns (note that a 310-helix is structurally equivalent to two consecutive type I β-turns). These bifurcated 310/α-helical hydrogen bonding patterns and the formation of turns is in good agreement with other simulations of helical peptides (Soman et al. 1991; Daggett and Levitt 1992; Topol et al. 2001).
The experimental αN(i,i + 2) NOE connectivities are on the N-terminal side of the MW peptide, as those beyond residue 7 are obscured by much stronger αN(i,i + 3) cross-peaks (Millhauser et al. 1997). In our 8 Å cutoff simulation, we observed significant turn formation only on the N-terminal side of the peptide from residues 1–9, in agreement with the αN(i,i + 2) NOEs. The most C-terminal αN(i,i + 2) NOE is αN(7,9), and it was never violated during the simulation (average value of 4.3 Å); in fact, it had its lowest instantaneous values from 10 to 16 nsec in the α/π mixed ensemble.
Although there were fewer 310-hydrogen bonds compared with π- and α-hydrogen bonds on average in a structure (16%, 30%, and 54%, respectively), bifurcated 310-helical hydrogen bonds were fairly evenly distributed throughout the sequence. Based on the interpretation of NOE volume integrals Iαβ(i,i + 3)/IαN(i,i + 3), Millhauser and coworkers suggest that small amounts of 310-helix form along the sequence and that they are populated to a greater extent at the N and C termini (Millhauser et al. 1997).
Role of main chain–side chain hydrogen bonding in structural transitions
Both mc–sc and i → i + 3 hydrogen bonding formed transiently during structural transitions. However, the major transitions in the simulation were mediated through mc–sc hydrogen bonding, which can explain how local side chain interactions dominate local conformational preferences. Main chain–side chain hydrogen bonding, such as helical N-capping interactions, can restrict conformational space between the residues in contact, and these restrictions have been proposed to assist in the nucleation of more stable structure (Presta and Rose 1988; Karpen et al. 1992). In a recent example, mc-sc hydrogen bonding between a threonine and a carbonyl group four residues before it in the sequence leads to a shift from α-helical structure to mixed 310/α/π-helical conformations, as assessed by MD simulations and NMR and IR experiments on a designed helical bundle protein (Walsh et al. 2003).
The experimental 3JHNα coupling constants for the MW peptide reflect systematically higher values (>6 Hz) for the longer i → i + 5 spaced side chains. Millhauser and coworkers (1997) suggest that this is because local folding/unfolding originates at the positions of the longer side chains, which is consistent with transitions observed via MD (for example, see Fig. 7 ▶). Both side chain mediated unfolding and the existence of π-helical intermediates can contribute to this i → i + 5 experimental trend in 3JHNα.
The MW peptide is a variant of canonical alanine-based peptides (AAAAK)n, and Shirley and Brooks (1997) have also observed formation of π-helical structure in (AAKAA)3 and (AAQAA)3 peptides. Related repeating sequences (AAQA), (AAQAAA), and (AAQ) were also studied, and they concluded that i → i + 5 interactions between side chains promoted π-helical structure formation. Similar α → π transitions were observed in a more complicated Ala-based peptide by Lee and coworkers (2000). In this case, π-helix seems to have been triggered by repulsive interactions between i → i + 3 spaced Glu residues, which after conversion show a 3 Å increase in the distance between their carboxylates. Both of these other MD studies were performed using CHARMM with a force-shifted potential, and a 10 Å to 12 Å cutoff range (Brooks et al. 1983). Despite differences in the integration method used, the cutoffs, the water models, and the sequences, both the CHARMM and ENCAD potential functions support the formation of π-helical structure, and the π-helical structure was stabilized significantly by side chain interactions.
Garcia and Sanbonmatsu (2002) have suggested that mc–sc hydrogen bonds contribute to the stabilization of α-helical structure. Our simulations showed similar results for interactions between Lys or Trp and the main chain of the C-terminal capping group, but, in general, rather than stabilizing α-helical conformations, our results indicate that these interactions facilitate structural transitions to and from nonhelical and π-helical states. The main chain carbonyl groups of Met, Trp, and Lys showed less hydrogen bonding with water compared with the Ala residues across the sequence. Furthermore, there was a tendency for Ala to be less hydrated when following a Lys residue (Fig. 6 ▶). This result is consistent with simulation studies of Scheraga and coworkers (2002), who find that solvation of Lys side chains decreases the solvation of the neighboring main chain groups. Side chain shielding of the main chain from hydrogen bonding with, and attack by, solvent may contribute more to α-helix stability than side chain-to-main chain hydrogen bonding, but water was still effective at reaching and interacting with carbonyl groups near lysine residues in our simulations and such interactions do not appear to be helix destabilizing per se in our simulations.
Comparison of 310-hydrogen bonding in simulations of peptides and proteins
Although we observed 310-hydrogen bonding in the simulations, these hydrogen bonds had lower populations than α- and π-hydrogen bonds and they did not play a dominant role in unfolding/refolding events. Therefore, the question remains as to why there are so many 310- helices in experimentally determined protein structure. It is possible that our simulations are underestimating the 310-helical content, or that force fields in general may be energetically biased against i → i + 3 hydrogen bonding arrangements. To test this idea, G. Millhauser (pers. comm.) suggested that we perform a simulation of the leucine-rich repeat variant, which is a protein with a high percentage of 310-helix (Peters et al. 1996). Only the repeat domain (residues 41–231) was used, which is composed of a 24-residue tandem repeat pattern of α-helix, turn, and 310-helix. In a 3-nsec simulation of this domain at 298 K, using the same 8 Å nonbonded cutoff, the protein retained the majority of its 310-helical hydrogen bonds. Thus, the low population of 310-helix in our simulations of the MW peptide does not appear to be an artifact (data not shown). Many of these 310-helical hydrogen bonds were stabilized by side chain-to-main chain hydrogen bonds that have been described as supporting 310-helical structure (Karpen et al. 1992). Recent quantum mechanical studies indicate that 310-helical structure is more stable in vacuo than in water (Topol et al. 2001), indicating that there may be a shift from 310 to α-helical structure in solution.
Conclusions
We conclude that both the 8 Å and 10 Å cutoff simulations are in reasonable agreement with the helix content of the MW peptide as assessed experimentally by CD, the 3JHNα coupling constants, and the NOEs. Both the 8 Å and 10 Å cutoff simulations underwent structural transitions between α-helix, 310-helix, and π-helix, and both simulations exhibited a large population of π-helix. However, the 8 Å cutoff is in better agreement with calculated Zimm-Bragg parameters and the CD data, and unfolds to more nonhelical conformers. Consequently, our results for the MW peptide show that short cutoffs can be not only reasonable, but can also be in better agreement with experiment than longer cutoffs. Our results indicate that both N-terminal 310-helical structure and turns contribute to the observed αN(i,i + 2) NOEs. Furthermore, the simulations indicate that contiguous 310-helix is not populated appreciably without bifurcation involving simultaneous i → i + 4 interactions. 310-Hydrogen bonds were involved in helix-coil transitions, as suggested by Millhauser and coworkers (1997), but the π-hydrogen bonds were more important in this regard. The major structural transitions in the simulations were nucleated by transient mc–sc hydrogen bonding and hydrophobic interactions between side chains. This type of side chain-assisted helix formation and destruction may explain the apparent sequence dependence of π-helix formation in peptides with i → i + 5 spaced side chains, as well as the specific side chain interactions that stabilize 310-helical structure in proteins.
Materials and methods
All energy minimization and molecular dynamics was performed using an in-house version of the program ENCAD (Levitt 1990). An all-atom representation was used for both the peptide and the water, using a previously described macromolecular potential function with a force-shifted atom-based truncation method (Levitt et al. 1995), and the flexible F3C water model (Levitt et al. 1997).
The 16-residue MW peptide was generated to have ideal helical φ and ξ angles (−57°, −47°, respectively), the N terminus was acetylated, and the C terminus was amidated. The peptide was minimized 500 steps in vacuo. Two different simulations were performed of the MW peptide using 8 Å and 10 Å cutoffs, each for 25 nsec of simulation time. For the 8 Å cutoff simulation, the peptide was then solvated by adding waters extending at least 8 Å, resulting in the addition of 1142 water molecules. For the 10 Å cutoff simulation, the peptide was solvated by adding waters extending at least 10 Å, resulting in the addition of 1670 water molecules. Structures were saved every 0.2 psec for analysis, resulting in 125,000 structures for each 25-nsec simulation.
The box volume was adjusted to give the experimental density of 0.997 g/mL for 298 K (Kell 1967). The solvent was prepared for molecular dynamics by performing 2000 cycles of minimization, followed by 2000 cycles of molecular dynamics, and another 2000 steps of minimization. The peptide was then minimized for 500 steps, followed by the minimization of the entire system for 500 steps. The system was then brought to the target temperature of 298 K. MD simulations were performed using the microcanonical ensemble (NVE) and periodic boundary conditions. The equations of motion were integrated using a modified Beeman algorithm and a 2-fsec time step (Levitt et al. 1995). The nonbonded lists were updated every 2 steps (4 fsec), and structures were saved every 0.2 psec for analysis.
Acknowledgments
We are grateful for financial support provided by a research grant from the National Institutes of Health (GM 50789 to V.D.) and a Molecular Biophysics Training Grant (National Research Service Award T32 GM 08268 to R.A). We thank Drs. Glenn Millhauser and Bill DeGrado for stimulating discussions.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked "advertisement" in accordance with 18 USC section 1734 solely to indicate this fact.
Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.0240103.
References
- Barlow, D.J. and Thornton, J.M. 1988. Helix geometry in proteins. J. Mol. Biol. 201 601–619. [DOI] [PubMed] [Google Scholar]
- Bradley, E.K., Thomason, J.F., Cohen, F.E., Kosen, P.A., and Kuntz, I.D. 1990. Studies of synthetic helical peptides using circular dichroism and nuclear magnetic resonance. J. Mol. Biol. 215 607–622. [DOI] [PubMed] [Google Scholar]
- Brooks, B.R., Bruccoleri, R.E., Olafson, B.D., States, D.J., Swaminathan, S., and Karplus, M. 1983. CHARMM—A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4 187–217. [Google Scholar]
- Chakrabartty, A., Kortemme, T., Padmanabhan, S., and Baldwin, R.L. 1993. Aromatic side-chain contribution to far-ultraviolet circular dichroism of helical peptides and its effect on measurements of helix propensities. Biochemistry 32 5560–5565. [DOI] [PubMed] [Google Scholar]
- Chandrasekhar, K., Profy, A.T., and Dyson, H.J. 1991. Solution conformational preferences of immunogenic peptides derived from the principal neutralizing determinant of the HIV-1 envelope glycoprotein GP 120. Biochemistry 30 9187–9194. [DOI] [PubMed] [Google Scholar]
- Daggett, V. and Levitt, M. 1992. Molecular dynamics simulations of helix denaturation. J. Mol. Biol. 233 1121–1138. [DOI] [PubMed] [Google Scholar]
- Daggett, V., Kollman, P.A., and Kuntz, ID. 1991. A molecular dynamics simulation of polyalanine—An analysis of equilibrium motions and helix-coil transitions. Biopolymers 31 1115–1134. [DOI] [PubMed] [Google Scholar]
- Ferguson, N. and Fersht, A.R. 2003. Early events in protein folding. Curr. Opin. Struct. Biol. 13 75–81. [DOI] [PubMed] [Google Scholar]
- Fiori, W.R., Miick, S.M., and Millhauser, G.L. 1993. Increasing sequence length favors α-helix over 3(10)-helix in alanine-based peptides: Evidence for a length-dependent structural transition. Biochemistry 32 11957–11962. [DOI] [PubMed] [Google Scholar]
- Fiori, W.R., Lundberg, K.M., and Millhauser, G.L. 1994. A single carboxy-terminal arginine determines the amino-terminal helix conformation of an alanine-based peptide. Nat. Struct. Biol. 1 374–377. [DOI] [PubMed] [Google Scholar]
- Fodje, M.N. and Al-Karadaghi, S. 2002. Occurrence, conformational features and amino acid propensities for the π-helix. Protein Eng. 15 353–358. [DOI] [PubMed] [Google Scholar]
- Gans, P.J., Lyu, P.C., Manning, M.C., Woody, R.W., and Kallenbach, N.R. 1991. The helix-coil transition in heterogeneous peptides with specific side-chain interactions: Theory and comparison with CD spectral data. Biopolymers 31 1605–1614. [DOI] [PubMed] [Google Scholar]
- Garcia, A.E. and Sanbonmatsu, K.Y. 2002. α-Helical stabilization by side chain shielding of backbone hydrogen bonds. Proc. Natl. Acad. Sci. 99 2782–2787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmanshin, R., Williams, S., Callender, R.H., Woodruff, W.H., and Dyer, R.B. 1997. Fast events in protein folding: Relaxation dynamics of secondary and tertiary structure in native apomyoglobin. Proc. Natl. Acad. Sci. 94 3709–3713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gratias, R., Konat, R., Kessler, H., Crisma, M., Valle, G., Polese, A., Formaggio, F., Toniolo, C., Broxterman, Q.B., and Kamphuis, J. 1998. First step toward the quantitative identification of peptide 3(10)-helix conformation with NMR spectroscopy: NMR and X-ray diffraction structural analysis of a fully developed 3(10)-helical peptide standard. J. Am. Chem. Soc. 120 4763–4770. [Google Scholar]
- Gunasekaran, K., Nagarajaram, H.A., Ramakrishnan, C., and Balaram, P. 1998. Stereochemical punctuation marks in protein structures: Glycine and proline containing helix stop signals. J. Mol. Biol. 275 917–932. [DOI] [PubMed] [Google Scholar]
- Huang, C.Y., Klemke, J.W., Getahun, Z., DeGrado, W.F., and Gai, F. 2001a. Temperature-dependent helix-coil transition of an alanine based peptide. J. Am. Chem. Soc. 123 9235–9238. [DOI] [PubMed] [Google Scholar]
- Huang, C.Y., Getahun, Z., Wang, T., DeGrado, W.F., and Gai, F. 2001b. Time-resolved infrared study of the helix-coil transition using (13)C-labeled helical peptides. J. Am. Chem. Soc. 123 12111–12112. [DOI] [PubMed] [Google Scholar]
- Huang, C.Y., Getahun, Z., Zhu, Y., Klemke, J.W., DeGrado, W.F., and Gai, F. 2002. Helix formation via conformation diffusion search. Proc. Natl. Acad. Sci. 99 2788–2793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hummer, G., Garcia, A.E., and Garde, S. 2000. Conformational diffusion and helix formation kinetics. Physical Rev. Lett. 85 2637–2640. [DOI] [PubMed] [Google Scholar]
- ———. 2001. Helix nucleation kinetics from molecular simulations in explicit solvent. Proteins 42 77–84. [PubMed] [Google Scholar]
- Karle, I.L. and Balaram, P. 1990. Structural characteristics of α-helical peptide molecules containing AIB residues. Biochemistry 29 6747–6756. [DOI] [PubMed] [Google Scholar]
- Karpen, M.E., Haseth, P.L., and Neet, K.E. 1992. Differences in the amino-acid distributions of 3(10) helices and α-helices. Protein Sci. 1 1333–1342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karplus, M. 1959. Contact electron-spin coupling of nuclear magnetic moments. J. Chem. Phys. 30 11–15. [Google Scholar]
- Kell, G.S. 1967. Precise representation of volume properties of water at one atmosphere. J. Chem. Eng. Data 12 66–69. [Google Scholar]
- Kuntz, I.D. 1972. Protein folding. J. Am. Chem. Soc. 94 4009–4012. [DOI] [PubMed] [Google Scholar]
- Lee, K.H., Benson, D.R., and Kuczera, K. 2000. Transitions from α to π helix observed in molecular dynamics simulations of synthetic peptides. Biochemistry 39 13737–13747. [DOI] [PubMed] [Google Scholar]
- Leeson, D.T., Gai, F., Rodriguez, H.M., Gregoret, L.M., and Dyer, R.B. 2000. Protein folding and unfolding on a complex energy landscape. Proc. Natl. Acad. Sci. 97 2527–2532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitt, M. 1990. ENCAD (computer program). Energy Calculations and Dynamics, Molecular Applications group, Palo Alto, CA and Yeda, Rehovot, Israel.
- Levitt, M., Hirshberg, M., Sharon, R., and Daggett, V. 1995. Potential-energy function and parameters for simulations of the molecular dynamics of proteins and nucleic acids in solution. Comput. Phys. Commun. 91 215–231. [Google Scholar]
- Levitt, M., Hirshberg, M., Sharon, R., Laidig, K.E., and Daggett, V. 1997. Calibrating and testing a water model for simulation of the molecular dynamics of proteins and nucleic acids in solution. J. Phys. Chem. B 101 5051–5061. [Google Scholar]
- Low, B.W. and Grenville-Wells, H.J. 1953. Generalized mathematical relations for polypeptide chain helixes. The coordinates for the π helix. Proc. Natl. Acad. Sci. 39 785–801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyu, P.C., Liff, M.I., Marky, L.A., and Kallenbach, N.R. 1990. Side chain contributions to the stability of α-helical structure in peptides. Science 250 669–673. [DOI] [PubMed] [Google Scholar]
- Marqusee, S., Robbins, V.H., and Baldwin, R.L. 1989. Unusually stable helix formation in short alanine-based peptides. Proc. Natl. Acad. Sci. 86 5286–5290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayor, M., Guydosh, N.R., Johnson, C.M., Grossmann, J.G., Sato, S., Jas, G.S., Freund, S.M.V., Alonso, D.O.V., Daggett, V., and Fersht, A.R. 2003. The complete folding pathway of a protein from nanoseconds to microseconds. Nature 421 863–867. [DOI] [PubMed] [Google Scholar]
- Merutka, G., Morikis, D., Brushweiler, R., and Wright, P.E. 1993. NMR evidence for multiple conformations in a highly helical model peptide. Biochemistry 32 13089–13097. [DOI] [PubMed] [Google Scholar]
- Miick, S.M., Casteel, K.M., and Millhauser, G.L. 1993. Experimental molecular dynamics of an alanine-based helical peptide determined by spin label electron spin resonance. Biochemistry 31 8014–8021. [DOI] [PubMed] [Google Scholar]
- Millhauser, G.L. 1995. Views of helical peptides: A proposal for the position of 3(10)-helix along the thermodynamic folding pathway. Biochemistry 34 3873–3877. [DOI] [PubMed] [Google Scholar]
- Millhauser, G.L., Stenland, C.J., Bolin, K.A., and van de Ven, F.J.M. 1996. Local helix content in alanine-rich peptide as determined by the compete set of (3)J(HN α) coupling constants. J. Biomol. NMR 7 331–334. [DOI] [PubMed] [Google Scholar]
- Millhauser, G.L., Stenland, C.J., Hanson, P., Bolin, K.A., and van de Ven F.J.M. 1997. Estimating the relative populations of 3(10)-helix and α-helix in Ala-rich peptides: A hydrogen exchange and high field NMR study. J. Mol. Biol. 267 963–974. [DOI] [PubMed] [Google Scholar]
- Osterhout, J.J., Baldwin, R.L., York, E.J., Stewart, J.M., Dyson, H.J., and Wright, P.E. 1989. 1-H NMR studies of the solution conformations of an analog of the C-peptide of ribonuclease A. Biochemistry 28 7059–7064. [DOI] [PubMed] [Google Scholar]
- Peters, J.W., Stowell, M.H., and Rees, D.C. 1996. A leucine-rich repeat variant with a novel repetitive protein structural motif. Nat. Struct. Biol. 3 991–994. [DOI] [PubMed] [Google Scholar]
- Presta, L.G. and Rose, G.D. 1988. Helix signals in proteins. Science 240 1632–1641. [DOI] [PubMed] [Google Scholar]
- Ramachandran, G.N. and Sasisekharan, V. 1968. Conformations of polypeptides and proteins. Adv. Protein Chem. 23 283–438. [DOI] [PubMed] [Google Scholar]
- Richardson, J.S. and Richardson, D.C. 1988. Amino-acid preferences for specific locations at the ends of α-helices. Science 240 1648–1652. [DOI] [PubMed] [Google Scholar]
- Rohl C.A. and Doig A.J. 1996. Models for the 3(10)-helix/coil, pi-helix/coil, and α-helix/3(10)-helix/coil transitions in isolated peptides. Protein Sci. 5 1687–1696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohl, C.A., Scholtz, J.M., York, E.J., Stewart, J.M., and Baldwin, R.L. 1992. Kinetics of amide proton exchange in helical peptides of varing chain lengths. Interpretation by the Lifson-Roig equation. Biochemistry 31 1263–1269. [DOI] [PubMed] [Google Scholar]
- Sabelko, J., Ervin, J., and Gruebele, M. 1999. Observation of strange kinetics in protein folding. Proc. Natl. Acad. Sci. 96 6031–6036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schellman, C. 1980. The αL-conformation at the end of helices. In Protein folding (ed. R. Jaenicke), pp. 53–61. Elsevier, New York.
- Scheraga, H.A., Vila, J.A., and Ripoll, D.R. 2002. Helix-coil transitions re-visited. Biophys. Chem. 101–102 255–265. [DOI] [PubMed] [Google Scholar]
- Schreiber, H. and Steinhauser, O. 1992a. Cutoff size does strongly influence molecular dynamics results on solvated polypeptides. Biochemistry 31 5856–5860. [DOI] [PubMed] [Google Scholar]
- ———. 1992b. Molecular dynamics studies of solvated polypeptides: Why the cutoff scheme does not work. Chem. Phys. 168 75–89. [Google Scholar]
- Sheinerman, F.B. and Brooks, C.L. 1995. 3(10)-Helices in peptides and proteins as studied by modified Zimm-Bragg Theory. J. Am. Chem. Soc. 117 10098–10103. [Google Scholar]
- Shirley, W.A. and Brooks, C.L. 1997. Curious structure in "canonical" alanine based peptides. Proteins 28 59–71. [DOI] [PubMed] [Google Scholar]
- Smythe, M.L., Nakaie, C.R., and Marshall, G.R. 1995. α-helical versus 3(10)-helical conformations of alanine-based peptides in aqueous solution—An electron-spin-resonance investigation. J. Am. Chem. Soc. 117 10555–10562. [Google Scholar]
- Soman, K.V., Karimi, A., and Case, D.A. 1991. Unfolding of an α-helix in water. Biopolymers 31 1351–1361. [DOI] [PubMed] [Google Scholar]
- Thompson, P.A., Eaton, W.A., and Hofrichter, J. 1997. Laser temperature jump study of the helix-coil kinetics of an alanine peptide interpreted with a `kinetic zipper’ model. Biochemistry 36 9200–9210. [DOI] [PubMed] [Google Scholar]
- Tirado-Rives, J., Maxwell, D.S., and Jorgensen, W.L. 1993. Molecular dynamics and Monte Carlo simulations favor the α-helical form for alanine-based peptides in water. J. Am. Chem. Soc. 115 11590–11593. [Google Scholar]
- Todd, A.P. and Millhauser, G.L. 1991. ESR spectra reflect local and global mobility in a short spin-labeled peptide throughout the α-helix–coil transition. Biochemistry 30 5515–5523. [DOI] [PubMed] [Google Scholar]
- Topol, I.A., Burt, S.K., Deretey, E., Tang, T.H., Perczel, A., Rashin, A., and Csizmadia, I.G. 2001. α and 3(10)-helix interconversion: A quantum-chemical study on polyalanine systems in the gas phase and in aqueous solvent. J. Am. Chem. Soc. 123 6054–6060. [DOI] [PubMed] [Google Scholar]
- Walsh, S.T.R., Cheng, R.P., Wright, W.W., Alonso, D.O.V., Daggett, V., Vanderkooi, J.M., and DeGrado, W.F. 2003. The hydration of amides in helices: A comprehensive picture from molecular dynamics, IR, and NMR. Protein Sci. 12 520–531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weaver, T.M. 2000. The π-helix translates structure into function. Protein Sci. 9 201–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Werner, J.H., Dyer, R.B., Fesinmeyer, R.M., and Andersen, N.H. 2002. Dynamics of the primary processes of protein folding: Helix nucleation. J. Phys. Chem. B 106 487–494. [Google Scholar]
- Williams, S., Causgrove, T.P., Gilmanshin, R., Fang, K.S., Callender, R.H., Woodruff, W.H., and Dyer, R.B. 1996. Fast events in protein folding: Helix melting and formation in a small peptide. Biochemistry 35 691–697. [DOI] [PubMed] [Google Scholar]
- Wong, K.B. and Daggett, V. 1998. Barstar has a highly dynamic hydrophobic core: Evidence from molecular dynamics simulation and NMR relaxation data. Biochemistry 37 11182–11192. [DOI] [PubMed] [Google Scholar]
- Wüthrich, K. 1986. NMR of protein and nucleic acids. Wiley, New York.
- Zhang L. and Hermans, J. 1994. 3(10)-Helix versus α-helix—A molecular dynamics study of conformational preferences of AIB and alanine. J. Am. Chem. Soc. 116 11915–11921. [Google Scholar]
- Zimm B.H. and Bragg, J.K 1959. Theory of the phase transition between helix and random coil in polypeptide chains. J. Chem. Phys. 31 526–535. [Google Scholar]