Human Olfactory Detection of Homologous n-Alcohols Measured via Concentration-response Functions

Abstract

We explored in humans concentration-detection functions for the odor of the homologous n-alcohols ethanol, 1-butanol, 1-hexanol, and 1-octanol. These functions serve to establish structure-activity relationships, and reflect the pharmacology of the olfactory sense at the behavioral level. We tested groups of 14 to 17 subjects (half of them females), averaging 31 to 35 years old. An 8-station vapor delivery device (VDD8) presented the stimulus under a three-alternative forced-choice procedure against carbon-filtered air. The VDD8 was built to meet the demands of typical human sniffs in a short-term (<5 sec) olfactory detection task, and to accurately control odorant generation, delivery, and stability. Actual stimulus concentration was quantified by gas chromatography before and during testing. The functions obtained were log normally distributed and were accurately modeled by a sigmoid (logistic) function, both at the group and at the individual level. Sensitivity to ethanol was the lowest and to 1-octanol the highest. Functions became steeper with increasing carbon chain length. For all alcohols the concentration detected halfway between chance and perfect detection (threshold) was at the ppb (or nM) level. Females were slightly more sensitive than males. Intersubject variability across participants was between one and two orders of magnitude. The present odor thresholds were lower than many reported in the past but their relative pattern across alcohols paralleled that in our earlier data and in compilation studies. A previously described quantitative structure-activity relationship for odor potency holds promise to model thresholds that, like those obtained here, best reflect the intrinsic sensitivity of human olfaction.

Introduction

Understanding dose-response relationships in olfaction represents an important step in the functional characterization of this chemosensory system. At perithreshold levels of stimulation, these relationships take the form of concentration-detection functions. Olfactory detectability functions can be investigated using different types and levels of responses, from the receptor to the integrated organismic level. A main aim of these functions is to understand the physicochemical basis for the olfactory activity of vapors, and to define the chemical tuning characteristics of the sense of smell within various parts or as a whole. Recent examples of structure-activity studies exploring dose-response functions have included testing human (Jacquier V et al., 2006; Wise PM et al., 2007), mouse (Katada S et al., 2005; Oka Y et al., 2006), and fly (Pelz D et al., 2006; Stensmyr MC et al., 2003) olfactory responses at the receptor, cell, olfactory bulb or antennal/antennal lobe, and behavioral levels.

Olfactory receptors are broadly selective (Katada S et al., 2005), albeit species differences have been reported (Rawson NE et al., 1997), and respond together in a combinatorial way (Rennaker RL et al., 2007; Zou Z, Buck LB, 2006). It is, then, important to complement experiments that use molecular, cellular, and tissue approaches with those that use system-integrated behavioral approaches. Most studies on odor detection by humans have measured “thresholds” according to a particular, fixed criterion, e.g., (Cometto-Muñiz JE, Cain WS, 1990; Tsukatani T et al., 2003; Wudarski TJ, Doty RL, 2004). Few have gone further and measured concentration-detection functions (Cain WS et al., 2005; Cain WS, Gent JF, 1991; Cain WS et al., 2007a; Cometto-Muñiz JE et al., 2002). Even fewer have measured these functions for a number of odorants in the context of addressing structure-activity, e.g., (Cometto-Muñiz JE et al., 2004; Wise PM et al., 2007). Our own previous work has included measuring odor thresholds along and across homologous series, using a uniform procedure (Cometto-Muñiz JE, 2001), with the goal of studying enough odorants to propose a structure-activity model for the short-term (1–3 sec) odor detection of volatile organic compounds (VOCs) by humans (Abraham MH et al., 2002; Abraham MH et al., 2007). Compared to other thresholds in the literature (Devos M et al., 1990), our values captured well the relative odor potency across VOCs but lay at the high end of the reported range. We have discussed some of the reasons for this, including dilution of the stimulus when delivered to the nose, and a stringent criterion for defining the threshold (Cometto-Muñiz JE, Cain WS, 1993).

The present study represents an initial step to measure and model odor concentration-detection functions, not just threshold values, for a number of homologous series, beginning here with the n-alcohols. In addition to gathering complete functions, the present work employs a vapor delivery device and methodology designed to capture the best conditions for human olfactory sensitivity (Cain WS et al., 2007b). On the stimulus side, we strived to optimize delivery and analytical stability. On the response side, the procedure aimed to maximize speed and efficiency of smell testing. If the various sources of variability and uncertainty, both analytical and psychophysical, are effectively minimized, the outcome should show thresholds lower than many reported in the past.

Materials and Methods

An institutional review board at the University of California, San Diego, approved the protocol for all experiments described here. All participants provided written informed consent.

Subjects

The pool consisted of 34 persons (17 female) of average age (±SD) of 31 (±13) years and ranging from 18 to 59 years old. Our recruitment of subjects focused on the 18–45 years age-range (29 subjects). Since we were interested in evaluating the performance of the newly designed 8-station vapor delivery device (see below) in a broad context, we remained open to include a 49 year-old (female) and a small group of participants in their 50’s (5 subjects, males, ages: 52, 54, 56, and 59). All subjects performed in the normosmic range on a clinical olfactory test (Cain WS, 1989), except one male (59 years old, smoker) who was mildly hyposmic in the left nostril. (This subject was only tested with ethanol and his inclusion or exclusion does not alter the outcome.) All subjects except two males (ages 52 and 59 years) were non-smokers.

The intensive testing performed per chemical stimulus and subject (see Apparatus and Procedure) precluded the ideal scheme that all subjects be tested on all stimuli, so subsets from the pool were used for individual alcohols, as follows: For ethanol: 14 subjects (6 female), average (±SD) age 35 (±14) years, ranging from 20 to 59 years old. For 1-butanol: 17 subjects (8 female), average age (±SD) 33 (±14) years, ranging from 19 to 57 years old. For 1-hexanol: 17 subjects (8 female), average age (±SD) 31 (±13) years, ranging from 18 to 56 years old. For 1-octanol: 14 subjects (6 female), average age (±SD) 32 (±13) years, ranging from 19 to 56 years old. Four subjects, all normosmic and non-smokers (three males, subject #s 19, 20, and 26, and one female, subject #12), were tested on all four alcohols. Two of these males (subjects #s 19 and 26) were 56 and 54 years old; the remaining male and the female were 20 and 38 years old, respectively.

Stimuli

Previous work established that odor sensitivity in humans and other primates increases orderly along homologous n-alcohols (Cometto-Muñiz JE, Cain WS, 1990,1995; Laska M, Seibt A, 2002). Thus, to maximize efficiency and the overall range of carbon chain length explored, we chose to test homologs with even numbers of carbons. The stimuli selected were (purity in parenthesis): ethanol (μ99.5%), 1-butanol (99.9%), 1-hexanol (μ99%), and 1-octanol (>99.5%).

Apparatus and Procedure

The chemicals were generated and delivered by means of an 8-station vapor delivery device (VDD8). The instrument has been described in detail in a recent publication (Cain WS et al., 2007b). It was designed to optimize speed and efficiency in testing subjects. Samples for smelling were delivered at a total flow of 40 L/min, high enough to fully accommodate human sniffs (Laing DG, 1982,1983), but not so high to create a sensation of draft since presentations occurred via glass cones at a linear velocity of μ13 cm/sec, similar to that found in mechanically-ventilated spaces (Knudsen HN et al., 1997; Knudsen HN et al., 1998). Briefly, the VDD8 consists of 8 stations delivering increasing concentrations (in this study we chose a factor of 2) of the stimulus, i.e., ascending concentration approach. Each station consisted of three cones, one (randomly selected) delivered the odorant (active cone) and the other two delivered carbon-filtered air (blanks), i.e., a three-alternative forced-choice procedure. We tested one alcohol per session with irregular order of alcohols. In a session, subjects lined-up and went through each station, starting with the one presenting the lowest concentration, selecting the cone that smelled different (typically stronger) from the other two. They also provided a rating to reflect confidence in the decision on a scale from “1” (not confident at all, just guessing) to “5” (extremely confident). Instructions heard through a speaker-system guided participants to sniff a cone in a 5-sec window and to wait 15 seconds between stations. After subjects progressed through all 8 stations, they waited elsewhere while the experimenter set a new random order of the active cones across stations and let 5-min elapse to re-establish steady state conditions. The subjects then repeated another round of testing. This cycle continued until each subject provided a minimum of 21 judgments per concentration for an alcohol.

Quantification of vapors was accomplished via gas chromatography (flame ionization detector). The procedure required measuring a calibration curve for each odorant (Cometto-Muñiz JE et al., 2003b). To confirm the stability of delivery of the odorant, the concentration feeding the active cones was measured both before and during actual testing, as described in detail for D-limonene in a recent paper (Cain WS et al., 2007b). The concentration range presented via the VDD8 in seven binary steps for each alcohol was the following: For ethanol, 12 to 1538 ppb; for 1-butanol, 0.25 to 32 ppb; for 1-hexanol, 0.21 to 27 ppb; and for 1-octanol, 0.34 to 43 ppb.

Data analysis

Results are summarized as detection probability (i.e., detectability) and confidence rating as a function of vapor concentration. Detection probability (P) was corrected for chance, producing a number between P=0.0, i.e., chance detection, and P=1.0, i.e., perfect detection, according to the equation:

$$\text{P}=(\text{m}·\text{p}(\text{c})-1)/(\text{m}-1)$$ eq. (1)

where P = detectability corrected for chance, m = number of choices per trial (in this case, three), and p(c) = proportion correct (i.e., number of correct trials/total number of trials) (Macmillan NA, Creelman CD, 1991).

Concentration-detection, called psychometric, functions for each alcohol were modeled by a sigmoid (logistic) equation:

$$\text{P}={\text{P}}_{max}/(1+{\text{e}}^{(-(\text{x}-\text{C})/\text{D})})$$ eq. (2)

where P = detection probability (0μPμ1), P_max = 1.0, x = vapor concentration (in log ppb by volume), and C and D are constants. C is the value of x when P=0.5, i.e., when detection probability is half way between chance (P=0.0) and perfect (P=1.0) detection. This value is taken as the odor detection threshold (ODT). In turn, the constant D describes the steepness of the function.

The data were also fitted to a log normal distribution by converting experimentally measured detection probabilities (P) to z scores, plotting z scores vs. log ppm (which followed a linear equation), and using this linear relationship to calculate back the best fitting function of P vs. log ppm. In this way one can also calculate the value of concentration (log ppb) at P=0.5, i.e., the ODT, for each alcohol. Both models (sigmoid and log normal) produced excellent fits and, as reported below, values of concentration at P=0.5 from both approaches were virtually the same. The similarity held both for the group and for individuals.

Results

Figure 1, upper four panels, shows the group results in terms of detectability and rated confidence as a function of vapor concentration for ethanol, 1-butanol, 1-hexanol, and 1-octanol, respectively. In all cases, the sigmoid model provided an excellent fit to the data, and confidence ratings increased with detectability. The lower panel of Figure 1 shows that the average psychometric function from the complete group for each alcohol fell quite well into register with that from the common group of four subjects tested on all alcohols. Table 1, upper section, presents the group average value (±standard error, SE) of constants C and D from eq. (2), and two measurements of goodness of fit, for the individual alcohols. The lower section of Table 1 presents the same data but for the group of four common subjects. Absolute and relative values compare well between the two groups.

Figure 1.

Upper four panels. Upper left. Average group detectability (left y-axis) and confidence rating (right y-axis) as a function of vapor concentration (log ppb) of ethanol. Each detectability point represents the outcome of 294 trials made by 14 subjects. Bars indicate standard error (SE). Upper right. Same for 1-butanol. Each detectability point represents the outcome of 357 trials made by 17 subjects. Lower left. Same for 1- hexanol. Each detectability point represents the outcome of 357 trials made by 17 subjects. Lower right. Same for 1-octanol. Each detectability point represents the outcome of 294 trials made by 14 subjects. Lower panel. Showing, for each alcohol, how the average psychometric function for the complete group compares to that for the group of four subjects tested in common across the four alcohols.

Table 1.

Upper section. Showing, for each alcohol, values (±SE) for constants C and D from eq. (2) applied to the group psychometric function (n: number of subjects). Also shown are two estimates of goodness of fit. Lower section. Same data but from the group of four common subjects tested on all four alcohols.

All subjects
	n	C (log ppb)	SE (C)	D	SE (D)	R2	Chi square
Ethanol	14	2.52	±0.020	0.43	±0.020	0.996	0.0028
1-Butanol	17	0.90	±0.032	0.41	±0.032	0.987	0.0080
1-Hexanol	17	0.91	±0.014	0.36	±0.014	0.997	0.0018
1-Octanol	14	0.64	±0.025	0.33	±0.023	0.993	0.0064
Common Subjects
	n	C (log ppb)	SE (C)	D	SE (D)	R2	Chi square
Ethanol	4	2.40	±0.053	0.57	±0.057	0.971	0.0148
1-Butanol	4	1.19	±0.049	0.46	±0.053	0.968	0.0126
1-Hexanol	4	0.96	±0.087	0.59	±0.097	0.919	0.0313
1-Octanol	4	0.73	±0.022	0.25	±0.019	0.994	0.0064

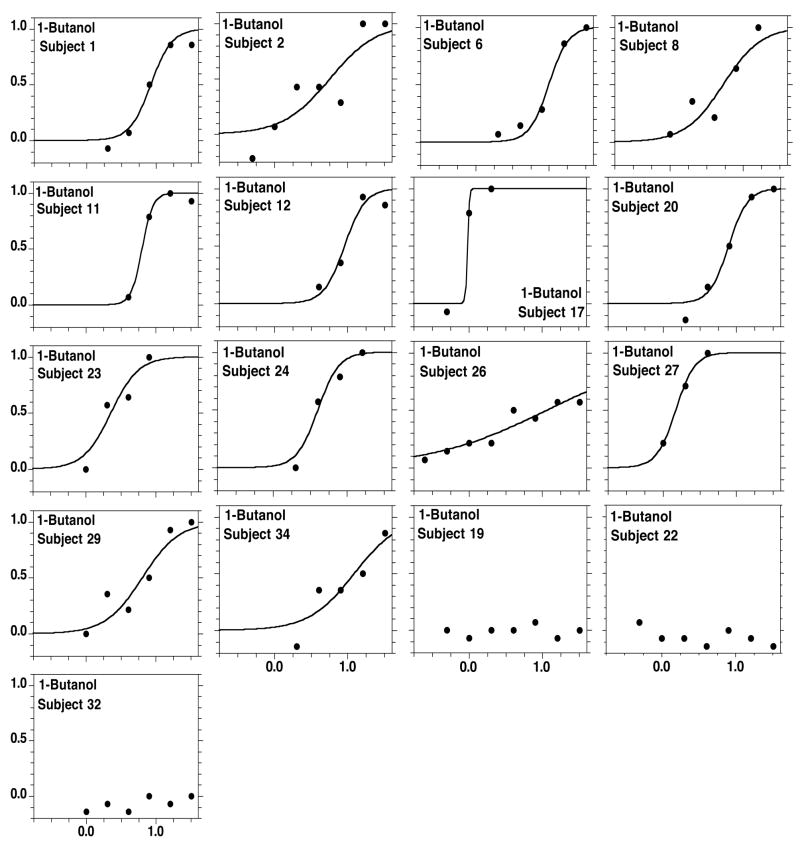
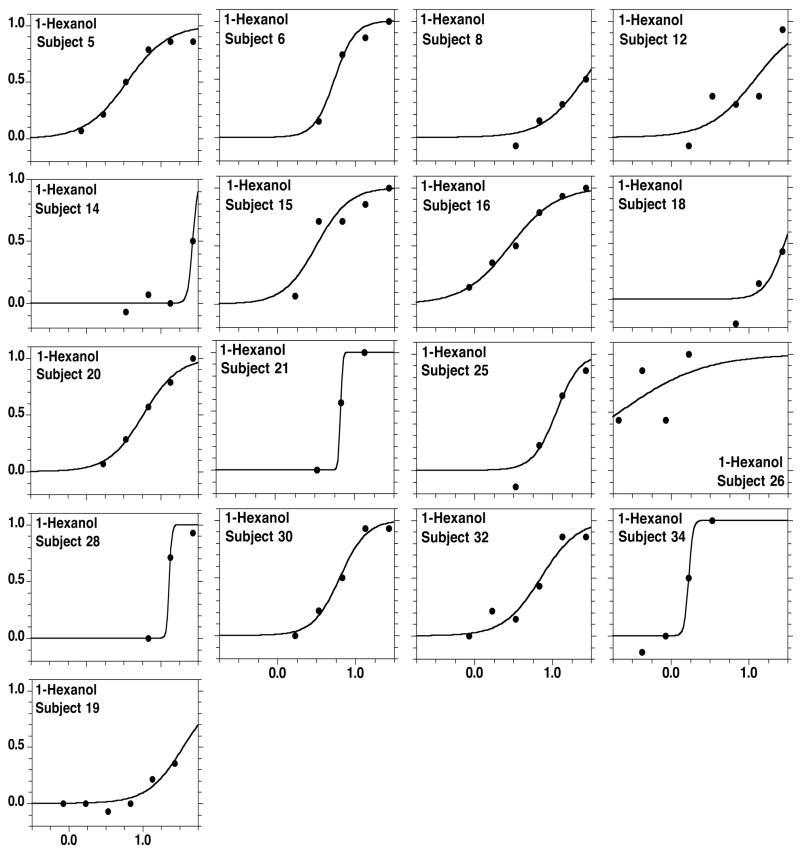
Figures 2 to 5 present, respectively, the individual detectability data for each alcohol, also fitted by the sigmoid equation. Individual data can also be satisfactorily modeled by the sigmoid. For 1-butanol only, three subjects (males, one smoker, ages 23, 52, and 57) performed around chance across all concentrations. Table 2 presents the values of C and D from psychometric functions fitted to each subject, excluding the three participants who performed around chance at all concentrations of 1-butanol.

Figure 2.

Individual detectability functions for ethanol fitted by the sigmoid eq. (2). Each point in a graph represents the outcome of 21 trials made by a subject. In each graph, the data shown spans the concentration range from chance detection (or lowest level presented) to perfect detection (or highest level presented). (For example, for Subject 14, all concentrations lower than the first shown were detected around chance level and are not depicted; for Subject 26, all concentrations higher than the last shown were detected around perfect detection and are not depicted).

Figure 5.

As in Figure 2, but individual functions for 1-octanol.

Table 2.

Showing, for each alcohol, the values of constants C and D from the psychometric function for each subject (identified by a unique S #), and an estimate of goodness of fit. (Excluding three participants for 1-butanol, as described in the text.)

	Ethanol (n=14)				1-Butanol (n=14)				1-Hexanol (n=17)				1-Octanol (n=14)
	S #	C (log ppb)	D	R2	S #	C (log ppb)	D	R2	S #	C (log ppb)	D	R2	S #	C (log ppb)	D	R2
	4	2.61	0.44	0.84	1	0.92	0.15	0.97	5	0.55	0.28	0.97	2	0.26	0.17	0.99
	7	2.02	0.21	0.87	2	0.76	0.32	0.77	6	0.74	0.13	0.97	3	1.03	0.12	1.00
	8	2.30	0.25	0.95	6	1.00	0.13	0.98	8	1.41	0.27	0.92	7	0.43	0.21	0.98
	9	3.18	0.42	0.97	8	0.73	0.26	0.84	12	1.08	0.30	0.75	12	0.74	0.017	0.88
	14	3.10	0.20	0.85	11	0.80	0.078	0.99	14	1.43	0.032	0.95	13	1.01	0.12	0.99
	18	2.61	0.22	0.90	12	0.96	0.14	0.94	15	0.50	0.21	0.85	14	1.56	0.20	0.96
	19	2.94	0.32	0.97	17	−0.016	0.013	0.99	16	0.46	0.30	0.99	17	−0.18	0.012	0.96
	20	2.30	0.23	0.93	20	0.90	0.13	0.97	18	1.46	0.13	0.74	19	0.88	0.089	0.95
	26	1.16	0.34	0.87	23	0.36	0.20	0.88	20	0.77	0.24	0.99	20	0.31	0.094	0.99
	29	2.40	0.42	0.93	24	0.61	0.14	0.95	21	0.83	0.013	1.00	26	1.03	0.47	1.00
	30	2.11	0.26	0.93	26	1.06	0.81	0.89	25	1.05	0.15	0.94	28	0.69	0.16	0.96
	31	2.35	0.25	0.97	27	0.18	0.13	1.00	26	−0.66	0.54	0.29	30	0.40	0.021	1.00
	32	2.97	0.34	0.98	29	0.81	0.26	0.89	28	1.11	0.017	0.99	33	0.82	0.15	0.67
	12	3.34	0.77	0.75	34	1.09	0.31	0.82	30	0.80	0.17	0.99	35	−0.22	0.23	0.96
									32	0.85	0.24	0.94
									34	0.23	0.027	0.97
									19	1.55	0.24	0.90
Average		2.53	0.34			0.73	0.22			0.83	0.19			0.63	0.15
±SE		±0.16	±0.04			±0.09	±0.05			±0.14	±0.03			±0.13	±0.03

Individual functions for subjects reaching at least P=0.5 were also fitted to a log normal distribution as described under “Data analysis”. A two-way analysis of variance (ANOVA) on the concentration producing P=0.5 for the factors n-alcohol (four levels: ethanol, 1-butanol, 1-hexanol, and 1-octanol) and model (two levels: sigmoid and log normal) revealed a significant effect for alcohol {F(3,108)=83.68, p<0.0001)}, but not for model (p=0.6), or for the interaction (p=0.3). The group function for ethanol was strongly shifted to the right (towards higher concentrations) compared to that for the other alcohols. The group function for 1-octanol was shifted to the left (towards lower concentrations) compared to the other alcohols. The group functions for 1-butanol and 1- hexanol were largely overlapping and much closer to the function for 1-octanol than to that for ethanol (Table 1 and Figure 1).

Table 1 shows that the parameter D decreased (i.e., functions became steeper) with increasing carbon chain length. A one-way ANOVA on the values of the constant D across subjects (as shown in Table 2) for the factor “alcohols” showed a significant effect {F(3,53)=2.90, p=0.04}, largely driven by the difference between ethanol (the least steep function) and 1-octanol (the most steep function).

Females were slightly more sensitive than males for every alcohol. A Wicoxon- Mann-Whitney test performed on C values from females and males across the alcohols revealed a significant higher sensitivity (i.e., lower thresholds) for females (p=0.02). Nevertheless, on average, females were younger than males by 9 years for ethanol (30 vs. 39 years), 1-hexanol (25 vs. 34 years), and 1-octanol (27 vs. 36 years), and by 1 year for butanol (30 vs. 31 years). Age has been shown to decrease olfactory sensitivity, e.g. (Cain WS, Gent JF, 1991; Doty RL et al., 1984). In a strategy to control for the possible influence of age, we performed a 2-way analysis of covariance (ANCOVA) on C values using age as the covariate (or regressor) and the factors gender (two levels: male and female) and alcohol (four levels). The outcome showed a significant effect for gender {F(1,41)=5.00, p=0.03} and alcohol {F(3,41)=5.96, p=0.0018} but no significance for age, for any of the interactions involving age, or for the gender X alcohol interaction.

Discussion

Group data

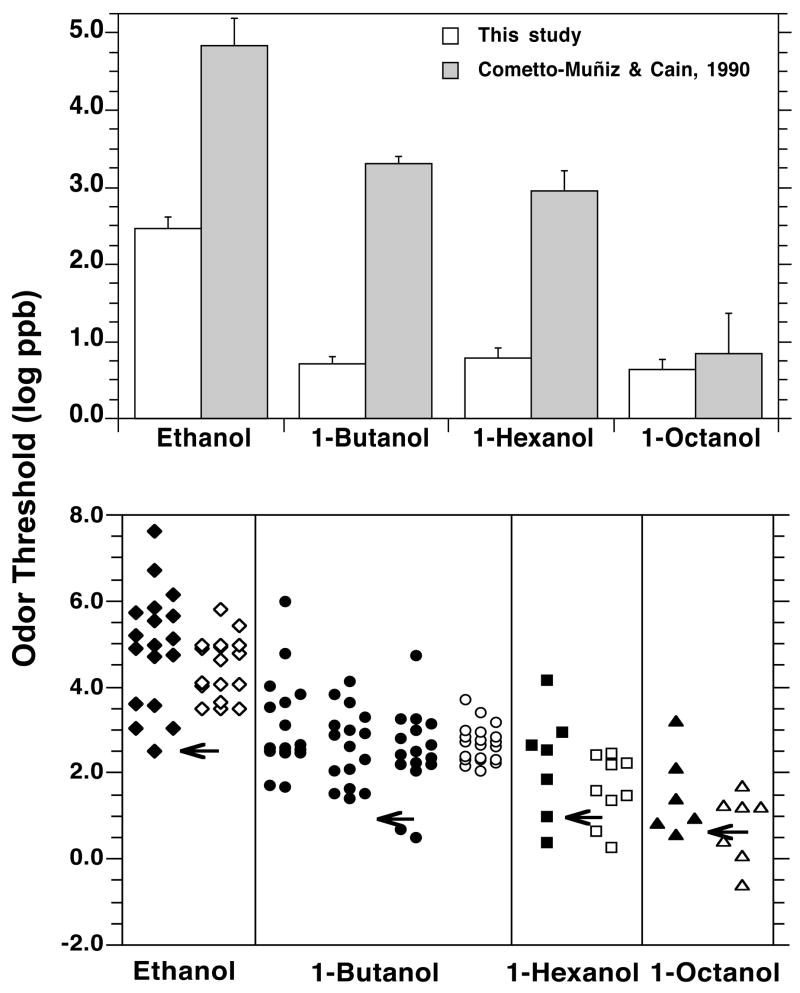
It is instructive to compare the present results with the standardized olfactory thresholds calculated by Devos et al. (Devos M et al., 1990) and with studies from the comprehensive compilation done by van Gemert (van Gemert LJ, 1999). (From the latter we included only odor detection, not recognition, thresholds in air.) (Figure 6.). Compilations of odor thresholds across studies are characterized by a staggering variability for any given odorant. This variability is at least partly due to the inclusion of studies employing inadequate stimulus delivery, stimulus control, threshold criteria, and/or number of subjects. In the van Gemert compilation, the difference between the highest and the lowest threshold for ethanol, 1-butanol, 1-hexanol, and 1-octanol, is 5.1, 5.5, 3.8 and 2.7 orders of magnitude, respectively. Devos et al. showed that an important part of the large variability across studies was systematic, and that it could be partially accounted for by given weighting coefficients to the values from the 105 references reviewed (Devos M et al., 1990). The outcome produced standardized thresholds. The difference between the highest and the lowest of these standardized thresholds for ethanol, 1-butanol, 1-hexanol, and 1-octanol, was 2.3, 1.7, 2.2, and 2.3 orders of magnitude, respectively. The variability is much lower but still ranges between 50 and 200 times across the extreme values for a given alcohol. Figure 6 shows that all data sources, to one or another degree, show decreasing thresholds (i.e., increasing potency) with increasing carbon chain length. It also shows that the present thresholds are considerably lower than those compiled or standardized from the literature and than our previous values, an outcome in line with the expectations stated in the Introduction. Among the values listed in both compilations (Devos M et al., 1990; van Gemert LJ, 1999) for each alcohol, the present thresholds rank the lowest for ethanol (out of 35 values), within the lowest three for butanol (out of 69), within the lowest four for hexanol (out of 16), and within the lowest five for octanol (out of 13) (Figure 6, lower part). Interestingly, the difference among the sources decreases as chain length increases. For example, compared to the Devos et al. average standardized values, the present thresholds are about 2.0, 1.8, 0.73, and 0.12 orders of magnitude lower for ethanol, 1- butanol, 1-hexanol, and 1-octanol, respectively. The effect probably reflects, in part, the difficulty in securing a stable and reliable stimulus delivery for the most volatile odorants, particularly under techniques employing static headspace dilution (Cain WS et al., 1992). With these techniques, thresholds for stimuli with high vapor pressure could appear to be higher to a larger extent than those with low vapor pressure.

Figure 6.

Upper part. Showing across the four n-alcohols the present group average results (expressed in terms of the value of constant C) and our previous odor threshold data (Cometto-Muñiz JE, Cain WS, 1990). Bars indicate standard error (SE). Lower part. Showing across the four n-alcohols the odor thresholds compiled by van Gemert (van Gemert LJ, 1999) (filled symbols) and those compiled and standardized by Devos et al. (Devos M et al., 1990) (empty symbols). (Values from the studies listed in each compilation are spread out along the x-axis for clarity.) The arrows point to the thresholds (i.e., constant C) obtained in the present study (see text).

Interindividual variability

The present group of subjects covered a wide range of ages (18 to 59 years old) and included two smokers. For this group, the ratio between the least and the most sensitive individual in terms of antilog C (i.e., ppb at P=0.5) equaled 152 for ethanol (n= 14 subjects), 13 for 1-butanol (n=14), 162 for 1-hexanol (n=17), and 59 for 1-octanol (n=14), i.e., between one and two orders of magnitude. Three subjects tested with 1- butanol (subjects # 19, 22, and 32) never rose above chance level (Figure 3). Two of them (#s 19 and 22) were males in their fifties (57 and 52 years old, respectively) and one (#22) was also a smoker, factors that likely contributed to their poor performance. Subject #19 was among the four least sensitive participants for ethanol and for 1- octanol, and was, in fact, the least sensitive individual for 1-hexanol (Table 2). The third subject that did not rise above chance level for 1-butanol (subject #32) was a young (23 years) male, nonsmoker. The reasons for his poor sensitivity are less clear. He also performed poorly for ethanol but did about average for 1-hexanol (Table 2).

Figure 3.

As in Figure 2, but individual functions for 1-butanol. Three participants (males, one smoker, ages 23, 52, and 57) out of 17 performed around chance level across all concentrations.

Few investigations of odor thresholds have reported the interindividual range in sensitivity. Early studies found ranges between 3 to 5 orders of magnitude (Brown KS et al., 1968; Jones FN, 1957), and even 16 orders of magnitude (Yoshida M, 1984). Some results indicate that interindividual variability can differ vastly among compounds, depending on chemical structure (Punter PH, 1983; Stevens JC, Cain WS, 1987). Other results favor a picture of general (rather than odorant-specific) and small (1 to 2 orders of magnitude) interindividual differences in sensitivity (Rabin MD, Cain WS, 1986). It is clear that a high enough amount of data per person is necessary in order to avoid an artificially high interindividual variability (Stevens JC et al., 1988). Here, we have measured concentration-detection functions under an approach that combines analytical stability of stimulus presentation with speed and efficiency of subject testing. Despite the considerable age spread among the subjects, our present results are in line with studies showing variations in sensitivity across individuals in the range of 1 to 2 orders of magnitude.

Structure-activity relationships: Previous thresholds vs. psychometric functions

Using our previously measured odor detection thresholds (ODTs) for 60 VOCs that included alcohols, esters, ketones, alkylbenzenes, aliphatic aldehydes, carboxylic acids, and terpenes {see review in (Cometto-Muñiz JE, 2001)}, we have correlated olfactory potency with six physicochemical properties, i.e., descriptors, of the VOCs in a quantitative structure-activity relationship (QSAR) based on a solvation equation (Abraham MH et al., 2002). The model is not only descriptive and predictive (Abraham MH et al., 2001), it also has mechanistic significance. It quantifies the characteristics and relative role of transfer processes governing the transport of odorants from the air phase, when they enter the nose, to the biophase where reception takes place (Abraham MH et al., 2007). In other words, the QSAR quantifies the physicochemical properties that make a VOC a potent (low threshold) or a weak (high threshold) odorant, and also serves to define the complementary properties of the receptor environment (Abraham MH et al., 2002).

The QSAR was built using threshold values measured under a fixed performance criterion and not as part of a psychometric function, see review in (Cometto-Muñiz JE, 2001). The technique and procedure employed resulted in values that correlated highly with those in the literature but that lay at the high end of the range (Cometto-Muñiz JE, Cain WS, 1993). In other words, the resulting ODTs reflected well relative olfactory potency across a wide variety of VOCs, but were much less indicative of actual potency under an ecological exposure. In contrast, the constant C obtained here from the psychometric function provides a measure of ODTs that reflects not only the relative magnitude of ODTs across n-alcohols but also the threshold values that would be observed in humans under natural, realistic exposures. Both our previous (Cometto-Muñiz JE, Cain WS, 1990) and present thresholds follow a similar pattern of odor potency across n-alcohols (Cometto-Muñiz JE, Cain WS, 1993) (Figure 6). (A pattern also present in two comprehensive compilations of ODTs.) It follows that the same QSAR can be applied to ODTs, now calculated as the constant C, when a large enough number of homologous series tested under the present methodology becomes available. Work in progress is testing additional series with the aim of building such a database.

Steepness of the psychometric functions

The psychometric function approach also produces the constant D, a parameter that defines the steepness of the function. Making an analogy with dose-response relationships in pharmacology, for each alcohol we can consider the set of individual D values, and the value of D obtained from the group data (Brody TM, 1994; Snyder R, 1984). The set of individual D values reflects the interaction between odorant and olfactory receptors, assuming that odor detection at the behavioral level reflects, at least in part, the ligand binding characteristics in olfaction. In turn, the value of D from the group reflects the mean response across subjects. From the perspective of ligandreceptor interactions, a VOC characterized by a relatively flat function (i.e., high individual values of D) requires a larger concentration range to increase its detection from chance to certainty than a VOC characterized by a steeper function (i.e., low individual values of D). The information can be used to suggest a mechanism of interaction between different VOCs and olfactory receptors, as exemplified below.

We assume a system where a VOC interacts with a set of receptors (R) to form a VOC-receptor complex that then breaks down into the receptor and VOC, which is transported away:

$$\text{VOC}+\text{R}\underset{{\text{k}}_{-1}}{\overset{{\text{k}}_1}{\rightleftarrows }}\text{Complex}\stackrel{{\text{k}}_2}{\to }\text{VOC}+\text{R}$$ eq. (3)

Assuming that the concentration of the complex reaches a steady state under a given set of conditions, the concentration will be given by eq. (4), where k₁′ in the numerator is k₁ times the constant receptor concentration, k₁′ = k₁ · {R}.

$$\text{Complex}={\text{k}}_1\text{'}·\text{VOC}/({\text{k}}_{-1}+{\text{k}}_2+{\text{k}}_1·\text{VOC})$$ eq. (4)

Eq. (4) is derived from the well-known Michaelis-Menten equation (Price NC et al., 2001), that gives the steady state concentration of the VOC-receptor complex as a function of the initial concentration of the VOC and the various rate constants. Derivation of eq. (4) assumes that all the components occupy the same volume, which will not be correct in the present case. However, the effect of variation of the rate constants on the complex concentration will qualitatively be correct.

Although alteration in k₁′ or k_-1 will alter the complex concentration, the most easily interpreted scenario is that k₂ varies from VOC to VOC. The smaller is k₂ the steeper is the slope of any plot of complex concentration against {VOC}. This means that k₂ should be small for octanol and large for ethanol. If the phase into which the VOC is empted after it leaves the receptor were more polar (less hydrophobic) than the receptor, we would expect the more polar ethanol molecule to be transported to this phase more rapidly than the less polar octanol molecule. Two potential phases that could carry the VOC away are the bloodstream and the nasal mucus. Both of these are largely aqueous and hence are likely to be more polar than the receptor. The observation of a steeper slope in the psychometric plots for octanol than for ethanol is commensurate with a smaller value of k₂, and with the above interpretation.

The steepness of the psychometric function has also important practical implications in the search for remedial strategies to solve problems of environmental odor pollution (Cometto-Muñiz JE et al., 2004). For homologous alcohols, the present outcome shows statistical evidence that individual values of D decrease with increasing carbon chain length. Further studies will determine whether this effect extends to other series. In any case, there is the possibility that not only C, but also D might be described by the solvation-based QSAR. This will be explored as well.

Vapor concentration range issues

Recent studies, particularly at the receptor level, have included olfactory concentration-response relationships (Abaffy T et al., 2006; Jacquier V et al., 2006; Kajiya K et al., 2001; Katada S et al., 2005; Oka Y et al., 2006; Pelz D et al., 2006; Shirokova E et al., 2005). Table 3 summarizes their characteristics and those of the present work. Across all approaches, the functions follow a sigmoid that defines an EC₅₀ (effective concentration 50) value, i.e., the odorant concentration at half-maximal response. Most EC₅₀s fall within the micromolar (μM) range, typically tens to hundreds. A few others fall within the nanomolar (nM) range, mostly tenths to tens, i.e., a concentration difference of about four orders of magnitude between the two EC₅₀ groups. Delivering an odorant directly in a liquid phase to a preparation, a common occurrence in receptor and cell studies, invariably produces EC₅₀s in the μM range. Delivering it in a vapor phase, very often produces EC₅₀s in the nM range. (Studies where the odorant is presented indirectly in the liquid phase — and, often, quantified only in such phase — but where the tested species actually samples the vapor above the liquid do not constitute liquid phase presentations.) Notably, experiments within the same study (Oka Y et al., 2006) have shown that whereas delivery of the odorant as a vapor still needs to reach μM concentrations when the response is measured at the cell level (e.g., HEK293 or isolated olfactory sensory neurons: OSNs), it only needs to reach nM concentrations when the response is measured at the glomerular level. Thus, responses measured beyond the individual cell level, be it at the olfactory bulb (mouse) (Oka Y et al., 2006), the antennal lobe (fly) (Pelz D et al., 2006), or the integrated olfactory system (human) (this study; (Cain WS et al., 2005; Cain WS et al., 2007b; Cometto-Muñiz JE et al., 2004; Wise PM et al., 2007), produce EC₅₀s at or below the nM range. In terms of concentration span, the odorant response often rises from background to maximum within approximately two log units of concentration but this span can vary from one {e.g., (Kajiya K et al., 2001)} to three {e.g., (Abaffy T et al., 2006)} log units, irrespective of stimulus phase (liquid or vapor) or level at which the olfactory path is probed.

Table 3.

Comparison of EC₅₀ values from dose-response functions for miscellaneous odorants, beginning with n-alcohols, among various recent studies.

Odorant	Species	Stimulus Phase	Response Level	Receptor(s) Tested	Fitting Model	EC50 (nM)	Reference
Ethanol	Human	Vapor	Behavioral	All	Eq. (2)	13	This study
Ethanol	Human	Vapor	Behavioral	All	Log normal	3.7	(Cain WS et al., 2005)
1-Butanol	Human	Vapor	Behavioral	All	Eq. (2)	0.32	This study
1-Butanol	Human	Vapor	Behavioral	All	Eq. (2)	15	(Cometto-Muñiz JE et al., 1999)
1-Butanol	Fly	Vapor	Antenna	Or22a	Eq. (6)	22,484	(Pelz D et al., 2006)
1-Butanol	Fly	Vapor	Antennal Lobe	Or22a	Eq. (6)	2,657	(Pelz D et al., 2006)
1-Hexanol	Human	Vapor	Behavioral	All	Eq. (2)	0.33	This study
1-Hexanol	Fly	Vapor	Antennal Lobe	Or22a	Eq. (6)	816	(Pelz D et al., 2006)
1-Heptanol	Fly	Vapor	Antennal Lobe	Or22a	Eq. (6)	347	(Pelz D et al., 2006)
1-Octanol	Human	Vapor	Behavioral	All	Eq. (2)	0.18	This study
2-Heptanone	Human	Vapor	Behavioral	All	Eq. (2)	3.0	(Cometto-Muñiz JE et al., 1999)
Butyl acetate	Human	Vapor	Behavioral	All	Eq. (2)	0.0041	(Cometto-Muñiz JE et al., 2002)
Butyl acetate	Human	Vapor	Behavioral	All	Eq. (2)	0.086	(Cometto-Muñiz JE et al., 2003a)
Ethyl propanoate	Human	Vapor	Behavioral	All	Eq. (2)	12	(Cometto-Muñiz JE et al., 2005)
Ethyl heptanoate	Human	Vapor	Behavioral	All	Eq. (2)	1.7	(Cometto-Muñiz JE et al., 2005)
TXIB*	Human	Vapor	Behavioral	All	Log normal	0.049	(Cain WS et al., 2005)
D-Limonene	Human	Vapor	Behavioral	All	Log normal	0.61	(Cain WS et al., 2007b)
Toluene	Human	Vapor	Behavioral	All	Eq. (2)	4.0	(Cometto-Muñiz JE et al., 2002)
Toluene	Human	Vapor	Behavioral	All	Eq. (2)	0.26	(Cometto-Muñiz JE et al., 2003a)
Helional	Human	Liquid	Cell (HEK293)	h-OR17-40	Eq. (3)	98,700	(Jacquier V et al., 2006)
Helional	Human	Liquid	Cell (HEK293)	h-OR17-40-EGFP	Eq. (3)	114,400	(Jacquier V et al., 2006)
Helional	Human	Liquid	Cell (HeLa/Olf)	Rho-tag(39)-Olfr43	Eq. (5)	3,600	(Shirokova E et al., 2005)
(−) Citronellal	Human	Liquid	Cell (HeLa/Olf)	Rho-tag(39)-Olfr43	Eq. (5)	2,100	(Shirokova E et al., 2005)
(−) Citronellal		Liquid	Cell (HeLa/Olf)	Rho-tag(39)-Olfr49	Eq. (5)	3,300	(Shirokova E et al., 2005)
(−) Citronellal		Liquid	Cell (HeLa/Olf)	Rho-tag(39)-MOR267-1	Eq. (5)	8,200	(Shirokova E et al., 2005)
Octanal	Human	Liquid	Cell (HeLa/Olf)	Rho-tag(39)-Olfr43	Eq. (5)	22,500	(Shirokova E et al., 2005)
Glutaraldehyde	Human	Vapor	Behavioral	All	Log normal	0.012	(Cain WS et al., 2007a)
E-4-Decenal	Human	Liquid	Cell (HeLa/Olf)	Rho-tag(39)-Olfr43	Eq. (5)	30,400	(Shirokova E et al., 2005)
Lilal	Human	Liquid	Cell (HEK293)	h-OR17-40	Eq. (3)	63,900	(Jacquier V et al., 2006)
Lilal	Human	Liquid	Cell (HEK293)	h-OR17-40-EGFP	Eq. (3)	124,100	(Jacquier V et al., 2006)
Foliaver	Human	Liquid	Cell (HEK293)	h-OR17-40	Eq. (3)	96,700	(Jacquier V et al., 2006)
Foliaver	Human	Liquid	Cell (HEK293)	h-OR17-40-EGFP	Eq. (3)	145,400	(Jacquier V et al., 2006)
Cyclosal	Human	Liquid	Cell (HEK293)	h-OR17-40	Eq. (3)	112,300	(Jacquier V et al., 2006)
Cyclosal	Human	Liquid	Cell (HEK293)	h-OR17-40-EGFP	Eq. (3)	142,900	(Jacquier V et al., 2006)
Aldehyde TPM	Human	Liquid	Cell (HEK293)	h-OR17-40	Eq. (3)	113,300	(Jacquier V et al., 2006)
Aldehyde TPM	Human	Liquid	Cell (HEK293)	h-OR17-40-EGFP	Eq. (3)	139,500	(Jacquier V et al., 2006)
Methyl-hydro-cinnamaldehyde	Human	Liquid	Cell (HEK293)	h-OR17-40	Eq. (3)	163,200	(Jacquier V et al., 2006)
Methyl-hydro-cinnamaldehyde	Human	Liquid	Cell (HEK293)	h-OR17-40-EGFP	Eq. (3)	168,000	(Jacquier V et al., 2006)
Methyl-phenyl-pentanal	Human	Liquid	Cell (HEK293)	h-OR17-40	Eq. (3)	157,000	(Jacquier V et al., 2006)
Methyl-phenyl-pentanal	Human	Liquid	Cell (HEK293)	h-OR17-40-EGFP	Eq. (3)	158,500	(Jacquier V et al., 2006)
Trifernal	Human	Liquid	Cell (HEK293)	h-OR17-40	Eq. (3)	154,600	(Jacquier V et al., 2006)
Trifernal	Human	Liquid	Cell (HEK293)	h-OR17-40-EGFP	Eq. (3)	120,300	(Jacquier V et al., 2006)
Compound 2	Mouse	Liquid	Cell (HEK293)	mOR-EG		175,000	(Katada S et al., 2005)
Compound 3	Mouse	Liquid	Cell (HEK293)	mOR-EG		71,000	(Katada S et al., 2005)
Compound 4 (Eugenol)	Mouse	Liquid	Cell (HEK293)	mOR-EG		47,000	(Katada S et al., 2005)
Eugenol	Mouse	Vapor	Glomerulus Ea	mOR-EG		6.5	(Oka Y et al., 2006)
Eugenol	Mouse	Vapor	Glomerulus Eb	mOR-EG		14	(Oka Y et al., 2006)
Eugenol	Mouse	Vapor	Glomerulus Ec	mOR-EG		26	(Oka Y et al., 2006)
Eugenol	Mouse	Vapor	cell (HEK293)	mOR-EG		46,000	(Oka Y et al., 2006)
Eugenol	Mouse	Vapor	Isolated OSNs	mOR-EG		51,000	(Oka Y et al., 2006)
Eugenol	Mouse	Vapor	Glomerulus			59	(Oka Y et al., 2006)
Eugenol	Mouse	Liquid	Cell (HEK293T)	mOR-EG	Hill equation	46,000	(Kajiya K et al., 2001)
Compound 5 (Vanillin)	Mouse	Liquid	Cell (HEK293)	mOR-EG		26,000	(Katada S et al., 2005)
Vanillin	Mouse	Vapor	Cell (HEK293)	mOR-EG		26,000	(Oka Y et al., 2006)
Vanillin	Mouse	Vapor	Isolated OSNs	mOR-EG		33,000	(Oka Y et al., 2006)
Vanillin	Mouse	Liquid	Cell (HEK293T)	mOR-EG	Hill equation	36,000	(Kajiya K et al., 2001)
Vanillin	Mouse	Liquid	Cell (HEK293T)	mOR-EV	Hill equation	930,000	(Kajiya K et al., 2001)
Ethyl vanillin	Mouse	Liquid	Cell (HEK293T)	mOR-EG	Hill equation	290,000	(Kajiya K et al., 2001)
Ethyl vanillin	Mouse	Liquid	Cell (HEK293T)	mOR-EV	Hill equation	440,000	(Kajiya K et al., 2001)
Compound 7	Mouse	Liquid	Cell (HEK293)	mOR-EG		660,000	(Katada S et al., 2005)
Compound 8	Mouse	Liquid	Cell (HEK293)	mOR-EG		160,000	(Katada S et al., 2005)
Compound 10	Mouse	Liquid	Cell (HEK293)	mOR-EG		41,000	(Katada S et al., 2005)
Compound 11	Mouse	Liquid	Cell (HEK293)	mOR-EG		57,000	(Katada S et al., 2005)
Compound 15 (4-hydroxy-3-methylbenzaldehyde)	Mouse	Liquid	Cell (HEK293)	mOR-EG		4,000	(Katada S et al., 2005)
Compound 16	Mouse	Liquid	Cell (HEK293)	mOR-EG		215,000	(Katada S et al., 2005)
Compound 17	Mouse	Liquid	Cell (HEK293)	mOR-EG		33,000	(Katada S et al., 2005)
Compound 18	Mouse	Liquid	Cell (HEK293)	mOR-EG		47,000	(Katada S et al., 2005)
Compound 19	Mouse	Liquid	Cell (HEK293)	mOR-EG		68,000	(Katada S et al., 2005)
Compound 22	Mouse	Liquid	Cell (HEK293)	mOR-EG		26,000	(Katada S et al., 2005)
Methyl isoeugenol (MIEG)	Mouse	Vapor	Glomerulus Ea	mOR-EG		3.3	(Oka Y et al., 2006)
Methyl isoeugenol (MIEG)	Mouse	Vapor	Glomerulus Ma	mOR-EG		2.3	(Oka Y et al., 2006)
Methyl isoeugenol (MIEG)	Mouse	Vapor	Cell (HEK293)	MOR204-34		21,000	(Oka Y et al., 2006)
Acetic acid	Human	Vapor	Behavioral	All	Log odds ratio (Eq. (7))	0.094	(Wise PM et al., 2007)
Butyric acid	Human	Vapor	Behavioral	All	Log odds ratio (Eq. (7))	0.0041	(Wise PM et al., 2007)
Isovaleric acid	Mouse	Vapor	Glomerulus Ia	mOR-EG		97	(Oka Y et al., 2006)
Hexanoic acid	Human	Vapor	Behavioral	All	Log odds ratio (Eq. (7))	0.041	(Wise PM et al., 2007)
Octanoic acid	Human	Vapor	Behavioral	All	Log odds ratio (Eq. (7))	0.080	(Wise PM et al., 2007)
Octanedioic acid	Mouse	Liquid	Cell (Xenopus oocyte)	MOR42-3	Eq. (4)	146,000	(Abaffy T et al., 2006)
Nonanoic acid	Human	Liquid	Cell (HeLa/Olf)	Ors86	Eq. (5)	3,300	(Shirokova E et al., 2005)
Nonanedioic acid	Mouse	Liquid	Cell (Xenopus oocyte)	MOR42-3	Eq. (4)	5,900	(Abaffy T et al., 2006)
Nonanedioic acid	Human	Liquid	Cell (HeLa/Olf)	Ors6	Eq. (5)	500	(Shirokova E et al., 2005)
Decanedioic acid	Mouse	Liquid	Cell (Xenopus oocyte)	MOR42-3	Eq. (4)	47,000	(Abaffy T et al., 2006)
Decanedioic acid	Mouse	Liquid	Cell (Xenopus oocyte)	MOR42-1	Eq. (4)	6,500	(Abaffy T et al., 2006)
Undecanedioic acid	Mouse	Liquid	Cell (Xenopus oocyte)	MOR42-1	Eq. (4)	63,000	(Abaffy T et al., 2006)
Dodecanedioic acid	Mouse	Liquid	Cell (Xenopus oocyte)	MOR42-1	Eq. (4)	36,000	(Abaffy T et al., 2006)

In all equations, EC50 = odorant concentration producing half maximal response

^*TXIB: 2,2,4-trimethyl-1,3-pentanediol diisobutyrate

Eq. (2): P = Pmax/(1 + e^(−(x−C)/D)) where P= detection probability corrected for chance, Pmax = 1, x = odorant concentration, C = log EC50, and D: constant (function steepness)

Eq. (3): F(x) = m0 + ((m1 × (x^n))/(C^n + x^n) where m0 = minimum, m1 = maximum, x = odorant concentration, C = EC50, and n = Hill coefficient

Eq. (4): I = Imax/(1 + (EC50/X)^n) where I = current response, Imax = maximal current response, X = odorant concentration, and n = apparent Hill coefficient

Eq. (5): F(x) = (a − d)/(1 + (x/C)^n) + d where a = minimum, d = maximum, x = odorant concentration, C = EC50, and n = Hill coefficient

Eq. (6): R(x) = Rmax (x^n/EC50^n + x^n) where R = maximal response, x = odorant concentration, n = Hill coefficient

Eq. (7): ln{p/(1−p)} = a.x + b, where p = chance-corrected proportion correct detection, x = odorant concentration, a = constant, b = slope

The observations above raise a couple of interesting issues. First, it might be revealing to investigate how the sensitivity to particular odorants changes from the periphery to central levels and from the unicellular to the multicellular (or anatomical structure, e.g., bulb) level. The outcome can provide a quantitative estimate on the gradual gain in chemosensory sensitivity along successive levels, or steps, along the olfactory pathway. This will include information on whether the gain is relatively uniform or different across odorant classes and, in the latter case, whether a physicochemical basis for the difference in gain can be established. Second, in species where olfactory detection of odorants occurs naturally via the vapor phase, it is important to understand the role that presentation of the odorant directly in a liquid phase to a cell or tissue preparation might play in the overall characterization of their olfactory system. This is important because, as noted recently (Goyert HF et al., 2007), stimulation with liquid odorants at high (i.e., micromolar) concentrations could result in non-specific binding and, for the most reactive odorants, e.g., aldehydes and carboxylic acids (Abraham MH et al., 2002), in chemical reactions with proteins that might not represent true “odorant ligand” binding.

Conclusions

Concentration-detection functions for the odor of homologous n-alcohols shift towards lower concentrations with increasing carbon chain length. This pattern has been observed before in our previous work and in comprehensive compilations of olfactory thresholds, where the outcome was measured as single odor threshold values instead of the full functions measured here. In addition, our present results were gathered under an experimental approach that probes the sensitivity of the human sense of smell in conditions that closely resemble a short and natural odor exposure. The outcome provides a more realistic picture of individual variability by minimizing external sources of variation associated with stimulus generation, delivery, and stability, and with subjects’ biases. Under such conditions, the concentration of each alcohol eliciting a probability of detection half-way between chance and perfect detection is in the ppb (by volume) or nM range, i.e., lower than most reported values. In addition, inter-individual variability in ODTs across these normosmic subjects is lower than previously suggested by many studies in the literature.

Figure 4.

As in Figure 2, but individual functions for 1-hexanol.