Skip to main content
PMC home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2003 Aug;12(8):1686–1693. doi: 10.1110/ps.0306603

Library analysis of SCHEMA-guided protein recombination

Michelle M Meyer 1,4, Jonathan J Silberg 1,4, Christopher A Voigt 3, Jeffrey B Endelman 1, Stephen L Mayo 2, Zhen-Gang Wang 1, Frances H Arnold 1
PMCID: PMC2323955  PMID: 12876318

Abstract

The computational algorithm SCHEMA was developed to estimate the disruption caused when amino acid residues that interact in the three-dimensional structure of a protein are inherited from different parents upon recombination. To evaluate how well SCHEMA predicts disruption, we have shuffled the distantly-related β-lactamases PSE-4 and TEM-1 at 13 sites to create a library of 214 (16,384) chimeras and examined which ones retain lactamase function. Sequencing the genes from ampicillin-selected clones revealed that the percentage of functional clones decreased exponentially with increasing calculated disruption (E = the number of residue–residue contacts that are broken upon recombination). We also found that chimeras with low E have a higher probability of maintaining lactamase function than chimeras with the same effective level of mutation but chosen at random from the library. Thus, the simple distance metric used by SCHEMA to identify interactions and compute E allows one to predict which chimera sequences are most likely to retain their function. This approach can be used to evaluate crossover sites for recombination and to create highly mosaic, folded chimeras.

Keywords: Chimera, lactamase, PSE-4, recombination, schema, TEM-1, directed evolution

Numerous protein traits can be improved or altered when recombination is coupled with a screening or selection strategy (for review, see Minshull and Stemmer 1999; Arnold 2001a,b). During laboratory evolution, as in nature, recombination promotes the rapid accumulation of beneficial mutations from multiple parents onto a single offspring (Stemmer 1994b; Moore et al. 1997; Crameri et al. 1998). It also explores a part of sequence space that is particularly rich in folded and functional proteins. Recombination plays a key role in natural evolution of proteins through the swapping of well-defined structural domains (Ostermeier and Benkovic 2001). Where a domain structure is not obvious, however, how recombination contributes to the evolution and diversification of protein sequence and function is less well understood.

Recently we developed an algorithm, called SCHEMA, for predicting which fragments of homologous proteins can be recombined without disturbing the integrity of the structure (Voigt et al. 2002). Based on the 3D structures of the parent proteins, the algorithm identifies pairs of amino acids that are interacting, defined as those residues within a cutoff distance of 4.5 Å, and determines the net number of interactions broken when a chimeric protein inherits portions of its sequence from different parents (defined as E). Because calculating E for all possible crossover combinations is computationally intractable, it is difficult to identify which crossover locations are optimal with respect to their ability to yield folded chimeras. One version of SCHEMA circumvents this computational difficulty by finding compact, contiguous polypeptides with the largest number of intrablock interactions—these polypeptides correspond to fragments which in theory can be swapped with minimal cost. This is achieved by scanning the protein sequence with a window of defined size to create a disruption profile whose minima are predicted to represent crossover locations that preserve more interactions. It was proposed that the resulting fragments, or schemata, could be recombined using available laboratory recombination methods (Horton et al. 1989; Solaiman et al. 2000; Gibbs et al. 2001; O’Maille et al. 2002) to generate novel mosaic sequences that retain the parental structure.

A strong correlation exists between SCHEMA disruption profiles and existing experimental data on chimeras from site-directed recombination and DNA-shuffling experiments. In particular, the vast majority of the crossovers found in functional chimeras containing one or two crossovers appear in or near the minima of their calculated disruption profiles (Voigt et al. 2002), suggesting that crossovers at other locations (e.g., profile maxima) are unfavorable. Furthermore, functional analysis of 12 lactamase chimeras revealed that proteins tolerate a limited level of E; only those with E ≤ 26 were functional (Voigt et al. 2002). However, the small numbers of functional and nonfunctional chimeras analyzed in these studies and the small number of crossovers incorporated make it difficult to determine just how SCHEMA predictions correlate with functional and structural disruption. We would like to know whether chimeras with low E have a higher probability of retaining parental function than those with the same effective level of mutation but chosen at random. We would also like to know whether the minima in the profile still correspond to the best recombination sites when multiple crossovers are allowed.

To better test how well SCHEMA predicts crossovers that generate new folded proteins, we have created a large library of chimeras with a broad range of E, and examined which recombination events conserve function. For this test, we recombined two β-lactamases, using antibiotic selection to identify functional proteins. The parent PSE-4 and TEM-1 β-lactamases share 40% amino acid identity, have very similar structures (0.98 Å RMS deviation; Jelsch et al. 1993; Lim et al. 2001), and exhibit similar substrate specificities and activities towards the antibiotic ampicillin (kcat/Km ca. 107 M−1s−1; Matagne et al. 1998; Savoie et al. 2000).

Results

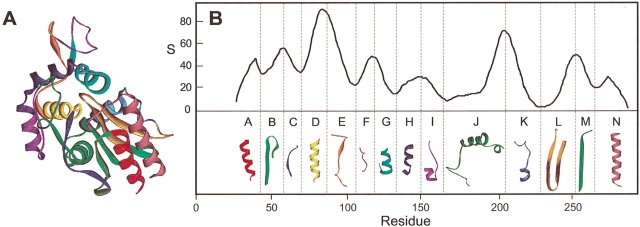
The SCHEMA-calculated profile shown in Figure 1 ▶ was used to guide the creation of a diverse library of lactamase chimeras exhibiting a broad range of disruption. Eight major peaks in the profile correspond to eight polypeptides with the largest number of intrablock interactions. We allowed recombination at seven minima and six maxima of the disruption profile, yielding a library containing 214 (16,384) possible unique chimeras. By calculating the exact disruption (E) of every sequence, we determined that the library contains chimeras with disruption values ranging from 7 to 113. Additionally, the chimeras display a broad range of effective mutations, from 7 to 75 amino acid substitutions relative to the closest parent.

Figure 1.

Figure 1.

Open in a new tab

Polypeptides recombined between TEM-1 and PSE-4. (A) Polypeptide modules swapped between lactamases are mapped onto the structure of TEM-1. (B) Profile disruption S was calculated for recombination of TEM-1 and PSE-4 using the crystal structure coordinates for TEM-1 (Jelsch et al. 1993) and a window size of 14 (see Materials and Methods). Residues are numbered based on the sequence of TEM-1. Vertical dashed lines represent crossover sites.

Twenty-eight gene modules were synthesized chemically or by PCR (14 for each parent). Gene modules encoding structurally related elements contained identical unique 5′ overhangs, but the sequences of the overhangs at each module boundary were distinct and nonpalindromic. Each parental gene was assembled to confirm that no mutations were present in the modules and to validate that full-length genes could be created. Because ligation efficiency decreased as the number of fragments increased, we used a serial assembly protocol. Two or three adjacent gene fragments were ligated and purified using an agarose gel to create six distinct sets of products. This process was repeated using the ligated products until the full-length genes were assembled. After assembly, pse-4 and tem-1 were amplified by PCR and cloned into the vector pMon•1A2; this bacterial vector contains a constitutive PSE-4 promoter and kanamycin selectable marker (Sabbagh et al. 1998). Escherichia coli transformed with pMonTEM1 and pMonPSE4 were selected on LB-agar plates containing a range of ampicillin concentrations (5 to 5000 μg/mL). Cells containing tem-1 and pse-4 grew on plates containing up to ~1000 and 3000 μg/mL of ampicillin, respectively, similar to that previously reported (Sabbagh et al. 1998). The minimum inhibitory concentration (MIC) of ampicillin for the strain of E. coli used was <5 μg/mL. Sequencing showed that no mutations were introduced into pse-4 or tem-1 during assembly.

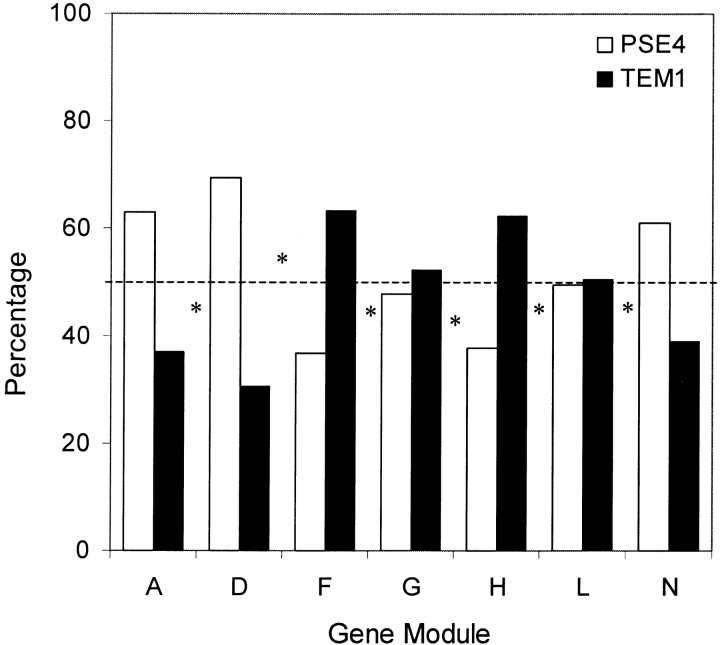
To create the library of chimeric lactamases, equimolar mixtures of modules from each parent were mixed and ligated using a procedure similar to that for assembling the parental genes. E. coli were transformed with this library, and thousands of variants were plated on nonselective medium, that is, LB-agar plates containing kanamycin. To determine if the library contained any significant sequence biases, we measured the distribution of pse-4 and tem-1 modules in 79 randomly chosen chimeras using oligonucleotide probe hybridization (Joern et al. 2002). Figure 2 ▶ shows the incorporation of the different parental sequences at seven positions throughout the genes and the frequency of crossovers between the modules probed, that is, how often adjacent probed positions had sequence from the same parent. All chimeras exhibited a near-random crossover frequency between the probed modules (46 ± 5%), and the average frequency of observing the rarer of the two parents at each position was 40 ± 6%. When we treat all chimeras as occurring with an equal frequency in the unselected library, we calculate that a selection of 200,000 variants will contain >99% of the unique chimera sequences.

Figure 2.

Figure 2.

Open in a new tab

Incorporation of tem-1 and pse-4 at different sequence positions in the unselected library. The presence of sequence from tem-1 and pse-4 at seven different module positions in 79 randomly picked unselected chimeras was determined using oligonucleotide probe hybridization. Asterisks represent the percentage of chimeras with crossovers occurring between adjacent probed positions. The dashed line represents the expected percentage of genes and crossovers in an unbiased library (50%).

Approximately 200,000 variants were plated on selective medium, LB-agar containing kanamycin and 20 μg/mL ampicillin. More than 100 colonies were observed, and sequencing 50 of these clones identified 23 unique functional lactamase chimeras, in addition to PSE-4 and TEM-1. Identification of the parental clones is consistent with predictions from hybridization results that suggest more than half of the chimeras were analyzed. Despite the PCR steps involved in library construction, the selected library displays a low point mutagenesis rate (0.005%). Only one chimera, the third sequence shown in Figure 3 ▶, has amino acid substitutions. In this chimera, PSE-4 residues 265 and 266 are mutated from glutamine to histidine and threonine to serine, respectively. Examination of the TEM-1 and PSE-4 crystal structures reveal that these residues are both on the surface of the protein, and neither is in the active site (Jelsch et al. 1993; Lim et al. 2001).

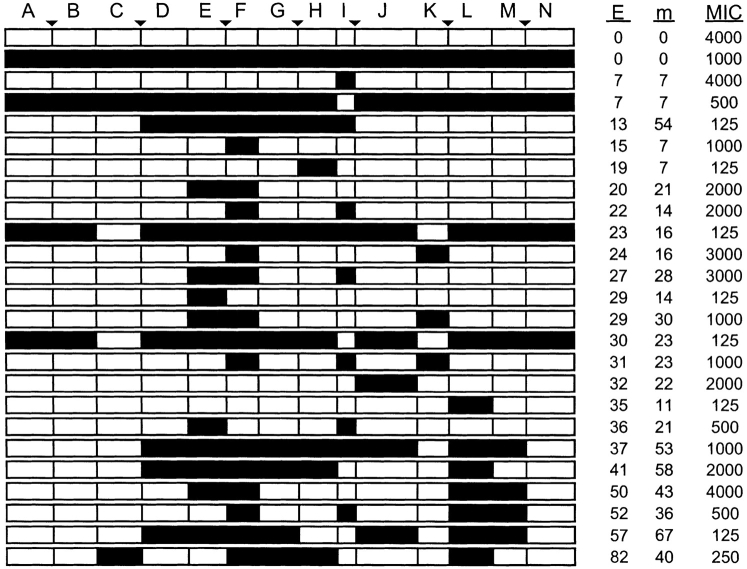
Figure 3.

Figure 3.

Open in a new tab

Sequences, calculated disruption, and effective level of mutation of functional lactamases. Closed triangles indicate profile minima, and filled and open blocks represent TEM-1 and PSE-4 sequences, respectively. The calculated disruption E represents the number of interactions broken by recombination. Minimal inhibitory concentrations of ampicillin (MIC) are in μg/mL and were determined using liquid cultures. Effective level of mutation (m) is the minimum number of mutations required to convert a chimera into one of its parents at only those residues recognized by SCHEMA, that is, residues whose coordinates are defined in the TEM-1 structure (Jelsch et al. 1993).

As shown in Figure 3 ▶, the functional chimeras are highly mosaic, with one, two, three, four, five, six, or seven modules swapped, and have between 7 and 67 effective mutations per chimera; the maximum possible in the library is 75. Furthermore, selected chimeras exhibited an average of 3.7 ± 1.5 crossovers, significantly lower than that expected from a random library (6.5 ± 1.8), and all chimeras have an even number of crossovers (two, four, or six), that is, each functional chimera derives the A and N modules from the same parent. Modules A and N are derived from different parents in 41% of the clones in the unselected library.

Of the 50 functional lactamases sequenced, only four derived both terminal fragments from TEM-1: three chimeras and one TEM-1. This indicates that chimeras that derive sequence from opposite parents at each position (chimera mirrors) are not functionally equivalent, even though SCHEMA does not distinguish them. Sequence analysis of randomly picked clones from the unselected library showed that 34% of the clones that acquire the A and N modules from the same parent contain TEM-1 at these positions. This small bias in the library does not account for the low level of TEM-1 terminal modules in functional chimeras (8%). The enrichment of one chimera from a mirror pair may arise because functional chimeras with TEM-1 terminal modules exhibit lower activity than those with PSE-4 at those positions. In fact, functional chimeras with TEM-1 terminal modules exhibit a significantly lower average MIC (250 μg/mL) than those with PSE-4 termini (1400 μg/mL). Also, for the mirror chimeras isolated, the TEM-like clone exhibits lower activity (Fig. 3 ▶).

To determine if conservation of function corresponds to low E, we compared the distribution of E for the functional sequences with every theoretically possible unique chimera in our library. Figure 4A ▶ shows the distributions of disruption for all chimeras in the selected and theoretical unselected libraries. The average E observed for functional clones (32 ± 17) is significantly lower than that calculated for the entire library (72 ± 16), indicating a strong association of low levels of disruption with maintenance of function. More than 90% of the functional chimeras have E ≤ 52, while only 11% of the chimeras in the theoretical library fall below this threshold. We quantified the fraction of functional chimeras at each E in Figure 4A ▶ by dividing the number of different functional sequences by the number of different sequences in the unselected library at each E (see Fig. 4B ▶). This analysis reveals that the fraction of chimeras that retain lactamase activity decreases exponentially with increasing disruption.

Figure 4.

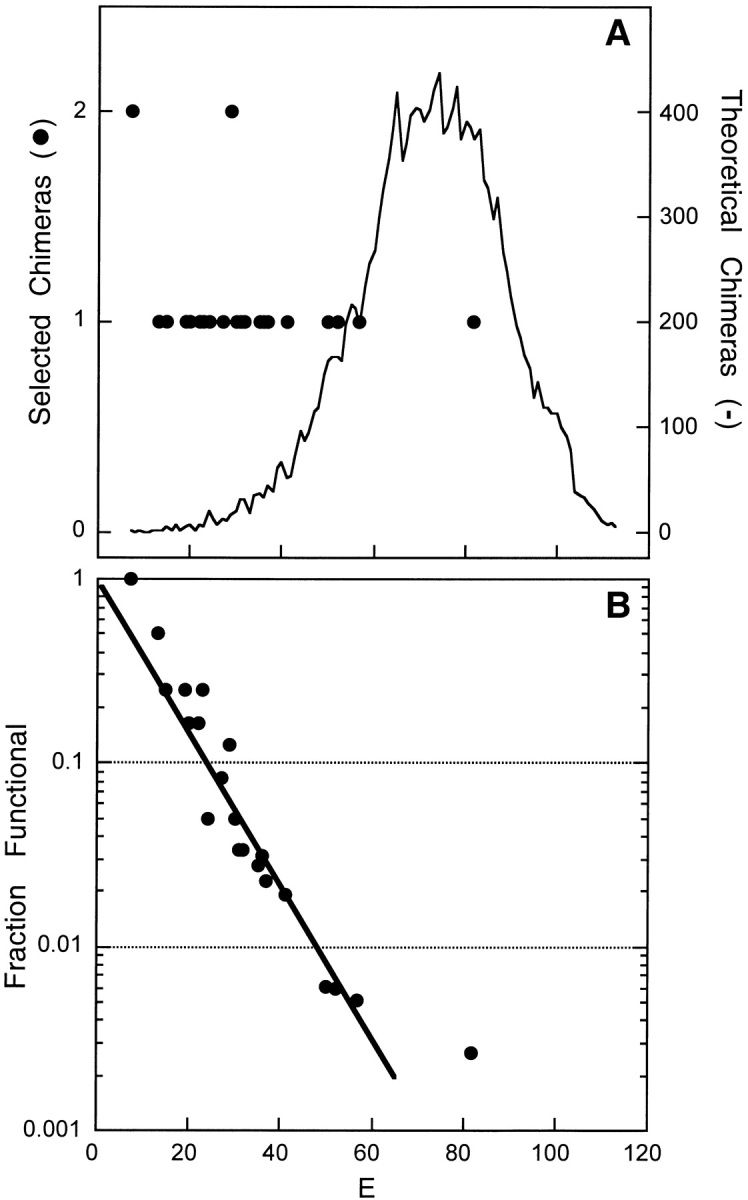
Figure 4.

Open in a new tab

Relationship between E and chimera function. (A) The disruption distribution of all possible chimeras (solid line) is compared with those discovered in the selection for activity (filled circles). (B) The fraction of theoretical chimeras identified as functional is shown for each E. The data were fit to Equation 1 using N = 322 to obtain the probability that a disruption leads to a nonfunctional chimera, fd = 0.095.

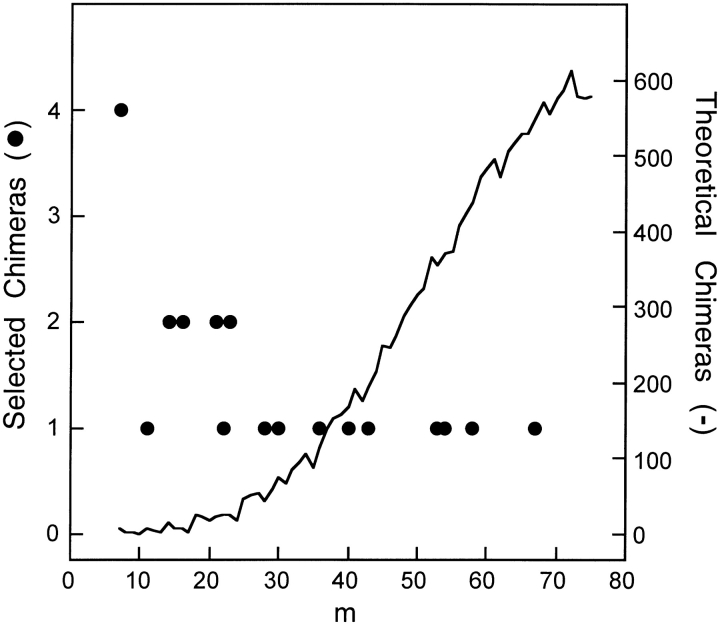
The fraction of chimeras in our library that retain function also depends on the level of mutation (see Fig. 5 ▶), which raises the possibility that the low average E of functional chimeras could arise because low E corresponds to a lower average number of mutations. To investigate this, we calculated the relative difference (Eselected − ≤E>)/≤E> for each functional chimera, where Eselected is the disruption of the functional chimera, and ≤E> is the average disruption of all chimeras in the theoretical library with the same effective level of mutation (see Fig. 6 ▶). The average relative difference for all functional chimeras in our library is −17.6%, suggesting that functional chimeras have lower disruption than those chosen at random with the same level of mutation. We then applied the Wilcoxon signed-rank test to evaluate the significance of these relative differences (Bernstein and Bernstein 1999). The Wilcoxon analysis yielded a ≥99% probability that the median relative difference for all functional chimeras in any library is <0. Thus, chimeras that minimize E will have a greater likelihood of exhibiting undisturbed function than those chosen at random with the same level of mutation.

Figure 5.

Figure 5.

Open in a new tab

Relationship between level of mutation and chimera function. The underlying distributions for the number of effective mutations (m) of all possible chimeras (solid line) and selected (filled circles) chimeras are shown.

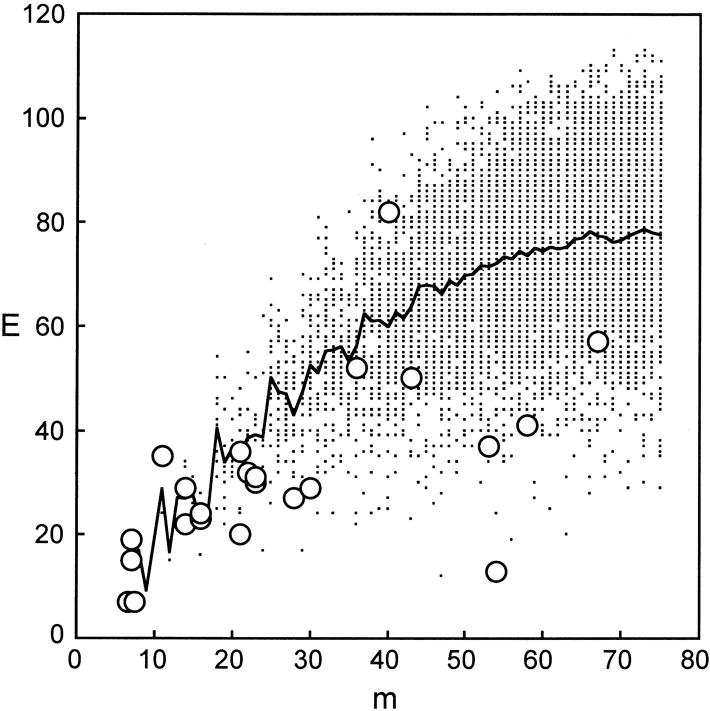
Figure 6.

Figure 6.

Open in a new tab

E and m for all possible chimeras. At each level of mutation (m) where functional chimeras were obtained, the possible E values (filled circles), the mean E for all possible chimeras (solid line), and the E of functional chimeras (open circles) are shown. Highly mutated chimeras have significantly lower disruption than the mean.

Discussion

Our results demonstrate that SCHEMA-calculated disruption (E) is a good metric for predicting functional conservation upon recombination. Sequence analysis of functional lactamases selected from a large library shows that chimeras with low E have a higher probability of retaining function than do chimeras with the same effective level of mutation but chosen at random. Our results also show that functional conservation decreases exponentially as E increases. This complements our previous finding, based on a small number of chimeras, that recombination disrupts protein function when it breaks many contacts in the three-dimensional structure (high E; Voigt et al. 2002).

A simple probabilistic model can be invoked to anticipate the likelihood that lactamase chimeras will retain function. Assuming all contacts defined by SCHEMA are statistically independent, the fraction of possible recombinants at each E that retain function Pf is

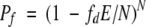graphic file with name M1.gif (1)

where N is the total number of interactions in the parental structures that can be disrupted upon recombination, and fd is the probability that a disrupted contact yields a nonfunctional chimera. When N is large, as it is for proteins, this model yields a Pf that decays exponentially with E. Fitting Equation 1 to our data yields fd = 0.095 (see Fig. 4B ▶). Because the experiment selected for functional chimeras, it could not uncover nonfunctional proteins that nonetheless retain proper fold. Furthermore, our use of a weak constitutive lactamase promoter to express chimeras in E. coli limits our ability to identify lactamases with very low activity. Therefore, this value for fd should be considered an upper bound on the probability that a disrupted contact yields unstructured or misfolded proteins, and the value of Pf that we calculate from fd is therefore a conservative estimate of the probability that a protein structure will not be disrupted by recombination.

Structure-guided recombination identifies highly mosaic chimeras that retain lactamase structure and exhibits greater effective levels of mutation than previously found with other methods. Several of our functional chimeras differ by more than 40 amino acids from the closest parent; one is 67 amino acids distant, and the sequences of these distant chimeras all contain four to six crossovers (see Fig. 3 ▶). Annealing-based recombination methods such as DNA shuffling (Stemmer 1994a; Moore et al. 1997; Crameri et al. 1998), StEP (Zhao et al. 1998), or in vivo techniques (Volkov et al. 1999) cannot recombine proteins exhibiting sequence identity as low as PSE-4 and TEM-1. Multiple-crossover chimeras can only be created using homologs with very high (often >70%) sequence identity; therefore, a maximum of ~40 effective mutations can be incorporated when two proteins the size of TEM-1 are recombined. The maximum level of mutation is often less than this because annealing-based techniques direct crossovers overwhelmingly to regions of high identity. Sequence-independent methods that can randomly recombine distantly related proteins to create high levels of mutation have also been described (Ostermeier et al. 1999; Lutz et al. 2001; Sieber et al. 2001). However, these methods have only created chimeras with one or two crossovers.

To simplify the identification of chimeras with low disruption, the SCHEMA algorithm generated a disruption profile such as shown in Figure 1 ▶ by calculating the contribution each residue makes to the internal interactions within a fragment covered by a sliding window of a given size. We previously found that nondisruptive crossovers frequently occur in or near minima of SCHEMA profiles in chimeras with one or two crossovers, suggesting these minima may be a useful guide for generating folded and functional chimeras (Voigt et al. 2002). Interestingly, crossovers in functional lactamase chimeras from our library did not occur predominantly at these minima. Almost half of all crossovers in the functional lactamases occurred at the sites corresponding to profile maxima (see Fig. 3 ▶). In addition, no functional chimeras were found with an odd number of crossovers: Only two, four, and six crossovers generated functional chimeras. This crossover distribution is similar to that predicted for chimeras with a ≥10% probability of exhibiting undisturbed function (E ≤ 24; see Fig. 4B ▶); of these chimeras, 88% have even numbers of crossovers, and almost half of the crossovers (46%) occur at maxima. These findings suggest that interactions between polypeptides distal in the primary sequence, that is, those not included in the profile calculation, should be considered when choosing crossover locations. In other words, profile minima become a poor guide for predicting nondisruptive crossover locations when many crossovers can take place.

A better way to identify crossover points that minimize functional disruption is to determine which chimeras have the lowest E. But, because crossovers that do not lead to mutation will always minimize E, we also have to maintain a desired level of mutation. For chimeras arising from a small number of crossovers, it is easy to enumerate E for all possible chimera and identify crossover locations that minimize disruption. However, complete enumeration becomes impossible when multiple crossovers are allowed. For example, it is computationally intractable to calculate E for all possible seven crossovers between PSE-4 and TEM-1 and identify which seven-crossover library encodes chimeras with the lowest average E values, among libraries encoding chimeras with similar average levels of mutation. However, it is not difficult to evaluate thousands of randomly-chosen seven-crossover libraries using SCHEMA to determine which ones encode chimeras with lower than average E. We find that this type of analysis is better than using profile minima to choose nondisruptive crossover locations for multiple-crossover libraries. For example, a PSE-4 and TEM-1 recombinant library made by allowing crossovers at the seven profile minima of Figure 1 ▶ is predicted to encode 10 times fewer functional chimeras (≤E> = 52 ± 17) than the best library found by searching 10,000 randomly generated libraries with seven crossovers (≤E> = 33 ± 10), even though both libraries encode chimeras with similar levels of mutation.

In future studies we will examine whether SCHEMA-guided recombination of distantly related proteins can yield libraries of shuffled sequences from which novel functions can be obtained by screening or selection. Recombination techniques such as DNA shuffling (Stemmer 1994b; Crameri et al. 1998), StEP (Zhao et al. 1998), ITCHY (Ostermeier et al. 1999), SHIPREC (Sieber et al. 2001), and in vivo techniques (Volkov et al. 1999) do not control the location or frequency of crossovers in combinatorial libraries, and therefore, do not minimize structural disruption or maximize sequence diversity. However, the results described here suggest that libraries created using targeted recombination methods (Horton et al. 1989; Solaiman et al. 2000; Gibbs et al. 2001; O’Maille et al. 2002; K. Hiraga and F.H. Arnold, in prep.) to make crossovers at sites predicted to minimize disruption will be simultaneously rich in folded proteins and diverse sequences. With such libraries we will be able to explore the evolution of protein function as well as rapidly assess sequence–function relationships (Joern et al. 2002).

Materials and methods

Materials

E. coli XL1-Blue was from Stratagene. Enzymes for DNA manipulations were obtained from New England Biolabs, Roche Biochemicals, or United States Biochemical Corp. Synthetic oligonucleotides were obtained from Invitrogen. DNA purification kits were from Zymo Research and Qiagen, and other reagents were from Sigma Chemical Co. or Fisher Scientific.

Calculations

For hybrids in which fragment(s) α and β are inherited from PSE-4 and TEM-1, respectively, the disruption (E) of the hybrid was calculated using Equation 2, where cij = 1 if residues are contacting (otherwise cij = 0), and Pij = 0 if i or j are identical in PSE-4 and TEM-1 (otherwise Pij = 1; Voigt et al. 2002). Two residues were considered contacting if any atoms in the TEM-1 structure (1BTL; Jelsch et al. 1993), excluding hydrogens, backbone nitrogens, and backbone oxygens, were within 4.5 Å.

graphic file with name M2.gif (2)

To calculate the SCHEMA profile, a window of w residues is defined, and the number of intrawindow interactions are counted. The profile disruption of all residues in this window is incremented by the number of contacts within the window. The window is then slid along the protein sequence, and a profile is generated by incrementing the disruption of each residue (Si) for all windows in which it resides. The numerical value of the SCHEMA–profile function S at residue i is defined by Equation 3; the magnitude of Si corresponds with the level of predicted structural disruption for a crossover at a residue. A window of 14 residues was used to calculate the profile in Figure 1 ▶.

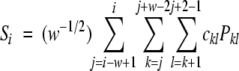graphic file with name M3.gif (3)

Software for performing SCHEMA calculations is available on the Web at www.che.caltech.edu/groups/fha/code.html.

Vectors

Lactamases were cloned into the vector pMon•1A2, which was created by cloning the gene encoding the heme domain of cytochrome P450 1A2 into pMon711 (Sabbagh et al. 1998). This vector was used for all selections. However, because this vector yields high background in oligonucleotide probe hybridization experiments, chimeras were cloned into pBC KS+ (Stratagene) for these studies. E. coli XL1-Blue transformed with these vectors were used for all analysis.

Library construction

Twenty-eight gene modules were created to assemble the lactamase genes (14 for each parent). The protein modules correspond to TEM-1 residues 1–39 (A), 40–57 (B), 58–67 (C), 68–84 (D), 85–102 (E), 103–115 (F), 116–131 (G), 132–146 (H), 147–163 (I), 164–204 (J), 205–222 (K), 223–249 (L), 250–264 (M), 265–286 (N), and structurally related residues in PSE-4 identified using a structure-based alignment with Swiss-Pdb Viewer (Guex and Peitsch 1997). All modules used in assembly were double stranded and contained unique nonpalindromic overhangs that allow for specific sequential ligation without concatamer production. Silent mutations were introduced into both genes at module boundaries (overhangs) to allow for facile assembly.

Chemically synthesized oligonucleotides used to create modules B, C, D, E, F, G, H, I, K, and M were phosphorylated using T4 polynucleotide kinase, and double-stranded modules were created from these by heating a reaction mixture containing 2.5 μM of complementary oligonucleotides, 10 mM Tris pH 8.0, 1 mM EDTA, and 50 mM NaCl at 95°C for 2 min and subsequently cooling the reaction to room temperature at a rate of 0.1°C per second. Modules larger than 70 base pairs (A, J, L, and N) were amplified with Vent DNA polymerase using primers containing SapI restriction sites; this allowed for rapid generation of complementary overhangs after amplification. Primers that amplified the terminal modules had a single SacI or HindIII site to allow for subsequent cloning. Amplified modules were purified by agarose gel electrophoresis, each (200 ng) was cut with 10 units of SapI at 37°C for 24 h, and digested modules were purified using agarose gel electrophoresis before assembly.

T4 DNA ligase was used to assemble pse-4, tem-1, and chimeric genes through a sequential process where pairs of adjacent modules were ligated, purified by agarose gel electrophoresis, and subsequently ligated to other assembled modules. Gene fragments composed of modules AB, CD, EFG, HIJ, KL, and MN were created in the first ligation reactions. For reactions in which the chimeric library was assembled, equimolar mixtures of modules derived from each parent were used in this step. The ligated module dimers and trimers were further assembled, using the ligated fragments that had been purified with an agarose gel, to construct ABCDEFG and HIJKLMN using T4 DNA ligase. Because yields were low, ABCDEFG and HIJKLMN were amplified using Vent DNA polymerase and cleaved by SapI prior to assembly of full-length lactamases in a third ligation step; SapI created complementary overhangs at the G and H termini. Full-length constructs were treated with SacI and HindIII, purified using a Zymo DNA Clean and Concentrator Kit, and ligated into pMon•1A2 and pBC KS(+), which were prepared similarly, to create the chimeric library.

Oligonucleotide probe hybridization

Sequences of 79 randomly-selected chimeras from the unselected library in pBC KS+ were determined for 7 modules (A, D, F, G, H, L, and N) using oligonucleotide probe hybridization (Joern et al. 2002; Meinhold et al. 2003).

Functional chimera selection

The minimal inhibitory concentration (MIC) of ampicillin for XL1-Blue E. coli containing pMon•1A2 is <5 μg/mL on LB-agar medium containing 10 μg/mL kanamycin. Therefore, functional selections using the pMon plasmid were performed under conditions that gave no background, that is, 20 μg/mL ampicillin and 10 μg/mL kanamycin. XL1-Blue were transformed with the unselected library using a heat-shock protocol recommended by the supplier, plated on selective medium, and incubated at 37°C for 24 h. Plasmid DNA was purified from all functional clones and digested with HindIII and SacI to confirm pse-4 and tem-1 length inserts (ca. 1 kb) were present. In addition, XL1-Blue were transformed with the purified DNA to verify the purified vectors conferred the ampicillin resistance. A majority of the clones had plasmids with an appropriate size insert and conferred resistance in a second selection; 50 of these were sequenced.

Wilcoxon signed-rank test

The Wilcoxon signed-rank test is a nonparametric technique for investigating hypotheses about the median of a population (Bernstein and Bernstein 1999). Although this test has less power than a t-test for small sample sizes, that is, less likely to yield as dramatic a P-value, we used this method because it makes no assumptions about the data being sampled from a normal distribution. To calculate the test statistic (W), we ranked the relative differences, (Eselected − 〈E〉)/〈E〉, at each level of mutation according to their absolute magnitude and summed the rank scores according to the sign of the relative difference. This yielded W+ and W− values of 58 and −218, respectively. The critical value (62) for a one-tailed Wilcoxon test for 23 functional chimeras with a P = 0.01 is larger than W+, indicating that there is a <1% probability that the median relative difference is ≥0.

Acknowledgments

This work was supported by the Army Research Office, NIH Fellowship F32 GM64949-01 (J.J.S.), Howard Hughes Medical Institute graduate research fellowship (M.M.M.), National Defense Science and Engineering Fellowship (J.B.E.), National Science Foundation (C.A.V.), and Burroughs-Welcome Fund (C.A.V.). Z.G.W. acknowledges support by the W.M. Keck Foundation. S.L.M. is supported by the Howard Hughes Medical Institute, the Ralph M. Parsons Foundation, and an IBM Shared University Research Grant.

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.

Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.0306603.

References

  1. Arnold, F.H., ed. 2001a. Advances in protein chemistry, Vol. 55. Academic Press, San Diego, CA.
  2. ———. 2001b. Combinatorial and computational challenges for biocatalyst design. Nature 409 253–257. [DOI] [PubMed] [Google Scholar]
  3. Bernstein, S. and Bernstein, R., eds. 1999. Elements of statistics II: Inferential statistics. McGraw-Hill, New York.
  4. Crameri, A., Raillard, S.A., Bermudez, E., and Stemmer, W.P. 1998. DNA shuffling of a family of genes from diverse species accelerates directed evolution. Nature 391 288–291. [DOI] [PubMed] [Google Scholar]
  5. Gibbs, M.D., Nevalainen, K.M., and Bergquist, P.L. 2001. Degenerate oligonucleotide gene shuffling (DOGS): A method for enhancing the frequency of recombination with family shuffling. Gene 271 13–20. [DOI] [PubMed] [Google Scholar]
  6. Guex, N. and Peitsch, M.C. 1997. SWISS-MODEL and the Swiss-PdbViewer: An environment for comparative protein modeling. Electrophoresis 18 2714–2723. [DOI] [PubMed] [Google Scholar]
  7. Horton, R.M., Hunt, H.D., Ho, S.N., Pullen, J.K., and Pease, L.R. 1989. Engineering hybrid genes without the use of restriction enzymes: Gene splicing by overlap extension. Gene 77 61–68. [DOI] [PubMed] [Google Scholar]
  8. Jelsch, C., Mourey, L., Masson, J.M., and Samama, J.P. 1993. Crystal structure of Escherichia coli TEM1 β-lactamase at 1.8 Å resolution. Proteins 16 364–383. [DOI] [PubMed] [Google Scholar]
  9. Joern, J.M., Meinhold, P., and Arnold, F.H. 2002. Analysis of shuffled gene libraries. J. Mol. Biol. 316 643–656. [DOI] [PubMed] [Google Scholar]
  10. Lim, D., Sanschagrin, F., Passmore, L., De Castro, L., Levesque, R.C., and Strynadka, N.C. 2001. Insights into the molecular basis for the carbenicillinase activity of PSE-4 β-lactamase from crystallographic and kinetic studies. Biochemistry 40 395–402. [DOI] [PubMed] [Google Scholar]
  11. Lutz, S., Ostermeier, M., Moore, G.L., Maranas, C.D., and Benkovic, S.J. 2001. Creating multiple-crossover DNA libraries independent of sequence identity. Proc. Natl. Acad. Sci. 98 11248–11253. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Matagne, A., Lamotte-Brasseur, J., and Frere, J.M. 1998. Catalytic properties of class A β-lactamases: Efficiency and diversity. Biochem. J. 330 581–598. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Meinhold, P., Joern, J., and Silberg, J.J. 2003. Analysis of shuffled libraries by oligonucleotide probe hybridization. Methods Mol. Biol. 231 177–188. [DOI] [PubMed] [Google Scholar]
  14. Minshull, J. and Stemmer, W.P. 1999. Protein evolution by molecular breeding. Curr. Opin. Chem. Biol. 3 284–290. [DOI] [PubMed] [Google Scholar]
  15. Moore, J.C., Jin, H.M., Kuchner, O., and Arnold, F.H. 1997. Strategies for the in vitro evolution of protein function: Enzyme evolution by random recombination of improved sequences. J. Mol. Biol. 272 336–347. [DOI] [PubMed] [Google Scholar]
  16. O’Maille, P., Bakhtina, M., and Tsai, M. 2002. Structure-based combinatorial protein engineering (SCOPE). J. Mol. Biol. 321 677. [DOI] [PubMed] [Google Scholar]
  17. Ostermeier, M. and Benkovic, S.J. 2001. Evolution of protein function by domain swapping. Adv. Protein Chem. 55 29–77. [DOI] [PubMed] [Google Scholar]
  18. Ostermeier, M., Shim, J.H., and Benkovic, S.J. 1999. A combinatorial approach to hybrid enzymes independent of DNA homology. Nat. Biotechnol. 17 1205–1209. [DOI] [PubMed] [Google Scholar]
  19. Sabbagh, Y., Theriault, E., Sanschagrin, F., Voyer, N., Palzkill, T., and Levesque, R.C. 1998. Characterization of a PSE-4 mutant with different properties in relation to penicillanic acid sulfones: Importance of residues 216 to 218 in class A β-lactamases. Antimicrob. Agents Chemother. 42 2319–2325. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Savoie, A., Sanschagrin, F., Palzkill, T., Voyer, N., and Levesque, R.C. 2000. Structure–function analysis of α-helix H4 using PSE-4 as a model enzyme representative of class A β-lactamases. Protein Eng. 13 267–274. [DOI] [PubMed] [Google Scholar]
  21. Sieber, V., Martinez, C.A., and Arnold, F.H. 2001. Libraries of hybrid proteins from distantly related sequences. Nat. Biotechnol. 19 456–460. [DOI] [PubMed] [Google Scholar]
  22. Solaiman, F., Zink, M.A., Xu, G., Grunkemeyer, J., Cosgrove, D., Saenz, J., and Hodgson, C.P. 2000. Modular retro-vectors for transgenic and therapeutic use. Mol. Reprod. Dev. 56 309–315. [DOI] [PubMed] [Google Scholar]
  23. Stemmer, W.P. 1994a. DNA shuffling by random fragmentation and reassembly: In vitro recombination for molecular evolution. Proc. Natl. Acad. Sci. 91 10747–10751. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. ———. 1994b. Rapid evolution of a protein in vitro by DNA shuffling. Nature 370 389–391. [DOI] [PubMed] [Google Scholar]
  25. Voigt, C.A., Martinez, C., Wang, Z.G., Mayo, S.L., and Arnold, F.H. 2002. Protein building blocks preserved by recombination. Nat. Struct. Biol. 9 553–558. [DOI] [PubMed] [Google Scholar]
  26. Volkov, A.A., Shao, Z., and Arnold, F.H. 1999. Recombination and chimeragenesis by in vitro heteroduplex formation and in vivo repair. Nucleic Acids Res. 27 e18. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Zhao, H., Giver, L., Shao, Z., Affholter, J.A., and Arnold, F.H. 1998. Molecular evolution by staggered extension process (StEP) in vitro recombination. Nat. Biotechnol. 16 258–261. [DOI] [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES