Structure-based phenotyping predicts HIV-1 protease inhibitor resistance

Abstract

Mutations in HIV-1 drug targets lead to resistance and consequent therapeutic failure of antiretroviral drugs. Phenotypic resistance assays are time-consuming and costly, and genotypic rules-based interpretations may fail to predict the effects of multiple mutations. We have developed a computational procedure that rapidly evaluates changes in the binding energy of inhibitors to mutant HIV-1 PR variants. Models of WT complexes were produced from crystal structures. Mutant complexes were built by amino acid substitutions in the WT complexes with subsequent energy minimization of the ligand and PR binding site residues. Accuracy of the models was confirmed by comparison with available crystal structures and by prediction of known resistance-related mutations. PR variants from clinical isolates were modeled in complex with six FDA-approved PIs, and changes in the binding energy (ΔE_bind) of mutant versus WT complexes were correlated with the ratios of phenotypic 50% inhibitory concentration (IC₅₀) values. The calculated ΔE_bind of five PIs showed significant correlations (R² = 0.7–0.8) with IC₅₀ ratios from the Virco Antivirogram assay, and the ΔE_bind of six PIs showed good correlation (R² = 0.76–0.85) with IC₅₀ ratios from the Virologic PhenoSense assay. ΔE_bind cutoffs corresponding to a four-fold increase in IC₅₀ were used to define the structure-based phenotype as susceptible, resistant, or equivocal. Blind predictions for 78 PR variants gave overall agreement of 92% (kappa = 0.756) and 86% (kappa = 0.666) with PhenoSense and Antivirogram phenotypes, respectively. The structural phenotyping predicted drug resistance of clinical HIV-1 PR variants with an accuracy approaching that of frequently used cell-based phenotypic assays.

Antiretroviral drugs targeting the RT and PR enzymes of HIV-1 may result in dramatic suppression of viral replication in infected individuals (Palella Jr. et al. 1998; Carpenter et al. 2000). However, when viral replication is incompletely suppressed, drug-resistant variants emerge through the accumulation of mutations in the HIV-1 RT or PR genes, leading to therapeutic failure (Hirsch et al. 2000). Genotypic testing for resistance is a relatively rapid and inexpensive method to identify PR and RT amino acid substitutions leading to drug resistance (Baxter et al. 2000; Schinazi et al. 2000; Shafer 2002). Genotyping is recommended for use in clinical practice (Hirsch et al. 2000). However, rules-based interpretation systems are retrospective in nature and must be frequently updated to accommodate new mutational patterns and new antiretrovirals. As a result, genotypic predictions for complex mutational patterns and for new antiretrovirals may be inaccurate (Baxter et al. 2000). Cell-based viral phenotyping assays (Hertogs et al. 1998; Petropoulos et al. 2000; Qari et al. 2002) have been correlated with favorable clinical outcomes (Cohen et al. 2002) and may offer a more reliable measure of resistance in cases in which mutational patterns are complex or the genotypic resistance pattern has not been determined (Haubrich et al. 2001). However, phenotypic assays are more time-consuming and expensive than genotypic assays, and the clinically significant cutoffs for the change in IC₅₀ for some drugs are still uncertain. A hybrid approach, matching viral sequence against a database of paired viral genotypes and phenotypes, is used to derive a VirtualPhenotype, a computational prediction of viral resistance (Tibotec-Virco; http://www.tibotec-virco.com). This method provides a quantitative estimate of drug resistance, although it may fail to give a prediction when few phenotypic matches for a particular variant are identified in the database, as is the case for rare mutational patterns or newly introduced drugs.

HIV-1 PR, a homodimer containing two identical 99 amino acid polypeptide chains, is a key enzyme involved in the catalysis of HIV protein cleavage in the viral replication cycle (Kohl et al. 1988). Processing by PR is essential for viral maturation and infectivity. Therefore, an intense effort has been made to rationally design and develop HIV-1 PIs (for review, see Wlodawer and Vondrasek 1998; Gulnik et al. 2000; Tomasselli and Heinrikson 2000). Six FDA-approved PIs (Fig. 1 ▶) are currently in clinical use. However, the rapid emergence of resistant HIV-1 variants can result in therapeutic failure (Schinazi et al. 2000; Shafer 2002). Individual mutations and combinations of mutations at more than 20 PR codons are known to contribute to PI resistance (Hirsch et al. 2000), including amino acids directly involved in the inhibitor binding, as well as some residues located up to 20 Å apart from the inhibitor binding site. The structural determinants of resistance for some of the PR variants have been characterized by X-ray crystallography (Baldwin et al. 1995; Hong et al. 2000; Mahalingam et al. 2001; King et al. 2002).

Figure 1.

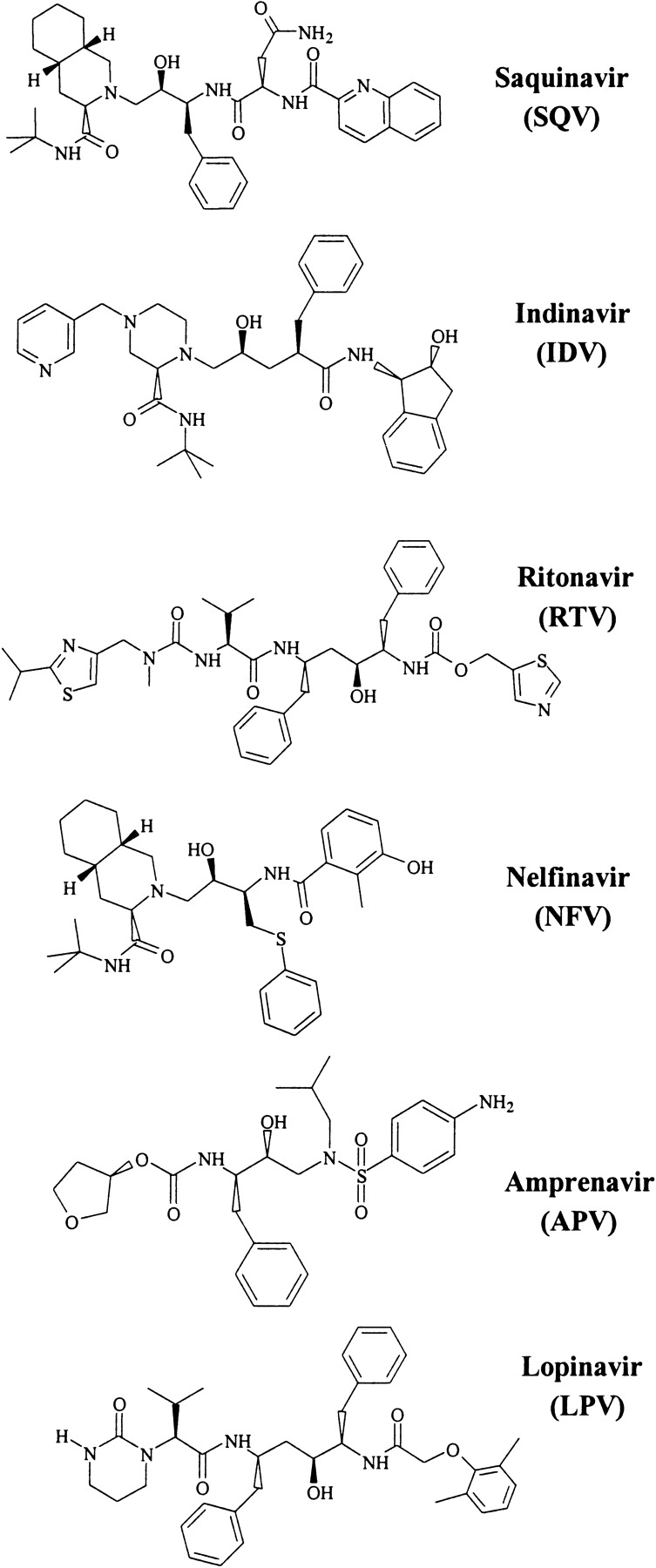
Structures of the FDA-approved HIV-1 PIs used in this study.

Several attempts have been made to develop computational methodologies for molecular modeling of PR–inhibitor complexes, and to build QSAR models for prediction of PI activity (Holloway et al. 1995; Perez et al. 1998; Nair et al. 2002). Molecular mechanics and molecular dynamics approaches have also been used to predict resistance of mutant PR variants to various PIs (Dominy and Brooks III 1999; McCarric and Kollman 1999). The approaches based on calculations of protein–ligand interaction energies resulted in significant correlations with experimental binding energies (Weber and Harrison 1999) or in the correct prediction of 75% of the single amino acid mutations causing resistance to commercial PIs (Wang and Kollman 2001). These computational methods, however, have not been developed to predict resistance of PR variants with multiple amino acid substitutions obtained from clinical HIV-1 isolates.

The present study tests the hypothesis that resistance to PIs results mainly from decreased inhibitor binding affinity to mutant PR variants, as was previously shown by inhibitor binding kinetics measurements for engineered PR variants containing known resistant mutations (Gulnik et al. 1995). We have further assumed that (1) mutant PR–inhibitor complexes can be accurately modeled based on X-ray crystal structures of WT PR complexes, (2) changes in the binding affinity on mutation may be approximated as changes in calculated binding energy of PR–inhibitor complexes, and (3) PI resistance may be predicted from a significant increase in the binding energy of an inhibitor with respect to the WT complex. We describe here a structural approach to predicting the resistance of HIV-1 PR mutants to the six FDA-approved PIs using molecular modeling of the PR complexes in order to calculate changes in the inhibitor binding energy to the mutant PR relative to the reference WT complex. In preliminary studies (Shenderovich et al. 2001a,b), we obtained statistically significant correlations between calculated and experimental values of binding energy of four FDA-approved inhibitors with engineered PR variants containing single and double amino acid mutations. In this study, we show that the changes in binding energy can be directly correlated to the fold changes in PI IC₅₀ values measured in two commercially available phenotypic assays. We propose a model for a structural phenotyping resistance assay based on these correlations.

Results

Accuracy of the models of mutant PR–inhibitor complexes

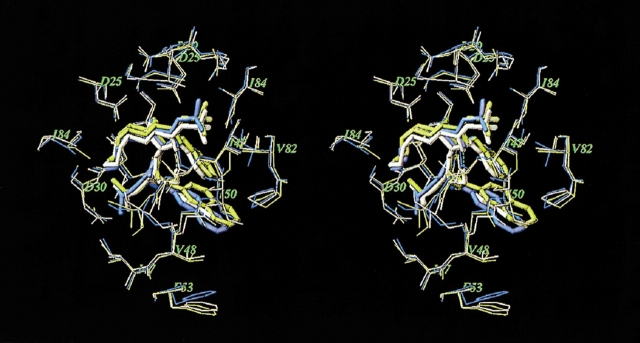
Accuracy of the models may be estimated by comparison with the X-ray crystal structure of the same or similar complexes. A few structures of PR–inhibitor complexes containing resistance-related mutations are available in the Protein Data Bank (PDB; Baldwin et al. 1995^; Mahalingam et al. 2001^; King et al. 2002), and only one crystal structure (Hong et al. 2000; PDB entry 1fb7) that involves an FDA-approved inhibitor, SQV, in complex with a highly resistant G48V/L90M PR mutant shows significant structural changes with respect to the WT PR–inhibitor complex (PDB entry 1hxb). In the preliminary study (Shenderovich et al. 2001a,b), we modeled SQV complexes with PR variants containing the G48V mutation. Figure 2 ▶ displays superposition of the crystal structure (yellow) and our model (white) of the mutant G48V PR–SQV complex. The crystal structure of the WT PR–SQV complex is shown in blue. In the WT complex, the quinoline moiety of SQV is tightly bound to the flap residues 47–50, and flexibility of the flap residues is restricted by interactions with the Phe 53 side chain. In the mutant complex, the bulky Val 48 side chain, which appears exactly between the quinoline ring of the ligand and the phenyl ring of Phe 53, causes a steric repulsion of the aromatic moieties that increases the van der Waals component of the binding energy (see Table 1). Both the crystal structure and the computational model show very similar displacements of the aromatic moieties of the ligand and Phe 53. The RMSD between the model and the crystal structure of the mutant complex are 0.5 and 1.0 Å for C^α atoms and all heavy atoms, respectively, of the PR residues located within a 7.0 Å shell from the ligand. It is noteworthy that our model was built from an optimized crystal structure of the WT complex before the crystal structure of the mutant complex was published.

Figure 2.

Superimposed stereo views of the crystal structure (yellow; Hong et al. 2000) and our model (white) of the SQV complex with the G48V/L90M mutant HIV PR. The crystal structure of WT PR–SQV complex (blue) is also shown for comparison. The SQV molecules are shown as tube models. Only PR residues closest to the ligand are displayed.

Table 1.

Calculated and experimental binding energy changes for known resistance mutations of HIV-1 protease

Mutations	PI	ΔEbind (calc), kcal/mole	ΔEvwa	ΔEhba	ΔEela	Fold resistanceb	ΔEbind (exptl), kcal/molec	Reference
G48V	SQV	3.5	2.1	0.5	0.5	160	3.1	Maschera et al. 1996
I50V	SQV	2.2	1.9	0.3	0.1	21	1.9	Markland et al. 2000
	APV	2.9	2.9	0.1	0.1	83	2.7	Markland et al. 2000
M46I/I47V/I50V	APV	3.6	1.5	1.8	0.4	270	3.4	Partaledis et al. 1995
M46I/G48V/I50V/I84L	SQV	3.8	1.6	1.3	0.6	300	3.5	Markland et al. 2000
	APV	0.9	1.0	−0.2	−0.1	2	0.4	Markland et al. 2000
V82A	IDV	1.8	1.2	0.0	0.5	22	1.9	Gulnik et al. 1995
	RTV	2.4	2.8	0.2	−0.5	10	1.4	Gulnik et al. 1995
I84V	SQV	2.2	2.1	−0.1	0.1	12	1.5	Partaledis et al. 1995
	APV	2.0	2.0	0.0	0.1	23	1.9	Partaledis et al. 1995
	IDV	1.5	1.0	0.0	0.4	20	1.8	Partaledis et al. 1995
V32I/I84V	IDV	2.9	2.2	0.2	0.2	80	2.7	Gulnik et al. 1995
	RTV	2.0	1.7	0.2	0.1	64	2.6	Gulnik et al. 1995
V82T/I84V	IDV	2.4	1.9	0.0	0.3	59	2.5	Schock et al. 1996
	RTV	2.9	2.6	0.1	0.0	158	3.1	Schock et al. 1996
M46I/I84V	NFV	1.7	1.5	−0.1	0.2	5–30d		Patick et al. 1996
D30N	NFV	1.5	−0.9	1.6	0.8	7d		Patick et al. 1996
L10F/V32I/M46I/ I47V/I84V	LPV	2.9	3.3	−0.3	−0.3	25–100	2.0–2.8	Carrillo et al. 1998

^a ΔE_vw, ΔE_hb, and ΔE_el are changes in the van der Waals, hydrogen bonding, and electrostatic components of binding energy (see equation 2 in Materials and Methods).

^b Fold changes in K_i or IC₅₀ values.

^c ΔE_bind(exptl) was calculated using equations 4 or 5 in Materials and Methods.

^d Ratios of EC₉₀ values; experimental binding energies were not estimated.

Crystal structures of the mutant L63P/V82T/I84V PR in complex with IDV and its analogs were recently solved (King et al. 2002). The mutant complex with IDV (PDB entry 1k6c) shows relatively small changes with respect to the crystal structure of the WT complex (PDB entry 1hsg) with all C^α atom RMSD = 0.46 Å. Our model of the mutant V82T/I84V PR–IDV complex is also close to the WT complex (all C^α atom RMSD = 0.42 Å). Furthermore, the crystal structure and our model of the mutant complex are reasonably close to each other: C^α atom and all heavy atom RMSD is 0.5 and 0.75 Å, respectively, for residues located in a 7.0 Å shell around the ligand. Both crystal structure and the model predict similar positions of the ligand and conformations of the mutated side chains, and the calculated change in the binding energy (Table 1) is very close to the measured value (King et al. 2002).

Evaluation of resistance-related mutations for HIV-1 PIs

Statistically significant correlations between calculated and experimental binding energy were obtained in our preliminary studies (Shenderovich et al. 2001a,b) for four clinically available PIs—APV, IDV, RTV, and SQV—in complex with genetically engineered PR variants. In the present study, we modeled complexes of six FDI-approved PIs (Fig. 1 ▶) with PR variants containing known resistance-related mutations. The calculated changes in the main components of the binding energy are given in Table 1 in comparison with energy values estimated from experimental K_i or IC₅₀ ratios. It may be noted that the computational mutagenesis procedure predicts significant change in the binding energy (ΔE_bind ≥ 1.5 kcal/mole) for the majority of known resistant single and double mutations: G48V for SQV; V82A for IDV and RTV; I84V in various combinations for SQV, NFV, IDV, RTV, and APV; and D30N for NFV. Furthermore, the most resistant mutations (>100-fold change in K_i values) can be reliably predicted by ΔE_bind values of ≥3.0 kcal/mole. For the majority of resistance-related single and double mutations, the increase in PI binding energy is due mainly to the van der Waals component of the binding energy function. Most of the conservative mutations in positions 50, 82, and 84 do not change significantly the ligand binding mode and structure of the complex, but only decrease the number of favorable van der Waals contacts between the ligand and the protein side chains. In particular, the crystal structure of IDV in complex with the mutant L63P/V82T/I84V PR (King et al. 2002) was similar to that of the WT PR–IDV complex, whereas thermodynamic measurements showed a 2.5 kcal/mole loss in the binding enthalpy of the mutant complex. This is in good agreement with the increase in the binding energy due to the reduced van der Waals contacts of the mutant side chains predicted for the IDV complex with the V82T/I84V mutant PR (Table 1). The noticeable exception is the complex of NFV with the mutant D30N PR, where substitution of neutral Asn for the charged Asp 30 that directly interacts with the m-phenol group of NFV weakens the hydrogen bonding and increases electrostatic components of the binding energy. More complex mutation patterns may cause significant changes in the 3D structure of the complex that leads to disruption of ligand–PR hydrogen bonding (APV complex with a triple mutant and SQV complex with a quadruple mutant; see Table 1). Only a combination of at least five mutations in residues close to the PR binding site causes a significant increase in the binding energy of the recently approved PI LPV (Table 1). This is consistent with experimental findings that clinical isolates resistant to LPV display complex mutational patterns involving positions 46, 47, and 84 (Carrillo et al. 1998).

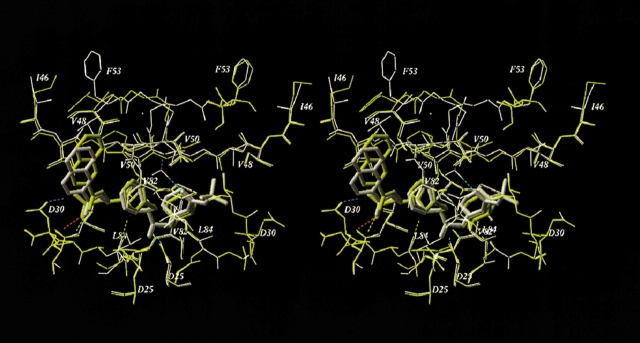
Using the computational mutagenesis procedure, we calculated the binding energy profiles of each PI for the set of single, double, and triple mutations that were described in the literature (Gulnik et al. 1995; Markowitz et al. 1995; Maschera et al. 1996; Pazhanisamy et al. 1996; Klabe et al. 1998; Markland et al. 2000). The profiles for SQV and APV shown in Figure 3 ▶ represent the histograms of calculated ΔE_bind ranked by increasing binding energy. The right shoulders of these profiles contain potentially resistant mutations. We assumed that ΔE_bind = 2.0 kcal/mole was a reliable threshold for resistance prediction from the binding energy profiles. The bars exceeding this threshold are colored gray in the histograms in Figure 3 ▶; the most resistant mutations (ΔE_bind ≥ 3.0 kcal/mole) are shown in black. Black bars in the binding energy profile of SQV correspond to PR variants containing the G48V mutation, known to cause a high resistance to SQV (Maschera et al. 1996). Other potentially resistant variants (gray bars in Fig. 3A ▶) contain mutations I84V and I50V. The latter mutation is known to cause resistance to APV (Pazhanisamy et al. 1996) but not to SQV. Indeed, mutation I50V, either alone or in combination with substitutions in positions 10, 46, or 47, comprised the most resistant variants in the binding energy profile of APV with ΔE_bind ≥ 3.0 kcal/mole (Fig. 3B ▶). Nonetheless, mutation I50V causes a 20-fold increase in the K_i value for SQV (Pazhanisamy et al. 1996; Markland et al. 2000), which is in good agreement with the calculated ΔE_bind of about 2.0 kcal/mole (Table 1, Fig. 3A ▶). The quadruple mutant (M46I/G48V/I50V/I84L) that combines single-residue mutations determining resistance to both inhibitors appears to be highly resistant to SQV but sensitive or only slightly resistant to APV (ΔE_bind = 3.8 and 0.9 kcal/mole for SQV and APV, respectively), which is consistent with the experimental observations (Markland et al. 2000). The model of the quadruple mutant complex with APV did not deviate significantly from the model of the WT complex (RMSD of 0.4 Å for heavy atoms of the ligand and binding site residues). Accommodation of the bulkier Leu 84 side chain in complex with APV resulted in tighter ligand packing in the vicinity of Val 50 and Pro 81. These small conformational rearrangements, together with favorable van der Waals interactions of APV with the Val 48 side chains, almost compensate for the ligand–protein van der Waals interactions lost because of the I50V mutation. Superposition of 3D models of the WT and the quadruple mutant PR in complex with SQV is shown in Figure 4 ▶. Conformational changes in the quadruple mutant complex with SQV were similar to those caused by the single G48V mutation (see Fig. 2 ▶) with similar displacements of the SQV quinoline ring. The RMSD of the ligand heavy atoms in both mutants is 0.4 Å compared with the RMSD of 0.7 Å between the ligand positions in WT and quadruple mutant models. However, additional mutations in positions 46 and 50 result in a more significant displacement of the flap residues: RMSD = 0.66 Å between C^α atoms of flap residues 46 to 54 in the single G48V mutant and the quadruple mutant complexes. Furthermore, the simultaneous substitution of bulkier residues in positions 46 and 48 may cause a rotamer transition of the Phe 53 side chain in the PR chain A from χ¹ ≈ −60° to χ¹ ≈ 60° (Fig. 4 ▶). In this case, unfavorable van der Waals interactions of the Val 48 side chains, combined with the losses in hydrogen bonding and electrostatic energy due to conformational changes in the complex, resulted in a high increase in binding energy consistent with the 300-fold increase in K_i (Markland et al. 2000).

Figure 3.

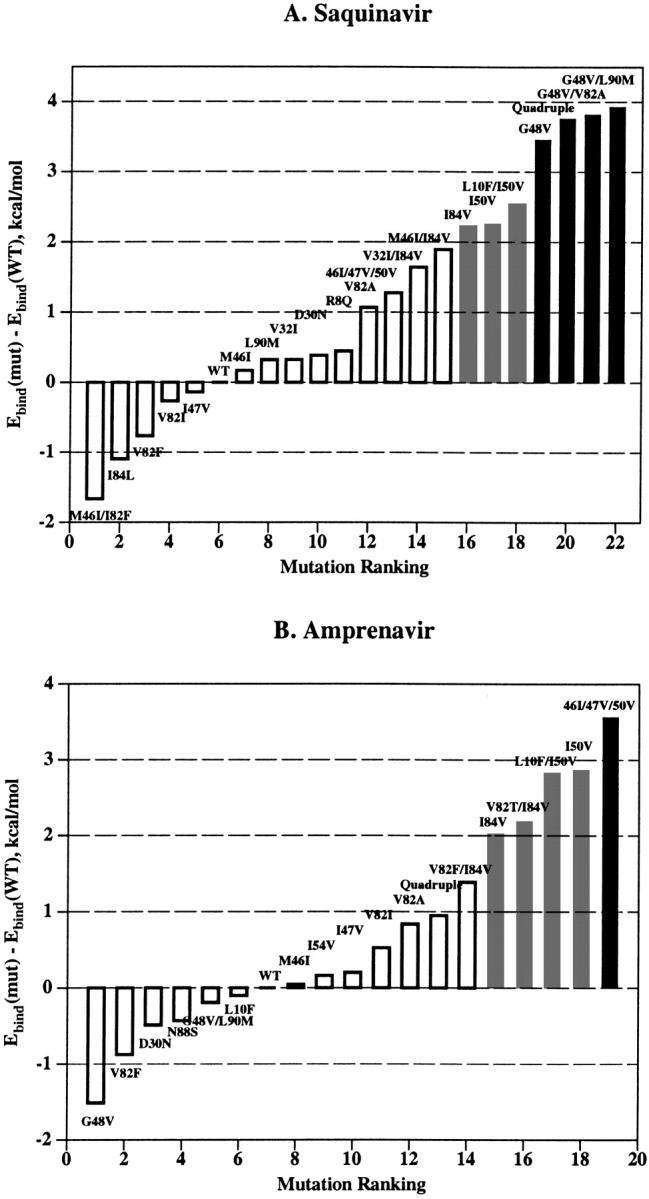
Binding energy profiles for SQV (A) and APV (B). PR mutations described in the literature are ranked by the increasing ΔE_bind. Predicted resistant (ΔE_bind ≥ 2.0 kcal/mole) and highly resistant (ΔE_bind ≥ 3.0 kcal/mole) mutants are shown as the gray and the black bars, respectively.

Figure 4.

Superimposed stereo views of the model SQV complexes with the WT (yellow) and the quadruple mutant (M46I/G48V/I50V/I84L, white) HIV-1 PRs. The SQV molecules are shown as tube models. Hydrogen bonds of the ligand and flap water molecule in the mutant complex are displayed. Mutated residues and other important residues are labeled.

Correlation between calculated binding energies and cell-based phenotypes of PR variants from clinical HIV-1 isolates

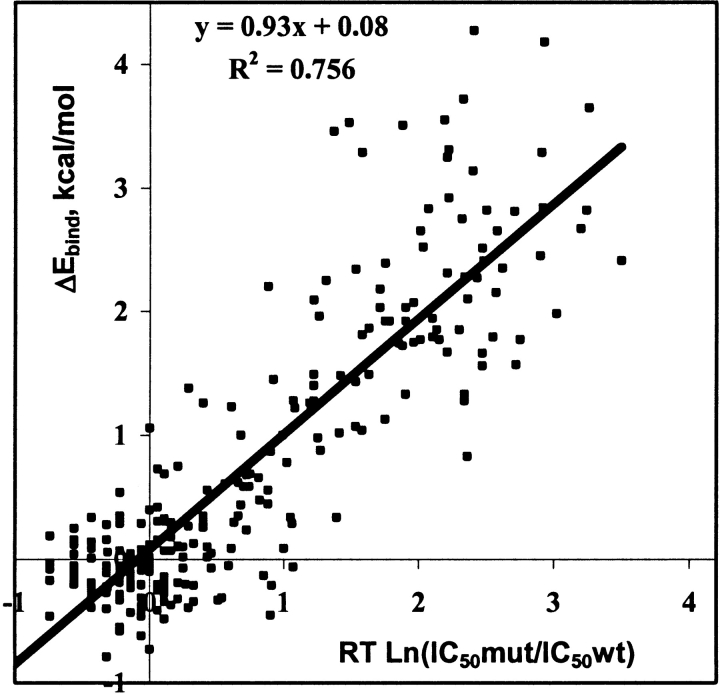
The changes in binding energies of mutant versus WT complexes calculated for 65 clinical HIV-1 PR variants with five PIs and 48 PR variants with LPV were correlated with PhenoSense cell-based phenotypic resistance assays from ViroLogic Inc. (Petropoulos et al. 2000). Characteristics of the regression analyses are given in Table 2A, and a cumulative correlation plot for all drugs is shown in Figure 5 ▶. The correlation coefficients R², ranging from 0.76 for NFV to 0.83 for APV and SQV, demonstrate statistically significant correlation with P < 0.001. Furthermore, the standard errors in prediction for these correlations ranged from 0.4 to 0.6 kcal/mole, corresponding to only a 2.0- to 2.5-fold standard error in predicted IC₅₀ ratios (see the last column in Table 2A). The entire data set of 65 PR variants with six PIs gave a correlation with R² = 0.76 and about a 2.5-fold standard error of prediction. Changes in binding energy calculated for a group of 63 PR variants were correlated with another commercially available phenotypic assay, the Antivirogram assay from Tibotec-Virco (Hertogs et al. 1998). Correlation coefficients R² ranging from 0.53 (APV) to 0.81 (LPV) with 2.0- to 2.5-fold standard errors in resistance prediction were obtained for this group (see Table 2B). Generally, the correlations of calculated binding energies with the Antivirogram phenotypes were less significant than the correlations with the PhenoSense phenotypes, especially for APV. To obtain significant correlations for five PIs with the Antivirogram phenotypes, we needed to exclude several outliers, that is, the data points with large discrepancies between calculated and observed resistance measures. Most of the outlying data originated from a small number of PR variants, indicating possible discrepancies between the genotyped sequence and the viral amplicon that was phenotyped in the cell-based system. The correlation coefficients obtained for five of six PIs after outlier exclusion were of the same range as the correlations between two different phenotypic assays, Virco Antivirogram and Viralliance Phenoscript (Dam et al. 2001). Interestingly, the correlation between APV phenotypes obtained in the two cell-based assays also was not significant (R² = 0.12; Dam et al. 2001).

Table 2.

Regression analysis of calculated ΔE_bind and experimental changes in binding energy^a

A: ViroLogic PhenoSense
Inhibitor	N	R2	S.E. (kcal/mole)	S.E. (fold)b
Amprenavir	65	0.83	0.36	1.8
Indinavir	65	0.80	0.43	2.0
Lopinavir	48	0.81	0.46	2.1
Nelfinavir	65	0.76	0.50	2.3
Ritonavir	65	0.78	0.57	2.5
Saquinavir	65	0.83	0.45	2.1

B: Virco Antivirogram
Inhibitor	N (outliers)c	R2 (+outliers)	S.E. (+outliers)	S.E. (fold)b (+outliers)
a Experimental changes in the binding energy were estimated as RT ln(IC50mut/IC50wt). The number of data points (N), correlation coefficients (R2), and standard errors (S.E.) in predicted binding energies are given.
b The standard error of prediction is expressed as a change in the fold resistance.
c Outliers are data points that were excluded to obtain statistically significant correlations. Characteristics of correlations obtained with outliers are given in parentheses.
Amprenavir	63 (6)	0.53 (0.34)	0.42 (0.55)	2.0 (2.4)
Indinavir	63 (8)	0.72 (0.51)	0.43 (0.57)	2.0 (2.5)
Lopinavir	63 (3)	0.81 (0.70)	0.35 (0.44)	1.8 (2.0)
Nelfinavir	63 (2)	0.70 (0.57)	0.47 (0.58)	2.1 (2.6)
Ritonavir	63 (3)	0.78 (0.68)	0.54 (0.68)	2.4 (3.0)
Saquinavir	61 (5)	0.66 (0.37)	0.56 (0.77)	2.5 (3.5)

Figure 5.

Total correlation between the calculated changes in binding energies (ΔE_bind ) of the WT vs. mutant HIV-1 PR–inhibitor complexes and the estimates of the changes in binding free energies obtained from experimental IC₅₀ ratios (see equation 5 in Materials and Methods). The correlation plot includes 35 PR variants in complex with LPV and 65 PR variants in complex with five other PIs (total 360 data points). Experimental IC₅₀ ratios were obtained from PhenoSence resistance assay (ViroLogic Inc., http://www.ViroLogic.com).

Semiquantitative resistance predictions

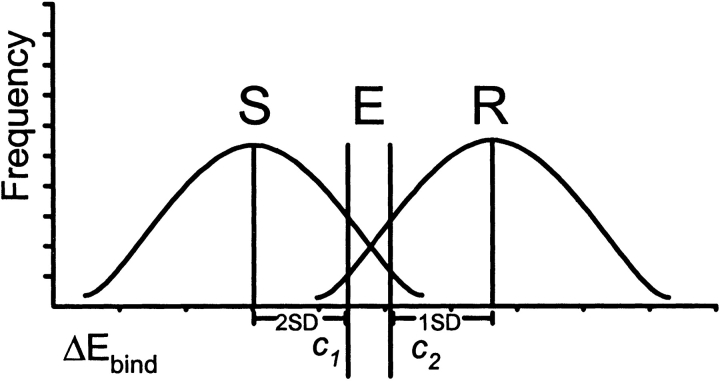
The ViroLogic PhenoSense data were used to group the variants into susceptible (less than fourfold increase in IC₅₀) and resistant (fourfold or higher increase in IC₅₀) classes for each PI. We determined the ΔE_bind distributions and calculated the cutoffs c₁ and c₂ for semiquantitative prediction of susceptibility and resistance, as described in Materials and Methods (Fig. 6 ▶). PR variants were then classified as resistant, sensitive, or equivocal. Excellent concordances between the structural ratings and the PhenoSense ratings (95% sensitivity, 88% specificity; 0.567 ≤ kappa ≤ 0.907, P < 0.0001) were obtained for this training set of 65 PR variants with six PIs. The same structural cutoff values were then applied to Virco Antivirogram data and were able to predict phenotypic resistance to five of six PIs with a high degree of concordance (79% sensitivity, 88% specificity; 0.561 ≤ kappa ≤ 0.743, P < 0.0001). Good concordance between structural prediction and Antivirogram phenotype was not obtained for APV (50% sensitivity, 87% specificity; kappa = 0.367). For the Antivirogram assay, phenotypic changes in APV resistance also showed the poorest correlation with the calculated binding energies (see earlier).

Figure 6.

A semiquantitative model for a structure-based PI resistance assay. Distributions of calculated ΔE_bind for PR variants phenotypically sensitive and resistant to six PIs were used to define the binding energy cutoffs c₁ and c₂ for prediction of sensitivity (S) or resistance (R) to each PI, respectively. Cases c₁ ≤ ΔE_bind ≤ c₂ are considered equivocal (E).

In order to evaluate the performance of the semiquantitative energy cutoffs, binding energy calculations and blind resistance predictions were performed for an additional set of 78 PR samples. The predictions were then compared with phenotypic data available from PhenoSense (46 samples) and Antivirogram (32 samples) assays. Drug-specific semiquantitative cutoffs and the observed concordances are shown in Table 3. For both data sets, the number of equivocal predictions was small, and rules-based genotypic prediction agreed with the phenotypic predictions in most cases (Table 3). The specificity of the structural predictions was high for all drugs, but sensitivities were better for the PhenoSense phenotypes (Table 4). Overall agreement between the structural predictions was 92% (kappa = 0.756) for the PhenoSense phenotypes and 86% (kappa = 0.666) for the Antivirogram phenotypes. For the 46 discordances, 20 (43%) of the structural predictions were concordant with genotypic rules, whereas for 26 (57%) of the discordances genotypic rules agreed with the phenotypic predictions; the proportions were nearly the same for the PhenoSense and the Antivirogram phenotypes. A comparable concordance of 89% was reported in a study comparing these two experimental phenotypic assays (Qari et al. 2002). Another study comparing the Virco Antivirogram assay with the Viralliance Phenoscript assay demonstrated 87% overall concordance for 30 PR samples and five PIs (Dam et al. 2001). Therefore, we conclude that the qualitative structure-based resistance predictions agree well with the resistance class assignments of cell-based phenotypic assays.

Table 3.

Concordance of structural phenotype predictions with the results of two phenotypic assays

A: ViroLogic PhenoSense
	ΔEbind cutoffsa		Phenotypic concordanceb				Equivocal predictionsd
PI	c1	c2	Sensitivity	Specificity	Kappac	P	Number	Genotypic concordance
APV	0.7	1.4	62.5%	100%	0.730	<0.0001	4/46	4/4
IDV	0.6	1.5	100%	94.1%	0.870	<0.0001	3/46	3/3
LPV	0.3	0.7	100%	87.1%	0.652	<0.0001	0/46	NA
NFV	0.7	1.0	64.3%	96.9%	0.665	<0.0001	0/46	NA
RTV	0.7	1.4	72.7%	100%	0.800	<0.0001	2/46	1/2
SQV	0.6	1.1	71.4%	100%	0.809	<0.0001	0/46	NA

B: Virco Antivirogram
a ΔEbind cutoffs in kcal/mole established as described in Materials and Methods.
b Sensitivity is the proportion of phenotypically resistant variants predicted to be resistant. Specificity is the proportion of phenotypically sensitive variants predicted to be sensitive.
cKappa is a measure of inter-assay agreement (Fleiss 1981). Kappa > 0.75, excellent agreement; 0.4 < kappa < 0.75, good agreement; kappa < 0.4, poor agreement.
d Genotypic predictions were performed in cases of equivocal structure-based predictions. The number of such predictions and their concordance with the phenotypic predictions are shown.
APV	0.7	1.4	85.7%	95.5%	0.812	<0.0001	3/32	2/3
IDV	0.6	1.5	69.2%	94.7%	0.664	<0.0001	0/32	NA
LPV	0.3	0.7	70.0%	90.5%	0.621	<0.0003	1/32	1/1
NFV	0.7	1.0	72.7%	88.9%	0.627	<0.0004	3/32	1/3
RTV	0.7	1.4	72.7%	100%	0.764	<0.0001	4/32	2/4
SQV	0.6	1.1	50.0%	95.5%	0.510	<0.002	0/32	NA

Table 4.

Overall concordance of structural phenotype with experimental phenotype for blind predictions

	PhenoSensea		Antivirogramb
Structural Prediction	S	R	S	R
S	196	13	112	19
R	7	41	7	43
Ec	6	3	4	6

^a 266 comparisons for 46 samples and 6 PIs. The overall agreement between structural phenotype and PhenoSense prediction of PI resistance was 92.2% (kappa = 0.756, P < 0.00001). (S) Sensitive; (R) resistant; (E) equivocal.

^b 191 comparisons for 32 samples and 6 PIs. The overall agreement between structural phenotype and Antivirogram prediction of PI resistance was 85.6% (kappa = 0.666, P < 0.00001).

^c Equivocal assignments where the change in binding energy was between the lower and the upper cutoffs. For equivocal structural predictions, genotypic resistance assignments agreed with the phenotypic predictions in 8 of 9 cases (PhenoSense) and 6 of 10 cases (Antivirogram).

Discussion

We have developed a computational approach for the prediction of resistance of clinical HIV-1 PR variants to PIs. This approach uses molecular modeling and binding energy evaluation for the WT and mutant PR–inhibitor complexes. The computational mutagenesis procedure can accurately reproduce the changes in 3D structure of the mutant complexes. Our model of the G48V/L90M mutant PR complex with SQV correctly reproduced significant changes in 3D structure with respect to the WT complex, including the ligand movement and conformational changes in the PR flap moiety (see Fig. 2 ▶), observed in the crystal structure of the same complex (Hong et al. 2000). The model of the IDV complex with the mutant V82T/I84V PR was also consistent with the crystal structure of a similar complex (King et al. 2002) and correctly predicted the experimentally observed change in the binding energy.

This study is based on the assumption that PI resistance is primarily determined by a reduction in binding affinity of PIs to mutant PR. This implies that mutations in the PR substrate cleft and in the flap regions are the major factors determining resistance to PIs. The influence of these mutations on affinity of PIs has been intensively investigated by site-directed mutagenesis and enzyme kinetic studies (Gulnik et al. 1995; Markowitz et al. 1995; Maschera et al. 1996; Pazhanisamy et al. 1996; Klabe et al. 1998), which showed significant increases in K_i for PR variants with known resistant mutations.

A second assumption of this study was that the changes in binding affinity might be accurately reproduced by changes in calculated binding energy of PR–inhibitor complexes. Previously we obtained statistically significant correlations with R² ranging from 0.69 to 0.81 between changes in experimental binding affinities derived from K_i ratios and calculated binding energies for complexes of four PIs with PR variants containing primary resistance mutations (Shenderovich et al. 2001a). It should be noted that in these studies we did not attempt to develop a QSAR procedure to evaluate and compare binding energies of different PIs. We developed a computational procedure that calculated relatively small changes in the binding energy on PR side chain substitutions in reference WT PR–inhibitor complexes derived from respective crystal structures. The binding energy function that included nonweighted van der Waals, hydrogen bonding, side-chain entropy, and electrostatic Coulomb and solvation terms (Schapira et al. 1999; Shenderovich et al. 2001b) was able to identify resistance mutations by a significant increase in binding energy. The primary resistance mutations (G48V for SQV, V82A for IDV and RTV, I50V for APV, D30N for NFV) caused more than a 1.5-kcal/mole increase in the binding energy of the respective PIs (Shenderovich et al. 2001b), whereas a strong (>100-fold) resistance could usually be predicted by more than a 3.0 kcal/mole increase in binding energy.

The majority of resistance-related mutations are conservative substitutions among hydrophobic side chains (Val, Ile, Leu, Met, Ala) that do not change the structure of the complex significantly, but modify van der Waals interactions between the ligand and the side chains of the PR active site. Respectively, changes in the binding affinity of PIs on resistance-related single and double mutations are mostly explained by changes in the van der Waals component of the binding energy (see Table 1). These calculations were able to predict both additive and differential effects of combined primary mutations on the resistance to different PIs. For example, the binding energy profile for IDV (not shown) predicts about 1.0 and 1.5 kcal/mole increases in the binding energy for single mutations V82T and I84V, respectively. A combination of two point mutations results in an additive 2.4 kcal/mole increase in binding energy of IDV (Table 1), which is consistent with the 2.5 kcal/mole increase in the binding enthalpy observed for a PR variant containing V82T/I84V mutations (King et al. 2002). Such additivity often appears when the WT side chains are substituted with less bulky ones and the structure of the mutant complex does not change significantly. On the other hand, a combination of the G48V mutation, which was highly resistant to SQV (Maschera et al. 1996), with the I50V mutation, which was highly resistant to APV and moderately resistant to SQV (Pazhanisamy et al. 1996), resulted in the quadruple mutant, M46I/G48V/I50V/I84L, which was highly resistant to SQV but, surprisingly, sensitive to APV (Markland et al. 2000). This effect was correctly reproduced by computational mutagenesis (see Results).

Generally, accumulation of several resistance-related active site and flap region mutations may cause significant structural changes of mutant PR–inhibitor complexes, which result in a partial disruption of the hydrogen bond network between the ligand and protein, as reflected in the increased hydrogen bonding component of the binding energy function. This is the case for the quadruple mutant complex with SQV and for the triple M46I/I47V/I50V mutant complex with APV (see Table 1). On the other hand, except for rare mutations that involve charged and polar residues located close to the active site (Arg 8, Asp 30, and Asn 88), Coulomb and electrostatic solvation components do not make significant contributions to changes in binding energy of mutant complexes. This is probably due to the specific structure of PR–inhibitor complexes, with a ligand completely buried between the mostly hydrophobic residues of the PR binding cleft and the flap loops (Wlodawer and Vondrasek 1998).

The presence of a deep, well-defined binding pocket, the prevalence of van der Waals and hydrogen bonding ligand–protein interactions, and the availability of numerous crystal structures that can be used both as templates and as benchmarks have made HIV-1 PR complexes a common target for molecular modeling and docking simulations. Quantitative structure–activity relationship studies based on various binding energy functions have been generally successful in obtaining significant correlation equations for a series of structurally related PIs (Holloway et al. 1995; Perez et al. 1998; Nair et al. 2002), but have had a limited predictive power for a more diverse set of inhibitors or for mutant PR variants. Successful attempts have been made to calculate binding free energies of PR substrates and inhibitors using molecular dynamics simulations and thermodynamic cycle calculations with empirical binding energy functions (Dominy and Brooks III 1999; McCarric and Kollman 1999). Although these methods supply relatively accurate binding energies, they are impractical for the routine screening of multiple PR variants against commercially available drugs. Molecular modeling of mutant PR–inhibitor complexes based on the crystal structures of WT complexes and evaluation of changes in the binding energy of mutant versus WT complexes using molecular mechanics binding energy functions were performed by Weber and Harrison (1999). They obtained significant correlations (R = 0.79 and 0.68 for SQV and IDV, respectively) between changes in binding energy and binding affinity calculated from K_i ratios for SQV and IDV complexes with nine single and double mutant PR variants. In our preliminary study (Shenderovich et al. 2001a,b), we modeled IDV and SQV complexes with 17 and 18 PR variants, respectively (including mutations studied by Weber and Harrison), and obtained stronger correlations between changes in binding energy and in binding affinity (R = 0.79 and 0.84, respectively). We also obtained significant correlations (R = 0.90) for two other commercial PIs, RTV and APV.

An attempt to predict HIV-1 PR resistance to five FDA-approved PIs using a complex binding energy function and a simplified molecular modeling approach was recently published by Wang and Kollman (2001). They calculated residue contributions (ΔG_res) to the binding free energy of WT complexes, and used a product of ΔG_res and residue variability to predict resistance of single residue mutations to five PIs. Mutant PR–inhibitor complexes were not modeled, and therefore any conformational changes that could influence binding energy were neglected. The residue contributions calculated for WT sequences neglected the nature of mutant residues and underestimated the consequences of substitution of a bulky side chain for a smaller one. In particular, this study failed to predict resistance of the G48V mutant PR to SQV. As was shown earlier, introduction of Val 48 in the PR–SQV complex causes significant steric strain that is accompanied by conformational changes in the complex. These effects could not be predicted by considering interactions of the parent Gly 48 residues only.

The primary aim of this study was to develop a relatively simple computational procedure for rapid discrimination between resistant and sensitive PR variants. A typical set of clinical PR variants included 20% to 30% of phenotypically resistant PR–inhibitor complexes that might undergo significant structural changes with respect to the WT complexes. Accumulation of multiple resistance-related mutations that may differentially affect binding modes of various ligands is often the case for clinical PR variants that emerge under therapeutic regimens involving multiple PIs. The total number of amino acids mutated with respect to a consensus WT sequence may amount to up to 20 for each of two 99 amino acid chains of the homodimeric HIV PR, and some clinical PR variants may contain more than 10 side-chain substitutions in the vicinity of the inhibitor binding site. Evaluation of structural and energetic effects of multiple mutations required the development of a stepwise computational procedure, which first introduces and locally optimizes all side-chain substitutions, gradually moving from the mutations closest to the ligand toward the periphery of the protein, and then minimizes the molecular mechanics energy of the complex over a flexible ligand and protein amino acids in the vicinity of the ligand. The minimization shell around the ligand (see Materials and Methods) should be large enough to include all mutations that may directly or indirectly influence ligand binding, but should be relatively narrow to avoid significant deviations from the WT complexes derived from the crystallographic coordinates. The computational protocol was separately optimized for each PI to get the best correlations between calculated and experimental binding energy for the training set totaling 127 PR variants obtained from clinical HIV-1. Furthermore, in the preliminary study (Shenderovich et al. 2001a,b), we found that optimization of the crystal structures of WT complexes that involved a Monte Carlo search and energy minimization (see Materials and Methods) was necessary to achieve significant correlation between experimental and calculated changes in binding energies. Modifications introduced in nonrefined crystallographic structures usually did not reproduce experimental changes in binding energies estimated from K_i ratios for engineered single and double mutant PR variants.

The computational mutagenesis procedure developed in this study was able to reproduce changes in binding affinity of clinical PR variants, as shown by statistically significant correlations between calculated changes in binding energy and experimental measurements of drug resistance. We obtained good overall correlation (R² = 0.76) between calculated changes in binding energy and experimental measures of phenotypic resistance (ViroLogic PhenoSense assay), with a standard error corresponding to only a 2.5-fold change in resistance, comparable with the standard error of cell-based phenotypic assays. This level of accuracy resulted in well-separated distributions of ΔE_bind that were used to determine binding energy cutoffs for phenotypically sensitive and resistant PR variants, allowing the qualitative classification of clinical isolates as susceptible or resistant to the six FDA-approved PIs, with a small number of equivocal assignments.

The remarkable concordance between the structural predictions and the measured resistance in two different cell-based assays indicates that changes in inhibitor binding affinity indeed explain most of the observed PI resistance, as was hypothesized. The failure to predict the phenotypic resistance in some cases may have been caused, in part, by mutations such as L90M (61% and 79% of the false negative calls for SQV and NFV, respectively) that do not greatly alter inhibitor binding affinity but may cause resistance by other mechanisms, such as decreasing the PR dimer stability (Xie et al. 1999; Hong et al. 2000). More than 40% of the predictions that were discordant with phenotype were nevertheless concordant with genotypic rules-based predictions of resistance or susceptibility. The inherent variability of cell-based phenotyping may be responsible for some of these variations. The differences in phenotypic technologies may also produce different results in a small number of cases (Qari et al. 2002). Structural predictions were complicated in some cases by the presence of multiple viral quasi-species encoding more than one amino acid variant at several PR codons that occasionally resulted in significantly different resistance predictions between these variants. In such cases, we arbitrarily selected the variant with the highest calculated ΔE_bind for our blind predictions, which was not always the variant in closest agreement with the experimentally measured phenotypic resistance.

Conclusions

We have developed a computational protocol for molecular modeling and binding energy evaluation for the WT and mutant PR–inhibitor complexes, and a structure-based approach for the prediction of resistance of clinical HIV-1 PR variants to PIs. The computational mutagenesis procedure accurately reproduced the changes in 3D structure of mutant PR–inhibitor complexes and correctly predicted mutations in the PR binding site and flap region that produce HIV-1 variants resistant to particular PIs. Applied to clinical HIV variants with multiple mutations, the procedure resulted in statistically significant correlations between calculated changes in the inhibitor binding energies and fold changes in inhibitor IC₅₀ values determined in experimental phenotypic assays. These correlations were used to define the binding energy cutoff values for semiquantitative prediction of HIV variants sensitive or resistant to each PI.

Our structure-based resistance predictions performed as well as the commercially available cell-based assays in categorizing viral variants as resistant or susceptible to PI inhibitors. The structure-based predictions may offer an alternative to rules-based genotyping for current PIs, and may be used as a rapid resistance prediction method for new PIs, for which genotypic rules are not yet known. The availability of a large database of clinical sequences and PR structures (the VARIOME database; Maggio and Ramnarayan 2001) can also enable investigators to perform rapid in silico screening of drugs under development to estimate the frequencies of resistant variants in the patient population. The structural phenotyping technology may be useful in prediction of probable resistance mutation patterns for prospective antiretroviral drug candidates prior to expensive clinical trials, and for selection of those drug candidates that are predicted to be most effective against viral variants resistant to the currently available drugs (Maggio et al. 2002). The computational mutagenesis technology may be extended to inhibitors of other viral and bacterial proteins, in which structure of the complex may be determined by X-ray crystallography or molecular modeling, and high variability of the target protein sequence is an issue for development of effective drugs. The similar approach may be applied for design and interpretation of site-directed mutagenesis studies of ligand interactions with protein targets of known 3D structure, and for design of ligands that would show selective affinities to protein targets with homologous active site structures.

Materials and methods

Wild-type HIV-1 PR–inhibitor complexes

WT complexes were built from crystal structures available in PDB. The PDB entries used were 1hxb for SQV, 1hsg for IDV, 1hxw for RTV, 1ohr for NFV, and 1hpv for APV. The crystal structure of the PR–LPV complex was obtained from Abbott Laboratories (PDB entry 1mui; Stoll et al. 2002). The chemical structures and abbreviations used for the inhibitors are shown in Figure 1 ▶. Covalent geometries of inhibitors were taken from the crystal structures and adjusted to ensure planarity of aromatic rings, rotational symmetry of particular groups, and so forth. The Gasteiger-Marsili algorithm (Gasteiger and Marsili 1980) was used to assign atomic charges to the ligands. Most of the inhibitors were considered to be electro-neutral compounds. IDV was protonated at piperazine nitrogen, which gave the best correlation with experimental binding energies in the preliminary study (Shenderovich et al. 2001a).

Molecular modeling and Monte Carlo simulations were performed using the ICM program, version 2.7 (Abagyan et al. 1994; MolSoft 1999), with the ECEPP/3 force field (Némethy et al. 1992). A regularization procedure (Maiorov and Abagyan 1998) was used to obtain relaxed structures of WT complexes with the standard ECEPP/3 amino acids and heavy atom RMSD of ≤0.5 Å from the crystal structures. Water molecules located in a 7.0 Å shell around the ligand were retained in the regularized complexes. A single “flap” water molecule (Wlodawer and Vondrasek 1998) was placed into the binding site of the PR–LPV complex. In order to find the optimal positions of ligands in the PR binding site with the force field used, Monte Carlo simulations with Minimization (Abagyan and Totrov 1994) were performed starting from the regularized crystal structures. Translational and rotational degrees of freedom, and single bond torsion angles of the ligand, as well as χ torsion angles of PR side chains located within 7.0 Å of any ligand atom were randomly perturbed during the Monte Carlo simulation steps. Movement of water molecules was allowed during the minimization. Protein–ligand interaction (binding) energies were calculated for the conformations accepted at 1000 K, and conformations with the lowest binding energies were selected as temporary models of the WT complex.

Modeling of mutant HIV-1 PR–inhibitor complexes

Modeling of mutant complexes was performed in two steps: (1) a search for an optimal conformation of each mutated side chain, and (2) optimization of the positions of the ligand and water molecules and conformations of the protein residues located near the binding site. The list of amino acid mutations was defined by alignment of the WT and mutant sequences. Individual mutations were introduced simultaneously in the two PR chains in the order of increasing distance from the mutated residues to the ligand. Initial conformation of a mutant side chain was “inherited” as much as possible from the WT side chain; that is, values of common χ torsion angles (like χ¹ angled of all non-β-branched residues) were assigned to the mutant side chain. A systematic search procedure (MolSoft 1999) was applied to χ torsion angles not common for the WT and mutant side chains, which generated all combinations of three rotamers (±60° and 180°) for the torsion angles involved, minimized energy of each combination, and selected the lowest-energy conformation. The minimization involved all χ angles of the side chains located in a 5.0 Å shell (see following) around the mutant residue. After the local optimization for individual mutations, energy minimization was performed for a substructure involving the ligand, surrounding protein residues, and water molecules. The energy function used for the final minimization included ECEPP/3 van der Waals, hydrogen bonding and torsion potentials (Némethy et al. 1992), electrostatic potentials with a distance-dependent dielectric ɛ = 4.0r_ij, side-chain entropy, and atomic solvation energy (Abagyan and Totrov 1994). Molecular variables of the mutant complex included (1) translation and rotation variables and all torsion angles of the ligand; (2) backbone and side-chain torsion angles of PR residues that had at least one atom within a distance ≤R₁ from any atom of the ligand (shell R₁); (3) all torsion angles of PR residues that had at least one atom within a distance R₂ from any atom of the mutated residues included in the shell R₁ (shell R₂); (4) translation and rotation variables of water molecules within shells R₁ and R₂. The radius R₁ of the shell surrounding the ligand was set to 7.0 or 8.0 Å. The radii R₂ of the secondary shells, which were included to relax the surroundings of mutated residues located at the periphery of the ligand-binding site, were varied between 0 and 5.0 Å.

The binding energies of PR–inhibitor complexes

Binding energies were estimated (Schapira et al. 1999, Shenderovich et al. 2001b) as

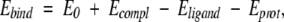(1)

where E₀ is an adjustable constant, E_compl is the energy of the complex, and E_ligand and E_prot are the energies of the ligand and protein when separated. The components of the binding energy were calculated using the following energy function:

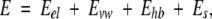(2)

where E_el is the exact-boundary electrostatics (Totrov and Abagyan 2001) that includes a Coulomb term and electrostatic solvation energy calculated with a dielectric constant ɛ = 8.0 (Schapira et al. 1999), E_s is the side-chain entropy (Abagyan and Totrov 1994), and E_vw and E_hb are the ECEPP/3 van der Waals and hydrogen-bonding terms.

For mutant PR–inhibitor complexes with known dissociation constants K_i, correlations between changes in the calculated binding energy

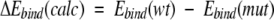(3)

and in the experimental estimate of binding free energy

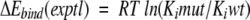(4)

were established by linear regression analysis (Shenderovich et al. 2001a). For clinical HIV-1 isolates, ratios of IC₅₀ measured in cell-based phenotypic assays (Hertogs et al. 1998; Petropoulos et al. 2000), were used to calculate a surrogate of experimental binding energies

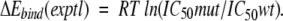(5)

For clinical HIV isolates containing a mixture of PR variants, separate ΔE_bind values were calculated for all essential PR variants, and either the maximum or the best-fit individual ΔE_bind(calc) value was used for correlation with experimental phenotypes.

Genotypic and phenotypic determinations

HIV-1 RNA was extracted from clinical samples submitted for RT and PR genotype determination to Quest Diagnostics Inc. or from 50 samples obtained from the California Collaborative Treatment Group 570 study (Haubrich et al. 2001) and genotyped at Quest Diagnostics Inc. The entire PR and the first 400 codons of RT were amplified by RT PCR and sequenced on an ABI 3700 capillary sequencer. Sequenced variants were aligned to an HIV-1 subtype B consensus sequence, and amino acid changes relative to the reference sequence were identified and tabulated. Genotypic resistance predictions were performed with the Quest-Diagnostics rules-based algorithm, an updated version of a published algorithm (Baxter et al. 2000). For the determination of the fold changes in IC₅₀ values of six PIs, plasma samples were submitted for phenotypic resistance assays to ViroLogic Inc. (PhenoSense assay, http://www.ViroLogic.com) or to Tibotec-Virco (Antivirogram assay, http://www.tibotec-virco.com).

Structure-based resistance predictions

In order to define semiquantitative binding energy cutoffs for resistance predictions, the phenotypic data set for 65 clinical isolates (Virologic PhenoSense) was divided into sensitive (less than four-fold increase in phenotypic IC₅₀) and resistant (four-fold or higher increase in phenotypic IC₅₀) groups for each PI, and mean ΔE_bind values and their standard deviations were calculated for all sensitive and resistant groups. The ΔE_bind cutoff c₁ defining susceptibility to each PI was set at two standard deviations above the mean of the group of samples sensitive to the respective PIs (Fig. 5 ▶). The cutoff c₂ defining resistance was set at one standard deviation (1.5 S.D. for LPV) below the mean for the group of samples resistant to the respective PIs (Fig. 6 ▶). Cases of c₁ ≤ ΔE_bind ≤ c₂ were considered equivocal. Inter-rater agreement between categorical resistance and susceptibility assignments was evaluated by the Kappa statistic (Fleiss 1981).

Abbreviations

• 3D, three-dimensional

• HIV-1, human immunodeficiency virus type 1

• PR, protease

• PI, protease inhibitor

• APV, amprenavir

• IDV, indinavir

• LPV, lopinavir

• NFV, nelfinavir

• RTV, ritonavir

• SQV, saquinavir

• RT, reverse transcriptase

• FDA, U.S. Food and Drug Administration

• RMSD, root mean square deviation

• QSAR, quantitative structure-activity relationship

• WT, wild type