Fast protein folding on downhill energy landscape

Abstract

Proteins fold in a time range of microseconds to minutes despite the large amount of possible conformers. Molecular dynamics simulations of a three-stranded antiparallel β-sheet peptide (for a total of 12.6 μsec and 72 folding events) show that at the melting temperature the unfolded state ensemble contains many more conformers than those sampled during a folding event.

Proteins are complex molecules with many degrees of freedom. Their ability to fold to a unique three-dimensional structure in a time range of microseconds to minutes seems to be at odds with the large amount of possible conformers (Dill and Chan 1997; Karplus 1997). One argument against this apparent conundrum (Levinthal’s paradox) is based on the results of a “toy” model of proteins, a string of 27 beads positioned at sites of a cubic lattice where beads interact only if they are nonbonded nearest neighbors and long-range interactions are neglected. Because the number of accessible conformations is of the order of 10¹⁶, folding of the lattice model in about 10⁷ Monte Carlo moves has suggested that it is possible to reach the folded state after searching through only a minute fraction of the denaturated state ensemble (Leopold et al. 1992; Dinner et al. 2000; Dinner and Karplus 2001). On the basis of explicit solvent molecular dynamics simulations of structured peptides (lasting up to 200 nsec) it has been proposed recently that the number of conformers that characterize the denaturated state is only on the order of 10⁹ for a 100-residue protein that folds on a millisecond time scale (van Gunsteren et al. 2001a). Furthermore, the significance of the results obtained by lattice simulations that model only short-range interactions (Dinner and Karplus 2001) has been questioned (van Gunsteren et al. 2001b).

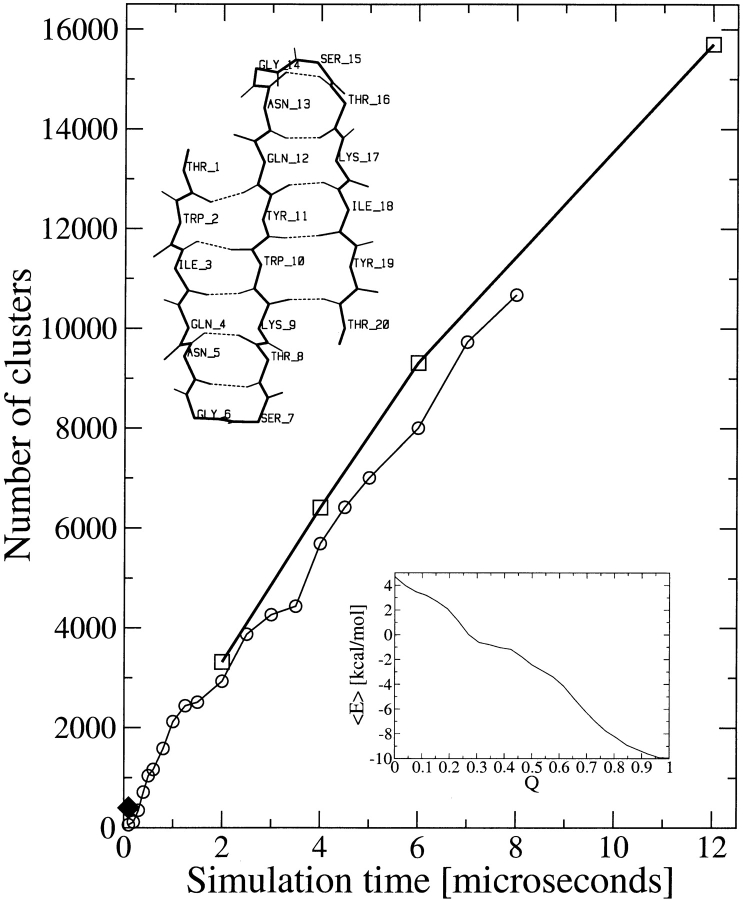
In this paper we show that the denatured state ensemble of a small protein cannot be characterized by a small number of statistically relevant conformations. Folding occurs through the exploration of a small number of conformations, and different conformations are sampled in different folding events. Beta3s is a designed 20-residue sequence whose solution conformation has been investigated by NMR spectroscopy (de Alba et al. 1999). The NMR data indicate that beta3s in aqueous solution forms a monomeric (up to 1 mM concentration) triple-stranded antiparallel β-sheet (Fig. 1 ▶, inset), in equilibrium with the random coil (de Alba et al. 1999). We have shown previously that in implicit solvent (Ferrara et al. 2002) molecular dynamics simulations beta3s folds reversibly to the NMR solution conformation, irrespective of the starting conformation (Ferrara and Caflisch 2000; Cavalli et al. 2002). Recently, four additional molecular dynamics simulations of beta3s were performed at 330 K for a total simulation time of 12.6 μsec. The length of each simulation (2.7 μsec, 2.7 μsec, 2.8 μsec, and 4.4 μsec) is more than 30 times longer than the average folding or unfolding time (about 85 nsec each), which are similar because at 330 K the folded and unfolded states are equally populated. At 330 K the peptide is within 2.5 Å C_α root mean square deviation (RMSD) from the folded conformation about 48% of the time. Figure 1 ▶ shows the results of a cluster analysis based on C_α RMSD. There are more than 15,000 conformers (cluster centers) and it is evident that a plateau has not been reached within the 12.6 μsec of simulation time. However, the number of significantly populated clusters (see Ferrara and Caflisch 2001 for a detailed description) converges already within 2 μsec. Hence, the simulation-length dependence of the total number of clusters is dominated by the small ones. At each simulation interval between an unfolding event and the successive refolding event additional conformations are sampled (Fig. 2 ▶). More than 90% of the unfolded state conformations are in small clusters (each containing < 0.1% of the saved snapshots) and the total number of small clusters does not reach a plateau within 12.6 μsec. Note that there is also a monotonic growth with simulation time of the number of snapshots in the folded-state cluster. After 12.6 μsec (and also within each of the four trajectories) the system has sampled at the equilibrium of folded and unfolded states despite the fact that a large part of the denaturated state ensemble has not yet been explored. In fact, the average folding time converges to a value around 85 nsec, which shows that the length of each simulation is much larger than the relaxation time of the slowest conformational change. Interestingly, in the average folding time of about 85 nsec beta3s visits < 400 clusters (diamond in Fig. 1 ▶). This is only a small fraction of the total number of conformers in the denaturated state. It is possible to reconcile the fast folding with the large conformational space by analyzing the effective energy, which includes all of the contributions to the free energy except for the configurational entropy of the protein (Dinner et al. 2000; Ferrara and Caflisch 2000). Fast folding of beta3s is consistent with the monotonically decreasing profile of the effective energy (Fig. 1 ▶, inset). Despite the large number of conformers in the denaturated state ensemble, the protein chain efficiently finds its way to the folded state because native-like interactions are on average more stable than non-native ones.

Figure 1.

Number of clusters as a function of time. The “leader” clustering procedure was used with a total of 120,000 snapshots saved every 0.1 nsec (thick line, squares). The clustering algorithm, which uses the C_α RMSD values between all pairs of structures, was used only for the first 8 μsec (80,000 snapshots) because of the computational requirements (thin line, circles). (Diamond) Average number of conformers sampled during the folding time, which is defined as the average time interval between successive unfolding and refolding events. (Inset, top) A backbone representation of the folded state of beta3s with main chain hydrogen bonds as broken lines; (inset, bottom) average effective energy as a function of the fraction of native contacts Q, which are defined in Ferrara and Caflisch 2000.

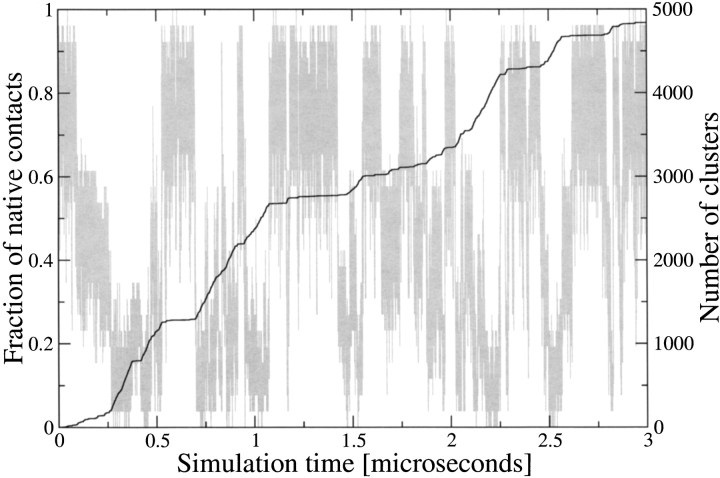
Figure 2.

Time series of the fraction of native contacts Q (gray line, axis labels on the left) and total number of clusters (thick line, axis labels on the right) along one of the four trajectories. The plot shows that the number of clusters grows in the simulation intervals during which beta3s is in the unfolded state, i.e., Q values close to zero.

In conclusion, we have shown using an atomic model of a small protein that the unfolded state ensemble at the melting temperature is a large collection of conformers differing among each other, in agreement with previous high-temperature molecular dynamics simulations (Wong et al. 2000; Shea and Brooks 2001). The energy “bias” that makes fast folding possible does not imply that the unfolded state ensemble is made up of a small number of statistically relevant conformations. The simulation results provide further evidence that the number of denaturated state conformations is orders of magnitudes larger than the conformers sampled during a folding event.

Materials and methods

The molecular dynamics simulations and part of the analysis of the trajectories were performed with CHARMM (Brooks et al. 1983). Beta3s was modeled by explicitly considering all heavy atoms and the hydrogen atoms bound to nitrogen or oxygen atoms (PARAM19 force field; Brooks et al. 1983). An implicit model based on the solvent-accessible surface was used to describe the main effects of the aqueous solvent on the solute (Ferrara et al. 2002). The CHARMM PARAM19 default cutoffs for long-range interactions were used, that is, a shift function (Brooks et al. 1983) was employed with a cutoff at 7.5 Å for both the electrostatic and van der Waals terms. This cutoff length was chosen to be consistent with the parameterization of the force-field and implicit solvation model. The model is not biased toward any particular secondary structure type. In fact, exactly the same force field and implicit solvent model have been used recently in molecular dynamics simulations of folding of structured peptides (α-helices and β-sheets) ranging in size from 15 to 31 residues (Ferrara and Caflisch 2000, 2001; Hiltpold et al. 2000), and small proteins of about 60 residues (Gsponer and Caflisch 2001, 2002). Despite the lack of friction attributable to the absence of explicit water molecules, the implicit solvent model yields a separation of time scales consistent with experimental data near room temperature: Helices fold in about 1 nsec (Ferrara et al. 2000; ≈0.1 μsec, experimentally [Eaton et al., 2000]), β-hairpins in about 10 nsec (Ferrara et al. 2000; ≈1μsec [Eaton et al. 2000]), and triple-stranded β-sheets in about 100 nsec (≈10μsec experimentally; de Alba et al. 1999).

The trajectories were started from the folded state with different initial assignment of the velocities. The temperature was kept constant at 330 K by weak coupling to an external bath with a coupling constant of 5 psec. The value of 330 K is close to the melting temperature in the model (Cavalli et al. 2002). The SHAKE algorithm (Ryckaert et al. 1977) was used to fix the length of the covalent bonds involving hydrogen atoms, which allows an integration time step of 2 fsec.

The fraction of native contacts Q is a progress variable whose time dependence is used to monitor folding/unfolding events (Ferrara and Caflisch 2000). A folding event is considered completed when Q reaches a value larger than 0.85 (Q > 22/26), while an unfolding event is considered completed when Q drops below 0.15 (Q < 4/26; Ferrara and Caflisch 2000). The folding time is defined as the temporal interval between the first time point with Q > 22/26 and the first time point with Q < 4/26. The unfolding time is defined analogously, that is, the interval between the first time point with Q < 4/26 and the first time point with Q > 22/26.

The method for cluster analysis (“leader” algorithm) is based on structural similarity. The first conformation along a trajectory is defined as the center of the first cluster. The remaining conformations are iteratively added to the cluster whose center has the lowest C_α RMSD if the C_α RMSD is smaller than a cutoff of 2 Å. If the closest cluster center deviates more, the conformation becomes the center of a new cluster. To estimate the statistical error the clustering was repeated several times. For this purpose, the four simulations were concatenated and the resulting composite trajectory was divided in subintervals of equal length (e.g., the number of clusters sampled in 4 μsec is calculated three times on the intervals 0–4 μsec, 4–8 μsec, and 8–12 μsec). The statistical error in the number of clusters is about twice the size of the square symbols in Figure 1 ▶. To show that the overall behavior does not depend on the clustering procedure a different clustering algorithm was also used. It evaluates the C_α RMSD for each pair of structures (Daura et al. 1999). Both clustering procedures gave a similar simulation-length dependence of the number of clusters for C_α RMSD cutoff values ranging from 1.5 to 2.5 Å.