Discrete restraint-based protein modeling and the Cα-trace problem

Abstract

We present a novel de novo method to generate protein models from sparse, discretized restraints on the conformation of the main chain and side chain atoms. We focus on Cα-trace generation, the problem of constructing an accurate and complete model from approximate knowledge of the positions of the Cα atoms and, in some cases, the side chain centroids. Spatial restraints on the Cα atoms and side chain centroids are supplemented by constraints on main chain geometry, ϕ/ξ angles, rotameric side chain conformations, and inter-atomic separations derived from analyses of known protein structures. A novel conformational search algorithm, combining features of tree-search and genetic algorithms, generates models consistent with these restraints by propensity-weighted dihedral angle sampling. Models with ideal geometry, good ϕ/ξ angles, and no inter-atomic overlaps are produced with 0.8 Å main chain and, with side chain centroid restraints, 1.0 Å all-atom root-mean-square deviation (RMSD) from the crystal structure over a diverse set of target proteins. The mean model derived from 50 independently generated models is closer to the crystal structure than any individual model, with 0.5 Å main chain RMSD under only Cα restraints and 0.7 Å all-atom RMSD under both Cα and centroid restraints. The method is insensitive to randomly distributed errors of up to 4 Å in the Cα restraints. The conformational search algorithm is efficient, with computational cost increasing linearly with protein size. Issues relating to decoy set generation, experimental structure determination, efficiency of conformational sampling, and homology modeling are discussed.

The three-dimensional structures of proteins play an increasingly important role in our understanding of biological phenomena. The growing rate of protein structure determination, prediction, and analysis, together with structural genomics efforts (Baker and Sali 2001) and large-scale modeling (Pieper et al. 2002), has increased the need for accurate, efficient, and reliable methods to model protein structures. Modeling of protein structures by satisfaction of spatial restraints (Sali and Blundell 1993) is a general framework for the generation of three-dimensional protein structures. Within this framework, the desired three-dimensional structure is described in terms of a network of restraints among atoms and between atoms and positions in space. These restraints can be derived from any source, including small-molecule studies (Engh and Huber 1991), surveys of protein structures (Lovell et al. 2000, 2003), relationships to other proteins (Blundell et al. 1987), or from experimental observations from X-ray crystallography or nuclear magnetic resonance (NMR) spectroscopy experiments. It remains a challenge to construct a three-dimensional model of the protein structure consistent with such restraints, however they are derived. A general approach to modeling by restraint satisfaction would support a general set of restraints and include an efficient algorithm capable of solving arbitrary networks of these restraints.

Cα-trace generation, the problem of constructing an accurate main chain or all-atom model from approximate knowledge of the positions of the Cα atoms, is a protein structure modeling problem with several interesting applications. Algorithms to solve the Cα-trace problem should be applicable to the broader class of restraint-based modeling problems. The Cα-trace problem is appealingly formal; it has unambiguous measures of success; and it is free from the errors and ambiguity caused by alignments in comparative modeling or experimental phases in X-ray crystallography.

Despite its idealized nature, the Cα-trace problem is surprisingly useful in structural biology. Experimental structure determination, comparative modeling, and ab initio structure prediction can be reduced to the solution of restraint networks similar to those used in Cα-trace generation. In X-ray crystallography, skeletonization is a widely-used image analysis technique for automatic electron density map interpretation capable of identifying likely centers for the main chain and side chains (Greer 1985). Following skeletonization, the crystallographer must build a complete model of the protein from the main chain and/or side chain guide positions. In comparative modeling, the approximate positions of the Cα atoms of the target protein can be inferred from an alignment to homologous proteins (Chothia and Lesk 1986; Blundell et al. 1987). Methods for ab initio prediction and analysis typically employ a limited representation of the protein structure (Levitt 1976; Park and Levitt 1995), providing predicted coordinates for the Cα atoms and, in some cases, centroids of the side chain atoms. Before journals required full disclosure of a structure’s coordinates following publication, many proteins were submitted to the Protein Data Bank (Berman et al. 2000) containing only the Cα positions or were unavailable altogether, perversely forcing researchers to reconstitute the complete model from the published Cα coordinates (Reid and Thornton 1989) or stereographic images (Rossmann and Argos 1980).

There have been many previous approaches to the Cα-trace problem, including labor-intensive manual reconstruction (Jones and Thirup 1986; Reid and Thornton 1989), methods based on fragment matching from the protein database (Holm and Sander 1991;Levitt 1992), and de novo methods that generate models without explicit reference to known protein structures (Purisima and Scheraga 1984; Correa 1990). Jones and Thirup (1986) described an early knowledge-based method to construct a complete protein structure from Cα coordinates. Following the observation that the unusual reverse turns in retinol binding protein (RBP) were easily identifiable in unrelated proteins in the Protein Data Bank, Jones and Thirup assembled a model of RBP from short peptide fragments selected for similarity to the RBP Cα coordinates. Though fragments were taken from only three unrelated proteins, a complete model was constructed with main chain RMSD of 1.0 Å from the crystal structure.

Following Jones’ work, Reid and Thornton (1989) used fragments from previously solved structures and extensive expert knowledge to rebuild an all-atom model of flavodoxin from Cα coordinates. Short stretches of backbone were fit to the Cα coordinates and side chains conformations added, until the model contained few atomic overlaps and passed several knowledge-based filters. Following energy minimization, the final model was close to native (0.6 Å main chain, 1.7 Å all-atom RMSD).

Two important papers brought full automation to knowledge-based methods. Holm and Sander (1991) matched stretches of Cα coordinates against a large set of high-quality protein structures, assembled the best overlapping fragments into a backbone model using a dynamic programming algorithm, and assigned side chains to this fixed backbone with a Monte Carlo simulation of side chain rotamers. Their method, implemented in a program called MaxSprout, produced models with 0.4–0.6 Å main chain RMSD and 1.6 Å side chain RMSD for buried residues, even with up to 0.4 Å of noise in the Cα coordinates. A similar approach was adopted by Levitt (1992) in the program SegMod, which automatically matched fragments from the protein database to the Cα coordinates, computed the mean model of all well-fit fragments, and applied restrained energy minimization to ameliorate poor covalent geometry and nonbonded interactions introduced by coordinate averaging. SegMod averaged 0.4/1.3 Å main chain/all-atom RMSD to native with Cα restraints on every residue over eight test proteins, though on flavodoxin the models have 0.4/1.9 Å main chain/all-atom RMSD. Further, SegMod proved insensitive to uniformly distributed random errors in the Cα coordinates up to 1 Å, a substantial improvement over MaxSprout. The fragment database used by SegMod, it should be noted, included proteins in the same homologous superfamily (the human lysozyme target 1LZ1 and the database structure E.coli lysozyme 2LZM) and structurally similar proteins (the aspartic proteinase target 3APP and the database structure aspartic proteinase 2RSP).

In contrast to knowledge-based methods, de novo methods rely heavily on geometric and energetic criteria to construct main chain and side chain conformations for the target protein. Purisima and Scheraga (1984) developed a purely geometric method to generate main chain coordinates by solving polynomial equations parameterized by the positions of the Cα guide positions. Correa (1990) next developed a largely automated Cα-trace method by coupling iterative chain building with energy minimization and molecular dynamics in the charmm forcefield. Though computationally expensive, Correa’s method successfully reconstructed α-lytic protease to 0.3/1.3 Å and flavodoxin to 0.5/1.6 Å main chain/all-atom RMSD.

Rey and Skolnick (1992) inferred the positions of the main chain and Cβ atoms from the geometric relationship among three neighboring Cα atoms, producing models around 0.7 Å RMSD over the main chain and Cβ atoms. Later, Milik et al. (1997) improved the method, achieving an accuracy of 0.2–0.6 Å main chain RMSD and a performance of over 8000 residues per second. Bassolino-Klimas and Bruccoleri (1992) applied their directed conformational search method to Cα-trace generation by using the Cα coordinates to guide their conformational search algorithm towards complete models free of van der Waals overlaps, producing models with 0.5–1.0 Å main chain RMSD over six proteins.

Payne (1993) reduced the problem of Cα-trace construction to determining the peptide plane rotations between adjacent Cα coordinates that minimize a semi-empirical Hamiltonian function describing internal peptide bonded geometry and the interaction between neighboring residues. Although models with extremely low main chain RMSD (below 0.3 Å) were generated, Payne’s method displayed significant sensitivity to errors in the Cα coordinates. Van Gelder et al. (1994) used molecular dynamics simulations and the backbone building routine of Correa to construct all-atom models from Cα coordinates, with main chain accuracies between 0.5–0.7 Å main chain and 1.5–1.9 Å all-atom RMSD. Mandal and Linthicum (1993), using a database of statistical relationships between Cα and main chain geometry, generated models with 0.3–0.8 Å main chain RMSD and 1.7 Å all-atom RMSD following energy minimization. Their modeling accuracy degenerated rapidly with Cα errors: The main chain RMSD of models for the α-chain of hemoglobin increased from 0.15 Å under error-free Cα’s to 1.28 Å under Cα’s with RMSD of 0.83 Å to the crystallographic Cα’s. Mathiowetz and Goddard III (1995) applied dihedral probability grid Monte Carlo (DPG-MC) to the Cα-trace problem, predicting six small proteins to 0.5 Å main chain and 1.7 Å all-atom RMSD. Based on discrete sampling of the ϕ/ξ and χ angles, the DPG-MC method first generates a complete main chain model, energy minimizes this chain, and adds side chains, before ultimately accepting the lowest energy all-atom model.

To convert the virtual-bond polypeptide chain produced by their ab initio protein structure prediction method into an to all-atom model for a more detailed analysis, Liwo et al. (1993) developed a method that constructed an initial main chain model with an optimal hydrogen-bonding network for subsequent minimization in the ECEPP/2 forcefield. A model within main chain RMSD of 1.1 Å to the crystal structure of bovine pancreatic trypsin inhibitor was generated given the crystallographic Cα atoms as guides. Kazmierkiewicz et al. (2002) recently extended the work of Liwo et al. with a fully automated Monte Carlo simulation in the ECEPP/3 force field, generating main chain models within 0.5 Å RMSD of two crystal structures. Finally, Iwata et al. (2002) describe an analytic method that predicts ϕ/ξ pairs from the Cα positions restrained to the favorable regions in the Ramachandran plot. Following energy minimization, the reconstructing main chain conformations have 0.25–0.48 Å RMSD, but like most de novo methods, their method was highly sensitive to errors in the Cα guide positions.

Cα-trace revisited

Despite considerable advances, current Cα-trace methods suffer from a number of serious problems and limitations that invite further investigation on the problem. For knowledge-based methods, the coverage of fragments extracted from the database of proteins can be a source of model inaccuracy on unusual conformations, such as loops that exhibit substantial structural variability (Fidelis et al. 1994). In general, unusual conformations will have few if any structural neighbors from which to generate a model, leading ultimately to reduced model quality. An ideal modeling method would perform equally well on all regions of the target protein, regardless of its conformational commonality.

Further, an ideal method should be general, supporting not only Cα atom restraints but also a range of restraints on other individual atoms such as the carbonyl oxygen or γ-carbon, on sets of atoms such as the centroid of the side chain, or even on the secondary structure character at each amino acid. Modeling under a greater number of restraints will be difficult for knowledge-based methods, as fewer fragments in the database will satisfy all the restraints. Many geometric de novo methods are overspecialized to solve the Cα-trace problem (Payne 1993) and cannot be easily extended to support further types of restraints, although methods relying on molecular dynamics or energy minimization have no such limitations.

An ideal method would be reliable, generating complete models with little variation in accuracy across a wide range of proteins. Previous knowledge-based and de novo methods suffer from substantial variability (ranging up to 0.3 Å while averaging 0.5 Å in main chain RMSD) across their target protein sets (Correa 1990; Holm and Sander 1991; Bassolino-Klimas and Bruccoleri 1992;Levitt 1992; Payne 1993; Mathiowetz and Goddard III 1995; Wang et al. 1998). When generating models under 1 Å main chain RMSD from native, as all of the Cα-trace methods do, reliability is an important factor to discriminate among the methods. A method that always produces models 0.5 Å RMSD from native is probably preferable to one that produces 0.25 Å models half the time, and 0.75 Å the other. Low variability across a wide range of proteins provides a statistical guarantee on model quality that is essential for use in structure determination or comparative modeling.

An ideal method would be insensitive to nonsystematic errors of up to several Å in the Cα restraint coordinates. In most applications of Cα-trace methods (e.g., structure determination and homology modeling), the position of the Cα restraints will be corrupted by both random and systematic errors due to experimental error or structural differences from the template structures. Knowledge-based methods have been superior in this respect, demonstrating a tolerance of up to 1 Å of noise in Cα coordinates. Several de novo methods explicitly place Cα atoms at the provided Cα restraints, and consequently modeling accuracy must degrade rapidly with increasing Cα restraint errors. The de novo methods that examined the effects of Cα errors have not fared well.

Given that proteins vary greatly in size, the efficiency of a Cα-trace generation method must be measured by its CPU consumption as a function of protein size, that is, its computational complexity. Several methods (Levitt 1992; Payne 1993) claim but do not demonstrate linear computational complexity. Most other methods, especially those using energy minimization or molecular dynamics (Liwo et al. 1993; van Gelder et al. 1994; Kazmierkiewicz et al. 2002), have superlinear computational complexity and consequently become prohibitively expensive on even moderately large proteins. An ideal Cα-trace method would have demonstrable linear computational complexity and be inexpensive in absolute CPU time on standard computer hardware.

In summary, an ideal Cα-trace method should be accurate, extensible, reliable, efficient, and robust. No previous approaches to Cα-trace generation have managed to combine all of these features. We present here an extension to our ab initio conformational sampling method for discrete restraint-based protein modeling (de Bakker et al. 2003; DePristo et al. 2003) that has all of these features. The method uses a novel conformational search algorithm to generate high-quality protein models by solving a network of constraints derived from analyses of protein structures and restraints on the Cα atoms and side chain centroids. The general constraints are idealized covalent geometry (Engh and Huber 1991), fine-grained propensity-weighted ϕ/ξ maps (Lovell et al. 2003), and accurate side chain rotamers (Lovell et al. 2000). For Cα-trace generation, the network is supplemented with restraints that enforce minimum interatomic separation (DePristo et al. 2003), restraints that ensure model Cα atoms lie near the provided Cα coordinates, and restraints on the model side chain centroids.

Results

Main chain modeling

Ensembles of 50 main chain only models were generated under 1 Å Cα restraints for the target proteins given in Table 1. The ensemble average RMSD varies between 0.75 and 0.85 Å over the target set, though the standard deviation within each target is low (Table 2). The ensemble average main chain RMSD is 0.80 (0.03) Å averaged over the target set. The low standard deviation indicates that the method performs consistently across the whole target set, with little variation among the target proteins.

Table 1.

Target proteins

IDa	Protein	dminb	Sizec
1A6M	Myoglobin	1.0	151
1CEM	Cellulase	1.65	363
1CRN	Crambin	1.5	46
1CTF	L7/L12 50 S ribosomal protein	1.7	68
1IGD	Immunoglobulin binding protein G	1.1	61
1LKS	Hen egg white lysozyme	1.1	129
1NIF	Nitrite reductase	1.6	333
1PHP	Phosphoglycerate kinase	1.65	394
1TPH:1	Triosephosphate isomerase	1.8	245
1UBQ	Ubiquitin	1.8	76
2ALP	Alpha-lytic protease	1.7	198
2PRK	Proteinase K	1.5	278
2WRP:R	Trp repressor	1.65	104
3APP	Penicillopepsin	1.8	323
3PTE	Transpeptidase	1.6	347
4ENL	Enolase	1.9	436
4GCR	Gamma-b crystalline	1.47	174
5CNA:A	Lectin (agglutinin)	2.0	237
5CPA	Hydrolase (c-terminal peptidase)	1.54	307
5NLL	Flavodoxin	1.75	138
6PTI	Bovine pancreatic trypsin inhibitor	1.7	56
7PCY	Plastocyanin	1.8	98
7RSA	Ribonuclease A	1.26	124
8ABP	Arabinose binding protein	1.49	305
8TLN:E	Thermolysin	1.60	316

^a PDB code and, optionally, chain identifier of the target protein.

^b Resolution of the crystal structure in Ångstroms.

^c Number of amino acids in the protein chain.

Table 2.

Accuracy of main chain only modeling under 1.0 Å Cα restraints

	RMSD [Å]
Target	Average Cαa	Best main chain	Average main chainb	Mean model Cαc	Mean model main chaind
1A6M	0.69 (0.02)	0.69	0.75 (0.02)	0.36	0.41
1CEM	0.69 (0.01)	0.73	0.76 (0.01)	0.32	0.39
1CRN	0.64 (0.04)	0.68	0.83 (0.07)	0.30	0.49
1CTF	0.66 (0.03)	0.64	0.76 (0.04)	0.31	0.41
1IGD	0.67 (0.03)	0.69	0.79 (0.05)	0.34	0.45
1LKS	0.68 (0.02)	0.71	0.78 (0.04)	0.30	0.41
1NIF	0.70 (0.01)	0.77	0.81 (0.02)	0.33	0.44
1PHP	0.69 (0.01)	0.73	0.77 (0.02)	0.31	0.39
1TPH	0.69 (0.01)	0.74	0.78 (0.02)	0.31	0.40
1UBQ	0.66 (0.03)	0.71	0.81 (0.04)	0.27	0.41
2ALP	0.69 (0.01)	0.78	0.84 (0.03)	0.31	0.45
2PRK	0.69 (0.01)	0.74	0.80 (0.02)	0.32	0.42
2WRP	0.68 (0.03)	0.69	0.74 (0.03)	0.35	0.41
3APP	0.69 (0.01)	0.75	0.80 (0.02)	0.32	0.42
3PTE	0.70 (0.01)	0.77	0.81 (0.02)	0.33	0.45
4ENL	0.70 (0.01)	0.76	0.81 (0.02)	0.34	0.45
4GCR	0.68 (0.02)	0.72	0.81 (0.04)	0.29	0.41
5CNA	0.70 (0.01)	0.79	0.84 (0.02)	0.34	0.49
5CPA	0.70 (0.01)	0.79	0.84 (0.02)	0.33	0.48
5NLL	0.69 (0.02)	0.76	0.82 (0.03)	0.34	0.49
6PTI	0.65 (0.04)	0.68	0.78 (0.05)	0.31	0.44
7PCY	0.68 (0.02)	0.74	0.84 (0.05)	0.33	0.47
7RSA	0.68 (0.02)	0.77	0.85 (0.04)	0.31	0.51
8ABP	0.70 (0.01)	0.77	0.80 (0.02)	0.34	0.47
8TLN	0.69 (0.01)	0.73	0.79 (0.02)	0.32	0.41
Average	0.68 (0.02)	0.73 (0.04)	0.80 (0.03)	0.32 (0.02)	0.44 (0.04)

^a Ensemble average Cα RMSD.

^b Ensemble average main chain RMSD.

^c Cα RMSD of the unregularized mean model derived from the ensemble.

^d Main chain RMSD of the unregularized mean model derived from the ensemble.

As the determinant of the radius of the Cα restraints, the Cα restraint threshold limits the distance the model Cα atoms can deviate from the origins of the Cα restraints. The average Cα and main chain RMSD across the target set rises with increasing Cα threshold for all Cα restraint thresholds (Table 3). More flexibility in the model Cα positions translates into greater deviation from the native structure.

Table 3.

Model accuracy as a function of Cα restraint threshold

	Cα restraint threshold [Å]
	0.25	0.50	0.75	1.00	2.00	3.00	4.00	5.00
No. targetsa	4	18	24	25	25	25	25	25
Cα RMSDb	0.18 (0.00)	0.36 (0.01)	0.53 (0.01)	0.68 (0.02)	1.31 (0.04)	1.97 (0.06)	2.63 (0.08)	3.33 (0.08)
Main chain RMSDc	0.50 (0.06)	0.55 (0.03)	0.67 (0.05)	0.80 (0.03)	1.38 (0.03)	1.99 (0.05)	2.60 (0.07)	3.26 (0.08)

The Cα restraint threshold determines the radius of the Cα restraint sphere associated with each model Cα atom. Values in parentheses are standard deviations.

^a Number of successfully modeled targets of the 25 target structures.

^b Ensemble average Cα RMSD [Å] over all successfully modeled proteins.

^c Ensemble average main chain RMSD [Å] over all successfully modeled proteins.

At every Cα restraint threshold, the best model is only marginally better than the ensemble average, as shown by the Cα and main chain RMSDs (Table 2, Fig. 1 ▶). The low variance in Cα and main chain RMSD within each ensemble of 50 models indicates that all generated models are equally accurate (Table 3). Increasing the number of generated models above 50 does not significantly increase the difference in accuracy between the best and average models (data not shown). The difference in model accuracy among different Cα restraint thresholds is much larger than between the best and ensemble average models (Fig. 1 ▶).

Figure 1.

Relationship between model accuracy and restraint specificity for (A) main chain only models generated under varying Cα restraints and (B) all-atom models generated under 1 Å Cα restraints and varying side chain centroid restraints. In both graphs, the average RMSD over all targets is shown for the closest model to the crystal structure (circles), the ensemble average RMSD (squares), (A) the main chain of the un-regularized mean model (diamonds), and (B) all atoms of the regularized mean model (diamonds). Error bars are drawn at one standard deviation from the mean.

The conformational search algorithm fails to find any models for some targets under 0.25–0.75 Å restraints (Table 3). The number of failed targets increases quickly with decreasing Cα restraint threshold, from a single failure at 0.75 Å to almost total failure at 0.25 Å. The failed targets are predominately large proteins, indicating that the conformational search algorithm itself begins to fail with very tight restraints. The truly problematic 0.25 Å Cα restraints, however, provide only a marginal improvement in model accuracy: reducing the main chain RMSD by 0.05 Å and 0.17 Å over 0.50 and 0.75 Å restraints, respectively.

Insensitivity to randomly distributed errors

The sensitivity of our method to nonsystematic errors in Cα coordinates has been assessed by introducing uniformly distributed random errors of varying magnitude into the origins of the Cα restraint spheres. For a given noise magnitude μ, each Cα restraint is centered on its corresponding crystallographic Cα atom and then displaced by a randomly oriented vector of length l, selected from a uniform random distribution between 0 and μ. To ensure reasonable restraints with large amounts of noise, restraints were accepted only if the distance between successive restraints was less than 3.8 Å plus the Cα restraint threshold. Further, after each pass of the conformation search algorithm, a new set of noisy restraints was derived. Due to these restrictions, the amount of noise is not entirely determined by the magnitude of the noise vector, and is consequently best measured by the restraint RMSD. The average restraint RMSD is in almost perfect agreement with the expected RMSD of uniformly distributed random deviations (Table 4), showing that the addition of noise to the Cα restraints described here is representative of randomly distributed errors in Cα coordinates.

Table 4.

Main chain only model accuracy as a function of errors in the origins of the Cα restraints

	RMSD [Å]
			Ensemble averaged		Mean modeld
Noisea	Expectedb	Restraintc	Cα	Main chain	Cα	Main chain
1 Å Cα restraint threshold
0.0	—	—	0.68 (0.02)	0.80 (0.03)	0.32 (0.02)	0.44 (0.04)
0.5	0.29	0.29	0.68 (0.01)	0.80 (0.03)	0.31 (0.02)	0.43 (0.03)
1.0	0.58	0.58	0.68 (0.02)	0.80 (0.03)	0.30 (0.02)	0.42 (0.03)
1.5	0.87	0.86	0.69 (0.02)	0.81 (0.03)	0.28 (0.02)	0.41 (0.03)
2 Å Cα restraint threshold
0.0	—	—	1.31 (0.04)	1.38 (0.03)	0.59 (0.03)	0.68 (0.05)
1.0	0.58	0.58	1.30 (0.04)	1.37 (0.04)	0.57 (0.02)	0.67 (0.04)
2.0	1.16	1.15	1.27 (0.03)	1.34 (0.04)	0.54 (0.03)	0.64 (0.05)
3.0	1.73	1.72	1.28 (0.04)	1.34 (0.04)	0.51 (0.03)	0.61 (0.05)
4.0	2.31	2.26	1.37 (0.04)	1.43 (0.04)	0.51 (0.03)	0.61 (0.04)

^a Width, in Ångstroms, of a uniform distribution used to sample the lengths of randomly oriented vectors added to the Cα restraints.

^b RMSD [Å] expected between the Cα atoms of the crystal structure and the Cα restraints for the given noise magnitude.

^c RMSD [Å] between the Cα atoms of the crystal structure and the Cα restraints enforced during model generation.

^d Mean model was not regularized because tinker requires all-atom models for energy minimization.

Conformations generated under 1 Å Cα restraints with less than 1 Å noise have identical Cα and main chain RMSD to native as those generated without any noise, though modeling accuracy begins to degrade slightly with noise at 1.5 Å (Table 4). At this level of error the restraint RMSD is actually greater than the Cα RMSD of the models, a counterintuitive result possible only because model Cα atoms are permitted to lie up to 1 Å from the center of the Cα restraints. It is almost impossible to generate sets of restraints for noise levels of 2 Å or greater consistent with 1 Å Cα restraints, though models generated for the small number of consistent restraint sets at 2 Å of noise again show only a minor decrease in model quality (main chain RMSD of 0.87 Å). Results are similar when models are generated under 2 Å Cα restraints with up to 4 Å of noise. The average main chain RMSD decreases from 1.38 Å to 1.34 Å as the noise level increases from 0 Å to 3 Å, but jumps to 1.43 Å under 4 Å noise. It was not possible to generate models with 5 Å of noise under 2 Å restraints. In conclusion, model accuracy is largely unaffected by random noise in the origins of the Cα restraints, tolerating a noise level of up to 1.5 Å under 1 Å restraints and up to 4 Å under 2 Å restraints.

All-atom modeling

All-atom models were generated by simultaneously adding side chain rotamers to the main chain at each extension step (see Materials and Methods). During unrestrained side chain modeling, all-atom models were generated under 1 Å Cα restraints but with reduced side chain van der Waals radii. Consequently, there was little available information to discriminate among side chain rotamers, and accurate side chain assignment was not expected. These low expectations were met, as the models had an average all-atom RMSD 1.92 Å and only 58.3% of χ₁ angles assigned correctly (Table 5).

Table 5.

Accuracy of all-atom modeling

	Ensemble average			Mean model
	Main chain RMSDa	All-atom RMSDb	χ1c	Main chain RMSDa	All-atom RMSDb	χ1c
rapper all-atom modeling
1 Å centroidsd,i	0.75	1.03	77.4	0.48	0.74	83.2
2 Å centroidsd	0.78	1.28	73.1	0.43	0.93	73.4
3 Å centroidsd	0.79	1.51	65.3	0.44	1.16	64.5
4 Å centroidsd	0.79	1.67	61.3	0.44	1.32	61.5
5 Å centroidsd	0.80	1.82	59.0	0.45	1.47	59.0
Unrestrainede	0.80	1.92	58.3	0.45	1.61	57.6
scwrl reassignment
1 Å centroidf	0.75	1.60	62.0	0.48	1.20	65.4
Unrestrainedg	0.80	1.82	59.1	0.46	1.33	62.5
Nativeh	—	1.13	80.3	—	—	—

^a Average main chain RMSD [Å] of the fifty models for each target protein, averaged over all target proteins.

^b Average all-atom RMSD [Å] of the fifty models for each target protein, averaged over all target proteins.

^c Percentage of side chains with χ₁ within 40° of the equivalent χ₁ in the crystal structure, averaged over all target proteins.

^d Side chain centroid threshold used for restrained side chain modeling.

^e These models were generated without any side chain centroid restraints.

^f Side chain assignment with scwrl onto backbones generated under 1 Å centroid restraints.

^g Side chain assignment with scwrl onto backbones generated without side chain centroid restraints.

^h Side chain assignment with scwrl onto the backbone of the target crystal structure. The slight discrepancy in the Cα and main chain RMSD between scwrl and rapper modeling is due to scwrl assignment failure on several models with restrained and unrestrained backbones, leading to their exclusion from the RMSD calculation. No mean model can be calculated as only a single conformation is produced for each target protein.

ⁱ No models could be generated for target 1NIF under 1 Å centroid restraints, due to a substantially non-rotameric side chain conformation at histidine:306.

During restrained side chain modeling, all-atom models were generated under 1 Å Cα restraints, reduced van der Waals radii, but with additional restraints on the centroid of the side chain conformation. The centroid restraints influence not only the orientation of the side chain relative to the main chain but also the absolute position and orientation of both the side chain and main chain. Centroid restraints affect large, bulky side chains such as phenylalanine more than short side chains such as valine. On the native backbone, 1 Å centroid restraints eliminate the majority of rotamers for bulky side chains but none for small side chains. Consequently, centroid restraints affect the all-atom RMSD more than χ₁ accuracy, as bulky side chains contribute disproportionately to the all-atom RMSD.

Restrained side chain modeling is very accurate under 1 Å centroid restraints, producing models with 1.03 Å all-atom RMSD and 77.4% of χ₁ assigned correctly (Table 5). These numbers are especially significant considering that main chain accuracy is largely unaffected by the additional centroid restraints, with 0.75 Å RMSD under 1 Å Cα and centroid restraints, in contrast to the 0.80 Å RMSD under only 1 Å Cα restraints. In fact, the side chains are modeled almost as accurately as the main chain, as demonstrated by the minor difference between the main chain RMSD and all-atom RMSD.

The accuracy of restrained side chain modeling is strongly dependent on the centroid threshold; both the all-atom RMSD and the χ₁ accuracy worsen with increasing centroid threshold. The χ₁ accuracy drops more rapidly than the all-atom RMSD, as seen by comparing the accuracy of modeling under 3 and 5 Å centroid restraints. Even large centroid restraints, of 4 or 5 Å, restrict the conformation of bulky residues and improve model accuracy relative to unrestrained side chain modeling.

Side chains were reassigned with scwrl on (1) the native backbone of each target protein, (2) the 50 models generated with unrestrained side chains under 1 Å Cα restraints, and (3) the 50 models under 1 Å Cα and 1 Å centroid restraints. Side chains reassigned to the native backbones had an average χ₁ accuracy of 80.3% over our target set, in excellent agreement with the published result of 80% (Bower et al. 1997), and indicating that the target set used in this work is equivalent to that used in the original scwrl assessment. On the backbones of all-atom models generated without side chain restraints, scwrl performs only marginally better than our naïve assignment algorithm: improving the χ₁ accuracy by 1% and all-atom RMSD by 0.1 Å. It appears that the quality of unrestrained side chain modeling is comparable to dedicated assignment methods.

Despite the low main chain RMSD to native of the unrestrained models, it is possible that the reduced van der Waals radii for side chain atoms lead to main chain conformations inconsistent with any accurate side chain assignment. Side chains were also assigned to main chain conformations generated under 1 Å Cα and centroid restraints. The main chain conformations of these models are clearly consistent with an accurate side chain assignment, as the side chains assigned during generation have on average 77.4% of χ₁ correct and a 1.03 Å all-atom RMSD (Table 5). Though the accuracy of scwrl reassignment improved, still only 62.0% of χ₁ angles were predicted correctly, far below the modeling accuracy under the 1 Å centroid restraints and only 4% above the assignment onto unrestrained backbones.

Insensitivity to local features of protein structure

The effects of secondary structure and solvent accessibility on model accuracy have been assessed by comparing the per-residue main chain RMSD over residues sharing the feature to all residues. Only an analysis of the best model generated under 1 Å Cα restraints without side chain modeling is shown, though the results are qualitatively similar for both unrestrained and restrained side chain modeling.

The per-residue Cα RMSD and main chain RMSD are 0.62 (0.22) and 0.71 (0.29) over all 5307 residues in the set of models, with average main chain RMSD of 0.73 Å (0.04; Table 2). There are 1577, 1242, and 2488 residues in the corresponding crystal structures in the helical, strand, and coil states, respectively. Residues in strands and coils are modeled equally accurately, with 0.73 (0.28) Å and 0.73 (0.34) Å per-residue RMSD, respectively, whereas the helical state residues are modeled slightly more accurately, with per-residue RMSD of 0.66 (0.22) Å. The per-residue Cα RMSD is completely independent of secondary structure content, at 0.62 (0.21), 0.63 (0.22), and 0.62 (0.22) over helices, strands, and coils. The slightly better performance over helices is due to improved orientation of the main chain and not superior spatial positioning. There is almost no difference in model accuracy over the 3431 accessible residues than the 1876 buried residues, with 0.71 (0.30) Å and 0.71 (0.28) Å per-residue main chain RMSD, respectively. In summary, the differences in model accuracy among secondary-structure and solvent accessibility classes are small compared to the variation within each class. Consequently, neither secondary structure nor solvent accessibility is a strong determinant of model quality.

Mean models are closer to native than any individual model

Following the approach described by Levitt (1992), the mean model was computed by averaging the atomic coordinates of equivalent atoms in each of the 50 generated models, without superposition. Because the averaging of atomic coordinates introduces large errors in covalent geometry, the raw mean model was regularized by energy minimization. Minimization under the bonded energy terms is very efficient, as the expensive O(n²) nonbonded calculation is avoided. Bonded-term regularization fixes most stereochemical problems; the mean models exhibit standard variation from ideal geometry and have reasonable ϕ/ξ characteristics (To conserve space, the term ‘mean model’ may be used for the regularized mean model. It will be explicitly noted when the raw or un-regularized mean model is used). These corrections require only minor rearrangements of the raw mean model, on the order of 0.3 Å all-atom RMSD between the mean and regularized models. Fortunately, the main chain and all-atom RMSD to native are almost completely unchanged following regularization, increasing by around 0.01 Å main chain and 0.03 Å all-atom RMSD.

The mean model is substantially closer (P < 0.001, paired t-test) to the native structure than even the best individual models, for every Cα and side chain centroid threshold (Table 5, Fig. 1 ▶). The improvement in main chain accuracy increases with larger Cα restraints, from 0.35 Å under 1 Å restraints to 1.51 Å under 5 Å restraints. On the other hand, side chain modeling improves only a constant amount of 0.3 Å all-atom RMSD over the ensemble average of structures from which it was derived.

In absolute terms, the mean models are very close to native. Under 1 Å Cα restraints and unrestrained side chains, the mean models have main chain RMSD of 0.45 (0.05) Å, closer to native than even models generated under 0.25 Å Cα restraints (Table 3). The mean models derived from the ensemble with 1 Å Cα and centroid restraints are extraordinarily close to the native, with an all-atom RMSD of only 0.74 Å and 83.2% of χ₁ angles assigned correctly. Further, the mean models under 1 Å Cα restraints with side chains reassigned with scwrl (0.46 main chain and 1.34 Å all-atom RMSD) are comparable to the accuracy of side chain assignment with scwrl onto the native backbone (1.14 Å all-atom RMSD).

The accuracy of the mean model as a function of Cα restraint error is given in Table 4. For every level of noise, it is substantially more accurate (P < 0.001, paired t-test) than the ensemble average and also the best individual model. The Cα and main chain RMSD both decrease slightly with increasing levels of noise in the Cα restraints. Though the improvements are small, the mean models under noisy Cα restraints are better than the mean models under noiseless restraints (P < 0.001, paired t-test). The cause of this observed decrease is unclear. Regardless, the improved accuracy of the mean model over any individual model clearly does not depend on the Cα restraints being centered on the native Cα atoms.

Mean models were derived from a variety of ensemble sizes, from 5 to 500 models. Small ensembles, below 10 models, produced worse mean models than the 50 model ensembles, whereas ensembles containing more than 50 models had only a marginal effect on the accuracy of the mean model.

Modeling accuracy summary

Though not the sole criterion of success, the ability to generate models within a reasonable proximity of the native structure is a necessity for any Cα-trace method. The accuracy of the individual models produced by main chain only modeling under 1 Å Cα restraints is comparable to that of previous methods, though slightly worse than the best methods. The mean models, on the other hand, are more accurate than even the best previous methods, consistently producing models with 0.4–0.5 Å main chain RMSD to native. The mean model derived from all-atom models with unrestrained side chains compare favorably with previous methods. The mean models computed with side chains reassigned with scwrl are even more accurate, well below the results obtained by all other methods except SegMod. Finally, all-atom modeling with side chain centroid restraints produces the most accurate models of all, with mean models within 1 Å all-atom RMSD of the native structure for reasonably strict centroid restraint thresholds. To put these numbers in context, scwrl side chain assignment on the native backbone produces models with an all-atom RMSD of 1.14 Å, including four heavy main chain atoms with no deviation from the crystal structure. So even with backbone flexibility, restrained side chain modeling is more accurate than side chain assignment onto the native backbone. In summary, our main chain only and side chain modeling methods consistently produce highly accurate models, improving main chain and all-atom modeling over all previous methods.

Computational cost scales linearly with protein size

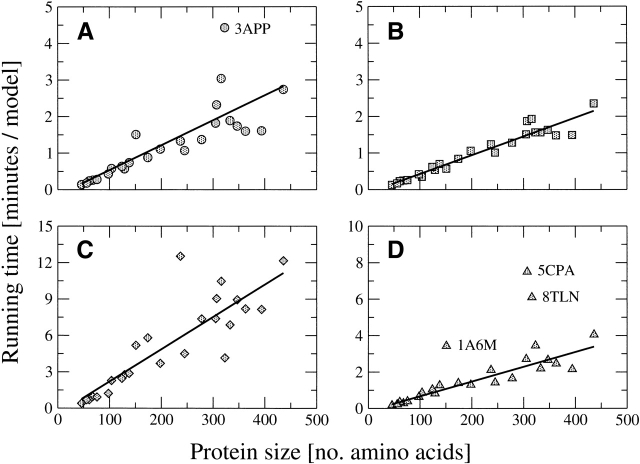
Here we assess the computational cost of the algorithm as a function of protein size for main chain only and all-atom modeling. The average-case behavior of the conformational search algorithm is linear in the length of the protein for main chain only generation (Fig. 3 ▶), excluding the outlier 3APP with an abnormally large number of pass failures caused by glycine:314, with forbidden ϕ/ξ angles, preceding a cis proline:315. The total cost to build a model can be decomposed into the actual cost to build a model plus the cost of all failed passes. Removing the cost of failed passes, the average running time per successfully built model shows less variability and a nearly perfect correlation with protein size (Fig. 3 ▶).

Figure 3.

Computational cost (average CPU time to generate one model, y-axis) as a function of protein size (number of amino acids, x-axis), for (A) main chain only modeling under 1 Å Cα restraints; (B) main chain only modeling under 1 Å Cα restraints but excluding the CPU cost of failed passes of the conformational search algorithm; (C) all-atom modeling under 1 Å Cα restraints and unrestrained side chains; and (D) all-atom modeling under 1 Å Cα and side chain centroid restraints. Linear regressions are plotted as thick lines, with correlation coefficients of (A) 0.80, (B) 0.96, (C) 0.86, and (D) 0.93 excluding the outliers 1A6M, 5CPA, and 8TLN.

Simultaneous modeling of side chains is more costly than main chain only modeling. Unrestrained side chain modeling is three times as expensive as main chain only, but has an only slightly worse linear relationship between running time and protein size (Fig. 3 ▶). As discussed previously, the lower correlation for unrestrained all-atom modeling is a consequence of the nonlocality of interactions between side chains: A fatally incorrect rotamer assigned for one residue may not be detected until further down the polypeptide chain. This nonlocal behavior increases the likelihood and cost of pass failures for the conformational search algorithm.

Restrained side chain modeling (with 2 Å centroid restraints) is less expensive than its unrestrained counterpart, due to fewer pass failures from fatally incorrect side chain assignments. Its computational cost is more variable as a function of protein size, as reflected by a correlation coefficient of 0.68 over the entire target set. This greater variability is a consequence of three targets (1A6M, 5CPA, and 8TLN) that have an unusually large number of failed passes. Excluding these three outliers increases the correlation between running time and protein size to 0.93 (Fig. 3 ▶).

The performance of restrained side chain modeling with 1 Å centroids is significantly worse than for 2 Å or larger centroids (data not shown). This is due to nonrotameric side chain conformations in the target structures, as ∼1% of residues have no conformation in the rotamer library satisfying the 1 Å centroid on the native backbone. These nonrotameric conformations make assignment extremely difficult under 1 Å centroid restraints, as substantial repositioning of the main chain is required to place such side chains.

The absolute computational costs of the conformational search algorithm are modest. Main chain only and all-atom with side chain centroids generation requires approximately equal amounts of time: 15–20 sec for 1IGD (61 residues) and 3–4 min for 4ENL (436 residues). Unrestrained all-atom generation is around three times as costly, requiring 40 sec for 1IGD and 12 min for 4ENL. These costs are well within reason for standard desktop computers. The algorithm is also easily parallelized, as an ensemble of models can be independently generated on separate processors.

Discussion

Among the most interesting issues addressed in this work is the relationship between conformational sampling, restraint specificity, and model accuracy. Considering that the ensemble average RMSD is so different under different sets of restraints, the accuracy of an individual model is determined almost entirely by the specificity of the restraints under which it is generated. The strong relationship between model accuracy and restraint specificity is both positive and negative. On one hand, reliable estimates of model accuracy can be provided for any given set of Cα and centroid restraint thresholds. On the other hand, the single largest factor determining model accuracy is the accuracy of the Cα and centroid restraints.

The ability to precisely control the radius of conformational sampling around the native structure has many interesting applications. In experimental structure determination with X-ray crystallography or NMR spectroscopy, controlled sampling can be used to search for similar conformations that better satisfy experimental data. It is now common to measure the discriminatory power of selection methods such as statistical potentials or molecular mechanics forcefields by their ability to identify native conformations against a background of decoy conformations (Park and Levitt 1996; Samudrala and Levitt 2000; de Bakker et al. 2003). High-quality decoy sets could be created by combining models generated by rapper under a variety of restraints. Models of a target sequence can be generated by tracing through restraints derived from homologous structures (P.I.W. de Bakker, M.A. DePristo, and T.L. Blundell, in prep.). We are also actively investigating the application of rapper to molecular docking against multiple structures, in which native restraints can be directly copied from the crystal structure to generate compatible receptor structures.

A statistical argument explains why the mean model is closer to the native structure than any individual model in an ensemble of 50 models. Each model is very likely to contain errors that keep its RMSD to native high. However, because each model is independently generated, models are unlikely to err in the same way at each position in the structure. When viewed as an ensemble, the errors in the models are nonsystematic and should be distributed evenly about the native structure. The mean model should be free of much of this nonsystematic error and thus closer to the crystal structure. Because the mean model is closer to native than the ensemble of models even under noisy Cα restraints, this effect is not dependent on Cα restraints centered on the native Cα atoms. However, each model is generated under different noisy restraints, so the ensemble should again be distributed equally around the native structure. The equivalent modeling accuracy of the models even under different noisy restraints suggests that the ensemble will be distributed even about the native even when derived under a single set of noisy restraints. An ensemble of independently generated models under discrete Cα restraints is largely free of systematic error. Reducing this ensemble to a mean model averages away the nonsystematic error in each model and thus produces a model substantially closer to the native structure than any individual model. The coordinate averaging, however, can introduce structural problems beyond covalent geometry, including poor van der Waals interactions, ϕ/ξ outliers, and nonrotameric side chains, that can be fixed by energy minimization.

The surprising degree of robustness to errors in the Cα restraint origins is probably the most significant and exciting result of this work. The insensitivity to nonsystematic noise is a consequence of our strict adherence to local conformational correctness and the discretization of the spatial Cα restraints. Idealized geometry ensures that only reasonable protein conformations are sampled, regardless of pressure from the Cα restraints. Propensity-weighted ϕ/ξ sampling further resists the influence of locally distorted Cα restraints. Further, the discrete Cα restraints only require models to lie within the Cα restraint spheres. Consequently, sampling is not biased toward the origin of the restraints, providing the freedom to accommodate the demands of local correctness from idealized geometry and ϕ/ξ angles. The chain-based competition of the conformational search algorithm introduces cooperation among individual residues that magnifies resistance to noise in the restraints. All of these features combine to overcome nonsystematic errors in the Cα restraints, effectively pulling the generated conformations toward the native structure even when subjected to a large amount of noise.

It must be emphasized that these results do not imply that our method is insensitive to systematic errors in the Cα restraints. The current algorithm alone is unlikely to correct systematically distorted Cα restraints, as occurs in practice from problematic electron density skeletonization, poor templates in comparative modeling, and incorrect positioning of secondary structures or noncompactness in ab initio calculations. Perhaps the effects of systematic distortions may be reduced by iterative sampling and refinement in an empirical forcefield.

Several interesting conclusions about the relationship between the main chain and side chain conformation can be drawn from a comparison of main chain only and restrained all-atom modeling. First, there are many conformations with 1 Å all-atom RMSD of the native structure that are consistent with both the native main chain and side chain conformations. Consequently, consistency with the native structure does not determine the structure of a protein to better than 1 Å all-atom RMSD. This suggests that when applying our method to comparative modeling, the most accurate models obtainable would have around 1 Å all-atom RMSD. That is, regardless of the errors inevitably introduced by an incorrect alignment and inaccurate restraints derived from homologous templates, the conformational search algorithm itself would limit the accuracy of the resulting models. This effect, which we suspect is a general feature of all modeling algorithms, would be a significant constraint for close homologs, where a large fraction of the distance from the native structure would result from inherent modeling difficulties and not from alignment errors.

More fundamentally, several pieces of evidence suggest that our method is incapable of generating models closer than 0.5 Å main chain RMSD to the crystal structure. First, extrapolating from Figure 1 ▶, a residual 0.5 Å main chain RMSD would remain even if the Cα restraints threshold could be tightened to 0 Å. Second, the mean models under 1 Å Cα restraints converge to an average of 0.5 Å main chain RMSD with increasing ensemble size. One interpretation of these results is that our approximations to protein structure limit our ability to reproduce the actual crystallographic models: as the latter may well deviate from the discrete sampling of ϕ/ξ angles in 5° bins and ideal main chain geometry, most notably the N—Cα—C (θ) bond angle and the ω dihedral angle.

However, it is cannot be overemphasized that the crystal structures are themselves models of experimental data derived from the time- and space-averaged diffraction of millions of conformations within the crystal lattice. The atomic B-factors, which relate to the variation of the protein atoms around their mean positions in the crystal structure, were not used in our comparisons of the Cα-trace models and crystal structures. These issues should not be disregarded when assessing the accuracy of models within 0.5 Å main chain RMSD from the crystal structure. We are currently investigating a direct comparison of the Cα-trace models to the experimental structure factors.

We show that side chain reassignment onto near-native backbones is significantly more difficult than assignment onto the native backbone. The accuracy of scwrl on both the unrestrained and restrained backbones is markedly reduced from the published values of x₁% of 80% onto native backbones and 74% onto gapless homologous structures (Bower et al. 1997). The large drop in accuracy from homologous structure assignment to near-native backbone suggests that assignment of a nonnative sequence onto a homologous but native backbone is far easier than assignment of the native sequence onto a near-native backbone. This is especially troubling for side chain assignment onto comparative models, where a target sequence must be assigned to an at-best near-native backbone.

The effect of near-native backbones on the quality of side chain assignment has clearly been underestimated. Because side chain assignment methods are useful primarily on near-native backbones, the accuracies reported here are more representative of the real-world accuracy of side chain assignment programs. We expect that near-native assignment will be equally difficult for other side chain assignment methods, as they focus even more exclusively on native side chain reassignment. The large effect of near-native backbones on side chain modeling accuracy demands that side chain assignment methods be evaluated on both native and near-native backbones. To encourage such evaluations, the models generated in this study will be made available from the rapper website.

Though effective and efficient most of the time, the conformational search algorithm tends to fail on overly restrictive restraint networks, leading to increased computational costs (Fig. 1 ▶) or total search failure (Table 3). This behavior is a natural consequence of attempting to build the entire polypeptide chain in a single pass. We are currently investigating whether this problem can be circumvented by dividing modeling into small segments of restraints, separately solving each segment, and then assembling them into a complete model. Segment assembly should decrease the number and cost of failed passes and increase the linear relationship between protein size and running time (Fig. 3 ▶).

In conclusion, our de novo method for Cα-trace generation is accurate, extensible, reliable, efficient, and robust, meeting all of the proposed criteria for an ideal Cα-trace method. We are currently investigating the application of our restraint-based conformational search method to experimental structure determination, comparative modeling, and protein-ligand docking.

Materials and methods

Target proteins

The target set of protein structures was chosen to cover the major target structures from previous papers (Table 1). Superceded entries have been replaced by their current structures. The first alternate location was used when multiple locations were given. Proteins 1CEM, 1NIF, 1PHP, 3PTE, and 8ABP were added to increase the number of larger protein targets. All target structures were solved with X-ray crystallography to better than 2 Å resolution and are structurally dissimilar according to CATH (Orengo et al. 1997).

Model representation

Our approach to high-fidelity protein modeling is founded on the belief that simple discrete restraints coupled with efficient algorithms for conformational sampling can generate ensembles of accurate model structures. This was implemented in the program rapper and used to assess the energetic discrimination of decoy ensembles of protein loops (de Bakker et al. 2003; DePristo et al. 2003). Here we introduce the standard model of protein structure employed in this work.

The covalent geometry of the standard amino acids has been well characterized by small-molecule crystallography (Engh and Huber 1991). Since amino acids in protein structures exhibit little deviation from their small-molecule values (Dauter et al. 1997), idealized geometry is an excellent approximation to real protein structures. Consequently, models are constrained to have idealized geometry for the main chain {N, Cα, C, O, H} and side chain {all heavy atoms}. Conformational freedom is thus restricted to the dihedral angles ϕ, ξ, ω, and χ_i, greatly improving the efficiency of conformational sampling.

Steric interactions between main chain and side chain atoms within an amino acid restrict its backbone dihedral angles ϕ and ξ to highly localized regions of the ϕ/ξ plot (Ramachandran and Sasisekharan 1968). In rapper we constrain ϕ/ξ angles to allowed regions in fine-grained, residue-specific, ϕ/ξ maps derived from the database of protein structures (DePristo et al. 2003; Lovell et al. 2003).

Due to the partial double-bond character of the peptide bond, the ω dihedral angle occurs almost exclusively in the trans or the cis conformations. The trans conformation is much more prevalent (99.96%) than cis (0.04%) across the whole database of protein structures. However, amino acids preceding proline are over 100 times as likely to adopt the cis conformation (6%; Jabs et al. 1999). In the present study, trans and cis conformations were sampled at their frequency of occurrence in the protein database for standard and pre-proline residues.

Hard-sphere excluded volume

A hard-sphere approximation to excluded-volume principle is used to enforce minimum interatomic separation. Despite its limitations, a hard-sphere model for excluded volume is an acceptable approximation for excluded-volume interactions with several advantages over more computationally expensive approaches. Grid algorithms permit constant-time overlap detection to a set of frozen atoms. Interactions such as disulfide and hydrogen bonding can be modeled by permitting a closer approach between the donor/acceptors and cysteine sulfurs. In this study, van der Waals radii were taken from probe (Word et al. 1999a), reduced by 20% to exclude only energetically infeasible atomic contacts.

Cα and side chain centroid restraints

The provided guide positions are incorporated into the restraint network by spherical restraints associated with each Cα atom. A Cα atom at position p satisfies a spherical restraint centered at O with radius r when

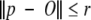The radius of the Cα restraints is called the Cα threshold. For benchmarking purposes, the Cα restraints are centered on the Cα atoms of the crystal structure.

Similar to Cα restraints, side chain centroid restraints are enforced by spherical restraints on the mean position of the side chain atoms (here we take the set of side chain atoms to be all atoms outwards from Cβ, excluding the Cα as seen in other work). A centroid restraint of radius r at position O is satisfied when

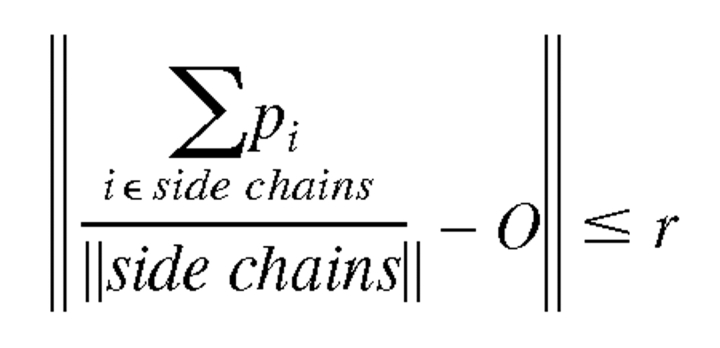For benchmarking, the centroid restraints are placed at the mean coordinates of the crystal structure’s side chain atoms with radii from 1 Å to 5 Å. Several targets have missing side chain atoms: 2PRK (residues 103-GLN, 167-ARG, 278-GLN), 2WRP (4-SER, 7-MET, 70-GLU), and 8ABP (2-ASN, 306-LYS); side chain centroid restraints were not enforced for these residues.

Conformational search algorithm

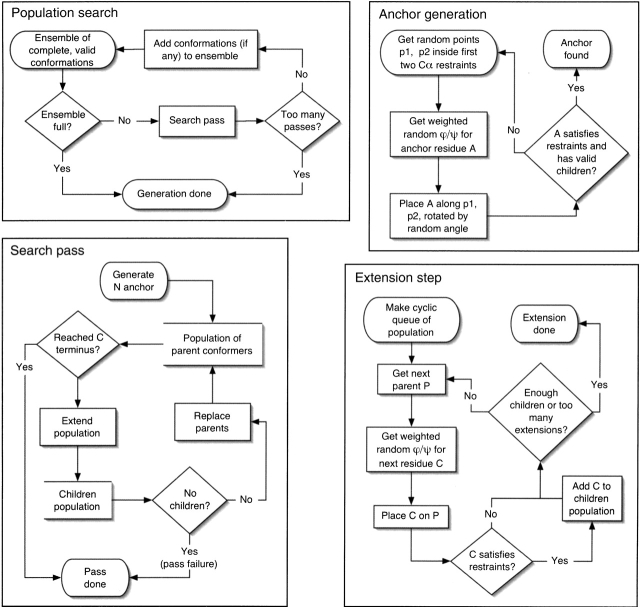
A novel conformational search algorithm, combining aspects of tree-search and genetic algorithms, was employed to solve restraint networks (shown schematically in Fig. 2 ▶). First, an N-terminal anchor residue must be generated to bootstrap the conformational search (Anchor generation). Two points are randomly chosen within the spheres of first and second Cα restraints. A residue is placed along the vector between the two points and rotated by a random angle around the vector. The anchor is accepted if it and at least some of its successor residues satisfy the restraint network; otherwise the process repeats.

Figure 2.

Flow diagram of the conformational search algorithm. See Materials and Methods for a detailed description of the algorithm.

Next, a population of 100 conformations (the parents) is extended from the N anchor residue to the C terminus, one residue at a time, generating at each step a new population of children conformations based on the parents (Search pass). During an extension step, the members of the parent population are examined in a round-robin fashion. For each parent P, a pair of backbone dihedral angles is randomly selected, weighted by propensity, and the corresponding child residue C is built. If C satisfies the Cα and clash restraints, then side chains are added as described below. The extension of the parent conformation proceeds until 100 children have been found or 100,000 extension steps have been tried. If the distance between the population and the closest common ancestor shared by all members of the population exceeds 20 residues, then the conformations sharing the most populous ancestor 20 residues back are kept and all others rejected from the population. This limits the diversity in the chain, and ensures that all residues preceding the common ancestor can be added to a grid-based cache for constant time excluded-volume checks. The maximum length of 20 is fairly arbitrary, and was selected because it enormously improves performance without any noticeable effect on the quality of the sampling algorithm.

Finally, when the population reaches the C terminus, only the unique chains from the population are selected as independent solutions. The whole process repeats until a complete ensemble of conformations has been found or the maximum number of passes has been exceeded (Population search).

Side chain modeling

Side chain conformations are taken from the penultimate rotamer library with secondary structure-specific rotamer propensities (Lovell et al. 2000). Rotamers are added to the main chain following each residue extension step of the conformation search algorithm. Given a residue with a valid main chain conformation, a random rotamer is chosen from the rotamer library based on the ϕ/ξ state of the residue and placed onto the main chain. If the rotamer satisfies all applicable restraints, the complete residue is accepted, otherwise the assignment iterates with another random rotamer until either a good conformation is found or all rotamers have been examined. This process is efficient using an elimination-based assignment algorithm (R.P. Shetty, P.I.W. de Bakker, M.A. DePristo, and T.L. Blundell, in prep.). During unrestrained side chain modeling, only excluded-volume restraints are enforced for side chain atoms, whereas restrained side chain modeling includes both excluded-volume and side chain centroid restraints.

Often residues distantly separated in the amino acid sequence are spatially in close proximity due to close contacts between side chains. During conformational search, an incorrectly chosen rotamer may affect only residues much later in the chain. The high sensitivity and nonlocality of side chain excluded-volume interactions give rise to a "needle-in-a-haystack" problem that the conformational search algorithm is particularly ill-suited to solve. In order to limit the long-distance effects between amino acids and ensure that the conformational search algorithm can construct models, the van der Waals radii for side chain–side chain and side chain–main chain interactions must be reduced by 50%.

Miscellaneous

The RMSD between two structures over a set of atoms was computed after optimal superposition of the structures. The Cα RMSD is the RMSD over only Cα atoms, the main chain RMSD is over the heavy backbone {N, Cα, C, O} atoms, and the all-atom RMSD is computed over all heavy main chain and side chain atoms present in the native structure. The restraint RMSD is the RMSD between the center of the (spherical) Cα restraints and the native Cα atoms. The ensemble average RMSD, over a set of atoms and an ensemble of structure, is the average RMSD over the set of atoms of each structure in the ensemble. It is an estimate for the RMSD of a randomly selected model from the ensemble. IUPAC atom name conventions were obeyed when comparing all-atom models.

Throughout the text, values in parentheses are standard deviations from the mean value. Secondary structure assignment was performed with dssp (Kabsch and Sander 1983), with ‘H’ state residues considered helical, ‘E’ state strand, and all other states coil. Surface accessibility calculations were performed with psa (Hubbard and Blundell 1987). A residue is considered buried when its normalized accessible surface area is less than 7% (Hubbard and Blundell 1987). Side chains were reassigned using scwrl (Bower et al. 1997; version 2.8, May 21, 2001). Side chains are considered correctly assigned when the χ₁ angle of the assigned rotamer is within 40° of the native χ₁ angle (Bower et al. 1997). Energy minimization was performed under the bonded terms of the AMBER forcefield (Cornell et al. 1995) using the program minimize from the tinker molecular mechanics software package (http://dasher.wustl.edu/tinker/, version 3.9, December 21, 2001) to a gradient root-mean-square of 10 kcal/mole/Å. Hydrogens were added to all models prior to minimization with reduce (Word et al. 1999b).

rapper is written in C using the Boehm garbage collector (http://www.hpl.hp.com/personal/Hans_Boehm/gc/) for automatic memory management and runs under Linux, FreeBSD, Mac OS X, and IRIX. All calculations were performed on a cluster of eight dual 2 GHz Althons running FreeBSD.