Abstract
In order to obtain adequate signal to noise ratio (SNR), stimulus-evoked brain signals are averaged over a large number of trials. However, in certain applications e.g. fetal magnetoencephalography (MEG), this approach fails due to underlying conditions (inherently small signals, non-stationary/poorly characterized signals, or limited number of trials). The resulting low SNR makes it difficult to reliably identify a response by visual examination of the averaged time course, even after pre-processing to attenuate interference. The purpose of this work was to devise an intuitive statistical significance test for low SNR situations, based on non-parametric bootstrap resampling. We compared a 2-parameter measure of p-value and statistical power with a bootstrap equal means test and a traditional rank test using fetal MEG data collected with a light flash stimulus. We found that the 2-parameter measure generally agreed with established measures, while p-value alone was overly optimistic. In an extension of our approach, we compared methods to estimate the background noise. A method based on surrogate averages resulted in the most robust estimate. In summary we have developed a flexible and intuitively satisfying bootstrap based significance measure incorporating appropriate noise estimation.
Keywords: bootstrap, statistical significance, evoked response, fetal magnetoencephalography, MEG
Introduction
Recording of brain activity by e.g. electroencephalography (EEG) or magnetoencephalography (MEG) is sometimes complicated by interference from unwanted signals. Interfering signals recorded during the measurement of an evoked brain response can be modeled as random noise relative to the triggered observation window of the response signal. To improve SNR, random noise is attenuated with signal averaging by the square root of number of events (K) which is at times limited by measurement conditions. Low SNR is exacerbated by inherently small signals (e.g. by stimuli at the perception threshold) or non-stationarity (due e.g. to latency jitter or poor attending to stimulus). The resulting time course may be difficult to interpret, with uncertain latency, especially when a physiological model of the response is not available to characterize the expected morphology. However, confidence intervals (CIs) can be computed and/or a statistical test can be applied to the data to determine significance of the response.
Statistical procedures which assume sufficient sampling and Gaussian distributions may not be well suited to this situation and we would like to avoid assumptions concerning the statistical distribution of the average. Traditionally, simple rank tests were applied in similar situations before the advent of modern computers (Maritz, 1995; Higgins, 2004). Later, more sophisticated permutation or randomization tests were developed for computerized significance computation (Edgington, 1995) and applied to many problems including evoked response studies (e.g. Blair and Karniski, 1993). This approach is attractive because it is non-parametric; however, it assumes that the statistical distributions of conditions to be compared are of the same shape or at least symmetric (Nichols and Holmes, 2001).
With the availability of high speed computers, there has been an increase in the use of bootstrap techniques which randomly resample a relatively small number of observations many times in order to estimate the population distribution (Zoubir and Boashash, 1998). This approach is similar to permutation in that both resample a relatively small collection of observations. However the bootstrap is more general because it does not require any assumption about distribution shape and resamples with replacement while permutation resamples without replacement. The method has recently been employed with evoked response data in a wide variety of applications, including modeled or parameterized time courses (Murata et al., 2002; Hammoudi et al., 2005; Rousselet et al., 2005), correlation measures (Martus et al., 2000), and frequency domain analysis (Furlong et al., 2004).
The immature or pathological brain may not produce a reliable response to stimuli so we would also like to avoid assumptions about response periodicity necessary for coherence or frequency domain approaches. A non-parametric bootstrap, which does not require a model of the response time course, may be most appropriate for such poorly characterized data. Numerous reports can be found in the literature on variations of the non-parametric bootstrap for the time domain averaged evoked response. Kruglikov et al. (2003) computed a bootstrap CI for the average over all trials of four stimulus conditions as a measure of background activity. A condition was considered significant in a time window where a single condition average fell outside the CI of the combined average. Given that the application of this scheme is limited to multiple stimuli paradigms, a more general approach would be preferred. Fujioka et al. (2004) used a nominal 95% bootstrap CI over the entire average window (subtracting the mean at each time point from the CI) as an estimate of the background and judged a post-stimulus average evoked response peak to be significant with a p-value < 0.05. This method may be overly optimistic since it does not account for the variation of the mean background. Lv et al. (2007) created an average from randomized triggers and applied the bootstrap procedure to estimate the distribution of the background and four different evoked response metrics. They tested the null hypothesis of no response for each metric applied to the true average. Although trigger randomization is an appealing and general method for estimating background activity, this implementation has no provision for estimating uncertainty due to the overlap of the mean peak distribution with the background distribution (statistical power).
Power analysis is useful when the application requires knowledge of reproducibility, often a concern with low SNR processes. It should be mentioned that there is some controversy in the use of statistical power analysis together with p-value for determination of statistical significance (Murphy and Myors, 2004). Detractors argue that statistical power should only be used for the purpose of experimental design to ensure that a properly designed experiment will necessarily have the required power, while proponents maintain that it is an important parameter in statistical significance of an experimental outcome. We did not find any report in the literature of evoked brain responses which has utilized the power measure in significance analysis. A related method is the use of a correction for false discovery rate (FDR) in test situations where multiple inferences are involved (Benjamini and Hochberg, 1995). FDR is defined as the proportion of errors in rejecting the null hypothesis while 1 – power is the probability that a random sample from the response distribution may also be found in the background distribution, even though the null hypothesis was rejected. Both concepts provide a mechanism for controlling overly optimistic conclusions.
The purpose of the present work was to devise a quantitative significance estimate including power analysis for difficult low SNR situations. The approach was based on the intuitive concept of overlapping signal and noise confidence intervals as an extension to the simple p-value threshold test and as an alternative to traditional equal means tests. We describe a bootstrap confidence interval calculation, two bootstrap-based significance measures, and a rank test in the next section and discuss three alternate methods for estimating the background distribution.
Performance of the proposed significance measure utilizing both p-value and power is compared with (a) p-value alone, (b) bootstrap equal means test, and (c) rank test using simulated data with variable SNR in the results section. We then provide a comparison of these four measures using three real example datasets. Finally, the effect on the proposed measure of using different estimates of the background distribution are demonstrated with the example datasets.
The example data was selected from a fetal MEG study. Fetal MEG (fMEG) is an emerging noninvasive technique with potential for monitoring fetal development and well-being. An array of MEG sensors is positioned over the surface of the pregnant abdomen and biomagnetic signals are recorded. Fetal brain signals are obscured by interference from environmental noise, fetal and maternal heart, and other biomagnetic activity; all of which must be attenuated by spatial and frequency domain filters before they can be observed. Spontaneous brain activity is usually identifiable after such processing; however, the amplitude of activity evoked by an external stimulus is around ten times smaller and requires further noise attenuation by signal averaging. The number of trials available for averaging is limited by practical considerations including the length of time that the mother can remain still (motionless) in the measurement position and the time interval between fetal movements. The immature fetal brain may not produce a reliable response to stimuli and latency may be uncertain, especially since fetal evoked response is not well characterized.
Materials and methods
The data used for evaluation of the significance measures was collected with a dedicated 151 channel fMEG system (Preissl et al., 2004; Eswaran et al., 2005) using a visual stimulation delivered to the pregnant abdomen from a fiber-optic cable terminated in a woven pad. Data was collected at 312.5 Hz with a randomized inter-stimulus-interval (ISI) of 3 +/− 0.5 s for a total of around 150 stimulus repetition trials. The data was post-processed with 0.5 − 10 Hz bandpass filter and averaged relative to the stimulus trigger over a window of −0.5 to 1.5 s. Interference by fetal and maternal magnetocardiogram (MCG) was attenuated by orthogonal projection of averaged MCG signal space vectors (McCubbin et al., 2006) and plausible MEG channel time courses were selected for best SNR (McCubbin et al., 2007). A selected time course was then tested for statistical significance.
For the description of the method we use the following notation convention: italic lower case character for a scalar, bold lower case character for a vector, lower case character with a subscript for a vector component, bold upper case character for a matrix, and plain upper case character with subscripts for a matrix component. A bold lower case character with a subscript indicates a member of a set of vectors. Curly brackets indicate a sequence of values and plain upper case character followed by square brackets represents an operation.
An estimate for the statistical distribution of the averaged evoked response at a time point of interest in the average window was devised by extending an algorithm for a bootstrap CI (Zoubir and Iskander, 2004). The collection of K trials used for the average at any time point, x = {x1, ..., xK}, is subjected to a bootstrap resampling operation where a random sample is drawn from the sequence of trial numbers {1,...,K} with replacement (such that some values may be repeated and some values may be omitted, but with same number of elements, K). The operation is repeated a number of times, N, to yield sequences {r1,..., rN} which remain static for analysis over the entire average window. Define Rb[x, rj] as the operation of selecting the sequence of trials rj from x. Repeat the operation N times to get a set of resamplings
| (1) |
At a selected time, t, in the average window define the set of sample observations as the collection of signal values for all trials, x(t) = {x1(t), ..., xK(t)}. Then the averaged evoked response at time t is given by the sample mean,
| (2) |
The variance of the mean, s2, may be estimated using a short bootstrap with N1 < N iterations (Zoubir and Iskander, 2004, p. 22). Then
| (3) |
where Ψ has dimensions of N1 by K. Compute N1 estimates of the bootstrap sample mean,
| (4) |
and
| (5) |
An estimate for the probability density function (PDF) of m(t) is determined using N realizations of a studentized statistic (Zoubir and Iskander, 2004, p. 52),
| (6) |
where
| (7) |
| (8) |
and
| (9) |
after obtaining bootstrap resamples
| (10) |
and
| (11) |
where Γ has dimensions of N by K and Λ has dimensions of N by N1 by K. Then the list of averaged evoked response estimates is formed
| (12) |
and {wi(t)} is sorted in ascending numerical order. A smoothed and normalized histogram of w(t) then provides an estimate of the PDF for m(t). We can extract the 100*(1 – a)% confidence interval from the sorted w(t) as
| (13) |
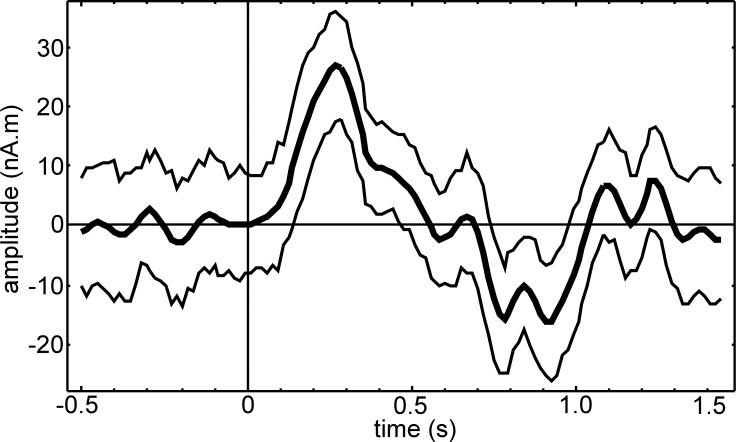
where indexes q1 = N a / 2 and q2 = N – q1 + 1 (Zoubir and Iskander, 2004, p. 81). The bootstrap procedure is repeated for every time point in the average window and the time courses of the confidence limits and averaged evoked response can be plotted together for interpretation , as shown in the example of Fig. 1.
Figure 1.
Example of time courses for an averaged flash evoked response, m(t) (thick line) and 95% confidence limits, wq1(t) and wq2(t) (thin lines). Stimulus trigger is at time zero.
The averaged evoked response in Fig. 1 exhibits a relatively flat pre-stimulus interval (−0.5 to 0 s, representing background noise) and a pronounced peak at about 300 ms post-stimulus which demonstrates a good SNR and would be readily accepted as a legitimate response latency even without the benefit of the CI. The CI provides additional assurance that the 300 ms peak is not likely to be due to a chance average of a few outlier trial values.
A judgment on the significance of the 300 ms peak in Fig. 1 can be made more concise by defining a statistical distribution of the background noise for comparison with the response distribution. Distributions are estimated via eq. 12. The statistics at a selected response point tb can be estimated relative to the worst case background point. For the example in Fig. 1, selecting e.g., tr = 300 ms, the worst case background point is at tb = −500 ms, because |m(tr)-m(tb)| is smallest. Based on this estimate we can determine the probability, p, that a mean value equal to or greater than m(tr) may be found in the background signal distribution by computing the tail area of the background PDF for values greater than m(tr). In addition we measure the probability, b, that a sample from the distribution of m(tr) will be less than the upper confidence limit of the background noise distribution by computing the tail area of the response PDF for values less than that limit.
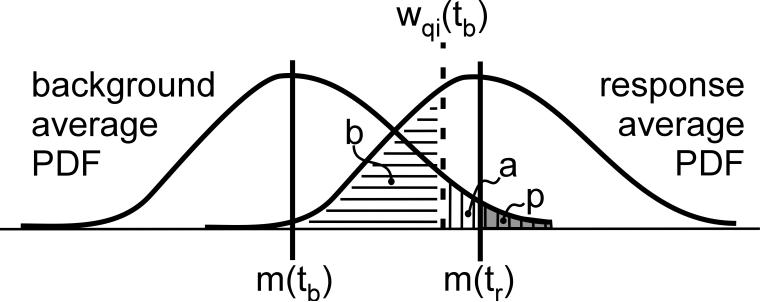
The situation can be visualized by the sketch in Fig. 2, where tb is a pre-stimulus time point chosen to represent the background distribution and tr is a post-stimulus time point of interest. These probabilities may be recognized as the familiar statistical measures commonly known as ‘p-value’ and power (1 – b). In general there are two cases to consider, m(tr) < m(tb) and m(tr) > m(tb), and Fig. 2 illustrates only the later. The schematic PDFs in Fig. 2 have a quasi-Gaussian character, however could be far from Gaussian in real situations.
Figure 2.
Schematic representation of significance for averaged evoked response, m(tr), given nominal background distribution with mean, m(tb), and confidence limit, wqi(tb). The area ‘a’ (vertical hatching) is the significance level associated with wqi(tb), ‘p’ (shaded) is the tail area of the background PDF for values larger than m(tr), and ‘b’ is the tail area of the response PDF for values smaller than wqi(tb).
An efficient estimation of p and b can be developed using the sorted bootstrap lists w(tb) and w(tr), where tb is the pre-stimulus time point chosen to represent the background distribution and tr is the post-stimulus time point of interest. The procedure is described as follows:
Step 1- find the sequence number (index, j) for the wj(tb) value closest to m(tr).
Step 2- compute the p-value as
| (14) |
Step 3- find the sequence numbers (indexes j1 and j2) for the wj(tr) value closest to wq1(tb) and wq2(tb).
Step 4- for the case where m(tr) > m(tb),
| (15) |
Step 5- for the case where m(tr) < m(tb),
| (16) |
Bootstrap equal means test
As an alternate measure, we apply an algorithm for the bootstrap comparison of two means using a standard two-sample t-statistic (Davison and Hinkley, 1997). The test statistic for the observed samples is computed as
| (17) |
Then N bootstrap estimates are computed using the same procedure as above,
| (18) |
The number, k, of values for which and the number, j, of values for which are found to cover both cases, m(tr) < m(tb) and m(tr) > m(tb) and the p-value is given by
| (19) |
Equal means by rank test
For comparison we also use a non-parametric rank test known as the Mann-Whitney test for equality of means of two populations (Higgins, 2004) which is a variation of the Wilcoxon rank sum test (Ostle and Malone, 1988). These tests assume symmetric distributions so that median = mean. The algorithm proceeds as follows.
First, a list of all possible pairs {xi(tb), xj(tr)}, i, j = 1,..., N, is created and the statistic u = number of pairs for which xi(tb) < xj(tr) is formed. A large value of u indicates that the background distribution has a tendency to produce larger values than the response distribution, small u is the converse, and intermediate u indicates equality. A normal distribution of the test statistic u may be assumed without significant error for sample size larger than about 10, so that a statistical table is not required to test the null hypothesis (Maritz, 1995). Following the above references,
| (20) |
where u is the test statistic value at a time point of interest,
| (21) |
is the expected value of the u distribution,
| (22) |
is the variance of the u distribution, c is a continuity correction (set to zero here), and G is the standard normal cumulative distribution function. P[.] represents the probability of an event.
Alternate background distribution estimates
We have considered 3 different methods to estimate the background distribution:
(a) maximum pre-stimulus: compute pi using w(ti) , i = 1,...,S, from each of the time points in the pre-stimulus interval, find k such that pk = Max[{pi}], and take w(tk) as the background distribution estimate.
(b) average zero mean: compute pi using w(ti) , i = 1,...,T from each of the time points in the entire average window, find k such that pk = Min[{pi - <p>}] where <p> is the mean of {pi}, and take w(tk) normalized to zero mean as the background distribution estimate.
(c) pooled random average: surrogate background data was created from the continuous, unaveraged data by averaging relative to 50 sets of randomized stimulus triggers. We have taken the set of randomized averages as a sample of background noise in the averaged time course. Since the randomized triggers have no meaningful temporal relationship to the averaged time course points, the time points from all randomized averages may be pooled and taken as independent random samples from the statistical distribution of the background noise. We have assumed a Gaussian distribution of the noise with mean and variance of the pooled sample. A Monte-Carlo investigation indicated that 50 randomizations was enough to reduce the spread of variance estimates to less than 1%.
The methods (a) and (b) involve the comparison of the response with multiple estimates of the background distribution and we have used a maximal (a) or mean (b) statistic (by taking the distribution that produced maximum or mean p-value) to avoid the problem of multiple comparisons (Nichols and Holmes, 2001).
Results
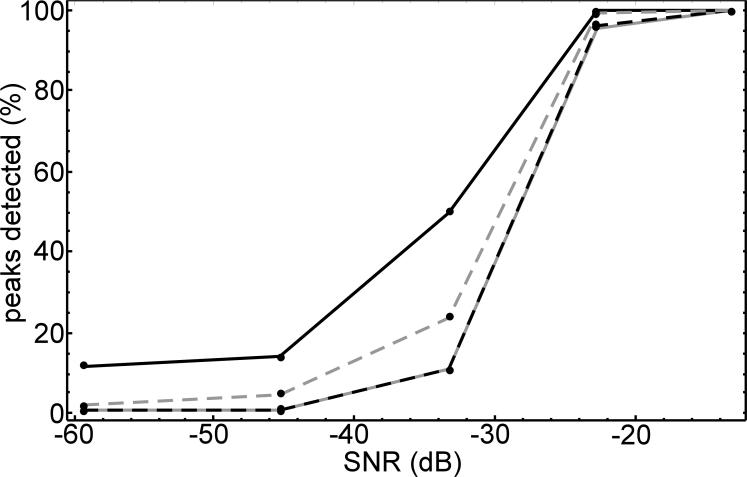
The significance measures described above were evaluated with a Monte Carlo study using simulated evoked response data consisting of 400 s of filtered random noise (bandwidth of 0.5 to 10 Hz) added to a sequence of Gaussian-shaped responses at intervals of 3 +/− 0.5 s. This provided about 115 trials with an average window of −0.5 to 1.5 s. The SNR was reduced in five steps from about −13 to −60 dB and 300 Monte Carlo repetitions were conducted for each step. As a performance measure we counted the percentage of correctly detected peaks in the 300 repetitions at a significance threshold of p = 0.05 (for all four measures) and b = 0.2 (for the p and b measure). Background noise distributions were computed using the average zero mean method. The evaluation is summarized in the plot of Fig. 3. As expected, all four methods performed similarly at high SNR. P-value and, to a lesser extent, rank were more optimistic than (p, b) or equal means. The (p, b) and equal means measures showed nearly identical behavior so that the plotted lines in Fig. 3 are overlapping. At very low SNR the detection rate was expected to drop to the threshold level of 5%, however the simple p-value test indicated a high false positive rate.
Figure 3.
Monte Carlo simulation, proportion of correctly detected peaks vs. SNR for four significance measures: p-value alone (solid black line), rank test (dashed gray line), bootstrap equal means test (solid gray line), and (p, b) (dashed black line).
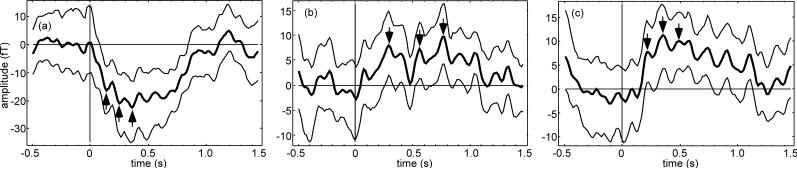
For comparison, the four significance measures were then applied to three selected examples from the collection of flash evoked response data. The examples were chosen to demonstrate significance measure performance on different characteristic time courses; one with a good SNR (pat5011), one with a poor SNR (pat5015), and one with a baseline drift but otherwise good SNR (pat5017). About 50% of selected channels had a time course similar to pat5011 example and about 30% exhibited baseline drift like the pat5017 example. The remaining 20% had time courses with SNR similar to the pat5015 example.
We have used N1 = 100 and N = 1000 for the bootstrap computation. These values were chosen as a compromise between convergence of the confidence interval (evaluated on one of the example datasets) and practical limitations of the computational burden. Resampling by 5 was employed after the 0.5 − 10 Hz bandpass filtering for expedience in processing the examples. Time course for the example averaged evoked responses is shown in Fig. 4 together with the bootstrap 95% confidence interval. The p-value threshold for significance was chosen as 0.05 to correspond to the 95% CI and b-value was taken as 0.2 which is a rule of thumb used in behavioral science applications (Cohen, 1988). The significance of prominent peaks indicated in Fig. 4 is provided in Table 1 for a comparison of p-value, b-value, equal means test value, and rank test value for each example. The significance parameters were computed using the average zero mean background noise method. The p-value measure was most optimistic with all nine peaks below the significance threshold. The (p, b) measure agreed with the equal means test (six peaks below the significance threshold) while the rank test (eight significant peaks) was nearly as optimistic as p-value.
Figure 4.
Example datasets: (a) pat5011, (b) pat5015, (c) pat5017: averaged evoked response time course (thick line) with bootstrap 95% confidence limits (thin lines). First three prominent peaks are indicated by arrows.
Table 1.
Significance values at prominent peaks for three example datasets of Fig. 4. Gray boxes indicate values below threshold, at which the response was deemed significant.
| Pat | Peak | Latency (ms) | p-value | b-value | Equal means | Rank |
|---|---|---|---|---|---|---|
| 5011 | 1 | 154 | 0.006 | 0.036 | 0.015 | 0.020 |
| 2 | 268 | 0.004 | 0.020 | 0.012 | 0.020 | |
| 3 | 379 | 0.001 | 0.009 | 0.007 | 0.014 | |
| 5015 | 1 | 299 | 0.008 | 0.287 | 0.060 | 0.026 |
| 2 | 572 | 0.010 | 0.300 | 0.070 | 0.090 | |
| 3 | 786 | 0.002 | 0.029 | 0.022 | 0.037 | |
| 5017 | 1 | 221 | 0.009 | 0.261 | 0.089 | 0.050 |
| 2 | 363 | 0.003 | 0.078 | 0.038 | 0.007 | |
| 3 | 505 | 0.006 | 0.088 | 0.041 | 0.013 |
We have investigated three alternative choices of background noise distribution estimate, described above, which are compared in Table 2 using the example datasets with p < 0.05 and b < 0.2 as significance measure. All three methods gave similar results except in the case of pat5017 where maximum pre-stimulus was considerably more conservative that either average zero mean or pooled random average methods.
Table 2.
Effect of background noise distribution estimate on significance measure for three example datasets of Fig. 4. Gray boxes indicate values below threshold, at which the response was deemed significant.
| Pat | Peak | Latency (ms) | Maximum prestimulus (p, b) | Average zero mean (p, b) | Pooled random average (p, b) |
|---|---|---|---|---|---|
| 5011 | 1 | 154 | (0.010, 0.196) | (0.006, 0.036) | (0.002, 0.084) |
| 2 | 268 | (0.005, 0.020) | (0.004, 0.020) | (0.005, 0.023) | |
| 3 | 379 | (0.005, 0.010) | (0.001, 0.009) | (0.005, 0.010) | |
| 5015 | 1 | 299 | (0.077, 0.679) | (0.008, 0.287) | (0.010, 0.246) |
| 2 | 572 | (0.108, 0.871) | (0.010, 0.300) | (0.018, 0.282) | |
| 3 | 786 | (0.034, 0.551) | (0.002, 0.029) | (0.005, 0.082) | |
| 5017 | 1 | 221 | (0.425, 1.000) | (0.009, 0.261) | (0.025, 0.354) |
| 2 | 363 | (0.172, 0.941) | (0.003, 0.078) | (0.004, 0.101) | |
| 3 | 505 | (0.238, 0.980) | (0.006, 0.088) | (0.006, 0.130) |
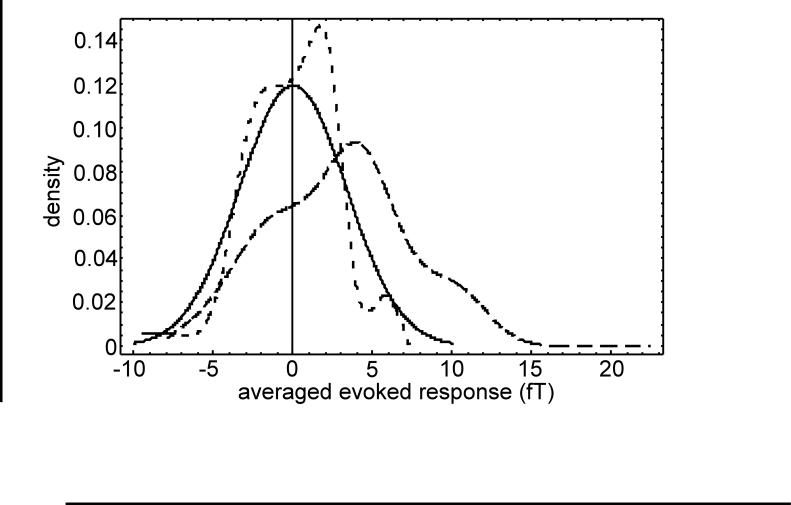
This raises concern for bias towards overestimation of the background due to the large excursion at the beginning of the pre-stimulus interval. The situation can be illustrated in another way by plotting the alternate background PDFs for pat5017 as shown in Fig. 5. Here it can be seen that the maximum pre-stimulus distribution is shifted towards larger values of the response and has a considerably broader extent than either of the other alternatives. It is also interesting to note the non-Gaussian character of the maximum pre-stimulus and average zero mean distributions compared to the Gaussian pooled random average distribution.
Figure 5.
Examples of alternate background PDFs for the averaged evoked response of pat5017; maximum pre-stimulus (long dash), average zero mean (short dash), and pooled random average (solid).
Discussion
The bootstrap significance measure based on the pair of parameters (p, b) has a similar behavior as the well-established bootstrap equal means test and the traditional rank test based on the simulation and the three examples presented above. Bootstrap p–value alone is overly optimistic compared to the other measures. This is not surprising since the shape of the test distribution is not considered; the mean may be a poor estimate of the expected value of the population for a distribution with large variance. The rank test provides a useful check on the bootstrap approach and is attractive because of its computational simplicity. However the assumption of symmetrical distributions may not be well supported for our data and we have not used it for routine processing.
Confidence intervals plotted together with the averaged evoked response represent a familiar and intuitive means to visually judge the significance of a peak in the response. We can quickly see if a peak average is outside the CI of the background noise observed over the pre-stimulus time segment and, if so, we can judge confidence in that estimate of the population average by checking the overlap of the peak's CI with the appropriate background confidence limit. The two parameter significance measure (p, b) provides us with a means to quantify this common intuitive assessment of the data. The bootstrap equal means test does provide similar information and could be used in place of the (p, b) measure (albeit with no control over power) or it may be used as validation of the (p, b) measure.
The choice of b-value threshold may depend on the experimental objective. If one is only interested to show that a physiologically reliable but low SNR process is active, as in the auditory brainstem response application of Lv et al. (2007), p-value alone may be sufficient. At the other extreme, where e.g. a critical diagnostic decision is based on the detection of a potentially unreliable response, a high level of certainty is required and b-value threshold should be low. We would consider our application to justify an intermediate threshold since we want to test for a reliable fetal evoked response but do not expect an exclusive clinical decision to be based on the outcome. Given this flexibility in setting b-value threshold and the intuitive linkage with the CI concept, we have chosen to base our significance analysis on the (p, b) measure.
The usual interpretation for evoked response data is that a time interval immediately preceding the stimulus trigger may be taken as background activity or noise with respect to the evoked response in the post-stimulus interval. The length of the time interval which may be used for a noise estimate is limited by the ISI and characteristic response duration for a particular experimental paradigm. We have used a relatively long ISI to account for the potentially prolonged response of the immature fetal brain to the stimulus in the example data. As such, we were reasonably confident that event related brain response above 0.5 Hz had subsided after two seconds and, with a three second ISI, assigned the 0.5 seconds before the trigger as unrelated background activity.
However, our examples have demonstrated a strong influence of the choice of background distribution on the significance analysis outcome. In situations with short ISI or where the background spontaneous brain activity may have a non-stationary bursting character as observed in premature newborn EEG (Stockard-Pope et al., 1992) (which is not sufficiently attenuated by averaging), the pre-stimulus time interval may not provide a good estimate of the noise. Small fetal body movements may also introduce non-stationary interference (due to residual MCG after attenuation by orthogonal projection of a nominal MCG signal subspace) which is not well characterized over the pre-stimulus interval.
The maximum pre-stimulus estimate may underestimate the noise or it may exaggerate it if an uncharacteristic drift is present, as in the pat5017 example (especially if the ‘drift’ is residual response due to insufficient ISI). The average zero mean method is a reasonable and convenient way to get the most conservative estimate of the variance of the process over the entire average window, but discards the un-attenuated slow background activity. As a result it may over-estimate significance. The pooled random method provides an arbitrarily large sample of the averaged background distribution which is unrelated to the stimulus-triggered average. With a sufficient number of random averages, it should account for non-stationary background activity.
Conclusions
We have described an application of the bootstrap method to quantify significance of averaged evoked response data which suffers from low SNR. We have chosen a familiar two parameter measure of p-value and statistical power and related it to the intuitive interpretation of bootstrap confidence intervals. The measure has been compared with a bootstrap equal means test and a traditional rank test using a simulation and example data from flash evoked fetal MEG data. Favorable comparison with these established tests has served to validate the chosen measure. The comparison illustrates the potentially optimistic bias of a test which relies only on p-value.
The (p, b) measure may fill a gap in descriptive statistics between p-value and the conservative equal means tests. The user may then choose a b-value threshold which matches the purpose of the study. If the hypothesis involves simple existence of a response then an appropriate b-value threshold may be near unity and thus dropped from the significance measure. At the other extreme may be a hypothesis which requires a highly reliable response. In that case one may choose a b-value similar to the p-value threshold. Accurate estimation of the background distribution is critical for reliability of the bootstrap significance measure. We found that for our fetal data application with non-stationary burst characteristic and insufficient attenuation from averaging, the background can be more reliably represented by using a pooled random average sample than by using maximum pre-stimulus or average zero mean distribution estimates.
Acknowledgements
The authors would like to thank R.B. Govindan for valuable suggestions. The work was supported by the U.S. National Institutes of Health under grants 1R01NS367704A1 and 1R33EB00978-01.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Statist. Soc. B. 1995;57(1):289–300. [Google Scholar]
- Blair RC, Karniski W. An alternative method for significance testing of waveform difference potentials. Psychophysiology, 1993;30:518–524. doi: 10.1111/j.1469-8986.1993.tb02075.x. [DOI] [PubMed] [Google Scholar]
- Chow SL. Statistical Significance. Sage Publications; London: 1996. [Google Scholar]
- Cohen J. Statistical Power Analysis for the Behavioral Sciences. L. Erlbaum Assoc.; Hillsdale NJ: 1988. [Google Scholar]
- Davison AC, Hinkley DV. Bootstrap Methods and their Application. Cambridge Univ. Press; Cambridge: 1997. pp. 171–172. [Google Scholar]
- Edgington ES. Randomization Tests. (3rd ed.) Marcel Dekker; New York: 1995. [Google Scholar]
- Eswaran H, Lowery CL, Wilson JD, Murphy P, Preissl H. Fetal magnetoencephalography – a multi-modal approach. Developmental Brain Research. 2005;154:57–62. doi: 10.1016/j.devbrainres.2004.10.003. [DOI] [PubMed] [Google Scholar]
- Fujioka T, Trainor LJ, Ross B, Kakigi R, Pantev C. Musical training enhances automatic encoding of melodic contour and interval structure. J. Cognitive Neuroscience, 2004;16(6):1010–1021. doi: 10.1162/0898929041502706. [DOI] [PubMed] [Google Scholar]
- Furlong PL, Hobson AR, Aziz Q, Barnes GR, Singh KD, Hillebrand A, Thompson DG, Hamdy S. Dissociating the spatio-temporal characteristics of cortical neuronal activity associated with human volitional swallowing in the healthy adult brain. 22. Neuroimage. 2004:1447–1455. doi: 10.1016/j.neuroimage.2004.02.041. [DOI] [PubMed] [Google Scholar]
- Hammoudi DS, Lee SSF, Madison A, Mirabella G, Buncic JR, Logan WJ, Snead OC, Westall CA. Reduced visual function associated with infantile spasms in children on vigabatrin therapy. Investigative Ophthamology and Visual Science. 2005;46(2):514–520. doi: 10.1167/iovs.04-0559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Higgins JJ. An Introduction to Modern Nonparametric Statistics. Brooks/Cole-Thompson: Pacific Grove. 2004:43–45. [Google Scholar]
- Kruglikov SY, Schiff SJ. Interplay of electroencephalogram phase and auditory-evoked neural activity. J. Neuroscience. 2003;23(31):10122–10127. doi: 10.1523/JNEUROSCI.23-31-10122.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lv J, Simpson DM, Bell SL. Objective detection of evoked potentials using a bootstrap technique. 29. Medical Engineering and Physics. 2007:191–198. doi: 10.1016/j.medengphy.2006.03.001. [DOI] [PubMed] [Google Scholar]
- Maritz JS. Distribution-Free Statistical Methods. 2nd ed Chapman and Hall; London: 1995. pp. 79–96. [Google Scholar]
- Martus P, Jünemann A, Wisse M, Budde WM, Horn F, Korth M, Jonas JB. Multivariate approach for quantification of morphologic and functional damage in glaucoma. Investigative Ophthamology and Visual Science. 2000;41(5):1099–1110. [PubMed] [Google Scholar]
- McCubbin J, Robinson SE, Cropp R, Moiseev A, Vrba J, Murphy P, Priessl H, Eswaran H. Optimal reduction of MCG in fetal MEG recordings. IEEE Trans. Biomed. Eng. 2006;53:1720–1724. doi: 10.1109/TBME.2006.876619. [DOI] [PubMed] [Google Scholar]
- McCubbin J, Murphy P, Wilson JD, Eswaran H, Preissl H, Robinson SE, Yee T, Vrba J, Lowery CL. Improved flash evoked response from fetal MEG. 1300. Int. Congr. Ser. 2007:749–752. [Google Scholar]
- Murata K, Budtz-Jørgensen E, Grandjean P. Benchmark dose calculations for Methylmercury-associated delays on evoked potential latencies in two cohorts of children. Risk Analysis. 2002;22(3):465–474. doi: 10.1111/0272-4332.00034. [DOI] [PubMed] [Google Scholar]
- Murphy KR, Myors B. Statistical Power Analysis. Lawrence Erlbaum Assoc.; Mahwah NJ: 2004. [Google Scholar]
- Nichols TE, Holmes AP. Nonparametric permutation tests for functional neuroimaging: a primer with examples. Human Brain Mapping. 2001;15:1–25. doi: 10.1002/hbm.1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ostle B, Malone LC. Statistics in Research. 4th ed Iowa State Univ. Press; Ames: 1988. pp. 95–106.pp. 131–132. [Google Scholar]
- Preissl H, Lowery CL, Eswaran H. Fetal magnetoencephalography: current progress and trends. 190. Exp. Neurol. 2004;(Suppl 1):28–36. doi: 10.1016/j.expneurol.2004.06.016. [DOI] [PubMed] [Google Scholar]
- Rousselet GA, Husk JS, Bennett PJ, Sekuler AB. Spatial scaling factors explain eccentricity effects on face ERPs. J. Vision. 2005;5:755–763. doi: 10.1167/5.10.1. [DOI] [PubMed] [Google Scholar]
- Stockard-Pope JE, Werner SS, Bickford RG. Atlas of Neonatal Electroencephalography. 2nd ed Raven Press; 1992. pp. 105–175. [Google Scholar]
- Zoubir AM, Iskander DR. Bootstrap Techniques for Signal Processing. Cambridge University Press; 2004. [Google Scholar]
- Zoubir AM, Boashash B. The bootstrap and its application in signal processing. IEEE Signal Processing Magazine. 1998 January;:56–76. [Google Scholar]