Sex-specific quantitative trait loci affecting longevity in Drosophila melanogaster

Abstract

Senescence, the decline in survivorship and fertility with increasing age, is a near-universal property of organisms. Senescence and limited lifespan are thought to arise because weak natural selection late in life allows the accumulation of mutations with deleterious late-age effects that are either neutral (the mutation accumulation hypothesis) or beneficial (the antagonistic pleiotropy hypothesis) early in life. Analyses of Drosophila spontaneous mutations, patterns of segregating variation and covariation, and lines selected for late-age fertility have implicated both classes of mutation in the evolution of aging, but neither their relative contributions nor the properties of individual loci that cause aging in nature are known. To begin to dissect the multiple genetic causes of quantitative variation in lifespan, we have conducted a genome-wide screen for quantitative trait loci (QTLs) affecting lifespan that segregate among a panel of recombinant inbred lines using a dense molecular marker map. Five autosomal QTLs were mapped by composite interval mapping and by sequential multiple marker analysis. The QTLs had large sex-specific effects on lifespan and age-specific effects on survivorship and mortality and mapped to the same regions as candidate genes with fertility, cellular aging, stress resistance and male-specific effects. Late age-of-onset QTL effects are consistent with the mutation accumulation hypothesis for the evolution of senescence, and sex-specific QTL effects suggest a novel mechanism for maintaining genetic variation for lifespan.

Although commonly acknowledged as one of life’s two certainties, the limited lifespan and characteristic postreproductive decline in survivorship and fertility with advancing age (senescence) (1) observed for most eukaryotic organisms remains an evolutionary conundrum. Explanations for the evolution of senescence and limited lifespan rest on the idea that the strength of natural selection on genes that express deleterious effects later in life is much weaker than selection against genes with equally deleterious effects earlier in life (2–4). Two, nonmutually exclusive hypotheses for the evolution of aging are predicated on different postulated properties of mutations affecting fitness. The “mutation accumulation” hypothesis (2) assumes that mutations affecting fitness have deleterious effects on all traits affecting viability and fertility but can vary for the age at which their deleterious effects are expressed. The “antagonistic pleiotropy” hypothesis assumes that mutations will preferentially accumulate that have beneficial effects on a component of fitness earlier in life but detrimental effects on either the same (3, 5) or a different (6) fitness component later in life.

In Drosophila, there is substantial segregating variation for longevity in nature, as evidenced by direct estimates of genetic variance for lifespan in random breeding populations (5, 7–11), response to selection for longer lifespan (12), correlated responses in lifespan to selection for late-age reproduction (5, 13–16), and divergence of average lifespan among inbred strains (7, 17). The existence of genetic variation for lifespan is consistent with both hypotheses; therefore, considerable effort has been expended to determine the relative contributions of mutations of each sort to variation in lifespan. The mutation accumulation hypothesis predicts that genetic variation of fitness in an equilibrium population should increase with age: Because the frequency of a gene in a mutation–selection equilibrium is proportional to the inverse of the selection coefficient, mutations that act late in life will reach higher frequencies than those with effects early on, and genetic variance increases when gene frequencies are less extreme (18). Empirical evidence both supports (9, 10, 19) and refutes (5, 8, 11, 20) this prediction. The antagonistic pleiotropy hypothesis predicts negative genetic correlations between early and late components of fitness. Again, empirical evidence both supports (5, 12–16) and refutes (10, 20–22) this prediction. Finally, if variation for lifespan is maintained by balancing selection for alleles with antagonistic pleiotropic effects, the dominance variance for longevity will be much larger than the additive variance. This prediction is not borne out; longevity in Drosophila melanogaster is a largely additive trait exhibiting little inbreeding depression (10, 11, 20, 21, 23–25).

The consensus from quantitative genetic studies is that genetic variation for longevity can be attributed to mutations with late-age specific effects as well as antagonistic pleiotropic effects on early and late fitness but that the relative contribution of each class of mutation is unknown (26, 27). This question can only be addressed by determining at what loci segregating variation for lifespan occurs in natural populations and by evaluating the distribution of allelic effects at each. Analyses of physiological correlates of longevity in Drosophila lines selected for postponed senescence have implicated loci involved in stress response and lipid biosynthesis in the selection response (12, 28–32). Additional candidate loci associated with the aging process are those affecting somatic mutation rate and cellular aging (27, 33–36). However, analyses of mutations, physiological correlates of long-lived lines, and changes in gene expression with aging do not directly address the question of the extent to which allelic variation at candidate loci causes quantitative genetic variation for longevity.

An approach that offers promise both for determining at which loci segregating variation affecting longevity occurs and the nature of allelic variation at these loci is quantitative trait locus (QTL) mapping (18, 37). Here we report the results of a genome-wide scan for QTLs affecting adult lifespan in D. melanogaster using a high resolution molecular marker map and a panel of 98 recombinant inbred (RI) lines constructed from two homozygous laboratory strains that were not selected for longevity.

MATERIALS AND METHODS

Drosophila Strains.

The RI lines were derived from two unrelated strains, Oregon R (38) and 2b (39), which were homozygous at all loci (39). The F₁ progeny of the parental lines were backcrossed to 2b, and the backcross progeny were randomly mated for four generations. At generation 5, 200 individual pairs were selected, and their progeny were inbred by full-sib mating for 25 generations. Ninety-eight lines that survived inbreeding were maintained by small mass matings of 20 pairs for 10 further generations. In the following generation, each RI line was split to produce individuals for longevity (20 pairs per vial) and marker (5 pairs per line) analysis.

Longevity Assay.

To obtain sufficient individuals for testing, all lines were multiplied for two generations at a density of 20 pairs per vial. In the following generation, 20 pairs of flies were placed in each of 5 vials per line for 3 days. Virgin females and males were collected over a 24-h period 9 days after the parents were discarded. The following day, 20–25 males and females (with only two exceptions when 8 and 19 females were collected, mean = 23) of each line were put individually in 10-ml plastic vials (total = 4519) with ≈1 ml of cornmeal–agar–molasses medium to eliminate the effect of density on longevity (29). No live yeast was added to the surface of the food. Deaths were recorded at 2-day intervals, and live flies were transferred to fresh vials every 8–10 days.

Molecular Markers.

Transposable element insertion sites were determined by in situ hybridization of a biotin-labeled plasmid containing the full length roo transposable element (40) to polytene salivary gland chromosomes of third instar larvae. Probes were labeled with biotinylated dATP (bio-7-dATP; BRL) by nick translation. Hybridization was detected using the Vectastain ABC kit (Vector Laboratories) and visualized with diaminobenzidine (40). Five slides were scored per line. Markers showing within-line heterozygosity were rechecked to eliminate the possibility of mis-scoring. The roo element markers were fixed in cytological positions 1B, 3E, 5D, 6E, 9A, 10D, 12E, 15A, 15F, 16A, 16D, 17C, 18A, 19A, 30A, 33E, 34EF, 35BC, 38A, 43A, 44C, 46A, 50F, 57C, 57D, 57F, 60E, 63A, 65A, 69D, 71E, 76A, 77E, 79C, 79E, 82D, 87B, 87F, 88E, 89B, 93A, 94D, 96A, 96F, 97E, 99E, 100A in 2b and at sites 4F, 7D, 7E, 11C, 11D, 14C, 15B, 19C, 21E, 22F, 27B, 29F, 30D, 38E, 39A, 43E, 44F, 46C, 48D, 49D, 50B, 50D, 61A, 61D, 65D, 67D, 68B, 68C, 70C, 72A, 73D, 76B, 77A, 78D, 85A, 85F, 87E, 91A, 91D, 92A, 93B, 97D, 98A, 99A, and 99B in Oregon, giving a total of 92 markers that were polymorphic between the parental lines, with an average spacing of 3.2 cm. The X chromosome is represented by cytological divisions 1–20, the second chromosome by divisions 21–60, and the third by divisions 61–100. The fourth chromosome of Oregon R line is marked by spa^pol.

Statistical Analyses.

Distribution statistics, correlations, and variance components were estimated using SAS procedures MEANS, CORR, GLM, and VARCOMP (41). F statistics (Type III SS) for regression of the line mean trait values on single or multiple markers were calculated using the GLM procedure. QTL cartographer, Ver. 1.09a (J. C. Basten, B. S. Weir, and Z.-B.Z., North Carolina State University, Raleigh, NC) was used for composite interval mapping of QTLs, and Macro SAS language (41) was used for permutations of the trait data and for repeated analysis of permuted data. Unless noted, heterozygous markers within an RI line were treated as missing data for this line.

RESULTS

Quantitative Genetic Analysis of Longevity.

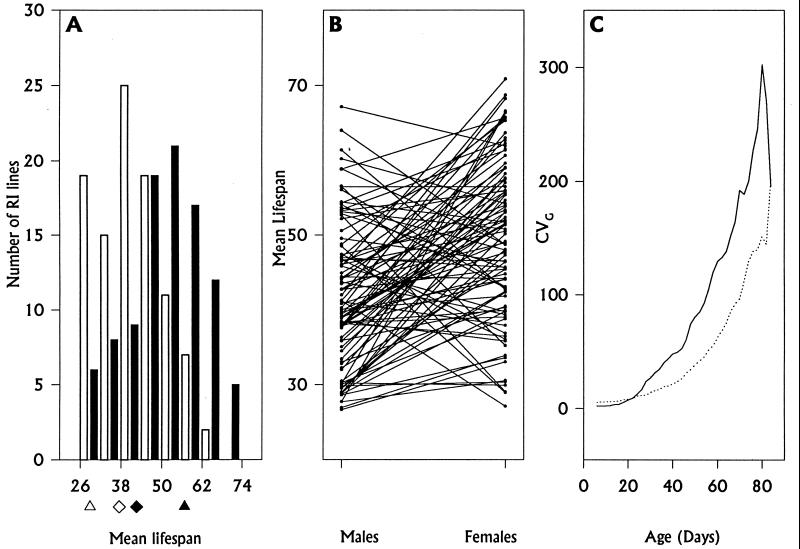
The mean lifespans of the parental lines were not significantly different from each other: 28.8 ± 2.64 (SE) and 56.8 ± 2.88 days for Oregon males and females and 37.4 ± 3.33 and 42.6 ± 4.21 days for 2b males and females, respectively. There was significant variation in mean lifespan for both sexes among the RI lines, the range of which exceeded that between the two parental lines (Fig. 1A). If we assume that the RI lines are completely inbred and that gene frequencies at loci causing variation in longevity are 0.5, the total genetic variance between the two parental strains, V_G, is estimated by the average among-line variance component for males and females (18), or 86.4. Females, with a mean lifespan of 49.53 days, were significantly longer-lived than males, with a mean lifespan of 41.88 days, averaged over all RI lines (F _{97, 97} = 35.62, P < 0.0001). However, this difference was not constant across lines; the sex × line interaction term was highly significant (Fig. 1B). The genetic correlation of male and female lifespan was low (0.304) indicating that the same loci do not affect longevity in the two sexes (7, 18).

Figure 1.

(A) The solid bars depict variation in mean female lifespan, and the open bars depict variation in mean male lifespan, among the Oregon and 2b RI lines. The solid and open symbols mark the mean lifespans of Oregon (triangles) and 2b (diamonds) females and males, respectively. The variation among RI lines for both sexes was highly significant by ANOVA (females: F_{97, 2129} = 6.568, P < 0.0001; males: F_{97, 2194} = 9.264, P < 0.0001). The estimates of among-line (σ_L²) and within-line (σ_E²) variance components were σ_LF² = 92.166 and σ_EF² = 376.117 for females and σ_LM² = 80.700 and σ_EM² = 228.383 for males. (B) There is highly significant sex × line (S × L) variation for lifespan among the RI lines (F_{97, 4323} = 6.111, P < 0.0001; σ_S×L² = 67.023), exhibited as crossing of reaction norms when the mean male and mean female longevity of each line are connected. The among-line variance component from ANOVA of lifespan including the fixed effect of sex (σ_LP²) was 26.180. The variance component estimate of the genetic correlation between the sexes (18) = r_G = σ_LP²/(σ_LF²×σ_LM²)^½ = 0.304. (C) The genetic variance in survival of the RI lines increases with age. The genetic variance, V_G, was estimated by the among-line variance in survival (σ_L²) at each time point for females (dashed line) and males (solid line). The coefficient of genetic variation, CV_G = 100(V_G)^½/x̄, where x̄ is the mean survival at each time point, is plotted against time.

The mutation accumulation theory predicts that genetic variation for survivorship should increase with age as late age-of-onset deleterious alleles are expressed (5). We analyzed the genetic variance of survivorship, scaled by the mean survivorship to partially remove any dependency of the variance on the mean, at different ages. There was a highly significant positive association of the coefficient of genetic variance (CV_G) with age (t) for both males (b_CVG, t = 2.29, P < 0.0001; r_CVG, t = 0.94, P < 0.0001) and females (b_CVG, t = 1.32, P < 0.0001; r_CVG, t = 0.91, P < 0.0001) (Fig. 1C).

Marker Genotype-Phenotype Associations.

The genotypic analysis of the RI lines confirmed that they were largely homozygous; the mean homozygosity averaged over all markers and lines was 0.956. However, 60 lines were heterozygous for at least one marker, and only eight markers were fixed in all lines. For any segregating marker, the genotype of the individuals for which lifespan was measured was unknown, so we determined associations between marker genotypes and lifespan phenotypes by treating heterozygous markers as missing data.

The genetic map for RI lines is expanded relative to an F2 or backcross map because more recombination events occur during their construction. Recombination rates (r) were computed from the marker data as r = 1/(4/R − 6), where R is the proportion of RI lines for which recombination between adjacent markers occurred (42); 17 markers were uninformative because they did not recombine with adjacent markers, and they were dropped from the analysis. No linkage disequilibrium was found between markers at 50°F and 57°C; therefore, the second chromosome was formally split into two linkage groups.

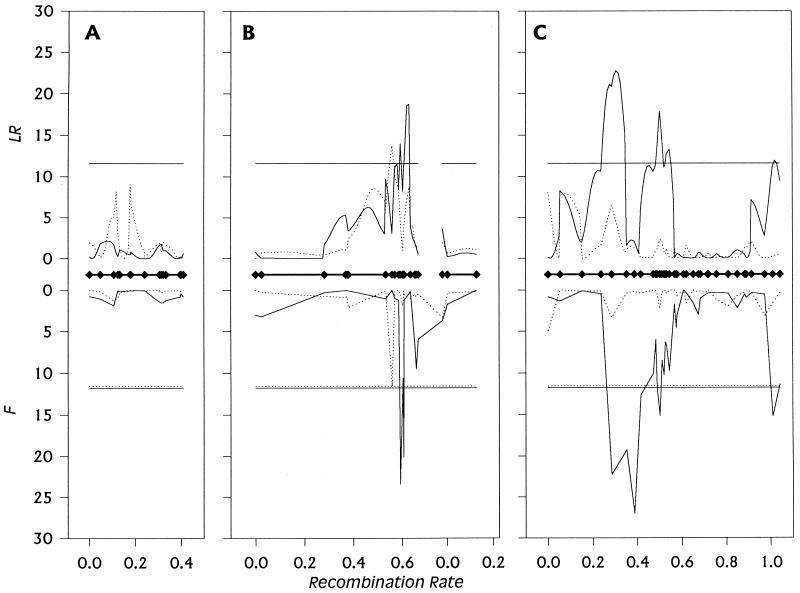
We used two different procedures to map QTLs affecting lifespan. Composite interval mapping (43, 44) tests the hypothesis that an interval flanked by two adjacent markers contains a QTL affecting the trait, while statistically accounting for the effects of additional segregating QTLs by multiple regression on markers outside the tested interval. Composite interval mapping results can depend on the number of background markers used and the size of the window around the tested interval within which linked markers are excluded from multiple regression. Fig. 2 depicts results using the Ri2 design of QTL cartographer (42), the Kosambi map function, 10 background markers, and a window size of 5 cm, for males and females separately. The likelihood ratio test statistic LR is −2ln(L₀/L₁), where L₀/L₁ is the ratio of the likelihood under the null hypothesis (there is no QTL in the interval) to the alternative hypothesis (there is a QTL in the interval). This test statistic at a genomic location is distributed as χ² with 1 df under the null hypothesis. The genome-wide critical threshold for α = 0.05, taking multiple tests into account, is estimated to be 11.6. In females, intervals in one region, 33E-34EF, showed a significant association with lifespan whereas in males, intervals in four regions were associated with variation in lifespan of the RI lines: 38E-46C, 65D-67D, 72A-85F, and 99B. We explored the effects of altering the window size and number of background markers on the location of significant intervals and found that three of the male-specific QTLs were consistent across a wide range of parameter combinations but that the LR test statistic for the female-specific interval and the male-specific interval at 99B did not always exceed the conservative threshold value, and additional significant intervals appeared and disappeared depending on the combination of parameters chosen.

Figure 2.

Plot of LR statistics from composite interval mapping (above the abscissa) and F statistics from multiple regression of lifespan on marker genotype (below the abscissa) against recombination rate on the first (A), second (B), and third (C) chromosomes for males (solid lines) and females (dotted lines). Marker positions are indicated on the abscissa by ⧫. The horizontal lines above the x axis mark the Bonferroni-corrected LR critical value for experimentwise α = 0.05, and the horizontal lines below the x axis mark the empirical F statistics for experimentwise α = 0.05 obtained from permutation tests of the final model for males (solid lines) and females (dashed lines). The F statistic for each nonsignificant marker was computed from a model that accounted for the effects of all significant markers. The F statistic for each significant marker was computed similarly, but markers closely linked to the significant marker under consideration were not included in the regression model. The abrupt declines in values of the F statistics flanking markers of the significant regions are artefacts of this procedure.

Because the choice of number of background markers and window size for composite interval mapping is somewhat arbitrary and exact results differ according to this choice, we also evaluated the robustness of our inferred QTL map positions by regressing RI line phenotype on marker genotype for each marker in turn, separately for males and females. With a dense map, the single marker problem of confounding map position with QTL effect is minimized. To overcome the problems of multiple tests and correlated markers in setting the correct experiment-wise type I error rate at α = 0.05, we determined the empirical F distribution under the null hypothesis of no association between any of the markers and trait values by randomly permuting the trait data among marker classes 1000 times and calculating the maximum F statistic (F_MAX) across all markers for each permutation. The 50th highest F_MAX is the empirical critical F corresponding to α = 0.05 under the null hypothesis (44, 45). To address the issue of segregating unlinked QTLs inflating the within-marker-class variance and hence reducing the power to detect additional QTLs (43, 44), a sequential search procedure for significant marker–QTL associations was used (46). In the second iteration, all significant markers from the first round were accounted for by treating them as fixed effects in a multiple regression, and marker–phenotype associations were recalculated for all remaining single markers. The threshold F statistic corresponding to α = 0.05 was determined by a permutation test for this model. We continued to add significant markers to the model in this fashion until no further significant markers were detected. The results of this analysis are given in Fig. 2. In good agreement with composite interval mapping, marker 34EF showed a significant association with female lifespan whereas four groups of closely linked markers at 38E-43E, 67D-69D, 72A-73D, and 99B-100A were associated with variation in male longevity among the RI lines.

QTL Effects.

The most significant marker in each of the five regions defined by the single marker analysis was included in a multiple regression analysis to estimate additive effects of the QTLs associated with the markers (Table 1). The effects ranged from 5 to over 14 days, or 0.6 to 1.5 additive genetic SD units. The proportion of the genetic variance contributed by each QTL was estimated as p(1 − p)a², where p is the marker frequency and a is the difference in lifespan, in days, between homozygous marker classes (this is less than the proportion of variance accounted for by multiple regression on the line means because the latter is inflated by sampling error). This estimate assumes strict additivity (we tested whether the mean longevity of lines containing heterozygotes differed from the average of the two homozygotes for each marker at which some lines segregated and found no significant deviations from additivity; see also 10, 11, 20, 21, 23–25) and that the markers and QTLs are tightly linked, so the frequencies of the markers and the QTLs are the same. In males, the four most significant markers account for 47.1% of the genetic variance among the RI lines, in good agreement with 47.4% of the variance among line means accounted for by regression. In females, marker 34EF alone accounted for 36.7% of the genetic variance, but the variance explained by regression, including all five markers, was only 16.4%. It is likely that there are two QTLs in repulsion linkage in the 34EF-38E region (see Table 1) and that the negative covariance between them reduces the overall variance explained in the full model. This could also account for the sensitivity of this region to model assumptions. The assumption of additive between-locus QTL effects in males is justified by analysis of all pair-wise combinations of significant markers; no significant interactions were observed between markers (data not shown).

Table 1.

QTLs affecting lifespan in Drosophila

Marker (map position)	Interval (map position)	Effect
		Days (SE)		σG
		♂	♀	♂	♀
34EF  (2-48)	33E, 35BC (2-46, 2-51)	0.61ns  (3.48)	−14.60*  (5.07)	0.07ns	−1.52*
38E  (2-54)	38A, 44C (2-54, 2-58)	10.92*  (3.82)	5.98ns  (5.56)	1.22*	0.62ns
68C  (3-35)	65D, 70C (3-22, 3-41)	−6.24*  (1.84)	1.91ns  (2.69)	−0.69*	0.20ns
73D  (3-44)	71E, 76A (3-43, 3-45)	−5.70*  (1.77)	−3.89ns  (2.58)	−0.63*	−0.41ns
99B  (3-100)	99A, 100A (3-100, 3-102)	−5.36*  (1.74)	2.88ns  (2.53)	−0.60*	0.30ns

Effects were estimated relative to the 2b strain markers by multiple regression of the most significant markers in each of the five regions to which QTLs for lifespan were mapped by single marker analysis. Approximate bounds on the intervals were determined by the position of the first nonsignificant markers flanking the significant regions. ∗, Markers that were significant on the basis of the permutation test; ^ns nonsignificant markers. Effects are given in days and as genetic SD units (σ_G). 

We assessed the age-specificity of the QTL effects on survivorship by regression of female survivorship at each age on the genotype of the single significant female marker and by multiple regression of male survivorship at each age on the four male marker genotypes. Applying the Bonferroni correction for multiple tests gives a threshold F statistic for an overall α = 0.05 of 11.4 for females and 11.6 for males. The five markers exceeded the critical F values at different ages, indicating age-specific QTL effects. Marker 34EF significantly affected female survivorship both early (days 4–22) and late (days 46–48) in life. For males, significant effects on survivorship were observed for marker 38E from days 44–92, marker 68C from days 30–46, marker 73D on day 34, and marker 99B on days 36–42. This analysis was repeated for mortality (17, 47) at each age. Age-specific QTL effects on mortality were observed in the time intervals immediately before those for which there were significant effects on survivorship. Marker 34EF significantly affected female mortality from days 4–12 and again at days 36 and 46. Marker 68C affected male mortality on days 26–36, marker 73D on days 28–34, and marker 99B on days 28–38. The exception was marker 38E, for which no age-specific mortality was detected.

DISCUSSION

We have used a panel of RI lines and a dense molecular marker map to conduct a genome-wide screen for QTLs affecting adult Drosophila lifespan that segregates between two homozygous parental lines, Oregon and 2b. Five genomic regions with moderate homozygous effects— over 0.5 genetic SD units—and that account for 37–47% of the genetic variance between the parental strains were detected using two different mapping algorithms. The usual caveats of statistical and genetic sampling applicable to initial QTL screens held here: QTLs with smaller effects that account for the remainder of the genetic variance segregating between these two particular strains could be detected by increasing the scale of the experiment, and similar studies of other strain combinations are necessary because genetic variation between pairs of inbred lines represents only a restricted subset of the total allelic variation (18). Nevertheless, our results demonstrate the power of the QTL mapping paradigm for determining the properties of mutations affecting lifespan and dissecting the multiple genetic causes of aging.

The longevity QTLs were highly sex- and age-specific. Sex-specific QTL effects on longevity are consistent with the low genetic correlation in lifespan between the sexes in these RI lines and with sex-specific longevity effects observed in unselected populations and inbred strains derived from wild populations (7). Although sex dimorphism in lifespan is a well known phenomenon in Drosophila (see, e.g., ref. 21), genetic variation in sex dimorphism has not been reported otherwise, presumably because most information on genetic variation for longevity comes from selection on both sexes, which increases the between-sex genetic correlation. Recently, mutational and segregating genetic variation in sex dimorphism has been observed for quantitative traits as different as Drosophila bristle number (40, 48–50) and olfactory behavior (51, 52). Such genotype × sex environment interaction means that a single genotype does not have the same effect in males and females. Sex-specific QTL effects could be an important mechanism maintaining segregating variation for quantitative traits in general and lifespan in particular, provided the relationship between fitness and trait value is the same for both sexes [i.e., provided there is QTL genotype by sex interaction for fitness (53–55)]. Late age-specific QTL effects on survivorship and mortality provide strong empirical support for the accumulation of late age-of-onset mutations that limit the mean and maintain the variation of lifespan, consistent with conclusions from studies of laboratory lines selected for postponed senescence (26). Antagonistic pleiotropic effects of lifespan QTLs have not been tested, and compensatory benefits early in life of QTLs that are deleterious later in life cannot be ruled out. The 2b strain was derived from a line that had been selected for reduced male mating activity (39). Male mating shortens male lifespan (56), so it will be of interest to determine whether the 2b and Oregon alleles associated with increased and reduced lifespan, respectively, also have antagonistic pleiotropic effects on early male mating.

The issues of the extent to which the QTLs detected here contribute to segregating variation for lifespan and whether naturally occurring alleles are also sex- and age-specific are matters for future experimentation. Variation between long inbred laboratory lines for any trait is due to fixation of different alleles that were segregating in the base population from which they were derived and to fixation of new mutations that occurred during laboratory maintenance. The problem of distinguishing initially segregating from mutational variation plagues all QTL studies, including those using divergent long term selection lines because mutation occurring during selection will contribute to the divergence from the base population and between replicate selection lines (57). Indeed, the mutational contribution to the divergence of selection lines is even greater than divergence between unselected lines because mutations with more deleterious effects can be fixed by artificial selection (58). However, discriminating old from new mutations is a moot point if the properties of new and segregating mutations are similar [sex-specific effects are observed for both mutational and segregating variation for other quantitative traits (40, 48, 49, 51, 52, 59, 60)] and if segregating and mutational variation for quantitative traits occurs at the same loci, as appears to be the case for numbers of Drosophila sensory bristles (40, 50, 59–61). One can therefore use QTL allelic variation to define a genetic locus and in future studies specifically address the question of the nature of mutational and segregating variation at that locus.

Mutations in genes affecting fertility, DNA repair and cellular aging, resistance to environmental stress, and lipid and glycogen content have been associated with altered lifespan and the aging process (12, 27–34). Candidate loci affecting all of these traits are found in the genomic regions to which QTLs affecting lifespan map (ref. 38; Table 1). Mutations in arrest (map position 2–48) are female sterile. mutagen sensitive (2–47, 2–54.9, 3–23, 3–44, 3–45) loci are deficient in excision and postreplication DNA repair. Loci implicated in cellular aging are elongation factor 2 (2–54), which catalyzes hydrolysis of GTP and the GTP-dependent translocation of tRNA on ribosomes, cyclin A (3–37), encoding cyclin, which is necessary for cell division, and acid phosphatase-1 (3–101.1), encoding the major adult phosphatase, levels of which increase during adult life. Resistance to oxidative stress is conferred by the products of the superoxide dismutase (3–34) and catalase (3–47) loci, resistance to thermal stress is conferred by heat shock proteins (3–28), and resistance to ethanol stress is associated with alcohol dehydrogenase (2–50.1). The cecropin loci (3–101) encode three bactericidal proteins. Candidate loci with male-specific effects are accessory gland protein K (2–54.1) and accessory gland peptide 70A (3–40), both produced exclusively in male accessory glands, and esterase 6 (3–39.5), the specific activity of which is two times higher in males than females and which is a component of seminal fluid. Finally, glyceraldehyde dehydrogenase 1 (2–57), phosphoglucomutase (3–43.4), and triosephosphate isomerase (3–101.3) are glycolytic enzymes that contribute to metabolic energy storage pools of glycogen and triglycerides. Fine-scale mapping and quantitative complementation tests (50, 61) to candidate loci should resolve which, if any, of the candidate loci harbor allelic variants that are associated with variation in lifespan.

ABBREVIATIONS

RI

recombinant inbred

QTLs

quantitative trait loci