A buried lysine that titrates with a normal pK_a: Role of conformational flexibility at the protein–water interface as a determinant of pK_avalues

Abstract

Previously we reported that Lys, Asp, and Glu residues at positions 66 and 92 in staphylococcal nuclease (SNase) titrate with pK_a values shifted by up to 5 pK_a units in the direction that promotes the neutral state. In contrast, the internal Lys-38 in SNase titrates with a normal pK_a. The crystal structure of the L38K variant shows that the side chain of Lys-38 is buried. The ionizable moiety is ∼7 Å from solvent and ion paired with Glu-122. This suggests that the pK_a value of Lys-38 is normal because the energetic penalty for dehydration is offset by a favorable Coulomb interaction. However, the pK_a of Lys-38 was also normal when Glu-122 was replaced with Gln or with Ala. Continuum electrostatics calculations were unable to reproduce the pK_a of Lys-38 unless the protein was treated with an artificially high dielectric constant, consistent with structural reorganization being responsible for the normal pK_a value of Lys-38. This reorganization must be local because circular dichroism and NMR spectroscopy indicate that the L38K protein is native-like under all conditions studied. In molecular dynamics simulations, the ion pair between Lys-38 and Glu-122 is unstable. The simulations show that a minor rearrangement of a loop is sufficient to allow penetration of water to the amino moiety of Lys-38. This illustrates both the important roles of local flexibility and water penetration as determinants of pK_a values of ionizable groups buried near the protein–water interface, and the challenges faced by structure-based pK_a calculations in reproducing these effects.

A small but significant fraction of the ionizable amino acids in proteins are buried (Rashin and Honig 1984; Kajander et al. 2000; Kim et al. 2005). These internal ionizable groups are of special interest because they play essential roles in energy transduction processes, including H⁺ transport (Luecke et al. 1998), e⁻ transfer (Deisenhofer et al. 1985), ion homeostasis (Jiang et al. 2003), and catalysis (Harris and Turner 2002). To understand the functional roles played by internal ionizable groups, it is necessary to know their pK_a values and to understand the molecular determinants of these values.

Previously we have shown that internal ionizable groups in staphylococcal nuclease (SNase) can titrate with pK_a values that are shifted significantly relative to the normal values. For example, Asp-66, Glu-66, and Lys-66 titrate with pK_a values of 8.9, 8.8, and 5.6, respectively (Stites et al. 1991; García-Moreno E. et al. 1997; Dwyer et al. 2000; Karp et al. 2007). Glu and Lys at position 92 titrate with pK_a values of 8.7 and 5.6 (Nguyen et al. 2004). In fact, an unpublished survey of Asp, Glu, and Lys at 25 internal positions in SNase shows that they are all destabilizing and that they titrate with pK_a values that are shifted toward the neutral state by an average of three pK_a units (D. Isom, B. Cannon, and B. García-Moreno E., in prep.). Similar observations have been made previously with other proteins (Li et al. 1993; Chivers et al. 1997; Czerwinski et al. 1999). The shifts in pK_a values are usually in the direction that promotes the neutral state (i.e., elevated for acidic groups and depressed for basic ones), which implies that the protein interior is neither as polar nor as polarizable as water. Exceptional cases have been reported of internal ionizable groups that are actually stabilizing (Kaushik et al. 2006), and where the polar atoms of the protein solvate the ionizable moieties better than water (Giletto and Pace 1999). However, in general it appears that factors such as Coulomb interactions, interactions with permanent dipoles, the reaction field of bulk solvent, the relaxation of permanent dipoles from the protein, and water penetration cannot fully compensate for the dehydration experienced by an ionizable moiety in the buried state.

Continuum electrostatics methods have been extremely useful to elucidate the determinants of pK_a values of surface groups (Tanford and Kirkwood 1957; Bashford and Karplus 1990; Nicholls and Honig 1991; Antosiewicz et al. 1994; Georgescu et al. 2002; Baker 2005), but it is becoming increasingly clear that these methods are inappropriate to treat internal groups (Schutz and Warshel 2001; Fitch et al. 2002; Karp et al. 2007). The problem is that these computational methods attempt to account for all the contributions to the dielectric effect implicitly (Warshel et al. 2006). This might be a valid approximation for surface ionizable groups, but it is probably not valid for internal groups; the chemical and dynamic heterogeneity and anisotropy of the protein interior cannot be ignored. Worse yet, the ionization of internal groups can be coupled to structural reorganization of the protein, not just through the reorientation of dipoles described implicitly by the protein dielectric constant, but also through more substantial local reorganization or subglobal unfolding that involves changes to the conformation of the backbone (Karp et al. 2007; A. Damjanović, X.W. Wu, B. Brooks, and B. García-Moreno E., in prep.). Physical insight into the factors that govern the pK_a values of internal groups is needed urgently to guide improvements to methods for structure-based calculation of electrostatic energies and pK_a values of internal groups.

The crystal structures of variants with Lys, Glu, and Asp at positions 66 and 92 in SNase show that the ionizable moieties of these groups are buried deeply in the hydrophobic core of the protein, surrounded primarily by hydrophobic matter. The only distinct feature observed in these crystal structures are internal water molecules associated with the buried carboxyl groups. The pK_a values of these internal groups cannot be reproduced with continuum electrostatics methods unless the protein is treated with artificially high dielectric constants of 10 or greater (García-Moreno E. et al. 1997; Dwyer et al. 2000). We have shown recently that in some cases these high apparent dielectric constants reflect local structural reorganization coupled to ionization of the internal group (Dwyer et al. 2000; Karp et al. 2007; A. Damjanović, X.W. Wu, B. Brooks, and B. García-Moreno E., in prep.). These dynamic processes are usually not treated explicitly in continuum calculations with static structures, thus they must be reproduced implicitly through the use of arbitrarily high protein dielectric constants.

Structure-based calculations of dielectric permittivity in proteins have suggested that the dielectric properties at the core can be different from those at the protein–water interface because the reaction field of bulk water can contribute significantly to the dielectric effect near the interface (King et al. 1991; Simonson and Brooks 1996; Simonson and Perahia 1996; Pitera et al. 2001). To examine the properties of ionizable groups that are buried but closer to the protein–water interface than to the core, we determined the crystal structure of the L38K variant of SNase, established that the side-chain of Lys-38 is indeed buried, measured its pK_a value with equilibrium thermodynamic experiments, and examined its interactions with nearby charges at the surface. In contrast with internal Lys residues in SNase described previously, the pK_a of Lys-38 is normal despite its being buried. The structural basis of this interesting observation cannot be explained with continuum electrostatics calculations. Extensive molecular dynamics (MD) simulations were performed to examine conformational dynamics in the region near the internal Lys-38. Overall, the data suggest that the flexibility at the protein–water interface is an extremely important determinant of pK_a values of ionizable groups buried near the protein–water interface. These findings have important implications for structure-based pK_a calculations, which are for the most part unable to treat flexibility realistically.

Results and Discussion

Crystal structure of the L38K protein

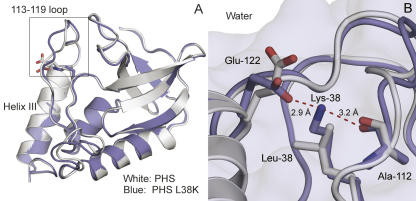
The structure of the L38K variant was obtained from a crystal of the PHS/L38K protein. The hyperstable PHS variant of SNase contains the P117G, H124L, and S128A substitutions. The L38K substitution had no detectable impact on the structure of SNase outside of the region near position 38. The C_α RMSD of the structure of PHS/L38K structure relative to the structure of the PHS protein was 0.7 Å (Fig. 1A).

Figure 1.

Crystal structure of PHS/L38K. (A) Structure of PHS/L38K (blue, accession code 2RKS), overlaid on the structure of PHS (white, accession code 1EY8) (Chen et al. 2000). The superposition highlights the minor rearrangement of residues in the loop composed of residues 113–119. (B) Close-up highlighting the fully internal Lys-38, the hydrogen bond with the backbone of Ala-112, and the ion pair with Glu-122.

Well-defined 1.5σ 2F_o − F_c density was observed for the Lys-38 side chain in electron density maps following molecular replacement. The side chain of Lys-38 is fully sequestered from solvent; the accessible surface area of the N_ζ atom of Lys-38 was 0.6 Ų (1.2%). The most interesting feature of the crystal structure is an ion pair between Lys-38 and the surface residue Glu-122. The conformation of the side chain of Glu-122 was different in the L38K variant than in other SNase variants; it is rotated 180° about the χ-angle, displacing the C_δ carbon by 1.6 Å and bringing the O_ε1 atom to within 2.9 Å of the Lys-38 N_ζ. The N_ζ atom of Lys-38 also formed a 3.2 Å hydrogen bond with the carbonyl oxygen of Ala-112 (Fig. 1B). A minor rearrangement of the backbone from 113 to 119 was also observed. This region forms a loop that packs against Lys-38. The backbone of this region had well-defined 1.5σ 2F_o − F_c density, but the density for the side chains was poor. This loop is often poorly resolved in crystal structures of SNase (Loll and Lattman 1989; Hynes and Fox 1991) as well as in the structures obtained by NMR spectroscopy (Wang et al. 1997). The backbone torsion angles of Lys-38 were unusual (φ = 59.5°, ψ = 6.4°), as has been noted previously in crystal structures with several types of amino acids at position 38 (Shortle et al. 1990; Stites et al. 1994). Data collection and refinement statistics are summarized in Table 1.

Table 1.

Crystallographic statistics of PHS/L38K

It is unlikely that crystal-packing forces induced the ion pair between Lys-38 and Glu-122. A symmetry-related molecule approaches this region of the protein, but the closest contact between Lys-38, Glu-122, and symmetry-related atoms is in the range 9–10 Å. PHS and PHS/L38K are also isomorphous; therefore, the interactions between symmetry-related molecules are comparable between these two proteins. There are no packing-induced structural changes that could explain the presence of the ion pair between Lys-38 and Glu-122.

pK_a value of Lys-38

All equilibrium thermodynamic and spectroscopy experiments were performed with the Δ+PHS/L38K variant. The Δ+PHS variant of nuclease is a hyperstable form consisting of PHS with additional G50F and V51N substitutions and a 44–49 deletion. We have shown previously that the structures of variants in the PHS or Δ+PHS backgrounds are identical (Dwyer et al. 2000; Karp et al. 2007).

The pK_a value of Lys-38 was determined by analysis of the pH dependence of stability of Δ+PHS nuclease and of the Δ+PHS/L38K variant with linkage relationships, as described previously (Stites et al. 1991; Fitch et al. 2002). This analysis is possible because the folding equilibrium of a protein is coupled to its proton binding equilibrium owing to differences in the pK_a values of ionizable groups in the folded and unfolded states (Wyman Jr. 1964). Measurement of the unfolding free energy (ΔG°_H2O) as a function of pH reports on the pK_a values of all ionizable residues in the protein. The pK_a value of a single group introduced by mutagenesis can be measured by subtracting ΔG°_H2O of the background protein (i.e., Δ+PHS nuclease) from ΔG°_H2O of the variant protein (i.e., Δ+PHS/L38K). Shifts in the pK_a value are reflected in the characteristic shape of the pH dependence of ΔΔG°_H2O (Stites et al. 1991; Fitch et al. 2002).

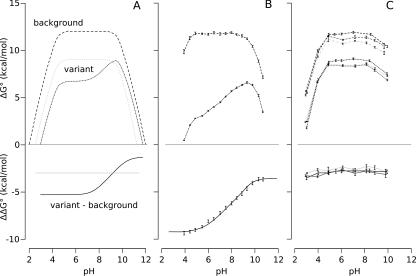
The pH dependence of ΔΔG°_H2O was simulated with Equation 1 (see Materials and Methods). The simulations plotted in Figure 2A illustrate how the pH dependence of ΔΔG°_H2O can be affected when a Lys residue introduced mutagenically titrates either with a normal pK_a value or with a depressed pK_a value. Figure 2B shows the pH dependence of ΔΔG°_H2O measured previously for Δ+PHS/V66K, a variant that has a Lys with a pK_a value of 5.6. These data illustrate how a depressed pK_a value would be readily apparent and resolvable from these data (Fitch et al. 2002). The pK_a value extracted with this method is equivalent to the pK_a value obtained from direct proton binding measurements using poteniometric methods (Fitch et al. 2002).

Figure 2.

Measurement of pK_a values with linkage thermodynamics. (A) Simulated pH dependence of ΔG°_H2O and ΔΔG°_H2O for proteins containing a Lys with a normal pK_a value (light dotted line) or with a depressed pK_a value (dark dotted line). The heavy dashed line represents the pH dependence of ΔG°_H2O for the background protein. The solid lines represent the pH dependence of ΔΔG°_H2O (variant: background). (B) Experimental ΔG°_H2O curves for Δ+PHS nuclease (heavy dashed line) and the Δ+PHS/V66K variant (dark dotted line) (Fitch et al. 2002). Lys-66 has a depressed pK_a value of 5.7. The solid line is the fit of Equation 1 to the experimental ΔΔG°_H2O points. (C) Measured pH dependence of ΔG°_H2O for the Δ+PHS/L38K (black), Δ+PHS/L38K/E122Q (dark gray), and Δ+PHS/L38K/E122A (light gray) variants. The dashed lines represent the pH dependence of ΔG°_H2O for the background proteins (Δ+PHS, Δ+PHS/E122Q, and Δ+PHS/E122A). The dotted lines represent the pH dependence of ΔG°_H2O for the variants (Δ+PHS/L38K, Δ+PHS/L38K/E122Q, and Δ+PHS/L38K/E122A). The solid lines trace the measured ΔΔG°_H2O for each variant. ΔΔG°_H2O is independent of pH for all three proteins.

The ΔΔG°_H2O of the Δ+PHS/L38K variant was independent of pH between pH 3 and 10, indicating that the pK_a value of Lys-38 was normal or higher than normal (Fig. 2C). The ion pair between Lys-38 and Glu-122 observed in the crystal structure suggested that the pK_a value of Lys-38 was normal because the dehydration penalty due to burial of the ionizable moiety of Lys-38 was offset by the favorable Coulomb interaction with Glu-122 and by the hydrogen bond with Ala-112. The Coulomb interaction could be quite strong as the interacting atoms are not water accessible. To test this, the pK_a value of Lys-38 was measured in the variants in which Glu-122 was replaced with Gln and Ala. Had the ion pair been the critical factor that compensated for dehydration, the pK_a value of Lys-38 should have been depressed in the absence of Glu-122. This was not observed. ΔΔG°_H2O was independent of pH for both the E122Q and the E122A variants (Fig. 2C). This suggests, contrary to the expectations set by the crystal structure, that the pK_a value of Lys-38 is normal even when the potentially favorable Coulomb interaction with Glu-122 was removed. This does not necessarily mean that Lys-38 and Glu-122 do not interact favorably because the pK_a value of Lys-38 in the presence of Glu-122 could actually be higher than 10.4. This cannot be established experimentally because ΔG°_H2O cannot be measured accurately above pH 10.4. We also deem it highly unlikely that a single hydrogen bond between Lys-38 and the carbonyl oxygen of Ala-112 is sufficient to compensate for dehydration. The most reasonable hypothesis to explain the normal pK_a value of Lys-38 is that conformational flexibility in this region of the protein is enhanced when Lys-38 is charged, allowing Lys-38 to contact water.

NMR and far-UV CD spectroscopy of variants with Lys-38

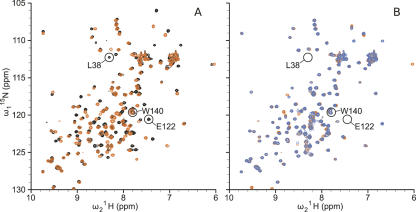
The possibility that structural reorganization was responsible for the normal pK_a value of Lys-38 was probed by comparing several spectroscopic properties of the L38K and L38K/E122Q variants. Two-dimensional (2D) ¹H,¹⁵N heteronuclear single quantum coherence NMR (HSQC) spectra, which correlate the amide ¹H chemical shift with the amide ¹⁵N chemical shift, were acquired for Δ+PHS nuclease and its L38K and L38K/E122Q variants. The HSQC spectrum of Δ+PHS nuclease and of the Δ+PHS/L38K variant were highly similar but distinct (Fig. 3A). One hundred thirty-one amide backbone resonances in the spectrum of Δ+PHS have been assigned previously by multidimensional NMR methods (C. Castañeda, pers. comm.). Ninety-eight of the 131 background assignments could be transferred by inspection to the spectrum of the Δ+PHS/L38K variant. The peaks that shifted in the spectrum of the L38K protein relative to Δ+PHS background, which therefore could not be assigned visually, corresponded to residues near Lys-38 in the crystal structure. Twenty of these 33 peaks belonged to backbone amides between residues 111 and 134, a stretch encompassing a loop and the N-terminal region of helix-3, both of which make contact with Lys-38 in the crystal structure (Fig. 1A). The remaining unassigned peaks corresponded to residues distributed throughout the protein, following no obvious pattern.

Figure 3.

2D [¹H, ¹⁵N]-HSQC spectra. (A) Superposition of HSQC spectra of Δ+PHS/L38K (orange) and Δ+PHS (black). (B) HSQC spectra of Δ+PHS L38K/E122Q (blue) overlaid on Δ+PHS L38K (orange). All spectra were acquired at pH 6.7 in 125 mM buffer at 298 K.

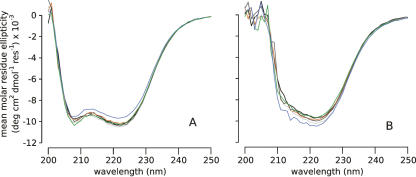
Although the HSQC results indicate that the L38K mutation altered this region of the protein, the chemical shift information in the HSQC cannot distinguish reliably between relatively minor changes in structure, dynamics, or electrostatics (Wishart and Case 2001). Other spectroscopic probes were necessary to examine the structural changes that might occur. For this reason, the far-UV circular dichroism (CD) spectra of all protein variants were compared. They are all quite similar, indicating that the overall secondary structure of the protein is not perturbed significantly (Fig. 4). Furthermore, the spectroscopic properties of Trp-140, an important residue that caps the C-terminal end of helix-3 and that has a strong fluorescence emission at 296 nm in folded SNase, indicate that helix-3 remains packed against the protein (Hirano et al. 2005). This fluorescence signal was strong in all variants (data not shown), fully consistent with helix-3 being packed in a native-like arrangement. The peak corresponding to Trp-140 in the HSQC spectra was also invariant in the different proteins, indicating that the side chain was in a similar environment in the Δ+PHS and Δ+PHS/L38K proteins. Together, the spectroscopic data suggest that the changes observed in the HSQC of the Δ+PHS/L38K variant are not caused by unfolding or by any other significant changes to secondary or tertiary structure. These small changes observed in the HSQC probably reflect subtle changes in the structure, dynamics, or electrostatics of the microenvironment of Lys-38.

Figure 4.

Far-UV CD scans at pH 7 (A) and 10 (B). Δ+PHS nuclease (black), Δ+PHS/L38K (orange), Δ+PHS/E122Q (dark gray), Δ+PHS/L38K/E122Q (blue), Δ+PHS/E122A (light gray), and Δ+PHS/L38K/E122A (green).

A comparison of the HSQC spectra of the Δ+PHS/L38K and Δ+PHS/L38K/E122Q variants showed that these proteins also did not differ significantly from each other (Fig. 3B). Significant changes in chemical shift would be expected if removal of Glu-122 led to structural rearrangement. Overall, the spectroscopic data suggest that neither the substitution of Leu-38 with Lys nor the substitution of Glu-122 with Gln affects the conformation of the protein in a substantial way. They support the hypothesis that the pK_a value of Lys-38 is normal because local conformational reorganization allows the ionizable moiety to experience more substantial contact with water than is reflected in the crystal structure.

Structure-based pK_a calculations

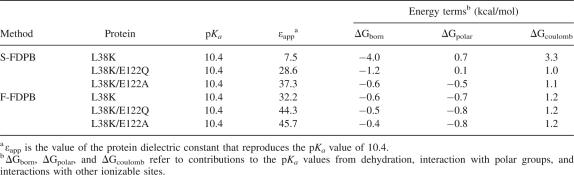
Continuum electrostatics calculations with a variety of different methods were performed to determine if an ion pair between Lys-38 and Glu-122 could be sufficient to compensate for dehydration of Lys-38. Two of these methods were implementations of standard finite-difference Poisson-Boltzmann (FDPB) calculations. In single-site calculations (S-FDPB), the charges of ionizable groups were placed on the titratable atom of a residue (i.e., the N_ζ of Lys) (Antosiewicz et al. 1994, 1996). In full-site calculations (F-FDPB), the charges on the ionizable groups are distributed over the entire residue using to the PARSE parameter set (Sitkoff et al. 1994). These calculations were performed using the crystal structure of the PHS/L38K variant and models of the PHS L38K/E122Q and PHS L38K/E122A variants derived from the structure of PHS/L38K.

Apparent dielectric constants (ε_app) refer to the protein dielectric constant (ε_p) needed to reproduce a measured pK_a value with a given model. To identify the ε_app values reported by Lys-38, calculations were performed using a wide range of values for the protein dielectric constant. Apparent dielectric constants are empirical parameters that capture implicitly all contributions to the dielectric response that are not treated explicitly in a given model (Schutz and Warshel 2001). In a calculation in which all contributions to the dielectric response are treated explicitly, ε_app = 1. Higher values of ε_app correspond to increasing levels of implicit treatment. For example, values of ε_app ∼ 2–4 presumably reproduce implicitly all contributions from electronic polarization (Harvey and Hoekstra 1972), values of 4–10 capture additional contributions from dipolar fluctuations (Sham et al. 1998), and values of 10–15 begin to include contributions from water penetration and structural reorganization (Dwyer et al. 2000).

The values of ε_app obtained from different calculations are listed in Table 2. The S-FDPB calculation on the PHS/L38K structure yields a pK_a value for Lys-38 of 10.4 with ε_app = 7.5. Under these conditions, the pK_a value of Lys-38 is normal because the unfavorable dehydration energy and the favorable Coulomb and polar interactions are balanced. When Glu-122 is removed, ε_app ∼ 30 is required to reproduce the pK_a value of Lys-38 with these calculations. This high apparent dielectric constant suggests that the protein structure reorganizes when Lys-38 is charged. According to the S-FDPB calculations, the ion pair between Lys-38 and Glu-122 is sufficient to compensate for dehydration experienced by the charged Lys-38 in the buried state. In contrast, ε_app > 30 is needed in F-FDPB calculations to reproduce the pK_a value of Lys-38, even in the presence of Glu-122. Thus, according to these calculations, the ion pair is never sufficient to compensate for burial of Lys-38. It suggests that more significant structural reorganization must be invoked to explain the normal pK_o value of Lys-38.

Table 2.

pK_a values of Lys-38 calculated with FDPB methods using static structures

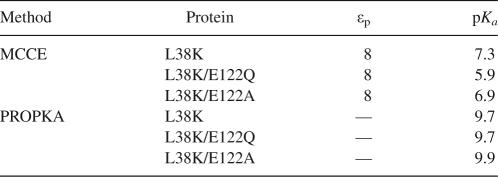
Calculations were also performed with the multiple-conformation continuum electrostatics (MCCE) method of Gunner and coworkers to explore how the explicit relaxation of side chains would affect the calculated pK_a value of Lys-38 (Alexov and Gunner 1997; Georgescu et al. 2002; Gunner et al. 2006). MCCE is an implementation of FDPB in which a Monte Carlo method is used to sample side-chain rotamers and tautomeric states without allowing the backbone to rearrange. Because the method does not allow arbitrary definition of the protein dielectric constant without extensive reparameterization, the pK_a values calculated using the highest available value (ε_p = 8) are reported. MCCE significantly underestimated the pK_a value of Lys-38 (Table 3), suggesting that relaxation of side chains is not sufficient to explain the normal pK_a value of Lys-38.

Table 3.

pK_a values of Lys-38 calculated using MCCE and PROPKA on static structures

pK_a calculations were also performed with the empirical PROPKA method (Dolinsky et al. 2004; Li et al. 2005). The pK_a value of Lys-38 calculated with PROPKA was depressed slightly and was insensitive to the presence of Glu-122. A small dehydration penalty was responsible for the depressed value. These calculations suggested that the pK_a value of Lys-38 is independent of the ion pair.

The results of calculations with the F-FDPB, MCCE, and PROPKA methods all suggested that the ion pair is not sufficient to compensate for the dehydration experienced by Lys-38. Overall, the pK_a calculations suggested that some form of structural reorganization was responsible for the normal pK_a value. S-FDPB suggested the opposite, but this is likely to be a consequence of the simplified charge distribution used for these calculations. In these calculations, the positive charge is placed on the N_ζ of Lys-38 (the atom closest to solvent), thereby lowering the energetic penalty due to dehydration. Furthermore, this charge distribution exaggerates the Coulomb interaction between Lys-38 and Glu-122 by placing all of the positive charge in the atom nearest Glu-122. When the charge is distributed in a more realistic fashion, as in the F-FDPB calculation, the energetic penalty due to dehydration increases and the favorable Coulomb interaction decreases. In this case, the results from F-FDPB calculations are probably more accurate than those with S-FDPB.

It is worth noting that none of the FDPB-based methods were able to reproduce the pK_a value of Lys-38 without arbitrary adjustment of the protein dielectric constant. Without previous knowledge of the pK_a of Lys-38, none of the methods would have estimated its pK_a value correctly using the values of ε_p = 4 commonly used in this type of calculation. These problems likely stem from the inability of these methods, including MCCE, to handle main-chain relaxation and other forms of reorganization of the protein. More microscopic methods (Kato and Warshel 2006) are becoming available that are useful for calculation of pK_a values of internal groups without assumptions about macroscopic dielectric constants.

Conformational reorganization probed with MD simulations

The spectroscopic measurements and electrostatics calculations suggested that structural reorganization, not an ion pair with Glu-122, was responsible for the normal pK_a value of Lys-38. MD simulations were performed to examine the nature of the structural reorganization. MD simulations sometimes suffer from incomplete sampling and can be force field dependent (Mackerell 2004). To ensure that sampling statistics were not limiting, ten 1-ns trajectories were compared to a single 10-ns trajectory (Damjanović et al. 2007). To examine how these results depended on the force field used, trajectories were generated using the CHARMM27 and the GROMOS96 53A6 force fields. GROMOS has been shown to sample more conformations than CHARMM (Yeh and Hummer 2002; Roccatano et al. 2004). It also tends to favor the β-sheet conformation, whereas CHARMM appears to favor the α-helix (Roccatano et al. 2004; Yoda et al. 2004).

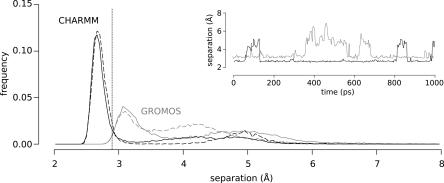
In the MD simulations, the ion pair between Lys-38 and Glu-122 broke and formed on the picosecond timescale (Fig. 5, inset). The populations of the ion-paired conformation in the ten 1-ns trajectories or in the one 10-ns trajectory were similar, suggesting that the relevant states were sampled adequately (Fig. 5). In a 10-ns GROMOS trajectory, a water-mediated ion pair between Lys-38 and Glu-122 was sampled more frequently than in the ten 1-ns trajectories. In the CHARMM simulations, a 2.7 Å ion pair was formed 70% of the time. In the GROMOS simulations, a 3.2 Å ion pair formed 50% of the time (Fig. 5). This is consistent with peptide simulations in which CHARMM favored ion pair formation more than GROMOS (Yoda et al. 2004). The difference in the distance between the closest heavy atoms of the ion pair in the GROMOS and CHARMM simulations reflect differences in the preferred orientations of the Glu-122 side chain in the two force fields.

Figure 5.

Distribution of distances between Lys-38 N_ζ and nearest Glu-122 O_ε during MD trajectories. Ion paired and non-ion paired states were populated in both CHARMM (black) and GROMOS (gray) simulations. Ten 1-ns trajectories combined (solid lines) give similar results to one 10-ns trajectory for short distances (dashed lines). The vertical line represents the distance between the ion paired atoms in the crystal structure (2.9 Å). Inset shows representative traces of the distance of separation between Lys-38 N_ζ and Glu-122 O_ε as a function of time for a CHARMM (black) and a GROMOS (gray) run.

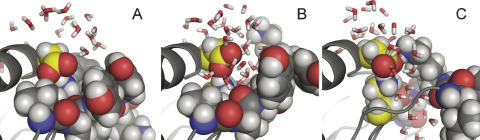
The most significant insight contributed by the MD simulations is that the side chain of Lys-38 is hydrated more extensively than is reflected in the crystal structures because slight movement of the loop consisting of residues 113–119 allows water to penetrate into the protein to hydrate Lys-38. This loop breaks van der Waals contact with Lys-38, forming a discrete channel that allows penetration of water to the region around Lys-38 (Fig. 6). A similar structural change was observed in simulations using the structural models of PHS/L38K/E122Q and PHS/L38K/E122A, but not in simulations with PHS or with PHS/L38K when Lys-38 was in the neutral state. This suggests that structural reorganization is coupled to the ionization of Lys-38 and is independent of the charge on Glu-122. The slight structural rearrangement suggested by the MD simulations is fully consistent with our observations with NMR and CD spectroscopy.

Figure 6.

Lys-38 is solvated by water penetration. Snapshots taken from a single CHARMM molecular dynamics run at 0 ps (A), 569 ps (B), and 818 ps (C). The side chains of Lys-38 and Glu-122 are highlighted in yellow. To illustrate the disruption of packing between the loop and Lys-38, residues 111–119 are shown in CPK representation in A and B. To illustrate the penetration of water into the protein, only residues 114–119 are represented as CPK in panel C.

To examine if the observed structural rearrangement could account for the implicit relaxation described by high values of ε_app in the continuum calculations, snapshots were taken at 0.1-ns intervals from the MD trajectories and used for pK_a calculations. ε_p = 4 was used in these calculations to account for electronic polarization and other factors (Warshel et al. 2006). This assumes that all other contributions related to structural reorganization are captured explicitly through relaxation of the protein structure with MD simulations. This approach is clearly an approximation and formally incorrect, as the electrostatic potential used to generate the states with the MD force fields are not the same as the potentials used to calculate the pK_a values with the continuum method, and, as independent MD simulations, should have been performed with Lys-38 in the neutral and charged states (Sham et al. 1997). The pK_a values calculated in this fashion are therefore only meant to assess whether the water penetration observed in the MD-relaxed state is sufficient to account for the normal pK_a of Lys-38. The water molecules that penetrated during the MD trajectory to solvate the N_ζ group of Lys-38 were not treated explicitly in these continuum calculations; they were treated implicitly with the dielectric constant of water.

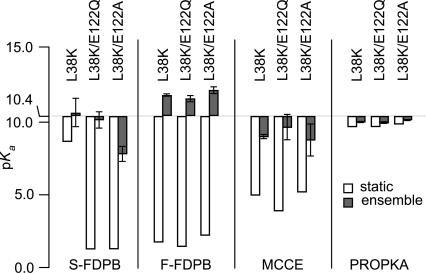
The results of these calculations are summarized in Figure 7. All calculations with continuum methods using the MD-relaxed structures gave pK_a values closer to the experimental value, although the different continuum methods did not all lead to normal pK_a values. Calculations with the S-FDPB on PHS/L38K/E122A continued to underestimate the pK_a value of Lys-38, as did MCCE on all variants. The MD calculations fully support the hypothesis that the pK_a of Lys-38 is normal because flexibility of this region of the protein allows Lys-38 to make more contacts with water than are reflected in the crystal structure. These results illustrate the potential usefulness of methods that combine continuum electrostatics calculations, in which many properties of the protein are described implicitly, with MD simulations (Srinivasan et al. 1998; van Vlijmen et al. 1998; Swanson et al. 2004).

Figure 7.

The calculated pK_a values of Lys-38 are higher when the structure is relaxed with MD. Calculations were done by using either a static structure (white bars) or an ensemble of snapshots from MD trajectories (gray bars). Error bars in ensemble calculations are the SD of calculated pK_a values. S-FDPB, F-FDPB, and MCCE calculations were all performed with ε_p = 4. S-FDPB, F-FDPB, and PROPKA used 100 snapshots per protein for ensemble calculation; MCCE used 10 snapshots per protein.

Conclusions

The pK_a values of internal ionizable groups can be very different from their normal pK_a values in water. The magnitude of the shifts in pK_a values experienced by internal groups are governed by the polarizability and polarity of the protein interior, and by a variety of factors that are poorly understood. Lys-66, Lys-92, and Lys-38 are all internal ionizable groups in SNase; Lys-66 and Lys-92 titrate with highly depressed pK_a values (Fitch et al. 2002; Nguyen et al. 2004), whereas Lys-38 has a normal pK_a value. This situation offered a unique opportunity to examine factors that govern the pK_a values of internal ionizable groups.

Ionizable groups buried in the protein interior are usually dehydrated or at least not as well hydrated as in bulk water. When this dehydration is not compensated by favorable interactions with the reaction field of bulk water, with backbone polar groups, or with charges of the opposite sign, the pK_a values shift in the direction that maximizes the range of pH over which the ionizable group remains neutral. The N_ζ atom of Lys-38 is ∼5 Å closer to bulk water than the N_ζ atom of Lys-66 and Lys-92. In principle, the reaction field of bulk water could compensate for dehydration in the case of Lys-38; however, according to the continuum electrostatics calculations, this effect was not sufficient to compensate for dehydration. Similarly, the N_ζ atom of Lys-38 makes a hydrogen bond with the carbonyl oxygen of Ala-112; but according to the continuum calculations, this interaction is also not sufficient to compensate for dehydration. The possibility that the Coulomb energy from the ion pair with the surface Glu-122 was sufficient to compensate for dehydration was eliminated by showing experimentally that the pK_a value of Lys-38 is insensitive to the presence of Glu-122.

The high dielectric constants required to reproduce the pK_a of Lys-38 in structure-based calculations with continuum methods suggested that conformational reorganization was necessary to explain the experimental data. On the other hand, the far-UV CD spectra, HSQC spectra, and the crystal structure suggested that the structure of the L38K variant was fully native-like, with all secondary structure intact and no overt sign of having reorganized in response to the ionization of Lys-38. Conformational reorganization coupled to the ionization of Lys-38 must therefore be local and modest. MD simulations revealed one possible form of structural reorganization that would allow Lys-38 to titrate with a normal pK_a value and that would be consistent with all experimental observations. They suggest that the ionization of Lys-38 causes a slight reorganization of the loop consisting of residues 113–119, which is packed against the side chain of Lys-38. This is enough to allow the penetration of water into the cavity where the charged and buried N_ε atom of Lys-38 is found. The results of the MD simulations were the same with the GROMOS and CHARMM force fields, and with one long or many short simulations. According to structure-based pK_a calculations, the water that penetrates following the opening of this passage is sufficient to normalize the pK_a value of the internal Lys. The structural changes needed to hydrate Lys-38 are sufficiently modest to be undetectable by CD or fluorescence measurements, yet sufficiently large to hydrate Lys-38 and completely normalize its pK_a value.

The ionization properties of Lys-38 and of ionizable groups at positions 66 and 92 in SNase are governed by different factors. Lys-66 and Lys-92 are buried deeply, beyond the influence of the reaction field of bulk water, in hydrophobic pockets without any polar groups that could compensate effectively for dehydration, and in relatively rigid regions where no readily accessible local conformational reorganization can lead to the large-scale hydration of the side chains in their buried state. For these reasons, these residues titrate with highly depressed pK_a values, and their ionization leads to local or subglobal unfolding (Kato and Warshel 2006; Karp et al. 2007; A. Damjanović, X.W. Wu, B. Brooks, and B. García-Moreno E., in prep.). In contrast, Lys-38 achieves a fully hydrated state without deleterious impact on the conformation of the native state. It is unclear if this will be the case with other ionizable groups that are buried near the protein–water interface. It is also not clear what the behavior of groups will be that are buried less deeply than those at positions 66 or 92 but are buried more deeply than Lys-38. What is clear is that small conformational reorganization followed by water penetration can have a large impact on the pK_a value of an ionizable group near the protein–water interface, and the important contributions made by these structural relaxation processes to the pK_a values of internal groups are very difficult to reproduce with structure-based calculations with continuum methods.

Materials and Methods

Staphylococcal nuclease

Two hyperstable variants of SNase, known as PHS and Δ+PHS, were used for crystallography and solution experiments, respectively. Both variants contain three substitutions: P117G, H124L, and S128A. Δ+PHS nuclease has two additional mutations (G50F and V51N) and a short deletion (residues 44–49). All genes were engineered into the pET24A+ vector (Novagen). Substitutions were introduced using QuikChange site-directed mutagenesis (Stratagene). All proteins were expressed in BL21(DE3) cells from Stratagene, and purified using the protocol of Shortle and Meeker (1989). Protein purity was determined to be >98% by SDS-PAGE. Protein concentration was determined by absorbance at 280 nm using an extinction coefficient of 0.93 mL mg⁻¹ cm⁻¹ (Fuchs et al. 1967).

X-ray crystallography

PHS/L38K was crystallized by the hanging-drop vapor diffusion method. Drops containing a 3 μL:3 μL mixture of 5.6 mg/mL protein and a reservoir solution of 45% (v/v) 2-methyl-2,4-pentanediol and 50 mM potassium phosphate, pH 10.5 were suspended over 1 mL of reservoir solution and equilibrated at 4°C. Diffraction data were collected from a single crystal suspended with mother liquor in a cryoloop and then flash-cooled in a stream of chilled nitrogen. Data were collected at 100 K using a Rigaku/MSC RU-H3R/Raxis4++ image plate system (Rigaku/MSC). Reflections were indexed and integrated in HKL and scaled and merged in SCALEPACK (Otwinowski and Minor 1997). Molecular replacement was performed in CNS (Brünger et al. 1998); the search model consisted of PHS/V66E coordinates (structure at 100 K) in which positions 38 and 66 were truncated to alanine, all waters were removed, and all B-factors were set to 20.0 Ų (Dwyer et al. 2000). Iterative model building in O (Jones et al. 1991) and crystallographic refinement in CNS (Brünger et al. 1998) were performed. Side chains for V66 and K38 were visible in the electron density maps and added in the first round of model building. Waters and phosphate ions were added in later model building iterations. A single round of model building was performed in COOT prior to the final round of refinement in CNS (Emsley and Cowtan 2004). The final model includes amino acids 7–141, 86 water molecules, and two phosphate ions. Crystallographic statistics are summarized in Table 1.

Measurement of pK_a values

Guanidine denaturation experiments monitoring Trp-140 fluorescence were performed as described previously, (García-Moreno E. et al. 1997; Dwyer et al. 2000; Whitten and García-Moreno E. 2000) with only a slight modification to ensure all measurements were performed with samples at equilibrium. All experiments were performed on an Aviv Automatic Titrating Fluorimeter 105 using an automated approach-to-equilibrium function to determine when equilibrium was reached after each addition of titrant. This entailed calculation of the change in signal as a function of time (dy/dt) by making fluorescence measurements at 2-min intervals after each injection. Samples were deemed to have reached equilibrium when dy/dt ≤ 5 × 10⁻⁵ s⁻¹. All solutions contained 25 mM buffer and 100 mM KCl. The different buffers used for measurements at different pH values have been described previously (Fitch et al. 2002).

The pK_a value of Lys-38 was determined by using the theory of linked functions (Wyman Jr. 1964) to analyze the pH dependence of the protein folding equilibrium (ΔG°_H2O). ΔG°_H2O was measured for a protein with and without the internal group of interest. The pK_a value of the inserted group in the native and denatured states of the protein could be extracted by fitting Equation 1 to the difference free energy curves (ΔΔG°_H2O) (Stites et al. 1991):

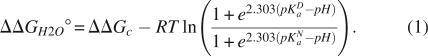ΔΔG°_c is the energetic cost of the substitution when the ionizable group that is being introduced is in the neutral state, and pK_a ^N and pK_a ^D are pK_a values of the group in the native and denatured states, respectively. Use of this method to measure pK_a value has been described previously (Stites et al. 1991; Dwyer et al. 2000; Karp et al. 2007).

NMR spectroscopy

Samples for NMR analysis were prepared by extensive buffer exchange of ¹⁵N-labeled protein into a phosphate buffer using a Millipore Ultracel YM-10 Centricon system. The NMR phosphate buffer contained 25 mM sodium phosphate, 100 mM sodium chloride, and 10% D₂O for field/frequency lock. The pH of the sample was measured on an Orion model 720A pH meter equipped with a Mettler Toledo 3-mm glass combination electrode. The pH was adjusted with 1 μL aliquots of concentrated HCl and NaOH at 25°C.

2D-¹H, ¹⁵N HSQC spectra of the Δ+PHS/L38K and Δ+PHS/L38K/E122Q variants were acquired at 298 K (actual temperature) and pH 6.7. The ¹H transmitter was set to the H₂O peak at 4.76 ppm, and the ¹⁵N carrier was set to 118.05 ppm. A total of four scans were signal averaged over 330 complex t ₁ points. Typical acquisition times in t ₂ were 128 ms (1280 complex points); in t ₁, 135 ms (330 complex points). Spectra were obtained on a cryoprobe-equipped Bruker 600-MHz spectrometer, located in the Johns Hopkins Department of Chemistry NMR Facility (Baltimore, MD). Typical sample volumes were ∼300 μL, and all samples were placed in Shigemi BMS-005TB solvent susceptibility-matched glass tubes. Uncertainties in chemical shifts were 0.01 ppm, 0.1 ppm in ¹H, ¹⁵N, respectively. Data conversion and processing was performed by using the nmrPipe software suite (Delaglio et al. 1995). Spectroscopic visualization and analysis was done by using Sparky (Goddard and Kneller).

Far-UV CD

Far-UV CD scans were performed in 1-nm increments with a 5-s averaging time using an Aviv CD-215 spectrophotometer. Signal was converted to mean residue ellipticity using the protein concentration and molecular weight (16,000 Da). Solutions contained 25 mM buffer and 100 mM KCl. Tris buffer was used at pH 7 and CAPS at pH 10.

Electrostatics calculations

The crystal structure described in this study was used for all calculations on the L38K variant. Models of the L38K/E122Q and L38K/E122A variants were made by manually editing the PHS/L38K PDB file. For the E122Q variant, OE2 was renamed to NE2. For the E122A variant, the side chain was truncated to the C_β atom. Polar hydrogens were added to the file using the HBUILD feature of CHARMM. The positions of the hydrogens and the side chain of residue 122 were minimized using CHARMM 22 (Brooks et al. 1983; Neria et al. 1996). The crystal structure of the PHS protein (accession code 1EY8) was used for calculations on the background protein (Chen et al. 2000).

FDPB calculations were done using the University of Houston Brownian Dynamics (UHBD) package, version 5.1 (Davis et al. 1991). Two different methods of FDPB calculations were done: single-site FDPB (Antosiewicz et al. 1994, 1996) and full-site FDPB using the PARSE parameter set (Sitkoff et al. 1994). All calculations were performed at 100 mM ionic strength as described previously (Fitch et al. 2006). MCCE calculations were done by using MCCE 2.2, downloaded from http://www.sci.ccny.cuny.edu/∼mcce/ (Alexov and Gunner 1997; Georgescu et al. 2002). The parameters distributed with the program were used for the ε_p = 4 and ε_p = 8 calculations. Calculations were done at 100 mM ionic strength. PROPKA calculations were performed by using PDB2PQR 1.1.2, downloaded from http://pdb2pqr.sourceforge.net/ (Dolinsky et al. 2004; Li et al. 2005). Solvent accessibility calculations were performed by using NACCESS 2.1.1, which is an implementation of the Lee and Richards algorithm (Lee and Richards 1971). A probe radius of 1.4 Å was used with the default van der Waal's radii for each atom (Chothia 1976). Relative accessible surface areas were calculated by comparison to a model of the amino acid in an extended, blocked, Ala-X-Ala peptide generated using Ribosome 1.0 (Srinivasan and Rose 1995).

MD simulations

MD simulations with CHARMM were performed by using NAMD 2.5 (Phillips et al. 2005) with the CHARMM 27 force field (MacKerell et al. 1998). Hydrogen atoms, N-terminal acetylation, and C-terminal N-methylation were added to structures by using the PSFGEN feature of NAMD (Phillips et al. 2005). The systems were energy minimized and immersed in a pre-equilibrated water box with TIP3 water molecules such that the protein was 10 Å from the closest edge of the box. All water molecules within 2.4 Å of a protein (except crystallographic water molecules) were removed. The systems were neutralized with the addition of 17 K⁺ and Cl⁻ ions, corresponding approximately to 100 mM salt. The ions were placed at random in the simulation box, but at least 6 Å away from the protein or from each other.

Systems were simulated with periodic boundary conditions by using the particle mesh Ewald (PME) method with a real space interaction cutoff of 10 Å. The PME grid spacing was ∼1 Å (60 × 60 × 60 grid dimensions) with an interpolation order of 4. The systems were first energy minimized, then equilibrated at 300 K for 500 ps. MD simulations were performed in an NPT ensemble at a pressure of 1 atm and a temperature of 300 K. The Langevin piston method was used for pressure control (Feller et al. 1995), together with Langevin dynamics for temperature control. The Langevin damping, piston period, and decay time were set to 1/ps, 200 fs, and 100 fs, respectively. A 2-fs time step was used and coordinates recorded every picosecond.

GROMOS calculations were done by using GROMACS 3.3.1 (Lindahl et al. 2001; Van der Spoel et al. 2005) and the GROMOS96 53A6 force field (Oostenbrink et al. 2004). Water molecules were added to the system using the genbox utility in GROMACS such that the protein was 10 Å from the closest edge of the box. The system was neutralized by using the genion utility in GROMOS by adding ∼25 K⁺ and Cl⁻ ions, corresponding to 100 mM salt. This was followed by minimization. Maxwellian initial velocities were generated, and the system equilibrated with 50 ps position-restrained MD. Systems were simulated with periodic boundary conditions using the PME method with a real space interaction cutoff of 10 Å. The PME grid spacing was ∼1 Å (60 × 60 × 60 grid dimensions) with an interpolation order of 4. MD simulations were performed in an NPT ensemble at a pressure of 1 atm and a temperature of 300 K by using Berendsen temperature and pressure coupling (Berendsen et al. 1984).

FDPB and PROPKA calculations were performed on structures extracted at 0.1-ns intervals from the ten 1 ns CHARMM trajectories (100 snapshots per variant). MCCE calculations were done on the last snapshot of each 1-ns trajectory (10 snapshots per variant). Average pK_a values were determined by taking the mean of the calculated pK_a value of Lys-38 in each snapshot (van Vlijmen et al. 1998).