An assessment of fixed-capacity models of visual working memory

Abstract

Visual working memory is often modeled as having a fixed number of slots. We test this model by assessing the receiver operating characteristics (ROC) of participants in a visual-working-memory change-detection task. ROC plots yielded straight lines with a slope of 1.0, a tell-tale characteristic of all-or-none mnemonic representations. Formal model assessment yielded evidence highly consistent with a discrete fixed-capacity model of working memory for this task.

The study of the nature and capacity of visual working memory (WM) is both timely (1) and controversial (2, 3). A popular conceptualization is that visual WM consists of a fixed number of discrete slots in which items or chunks are temporarily held (2, 4, 5). Nonetheless, there are dissenting viewpoints in which the discreteness is taken as, at most, a convenient oversimplification (6, 7). In this article, we provide a rigorous test of the fixed-capacity model for a visual WM task. Herein, we apply this test to items that differ in color, although the test is suitable to examine the generality of capacity limits across various materials.

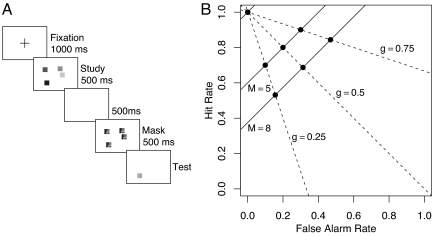
We used a common version (8–15) of the task popularized by Luck and Vogel (4, 16) (see Fig. 1A). At study, participants are presented with an array of colored squares. At test, a single square is presented; this square is either the same color as the corresponding square in the study array (a “same trial”) or a novel color (a “change trial”). Participants simply decide whether the test square is the same as or different from the corresponding studied square. In this task, where the color of each square is unique and the colors are well separated, capacity is the number of squares (objects) that may be held in visual WM. This object-based view of capacity is supported by previous research (4), in which performance does not vary with the number of manipulated features per object.

Fig. 1.

Experimental paradigm and fixed-capacity model predictions. (A) Structure of a trial in the experiment. The squares and masks in the experiment varied in color rather than gray scale. (B) Selective influence predictions for ROC plots. The predicted points are constrained to be at the intersections of equal-sensitivity and equal-bias lines.

Previous demonstrations of fixed capacity have relied on plotting capacity estimates as a function of the number of to-be-remembered items. Fixed capacity is claimed because capacity estimates tend to asymptote at three to four items for array sizes of four to six items. This approach, however, is not the most rigorous for this model. There are three weaknesses in previous demonstrations: (i) The asymptote of the capacity estimated may be mimicked by models without recourse to fixed capacity; (ii) previous demonstrations are made with aggregate data, and an asymptote in the group aggregate does not necessarily imply asymptotes in all or any individuals; and (iii) the stability of these asymptotes has not been formally assessed. These weaknesses motivate a more constrained test, to be presented subsequently.

The Fixed-Capacity Almost-Ideal Observer Model.

We define the fixed-capacity ideal observer as one who maximizes the probability of a correct response given the constraint that visual WM is discrete and limited in the number of items that may be held. Here, we derive the ideal observer model and show that it is closely related to Cowan's formula (2, 17) for visual WM capacity. Cowan's formula has been applied in a growing number of studies (9, 18, 19), often in combination with electrophysiological measures (20, 21) or functional neuroimaging (12–14). The measures seem to converge on a human capacity of approximately four simple objects in WM. However, all of this work is tenuous inasmuch as the theoretical assumptions underlying the model have not been examined rigorously. Later in this section, we relax an assumption of the model to approximate ordinary nonideal human decision processes (almost-ideal observer model) and, in Results, we include effects of inattention to the display.

The ideal observer conditions her or his response on whether the item is in memory. If so, the ideal observer responds accordingly, and performance is perfect. The probability that a cued square is in memory is a function of capacity, denoted k, and the number of squares in the study array (array size), denoted M. If capacity is as great as the number of squares, all may be held in memory. If capacity is smaller, however, only k may be held, and the probability of any one square being in memory is k/M. Combining these facts yields:

If the test item is out of memory, the ideal observer responds “change” only if a change is more likely a priori. Let g denote the probability of a change response when the item is out of memory, and let π be the probability of a change trial. Then,

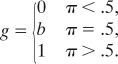The parameter b is a bias that holds if change and same trials are equally likely (i.e., π = 0.5) and does not affect the overall probability of a correct answer. The above equation is valid when the probability that the tested item changed (π) is known. It is not valid for other paradigms in which any one of several items presented at test may have changed (e.g., ref. 22).

Model predictions are easily derived for hit and false alarm rates, the probability of a “change” response for change and same trials, respectively. Let these rates be denoted by h and f, respectively. A hit occurs if an item is remembered, or failing this, a change is guessed. A false alarm comes about from guessing when the item is not remembered:

An equation for capacity may be derived by subtracting the false alarm rate from the hit rate and solving for k:

Eq. 3 is the same as Cowan's formula (2, 17), except that Eq. 3 is properly qualified for k≤ M.

The ideal observer model predicts a degree of determinism that seems unrealistic. When an item is not in memory, the model predicts response rates of 0.0 or 1.0, depending on whether π is less than or greater than 1/2, respectively. This deterministic rule is in conflict with the well known phenomenon of probability matching (23, 24), in which participants' response rates are more intermediate than these extremes. Our goal is to test WM models rather than models of response strategies. Therefore, we relax the model by allowing g to be any monotonic function of π. Although g is free to vary across conditions with different probabilities π, it does not depend on the array size. Because this relaxation allows for suboptimalities such as probability matching, the model may be characterized as a fixed-capacity almost-ideal observer. For brevity, we term it the fixed-capacity model. In fact, as will be shown, the model will need further generalization to fit data.

Testing the Fixed-Capacity Model.

The goal of this article is to provide a selective influence test (25) of the fixed-capacity model for a visual WM task. We factorially manipulated the array size (arrays of two, five, and eight squares) and the probability that there was a change in the array (probabilities of 0.3, 0.5, and 0.7). According to the model, capacity estimates should not vary with either manipulation. The guessing parameter g should vary with the probability of change (π) and not with array size. Consideration of selective influence allows for a more competitive and rigorous test of the fixed capacity model than previously attempted.

We express these constraints as follows. Let M_i, i = 1,…, I and π_j, j = 1,…, J denote the levels of the array-size and change-probability factors, respectively. Let h_ij and f_ij denote the hit and false alarm rates for ith array size and jth change-probability condition, respectively:

where d_i = min(k/M_i, 1). The model is equivalent to the double high-threshold model (26). This model makes well specified predictions for how receiver operating characteristics (ROCs) change as a function of array size and the change-probability manipulation. The ROCs for a fixed array size and varying change probability trace a straight line with a slope of 1.0 and an intercept min(k/M_i, 1). Fig. 1B shows these predicted equal-set-size ROC lines (solid lines) for the case where capacity k = 3 and M = (2, 5, 8). The ROCs for fixed-change probability and varying array size also trace a straight line with a slope of 1−1/g and an intercept of 1.0. The dashed lines show these equal-bias ROC lines for g = (0.25, 0.5, 0.75). These constraints on equal-set-size and equal-bias ROC curves form a strong test of the fixed-capacity model not easily mimicked by other models.

Signal-Detection Alternatives.

We also compared the fit of the fixed-capacity model to a signal-detection model of WM (7). In the signal-detection model, items are neither in nor out of memory. Instead, they have variable strength or familiarity (27). As with the development of the fixed-capacity model, we relied on an ideal-observer framework as a guide and, consequently, adopted the likelihood-ratio version of the signal-detection model (28). The model is described as follows: If the test square is the same, then its strength is distributed as a standard normal; if it has changed, then its strength is distributed as a normal with mean and variance as free parameters (denoted d′ and σ², respectively). The participant observes a strength, x, from the test square and calculates the likelihood ratio of this strength under these two hypotheses:

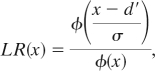where φ is the density of the standard normal. The participant responds “change” or “same” if the likelihood ratio is above or below a criterion, respectively. When parameterized in terms of likelihood ratios, the model has a natural selective-influence prediction: (i) set size should affect only the memory strength parameter, d′, and not the criterion; and (ii) change probability should affect only the criterion and not the memory strength parameter. A seven-parameter selective-influence model is constructed with three d′ parameters (one for each set size), three criteria (one for each change probability), and σ². A simpler six-parameter version is constructed by assuming equal variance in mnemonic strength (i.e., σ² = 1). Derivations for this model are provided as supporting information (SI).

Results

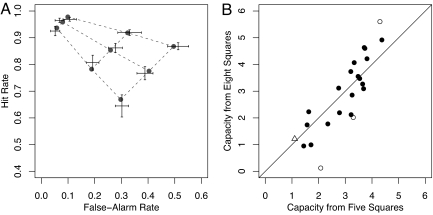
Averaged hit and false alarm rates are shown in Fig. 2A as two-dimensional error bars. These points fall at the vertices of straight lines. Moreover, the points lie very close to an isosensitivity line of slope 1.0, as predicted by the fixed-capacity theory.

Fig. 2.

Results. (A) ROC results (2D error bars) and predictions (lines and small points) from the five-parameter fixed-capacity model. Error bars denote standard errors of means in each measure. (B) Scatter plot of capacity in the eight-square arrays as a function of that in the five-square arrays. Filled points indicate participants for whom fixed capacity may not be rejected in favor of variable capacity. Open points are exceptions; see text.

The fixed-capacity model may be formally fit by assuming that the frequencies of hits and false alarms, denoted H_ij and F_ij, respectively, are distributed as conditionally independent binomials:

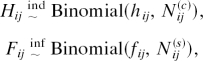where N_ij^(c) and N_ij^(s) are the number of change and same trials, respectively, for the ijth condition. For the experiment with three levels of change probability (J = 3), there are four parameters: k, g₁, g₂, and g₃. Estimation is performed by maximizing likelihood (29), and goodness of fit is assessed by comparing the likelihood of the model to that of a vacuous binomial model in which there are no constraints on h_ij and f_ij. For the experiment, the total number of parameters in the vacuous model is I × J × 2 = 18. The substantive model can be tested against the vacuous model with a log-likelihood test statistic (ref. 30) (G²). Given the large number of trials collected per individual, the model may be fit to individual rather than aggregated data.

The four-parameter fixed-capacity model fits poorly for 16 of 23 participants, as indicated by G² fit statistics that correspond to P values <0.05 [G²(14)>23.68]. The reason for these poor fits is both easy to diagnose and of secondary importance. One facet of the data is that accuracy with two squares at study is near but not at ceiling. Accuracy averaged 0.945 with none of the 23 participants achieving perfect performance. Any error in the two-square condition implies that capacity for all set sizes is <2.0. The data from the higher set sizes, however, are compatible with higher-capacity estimates, which leads to poor fits of the fixed-capacity model.

Adding Attention.

It seems plausible that below-ceiling performance with two squares may reflect an occasional lapse of attention. The fixed-capacity model, unfortunately, is not at all robust to this misspecification. For example, even for a person with a very high true capacity, the presence of a single error in the two-item condition will result in no likelihood for k ≥2. This lack of robustness can easily be modified by assuming that performance on each trial is a mixture of attentive and inattentive states. When the participant is attentive, performance is governed by the fixed-capacity model. When the participant is inattentive, the hit and false alarm rate probabilities are governed by the guessing parameters. The following five-parameter model reflects this role of attention:

where a denotes the probability that attention is engaged on a trial. This model also predicts straight-line ROCs with a slope of 1.0. Decreases in a lower the intercept of the ROC line. Thus, the five-parameter model is still highly falsifiable in the current experiment.

The addition of an attention parameter represents a type of trial-to-trial variability in the underlying process. In this case, the variability is coarse, varying between full attention and no attention. In a more fine-grained view, attention may vary across several levels. The experimental paradigm and subsequent data, however, do not provide sufficient precision to adjudicate between the all-or-none approach to trial-by-trial variability and a more fine-grained view. The current approach is simple and tractable and provides a parsimonious account of the data.

The five-parameter model was fit to each individual by maximizing likelihood. Overall capacity was at 3.35 items, and participants paid attention on 88% of trials. Guessing rates were ĝ = (0.47, 0.64, 0.79) for the base rates of π = (0.3, 0.5, 0.7), respectively. These guessing rates indicate a biased and probabilistic response strategy when items were out of memory and are approximately concordant with previous probability matching results (23, 24).

The model fit sufficiently well for 20 of the 23 participants, as indicated by G² fit statistics that correspond to P values greater than the 0.05 criterion [G²(13)<22.36]. Individualized maximum-likelihood estimates of model parameters are used to derive individualized ROC predictions for each participant. The average of these predictions is also shown in Fig. 2A as the smaller points connected by dotted lines. As can be seen, the averaged predictions are within the standard errors of averaged data. That is, the five-parameter fixed-capacity model does an excellent job of accounting for the selective-influence manipulations.

Fixed vs. Variable Capacity.

To test the fixed-capacity assumption more critically, we contrasted it to a six-parameter variable-capacity model with separate capacities for each array size. This model had six parameters: three capacities and three guessing parameters.^§ The five-parameter model can be rejected in favor of this six-parameter alternative for 4 of the 23 participants [G²(1)>3.84]. The nature of these few constant-capacity violations may be seen in the scatter plots of capacity estimates in Fig. 2B for the five- and eight-square arrays. Had capacity been exactly the same across array sizes, then the points would lie on the diagonal. The open circles indicate participants for whom capacity differs between the five- and eight-square arrays. The triangle indicates a participant who also violates fixed capacity; in this case, the participant had a capacity of 1.8 for two-square arrays but a capacity of 1.15 for five- and eight-square arrays. Overall, however, there is no apparent trend away from the diagonal; that is, the distribution of capacities across individuals does not appear to vary across the array size conditions. This fact serves as supporting evidence for the fixed-capacity model.

Even though the fixed-capacity assumption holds across a majority of participants, it does fail for a few. For a few participants, capacity decreases markedly with increasing array size. We suspect these participants may have been intimidated by the larger arrays and failed to encode much of them. Only one participant showed substantially increasing capacity across all three set sizes; perhaps this participant tried harder to encode the study array when more items were presented (31). In sum, fixed capacity is the norm, although subtle individual response characteristics, which seem orthogonal to the process of interest, are observable, too.

A Comparison to Signal Detection.

We also benchmarked the five-parameter fixed-capacity model against the signal-detection models. The six-parameter (equal variance) and seven-parameter (unequal variance) signal detection models fit well compared with the vacuous model for 19 and 20 of 23 participants, respectively. Whereas the signal-detection and discrete-capacity models are not nested, model comparisons are made with the following three model-selection statistics: Akaike information criterion (32), Bayesian information criterion (33), and an asymptotic approximation to normalized maximum likelihood (34, 35). We computed omnibus model selection statistics by computing the total likelihood of all parameters. For these three model-selection statistics, lower values indicate better fit. As shown in Table 1, the methods provide for converging results: the fixed capacity model fits best followed by the variable-capacity discrete-model and signal-detection models. As a final check of these model-selection results, we constructed bootstrapped sampling distributions (36) of the difference in deviance between the five-parameter discrete-capacity model and the six-parameter signal-detection model. Two such distributions were constructed, each assuming that one of the models being compared was true. These two distributions were well separated (z = 4.9), and the observed difference in deviance favored the fixed-capacity model.

Table 1.

Model-selection statistics

Model-selection statistic	Discrete capacity			Signal detection
	Full attention, four parameters	Fixed capacity, five parameters	Variable capacity, six parameters	Equal variance, six parameters	Unequal variance, seven parameters
Akaike Information Criterion	10,304.0	9,774.3*	9,775.8	9,791.5	9,796.8
Bayesian Information Criterion	10,674.3	10,237.3*	10,331.4	10,347.1	10,444.9
Normalized Maximum Likelihood	10,505.3	10,025.9*	10,077.7	10,093.4	10,149.0

*Indicates lowest value (best fit) across models.

Discussion

We have provided strong experimental support for a fixed-capacity model of visual WM in a task in which participants are asked to remember squares of various colors. Observed ROC functions have slopes near 1.0, and the five-parameter fixed-capacity model fits well when compared with a vacuous binomial model, a variable-capacity discrete model, and a variable-capacity signal-detection alternative. Perhaps the greatest advantage of the fixed-capacity model is its simplicity; it explains the extant data with far more parsimony than variable-capacity competitors. The paradigm and model are therefore well suited for exploring more advanced aspects of human visual WM, such as the role of chunking (5).

Although the fixed-capacity model fits well overall, there are violations in some participants. We suspect these may reflect idiosyncratic response characteristics, for example, being intimidated by large array sizes. Researchers need be aware of these possibilities, especially when attempting individual-level capacity estimation.

Software for fitting the fixed-capacity model across several array sizes is available at web.missouri.edu/∼umcaspsychpcl.

Methods

Participants.

Twenty-three students from an introductory psychology class at the University of Missouri, Columbia, served as participants.

Design.

Change probability (π = 0.3, 0.5, 0.7) and array size (M = 2, 5, 8) were manipulated in a within-participant factorial design. Change probability was held constant for blocks of 60 trials, whereas array size varied from trial to trial. The dependent variable of interest was the number of hits and false alarms in each condition.

Stimuli.

Study arrays were squares whose colors were sampled without replacement from 10 colors (black, white, red, blue, green, yellow, orange, cyan, purple, dark-blue-green). Squares were randomly positioned on the screen as described previously (17). Patterned masks consisted of identical multicolored squares as in Fig. 1A. Stimuli were presented on 17′′ cathode ray tube monitors (640 by 480 pixels, 120-Hz refresh).

Procedure.

The structure of a trial is shown in Fig. 1A. Participants depressed one of two keys on a keyboard to indicate whether the test square was the same as or different from the corresponding square in the study array. The experiment was composed of nine blocks of 60 trials each, for a total of 540 trials. To make the change-probability manipulation salient from the outset of a block, participants were first shown a pie chart of the change probability. The change probability was also presented, as a percentage, before every trial. The session took ≈45 min to complete.

Our experimental procedure had three features that may be necessary to isolate WM capacity. The first feature is that only a single square was presented at test. In a separate pilot experiment, we presented all squares at test and cued a specific target square by encircling it. In this case, there was evidence that capacity was not constant but rose with increasing array size. We attribute this phenomenon to the use of nontested squares as contextual cues, possibly allowing chunking or grouping of squares (15). Participants may quickly learn that squares can be stored and successfully retrieved as a group. The presentation of a single square at test may lessen the benefit of grouping. The second feature is that each studied square has a unique color within the array. It is our experience that if grouping were to happen, it would be across squares of the same color. Therefore, the constraint of unique colors limits grouping. The final feature was the insertion of a patterned mask between study and test. The patterned mask is useful, because it allows the relative participant to know the relative location of the tested square to the other squares and prevents any residual of perceptual or iconic memory (37) from contributing to the capacity score (18).