Abstract
S6K1 is a member of the AGC subfamily of serine-threonine protein kinases,
whereby catalytic activation requires dual phosphorylation of critical
residues in the conserved T-loop (Thr-229) and hydrophobic motif (Thr-389).
Previously, we described production of the fully activated catalytic kinase
domain construct, His6-S6K1αII(ΔAID)-T389E. Now, we
report its kinetic mechanism for catalyzing phosphorylation of a model peptide
substrate (Tide, RRRLSSLRA). First, two-substrate steady-state kinetics and
product inhibition patterns indicated a Steady-State Ordered Bi Bi mechanism,
whereby initial high affinity binding of ATP
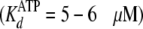 was
followed by low affinity binding of Tide
was
followed by low affinity binding of Tide
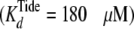 , and
values of
, and
values of 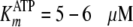 and
and 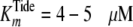 were
expressed in the active ternary complex. Global curve-fitting analysis of ATP,
Tide, and ADP titrations of pre-steady-state burst kinetics yielded
microscopic rate constants for substrate binding, rapid chemical
phosphorylation, and rate-limiting product release. Catalytic trapping
experiments confirmed rate-limiting steps involving release of ADP.
Pre-steady-state kinetic and catalytic trapping experiments showed osmotic
pressure to increase the rate of ADP release; and direct binding experiments
showed osmotic pressure to correspondingly weaken the affinity of the enzyme
for both ADP and ATP, indicating a less hydrated conformational form of the
free enzyme.
were
expressed in the active ternary complex. Global curve-fitting analysis of ATP,
Tide, and ADP titrations of pre-steady-state burst kinetics yielded
microscopic rate constants for substrate binding, rapid chemical
phosphorylation, and rate-limiting product release. Catalytic trapping
experiments confirmed rate-limiting steps involving release of ADP.
Pre-steady-state kinetic and catalytic trapping experiments showed osmotic
pressure to increase the rate of ADP release; and direct binding experiments
showed osmotic pressure to correspondingly weaken the affinity of the enzyme
for both ADP and ATP, indicating a less hydrated conformational form of the
free enzyme.
A key requirement for higher eukaryotic cells in sustaining prolific capacity is growth regulation, whereby increasing cellular mass and size prerequisite to division derive from coordinate macromolecular biosynthesis. The 70-kDa 40 S ribosomal protein S6 kinase-1 (S6K1)2 is a key enzyme in coordinating cell growth with proliferation, as mitogen, nutrient, and energy status signaling pathways converge to activate S6K1 and initiate protein translation (1–5). Two S6K1 isoforms (accession no. NM003161, αI and αII isoforms) are produced from a single gene by alternative mRNA splicing and the use of an alternative translational start site (6). The 525-residue αI isoform contains an N-terminal 23 residue segment that encodes a polybasic nuclear localization motif, whereas the cytoplasmic αII isoform starts at a Met residue equivalent to Met-24 in the αI isoform, and the sequences of both isoforms are identical thereafter.
S6K1 is a member of the AGC subfamily of serine-threonine protein kinases in which amino acid sequences are conserved in a segment of the catalytic kinase domain known as the activation loop or T-loop, as well as in a segment near the C terminus of the kinase domain known as the hydrophobic motif (7). Similar to other AGC kinase family members, catalytic activation of S6K1 minimally requires dual phosphorylation of a critical residue in both the T-loop and hydrophobic motif. For the full-length S6K1αI isoform these residues correspond to Thr-252 and Thr-412, respectively (8), whereas in the S6K1αII isoform the identical residues correspond to Thr-229 and Thr-389 (9). With combined knowledge from available amino acid sequence alignments and x-ray structures, molecular modeling and biochemical testing now provide strong evidence for a common AGC kinase activation mechanism in which the C-terminal phosphorylated hydrophobic motif interacts with a phosphate binding pocket located in the small N-lobe of the kinase (10). This intramolecular interaction acts synergistically with T-loop phosphorylation to stabilize the active conformation, whereby a critical Glu residue in the αC-helix forms an ion pair with the catalytic Lys that functions to position the terminal phosphate of ATP for phosphotransfer in the kinase reaction.
In recognizing the synergistic role of AGC kinase dual site phosphorylation, neither an x-ray three-dimensional structure nor a kinetic mechanism has been reported for any S6K1 isoform or domain construct. This derives largely from the inability to generate fully Thr-229 phosphorylated and activated S6K1. In previous work, we demonstrated by (i) Western analysis, (ii) electrospray ionization-time-of-flight, (iii) Mono Q anion exchange chromatography, and (iv) kinetic assays that the N-terminal His6 affinity-tagged catalytic kinase domain construct of the αII isoform of S6K1 (His6-S6K1αII(ΔAID)-T389E; residues 1–398) could be generated in its fully Thr-229 phosphorylated most highly active form (250 nmol/min/mg) by baculovirus-mediated expression and purification from Sf9 insect cells that are co-infected with recombinant phosphoinositide-dependent protein kinase-1, the upstream Thr-229 kinase (11).
Herein, we report that fully activated His6-S6K1αII(ΔAID)-T389E catalyzes peptide phosphorylation by a Steady-State Ordered Bi Bi mechanism, whereby high affinity ATP binding precedes low affinity peptide binding. Rapid chemical phosphorylation and release of phosphopeptide is followed by steady-state rate-limiting steps involving release of ADP. Pre-steady-state kinetic and direct binding experiments showed osmotic pressure to correspondingly weaken nucleotide affinity and increase the dissociation rate, indicating a less hydrated conformational form of the free enzyme.
EXPERIMENTAL PROCEDURES
Materials—His6-S6K1αII-T389E was generated in its fully Thr-229 phosphorylated and activated form by baculovirus-mediated expression and purification from Sf9 insect cells that were co-infected with recombinant baculovirus expressing the catalytic domain of phosphoinositide-dependent protein kinase-1 (11). Minor amounts of high molecular weight protein impurities observed with His6 affinity-purified His6-S6K1αII-T389E were removed by heparin-Sepharose chromatography. Protein concentration was determined using the Bio-Rad Protein Assay Kit with bovine serum albumin as a standard. Fmoc-l-arginine, Fmoc-l-leucine, Fmoc-l-alanine, Fmoc-l-serine, and Wang resin were from Advanced Chemtech (Louisville, KY). N-α-Fmoc-O-benzyl-l-phosphoserine (Fmoc-Ser[PO(OBzl)-OH]-OH) was from AnaSpec, Inc. (San Jose, CA). [γ-32P]ATP, [8-14C]ATP, and [8-14C]ADP were from MP Biomedical (Irvine, CA). All other chemicals, salts, and buffers were from Sigma.
Peptide Synthesis—The S6K/RSK model peptide substrate (Tide, RRRLSSLRA) and phosphorylated peptide product (pTide, RRRLSpSLRA) were prepared by the solid-phase methodology on Wang resin (1.3 mmol/g). Briefly, coupling reactions were carried out with a 3-fold excess of Fmoc amino acids with diisopropylcarbodiimide/1-hydroxybenzotriazole as activating agent in dimethylformamide. Intermediate deprotection was achieved with 20% (v/v) piperidine in dimethylformamide for 30 min. After an average coupling period of 1 h, the extent of acylation was monitored by the standard ninhydrin test. In the event of incomplete coupling, the coupling procedure was repeated. Cleavage of the peptide from the resin was performed with trifluoroacetic acid in the presence of 8% anisole, 2% dimethyl sulfide, 2% p-cresol, and 2% thiocresol at 0 °C for 2 h, which also effectively removed the monobenzyl protecting group of phosphoserine. After removal of trifluoroacetic acid under a stream of nitrogen followed by vacuum, crude peptide was (i) precipitated with diethyl ether, (ii) filter washed with water and diethyl ether, (iii) extracted with 50% (v/v) aqueous acetic acid, and (iv) lyophilized. Crude peptide was purified by semipreparative reversed-phase high-performance liquid chromatography using a Vydac 219TP1010 column (diphenyl, 10 μm, 10-mm inner diameter × 250 mm) with 0.1% trifluoroacetic acid in water/0.1% trifluoroacetic acid in acetonitrile as the eluant system. Purified Tide (≥95%) and pTide (≥95%) were confirmed by analytical reversed-phase high-performance liquid chromatography (Vydac 219TP54, diphenyl, 5 μm, 4.6-mm inner diameter × 150 mm) and matrix-assisted laser desorption ionization time-of-flight mass spectrometry.
Two-substrate Steady-state Kinetic Assays—Steady-state kinetic assays were carried out for His6-S6K1αII(ΔAID)-T389E-catalyzed phosphorylation of the S6K/RSK model peptide substrate (Tide, RRRLSSLRA). The residue of the Tide substrate that undergoes phosphorylation is underlined. The 100-μl Tide phosphorylation reactions were performed at 25 °C in 40 mm MOPS buffer, pH 7, containing 0.1% 2-mercaptoethanol, 10 mm MgCl2, and 0.2 mm sodium vanadate. Initial velocities were measured for varying Tide concentrations (1, 2, 3, 5, 10, 25, and 50 μm) at different fixed concentrations of [γ-32P]ATP (∼500–1000 cpm/pmol, 1, 2, 3, 5, 10, 25, and 50 μm). Data collection in this manner provided all information necessary to construct companion reciprocal plots for the two varied substrates. The assays were initiated by addition of 10–30 nm kinase.
For all kinase assays, 20-μl aliquots were removed at three different times (ranging from 5 to 15 min) and mixed with 20 μl of 75 mm phosphoric acid and applied to P81 phosphocellulose paper (2 × 2 cm). After 30 s, the papers were washed (3×) in 1 liter of fresh 75 mm phosphoric acid for 10 min, then rinsed with 50 ml of acetone, and placed in the hood (≤5 min) to dry. The specific radioactivity of 32P-radiolabeled Tide (SATide, cpm/pmol) was determined from radioactivity detected by scintillation counting of the known amount of total Tide that was applied to the P81 paper; the micromolar amount of phosphorylated Tide product formed at each time point was determined by reference to the specific radioactivity of [γ-32P]ATP (SAATP, ∼500–1000 cpm/pmol) and the volume of the aliquot removed for quenching (20 μl). Initial velocities (v, μm s–1) were measured under conditions where total product formation represented ≥10% of the initial concentration of the limiting substrate. To better facilitate kinetic comparisons between steady-state and pre-steady-state kinetic results, initial velocities were normalized to enzyme concentration to yield apparent first order rate constants, k (s–1) = v/[Etot].
Control assays were carried out in which either the enzyme or Tide were omitted; these values were always ≤5% of the activity measured in the presence of both the lower- and upper-bound concentrations of these reagents (0.5 and 50 μm [γ-32P]ATP; 10 and 30 nm enzyme). Control assays containing the enzyme and only the [γ-32P]ATP substrate were further analyzed to measure ATPase activity. The amount of [32P]inorganic phosphate released from [γ-32P]ATP was determined by addition of 50 μl of the reaction mixture to 100 μl of a quench solution containing a 21% suspension of acid-washed (HCl) activated charcoal in 75 mm phosphoric acid. The quenched solution was mixed and placed on ice for 5 min, which provided for effective removal of the [γ-32P]ATP nucleotide from solution by the charcoal. The charcoal with bound [γ-32P]ATP was pelleted by centrifugation for 10 min, and a 60-μl aliquot of the supernatant was analyzed for [32P]inorganic phosphate. The 32P radioactivity in the supernatant was always ≤5% of the radioactivity measured in the absence of enzyme, indicating that the ATPase activity of His6-S6K1(ΔAID)-T389E is significantly lower than activity to the Tide substrate.
Product Inhibition Steady-state Kinetic Assays—Diagnostic enzyme inhibition studies were carried out for His6-S6K1(ΔAID)-T389E-catalyzed phosphorylation of Tide exactly as described for two-substrate kinetics. Both ADP and phospho-Tide (pTide, RRRLSpSLRA) were tested as true product inhibitors. For ADP inhibition, initial velocities were measured
| SCHEME 1 |
for varying ATP substrate concentrations (5, 10, 15, 20, 30, 50, and 100 μm) at different fixed concentrations of ADP (0, 5, 10, 15, and 20 μm) at a saturating concentration of Tide (200 μm). For pTide inhibition, initial velocities were measured for varying ATP substrate concentrations (0.5, 1, 2, 3, 5, 10, 15, and 20 μm) at different fixed concentrations of pTide (0, 100, 200, 300, and 400 μm) at a saturating concentration of Tide (200 μm).
Pre-steady-state Kinetic Assays—Pre-steady-state kinetic assays were carried out for His6-S6K1(ΔAID)-T389E-catalyzed phosphorylation of Tide using a KinTek Corp. (Austin, TX) Model RQF-3 rapid-quench-flow apparatus thermostatted at 25 °C. Reaction buffer refers to 40 mm MOPS buffer, pH 7, 0.1% 2-mercaptoethanol, 10 mm MgCl2, and 0.2 mm sodium vanadate. The left and right drive syringes in the rapid quench flow apparatus were filled with reaction buffer, and the middle (quench) syringe was filled with 75% acetic acid. One sample loop was loaded with 15 μl of reaction buffer containing designated amounts of Tide, [γ-32P]ATP, and ADP; the other sample loop contained 15 μl of His6-S6K1(ΔAID)-T389E enzyme in reaction buffer. The phosphorylation reaction was initiated by mixing the contents of the sample loops and acid quenched after varying reaction times t (0.2, 0.3, 0.5, 0.7, 1.0, 1.5, 2.0, and 3.0 s). For each time point, two 20-μl aliquots of each quenched reaction solution were individually applied to P81 phosphocellulose paper (2 × 2 cm), and the amount of Tide phosphorylation was quantified as described for the steady-state kinetic assays. The time courses were performed in triplicate, and the data points represent averaged values.
Three companion sets of pre-steady state kinetic experiments were carried out in which 2 μm enzyme (concentration after mixing) was reacted with the following final concentrations of other reactants: (i) [Tide] = 200 μm and [ATP] = 5, 10, 20, 50, and 200 μm; (ii) [ATP] = 200 μm and [Tide] = 5, 10, 20, 50, and 200 μm; and (iii) [ATP] = [Tide] = 200 μm and [ADP] = 0, 100, 200, 500, and 1000 μm. Data collection in this manner permitted global kinetic analysis to obtain exact or limiting fitted values of the microscopic rate constants in the Ordered Bi Bi mechanism (Scheme 1). Control assays were carried out in which the Tide substrate was omitted for enzyme in the presence of 200 μm [γ-32P]ATP. The amount of 32P radioactivity detected on the filter paper was always ≤5% of the measured radioactivity in the presence of Tide, indicating that purified active His6-S6K1(ΔAID)-T389E catalyzes little or no nonspecific autophosphorylation during reaction times ≤3 s. In addition, the amount of 32P radioactivity hydrolyzed from [γ-32P]ATP during this time period was shown to be negligible by the charcoal-filtration assay.
Catalytic Trapping Assays—Catalytic trapping assays were carried out at 25 °C using the rapid-quench-flow apparatus exactly as described for pre-steady-state assays except that enzyme was preincubated with ADP prior to mixing with ATP and Tide substrates. The final concentrations after mixing were 2 μm active His6-S6K1(ΔAID)-T389E and 200 μm each of ADP, ATP, and Tide in reaction buffer either in the absence or presence of 5% (w/v) polyethylene glycol with an average molecular weight of 8000 (PEG-8000).
Nucleotide Binding Assays—Nucleotide binding to His6-S6K1(ΔAID)-T389E was measured using a filter binding assay, whereby 0.5 μm enzyme was preincubated at 25 °C in 70 μl of phosphorylation reaction buffer, either in the absence or presence of 5% (w/v) PEG-8000, containing varying concentrations of either [8-14C]ATP (∼500 cpm/pmol, and 1, 2, 3, 5, 10, 25, and 50 μm) or [8-14C]ADP (∼500 cpm/pmol, and 1.5, 2.5, 4, 7.5, 17.5, 37.5, and 62.5 μm). After 15 min, three separate 20-μl aliquots were removed and applied to three separate wells of a Bio-Rad Bio-Dot microfiltration apparatus with a fitted P81 phosphocellulose paper under vacuum. Radiolabeled nucleotide bound to the enzyme was retained by the P81 paper, whereas unbound nucleotide was collected in a vacuum flask. The P81 paper was removed from the apparatus and cut into individual sections. The amount of 14C background radiation was also determined for each nucleotide concentration by control assays carried out in which the enzyme was omitted. The amount of 14C background radiation (≤10%) was subtracted from the total radioactivity measured in the presence of the enzyme. The corrected radioactivity was used to calculate the micromolar amount of bound nucleotide, [A]bound, according to the specific radioactivity of the nucleotide and the volume of the aliquot applied to the paper. Because titrated nucleotide exceeded enzyme concentration, the total nucleotide concentration, [A]total, approximated its free concentration, [A]free, for each measurement. Data points represent averaged values from triple measurements.
Data Analysis—Steady-state kinetic data were plotted and
fitted using the GraFit 4.0 software (Erithacus Software, UK). The kinetic
formulation of an Ordered Bi Bi system, taking into account an irreversible
chemical phosphorylation step in the ternary complex
(Scheme 1), is fully described in
the supplemental material. Initial rates determined in the two-substrate
steady-state kinetic studies were globally fitted to Equation S8 (supplemental
material), which yielded values for kcat,
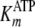 ,
,
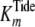 , and
, and
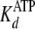 . Secondary plots of
kcat(app) determined from direct Michaelis-Menten fits of
(i) k versus [ATP] and (ii) k versus [Tide] at different
fixed concentrations of the other substrate were further analyzed by Equations
S11 and S15, respectively, which confirmed the fitted values for
kcat,
. Secondary plots of
kcat(app) determined from direct Michaelis-Menten fits of
(i) k versus [ATP] and (ii) k versus [Tide] at different
fixed concentrations of the other substrate were further analyzed by Equations
S11 and S15, respectively, which confirmed the fitted values for
kcat,  , and
, and
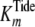 .
.
Initial rates determined in steady-state kinetic ADP and pTide inhibition
studies were globally fitted to Equations S23 and S31, respectively, to yield
values for kcat,
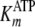 , and the inhibition constant for
the designated product (either
, and the inhibition constant for
the designated product (either 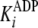 or
or
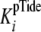 ). The secondary plot of
). The secondary plot of
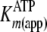 determined from
direct Michaelis-Menten fits of k versus [ATP] at different fixed
[ADP] was further analyzed by Equation S25, which confirmed the fitted values
for
determined from
direct Michaelis-Menten fits of k versus [ATP] at different fixed
[ADP] was further analyzed by Equation S25, which confirmed the fitted values
for 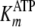 and
and
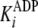 ; secondary plots of
kcat(app) and
; secondary plots of
kcat(app) and
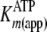 determined from
direct fits of k versus [ATP] at different fixed [pTide] were
analyzed by Equations S32 and S33, respectively, which confirmed the fitted
values for kcat,
determined from
direct fits of k versus [ATP] at different fixed [pTide] were
analyzed by Equations S32 and S33, respectively, which confirmed the fitted
values for kcat,
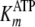 and
and
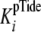 .
.
Pre-steady-state kinetic data were analyzed using the DynaFit 3.28 software (BioKin, Ltd., Pullman, WA) (12). The time dependence of phosphopeptide product formation as a function of [ATP], [Tide], and [ADP] was globally fitted to obtain the microscopic rate constants depicted in Scheme 1. As demonstrated in the supplemental material, Equations 1, 2, 3, 4, 5, 6 relate values of the microscopic rate constants in Scheme 1 with the kinetic constants determined in steady-state kinetic studies.
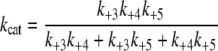 |
(Eq. 1) |
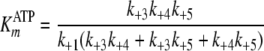 |
(Eq. 2) |
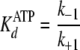 |
(Eq. 3) |
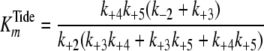 |
(Eq. 4) |
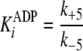 |
(Eq. 5) |
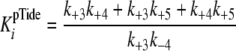 |
(Eq. 6) |
With regard to ADP inhibtion, 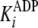 represents the true dissociation constant,
represents the true dissociation constant,
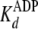 . For pTide inhibition,
. For pTide inhibition,
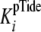 closely approximates the true
dissociation constant of phosphopeptide product,
closely approximates the true
dissociation constant of phosphopeptide product,
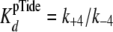 under conditions where both k+3 and
k+4 exceed k+5.
under conditions where both k+3 and
k+4 exceed k+5.
The nucleotide dissociation constants
(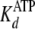 and
and
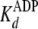 ) and binding capacity (C)
were obtained from direct fittings of plots of concentrations of bound
nucleotide, [A]bound, versus concentrations of
free nucleotide, [A]free, to
Equation 7.
) and binding capacity (C)
were obtained from direct fittings of plots of concentrations of bound
nucleotide, [A]bound, versus concentrations of
free nucleotide, [A]free, to
Equation 7.
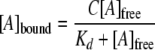 |
(Eq. 7) |
RESULTS
Two-substrate Steady-state
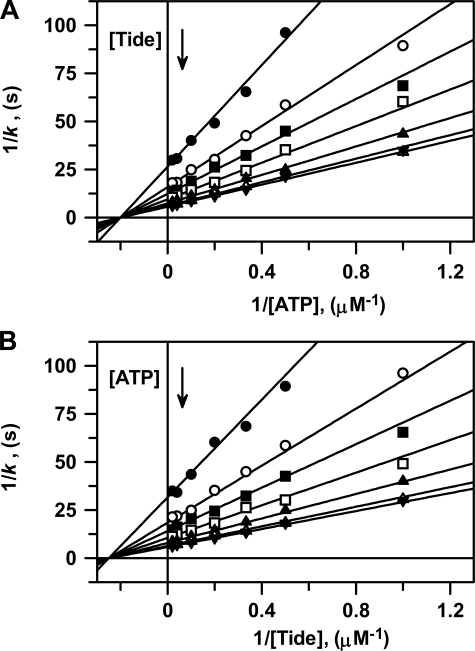
Kinetics—Fig. 1
shows double reciprocal plots of all steady-state kinetic data for titration
of active His6-S6K1αII(ΔAID)-T389E with varying
concentrations of one substrate at different fixed concentrations of the other
substrate. Due to the results obtained in product inhibition studies (see
below), analysis of these data was best approximated and described for a
Steady-State Ordered Bi Bi system, whereby binding of ATP precedes binding of
peptide substrate (Scheme 1).
Global fitting of the data to Equation S8 yielded values of
kcat = 0.192 ± 0.002 s–1,
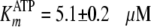 ,
,
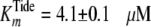 ,
and
,
and
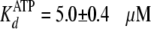 .
.
FIGURE 1.
Two-substrate steady-state kinetics. Double reciprocal plots of A, 1/k versus 1/[ATP] and B, 1/k versus [Tide] performed at 25 °C. In both reciprocal plots, the concentration of one substrate was varied at seven different concentrations of the fixed substrate (1 μm (•), 2 μm (○), 3 μm (▪), 5 μm (□), 10 μm (▴), 25 μm (▵), and 50 μm (▾)). The solid lines were generated using the kinetic constants determined from the global fit of the data to Equation S8, and the reciprocal forms of this equation were generated with either ATP (Equation S13) or Tide (Equation S17) as the varied substrate.
To better illustrate this analysis, these data are further given in direct and secondary plots, where both the global fit to Equation S8 and individual direct fits to the Michaelis-Menten equation are displayed and tabulated (supplemental Fig. S1 and Tables S1 and S2).
Product Inhibition Steady-state Kinetics—The pattern of intersecting lines shown in two-substrate steady-state kinetics (Fig. 1) provided little evidence toward the kinetic mechanism of peptide phosphorylation other than ruling out both (i) Ping-Pong and (ii) Rapid Equilibrium Ordered Bi Bi systems. For these mechanisms, respectively, either parallel lines are observed or lines intersect on the y-axis for the second binding substrate. Discrimination between other possible mechanisms (e.g. Steady-State Ordered, Steady-State Random, or (Partial) Rapid Equilibrium Random Bi Bi systems) may be achieved by comparing the effects of product inhibitors in double reciprocal plots constructed for varying one substrate concentration at a fixed concentration of the other substrate.
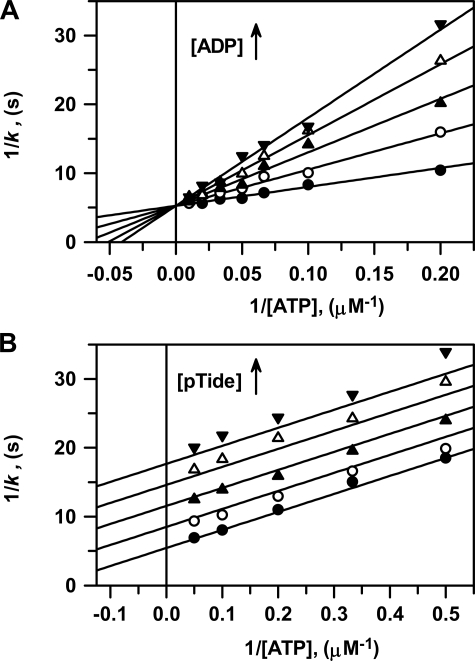
Fig. 2 shows double
reciprocal plots of both ADP and pTide product inhibition steady-state kinetic
data for titration of active His6-S6K1αII(ΔAID)-T389E,
whereby [ATP] was varied using a fixed [Tide] (200 μm) far
exceeding 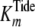 (4.1 μm).
Fig. 2A shows the ADP
product to be competitive with respect to the varied ATP substrate, and global
fitting of the data to Equation S23 yielded very close approximations of the
true values of kcat = 0.190 ± 0.003
s–1,
(4.1 μm).
Fig. 2A shows the ADP
product to be competitive with respect to the varied ATP substrate, and global
fitting of the data to Equation S23 yielded very close approximations of the
true values of kcat = 0.190 ± 0.003
s–1,
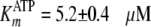 ,
and the inhibition constant
,
and the inhibition constant
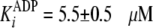 .
In this case, the measured
.
In this case, the measured 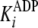 equates
with the true dissociation constant for ADP product release,
equates
with the true dissociation constant for ADP product release,
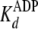 (Scheme 1 and
Equation 5).
(Scheme 1 and
Equation 5).
FIGURE 2.
Product inhibition steady-state kinetics. Double reciprocal plots of 1/k versus 1/[ATP] performed at 25 °C. A, ADP product inhibition was measured using (i) varying [ATP] = 5, 10, 15, 20, 30, 50, and 100 μm, (ii) saturating fixed [Tide] = 200 μm, and (iii) [ADP] = 0 μm (•), 5 μm (○), 10 μm (▴), 15 μm (▵), and 20 μm (▾). Solid lines were generated using the kinetic constants determined from the global fit of the data to Equation S23 and its reciprocal Equation S26. B, pTide product inhibition was measured using (i) varying [ATP] = 0.5, 1, 2, 3, 5, 10, 15, and 20 μm, (ii) saturating fixed [Tide] = 200 μm, and (iii) [pTide] = 0 μm (•), 100 μm (○), 200 μm (▴), 300 μm (▵), and 400 μm (▾). Solid lines were generated using the kinetic constants determined from the global fit of the data to Equation S31 and its reciprocal Equation S34.
Fig. 2B shows the
pTide product to be uncompetitive with respect to the varied ATP substrate,
and global fitting of the data to Equation S31 yielded values of
kcat = 0.184 ± 0.004 s–1,
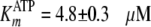 ,
and
,
and
 .
In this case, the measured
.
In this case, the measured 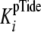 is
defined by Equation 6. The
combined observation that ADP and pTide behave as competitive and
uncompetitive inhibitors, respectively, with respect to the varied ATP
substrate under saturating [Tide] conditions clearly indicates a Steady-State
Ordered Bi Bi system, whereby binding of ATP precedes binding of peptide
substrate (Scheme 1).
is
defined by Equation 6. The
combined observation that ADP and pTide behave as competitive and
uncompetitive inhibitors, respectively, with respect to the varied ATP
substrate under saturating [Tide] conditions clearly indicates a Steady-State
Ordered Bi Bi system, whereby binding of ATP precedes binding of peptide
substrate (Scheme 1).
To better illustrate this analysis, the ADP and pTide inhibition data are further given in direct and secondary plots, where both the global fits to Equations S23 and S31 and individual direct fits to the Michaelis-Menten equation are displayed and tabulated (supplemental Fig. S2 and Tables S1 and S3). Table 1 summarizes the range of values obtained for the steady-state kinetic constants obtained from all two-substrate and product inhibition analyses.
TABLE 1.
Comparison of kinetic constants determined for phosphorylation of Tide by His6-S6K1 (ΔAID)-T389E
| Constant | Steady statea | Pre-steady stateb | Equation |
|---|---|---|---|
| kcat (s-1) | 0.18-0.19 | 0.22 | 1 |
| KmATP (μm) | 4.9-5.5 | 5.9 | 2 |
| KdATP (μm) | 5.0-5.5 | 5.9 | 3 |
| KmTide (μm) | 4.1 | 5.1 | 4 |
| KdADP (μm) | 5.5-6.0 | 5.8 | 5 |
| KipTide (μm) | 170-180 | 185 | 6 |
These numbers represent the range of values obtained from global and secondary fits of data obtained in both two-substrate and product inhibition steady-state kinetics. A detailed listing of all determined values ± S.E. is given in supplemental Table S1.
These numbers were calculated using the designated equation and microscopic rate constant values in Table 2.
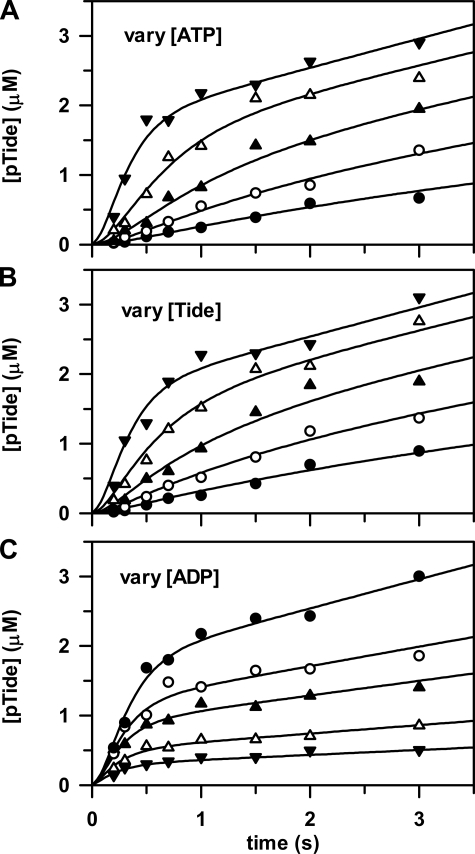
Pre-steady-state Kinetics—Fig. 3 shows three companion plots of pre-steady-state time progress curves measured for pTide product formation, which were simultaneously fitted to yield microscopic rate constants of the Ordered Bi Bi mechanism (Scheme 1 and Table 2). The rapid-quench-flow apparatus was used to mix free enzyme from one sample loop with varying concentrations of ATP, Tide, and ADP from the other sample loop. In all cases the final active His6-S6K1αII(ΔAID)-T389E concentration after mixing was 2 μm.
FIGURE 3.
Pre-steady state kinetics. The rapid-quench-flow apparatus was used to measure three companion sets of pre-steady state kinetic data, whereby free enzyme from one sample loop (2 μm, concentration after mixing) was reacted at 25 °C with the following final concentrations of reactants from the other sample loop: A, [Tide] = 200 μm and [ATP] = 5 μm (•), 10 μm (○), 20 μm (▴), 50 μm (▵), and 200 μm (▾); B, [ATP] = 200 μm and [Tide] = 5 μm (•), 10 μm (○), 20 μm (▴), 50 μm (▵), and 200 μm (▾); and C, [ATP] = [Tide] = 200μm and [ADP] = 0μm (•), 100μm (○), 200μm (▴), 500μm (▵), and 1000μm (▾). The curves are from global fitting of all time progress data to the Ordered Bi Bi mechanism in Scheme 1 with DynaFit (12), which yielded the rate constants given in Table 2.
TABLE 2.
Microscopic rate constants for phosphorylation of Tide by His6-S6K1(ΔAID)-T389E
The reaction steps and rate constants refer to the Ordered Bi Bi system depicted in Scheme 1.
| Reaction step | Rate constant | Value |
|---|---|---|
| E + ATP → E·ATP | k+1 (m-1 s-1) | (3.8 ± 0.2) × 104 |
| E·ATP → E + ATP | k-1 (s-1) | 0.22 |
| E·ATP + Tide → E·ATP-Tide | k+2 (m-1 s-1) | ≥106 |
| E·ATP-Tide → E·ATP + Tide | k-2 (s-1) | ≥190 |
| E·ATP-Tide → E·ADP-pTide | k+3 (s-1) | 8.6 ± 1.0 |
| E·ADP-pTide → E·ADP + pTide | k+4 (s-1) | ≥180 |
| E·ADP + pTide → E·ADP-pTide | k-4 (m-1 s-1) | ≥106 |
| E·ADP → E + ADP | k+5 (s-1) | 0.23 ± 0.01 |
| E + ADP → E·ADP | k-5 (m-1 s-1) | (4.0 ± 0.2) × 104 |
Figs. 3A (varying [ATP]) and 3B (varying [Tide]) show time progress curves, whereby the final concentration of one substrate was fixed at 200 μm and the other substrate was varied from 5 to 200 μm. Fig. 3 (A and B) shows significant burst kinetics appearing at very high substrate concentrations, indicating that the rate-limiting step occurs after chemical phosphorylation. In addition, the burst amplitude approaches the concentration of the enzyme (2 μm), indicating fully reactive enzyme.
Further inspection of the data in Fig. 3
(A and B) revealed that burst kinetics required
very high concentrations of both [ATP] and [Tide], indicating unusually slow
association of the first binding substrate, ATP. This is consistent with the
measured values of
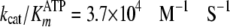 and kcat = 0.19 s–1
(Table 1), which approximate
the microscopic rate constants for association (k+1) and
dissociation (k–1) of ATP
(Scheme 1) under conditions where
and kcat = 0.19 s–1
(Table 1), which approximate
the microscopic rate constants for association (k+1) and
dissociation (k–1) of ATP
(Scheme 1) under conditions where
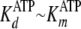 (Equations 1,
2,
3).
(Equations 1,
2,
3).
Fig. 3C shows time
progress curves, whereby the final concentrations of ATP and Tide were fixed
at 200 μm and ADP was varied from 0 to 1 mm. In this
case, decreasing linear steadystate velocities were observed with increasing
[ADP] in accordance with increasing values of
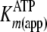 . In addition,
decreasing burst amplitudes were observed with increasing [ADP], reflecting
the competition between ATP and ADP for binding to the free enzyme upon
mixing. Most significantly, it can be seen that the burst amplitude was
reduced ∼50% when [ADP] = [ATP] = 200 μm. Making note of the
approximately equal values measured for
. In addition,
decreasing burst amplitudes were observed with increasing [ADP], reflecting
the competition between ATP and ADP for binding to the free enzyme upon
mixing. Most significantly, it can be seen that the burst amplitude was
reduced ∼50% when [ADP] = [ATP] = 200 μm. Making note of the
approximately equal values measured for
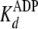 and
and
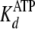 , the ADP association
(k–5) and dissociation rate constants
(k+5) must approximate those of ATP
(
, the ADP association
(k–5) and dissociation rate constants
(k+5) must approximate those of ATP
(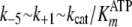 ;
k+5 ∼ k–1 ∼
kcat), strongly suggesting that release of ADP is the
rate-limiting step.
;
k+5 ∼ k–1 ∼
kcat), strongly suggesting that release of ADP is the
rate-limiting step.
Preliminary analysis of the pre-steady state kinetic data to the mechanism
in Scheme 1 revealed that good
fitted values could not be obtained for k–1,
k+2, k–2,
k+4, and k–4. The insensitivity
of the rate constants for association and dissociation of Tide
(k+2 and k–2) and pTide
(k+4 and k–4), together with the
measured weak inhibition constant of pTide
(Table 1,
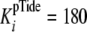 μm), are
consistent with rapid equilibrium peptide binding. Using the measured value of
μm), are
consistent with rapid equilibrium peptide binding. Using the measured value of
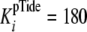 μm, ratio
fixed values of k+4 = 1.8, 18, 180, and 1800
s–1 with k–4 104,
105, 106, and 107
m–1 s–1, respectively, were
assigned and held constant during the fitting analysis. Assuming that pTide
and Tide association rates are approximately equal, fixed values of
k+2 = k–4 = 104,
105, 106, and 107
m–1 s–1 were also assigned and
held constant during the fitting analysis. Finally, the calculated value of
k–1 = kcat = 0.19
s–1 was assigned and held constant.
μm, ratio
fixed values of k+4 = 1.8, 18, 180, and 1800
s–1 with k–4 104,
105, 106, and 107
m–1 s–1, respectively, were
assigned and held constant during the fitting analysis. Assuming that pTide
and Tide association rates are approximately equal, fixed values of
k+2 = k–4 = 104,
105, 106, and 107
m–1 s–1 were also assigned and
held constant during the fitting analysis. Finally, the calculated value of
k–1 = kcat = 0.19
s–1 was assigned and held constant.
In all cases where k+2 = k–4
≥ 106 (and k+4/k–4
= 180 μm), global fitting of the pre-steady state kinetic data
(Fig. 3) yielded identical
values of k+1 = (3.8 ± 0.2) × 104
m–1 s–1, k+3
= 8.6 ± 1.0 s–1, k+5 = 0.23
± 0.01 s–1, and k–5 = (4.0
± 0.2) × 104 m–1
s–1 (Table 2).
In addition, the fitted values of k–2 (= 190
± 27 s–1 and 1900 ± 270 s–1
when k+2 = k–4 were
correspondingly fixed at 106 and 107
m–1 s–1, respectively) yielded
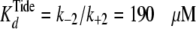 ,
which approximates the measured value of
,
which approximates the measured value of
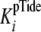 . In cases where
k+2 = k–4 ≤ 105
such that k+4 ≤ 18 s–1, global fitting
procedures were increasingly unable to converge, yielding systematic deviation
of the fitted lines from the data and surely indicating that release of ADP
(k+5 = 0.23 ± 0.01 s–1) is the
rate-limiting step. Thus, limiting lower values were assigned to rate
constants for association and dissociation of Tide (k+2
and k–2) and pTide (k+4 and
k–4) (Table
2). Using the microscopic rate constants in
Table 2, Equations
1,
2,
3,
4,
5,
6 were used to calculate values
of the steady-state kinetic constants; and these values agree well with the
values measured in steady-state kinetics
(Table 1). According to
Equations 1,
2,
3, the calculated value of
kcat = 0.22 s–1 was assigned to be the
value of k, because
. In cases where
k+2 = k–4 ≤ 105
such that k+4 ≤ 18 s–1, global fitting
procedures were increasingly unable to converge, yielding systematic deviation
of the fitted lines from the data and surely indicating that release of ADP
(k+5 = 0.23 ± 0.01 s–1) is the
rate-limiting step. Thus, limiting lower values were assigned to rate
constants for association and dissociation of Tide (k+2
and k–2) and pTide (k+4 and
k–4) (Table
2). Using the microscopic rate constants in
Table 2, Equations
1,
2,
3,
4,
5,
6 were used to calculate values
of the steady-state kinetic constants; and these values agree well with the
values measured in steady-state kinetics
(Table 1). According to
Equations 1,
2,
3, the calculated value of
kcat = 0.22 s–1 was assigned to be the
value of k, because
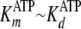 (Table 2). In addition, this
kinetic mechanism is consistent with conditions where both
k+3 and k+4 exceed
k+5 so that the
(Table 2). In addition, this
kinetic mechanism is consistent with conditions where both
k+3 and k+4 exceed
k+5 so that the
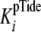 (Equation 6) approximates
(Equation 6) approximates
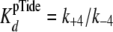 .
.
Effects of Cosolutes on ADP Release and Nucleotide Binding—“Stressing” cosolutes are known to exert effects on enzymatic equilibrium and kinetic constants by any number of a variety of mechanisms, including (i) specific interactions between the cosolute and enzyme and (ii) changes in solution properties such as water activity, dielectric constant, and viscosity (13). Most typical to enzymatic kinetic studies, a microviscogen cosolute (e.g. sucrose and glycerol) is used to detect rate-limiting diffusional release of products, whereby kcat is decreased proportionately with increasing solution viscosity (14). To rule out effects from specific interactions, the observed rate decreases should be determined to be the same when using amounts of different microvisogens that produce the same relative viscosity. One further important control involves testing the reaction in the presence of a high molecular weight macroviscogen (e.g. PEG-8000), which should not affect the rate of diffusion of a small molecule product.
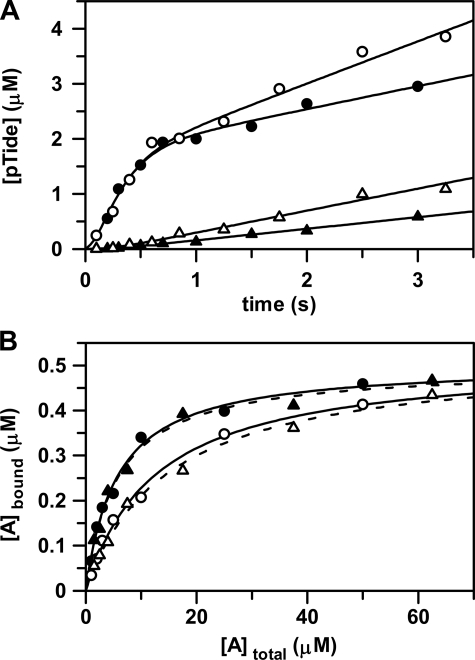
During preliminary steady-state kinetic studies, we made the unusual observation that reaction mixture solutions utilizing increasing amounts of either sucrose or glycerol as microviscogens increased kcat; the small amounts of rate enhancements were nonlinear with measured buffer viscosities. Moreover, this same effect was observed in the presence of much lower amounts of the macroviscogen PEG-8000. Although the rate of diffusion of ADP away from enzyme was surely decreased in the presence of the microviscogens, it certainly remained faster than a rate-limiting step preceding ADP release; and this rate-limiting step was activated by cosolutes of differing chemical nature (i.e. sucrose, glycerol, and PEG). In addition, we early noted that preparations of His6-S6K1αII(ΔAID)-T389E were sensitive to enzyme inactivation and that stability could be conferred by storage in buffers containing a known protein “stabilizing” agent such as sucrose (12). Hence, the activating effect of cosolute in pre-steady state kinetic and equilibrium binding experiments (Fig. 4) will be discussed in terms of it acting as “protecting” osmolyte.
FIGURE 4.
Effects of osmolyte on ADP release and nucleotide binding. A, the rapid-quench-flow apparatus was used to measure: (i) pre-steady state kinetic experiments in the absence (•) and in the presence of 5% (w/v) PEG-8000 (○) and (ii) catalytic trapping experiments in the absence (▴) and in the presence of 5% (w/v) PEG-8000 (▵). For pre-steady state kinetic experiments, free enzyme from one sample loop was reacted at 25 °C with ATP and Tide from the other sample loop. The concentrations after mixing were [E] = 2 μm with [ATP] and [Tide] = 200 μm. For catalytic trapping experiments, enzyme preincubated with ADP from one sample loop was reacted at 25 °C with ATP and Tide from the other sample loop. The concentrations after mixing were [E] = 2 μm with [ADP], [ATP], and [Tide] = 200 μm. The curves for pre-steady state (•) and catalytic trapping (▴) in the absence of 5% (w/v) PEG-8000 were generated with the kinetic constants in Table 2. The curves for pre-steady state (○) and catalytic trapping (▵) in the presence of 5% (w/v) PEG-8000 were generated with the kinetic constants in Table 2, but with 2-fold increased values of k–1 and k+5. B, the radiometric filter-binding assay was used to measure equilibrium binding of enzyme (0.5 μm) at 25 °C (i) with varying concentrations of [8-14C]ATP (∼500 cpm/pmol, and 1, 2, 3, 5, 10, 25, and 50 μm) in the absence (•) and in the presence of 5% (w/v) PEG-8000 (○) and (ii) varying concentrations of [8-14C]ADP (∼500 cpm/pmol; and 1.5, 2.5, 4, 7.5, 17.5, 37.5, and 62.5 μm) in the absence (▴) and in the presence of 5% (w/v) PEG-8000 (▵). The curves were generated by direct fitting of the data to Equation 7. In each case, the limiting amount of bound nucleotide approximately equaled the amount of enzyme, indicating one nucleotide binding site (i.e. C ∼ [Etot] = 0.5 μm).
In cases where the free and ligand-bound forms of a protein are differentially solvated, osmotic pressure will shift the binding equilibrium toward the protein conformation that is in the less hydrated form (15–18). For osmotic pressure studies, PEG-8000 is an optimal “nonbinding” high molecular weight cosolute compared with either sucrose or glycerol on several accounts (15–18). First, it tends to be excluded from the layer of water molecules near the protein surface. As an osmolyte, PEG-8000 reduces the activity of protein surface water by forcing water molecules to migrate from solvent-exposed surfaces, interfacial surfaces, and internal clefts into the bulk solution. In contrast, numerous other small molecule osmolytes are known to exert conformational effects more proximate to the protein surface. Second, PEG-8000 is a very strong osmolyte so that minimal amounts can be used to obtain significant osmotic pressure levels. Finally, small molecule diffusional processes will not be complicated since PEG-8000 behaves as a macroviscogen.
To better probe the nature of the rate-limiting step, the rapid-quench-flow apparatus was used to determine and compare pre-steady-state time progress curves obtained in the absence and in the presence of PEG-8000. As might be expected, the presence of 5% (w/v) PEG-8000 in the reaction buffer exerted no effect on the initial chemical burst for pTide formation. In accordance with steady-state kinetic observations, the slope of the subsequent rate-limiting linear phase increased ∼2-fold (Fig. 4A), suggesting that release of ADP generates an enzyme conformation that is less hydrated.
To more directly observe and confirm osmolyte-induced activation of ADP product release, the rapid-quench-flow apparatus was used to determine and compare time progress curves in “catalytic trapping” experiments. In this case, enzyme preincubated with a saturating amount of ADP from one sample loop was reacted with saturating amounts of ATP and Tide from the other sample loop. That the overall process associated with release of ADP is rate-limiting is clearly indicated by complete loss of the burst phase, which became a significant lag phase. Again, the presence of 5% (w/v) PEG-8000 in the reaction buffer increased the subsequent linear steady-state accumulation of product by 2-fold (Fig. 4A).
Finally, a radiometric filter-binding assay was used to measure the effect
of PEG-8000 in the reaction buffer on equilibrium binding of both
[8-14C]ATP and [8-14C]ADP
(Fig. 4B). In the
absence of PEG, the enzyme showed similar values of
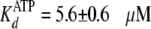 and
and
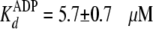 ,
which agreed with the values determined in steady-state and pre-steady state
kinetics (Table 1). But in the
presence of 5% (w/v) PEG-8000, the enzyme exhibited ∼2-fold weaker
affinities
(
,
which agreed with the values determined in steady-state and pre-steady state
kinetics (Table 1). But in the
presence of 5% (w/v) PEG-8000, the enzyme exhibited ∼2-fold weaker
affinities
(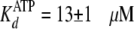 and
and
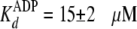 ),
consistent with the 2-fold increased rate of ADP dissociation measured in
pre-steady state kinetics (Fig.
4A). Thus, the weakened nucleotide affinity and
correspondingly increased dissociation rate most likely result from
osmolyte-induced stabilization of a less hydrated nucleotide-free form of the
enzyme. That ADP release is coupled to a rate-limiting conformational
transition is further supported by the unusually slow rate constants measured
for association and dissociation of both ATP substrate
(k+1 = 3.8 × 104
m–1 s–1 and
k–1 = 0.22 s–1) and ADP product
(k–5 = 4.0 × 104
m–1 s–1 and
k+5 = 0.23 s–1)
(Table 2).
),
consistent with the 2-fold increased rate of ADP dissociation measured in
pre-steady state kinetics (Fig.
4A). Thus, the weakened nucleotide affinity and
correspondingly increased dissociation rate most likely result from
osmolyte-induced stabilization of a less hydrated nucleotide-free form of the
enzyme. That ADP release is coupled to a rate-limiting conformational
transition is further supported by the unusually slow rate constants measured
for association and dissociation of both ATP substrate
(k+1 = 3.8 × 104
m–1 s–1 and
k–1 = 0.22 s–1) and ADP product
(k–5 = 4.0 × 104
m–1 s–1 and
k+5 = 0.23 s–1)
(Table 2).
DISCUSSION
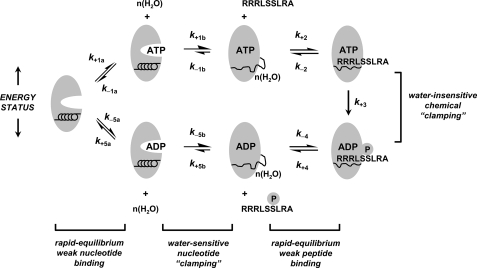
To account for observations (i) that the rates of nucleotide association
and dissociation were unusually slow and (ii) that nucleotide binding kinetics
and equilibria were sensitive to water activity, the deduced kinetic mechanism
of Scheme 1 is elaborated to that
shown in Fig. 5. In specific,
the single-step ATP and ADP forward binding reactions
(Scheme 1;
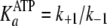 and
and
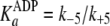 )
are now modified to behave as sequential two-step binding reactions, whereby
initial rapid equilibrium weak association of enzyme with either ATP
(
)
are now modified to behave as sequential two-step binding reactions, whereby
initial rapid equilibrium weak association of enzyme with either ATP
(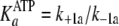 )
or ADP
(
)
or ADP
( )
is converted to an overall high affinity complex by a fast and favorable
conformational change
(
)
is converted to an overall high affinity complex by a fast and favorable
conformational change
(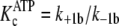 and
and
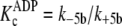 ).
Thus, the degrees to which such nucleotide “clamping” yields
apparently higher affinity complexes
(
).
Thus, the degrees to which such nucleotide “clamping” yields
apparently higher affinity complexes
( or
or
 ) is represented by
the amount that either k+1b exceeds
k–1b(ATP) or k–5b exceeds
k+5b(ADP), according to Equations
8 and
9, respectively.
) is represented by
the amount that either k+1b exceeds
k–1b(ATP) or k–5b exceeds
k+5b(ADP), according to Equations
8 and
9, respectively.
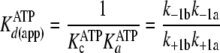 |
(Eq. 8) |
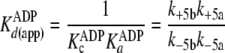 |
(Eq. 9) |
FIGURE 5.
Proposed mechanism for nucleotide binding coupled to water-sensitive conformational change. An Ordered Bi Bi mechanism is depicted for S6K1, whereby the free enzyme initially competes for rapid equilibrium binding to either ATP substrate (k+1a and k–1a) or ADP product (k+5a and k–5a). A distribution of overall high affinity E·ATP (Equation 8) and E·ADP complexes (Equation 9) is generated by fast and favorable conformational changes (k+1b > k–1b and k–5b > k+5b) leading to partial unfolding and hydration of a peptide region of the enzyme. Next, the nucleotide-bound enzyme engages rapid equilibrium weak binding of either the Tide substrate (k+2 and k–2) or pTide product (k+4 and k–4). Rapid equilibrium weak binding of the Tide substrate is converted to apparently high affinity binding and specificity by fast and favorable phosphoryl transfer (k+3), which serves as a chemical clamp.
The two-step nucleotide binding reactions in
Fig. 5 can account for the
apparently slow bimolecular association rates
(Table 2,
k+1(app) and k–5(app)) in that
fast first order rates of clamping (k+1b and
k–5b) are augmented by initial rapid equilibrium
weak binding (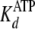 and
and
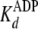 ), according to Equations
10 and
11,
), according to Equations
10 and
11,
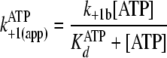 |
(Eq. 10) |
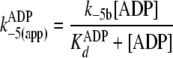 |
(Eq. 11) |
whereas the apparently slow first order nucleotide dissociation rates (Table 2, k–1(app) and k+5(app)) represent the overall rate-limiting conformational change that precedes a more rapid diffusional separation (kcat = k–1b = k+5b). In addition, the two-step nucleotide binding reactions most readily explain how rate-limiting ADP release can be increased in the presence of cosolutes, which are typically used as viscogens to decrease diffusional rates of product release. In this case, rate-limiting conformational “unclamping” (Fig. 5, kcat = k–1b = k+5b) is enhanced by osmotic pressure induced by added cosolute, which favors a less hydrated nucleotide-free form of the enzyme.
Protecting osmolytes are routinely added to enzyme preparations to increase enzyme stability during freezing and storage. The emerging view is that protecting osmolytes raise the free energy of a more hydrated partially “unfolded” state, which favors a less hydrated and more “folded” population (15–18). Accordingly, we may postulate that nucleotide clamping results in some peptide region(s) becoming more unfolded and solvent exposed.
After utilizing a conformational “clamp” for
sequential nucleotide and peptide binding, fully activated S6K1 then utilizes
fast and favorable phosphoryl transfer as a chemical clamp
(k+3) (Fig.
5) in the transient ternary complex, which converts rapid
equilibrium weak binding of the peptide substrate
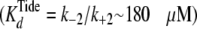 to apparently high affinity
(Equation 4,
to apparently high affinity
(Equation 4,
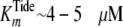 ).
Adams and coworkers first noted and coined “catalytic clamping” in
the reactions of (i) yeast Sky1p protein kinase with the RNA carrier protein
Np13 (19) and (ii) the human
C-terminal Src kinase with Src
(20); we agree that natural
selection of the fast chemistry coupled to weak peptide binding mechanism has
been advantageous, because it facilitates high peptide specificity but with
quick production and release of the phosphorylated downstream protein target
(21).
).
Adams and coworkers first noted and coined “catalytic clamping” in
the reactions of (i) yeast Sky1p protein kinase with the RNA carrier protein
Np13 (19) and (ii) the human
C-terminal Src kinase with Src
(20); we agree that natural
selection of the fast chemistry coupled to weak peptide binding mechanism has
been advantageous, because it facilitates high peptide specificity but with
quick production and release of the phosphorylated downstream protein target
(21).
Supplementary Material
This work was supported by NIGMS, National Institutes of Health Grant GM69868 (to T. K. H.) and a Maytag Fellowship (to M. M. K.). The costs of publication of this article were defrayed in part by the payment of page charges. This article must therefore be hereby marked “advertisement”in accordance with 18 U.S.C. Section 1734 solely to indicate this fact.
The on-line version of this article (available at http://www.jbc.org) contains supplemental Figs. S1 and S2, Tables S1–S3, text, references, and Equations S1–S34.
Footnotes
The abbreviations used are: S6K1, 70-kDa 40 S ribosomal protein S6 kinase-1; AID, C-terminal autoinhibitory domain of S6K1; His6-S6K1αII(ΔAID)-T389E, N-terminal His6 affinity-tagged recombinant catalytic domain of the αII isoform of S6K1 (residues 1–398) and including the T389E mutation; PEG, polyethylene glycol; Fmoc, N-(9-fluorenyl)methoxycarbonyl; MOPS, 4-morpholinepropanesulfonic acid.
References
- 1.Holz, M. K., Ballif, B. A., Gygi, S. P., and Blenis, J. (2006) Cell 123 569–580 [DOI] [PubMed] [Google Scholar]
- 2.Tee, A. R., and Blenis, J. (2005) Semin. Cell Dev. Biol. 16 29–37 [DOI] [PubMed] [Google Scholar]
- 3.Fingar, D. C., and Blenis, J. (2004) Oncogene 23 3151–3171 [DOI] [PubMed] [Google Scholar]
- 4.Richardson, C. J., Schalm, S. S., and Blenis, J. (2004) Semin. Cell Dev. Biol. 15 147–159 [DOI] [PubMed] [Google Scholar]
- 5.Martin, K. A., and Blenis, J. (2002) Adv. Cancer Res. 86 1–39 [DOI] [PubMed] [Google Scholar]
- 6.Grove, J. R., Banerjee, P., Balasubramanyam, A., Coffer, P. J., Price, D. J., Avruch, J., and Woodgett, J. R. (1991) Mol. Cell Biol. 11 5541–5550 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Peterson, R. T., and Schreiber, S. L. (1999) Curr. Biol. 9 R521–R524 [DOI] [PubMed] [Google Scholar]
- 8.Alessi, D., Kozlowski, M. T., Weng, Q.-P., Morrice, N., and Avruch, J. (1997) Curr. Biol. 8 69–81 [DOI] [PubMed] [Google Scholar]
- 9.Pullen, N., Dennis, P. B., Andjelkovic, M., Dufner, A., Kozma, S. C., Hemmings, B. A., and Thomas, G. (1998) Science 279 707–710 [DOI] [PubMed] [Google Scholar]
- 10.Frödin, M., Antal, T. L., Dümmler, B. A., Jensen, C. J., Deak, M., Gammeltoft, S., and Biondi, R. M. (2002) EMBO J. 21 5396–5407 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Keshwani, M. M., Ross, D. B., Ragan, T. J., and Harris, T. K. (2007) Prot. Express. Purif. 58 32–41 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kuzmic, P. (1996) Anal. Biochem. 237 260–273 [DOI] [PubMed] [Google Scholar]
- 13.Timasheff, S. N. (1993) Annu. Rev. Biophys. Biomol. Struct. 22 67–97 [DOI] [PubMed] [Google Scholar]
- 14.Adams, J. A. (2001) Chem. Rev. 101 2271–2290 [DOI] [PubMed] [Google Scholar]
- 15.Parsegian, V. A., Rand, R. P., Colombo, M. F., and Rau, D. C. (1994) Adv. Chem. Series 235 177–196 [Google Scholar]
- 16.Parsegian, V. A., Rand, R. P., and Rau, D. C. (1995) Methods Enzymol. 259 43–93 [DOI] [PubMed] [Google Scholar]
- 17.Robinson, C. R., and Sligar, S. G. (1995) Methods Enzymol. 259 395–427 [DOI] [PubMed] [Google Scholar]
- 18.LiCata, V. J., and Allewell, N. M. (1998) Methods Enzymol. 295 42–62 [DOI] [PubMed] [Google Scholar]
- 19.Aubol, B. E., Ungs, L., Lukasiewicz, R., Ghosh, G., and Adams, J. A. (2004) J. Biol. Chem. 279 30182–30188 [DOI] [PubMed] [Google Scholar]
- 20.Leiser, S. A., Shindler, C., Aubol, B. E., Lee, S., Sun, G., and Adams, J. A. (2005) J. Biol. Chem. 280 7769–7776 [DOI] [PubMed] [Google Scholar]
- 21.Leiser, S. A., Aubol, B. E., Wong, L., Jennings, P. A., and Adams, J. A. (2005) Biochim. Biophys. Acta 1754 191–199 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.