Osmoviscoelastic finite element model of the intervertebral disc

Abstract

Intervertebral discs have a primarily mechanical role in transmitting loads through the spine. The disc is subjected to a combination of elastic, viscous and osmotic forces; previous 3D models of the disc have typically neglected osmotic forces. The fibril-reinforced poroviscoelastic swelling model, which our group has recently developed, is used to compute the interplay of osmotic, viscous and elastic forces in an intervertebral disc under axial compressive load. The unloaded 3D finite element mesh equilibrates in a physiological solution, and exhibits an intradiscal pressure of about 0.2 MPa. Before and after axial loading the numerically simulated hydrostatic pressure compares well with the experimental ranges measured. Loading the disc decreased the height of the disc and results in an outward bulging of the outer annulus. Fiber stresses were highest on the most outward bulging on the posterior-lateral side. The osmotic forces resulted in tensile hoop stresses, which were higher than typical values in a non-osmotic disc. The computed axial stress profiles reproduced the main features of the stress profiles, in particular the characteristic posterior and anterior stress which were observed experimentally.

Introduction

Recent studies of low back pain disorder demonstrate that back pain is a major health problem within Europe, resulting in large economic losses. The report of the European agency for safety and health at work [1] indicates that the number of people who will suffer from back pain during their life time lies between 60 and 90%.

The mechanics of load transfer in the spine, and particularly the intervertebral disc, are an important factor in understanding the patterns and mechanisms of back pain. Intervertebral disc tissue is a cartilaginous structure connecting the vertebral bodies and allowing the movement of the spine. The disc consists of a gelatinous core know as the nucleus pulposus, which is surrounded by a fibrous ring know as the annulus fibrosus. The mechanical function of the disc is regulated by its biochemical composition. The annulus fibrosus consists mainly of type I and type II collagen, which provide tensile strength, and the proteoglycans, which due to the strong swelling ability [2–4] assure the tissue hydration. This swelling tendency is magnified by the partial shielding of the water by the collagen [3]. A high intradiscal pressure in the nucleus is the consequence of (1) the swelling propensity. This is counteracted by the dense collagen fiber structure of the annulus and (2) the external load which is transformed by the intradiscal pressure to a tensile stress in the collagen fiber structure of the annulus. The disc is subjected to a combination of elastic, viscous and osmotic forces [2] and is less stiff than the adjacent vertebral bodies. Degeneration in the disc, which is closely associated with back pain, occurs much earlier than in other tissues for reasons that are still unclear, but daily loads may play a role [4]. The environment of the disc cells, which make and maintain the disc’s composition and integrity, is influenced through loading. The degree of change in their extra cellular environment depends on the magnitude, duration and type of loading [4]. Because the cells in the intervertebral discs are sensitive to hydrostatic and osmotic pressure, quantification of these stresses with regard to disc degeneration is important.

Experimental measurements of in vivo intradiscal stresses are difficult. Therefore, different finite element approaches have been made in recent years to gain a better understanding of the load distribution in the spine and especially in the disc. In recent studies the poroelastic model has been widely used. A major problem associated with this type of model is that intradiscal pressure always tends ultimately to zero under constant load, which does not mirror physiological reality [5].

Different approaches for the implementation (e.g., stresses) of collagen fibers have been made [6, 7]. Elliot and Setton [8] recommend applying a linear fiber-induced anisotropic model to the annulus fibrosus. Wagner and Lotz [9] developed a theoretical model for the nonlinear elastic behavior of the human annulus fibrosus. However, different material laws have been considered to explain the complex tissue behavior. Wang et al. [10] applied a viscoelastic material law, which we applied as well. All of these models assume that the in vivo disc is stress-free in the supine position. This assumption is in conflict with experimental results which show hydrostatic pressure in the order of 0.1 MPa in an unloaded disc [5, 11]. Few models calculate the distribution of osmolarity in the disc and to our knowledge no such finite element model is currently available in the literature. Osmolarity is important as it regulates swelling pressure and disc hydration and hence contributes to load bearing [12]; it also affects the cellular responses [13]. Furthermore, recent study suggested an important role of osmolarity changes in the propagation of cracks in the disc [14]. Therefore, a finite element model, which accounts for both the collagen fibers and the swelling properties of the tissue, is a very useful tool to study stress distribution in the disc.

Several authors have proposed models of osmotic prestressing in cartilaginous tissues. However, few have been applied to the disc. Lanir [15, 16] recommended a bicomponent fluid–solid model which includes the Donnan-osmotic pressure generated by the proteoglycan molecules that are entangled in the collagen network of articular cartilage. While neglecting the effect of the diffusion–convection of counter- and coions, which are responsible for the osmotic forces, Lanir [15, 16] assumed that the ionic distribution is always in equilibrium with the surrounding physiological salt concentration of the blood. This simplification cannot be justified in unsteady state conditions where loading changes lead to fluid expression or imbibitions, as diffusion times of ions in cartilages are of the same order of magnitude as the diffusion or flow of the water.

Lai et al. [17] included a diffusing ionic component in a cartilage model, hence making it a triphasic model. Huyghe and Janssen [18] further generalized the model to finite deformation and showed that the full constitutive behavior of the swelling tissue can be described by one free energy function and one frictional coefficient matrix. This electrochemical model of Huyghe and Janssen [18] was used by Frijns et al. [19] to reproduce swelling and compression of canine annulus fibrosus. This finite deformation model was further extended by Van Loon et al. [20] in a 3D finite element study.

A detailed comparison of Lanir’s two-component model [16] and the electro-chemo-mechanical models of Lai et al. [17] and Huyghe and Janssen [18] was carried out by Wilson et al. [21]. They showed that the bicomponent model is a reasonable approximation of the more complex electro-chemo-mechanical models under physiological conditions. Iatridis et al. [22] developed a 2D plane stress poroelastic and chemical (PEACE) model to study the influence of the fixed charge density magnitude and the distribution in a slice of disc material. Results showed that the influence of the fixed charge density on the mechanical, chemical and electrical behavior of the tissue should definitely be taken into account for finite element modeling of the disc. Sun and Leong [23] developed a nonlinear hyperelastic mixture theory model for the annulus fibrosus, which takes the anisotropy, transport, and swelling tendency into account. Unfortunately, to our knowledge their computations are not yet published.

Wilson et al. [24] combined the bicomponent model [21] with their fibril-reinforced poroviscoelastic model [25]. This allows the inclusion of the fibril structure of articular cartilage. Natarajan et al. [26] compared analytical models which have been used to study disc degeneration. They found that the implementation of the osmotic pressure and the strain-dependent-permeability into poroelastic finite element models is an essential factor for simulations and understanding disc degeneration. Experimental validation of the analytical model is an additional requirement.

The swelling tendency of the disc tissue and the tensile stresses in the collagen structure are highly interdependent, as Urban and Maroudas [27] demonstrated experimentally. The swelling propensity is counteracted by the viscoelastic stiffness of the dense collagen fiber structure of the annulus, resulting in high hydrostatic pressure in the nucleus [28]. However, no published 3D finite element model of the disc includes osmotic prestressing. In our group we have thought to overcome this problem by developing a 3D model that takes the interdependency of the swelling and the collagen structure into account. Because intervertebral disc cells are sensitive towards osmotic pressure and hydrostatic pressure changes, the primary aim of our work was to predict these quantities in the disc. This paper describes the 3D model in detail and presents numerical results.

Method

A fibril-reinforced poroviscoelastic swelling model of Wilson et al. [24], based on the theory of Biot [29], Mow et al. [30] and Lanir [15, 16], is used to describe the intervertebral disc; it consists of a swelling non-fibrillar part and a fibrillar part [24, 25]. The model distinguishes between an elastic non-fibrillar solid matrix, a 3D viscoelastic collagen fiber structure and an osmotically prestressed extrafibrillar fluid. Because we assume no oriented collagen fiber structure in the nucleus pulposus, it only consists of an elastic non-fibrillar solid matrix and the osmotically prestressed fluid, while the annulus consists of all three parts.

Intrafibrillar water is water which is located in the collagen fibrils. We assume intrafibrillar water content to be constant in time and we deal with it as an integral part of the solid. Water located between the fibrils is extrafibrillar [31]. Literature [31–33] shows that accounting for this difference has an amplifying effect on the swelling pressure of the tissue.

The key equations of the main components are given here, for further details refer to [24] and Appendix.

Finite element model

Non-fibrillar solid matrix

The extracellular matrix of the disc, consisting of many components, is a structure that continually renews itself. However, in our simulation we assume the matrix to be solid. The elastic material behavior of the non-fibrillar part of the extracellular matrix is accounted for through a compressible neo-Hookean model [24].

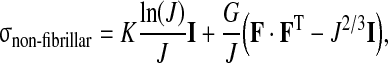1

where J is the determinant of the deformation tensor F relative to the stress-free state of the tissue. I is the unit tensor. K is the bulk modulus, and G is the shear modulus. The hydraulic permeability (k) is assumed to be fluid fraction-dependent [17], and is given by [34].

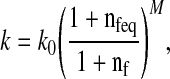2

with k₀ the initial permeability, M a positive constant, n_f and n_feq the current and initial extrafibrillar fluid fraction, respectively.

Collagen fibers

Within each lamella the collagen fibers run in parallel and are oriented approximately ± 30° to the transversal plane [35].

Data in the literature reveals the viscoelastic behavior of the extracellular matrix, especially for collagen [36–39]. Therefore, a viscoelastic material law [24, 25] describes the behavior of the collagen fibrils. Assuming that the fibrils only resist tension, the stresses in the viscoelastic fibrils are given by:

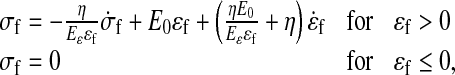3

where σ_f and σ_f are the fibril stress and strain, respectively. E₀ and E_ɛ are stiffness constants and η is a damping coefficient. A more detailed description of this viscoelastic law can be found elsewhere [24, 25, 40]. The strain is defined with respect to an initial stress-free state. The differential equations are numerically integrated using an implicit backward Euler scheme.

Osmotic swelling

The osmotic pressure (Δπ) of the intervertebral disc tissue depends on the fixed charge concentration (c_F) of the proteoglycans [3]:

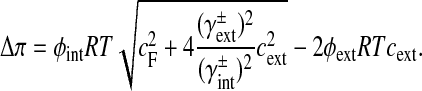4

The fixed charge density (c_F) is calculated per unit of extrafibrillar fluid volume. R is the universal gas constant, T is the absolute temperature and c_ext is the external salt concentration. The osmotic (ϕ_int, ϕ_ext) and activity coefficients (γ_int, γ_ext) are implemented as proposed by Huyghe and Janssen [18].

At each integration point the total stress is given by the sum of the stresses in the non-fibrillar matrix and the fibril stresses minus the intradiscal pressure:

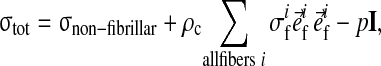5

where 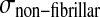and σⁱ_f are the stresses in the non-fibrillar matrix, I the unit tensor, ρ_c is collagen density, and in each fibril 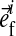is the unit vector pointing in the direction of the i^th fibril (Fig. 1). The intradiscal pressure p is defined through:

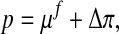6

with the chemical potential μ^f and the osmotic pressure Δπ.

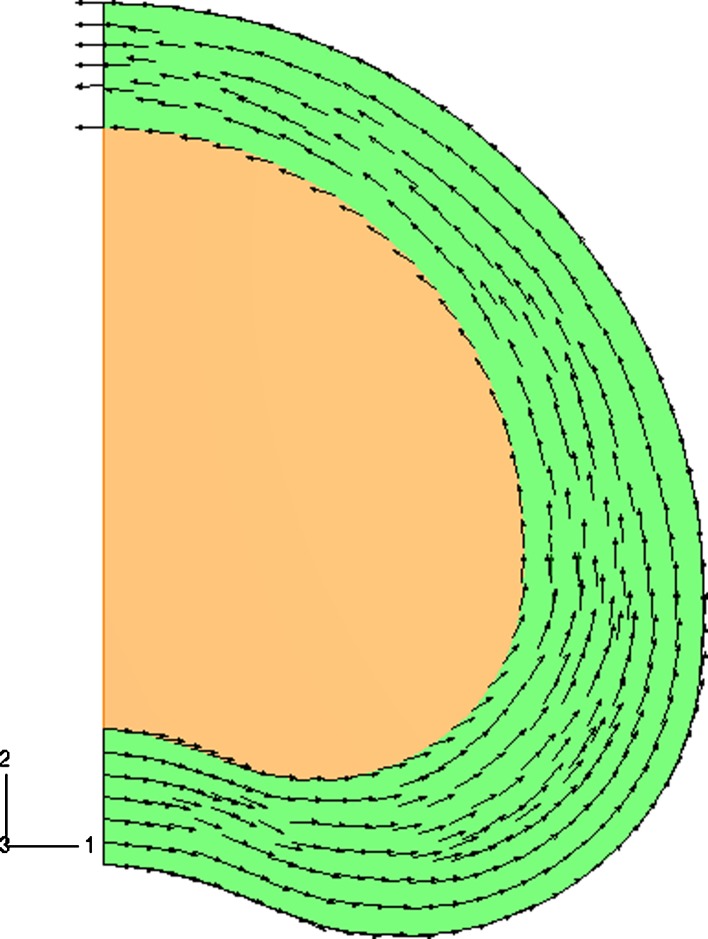
Fig. 1.

Two-dimensional fiber plot of one family of fibers in the disc model. The arrows show the projected fiber orientation in each integration point. The fiber density is uniformly distributed over the annulus (green). The fibers are oriented parallel to the outer curvature of the FE model at an angle of ± 30° to the transversal plane. No fibers in the nucleus (orange)

The stress-free state is different from the unloaded state of the disc. The stress-free state is defined as the state of the tissue when in contact with a saturated salt solution, i.e., the state of the tissue in which osmotic pressure (Δπ) in Eq. 4 approaches zero.

The model was implemented in ABAQUS v6.3 (ABAQUS Inc., Pawtucket, RI, USA). The subroutine UMAT was used to define the material behavior of the total solid matrix. An updated Lagrange procedure was used to account for geometric and physical non-linearities of the model.

The element type, a 3D 8-node brick element, used for this computation has eight integration points. Each node has 4 degrees of freedom: the 3 displacements plus the chemical potential of the fluid, which is the difference between the hydrostatic pressure and the osmotic pressure. To account for the fiber orientation independently from the discretization of the finite element mesh, the fibril stresses are computed in each integration point of the element [24, 25].

Disc mesh

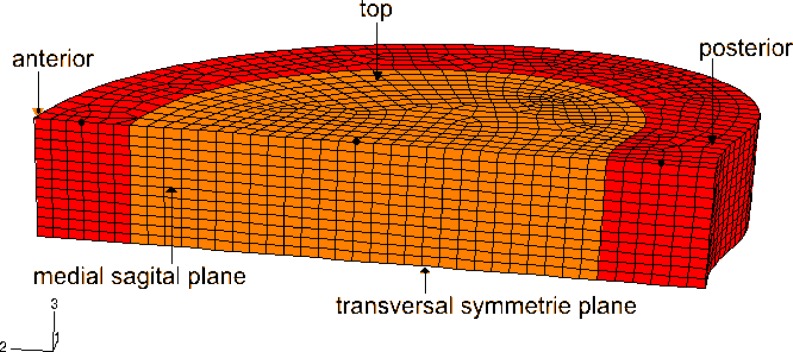
A simplified geometry of a human lumbar disc is chosen (Fig. 2). The model disc geometry is based on anatomical measurements of the typical geometry (outer curvature, bulging posterior, lateral) of a human lumbar vertebra. Because symmetry towards the transversal and sagittal plane is assumed, the whole disc geometry is reduced to 1/4 of the size. The mesh consists of 4,776 3D 8-node elements for the nucleus pulposus and 4,188 3D 8-node elements simulating the annulus fibrosus.

Fig. 2.

Finite element mesh of 1/4 of an intervertebral disc with differentiation in the nucleus pulposus (orange) and the annulus fibrosus (red), in the stress-free state; black dots show node selection for Fig. 3

The upper (top) surface of the mesh is the interface between the vertebra and the disc. The lower surface of the mesh is the transversal symmetry plane of the disc. The vertical plane is the sagittal symmetry plane. The height of the finite element mesh is 6 mm, the length from anterior to posterior is 36 mm and the distance from medial to lateral is about 22 mm, ensuing in a whole disc of 12 mm height and a surface of 15 cm² in total. In the analysis it is assumed that the interfaces between vertebrae and disc are flat surfaces parallel to each other. The initial mesh is the shape of the tissue in equilibrium with a saturated salt solution.

The disc geometry, material parameters and boundary conditions are symmetric with respect to the medial and transversal plane. Across the interface between nucleus and annulus there is free fluid flow and no sliding.

Boundary conditions

Along the transversal symmetry plane, because of symmetry, we assume no axial displacement and no fluid flux across the plane. Along the sagittal symmetry plane, again because of symmetry, we assume the displacement normal to the plane and the fluid flux across the plane to vanish. Along the vertebra-disc interface we assume the anterior–posterior displacement and the lateral displacement to vanish because the bone is stiff relative to the disc. For the same reason we tie the axial displacement of all the nodes along the vertebra-disc interface to each other, allowing the distance between the 2 vertebrae to change. The fluid chemical potential along the interface is set equal to the chemical potential of the blood plasma in the vertebra. Along the outer boundary of the disc, we neglect the force exerted by the surrounding tissues and we assume the fluid chemical potential to be equal to the same value as along the vertebra-disc interface, i.e., that of physiological salt concentration.

The initial mesh is equilibrated with a hypertonic salt solution. First the stress, the pressure and the chemical potential are calculated for the physiological unloaded state of the disc by reducing the saturated external salt concentration to 0.15 M. In other words, the disc is brought into its physiological unloaded state in equilibrium with a physiological salt solution (step 1), while the disc is gripped between the two vertebrae. This restrains the disc from swelling freely and allows the disc to develop its osmotic pressure. During the first step ions flow out of the mesh and water flows in, this causes the tissue to swell. Due to this the annulus bulges out (Fig. 4, top). In steps 2–4 the disc is axially loaded and step 6 again simulates the physiological unloaded state (Table 1). The magnitudes of load have been chosen from frequently applied values in the literature.

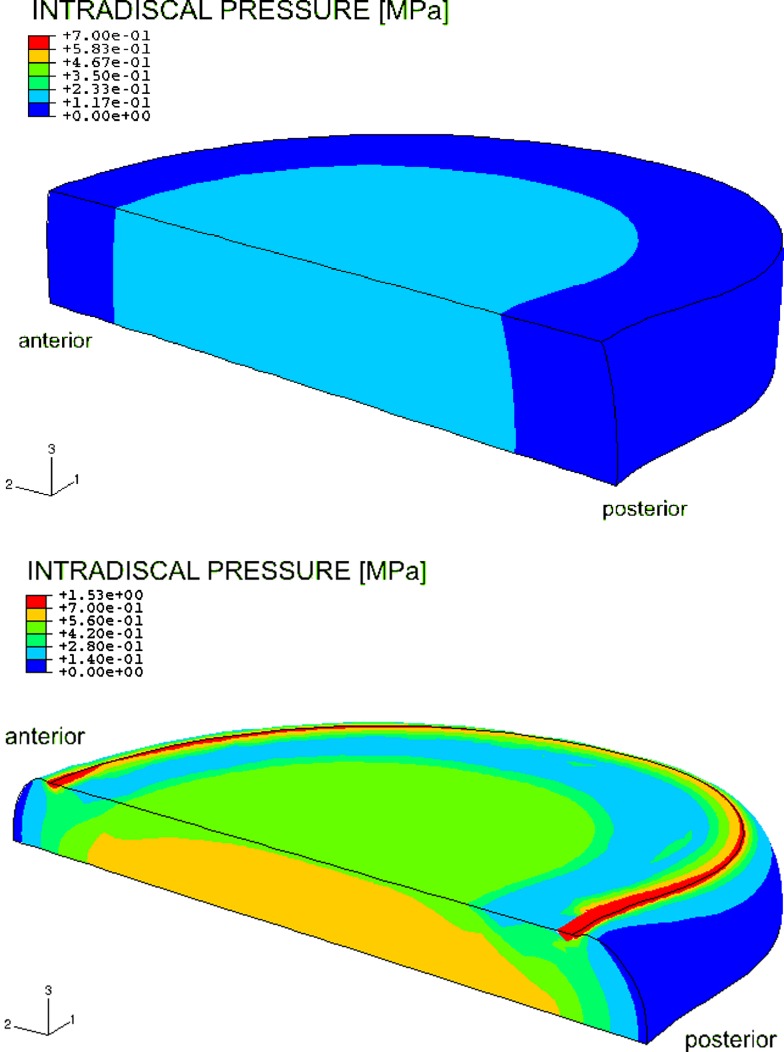
Fig. 4.

Color plot of unloaded model (top) and axially loaded model with 1,000 N (bottom) showing the intradiscal pressure. The highest noticeable pressure (ca. 0.7 MPa) starts from the transversal plane to the top plate on the medial sagittal plane with a concentration in the center of the nucleus. The pressure in the inner annulus neighboring the nucleus also increased

Table 1.

Different loading steps for the simulations and the salt concentration applied at the endplate and outer annulus

Step	Loading	Salt concentration (M)
1	Constrained swelling, no axial loading	0.15
2	Increasing axial load from 0 to 500 N over time step	0.15
3	Constant axial load of 500 N	0.15
4	Increasing axial load from 500 to 1,000 N over time step	0.15
5	Constant axial load of 1,000 N	0.15
6	Decreasing axial load to 0 N	0.15

Material parameters

The material properties include extra-fibrillar fluid fraction, hydraulic permeability, fixed charge density, matrix stiffness, Poisson’s ratio and viscoelastic properties of collagen fibers (Table 2). To account for the shielding of the intra-fibrillar water by the collagen, the values of fixed charge density are the extrafibrillar values. During the simulation the gas constant is 8.3145 Nm/mol, the absolute temperature is 310 K and the external salt concentration (c_ext) of 0.15 M is kept constant during all loading steps. The material parameters chosen from literature are mostly derived from measurements of tissue in an equilibrium state. This leads to a conflict with our assumption of a stress free state before starting the simulation. To account for this discrepancy between initial conditions in experiments and models, Wilson et al. [24] integrated an initial step into the simulation. During this first step the model is allowed to equilibrate to a physiological salt solution of 0.15 M. The chosen material parameters, taken from literature, are derived from measurements of disc tissue in a swollen equilibrium, i.e., the state of the model at the end of the first step. Therefore, the initial material properties of the model (fixed charge density, fluid fraction)—i.e., the material properties at the beginning of the first step—were estimated recursively through an initial step. For more details the reader is referred to Wilson et al. [24].

Table 2.

A set of material parameters for finite element simulation with fibril-reinforced poroviscoelastic swelling model

Material parameters	Input value		References
	Nucleus	Annulus
Young’s modulus	0.15 MPa	1.5 MPa	[2, 19]
Extrafibrillar fluid fraction	70%	60%	[27, 41]
Fixed charge density	0.24 mEq/ml	0.18 mEq/ml	[19, 27]
Viscoelastic properties of collagen fibers	–	E0 = 3.337 MPa, Eε = 380.8 MPa η = 1,532.39 MPas	[38]
Poisson ratio		0.17	[28, 42, 43]
Hydraulic permeability		5.0 × 10−16  m4N−1s−1	[2, 19, 43, 44]

Because the model is poroviscoelastic, Poisson’s ratio in the table relates to the porous solid, not to the solid filled with fluid. Therefore, Poisson’s ratio is very different from its incompressibility value of 0.5 [28]

Results

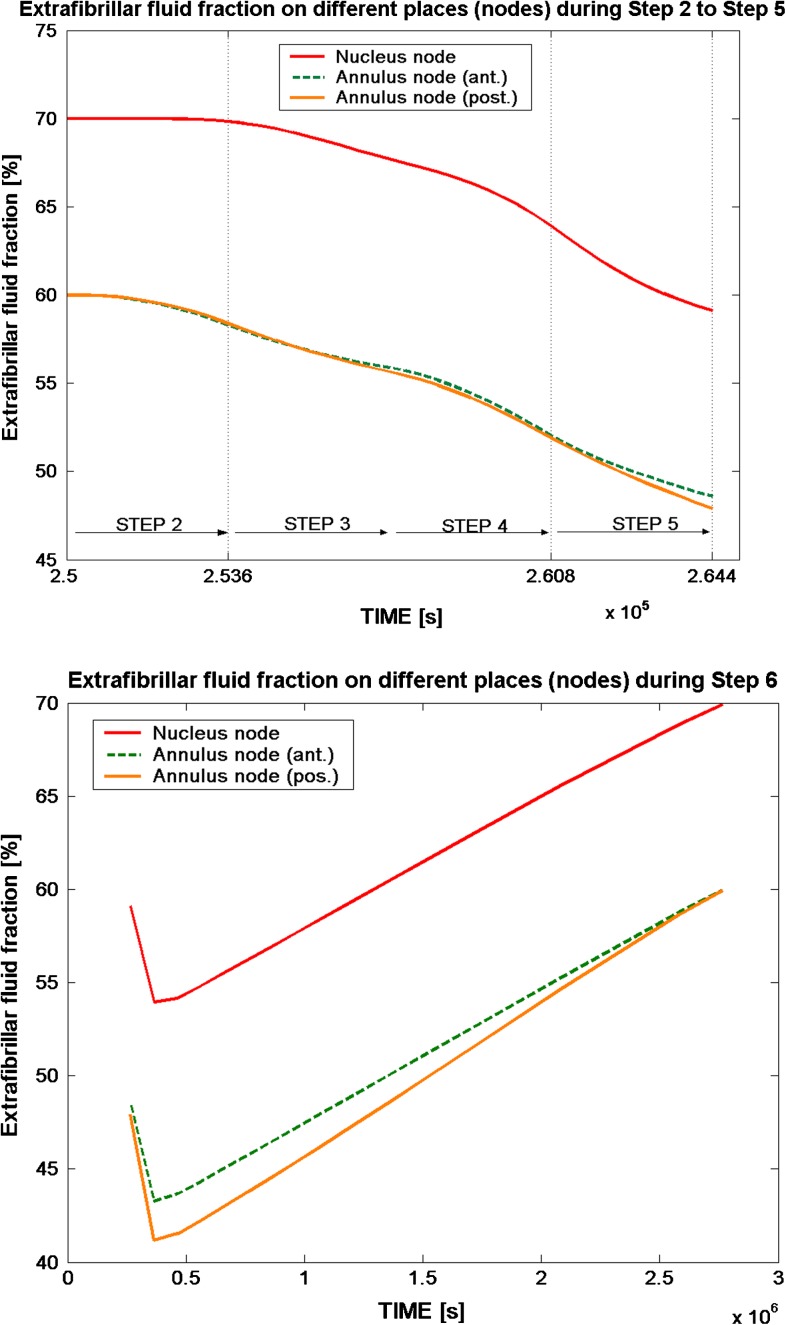
The extrafibrillar fluid content reaches about 70% for the nucleus at the beginning of step 2, while the fluid content for the annulus is about 10% lower. Thereafter, loading of the disc tissue decreases the water content of the disc. Applying an axial load of 1,000 N to the model decreased the fluid content in the annulus by about 8%, which is an average value between anterior and posterior side. A fluid decrease of about 6% was seen in the nucleus region after step 4. By the end of step 5 (loading disc with 1,000 N for 3,600 s) the fluid content decreased by about 11–12% for both nucleus and annulus. Following the load removal in step 6 the fluid content of the disc model reached the same condition subsequent to step 2 (Fig. 3).

Fig. 3.

The extrafibrillar fluid fraction on different nodes (black dots in Fig. 2) from the anterior to the posterior side in the nucleus and annulus during step 2 (start loading) to step 6 (fully unloaded). The top figure shows the loading steps 2–5, with a time scale of 3,600 s for each step, while step 6 (bottom figure) simulates a resting period; in with the fluid is regained after load removal

The disc generated an intradiscal pressure of 0.18 MPa in the nucleus pulposus after step 1 (Fig. 4). The different loading steps had the following impact on the pressure: a linear increasing axial load of 500 N (over 3,600 s) rose the intradiscal pressure to 0.56 MPa in the nucleus. During step 3 no load change occurred and the load was kept constant, which slightly decreased pressure in the center of the nucleus. A linear increasing axial load (step 4) of 1,000 N (over 3,600 s) enlarged the pressure to a maximum of 0.70 MPa in the nucleus (Fig. 4).

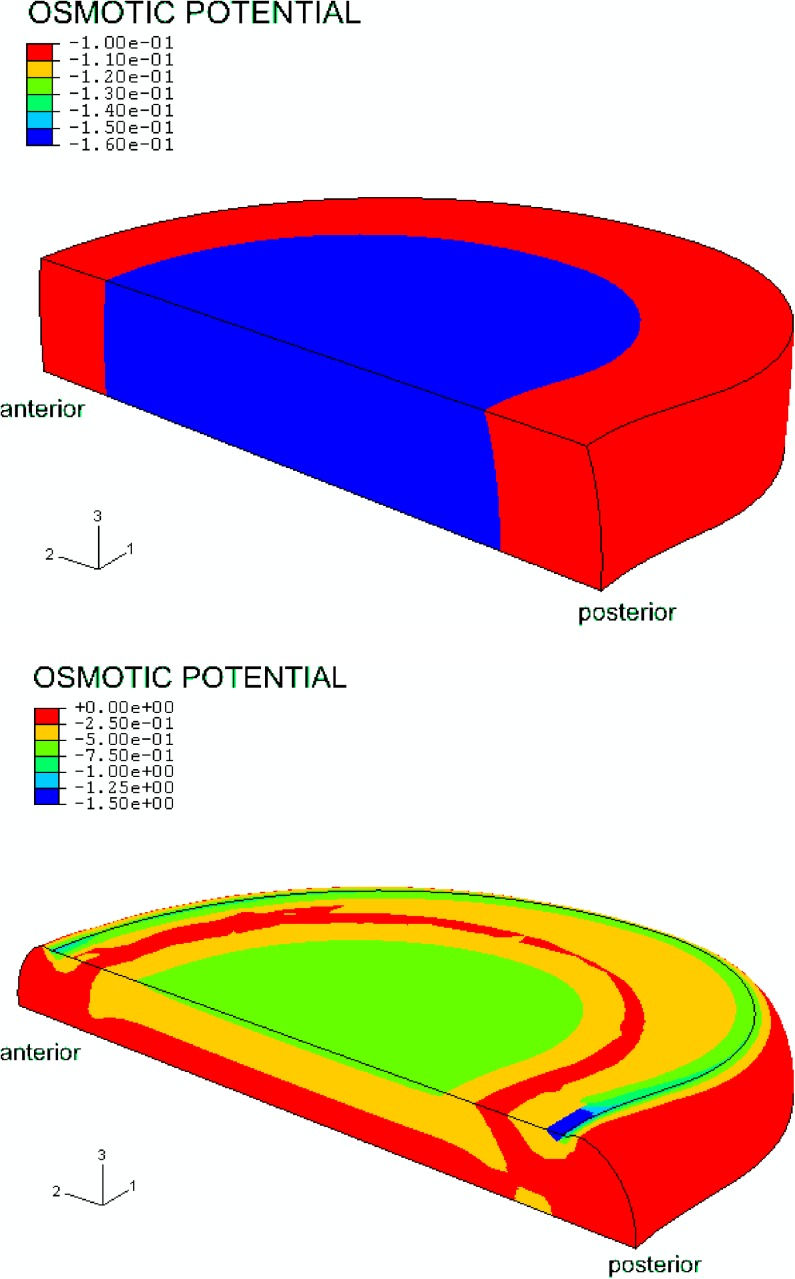
After swelling, during the first step, the osmotic pressure was highest in the nucleus pulposus. The osmotic pressure in the annulus was about 40% lower and was distributed evenly from the anterior to posterior side. Loading the disc changed the osmotic pressure distribution as follows: the osmotic pressure rose sharply at the outflow boundaries. When the fluid was pressed out, the fixed charge density concentration was rising correspondingly, which resulted in an increase of osmotic pressure (Fig. 5). As time proceeded and the load was maintained the high osmotic pressure region spreads away from the outflow boundary.

Fig. 5.

Color plot of an unloaded model (top) and an axially loaded model with 1,000 N (bottom), showing the osmotic potential (the negative of the osmotic pressure). After swelling, during the first step, osmotic pressure is highest in the nucleus pulposus, while the osmotic pressure in the annulus is about 40% lower. After loading, the osmotic pressure rises first close to the outflow boundaries. When the fluid is pressed out, the fixed charge density concentration increases, which results in an increase of osmotic pressure

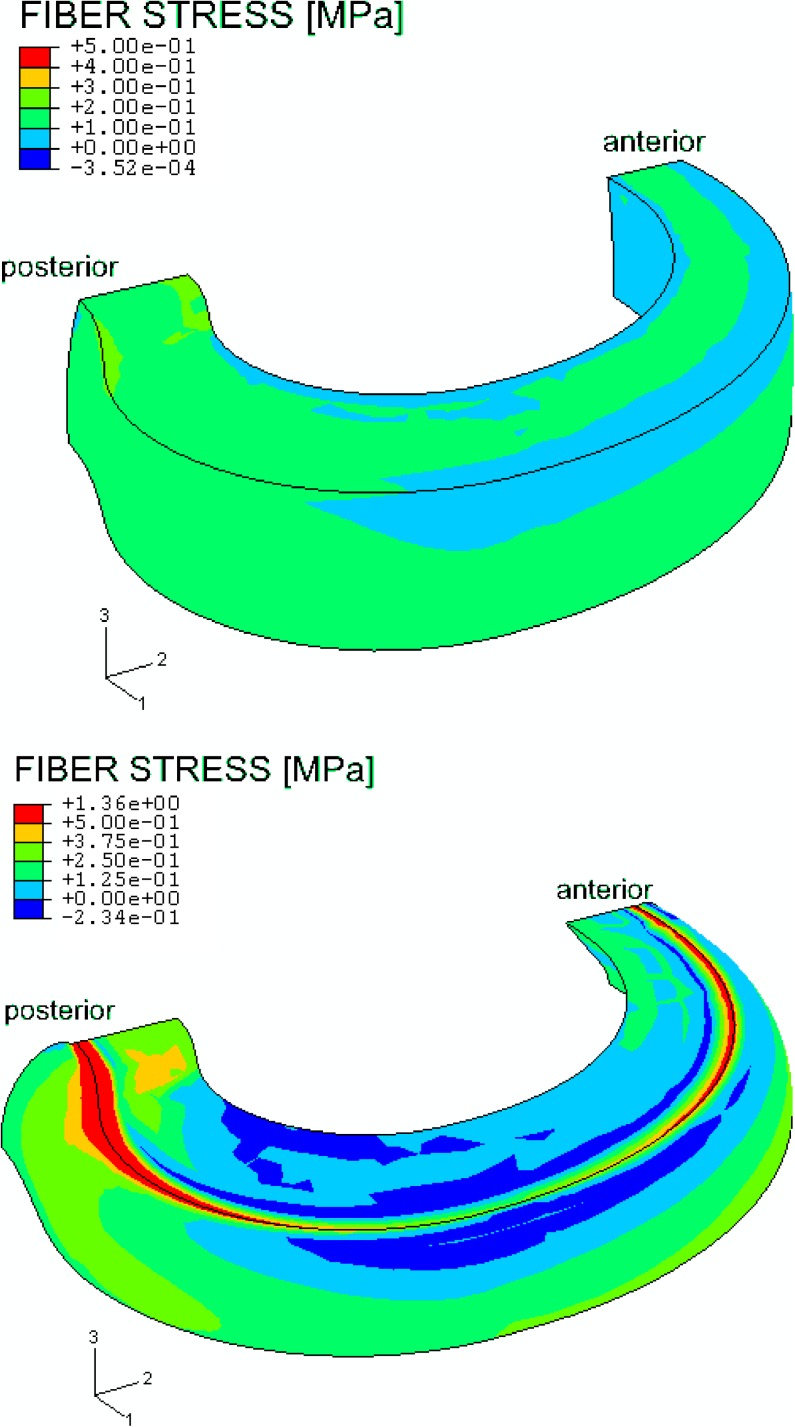
The color plots in Fig. 6 show the stresses for one family of fibers. The impact of the tissue swelling tendency on the collagen fibers can clearly been seen after step 1. A prestressing of the collagen fiber is noticed without any external loading. Stresses are high on the outward bulging of the disc starting from the posterior and anterior side and decreasing slightly towards the lateral side of the annulus. Stress concentrates posteriorly and anteriorly on the top plate of the model, while the area of high stress is much larger on the posterolateral side than on the anterior side. Much lower stresses were observed in the nucleus since the model only implements fibers in the annulus.

Fig. 6.

Color plot of an unloaded model (top) and an axial loaded model with 1,000 N (bottom) showing the fiber stress in one family of fibers. While unloaded, a prestressing of the collagen fibers in the model during the constrained swelling (step 1) was observed. Because the fiber stress in the nucleus is set to zero, the nucleus was not plotted here

Discussion

Because intervertebral disc cells are sensitive towards osmotic pressure and hydrostatic pressure changes, the primary aim of our work was to predict these quantities. For the first time in this paper a very useful tool was described in detail, the 3D osmoviscoelastic finite element model of the disc, to simulate finite deformations 3D osmoviscoelasticity of the swelling intervertebral disc.

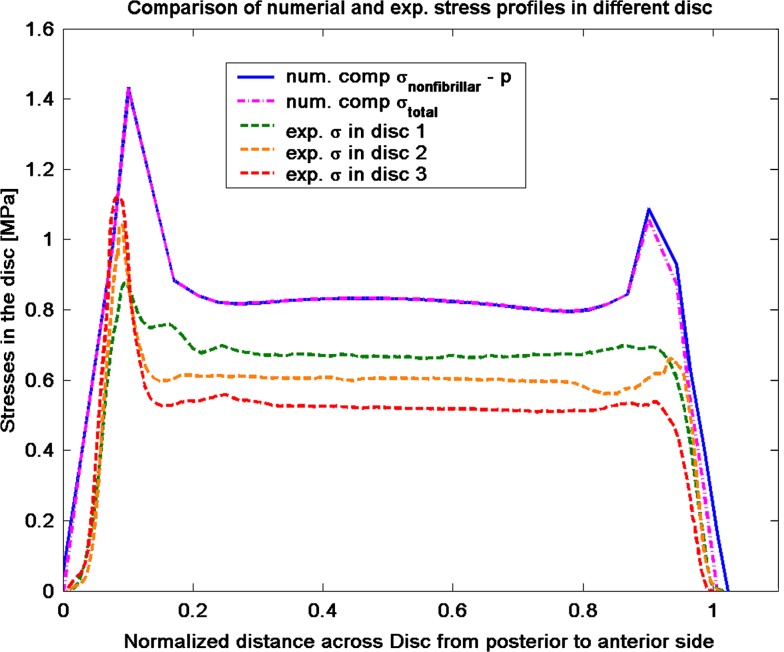
The computed axial stress profiles reproduced the main features of stress profiles, in particular the characteristic posterior and anterior stress peaks, which were observed experimentally by McNally and McKinlay (personal communication). McNally and McKinlay measured compressive stress profiles in post mortem human discs. The stresses in the nucleus are nearly constant, whereas high peaks of compressive stress are found on the posterior and anterior side of the annulus. The posterior side experiences the highest compressive stress peaks in the experimental [45, McNally and McKinlay, personal communication] as well in the numerical results (Fig. 7). The comparison of the stress profile shows that the computed stress peaks are larger than the experimental measured stress peaks. One of the reasons could be that the model does not account for a transition zone between annulus und nucleus, which results in a discontinuity of the material parameters. Another reason could be the choice of material parameters for the non-fibrillar matrix and the fibrillar matrix. The non-fibrillar matrix properties are based on literature data of the intervertebral disc, while the fibrillar matrix properties are from validated articular cartilage properties [24, 40]. However, these peaks may partly explain the prevalence of postero-lateral herniation in humans [46, 47]. The non-homogenous stress distribution observed experimentally and numerically questions the plane stress assumption by Iatridis et al. [22] in their simulations with the PEACE model. The plane stress assumption requires the total stress to be homogeneous while the present simulation clearly demonstrates gradients in total stress in the outer annulus region (Fig. 7).

Fig. 7.

Comparison of experimental stress results from McNally and McKinlay (personal communication) of human disc with the numerical predictions of compressive (comp) stress from the presented model. For the total stress 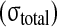and the nonfibrillar matrix stress 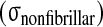minus the hydrostatic pressure (p), stress peaks are seen on the posterior and anterior side of the annulus, while nearly constant stresses are noticed in the nucleus

Unlike previous models [28, 48, 49] our model took the intradiscal pressure in the unloaded state was to be non-zero, and it’s predictions showed that it maintained a finite value even after hours of loading. This finding is in agreement with the pressures measured in vivo by Nachemson and Morris [11] and Wilke et al. [5]. The high intradiscal pressure along the edge of the vertebrae may be un-physiological. The same holds for the high osmotic pressure along the edge of the vertebrae (Fig. 5). These findings may be due to the rigid body behavior of the vertebrae in the model which, according to Brinckmann et al. [50] and Iatridis et al. [51], is not realistic.

During constrained swelling—the first step of our simulation—an increase in intradiscal pressure was observed, which led to prestressing of the collagen fibers even before load was applied; neglecting this effect underestimates the stresses and strains in the collagen structure. This prestress has been considered by others; one approach for considering the prestressing of the annulus fibers is through the implementation of a stress offset (σ_offset), as done by Iatridis et al. [52]. Their in vitro experimental findings were consistent with the in vivo experimental results of subjects in the supine position [5, 11] as these findings indicated the presence of residual stresses in the unloaded disc. Huyghe et al. [18] found significant offset stresses in in vitro confined compression and swelling in canine annulus explants.

The present numerical analysis—in contrast to Iatridis et al. [52]—does not include a priori-offset stress; it computes the prestressing from physical principles of osmosis and experimentally quantified material parameters. This high osmotic pressure in the unloaded disc is achieved in the model by reducing the hypertonic external salt concentration to a physiological salt concentration. These changes result in swelling (step 1), which is constrained by sandwiching the disc between two vertebral bodies; a hydrostatic pressure of 0.2 MPa arises in the nucleus pulposus (Fig. 4), and the fluid content increases to almost 72% (Fig. 3).

Recent experimental results demonstrate that disc cell responses are strongly influenced by osmolarity [13]. Therefore, in order to correctly understand the patters of disc degeneration the inclusion of the swelling process into the disc model is required.

As the collagen fibers are introduced individually into the poroviscoelastic swelling model [24], separate predictions of stresses in the collagen fibers and in the matrix are possible. The total stress of the tissue is the sum of the effective stress in the ground matrix (solid) plus the fiber stresses minus the hydrostatic pressure (Eqs. 5, 6). The computed stresses are defined per unit area of disc tissue. To evaluate the fiber stresses per unit area of fiber, the computed stresses have to be divided by the fiber volume fraction, resulting in much higher values.

Because the model explicitly includes swelling, properties evaluated for biphasic or monophasic models [8, 53] only give indirect clues for the elastic properties to be substituted into the model. Because the contribution of the proteoglycans to the aggregate modulus is mostly integrated into the model through osmosis, the value of the model parameters should be closer to the trypsin treated values than the non-trypsin treated values.

The Young’s modulus of the nucleus pulposus was chosen to be 0.15 MPa. Together with the Poisson ratio of 0.17, this results in an aggregate modulus of 0.16 MPa. Perie et al. [54] measured aggregate moduli of nucleus pulposus and found 0.04 ± 0.02 MPa for trypsin treated nucleus pulposus and 0.58 ± 0.12 MPa for non-trypsin treated. It has been shown that the permeability [43, 54] for the nucleus and annulus are different. For simplicity, we assume homogenous hydraulic permeability. Maroudas et al. [32] presented swelling data showing that intrafibrillar water content is modulated by the extrafibrillar osmotic pressure. For simplicity this effect has not been integrated into our disc model.

The volume and fluid content of the disc depends on the loading condition. This condition leads to an outward bulging of the outer annulus. The largest noticeable deformations were on the posterior side of the model. Observed strains exceed locally up to 20%, hence justifying the need for a finite deformation analysis.

Appendix

Abaqus has a biphasic model of the form:

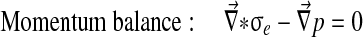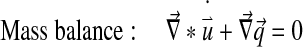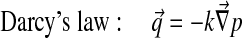With Dirichlet boundary conditions: [u] =0 and [p] =0.

Here 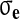is the effective stress, p the fluid pressure, 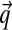the fluid flux, k the permeability and u the displacements.

The swelling behavior through the Donnan osmotic theory was included into the biphasic theory as follows:

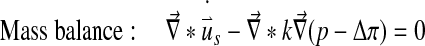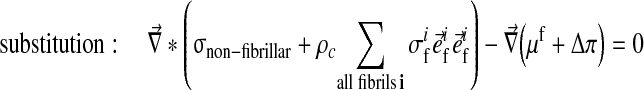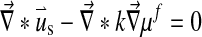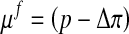Here μ^f is the chemical potential and Δπ is the osmotic pressure given by Eq. 4 with Dirichlet boundary conditions: [u] = 0 and [μ^f] = 0.