ALLPATHS: De novo assembly of whole-genome shotgun microreads

Abstract

New DNA sequencing technologies deliver data at dramatically lower costs but demand new analytical methods to take full advantage of the very short reads that they produce. We provide an initial, theoretical solution to the challenge of de novo assembly from whole-genome shotgun “microreads.” For 11 genomes of sizes up to 39 Mb, we generated high-quality assemblies from 80× coverage by paired 30-base simulated reads modeled after real Illumina-Solexa reads. The bacterial genomes of Campylobacter jejuni and Escherichia coli assemble optimally, yielding single perfect contigs, and larger genomes yield assemblies that are highly connected and accurate. Assemblies are presented in a graph form that retains intrinsic ambiguities such as those arising from polymorphism, thereby providing information that has been absent from previous genome assemblies. For both C. jejuni and E. coli, this assembly graph is a single edge encompassing the entire genome. Larger genomes produce more complicated graphs, but the vast majority of the bases in their assemblies are present in long edges that are nearly always perfect. We describe a general method for genome assembly that can be applied to all types of DNA sequence data, not only short read data, but also conventional sequence reads.

Recently introduced DNA sequencing technologies yield short “microreads” only 25–50 bases long, at per-base costs that might better Sanger-chemistry sequencing by two orders of magnitude (Sanger et al. 1975; Shendure et al. 2005). Two systems (Illumina-Solexa and ABI-SOLiD) are presently available. These yield data suitable for straightforward mapping of biological features such as transcription factor binding sites and chromatin modifications (Johnson et al. 2007; Mikkelsen et al. 2007), and also for the more demanding problem of detecting differences between an unknown genome and a previously sequenced close relative (T.K. Ohsumi, M.G. Grabherr, C. Nusbaum, B.W. Birren, and D.B. Jaffe, in prep.).

A much harder problem is de novo assembly of whole-genome shotgun microreads. In this study, we present a theoretical analysis of this problem and describe an algorithm for addressing it, which we apply to simulated data based on real Solexa reads. We present results for small- to mid-size (39 Mb) genomes, describing assembly completeness, continuity, and correctness.

Briefly, the paper proceeds as follows: (1) We start by discussing the difficulty of applying conventional assembly methods to this type of data, which would involve finding all overlaps between reads. The very large number of (mostly false) overlaps makes this approach intractable. (2) Next, we consider the case of unpaired reads. We determine exactly how good an assembly of such data could possibly be. The answer is captured by a graph, allowing for alternatives in cases where the data lack power to determine the correct answer. (3) Then, we consider the case of paired reads, which in principle enables much better assemblies. Paired-read assembly turns out to be considerably more complicated than unpaired assembly, and although we cannot describe a simple answer as to its best possible result, we do describe an algorithm for it and a research software system, ALLPATHS, that instantiates this algorithm.

There are two key concepts in the ALLPATHS algorithm: (1) finding all paths across a given read pair, i.e., all sequences from one read to the other that are covered by other reads, and (2) localization, a way of using pairs to isolate small regions of the genome and assemble them independently.

Importantly, an ALLPATHS assembly is presented as a graph that retains intrinsic ambiguities, arising from limitations of the data set and also from polymorphism in diploid genomes. Thus, in principle, the assemblies capture exactly what can be known from the data. We have implemented this here for microreads. The same conceptual framework can apply to DNA sequence data of any type.

The reference sequences used in this paper are described in the Supplemental material (Part a). The Source code used in computations is distributed with the paper (Supplemental material Part b).

The challenge of microread assembly

The goal of microread assembly is to build an assembly from reads of size L = 25–50 bases. This is challenging because there are far too many overlaps between reads to compute and most of these overlaps are wrong. A direct approach to assembly would compare reads to each other, glue overlapping ones together, and thereby progressively agglomerate the genome. Table 1A shows that when the size of the minimum allowed overlap (K) is small, the probability of gluing correctly along such overlaps is very low, but can improve dramatically with increase in K. The value of K is limited both by read length and by coverage: Two different reads can overlap by at most L − 1 bases, but many of these “long” overlaps will be missing unless coverage is very high; thus, increasing K requires increasing read length or raising coverage.

Table 1A.

Mean number of false placements of K-mers on the genome

For a given K and a given genome, we show the mean number of perfect placements on the genome for a K-mer drawn at random from the genome, excluding the true placement. This number is the expected ratio of false to true overlaps between reads overlapping by exactly K bases. Values were estimated using a sample size of 10⁶. The procedure used to generate this table is in the Supplemental material Part c. To provide context for Table 1A, we also show the fraction of K-mers having a unique placement on the genome in Table 1B.

Table 1B.

Fraction of K-mers having a unique placement on the genome

For a given K and a given genome, we show the fraction of its K-mer that have a unique placement on the genome. Values were estimated using a sample size of 10⁴.

Finding all overlaps between microreads is also computationally very expensive because there are so many overlaps. Reads are shorter than the long reads from Sanger-chemistry sequencing, thus at the same level of coverage there will be more reads and hence more true overlaps. But the same level of coverage is not enough: One needs to raise coverage to get a usable minimum overlap K, and as one does this, the number of true overlaps rises further (increasing quadratically as coverage rises). To make matters worse, the true overlaps may be swamped by false overlaps (Table 1A). In all, there are too many overlaps, and thus the standard assembly paradigm of finding all overlaps is unlikely to be the best approach for microreads.

Limits of unpaired-read assembly

Setting aside the problem of how genomes might be assembled from microreads, we first describe how good an assembly could possibly be if it were based solely on unpaired reads. While the answer for unpaired reads is not simple, it is precisely computable from the genome. In the process of explaining how this is done, we introduce key concepts needed to assemble genomes from paired microreads.

First, for given minimum overlap K, a “branch” in a genome is a place where there is a sequence of K bases (K-mer) that appears in two or more places and for which the next (or previous) bases are different. By breaking the genome at every branch, we decompose it into a collection of sequences that we call “unipaths” (see Methods, “K-mer Terminology” and “Unipath and Unipath Graph Definitions”). These unipaths form the edges of a “sequence graph,” by which we mean a directed graph whose edges are sequences (Fig. 1; Pevzner et al. 2001; see Methods, “Sequence Graphs”). In fact, the unipath graph is the best possible assembly of the genome from reads of length K + 1, achievable in theory given infinite coverage by perfect reads, which contain all genomic (K + 1)-mers and hence reveal all branches. We will see in the next section that imperfect reads at high coverage will suffice, provided that the reads are longer.

Figure 1.

Unipath graph of the 1.8-Mb genome of C. jejuni for K = 6000, which is also the best possible assembly of its genome from unpaired reads of length 6001. The genome was treated as linear to simplify computation. Each unipath is labeled with its number of copies (multiplicity) in the genome and with a letter to facilitate discussion. Formally, the graph also includes a reversed copy corresponding to the reverse-complemented sequence (data not shown). The middle horizontal edge represents a 6.2-kb perfect repeat present three times in the genome. This edge is present exactly because the reads are shorter than the repeat. If the reads were longer than 6.2 kb, then the graph would be a single edge. This graph (along with edge sequences and multiplicities) represents exactly what can be known from the data: There are exactly two ways to traverse the graph from end to end, ABCDBCEFCEG and ABCEFCDBCEG, but it is not possible to know from the data which of these alternatives represents the true genome. When K = 20, one instead has 4161 unipaths in total, and the graph is far too tangled to display, or even to separate the genome from its complemented copy.

Figure 1 exhibits the unipath graph for the 1.8-Mb genome of Campylobacter jejuni, for a huge value of the overlap parameter K (6000). The graph is simple, as is its relation to the genome: There are two ways to traverse the graph from beginning to end, one of which is correct and one of which is a misassembled version of the genome. It is impossible to do better using unpaired reads unless one has reads longer than 6.2 kb. The graph thus encodes exactly what can be known from the data: it tells us that there are two possibilities for the complete sequence of the genome, but it does not tell us which one is right.

When the minimum overlap K is lowered to 20, we find instead that the unipath graph of C. jejuni has 4161 edges, and it is very tangled. The N50 size of the unipaths is 3.1 kb; that is, half of the total bases in the unipaths are present in unipaths of size 3.1 kb or larger. Moreover, 87% of the genome is in unipaths of size ≥1 kb; thus, there is some continuity in spite of the tangle. Raising K to 24 improves matters strikingly: although there is still a tangle of 1106 unipaths, the N50 size rises to 35.7 kb, corresponding to a level of completeness and continuity that might be adequate for some applications. We see that potential assembly quality is highly sensitive to the minimum overlap K, and hence to both read length and coverage.

As a sequence graph (see Methods, “Sequence Graphs”), the unipath graph captures exactly what can be known about a genome from unpaired reads of a given length, at least under ideal conditions (perfect reads, essentially infinite coverage). It reveals both what can be known from the data and what cannot be known. We set the same goal for assemblies of reads, thus building a sequence graph that retains intrinsic ambiguities arising from polymorphism in the genome or the limited power of the data. If this is done correctly, errors should be exceedingly rare, and where there is uncertainty, the assembly will display the alternatives, rather than picking the one that is judged to be true.

Algorithmic ingredients for unpaired-read assembly

We have not yet explained how unipaths may be constructed from reads. Here we outline the basic ideas. The first step is to correct as many errors as possible in the reads (see Methods, “Error Correction”). Next we assign numbers to K-mers in the reads and build a compact searchable data structure based on these numbers (see Methods, “K-mer Numbering and Database” and “K-mer Numbering Algorithm”). This strategy allows us to avoid the standard operation of computing all overlaps between reads, which is unsuitable for microreads (see “The Challenge of Microread Assembly,” above). Approximate unipaths can then be computed from this data structure (see Methods, “Unipath Generation”), roughly by walking along the reads until a branch is encountered.

At least for simulated reads (modeled on real data), these approximate unipaths closely match the true genomic unipaths. For example, computing unipaths from simulated reads for the linearized Escherichia coli genome (see “Results for Assemblies of Simulated Data,” below) yields approximate unipaths that agree essentially exactly with the true genomic unipaths. (The only exception is that the first and last seven bases are missing; this is an artifact of linearizing a circular genome for this analysis.)

Algorithmic ingredients for paired-read assembly

For paired reads, the assembly problem is far more complex. If we sequence both ends of DNA fragments of size N, then the resulting assemblies can be no better than assemblies from unpaired reads of size N, and the best possible assembly of these can be understood as in the section “Limits of Unpaired-Read Assembly,” above. But this represents an absolute limit, which is not necessarily achievable. To approach this limit, new paired-read assembly algorithms are needed.

In this direction, we begin by describing two core concepts at the heart of the ALLPATHS algorithm. We then elaborate in subsequent sections.

Find all paths across a read pair

Given a read pair (representing the two ends of a single DNA fragment), one may computationally bridge the gap between the two reads by filling in using other reads (without regard to their pairing) having some minimum overlap K with each other, via a process of “walking” from one read to the other (see Methods, “All Paths Definition” and “How to Find All Paths across a Given Read Pair”). Each such sequence, going from the beginning of the one read, across the gap, and on to the end of the other read, is called a “path” (or closure). If the coverage is high enough, this approach is guaranteed to yield the correct path, that is, the true closure of the read pair. However, the approach will typically also yield other, incorrect paths. Our assembly method involves initially finding all of the paths, keeping track of them, and ultimately sorting out which one is right, where possible.

Localization

We use pairs to group together most or all of the reads from a given region of the genome (sometimes accidentally including reads from other regions), then assemble each group separately, in an in silico analog of clone-by-clone sequencing. The idea is to tile the genome by overlapping regions (even though we do not know the genome in advance), assemble each of these in turn, then glue all these local assemblies together to form one big assembly of the entire genome.

The results of the algorithm depend on the variation in the size of the DNA fragments. Table 2 illustrates how the number of paths connecting a given read pair can vary, both across pairs and also as a function of the standard deviation (SD) in the size of the DNA fragment. First, consider walking across read pairs using reads from the entire E. coli data set (left half of table). We find that for tight variation in fragment size (500 bp ±1%, i.e., mean = 500 bp, SD = 5 bp), 94.3% of read pairs have a unique closure, while 0.3% have ≥10³ closures (which arise from repetitive sequence). For the larger variation in fragment size (500 bp ±10%), we instead find that 1.9% of read pairs have ≥10³ closures. In either case, there are some read pairs that have >10⁷ closures; in these cases, the all paths process might be said to “blow up.”

Table 2.

Number of read pair closures in E. coli using 30-base reads and K = 20

Pairs of simulated 30-base reads with separations ∼500 bp from E. coli were walked, using high coverage (100×) (Supplemental material Part d). The table shows the histogram of the number of closures found per read pair, for each of two choices of library SD, and for each of two strategies. (Rows give the nonoverlapping closure count ranges.) In the first strategy, reads from the entire genome are used in the walk. In the second strategy, we picked 20-kb regions and walked short fragments from them using only the reads within a given region. For strategy 1, the sample size was 100 K for 500% ± 1% and 10 K for 500% ± 10%. For strategy 2, we used 200 randomly chosen 20-kb regions and 500 short fragments from each. It is possible for a pair to be reported as having zero closures because whereas we searched for closures having no more than 3 SDs of stretch, the underlying distribution of fragments includes some that are stretched more. It is also possible that zero closures could result from lack of coverage, although this would be a rare event.

These read pairs having large numbers of closures pose a complex series of problems. First, the number of closures could easily be so large that it would be impossible to store them, let alone compute them. More importantly, even if we could compute all these closures, there would be no way to sort them out so as to ultimately yield a usable and relatively untangled final answer for the assembly.

Finally, since we cannot compute, store, or use such a gargantuan set of closures, the algorithms must be designed to terminate in the worst cases, thereby failing to return any closures at all. This will lead to holes in the final assembly, generally in the most repetitive places. This is also where errors in ALLPATHS assemblies originate. Indeed, if we always found all paths, we would expect assemblies to have ambiguities rather than errors, in all cases. However, if some paths are missing, as is the case when all paths “blows up,” errors can occur. As we shall see in the section “Results for Assemblies of Simulated Data,” below, they are very rare.

One approach to this problem of too many closures is to localize the reads, so that only reads from the correct region are used to construct closures. Table 2 offers an optimistic preview of how well this might work: If we could localize, then the all paths problem would become much simpler. The right half of Table 2 reports the results that would be obtained if one could use only reads from a 20-kb region containing the read pair. With tightly constrained fragment size (500 bp ±1%), the fraction of pairs having a unique closure rises from 94.3% to 98.7%. Moreover, all read pairs have fewer than 10³ closures (whereas some have >10⁷ when global data are used).

Sketch of ALLPATHS paired-read assembly algorithm

We now outline the ALLPATHS algorithm for assembling paired reads, postulating a mix of fragment sizes for the paired reads, ranging from short (∼0.5 kb) to long (∼50 kb).

Step 1: Creating approximate unipaths

As with unpaired reads, the first step is to use the reads to compute an approximation to the unipaths (see “Algorithmic Ingredients for Unpaired-Read Assembly,” above). We do this without ever computing the set of all overlaps between reads, since, as discussed in “The Challenge of Microread Assembly” above, this would be computationally prohibitive. The unipath computation ignores the pairing of reads.

Step 2: Selecting seeds

Now with the unipaths and read pairs in hand, we are ready to localize. The first step is to pick “seeds”: these are unipaths around which we will build assemblies of genomic regions. The ideal seed unipaths are long and of low copy number (ideally one). Copy number is inferred from read coverage of the unipaths. (Implementation for real reads will need to take account of deviations from even coverage that are characteristic of particular sequencing technologies.) Using read pairing, we can choose seeds judiciously, spacing them so that the regional assemblies will overlap by a few kilobases where possible, facilitating subsequent gluing (see Methods, “Finding Seed Unipaths”). It is not necessary to use every ideal unipath as a seed.

Step 3: Building neighborhoods around the seeds

The genomic region containing the seed and extending 10 kb on each side is called the “neighborhood” of the seed. Our goal is to assemble the neighborhood. To that end, we first build a collection of sequences (reads, unipaths, etc.) that lie mostly within it.

First, define a collection of low-copy-number unipaths that partially cover the neighborhood. This is done by iterative linking (Fig. 2A). Each unipath is assigned coordinates relative to the seed, with error bars. Because the error bars are in general large, the precise order of the unipaths is unknown, and thus the structure is better thought of as a “cloud” rather than a “scaffold.”

Figure 2.

Localization. (A) Lines represent unipaths, and curves represent paired-read links between them; from seed, iteratively link to low-copy-number unipaths within a 10-kb radius of it. (B) Reads aligning to these unipaths have partners (red) that dangle in repetitive gaps between them.

Next, we construct two sets of reads for the neighborhood: the “primary read cloud,” generally containing only reads whose true genomic locations are near the seed (but not all such reads), and the “secondary read cloud,” generally containing all the short-fragment read pairs near the seed, and some outsiders as well. In more detail, the primary read cloud consists of those reads incident upon one of the neighborhood unipaths, plus their partners, some of which reach into gaps (Fig. 2B). If both reads in a pair land entirely within high-copy-number unipaths, the pair will not be in the primary read cloud; thus, sufficiently repetitive read pairs are excluded. The secondary read cloud consists of all short-fragment read pairs (∼0.5 kb) from the entire data set for which the sequence of both reads could be assembled from reads in the primary cloud (Fig. 3). This operation pulls in some pairs from outside the neighborhood, but usually finds all short-fragment pairs from inside the neighborhood, including highly repetitive ones; thus, the secondary read cloud is complete but can be contaminated.

Figure 3.

Finding pairs in secondary read cloud. An arbitrary short-fragment read pair is shown (red). If both its reads can be separately subsumed as perfect matches to contigs built from reads from the primary cloud (black), the pair is placed in the secondary read cloud. The black contigs represent all possible ways of combining reads from the primary read cloud using perfect overlaps that are at least K bases long.

In addition to completeness, the secondary read cloud has the advantage that it consists of short-fragment pairs, which generally have far fewer closures than longer-fragment pairs. Nevertheless, the same problem of “too many closures” (see “Algorithmic Ingredients for Paired-Read Assembly,” above) persists. There are parts of genomes that are locally repetitive, typically consisting of low-complexity sequence. Thus, even though localization allows us to zoom in on a small region of the genome (∼20 kb), and even though short-fragment (∼0.5 kb) read pairs capture a very small piece of this region, there are still many cases in which the number of closures of these pairs is too large to compute or store or use. This does not happen for E. coli (Table 2) but can happen for more complex genomes. The problem is compounded by the large number of short-fragment read pairs.

To mitigate this problem, we take the short-fragment read pairs in the neighborhood (the secondary read cloud) and progressively merge these pairs together (see Methods, “Short-Fragment Pair Merger”). The end result is that we obtain a smaller number of pairs, and the pairs themselves are more informative: the reads are lengthened (effectively turned into contigs), and the pair separations and their SDs are reduced. Because there are fewer pairs and they are more informative, they will have fewer closures.

Step 4: Finding all paths

Next, we compute the closures of all the merged short-fragment pairs, using only the reads from these pairs. The resulting set of closure sequences should cover the neighborhood correctly, but in general will also include false closures that do not align perfectly to it. These closures are then used, as though they were reads, to walk a selection of mid-length (∼5 kb) read pairs from the primary read cloud.

Step 5: Gluing together the local assembly

The closures of these mid-length read pairs are glued together, yielding a sequence graph: the assembly graph for the neighborhood. This gluing process works by iteratively joining closures that have long end-to-end overlapping stretches (Fig. 4). This process will join together some identical sequences that come from different parts of the genome. See Step 7, below, for how these may be subsequently pulled apart.

Figure 4.

Merger of sequence graphs in ALLPATHS. The process is iterative. It starts with a collection of sequence graphs, and progressively glues them together. Note the simplest case: all the sequence graphs might consist of single edges. Example: (A) two sequence graphs match at graph and sequence level along common portion consisting of bubble extended on both ends; (B) the algorithm identifies a common linear stretch (blue) that extends from a source on one graph to a sink on the other, then glues the graphs along this stretch; however, parallel black and red edges at the bottom are not yet glued; (C) now these edges are zipped up.

As suggested in “Algorithmic Ingredients for Paired-Read Assembly,” above, both the local and the global fragmentwalking processes can blow up in sufficiently repetitive regions, by exceeding predetermined computational limits. The typical effect of this computational failure is that the neighborhood assembly contains a hole, where sequence from the neighborhood is completely missing. This effect will be seen in the final assemblies (see “Results for Assemblies of Simulated Data,” below), where, for example, a few percent of the genome may be absent.

Step 6: Building the global assembly

The local assemblies run in parallel. Once complete, their outputs (local assembly graphs) are glued together formally (Fig. 4), yielding a single sequence graph (see Methods, “Sequence Graphs”), which may have several components, depending on the number of chromosomes in the genome and the success of the assembly process. At this stage, if there are long perfect repeats, they are likely assembled on top of each other. These collapsed parts of the assembly may be pulled apart in the next step, provided that the repeat length is less than the longest library fragment size.

Step 7: Editing the assembly

This graph generally provides an imperfect representation of the genome, and can be improved. To do so, we first find all perfect placements of the error-corrected reads on the assembly graph. Then we find all consistent placements for read pairs. This step is time- and memory-intensive, and we note that it would not necessarily work in precisely the same fashion for mammalian-size genomes, where a read pair with two repetitive ends could have a huge number of placements on the genome. We next carry out a series of editing steps (Fig. 5) to create the final assembly, which is again a sequence graph. These editing steps remove detritus, eliminate ambiguity in some cases, and where possible pull apart regions where repeats are assembled on top of each other.

Figure 5.

Editing assembly graphs. Assembly graphs are edited to improve their quality. (A) Clean-up operations, for example, removal of short “hanging ends,” like the middle vertical edge; other clean-up operations include deletion of sequence that is not covered by paired reads and deletion of tiny graph components. (B) Disambiguation operations. Here, given sufficient paired-read links from the left to the right edge, the precise number of copies of the loop edge may be determined, and it may then be unrolled, thereby replacing all three edges by a single edge. (C) Pulling-apart operations. If paired-read links go from the left red edge to the right red edge, and from the left black edge to the right black edge, but not from red to black or black to red, the middle edge may be duplicated, yielding as output two composite edges.

Results for assemblies of simulated data

To test the algorithm, we chose 10 finished reference genomes from bacteria and fungi (ranging from 2 to 39 Mb) and a 10-Mb segment of the human genome (Supplemental material Part a). Circular genomes were linearized to simplify simulation. The microbial genomes were all treated as haploid (i.e., without polymorphism). The human genomic segment was treated as diploid, in that we randomly introduced single nucleotide polymorphisms (SNPs) at 1/1200 bp, approximately the rate of SNPs in the human genome (Sachidanandam et al. 2001), thereby using both the original reference sequence and a second version having alternative alleles.

For each reference genome, we generated simulated 30-base reads to a total of 80× coverage. The simulated reads consisted of 1× coverage in paired reads from long fragments (50 kb ± 10%), 39.5× coverage in paired reads from moderate-size fragments (6 kb ± 10%), and 39.5× coverage in short fragments (0.5 kb ± 1%) (see the formal simulation procedure in the Supplemental material Part e). These fragment sizes are similar to those used in current genome assembly strategies; we note that the short fragment library has a particularly narrow size distribution; the effect of broadening the distribution is discussed below. The genomic positions of the fragments were chosen at random.

We introduced errors into the reads, at a frequency of ∼0.3%, as follows (Batzoglou et al. 2002). We took actual reads generated by Solexa sequencing of a human BAC clone with a known finished sequence (see Supplemental material), filtered them to eliminate failing reads based on intrinsic criteria (see Methods, “Filtering of Solexa Reads”), aligned the reads to the known reference, and marked the positions of errors. In this fashion, we created a set of “error templates” (distributed as Supplemental), indicating the position and nature (substitution, insertion, or deletion) of the errors in each read, if any. For each simulated read, we randomly selected an error template and introduced errors into the simulated read at the exact same positions indicated by the template. We also defined quality scores for the simulated read by copying them from the Solexa read that gave rise to the template.

We then applied the ALLPATHS code (minimum overlap K = 20) to the simulated reads to generate an assembly for each genome. The ALLPATHS software is distributed with this paper, as are the assemblies themselves (Supplemental material). The assemblies were all run with essentially the same version of the code, apart from slight modifications. The arguments to the software, including modifications for the diploid case and the computational resources (time and memory), are described in the Supplemental material Parts f and g.

We assessed each assembly by aligning it back to its reference genome, noting all defects (Supplemental material Part h). Summary statistics for completeness, continuity, ambiguity, and accuracy are shown in Table 3. (For E. coli, there is a parallel table [Supplemental material Part i] showing what happens when the small-fragment library is broadened: not too much, other than a modest increase in the number of ambiguities.) Some representative parts of these assemblies are shown in Figure 6.

Table 3.

ALLPATHS assemblies of simulated 30-base microreads

Statistics for assemblies of 11 genomes. All are entire genomes except for H. sapiens, for which we used the 10-Mb region on chromosome 22 starting at base 28,939,432 in NCBI build 36. Ploidy and genome size are characteristics of the input data sets, as is reference N50, which depends on both the genome and the connectivity of the reference. For ploidy 1, we treated the genome as having no polymorphism. For ploidy 2, we introduced SNPs at random every 1200 bp. The remaining columns provide summary statistics for the assemblies. Continuity: The N50 size of the assembly graph components, and edges. Ambiguity: We define the number of ambiguities in the assembly to be the total number of bubbles, loops, and so forth that appear in the graph, formally computed as (the number of components) + (the number of edges) − (the number of vertices), and report the number of ambiguities per megabase of genome, excluding ambiguities arising from SNPs in the diploid case. Completeness (coverage): The fraction of the genome that is covered by the assembly. Last column: fraction of genome covered by assembly edges that are perfect and have length ≥10 kb. The number for the H. sapiens region is low because edges are interrupted every ∼1200 bp at SNPs: there are virtually no long edges.

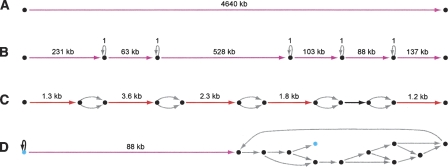
Figure 6.

ALLPATHS assemblies of simulated 30-base microreads. Four assembly graphs or parts are shown, with edges color-coded to reflect length: (gray) <100; (black) 100–1000; (red) 1000–10,000; (magenta) >10,000. (Image created using Graphviz [Low 2004].) None of the graph parts have errors, but some have ambiguities. (A) Assembly of E. coli is one edge. (B) 1.1-Mb component from assembly of 21-Mb fungal genome Y. lipolytica. Five ambiguities are seen: All are loops labeled “1” corresponding to mononucleotide runs whose exact length is unknown. (C) Tiny section of component of assembly of diploid human 10-Mb region. Five ambiguities are seen: All are bubbles arising from SNPs, which are intrinsic to the genome. (D) Correct but tangled component of Pichia stipitis assembly. There is a unique path between the two light blue vertices that matches the reference perfectly.

Completeness and contiguity

All of the assemblies are highly complete and contiguous. The proportion of the genome covered is >96% in all cases. For the haploid genomes, the N50 sizes of the components are typically at least half of the theoretical upper limit (the N50 sizes of the reference sequences), and the N50 sizes of the edges are typically hundreds of kilobases. For the human diploid region with polymorphism, the N50 sizes are lower. The N50 component size is ∼0.5 Mb. The N50 edge size is ∼2 kb, which is as expected given the SNP frequency. (Every SNP introduces a bubble.) If we collapse the SNP bubbles, effectively putting ambiguity codes in for the SNP bases, the N50 edge size increases to 32 kb.

Assembly ambiguities

Most of the assemblies contain at least some inherent ambiguities, regions where there are alternative solutions that could not be resolved with the available data. However, these are generally <20 per megabase. Figure 6 illustrates the nature and distribution of these ambiguities. For the haploid assemblies, there are both isolated and clustered ambiguities. Isolated ambiguities include loops, typically at long homopolymers, where the exact length has not been determined. Figure 6D exhibits a cluster of ambiguities. In the haploid cases, such small clusters account for most ambiguities and tend to occur in small (100–1000 bp) isolated regions of the genome (as is suggested by the large N50 edge size). For the diploid human data set, ambiguities should occur at SNPs (approximately every 1.2 kb), and they do: 96.1% of the SNPs in the reference are present as ambiguities in the assembly.

Assembly accuracy

The assemblies of the two smallest genomes (C. jejuni and E. coli) have no errors. In fact, these assemblies are perfect: in each case, the assembly graph is a single edge that matches the reference perfectly (exclusive of a few missing bases at the ends, because the genomes were linearized for convenience of simulation). Although these genomes are small, they do contain significant repeats. For example, C. jejuni has a 6-kb perfect repeat that occurs three times and yet is perfectly resolved (cf. Fig. 1). The assembly of Eremothecium gossypii also has no errors.

The other assemblies each contain only a very few errors, ranging from single-base errors to large-scale incorrect joins, in total at a rate of less than one event per megabase. We illustrate this by enumerating all errors in three of the assemblies:

• The assembly of Burkholderia thailandensis (6.7 Mb) has only one error: a misjoin between two large components that arises from a 5-kb perfect two-copy repeat.

• The assembly of Yarrowia lipolytica (21 Mb) has two errors: a single-base mismatch (the first base of a 44-kb edge) and a 412-base deletion that occurs between 55-copy and 44-copy pentanucleotide repeats.

• The assembly of Cryptococcus neoformans (19 Mb) has more errors: 12 single-base mismatches (of which 10 occur in the last 19 bases of one 257-kb edge) and three incorrect joins of segments (a component consisting of 12- and 15-kb segments that are incorrectly glued along a 9-kb perfect repeat; a component consisting of two edges of size 6 kb and 2 kb, of which the latter does not align to the genome; and a component consisting of two edges of sizes 69 kb and 0.1 kb, from different parts of the genome).

The overall base accuracy is extremely high, exceeding Q60, or less than one error per 10⁶ bases. The vast majority of the sequence occurs in large edges (>10 kb), and sequence errors are rare in these edges; there are only a dozen exceptions, all minor (Table 4). In most cases, a very high proportion of the genome is covered by long perfect edges (Table 3, last column). In addition, the sequence errors cluster near the ends of the edges. Outside the terminal 30 bases of edges, the sequence quality is Q70.

Table 4.

ALLPATHS assemblies: All edges of size ≥10 kb that contain errors

All edges of size ≥10 kb from the 11 assemblies of Table 3 were aligned to the reference. We report all edges that did not align perfectly from end to end. For N. crassa, there were in addition five cases whose interpretation is problematic, all involving the ends of incompletely finished reference contigs. In all five cases, the assembly is wrong, in the sense that it does not match the reference sequence. However, in three of the five cases, the assembly might match the true Neurospora genome. In each of these cases, the assembly contains an end-to-end perfect join along reference contigs overlapping perfectly by several hundred bases. In these cases, the assembly could correctly represent the genome. Of the two remaining cases, one joins the 140-kb end of one reference contig to the 2-kb interior of another. In the last case, the assembly extends 28 bases off the end of a reference contig.

Results for assemblies of artificially paired real reads

Finally, we applied ALLPATHS to actual data generated from Solexa sequencing. Because read pairs with high-quality and library parameters as in the section “Results for Assemblies of Simulated Data,” above, are not yet routinely available, we instead took single-read data from Solexa sequencing and imposed artificial pairing. Specifically, we started with a large pool of passing 36-base Solexa reads from E. coli (see Methods, “Artificially Paired Solexa Reads”) and mapped these reads to their position on the reference genome. (All reads were mapped.) In parallel, we defined simulated paired reads at 80× coverage, exactly as in the section “Results for Assemblies of Simulated Data,” above. For each such simulated pair, we noted the start point of the first read and the end point of the second read on the reference, and searched the pool for two real reads in opposite orientations having the exact same start and end points. If two such reads were not in the pool, we shifted both start and end by the smallest possible amount so that the corresponding reads were present in the pool. We then created an artificial read pair from these two reads and marked the two reads to avoid reuse. The read pairs thus have real error characteristics, but a coverage pattern and pairing parameters taken from the simulation.

We then trimmed each read, using the other reads as a guide (see Methods, “Artificially Paired Solexa Reads”), and assembled the data using ALLPATHS exactly as in the section “Results for Assemblies of Simulated Data” above, with no change to its parameters. The resulting assembly has 58 components and covers 99.1% of the genome. The N50 size of the components is 145 kb, the N50 size of the edges is 129 kb, and there are a total of 11 ambiguities (2.4 per Mb). All but four of the components consist of single edges, with the smallest component having a size of 6 kb.

We then used the read pairs to order and orient the components into “scaffolds,” by linking together components joined by multiple read pairs. A simple algorithm connected the 58 components into a single scaffold, having a median gap size of 11 bp and an N50 gap size of 4.6 kb.

The final assembly matches the reference sequence exactly, with only 12 exceptions: there were four single-base mismatches (three at the first or last base of an edge), seven indels (of sizes 2, 3, 5, 5, 5, 7, and 16 bp), and a single graph defect (an edge of size of 245 bp was missing). We studied the 11 cases of mismatches or indels to see if they corresponded to inherent defects in the assembly: we observed that in every case, the reads aligned discrepantly to the assembly; this suggests that, at a minimum, the assembly could have been marked to suggest possible errors at these loci.

In summary, the ALLPATHS assembly using actual Solexa read data (but artificial read pairing) is slightly worse than that obtained with simulated data, but is nonetheless quite good. It has high coverage (99.1%), high continuity (a single scaffold), and high accuracy (only 12 discrepancies with the reference). With better understanding of the error properties of the data, it should be possible to further improve the results.

Discussion

Genome sequencing has entered a new era, one that may be dominated by very short and inexpensive reads. Each application of these new data will require significant algorithmic development. Among the many applications, de novo assembly is likely the hardest, both in the laboratory and computationally. A growing base of installed instruments is beginning to generate huge quantities of data. In preparation for this, we have begun this theoretical investigation.

Several recent papers (Dohm et al. 2007; Jeck et al. 2007; Warren et al. 2007) have demonstrated assembly of unpaired microreads (for comparison, see Supplemental material Part j), but the quality of such assemblies is limited by the use of unpaired-read data. Here, we establish that it is possible to produce very high-quality assemblies based entirely on paired microreads at high coverage. We have demonstrated that short read assembly can succeed for genomes up to 40 Mb. The next step will be to move from simulated data to real data. Real data will not perfectly fit our model. Real reads may not land randomly on the genome, and certain positions in the genome may be particularly susceptible to sequencing errors. Nonetheless, the results here suggest that high-quality assemblies should be achievable with microreads. With sufficient amounts of real data, we will be able to establish the parameters of these assemblies, including, for example, read length, pairing rate, and depth of coverage.

The ALLPATHS approach of representing assemblies by graphs also offers the tantalizing prospect of accurately capturing polymorphism within the assemblies themselves, and more generally the systemic capture of ambiguity, regardless of source. In addition to the power of this approach in assembling short reads, ALLPATHS provides a generalized representation suitable to all types of DNA sequence data including traditional sequence reads. By accurately representing ambiguities, this richer view of draft assemblies offers greater capability in applying genome assemblies to biological problems. At the same time, the large edges in these graphs for haploid data sets are nearly all perfect and contain nearly all the genome, thus an excellent “traditional” assembly could be obtained by treating the large edges as contigs and putting aside the graph structure. For diploid assemblies, the same idea will work so long as the principal ambiguities (bubbles from SNPs) are “flattened” by substituting ambiguous base codes.

Methods

K-mer terminology (Pevzner et al. 2001)

A K-mer in a genome is a sequence of K consecutive bases in it. K-mer x is adjacent to K-mer y (written x → y) if there is a (K + 1)-mer in the genome whose first K bases are x and whose last K bases are y. (It follows that x and y overlap by K − 1 bases.) By taking the K-mers as vertices and the adjacencies as edges, one obtains a graph, called the de Bruijn graph. This is related to, but distinct from, the unipath graph described next.

Unipath and unipath graph definitions

Informally, a “unipath” is a maximal unbranched sequence in a genome G, relative to a given minimum overlap K. Formally, consider the de Bruijn graph of G. A sequence U of length ≥K in the genome is expressible as a sequence of successively adjacent K-mers x₁, . . . , x_N, in which case N = length(U) − K + 1. If x₁, . . . , x_{N − 1} have outdegree one and x₂, . . . , x_N have indegree one, and U cannot be lengthened without violating these constraints, U is a “unipath” (Fig. 7). Branchpoint-free circles are also unipaths.

Figure 7.

Unipaths in a genome. A hypothetical genome has 12 K-mers, represented here as vertices. There are five unipaths, one for each of five colors. Vertex L has indegree 2 and vertex R has outdegree 2, delineating branches.

A given K-mer from G can occur in only one unipath, and every K-mer in a unipath is represented by one or more instances in G. In this sense, every K-mer in G lies in exactly one unipath. Two unipaths x, y are “adjacent” if the last K-mer of x is adjacent to the first K-mer of y. This allows us to define a graph, that we call the “unipath graph,” whose edges are the unipaths.

Sequence graphs

We represent knowledge about a given genome using a directed graph whose edges are DNA sequences. We call this structure a “sequence graph.” A unipath graph, which we compute exactly from a genome or approximately from reads, is one example, as are the assemblies that ALLPATHS produces. A connected component of a sequence graph is a connected component of it as a graph, that is, a physically connected subgraph, that is disconnected from all vertices and edges not included within it. Any sequence graph may be divided into its connected components. For a haploid genome whose sequence is completely known, there is one connected component for each chromosome, and each component has no branches, that is, each component is a single edge. In all other cases, branches represent our uncertainty about the exact genomic sequence. For a diploid genome, homologous chromosomes are merged in the graph, generally leading to bubbles (Fig. 6C) in places where there is polymorphism.

Formally, for fixed K, a “sequence graph” is a directed graph whose edges are sequences, having the property that whenever x → y → z are edges, the end of the first edge perfectly overlaps the beginning of the second edge by exactly K − 1 bases. (The case K = 1 is allowed, in which case these edges abut but do not overlap.) Note that if we represent edges as sequences of adjacent K-mers, then the last K-mer of the first edge is adjacent to the first K-mer of the second edge. This is computationally convenient. The value of K can be changed by adjusting the edge sequences.

A sequence graph has a natural output format: a FASTA file of the edge sequences, with header lines of the form

where v₁ and v₂ are vertex indices for the edge (v₁ → v₂). Note that the overall numbering of vertices is arbitrary. The vertex numbering does not contain any genomic information, other than indicating which edges are juxtaposed in the graph.

Error correction

We correct errors in reads using an approach related to Pevzner et al. (2001). For each read, we either keep it as is, edit it, or discard it. The process for this is as follows:

Create a list of all K-mers in the reads. If there are N reads of length L, then the list has N(L − K + 1) entries. Any given K-mer occurs a certain number of times in the list. Let f(m) denote the total number of entries in the list that occur m times in the list. For example, if the list were AC, AC, AC, AT, AT, CG, CG, then f(2) would be 4.

We expect the graph of f to have a sharp peak for low m, especially m = 1, arising primarily from incorrect K-mers (those containing sequencing errors), and a smooth hump for higher m, arising primarily from correct K-mers (those not containing sequencing errors).

Let m₁ be the first local minimum of f, expected to lie between the “sharp peak” and “smooth hump,” as above. Most K-mers having multiplicity less than m₁ are incorrect, whereas most K-mers having multiplicity at least m₁ are correct. We call these high-frequency K-mers “strong.”

We consider various values of K (16, 20, 24) and compute m₁ (and thus define strong) for each. If for all values of K, all the K-mers in a read are strong, we leave the read as is. Otherwise, for each K, we attempt to correct the read by making a “change”: one or two substitutions. (More could be allowed, but the process would take longer.) Each change is assigned a probability based on the quality scores at the changed bases. We consider only changes that make all the K-mers in the read strong, for all K values. If the most probable change is 10 times more likely than the next most probable change, we make the most probable change. Otherwise we discard the read.

K-mer numbering and database

In ALLPATHS, genome sequence is represented in one of three ways: as a sequence of bases, via K-mer numbering (as described here), and as a sequence of unipaths. For fixed K and a fixed collection S of DNA sequences closed under reverse-complementation, a “numbering of K-mer space” is an assignment of a unique integer to each K-mer that appears in S. If the same K-mer appears more than once, each instance must be assigned the same integer. We regard a numbering as “good” if it tends to assign consecutive numbers to K-mers appearing consecutively in the genome. It is reasonable to assume that there exists such a good numbering because if we knew the sequence of the genome, we could walk through it from beginning to end, numbering K-mers as 1, 2, 3, and so on, changing the numbering only when we hit a K-mer that had already been assigned a number. If we do not know the genome in advance, we need an algorithm that takes reads as input (see Methods, “K-mer Numbering Algorithm”). Given a good numbering of the K-mers of S, any DNA sequence that is in S may be translated first into a sequence of K-mers, then into the corresponding sequence of K-mer numbers (e.g., 100, 101, 102, 500, 501, 502, 503, 504, 505), and thence into a sequence of closed intervals of K-mer numbers (e.g., [100, 102], [500, 505]), which we call a “K-mer path.” A good K-mer numbering thus enables a compact representation of each sequence in S. More importantly, these K-mer paths, once computed, may be represented as a searchable database in the form of a sorted vector of pairs (x, y), where x is a K-mer path interval (e.g., [100, 102]) and y identifies the K-mer path from whence it came. Given any sequence s from S, represented as a K-mer path, this database allows rapid identification of all sequences in S that share a K-mer with s. (Software note: see KmerPath.{cc,h} and KmerPathInterval.{cc,h} for implementation.)

K-mer numbering algorithm

First we fix some terminology. A collection of reads is given. We distinguish between a K-mer, and an “occurrence” of that K-mer in the reads (or their reverse complements). A given K-mer may occur several times, but all will be assigned the same K-mer number. Now we describe the process for defining K-mer numbers, which has three steps.

1. Given two sequences, a “maximal perfect alignment” between them is a choice of a window of equal length on each sequence, such that the bases in the respective windows match exactly, and such that the windows cannot be extended in either direction without violating this matching. We build certain maximal perfect alignments between the reads (and also their reverse complements). We do not build all such alignments, which would be computationally prohibitive. Rather, for a given K-mer x occurring in the reads (or their reverse complements), we consider the set S of all its occurrences (id, or, pos) where “id” is the numerical identifier of a read, “or” is the orientation of x on read id (forward or reverse), and “pos” is the start position of x on read id. We define the “canonical” occurrence of x to be the element of S that is lexicographically first. Read id is called the canonical read associated to x. For each other occurrence of x, we create a maximal perfect alignment between the read for the given occurrence and the read for the canonical occurrence, seeding on x. These alignments are shared in the sense that two different K-mers may ultimately contribute to the same alignment, and by so doing, we reduce the number of alignments to a manageable level. (The methodology of this step is adapted from the algorithm in Batzoglou et al. 2002 for finding all proper alignments between reads seeded on a K-mer not occurring more than a given number of times in the reads.)

2. Assign temporary numbers to the occurrences of K-mers in the reads and their reverse complements. This temporary numbering system assigns different numbers to occurrences of the same K-mer. It numbers the occurrences in read 0 consecutively, starting with the number 0, then continues this consecutive numbering with the occurrences in read 1, and so forth. Now if n is the number of an occurrence of a K-mer on a read, then the number of the reverse complemented K-mer on the reverse complemented read is set to M − n, where M is a large fixed constant, unless the K-mer is a palindrome, in which case the number is set to n.

3. Use the alignments of Step 1 to map K-mers on an arbitrary read to K-mers on the canonical reads associated to those K-mers, then assign them numbers via Step 2, thereby causing all occurrences of a given K-mer to have the same number. (Software note: see ReadsToPathsCore.cc for implementation.)

Unipath generation

We build the unipaths as K-mer paths (see Methods, “K-mer Numbering and Database”). The unipaths can then be converted into sequences as needed. Each K-mer path is a sequence of K-mer path intervals. The first step in generating unipaths is to find all the K-mer path intervals that will appear in any of them. Then we string together the intervals to form the unipaths.

To find the intervals that make up the unipaths, we note for each interval in the K-mer path database the K-mer number before and after it, if any, in the path from which it came. Starting with the first K-mer number of the first interval in the table, we set the goal of finding the longest branchless interval of K-mer numbers containing that K-mer number, which will form a K-mer path interval in some unipath. To do this, starting with the first interval that contains that K-mer number, a branchless interval is posited beginning at the first K-mer number of that interval and ending at the last K-mer number of that interval. We proceed forward through the database looking for intervals that extend the posited interval or that indicate branches within it, lengthening or shortening the posited interval accordingly. As soon as an interval in the database is encountered that begins after the posited interval ends, work on the posited interval is complete, and it is a unipath interval, since all subsequent intervals in the database will not intersect the posited interval. The process is repeated for the next highest K-mer number not yet in a unipath interval, until no K-mers remain.

With the unipath intervals in hand, it is a simple matter to build the unipaths. All we have to do is take the first (last) K-mer number in a given unipath interval, look it up in the database, thereby determine its possible predecessors (successors), and if there is exactly one, join the given unipath interval to the one on its left (right). This iterative joining process produces the unipaths.

All paths definition

Given a read pair (L, R) from a library with fragment size distribution D ± d, given K, and given a fixed constant e (typically ∼3), a path across the read pair (or closure) is a sequence that starts with L, ends with R, has length between D − ed and D + ed, and that can be covered by reads that perfectly match it, in such a way that one can walk from L to R using overlaps between reads that are all ≥K. That is one path across the read pair. By all paths across a read pair, we mean all the paths that can be obtained in this way.

How to find all paths across a given read pair

First, we assign numerical identifiers to each read in the set to be used in the search, including the reads in the pair. Then we find the minimal extensions of each read in that set. Conceptually, these are the reads that extend the given read in distinct ways by the smallest amount. Most reads have exactly one minimal extension; reads that have multiple minimal extensions border on branches in the genome. The search for closures over the minimal extensions therefore branches only when such a branch is determined by the content of the genome.

To define an extension, we must choose a direction; without loss of generality, we consider extensions to the right. An extension is a read that aligns perfectly with the given read such that it overhangs the given read to the right, or it ends at the same base and has an identifier greater than that of the given read. A minimal extension is an extension that cannot be found transitively, i.e., if B is a minimal extension of A, then there is no extension X of A where B is also an extension of X. We also find the subsumptions of each read, where read A subsumes B if they align perfectly and A overhangs B to the left and right. The computation of minimal extensions and subsumptions can be done collectively for a large set of pairs that will be crossed using the same set of reads, as is the case with localized assembly.

We then perform a depth-first search with these minimal extensions, beginning with one read of the pair and terminating a branch of the search either when the other read is encountered at a suitable distance (either directly or indirectly through a read that subsumes it), or the maximum distance (D + ed) has been exceeded. To make the results of this search usable, the solutions are stored as a graph structure in which the nodes are reads annotated with their offset from the start of the search. If the read under consideration can be extended by a read that has already led to solutions, the reads in the current search path are added to the solution graph, and the last read is linked to its previously encountered extending read, sharing the search results from that read on. This allows a further optimization: if a read has already been seen at a given offset and it is not part of the solution graph, that branch of the search can be pruned.

Finding seed unipaths

To find the seed unipaths, the idea is to start with all unipaths, then iteratively remove unipaths from that set. On a given iteration, we test unipaths for removal, in an order that favors unipaths of higher copy number, and secondarily to that, shorter unipaths. To see if a given unipath can be removed, we use read pairing to find the closest unipaths in the set that are to the left and to the right of the given unipath. We infer the distance between these left and right neighbors. If this distance is less than a threshold (set to 4 kb), then the given (middle) unipath can be removed. The iterations continue until no further unipaths can be removed from the set. (Software note: see UnipathSeeds.cc for implementation.)

Short-fragment pair merger

We start with the set of short-insert pairs for a neighborhood, that is, the secondary read cloud. The goal is to condense this set, reducing to a smaller set of pairs, and in the process making the residual pairs more informative, both by lengthening their “reads” and by reducing the SD of the separation between them.

To that end, we first translate to a natural and highly compact local representation for all the short-fragment read pairs in the neighborhood. More specifically, we use the reads in the neighborhood to define local unipaths, in exactly the same way that approximate unipaths for the entire data set are defined. Each read may then be expressed as a sequence of local unipaths. (If a read does not fall on a unipath end, we extend it to the end of the unipath.) Furthermore, every read pair has a representation in terms of local unipaths, which might look like the following:

where the local unipaths are symbolized A, B, C, . . . for convenience, and the notation means that the predicted gap between the reads is 50 ± 5 K-mers. The right read has been reverse complemented so that a closure for the read pair has the form B.C. . . . .W.X.X.Y, where the ellipsis is filled with local unipath symbols.

Each local unipath is itself expressible as a sequence of global unipaths. We assign to each local unipath the minimum of the predicted copy numbers for each of its constituent global unipaths. This “local copy number” is an upper bound on the number of times that the local unipath can appear in the genome.

With these tools in hand, the short-fragment read pairs now admit a certain calculus that enables their condensation into a smaller set of pairs, whose reads are longer and whose separation SDs are smaller (and hence which tend to have fewer closures). For example, suppose we have pairs

where B has local copy number one and C is 10 K-mers long. Then we may merge the two pairs together, yielding a single pair

one of whose reads is longer and whose separation SD is smaller. Via several similar rules, the short-fragment read pairs may typically be condensed to a much smaller and more specific set. In relatively easy parts of haploid genomes, it is common for all the short-fragment pairs to reduce to a single “degenerate” pair, for example:

where n is the length of D.E.F in K-mers—so that the read pair is its own closure and this closure is itself the assembly of the neighborhood.

Filtering of Solexa reads

Reads were filtered based on their intrinsic quality by removing non-passing reads. We describe here the definition of a passing read. The Solexa system reports an intensity for each possible base (A,C,G,T) at each position on the read. We define a read to be “passing” if for each of the first 10 bases of the read, the intensity at the called base is at least 1000 and the ratio of the intensity at the called base to the next highest intensity is at least 2.

Artificially paired Solexa reads

A DNA isolate for E. coli K12 MG1655 from the Weinstock Lab at Baylor University was sequenced by Solexa. We combined the reads from 14 lanes on six flowcells: 7986.{1,2}, 7987.{1,2}, 8009.{1,2}, 7706.{1,2}, 9547.{1,2,3}, 8898.{2,3,4}. Passing reads were selected as in the “Filtering of Solexa Reads” section, above, except that we required intensity ≥1500. (Non-passing reads were discarded.) Then we aligned each read to the reference, picking at random one of its best placements. If a read was not aligned, we placed it randomly on the reference, thereby ensuring that every read was placed. The order of the reads was randomized. We then selected simulated read pairs, as described in the text. Prior to assembly, we trimmed the reads, using the following procedure. (1) For each read X, find all other reads that have a gap-free end-to-end alignment with it of length ≥20, seeded on a 12-mer, with four or less errors. (2) Call a base on X “supported” if there exist two such reads, with different orientations or offsets, that agree with the given base. Treat all other bases as “errors.” (3) Trim bases from the end of X until at most two errors remain.