Broken symmetry and critical transport properties of random metals

Abstract

Recent experimental data on the conductivity σ₊(T), T → 0, on the metallic side of the metal–insulator transition in ideally random (neutron transmutation-doped) ⁷⁰Ge:Ga have shown that σ₊(0) ∝ (N − N_c)^μ with μ = ½, confirming earlier ultra-low-temperature results for Si:P. This value is inconsistent with theoretical predictions based on diffusive classical scaling models, but it can be understood by a quantum-directed percolative filamentary amplitude model in which electronic basis states exist which have a well-defined momentum parallel but not normal to the applied electric field. The model, which is based on a new kind of broken symmetry, also explains the anomalous sign reversal of the derivative of the temperature dependence in the critical regime.

The impurity band metal–insulator transition (IBMIT) in randomly doped semiconductors provides challenging problems for both experimentalists and theorists. The theoretical situation on the insulating side of the transition is partially satisfactory. Carriers hop between impurities along percolative paths, but the hopping occurs in a characteristically quantum rather than classical way. The most probable jumps are not between states centered on nearest neighbors (which in general have quite different energies because of randomly varying local fields) but between states centered on neighbors that are close to each other both spatially and energetically. This is Mott’s variable-range hopping model (1). On the insulating side of the transition one must recognize that Coulomb interactions produce a pseudogap in the density of localized states at the Fermi energy that reduces the effects associated with energetic resonances. The density of states of the pseudogap was calculated approximately self-consistently by Efros and Shklovskii (2) and used to modify Mott’s formula for the conductivity σ. The modified formula, logσ₋(T) ∝ (const. − (T₀/T)^1/2), is in excellent agreement with experiment (3). However, the density and compensation dependence of the pseudogap parameter T₀(N) is not understood.

On the metallic side of the transition the theoretical situation is unsatisfactory. The basic problem is that the nature of the current-carrying quantum states in a “random” metal is not clear. This issue does not arise in connection with equilibrium properties near thermodynamic transitions. Because density changes in the IBMIT are small, this quantum transport transition has often been compared with a classical critical point equilibrium transition, but this comparison is misleading in some ways. On the insulating side of the transport transition we know that the current is carried diffusively (that is, without phase coherence) by localized hopping states that are subject primarily to the nonclassical variable range and Coulomb gap quantum resonance effects (1, 2). On the metallic side the basis states that carry current may have some nonclassical phase-coherent or ballistic character, just as in normal Sommerfeld quasiparticle metals with a periodic potential. If some of the metallic states are fully ballistic, one obtains a jump in σ at T = ΔN = N − N_c = 0 which can be formally represented by

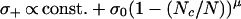1

with μ = 0.

In two dimensions the one-particle current-carrying states are always diffusive and classical. In this case the analogy with classical equilibrium critical points (where particle motion is diffusive and never phase-coherent) is instructive and appropriate. A great deal of theoretical work has been based on the assumption that the current-carrying metallic quantum states for d = 3 are also classical and diffusive in all directions, so that μ_d(d = 3) = μ₃ can be expanded in powers of ɛ = d − d_m. If this were to be so, then μ₃ could be evaluated by a variety of classical scaling methods (4, 5) whose characteristic feature is that they depend on one variable that can be chosen to be real (a diffusive correlation length), in contrast to quantum states, which must be complex and depend on two variables to carry current. Extensive numerical calculations (6) suggest that in the absence of electron–electron interactions the diffusive value for μ₃ should be close to its phase-space value (7), d/2 or 1.5. However, for randomly homogeneous n-type Si:P with very low temperatures and uniaxially tuned effective densities, Thomas, Paalanen, and Rosenbaum (8) found the intermediate value μ₃ = ½ or (d − d_m)/2, and this value has been confirmed by the “Gang of Fourteen” for randomly homogeneous (neutron transmutation doped) uncompensated p-type ⁷⁰Ge:Ga (3). It is apparent from these two classic experiments that there must be a significant ballistic Sommerfeld quantum character to the current-carrying states on the metallic side of the transition. The extent of this quantum character is determined by the new symmetry-breaking principles discussed here.

Unitary Transformations

We suppose that there are N^d uncompensated impurity centers in our sample, with one electron or hole per impurity. The basis set of wave functions used to describe current-carrying states consists of hydrogenic atomic orbital envelopes multiplied by band-edge Bloch functions. To describe randomly distributed impurity centers it is necessary at the outset to assume that N will eventually tend to ∞. This presents a problem for matrix diagonalization methods because there are no techniques for identifying through unitary transformations in Hilbert space the eigenfunctions of an infinite disordered set which are simultaneously eigenfunctions of the boundary-sensitive anti-Hermitian current operator

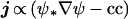2

and the boundary-insensitive but divergent Hermitian Hamiltonian

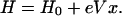3

In the crystalline case eigenfunctions of the periodic internal electric field are always chosen to be complex (Bloch) functions, and this is done because it produces the maximum (correct) electronic conductivities from a Boltzmann equation when off-diagonal elements of the density matrix are neglected in the relaxation time approximation to the collision operator. (Of course, in the same approximation real wave functions produce zero current.) For randomly distributed impurities the Bloch construction is excluded because of the nontranslationally invariant Gaussian noise of the impurity potentials. The characteristic feature of such noise is that its dimensionality is d/2, that is, there are (N_d)^1/2 = N^d/2 constraints that hinder the formation of ballistic extended states (9, 10). (These constraints include, of course, the effects of electron interactions, which are responsible for the first-order metal–insulator transition in a free-electron gas.) This point is crucial to our discussion; we do not need to know in detail what these constraints are, or how they depend on dynamical details such as the strength of the electron–electron interactions compared with the electron–impurity interactions, but we do need to know how many of them there are.

We can now imagine constructing optimized wave functions as linear superpositions of atomic wave functions centered on the dopant impurities. We show that the set of such states separates into two subsets, one consisting of localized states that carry no current at T = 0, the other consisting of suitably phased states that are only partially ballistic, that is, they are complex and have crystal momentum k only parallel to F or to the local drift velocity v_d, whose spatial average is parallel to F; normal to the drift velocity, as a result of the randomly distributed impurities, the wave functions can and must remain real and diffusive. This point is established by a simple counting argument based on the relative dimensionalities of several relevant Hilbert spaces. There is a subtle point here: to be able rigorously to carry out this construction in principle, even though it is not computable in practice, the axiom of choice must be valid; this has been proved to be so (11) whenever a basis set exists, which is the case here.

We know that the boundary conditions at the sample electrodes that change wave functions from real to complex need change eigenfunction energies only by an amount W/N, where W is the band width. In this energy interval there are bN^(d−1) states subject to a unitary transformation that will construct extended ballistic states with 〈j〉 maximized in the presence of Gaussian noise represented by cN^d/2 constraints, where b and c are constants of order unity. After the noise has localized cN^d/2 states (which can be chosen to be real), there will remain (bN^(d−1) − cN^d/2) states from which complex states (extended parallel to F) can be formed. Thus the existence condition for such partially ballistic states is (9)

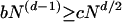4

which becomes (N → ∞)

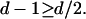5

Thus partially ballistic states exist (or not) for d > (<) 2. The case d = d_m = 2 is marginal in principle, but in practice there will always be background impurities that suppress these states for d = 2. Also for d = 3 it is not possible to extend the longitudinal ballistic character in transverse directions because d_⊥ − d_m = 0.

Broken Symmetry

The physical significance of the existence of partially ballistic states is that in the presence of an applied field these states carry a current with average drift velocity v_D. This effect can be described formally by a term H_F = Σm(v_i − f_b⁻¹v_D)²/2 in the Hamiltonian, where v_D ∝ F is the average drift velocity of all the carriers and f_b = N_b/(N_b + N_l), where N_b(N_l) is the number of ballistic (localized) states which are occupied at T = 0. The summation is taken only over the ballistic states; alternatively, one could use a projection operator for these states. For kT ≪ W the drift velocity is much larger for ballistic metallic states (which are scattered only by background impurities) than for diffusive hopping states (which are scattered by fluctuations in the dopant spacings). The limit of very small applied voltage (eV_a < W/N) is never attained in the laboratory, and were voltages this small to be used, the noise level resulting from thermal fluctuations in the occupancies of ballistic metallic states would render measurement of the conductivity very difficult, if not impossible. Thus, in the limit T → 0 where H_F/kT → ∞, there is in practice no mystery as to the origin of the broken symmetry associated with partially ballistic states generated by unitary transformations.

It is worth emphasizing that use of the term H_F to identify the characteristic basis states is proper procedure, because it embodies the intensive concept of “local equilibrium.” When this is not done in solving the Boltzmann equation, and electrode boundary conditions are applied instead (12), d-dimensional transport collapses and becomes one-dimensional (13), which produces spurious results because all states are localized in one dimension.

Domain Walls, Spin Waves, and Filaments

Some time after this analysis was first proposed (9) it was realized that it closely parallels that used to discuss localization (or domain formation) in spin models of magnetic materials disordered by random internal magnetic fields (10). In fact, mathematically the two procedures are identical, but the physical interpretations in the two cases are, of course, quite different. Strictly speaking, the parallel with spin waves would be even closer. We can examine this point by representing our N^d-electron product states in terms of antisymmetrized products of N^d complex one-electron states centered on the impurities labeled by n,

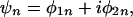6

where φ₁ and φ₂ are real. To take into account the smoothness of the N^d-electron states we must look at the gradients of the wave function amplitude and phase at each impurity; there are N^2d ways of combining the components of these 2d-dimensional vectors (▿∼φ₁, ▿∼φ₂) to form many-electron product states traversing electrode-to-electrode percolative paths that potentially utilize the entire sample volume.

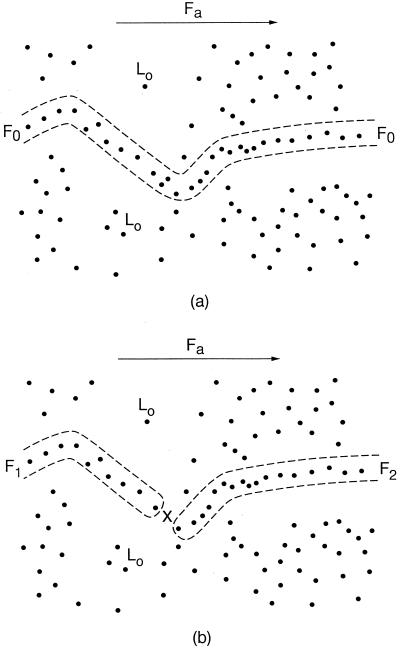
In this model we again begin by separating (8) the one-electron basis states into states that are localized and states that are extended relative to the electric field F, which we place parallel to the x-axis with electrodes in the (y, z) planes at x = 0, L*. (See Fig. 1, where examples of localized states are indicated.) By analogy with plane-wave ballistic states which have energies E(k, N) = E(0, N) + const.k² a similar inversion-symmetric relation is assumed to hold for k_x, the component of k parallel to F in the limit k_x → 0 for extended states. The problem is to identify those partially ballistic extended states which actually carry current as T and ΔN = (N − N_c) → 0 compared with the localized states that coexist at the same energies as a result of the Gaussian noise associated with random disorder (9).

Figure 1.

(a) Small localized clusters are indicated by L_o. A filamentary path F₀ mostly parallel to F_a is also shown. Many of the states on filamentary paths are also localized, as they are associated with filamentary blobs. Other candidates for such paths, which would be acceptable classically, are excluded if they are metallically connected to the best local path for a given value of E_F. (b) Same as a, except that now there is a residual oxygen impurity at X. As a result the single filamentary path of a is broken into two segments, F₁ and F₂, separated by a tunneling barrier. Carriers thermally activated over this barrier can make the slope dσ/dT > 0, while thermally excited filamentary disruption (loss of phase coherence by scattering inside the filaments) can produce the reverse sign. Which process dominates is determined by how wide the barriers are relative to the filament thickness, as measured by α = k_FL; for small ΔN/N the barriers are wide and the barrier resistance is large, so the former process dominates, but for larger ΔN/N the former dominates, in agreement with the results shown in figure 3 of ref. 3. The slope sign reversal actually occurs at α ≈ 4. This value of α is reasonable, because if the background impurities were to form a lattice, the IBMIT would be quite analogous to the Wigner electron gas-lattice transition, which occurs at comparable densities. Moreover, this sign reversal can be regarded as direct evidence for the existence of interrupted dendritic metallic percolation paths as N → N_c⁺.

We consider an array of curvilinear filaments as illustrated in Fig. 1. To have phase-coherent partially ballistic current-carrying states in a disordered medium it is necessary that these states propagate in filaments or channels that neither branch nor cross; this is achieved by limiting the density of filaments to one per unit volume L³; in effect, the filaments are confined to the interstitial volumes between background impurities with an average spacing L. The filamentary occupation number n_f of these sites is limited by the filamentary exclusion principle, n_f = 0, 1. Were branching or crossing to happen, because of multiple pathways with different dynamically fluctuating potentials the phase associated with those k_x-indexed states would no longer be well defined, and destructive interference would result. Transverse to F there are N^2(d−1) degrees of freedom associated with gradients of {φ₁, φ₂} that can be used to construct extended states. The number of filaments, each of which contains at least one such state and that we wish to construct, must have constant areal density to carry current, and thus this number must be proportional to N^(d−1). Finally, the Gaussian noise still scales as N^d/2. Thus the necessary condition for filaments carrying appreciable current to exist is

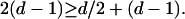7

Although the reasoning leading to inequality 7 addresses a question which is different from that leading to inequality 5, the result is the same, suggesting that the two approaches are mutually consistent.

Because the mean free path is fixed by L, the conductivity per filament is determined entirely by the number of metallic carriers per filament, and this is proportional to k_F. With the total number of carriers N = N_e + N_l dominated by localized states N_l (the number of extended states N_e ≪ N_l for N near N_c)

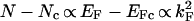8

we immediately obtain in the asymptotic regime

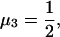9

in good agreement with experiment on randomly doped homogeneous samples (3, 7). It is believed that this axiomatic asymptotic model provides a consistent microscopic description of these data that has previously been lacking (14).

Temperature Dependence

The axiomatic quantum filamentary model also provides valuable guidance on the way temperature affects σ(ΔN, T). Guided by nonpercolative theories, the authors of refs. 15 and 16 had suggested that only samples with positive thermal slopes should be used to determine μ. In ref. 3, ten samples were classified as metallic and were studied to determine N_c⁺ and μ, but only two of these showed dσ₊/dT^1/2 > 0, as predicted by scaling theory; the eight remaining samples with larger ΔN have dσ₊/dT^1/2 < 0. The percolation model also suggests (17) that σ₊ should be linear in T^1/2, but the coefficient can have either sign, depending on whether thermal effects are larger inside the filaments or at their ends. This is because for small ΔN thermal fluctuations can thermionically heal or increase the conductivity in tunneling regions near background impurities (see Fig. 1), but for larger ΔN, where the background impurity tunneling barriers are thinner and less important and the blobs are larger, the effective value of L can be decreased by thermal fluctuations as these internally disrupt coherent filamentary ballistic conductivity by punching hot spots in filamentary blobs. In ref. 3 the eight samples with negative thermal slopes were included in the analysis for phenomenological reasons, because they gave results for N_c⁺ and μ fully consistent with those obtained from the two samples with positive slope. The filamentary quantum percolation model supports the procedures used in ref. 3.

There is an important general observation that can be made here which transcends the details of any specific model. If dσ₊/dT reverses sign while ΔN is within the critical region, then any model that averages over impurity configurations before calculating critical properties must fail, even if it includes electron–electron interactions, as the latter are critical only at the edge of the region, that is, at the transition itself. To explain an interior sign reversal there must be some feature of the internal structure associated with the impurity configurations. As the latter are random, this feature must be topological in nature. In the filamentary model such a feature is obviously the distinction between filament ends and filament interiors. Another way of making the same point is that the sign reversal must be associated with an extra length scale in addition to the average dopant spacing. That extra length scale is the spacing of the background impurities.

Conclusions

When the treatment presented here is compared with that of earlier work, it is easy to see why earlier theories, which were all based on the effective medium approximation (EMA) [Landauer (18) has traced the history of the EMA at least back to Faraday (1837) and perhaps to Avogadro (1806)], were unable to explain the experimental data. The justification, explicit or implicit, which has generally been given for the EMA is that at a critical phase transition, so long as the forces are all short range, only the average properties are needed as all lengths become infinite. Thus it has been thought that only Coulomb interactions could invalidate the EMA. Of course, the applied electrode-to-electrode potential itself is a Coulomb potential, and therefore the present model based on broken symmetry and counting of microscopic phases is consistent with this picture, but it should be noted that in most discussions of Coulomb effects it is only isotropic electron–electron interactions that are considered. This is the case in the “weak localization” model (19), but this EMA model does not explain the observed reversal of sign of the derivative of the T^1/2 term as a function of ΔN within the critical range where μ = ½. In particular, earlier effective medium theories assumed that all changes that occur at the phase transition are isotropic, but we find for d > 2 that some of the basis functions change from localized to ballistic extended only parallel to the applied electric field. Finally, it should be noted that the very good agreement between experiment and the present theoretical model for μ shows that electron–electron interactions have negligibly small effects on filamentary dynamics within the metallic critical region.

All the recent examples of metallic transport experiments that require an explanation that involves both quantum phases and amplitudes have involved either superconductivity or large magnetic fields, and the example with μ = ½ on the metallic side of the IBMIT discussed here seems to be the first exception to this rule since Sommerfeld. The necessity to invoke unitary transformations that produce broken symmetry for very small electric fields makes the demonstration of the correctness of the present theory of the results of refs. 3 and 7 more difficult, but at the same time it emphasizes the conceptual importance of this problem and these experiments. It also shows that randomness, by itself, can be a surprising yet powerful tool for diagnosing quantum interference effects in a many-electron metal at T = 0.

ABBREVIATIONS

IBMIT

impurity band metal–insulator transition

EMA

effective medium approximation