Critical transport properties of random metals in large magnetic fields

Abstract

The threshold behavior of the transport properties of a random metal in the critical region near a metal–insulator transition is strongly affected by the measuring electromagnetic fields. In spite of the randomness, the electrical conductivity exhibits striking phase-coherent effects due to broken symmetry, which greatly sharpen the transition compared with the predictions of effective medium theories, as previously explained for electrical conductivities. Here broken symmetry explains the sign reversal of the T → 0 magnetoconductance of the metal–insulator transition in Si(B,P), also previously not understood by effective medium theories. Finally, the symmetry-breaking features of quantum percolation theory explain the unexpectedly very small electrical conductivity temperature exponent α = 0.22(2) recently observed in Ni(S,Se)₂ alloys at the antiferromagnetic metal–insulator transition below T = 0.8 K.

Metal–insulator transitions, whose theory was pioneered by Mott (1), provide challenging problems for both experimentalists and theorists. Excellent studies of the impurity band metal–insulator transition (IBMIT) in Si:P (2) and neutron transmutation-doped ⁷⁰Ge:Ga (3) have shown that near the critical dopant density N_c on the metallic side, ΔN = N − N_c > 0, the conductivity has the form

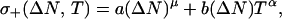1

where a is a constant and b(ΔN) is a slowly varying function whose derivative is positive for small argument, gradually turning to negative for values of ΔN still small enough that the first term accurately describes the T = 0 limit.

Theory’s task is to explain the observed (2, 3) exponent values μ = 0.50(1) and α = 0.5(1) and the sign and its reversal of b′(ΔN). As discussed in a preceding paper (4), effective medium models (5, 6) do not account either for μ or for the sign reversal of the derivative of b. These quantities can be understood by a percolative approach that includes the effects of applied fields on quantum-mechanical wave packets, which is called quantum percolation theory (4). In this paper quantum percolation concepts are extended to the case of strong magnetic fields, where we may well expect to encounter a new kind of broken symmetry. Our discussion is focused on two cases, the IBMIT in Si:B in a large external magnetic field H (7), and Ni(S,Se)_2−y (8), which is antiferromagnetic at low temperatures. The latter case is, I believe, the first alloy to show a quantum metal–insulator transition. The key to this discovery appears to be a novel method of sample preparation (in a Te flux) that excluded the halide dopants with strong phase-quenching effects generally present in transition metal dichalcogenides prepared by halide vapor transport methods. Each of these two cases presents unambiguous conductivity parameters that cannot be explained by scaling theory or by classical quasiparticle Fermi liquid models, which means that each case provides a significant challenge for quantum percolation theory.

Magnetoconductance of Metallic Si:P and Si:B: Experiment

The Si:B data (7) are very extensive and determine σ(ΔN, T, H) for 0.01 < ΔN/N_c < 0.22, for 0.07 < T/K < 0.5, and for gμ_BH/k_BT as large as 10. It appears that the most significant result obtained by Bogdanovich et al. (7) is that the form of the magnetoconductance for large H is given by

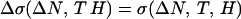2

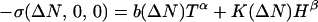with α = β = ½ and K(ΔN) > 0. The partial duality [K′(ΔN) does not switch sign] between T and H in Eq. 2 suggests that a model that predicts the value of α should also be able to predict that of β. In this context the Fermi liquid model (5) encounters even more problems with the H term than it did with the coefficient b(ΔN) of the T term. The derivative of the latter was predicted to be always positive, whereas it is positive only for small ΔN, where Fermi liquid theory is expected to break down, and negative for large ΔN, where Fermi liquid theory should be more appropriate. This is certainly not good, but the situation for the H term is even worse. It is always positive, whereas the diffusive Fermi liquid model with spin splitting predicts that it should always be negative (9). The p-type Si:B result disagrees with that observed in n-type Si:P (9), where it was found that the H term was indeed negative, as expected from diffusive Fermi liquid theory with spin splitting. One would not expect e–e (electron–electron) interactions to be qualitatively different in Si:P and Si:B, however, so it appears that there is a major problem here. We also note here that it is not necessary to invoke weak localization by e–e interactions to obtain a negative magnetoconductance. In the presence of a magnetic field H there will be different numbers N of up/down spin carriers, with δN ∝ H and with σ ∝ N^μ, ∂²σ/∂N² ∝ ∂σ/∂H < 0 for the observed value (not explicable by Fermi liquid theory) of μ = ½. Thus the real puzzle is the positive magnetoconductance, and here quantum percolation theory (4) may well provide a natural remedy, because it has already explained why μ = ½ (instead of the scaling value 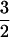) and why the derivative of b(ΔN) reverses sign (instead of always being positive, as predicted by Fermi liquid theory).

Magnetoconductance of Si:P and Si:B: Theory

The diffusive quasiparticle explanation (9) for the negative magnetoconductance of Si:P gives β = 0.5 as follows. The e–e interaction term associated with singular correlations between wave functions nearby in energy (10), which was used to explain the temperature term with α = ½, is unaffected by Larmor orbital motion, but it is modified by spin splitting, because the Altshuler–Aronov singularity (10) is now cut off at gμ_BH instead of at kT. In effect, the thermally induced reduction of e–e scattering by weak localization is in turn reduced itself by the Zeeman lifting of the spin degeneracy. This effective medium quasiparticle spin effect explains the data in Si:P very well (9), but it obviously fails to describe the effects in Si:B, where the magnetoconductance is always positive, regardless of the sign of the derivative of b(ΔN).

We can now examine the same data from the point of view of quantum percolation theory (4). Magnetic-field-induced differences in the number of up/down spins will always be present in both n- and p-type samples, but in p-type samples we must pay special attention to valence band edge orbital degeneracy. The effect of this degeneracy on collective e–e interactions was already discussed in ref. 9, but there is also a single-particle orbital effect to be considered. In the Fermi liquid effective medium model, single-particle orbital effects are zero (9) because of ensemble-averaged cylindrical symmetry around the applied fields. However, in quantum percolation theory we do not make such a premature average, and a new effect emerges. Application of a magnetic field lifts the m_J = ½, 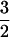degeneracy and this has a profound effect, as illustrated in Fig. 1.

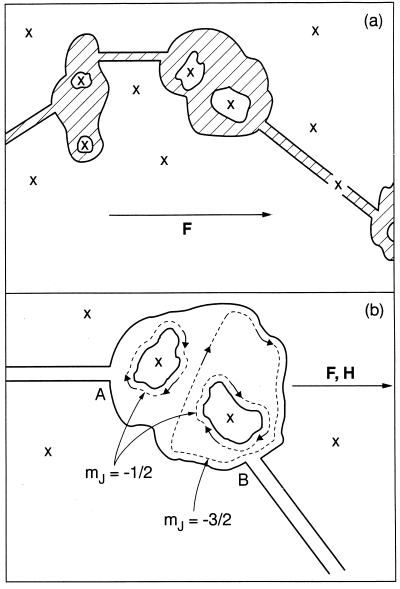
Figure 1.

Percolative paths near threshold are not always thin; instead, they alternate between thin and fat regions, or dendrites and blobs, as shown in a. The metallic regions are shaded and the blobs resemble Swiss cheeses. The holes in the blobs may (or may not) contain phase-breaking background impurities (denoted by ×), which for the samples described here are supposed to be randomly distributed. Very near threshold the applied field itself contributes to the formation of ballistic wave packets because of the broken symmetry discussed at length in ref. 4. In b the effects of a strong magnetic field on the basis states in a blob are illustrated. For the sake of clarity, the metallic regions are not shaded in b, and the applied fields are collinear. The reader is asked to imagine that the blob itself is tilted out of the plane of the paper, so that the Larmor orbits, which are normal to the applied fields, can be shown. The point of b is to illustrate the tendency of parts of the large orbits, which are preferentially associated with large magnitudes of m_J and which have dimensions of the order of the blob, to serve more effectively as connecting segments between the dendrite entrance A and exit B points, themselves separated by distances of the order of the blob dimensions, compared with the small orbits that encircle the holes in the blob.

Fig. 1a illustrates a percolative filament. In general, filaments actually consist of dendrites alternating with blobs. A dendrite is a chain in which each dopant sees at least two nearest neighbors (Z = 2), which are close enough to generate locally metallic basis states close to E_F in spite of e–e interactions that promote localization. (This is the usual competition between Coulomb repulsion and kinetic energies that is responsible for the Wigner transition in a free electron gas.) A blob is a cluster in which the average value of Z, 〈Z〉, is much larger than 2. A blob can contain several localized states and at most one extended state that connects electrodes in the energy range of interest (4) with |E − E_F| < W/N^1/3. One can picture a wave packet in an extended state as performing ballistic motion parallel to the applied field and a kind of random walk transverse to the field as it crosses the blob. Note that with the applied field F parallel to the x-axis, the (y, z) or (ρ, θ) coordinates of the dendrites that enter and leave the blob are generally different, so that with H = 0 the extended-state wave packet moves diffusively within the blob transverse to F at the same time that it is moving ballistically parallel to F (4). Note also that the blob is in general not simply connected; instead, it has a multiply connected Swiss cheese structure, with metallic regions surrounding insulating regions. Because the blob is multiply connected one can find alternate metallic paths across the blob, and current amplitudes flowing along such paths generally interfere destructively because their relative phases are randomized by e–e interactions. Such interference reduces the effective conductivity of the blob considerably, from the metallic level to the diffusive level, apart from the conductivity associated with the single extended metallic state whose properties we now discuss.

Now consider the effect of a magnetic field H parallel to F on the conductivity. It has essentially no effect on the dendritic conductivity, but for μH ≫ kT it can affect the blob conductivity considerably. This is because Landau orbits are formed around the insulating regions embedded in the blobs, as shown in Fig. 1b. An extended-state wave packet passing through the blob will of course avoid these localized Landau orbitals, which means that the magnetic field guides the extended-state wave packet away from the insulating regions. Within those regions there are charged background impurity states, and scattering from the long-range Coulomb potentials of those weakly screened impurities reduces the conductivity. That scattering, in turn, will be reduced when the extended states of the blobs are so guided; in other words, this mechanism will always make a positive contribution to the magnetoconductivity.

The quantum percolation method does not enable us to calculate the prefactor associated with this orbital contribution, but we can draw an important inference concerning chemical trends in the magnitude of this positive term. It will be much larger when the band edge is orbitally degenerate (p-type), while it is essentially absent when it is not (n-type). The reason for this is that the magnetic field lifts the orbital degeneracy between m_J = ½ and 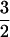, for example, and resistive scattering between orbitally degenerate states is especially strong for long-range interactions (10). In contrast, the lifting of spin degeneracies is an effect that occurs equally well for n- as for p-type samples, and so it cannot explain the difference between n- and p-type samples, which must be an orbital effect. As remarked above, orbital occupancy redistribution effects are absent not only from scaling theory, but also from the dirty Fermi liquid model, and this is a direct result of the effective medium approximation (premature averaging) which produced cylindrical symmetry.

To understand the effects of orbital degeneracy more completely, we examine the partitioning of m_J values between blob states that are localized or extended when projected on the (y, z) plane. These are illustrated in Fig. 1b, where the origin has been located at the center of mass of the blob. The dendrites enter the blob at A (−x_A, ρ_A, θ_A) and leave it at B (x_B, ρ_B, θ_B). The basis states are reoccupied in such a way as to produce ballistic motion along x due to F, as discussed before (4). Similarly, when μH ≫ kT we also have ballistic motion with the complex amplitude ψ_θ ∼ exp(im_Jθ) along the cylindrical angle θ produced by H, while along the cylindrical radius ρ the motion remains diffusive, as described by ϕ_ρ. The extended state that connects A to B is formed as a coherent superposition of segmental amplitudes ψ_x and ψ_θ that contain ballistic motion along x and θ, and

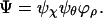3

The orbital moments associated with the segments contributing to extended states which connect A to B and the localized states which surround the insulating holes in the blobs are proportional to |m_J|A, where A is the area enclosed by the appropriate orbital, which is the cross section of the blob for the extended states, and the smaller cross section of an insulating hole in the localized case. These states will be occupied thermally in such a way as to maximize the diamagnetic screening of H. The extended state segments with the larger A will thus be preferentially occupied with m_J = −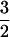 states, while the localized states will take what is left, that is, preferential occupation of m_J = −½ states.

Now we can identify the most probable origin of the large positive magnetoconductance in Si:B. The central cell correction is about 20 meV, which one may compare with a spin-orbit splitting of 40 meV (11). Thus impurity band states will contain an appreciable admixture of split-off J = ½ states into J = 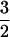band edge states. For large H long-range background impurity scattering between states with Δm_J = 0 is strongest, and this scattering for extended states is greatly reduced by the above-described spatial partitioning which reduces the J = ½, m_J = −½ content of the extended states. In fact, this redistribution is the precise non-effective medium orbitally degenerate orbital analogue of the effective medium spin-splitting effect that contributes a negative magnetoconductance in Fermi liquid theory and that was used to explain the negative magnetoconductance of Si:P (9). One can go even further and identify two mechanisms that make the positive orbital contribution much larger than the negative spin one in the orbitally degenerate case. The first is that with ballistic motion in the (x, θ) coordinates, instead of the x coordinate alone, the blobs become much more “metallically” conductive. The second is that in the effective medium approximation it is electron–electron interactions that are responsible for the negative spin contribution, whereas in quantum percolation theory it is electron–dopant interactions that are responsible for the orbital contribution. Generally speaking, because the electron charge is distributed, whereas the dopant charge is localized at points, the noneffective medium orbital effect should be larger. Even if we ignore these mechanisms altogether, on the grounds that quantum percolation theory does not claim to be able to calculate prefactors, it is still worth noting that for Si:B we have L = 1 and S = ½. Thus, all other things being equal, the positive ballistic orbital term should outweigh the negative spin term for Si:B, but not for Si:P, where L = 0.

Having rectified the magnetoconductance sign difficulties, which are fundamental if the theory is to be taken seriously, we can go on to evaluate β. The quantum percolative argument here is the same as that previously given (4) for α. Application of a large magnetic field enhances the θ conductivity by making it more ballistic and less diffusive, and this is equivalent to increasing the effective number of current carriers N_θ in the blobs. However, 〈(ΔN_γ)²〉 ∼ either kT or μH (for γ = x or θ, as the case may be), so that 〈ΔN_γ〉 ∼ T½ or H½, respectively. In non-effective medium ψ²ϕ theory the values α = β = ½ are essentially model-independent and material-independent and are the same as in effective medium ψ³ Fermi liquid theory. However, the latter is unable to explain the sign reversal between the orbitally degenerate and nondegenerate cases, just as it was unable to explain the sign reversal of the derivative of b(ΔN).

Antiferromagnetic Random Metals

We begin by reviewing the most remarkable aspect of the data (8) on NiS_2−x−ySe_x□_y alloys, the very rapid variation of metallic properties with alloy composition near the metal–insulator transition (MIT) temperature T_c. The (x, T/K) coordinates of the vertices of the nearly triangular region that is occupied by the metallic phase are at A = (0.47, 0); B = (1.0, 0), and C = (0.55, 1.0). Note that although these alloys are fully misicible, the MIT is re-entrant, that is, the metallic regime occurs not at x ∼ 0 or 2, but near x = 1. This is where the effects of disorder are largest. What has happened is that in the absence of disorder the pure materials are antiferromagnetic insulators, but with enough disorder (which presumably suppresses spin density waves) a special kind of metal exists at low T; this metal still contains large magnetic fluctuations. The MIT was studied along the line AB with a sample with x = 0.44 that was driven metallic at T = 0 by applied pressure ∼ 1.5 kbar. For T > 5 K the resistivity ρ showed the usual T² dependence characteristic of strong e–e interactions, unexpectedly switching to Δσ(T) = σ(T) − σ(0) ∼ T^α with α ∼ 0.5 for 0.8 < T/K < 1, and very unexpectedly to α = 0.22(2) for 0.035 < T/K < 0.8. The former value is interesting because it coincides with the value obtained for random impurity bands, whereas the present theory will explain the latter in terms of a new mechanism, double randomness.

Double Randomness

This new mechanism will be explained in terms of axiomatic analogies with other examples involving hindered redistributive percolative transport that are well documented either by numerical simulations or by experiments; in disordered systems rigorous proofs of even relatively simple ideas, such as the Imry–Ma model of domain formation in random-field Ising models, require 10–15 years, as noted in ref. 12. The concept of doubly random quantum percolation is very complex, and so it is introduced here in the simplest way possible. The explanation can be described as a hitchhiker’s (nonspecialist’s) guide to a universe of theoretical models in abstract configuration spaces.

Our first example concerns structural relaxation in quasicrystals. Recall that quasicrystal diffraction patterns are obtained by starting with a cubic lattice in a product Penrose hyperspace of 2d dimensions, a “parallel” space of d dimensions multiplied by a “perpendicular” space also of d dimensions; formally E_d^∥ ⊗ E_d^⊥. By using a suitably chosen irrational angle one obtains the actual atomic structure in parallel space by a probabilistic projection from the product hyperspace to the laboratory (parallel) space that gives the characteristic fivefold quasicrystalline symmetry. Very accurate numerical simulations (13) then showed that on the nanosecond time scale (times long compared with atomic vibrational periods of the order of picoseconds) diffusion in parallel space takes place as if the effective dimension of parallel space were d/2 instead of d. The reason for this is that thermalized diffusion actually takes place in the product hyperspace but that diffusion along the “perpendicular” directions corresponds to phason motion, which does not produce diffusion in parallel (laboratory) space, but only local rearrangements, so that a random hop is only 50% effective. This “ineffectiveness” is an immediate consequence of projection from the 2d-dimensional hyperspace to the d-dimensional laboratory space, and what we are describing can be called projective transport. The success of the microscopic theory (14) in explaining structural relaxation dynamics in this way demonstrates, in some sense, that the Penrose product hyperspace is more “real” than the laboratory space. There are many other examples of configurational ineffectiveness (14).

J Product Hyperspace

The foregoing analogies, together with the recent data (8) on the antiferromagnetic metallic ABC phase of Ni(S,Se)₂, lead to an orbital-spin product hyperspace model of the metal–insulator transition in such an antiferromagnetic doubly random alloy, E_2d^J = E_d^L ⊗ E_d^S, which is analogous to several of the molecular product hyperspaces discussed above. The basis states in this product hyperspace are the complex orbital amplitude ψ_n of the nth formula unit, evaluated at Ni, suitably averaged over the Fermi surface, and the similarly sited and averaged spin σ_n(−1)^j weighted by ±, depending on the sublattice j = 1, 2 to which the nth formula unit belongs. Current is carried only in orbital space, but because of spin–orbit coupling, every percolation path, and indeed every elementary excitation, must be described in the product hyperspace J = L ⊗ S; every particle current is paired with a spin current, and vice versa. In the limit T → 0 the thermal energy kT ≪ λ_a²/W, where λ_a is the spin–orbit coupling parameter averaged over the atoms in the formula unit weighted by their representation in states with E = E_F. The energy λ_a²/W = U is the appropriate measure for the condensation energy of the J phase because the orbital energy bands are nondegenerate. With x = 0.5 we estimate from the atomic values of λ (15) that λ_a ∼ 0.15 eV, so U ∼ 25 meV or 300 K. This is comparable to the maximal temperature of the ABC phase, as it should be. However, it is much larger than the observed transition temperature T_c = 0.8 K for the low-temperature electronic J phase, but the latter is affected by disorder and the fact that only a few coherent J states actually percolate; most of them are localized, which increases their kinetic energy on a scale W(a/l)², where a is the dimension of the formula unit and l is that of a localized metallic J cluster. Thus we would expect that kT_c ≪ U, and its actual value should be very sensitive to sample quality (randomness). Even in completely random samples the ABC metallic phase must compete with insulating antiferromagnetic phases of a nonpercolative semiconductive or insulating nature.

While we cannot calculate T_c, we can say quite a bit about α, which may be less sensitive to compensation or alloying effects. From our earlier analysis (4) we expect

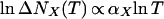4

for X = L, S, and J. The special feature of J states is that the phase-coherent current-carrying states involve both orbital L and spin S phase coherence, so the thermal relation 4 applies to X = J with α_J = ½. Because of this phase coherence we also have in our J = L ⊗ S product space

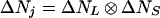5

so that

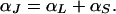6

The only question that now arises is how to partition α_J between α_L and α_S. As we saw above, in the limit T → 0 there is no way to distinguish between the two component spaces. Moreover, the observed value of T_c is very low compared with U/k, so that we do not expect the partition ratio to vary significantly as T increases from 0 to T_c. This means constant equipartitioning with α_L = α_S = ¼. (Equipartitioning is also observed in the phonon–phason and phonon–plasmon relaxation examples discussed above.) In the presence of an external applied electric field J coherence is broken, and the selected current-carrying states are L states. Thus the experimental value of α = 0.22(2) corresponds to α_L and α_L = 0.25 is in excellent agreement with experiment. Note that in this case the symmetry-breaking electric field acts as a projection operator that projects the J product or hyperspace onto the L laboratory space, just as the laboratory quasicrystal is projected from the cubic 2d hyperspace in the Penrose tiling construction.

Conclusions

In the presence of applied fields that produce measurable currents, random metals develop broken symmetries and phase coherence that are absent classically and in any effective medium approximation (4). Here we have analyzed two experiments that have revealed the nature of such broken symmetries in the presence of large magnetic fields.

First, one would expect that such quantum effects would be greatly enhanced by band degeneracies, and it turns out that such degeneracies, together with multiple connectivity of the random metal in the critical region, explain the sign reversal of the magnetoresistance between n-type and p-type samples. Of course, the multiple connectivity is absent from an effective medium model, and that is why Fermi liquid theory was unable to explain this effect.

Second, it is quite striking that the more ideally random the sample, the closer the exponents for the density-dependent factors approach integral or half-integral values. This is because of broken symmetry (4), which apparently makes dynamical renormalization corrections very small. The temperature exponents in the impurity band case have always been ½ (within the experimental uncertainties), so it is quite surprising that the exponent for antiferromagnetic Ni(S,Se)₂ alloys turned out to be essentially ¼. This has been explained here as the result of equipartitioning the thermal activation energy between orbital and spin motion. The equipartitioning principle has been tested in many classical contexts, but this is to my knowledge the first time it has appeared to determine a critical quantum transport exponent. Just as with the density exponents, a very simple result is explained, and there are no dynamical renormalization corrections.