Abstract
The time-varying dynamics of epileptic seizures and the high interindividual variability make their detection difficult. Osorio et al. (1998, Epilepsia, 39, 6) developed an algorithm that has had success in detecting seizures. We present a new strategy for adapting this algorithm or other algorithms to an individual's seizure fingerprint using both seizure and non-seizure training segments and a novel performance criterion that directly incorporates the non-linearity and lack of differentiability of the algorithm. The joint optimization of a linear filter chosen from a bank of candidate filters and of a percentile used in order statistic filtering provides an empirical solution that is both practical and useful, which should translate into improved sensitivity, specificity and detection speed. This premise is strongly supported by the results obtained in a large validation study and the examples illustrated in this article. This strategy is generalizable to other detection algorithms with modular architecture and spectral filters.
Keywords: Epilepsy, Electroencephalogram signal processing, Seizure Detection
1 Introduction
Epileptic seizures are highly non-stationary phenomena. Electrocorticogram (ECoG) signal characteristics vary inter- and intra-individually as seizures evolve temporally and spatially. This variability makes accurate, automated detection of seizures using algorithms difficult and underscores the need for adaptable algorithm architectures.
Osorio et. al. in [1] developed an algorithm for real-time detection of epileptic seizures. Their generic method (i.e., without any individual subject-specific tuning) achieved perfect sensitivity (zero false negatives) and perfect specificity (zero false positives) when tested on 125 seizures contained in short segments obtained from 16 subjects, providing new means for multidimensional quantification of seizure intensity and an average warning time of 15.5 s before clinical onset. Moreover, the architecture of this algorithm is such that it may be readily adapted to further improve its performance if necessary.
The generic Osorio-Frei algorithm (GOFA) cascades a wavelet-based, bandpass finite impulse response (FIR) digital filter, a rectifier that squares the FIR output, and a two second median (order statistic) filter to produce a ‘foreground signal.’ After normalization by a background reference, the resulting ratio is compared to a threshold for a pre-specified duration to determine a seizure detection. A complete mathematical description of the detection algorithm is provided in Appendix 1.
In this paper we propose a new approach to seizure detection adaptation that recognizes not only the role that seizure segments play in the detection process, but also that of interictal (non-seizure) segments. The rationale for inclusion of both seizure and non-seizure data in the adaptation is that it enables a detection algorithm to more accurately distinguish between the two compared to what it could do using exclusively seizure data. We describe in detail a procedure for tuning the detection algorithm's FIR and foreground order statistic filters to the subject's seizure fingerprint.
An overview of the adaptation methodology is as follows. A seizure segment and an interictal (non-seizure) segment are used as adaptation input, each representative of the type of activity the user wishes to detect and ignore, respectively. The optimization goal is to find an FIR filter of a specified order and a percentile value, p, such that, when the filter is applied to the seizure and non-seizure segments, the resulting outputs are maximally statistically separated, in the sense of having the largest ratio of pth-percentile of filtered seizure power to pth-percentile of filtered non-seizure power.4 However, the non-differentiability of the performance criterion does not permit a closed-form solution. Therefore, we attempt to find a good (but sub-optimal) solution by performing a limited search over a bank of candidate filters and percentile values. These candidate filters are computed utilizing the following well-known deterministic digital filter design methods:
Window methods that use the inverse Fourier transform,
Parks-McClellan optimal equiripple,
Linear predictor coefficient (LPC)-based design,
Eigenfiltering, and
Wiener filtering.
These design methods were selected because of their popularity, availability, efficiency, ability to use training data input, and because they each guarantee designs that are optimal in some sense, although not in the sense of our performance criterion. For each design method mentioned, some filters are created using only seizure training data, some using only non-seizure training data, and some using both seizure and non-seizure training data. We provide details on how these methods are used, including practical choices for input design spectra based on the training segments for use in the first three mentioned (frequency domain) design methods. The best FIR filter and percentile value (i.e., maximizing our performance criterion over all candidates) are selected to replace the wavelet FIR and foreground median order statistic filters, respectively, from the GOFA.
This paper is structured as follows. In the next section we describe the GOFA in more detail, and provide further justification for the adaptation procedure we propose. Section 3 describes the method for adapting the FIR and percentile filters of this algorithm to a particular subject's seizure characteristics, using a new performance criterion. We then present examples in Section 4 that compare the performance of the generic and adaptive detection algorithms. Although this paper is not meant as a validation study of the proposed method, we provide examples that demonstrate the ability of this adapted algorithm to: (a) detect epileptiform activity outside the frequency bands emphasized by the generic FIR filter, (b) selectively detect seizures at different stages in their evolution, and (c) speed up detections over those attained by GOFA without causing false positive detections. Finally, in Section 5 we conclude with a discussion of our methods and examples, and propose other ways to adapt the algorithm.
2 The Generic Osorio-Frei Algorithm for Seizure Detection
2.1 Description of the Algorithm
The generic Osorio-Frei algorithm continuously measures the signal's current seizure content in a moving window and compares it to past seizure content computed from a moving window on a larger time-scale. A threshold and duration-based criteria are applied for detection of seizures.
The first step in ECoG processing is the filtering of the raw input signal with a digital FIR filter, chosen because of its ability to improve sensitivity by retaining/enhancing waveforms that are epileptiform in nature and removing/reducing those outside frequency bands relevant for seizure detection. The generic FIR used for this purpose is the 22 coefficient, level 3, ‘DAUB4’ Daubechies wavelet filter [3], that essentially functions as a bandpass filter in the 8-42 Hz range (given the 240 Hz sampling rate of the input signals). The algorithm then squares the output of the FIR filter and uses a moving 50th-percentile order statistic (i.e., median) filter to increase specificity by removing single or brief bursts of epileptiform activity that do not qualify as seizures.
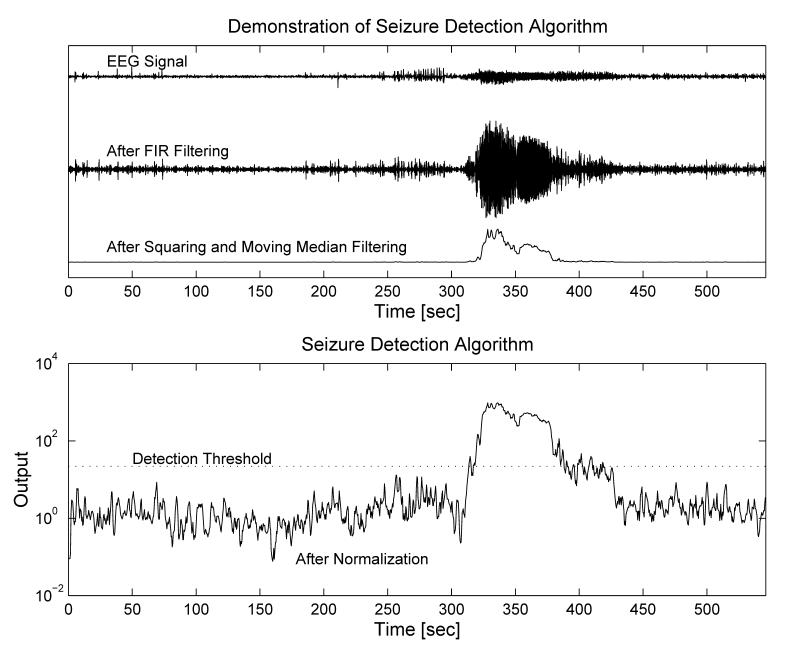
The two second median filter output (i.e., the ‘foreground signal’) is then normalized with respect to its own adaptive background reference prior to its use in the detection decision. The background signal is constructed by first decimating the foreground (sampling it at 2 Hz), then passing the result through a longer median filter and applying an infinite impulse response (IIR) filter to smooth the output with an exponentially forgetting time-weight. For the last step, the algorithm compares the foreground to background ratio to a pre-specified threshold value, T, and produces a detection provided it remains at or above this level for a pre-specified duration, D. A group optimization was performed in [1] to arrive at T = 22, D = 0:84 s for GOFA, as well as details of the procedure that may be followed to optimize T and D for a new (training) data set. An illustration of the signal analysis and detection processes are provided in Figure 1 and mathematical details are provided in Appendix 1. The procedure we present will utilize seizure and non-seizure signal training segments to jointly select an adapted FIR filter and the corresponding best percentile for use in the foreground order statistic filter of the detection algorithm.
Fig. 1.
The Osorio-Frei generic seizure detection algorithm first filters the input ECoG signal with a bandpass FIR digital filter. The output is squared and then passed through a (median) percentile filter. Following a background normalization, the result is compared to a threshold. If it remains at or above this threshold for a given duration, a detection occurs.
2.2 Motivation for Adaptation
The large intersubject variability in seizure characteristics makes it difficult to achieve the goal of a “universal algorithm that detects all seizures.” However, the intrasubject homogeneity in seizure characteristics clearly can be taken advantage of by an adaptable algorithm. The GOFA's modular and flexible structure (see [1]) make this algorithm ideal for parameter tuning to improve its performance when appropriate by utilizing available seizure and non-seizure signal information. The relatively broad frequency band of the generic wavelet FIR filter allows it to detect seizures in the 8–42 Hz range, but not those outside this range. Additionally, while the choice of the median is the most practical in the absence of a priori knowledge about the distribution of instantaneous power in the filtered signal, once some information about this distribution is known the percentile utilized in the foreground order statistic filtering can be adjusted to improve performance. The most common indications for adaptation in clinical practice are
to improve speed of detection,
to preferentially detect one type of seizure signal (or one portion of a multipart seizure evolution) over another,
to prevent future detections of activity the user wishes to ignore, whether epileptiform or artifactual,5 and
to improve sensitivity of detection (e.g., to detect signal changes that are outside the frequency range of the generic FIR filter or which have very low voltage).
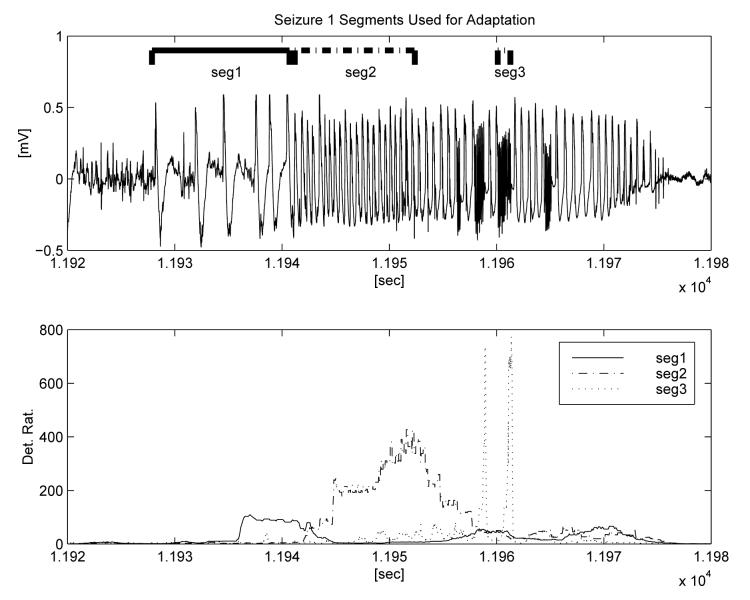
As we describe below, our adaptation procedure uses one seizure and one non-seizure segment as input. These segments serve as samples of what the user wishes to detect and not detect, respectively. The selection of the seizure segment is subjective and dictated by the type of signal characteristics or changes the physician/user wants to detect (or not detect). For example, seizures in certain subjects are sometimes preceded by distinct signal patterns that we term ‘precursors’. This terminology is used to describe epileptiform activity that may precede the unequivocable onset of seizures, but may also occur in isolation during the interictal period (i.e., without evolving into a ‘full blown’ seizure) and that is rarely, if ever, associated with behavioral manifestations. These include, for example, quasi-periodic, large-amplitude, low-frequency epileptiform discharges (see, e.g., Figure 4, seg1). The GOFA is not designed to detect these particular changes (as they are predominantly below 5 Hz) but rather to rapidly and accurately detect the rhythmic fast activity commonly associated in ECoG recordings with an impending clinical seizure. If ‘precursor’ detection is warranted to lengthen warning, then a representative sample of this activity should be chosen as the ‘seizure’ training segment.
Fig. 4.
A seizure with different annotated segments used as input for three separate adaptations (upper panel). The output ratios from the corresponding three adapted algorithms are also shown, indicating the success of the adaptation in recognizing the signals the respective adaptations were designed to detect.
If the user desires to detect some other pattern present in the later evolution of the seizure, then that segment should be used as the seizure segment input for adaptation purposes. Also, if the method produces undesired detections of a certain type of activity, a representative sample of this activity can be included in the non-seizure sample to prevent similar undesired detections in the future. In section 4 we provide examples to demonstrate the ability of this methodology to detect common different types of seizure characteristics.
3 Methodology for Adaptation
This section explains the procedure to adapt the Osorio-Frei algorithm to a given subject's seizures. Section 3.1 outlines the general procedure, while Section 3.2 elaborates on designing the FIR filter.
3.1 Adaptation Procedure
Seizures originating from the same site are highly stereotyped in the majority of subjects. This observation justified adaptation of the detection algorithm using data from the first available seizure. The procedure for adaptation is as follows:
Select representative ‘interictal’ (non-seizure) and ‘seizure’ segments (one of each) for training purposes. The interictal segment may or may not contain epileptiform activity, but should be free of any seizure activity similar to that which the user wishes to detect. The segments should be at least as long as the order of filter to be designed, and long enough to accurately determine the spectral characteristics of the segments. Typically segments of 2 s or more accomplish these objectives, but one may use longer segments or concatenate multiple interictal or seizure segments with different types of activity for use in tuning the filters. Since the filter designs are generally intended to enhance energy in the frequency band(s) that are predominant in the seizure segment and remove or reduce energy in the frequency bands predominant in the interictal segment, the choice of segments may be guided by review of the respective power spectral density estimates of the raw signal at different points in time, to ensure that the spectral characteristics of the two training segments adequately represent those of the longer time series.
Compute a bank of FIR filters based on the chosen seizure and interictal segments. For this paper, this bank consisted of 48 filters obtained using different design methods and input design spectra. The next section discusses this step in detail.
- Choose the filter and percentile value, p, that maximize the ratio of the pth percentile of squared, filtered seizure and interictal segments (the seizure to non-seizure ratio, ‘SNSR’). This new performance criteria that we use for optimization derives from the architecture of the seizure detection algorithm and is somewhat different from common criteria in classical detection theory (that are typically based on moment comparisons). The performance criterion here is defined for each filter and percentile pair by
where ℘p{𝒮} denotes the pth percentile of the set 𝒮. The pth percentile is evaluated by sorting the squared filter outputs and selecting the (pN)th largest, where N = the number of points in the segment. This step is performed by applying each candidate filter to the two segments, squaring the outputs, computing the candidate percentile values for the distribution of each result, and performing a search over the two-dimensional (rectangular) grid of (filter design, percentile) pairs.(1)
The end result of this procedure is a functional of two variables that quantifies performance as a function of filter design and order statistic filter percentile. The filter design and percentile that provide the best performance (i.e., the global maximum of the functional over the filter bank and percentile candidates) then replace the wavelet and median filters in the generic seizure detection algorithm, thereby optimizing the SNSR of the detection method. In this sense, the adapted algorithm (AOFA) parameters provide improved statistical separation between representative seizure and non-seizure data for the subject.
3.2 Design of the FIR Filters
This subsection describes the procedure used to generate a bank of candidate FIR filters for comparative performance assessment according the the criteria defined in Eq. 1. All of the design methods described below create FIR filters6 using standard filter design methods. In addition to the seizure segment and non-seizure segment used for training, the following other parameters and typical values are used:
NB – Number of coefficients in the FIR filter. The wavelet filter used in the generic algorithm has 22 coefficients (for 240 Hz processing) and this number is adequate for broad band detection in frequencies above the 8 Hz range. However, this number must be increased to obtain narrow band discrimination and/or for detection of lower frequency activity. A rule-of-thumb is to set NB to be at least as long as the single waves one is attempting to detect. For example, if the slow-waves in a spike/slow-wave train last 500 msec, then one might use a 120 coefficient FIR filter to detect them.
Fs – Signal sampling rate, typically 200 – 512 Hz for EEG/ECoG data, 240 Hz for the data used in this paper's examples.
NFFT – Parameter indicating how many points are used in computation of discrete Fourier transform (used in obtaining power spectral density estimates of training segments in frequency domain design methods. Typical values are 256 or 512. Power of two is desirable. Since our data sampling rate is 240 Hz, NFFT of 512 provides approximately 0:5 Hz resolution in frequency domain information.
Cutoff frequencies, flo and fhi – These cutoffs allow the user to ignore frequencies outside the [flo, fhi] band in the frequency domain design of the filters. Typical values used are flo = 1 Hz, fhi = 58 Hz (just below the 60 Hz ‘mains’ frequency).
We have utilized four frequency domain and two time domain filter design methods. The frequency domain approaches use as input various design spectra which we have developed from the seizure and non-seizure training segments by first computing the following three basic spectra:
Ratio Spectrum - The ratio of power spectral densities (PSD) for the seizure and interictal segments as estimated by Welch's averaged periodogram method with a Hanning window (computed via the MATLAB function PSD()). This is done to compute filters which magnify waveforms in the seizure frequency bands while filtering out waveforms with frequencies that are predominantly non-seizure.
Seizure Spectrum - The PSD of the seizure segment. This design spectra is chosen to amplify seizure components without attempting to remove activity with non-seizure frequencies.
Reciprocal Interictal Spectrum - The reciprocal of the PSD of the interictal segment. This spectra is meant to exclude typical non-seizure frequencies without regard for dominant seizure frequencies.
The following two optional design spectra modifiers were added to increase user control over the design spectra:
Bandlimited Spectrum - The PSD estimate is set to a near-zero value outside a given frequency range defined by the flo and fhi parameters discussed above. This alternative provides additional user control to restrict frequency focus, for example, to avoid designs which may erroneously rely on low or high frequency artifacts outside the range of front-end analog filters applied to the signal prior to digitization.
Peak Spectrum - The PSD estimate is set to a near-zero value outside the frequency bands containing the maximum power. A power percentile is input by the user to determine the level indicative of a peak (typically in the 0:75 to 0:95 range). This adds focus to dominant frequencies in the design.
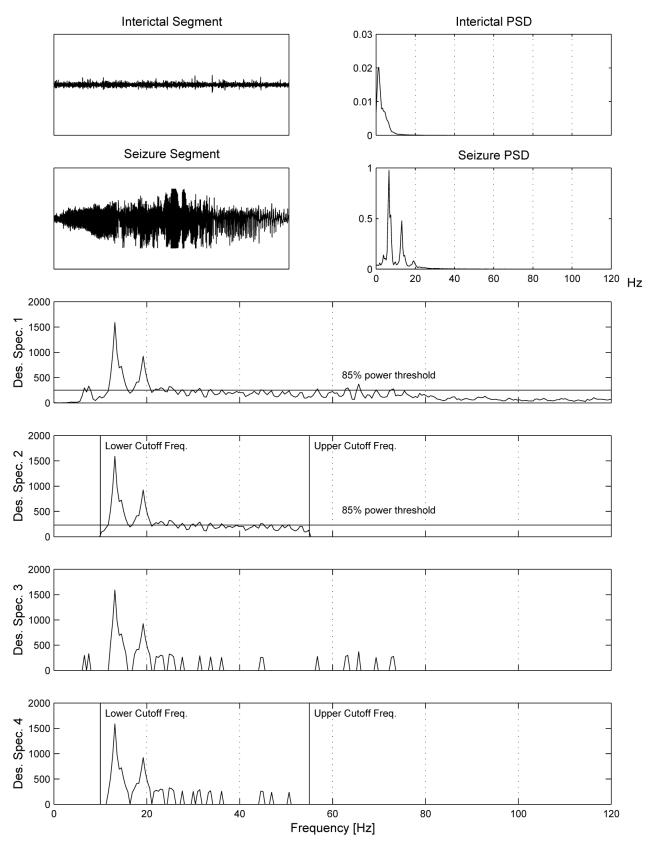
These variations on design spectra are illustrated in Figure 2.
Fig. 2.
Illustration of variations on design spectra. The upper four panels display a seizure and interictal segment (top-left) used as input to the adaptation procedure, along with their respective PSD estimates (top-right). The lower four panels display the Ratio Spectrum (i.e., the ratio of seizure PSD and interictal PSD) for the input data, illustrating variations obtained with and without the use of Peak Spectrum and Bandlimited Spectrum options. Design spectrum 1 illustrates the Ratio Spectrum and the corresponding 85th percentile threshold level. Design spectrum 2 again uses the Ratio Spectrum, but incorporates cutoff frequencies of 10 and 55 Hz limiting the frequency range used in filter design. Design spectra 3 and 4 are obtained in the same manner as Design spectra 1 and 2, respectively, except that power at all frequencies below the 85th percentile threshold level are set to zero.
The four well-known frequency domain filter design methods used to design candidate FIR filters were based on the MATLAB Signal Processing Toolbox functions7 fir1(), fir2(), remez(), and lpc(). The following provides a brief summary of each of the approaches:
- Bandpass Filters (see, e.g., [4], pp. 5.2-1, [5], pp. 630-632)
- Peaks were identified in the design spectra and used to create bandpass filters centered at these peaks with the fir1() function. For example, if the Ratio Spectrum had peaks in the [20:1, 25:7] Hz and [40, 46:3] Hz bands, indicating that these bands have the greatest increase in relative power between the seizure and non-seizure input segments, then an FIR filter, b, is designed in MATLAB using the command b = fir1(NB – 1, [20:1 25:7 40 46:3]/(Fs/=2)), where NB is the desired number of coefficients for the filter.
- Windowing (see, e.g., [4], pp. 5.2-1, [5], pp. 630-632)
- This method computes the inverse fast Fourier transform (IFFT) of the design spectra and multiplies it by a windowing function, using the function fir2(). For example, if p is a vector corresponding to the design spectrum values at normalized frequencies contained in the vector, f, then we obtain an FIR filter, b, with N − 1 coeffcients using the MATLAB command b = fir2(NB − 1, f, p.^(.5)).
- Parks-McClellan (see, e.g., [4], pp. 5.1-1, [5], pp. 637-652)
- This method uses the Parks-McClellan optimal equiripple FIR filter design method to minimize the maximum error between the design spectrum and the filter's frequency response. The MATLAB function remez() computes this optimal filter with a calling syntax similar to that for fir2().
- Linear redictor Coefficient (see, e.g., [5], pp. 864-868)
- This method uses a modified spectral factorization algorithm based on linear predictor coefficients. It is based on the function lpc(), illustrated in the following pseudo-code:
p=[p;p(NFFT/2:-1:2)]; %Make design spectrum, p, 2-sided for IFFTX=real(ifft(1./(p.^(.5)))); %IFFT reciprocal element-wise square-root of pY=fftshift(X); %Shift DC component to center of spectrum[b(:)]=lpc(Y,N_B-1)'; %Calculate the LPCs for use as a filter
A total of 42 filters are obtained using the frequency domain design methods described above. They are derived from permutations of the basic spectra and their variations when generating input to each design method. For example, the six design spectra for the fir1() bandpass filters are the ratio spectrum, bandlimited ratio spectrum, seizure spectrum, bandlimited seizure spectrum, reciprocal interictal spectrum, and bandlimited reciprocal interictal spectrum. Windowing, Parks-McClellan, and LPC-based designs each obtain an additional six filters by making use of the peak spectrum variation that was redundant for the bandpass filters.
In addition to the frequency domain design methods listed above, eigenfiltering and Wiener filter methods are used to each produce three candidate filters. These methods both use the time domain seizure and interictal segments directly and do not require frequency domain information as inputs.
- Eigenfiltering (see, e.g., [6])
- There are three eigenfilter designs utilized in construction of the filter bank. The first, which very often results in the best overall candidate, maximizes the ratio of mean squared filtered seizure to mean squared filtered interictal, i.e.,
where(2) (3)
∥·∥2 denotes the standard Euclidean norm, and B = [b1, … , bNB]. The following pseudocode fragment presents the procedure for computing these coefficients:(4) % Ratio eigenfilter design%% Inputs: N_B = number of coefficients for FIR filter% x_sz = seizure training segment vector% x_int = interictal training segment vector% Time-delay embed x_sz to create N_B x (length(x_sz)−N_B+1) matrixn=length(x_sz); k=length(x_sz)−N_B;y_sz=ones(N_B,k+1)+ones(N_B,1)×[0:k]+[0:N_B−1]'×ones(1,k+1);y_sz(:)=x_sz(y_sz); %Index into x_sz and store ouptut in index matrix% Time-delay embed x_int to create N_B x (length(x_int)−N_B+1) matrixn = length(x_int); k = length(x_int)−N_B;y_int = ones(N_B,k+1)+ones(N_B,1)×[0:k]+[0:N_B−1]'×ones(1,k+1);y_int(:)=x_int(y_int); %Index into x_int & overwrite to store ouptut% Now perform the eigenfilteringcsz = cov(y_sz');cint = cov(y_int');[V,D] = eig(cint\csz);[max_eigv,pos_max] = max(diag(D));b = (:,pos_max); %Store filter coeffs
- The other two eigenfilter designs are similar, but maximize mean squared filtered seizure alone, and the reciprocal of mean squared filtered interictal alone, respectively8.
- Wiener Filtering (see, e.g., [7], pp. 547-549)
- This method also creates three filters, each of which produces an output that is the least squares estimate of the unobserved seizure component embedded in an observed signal that consists of a mixture of seizure and non-seizure data constructed according to three specific models. To accomplish this, we first create a synthetic observation signal, consisting of weighted sums of the (training) interictal and seizure segments. Model 1 uses unity weights, Model 2 selects the weights to normalize the input segments by their average power, and Model 3 consists only of the interictal segment, i.e., the seizure segment has zero weight. More precisely, if we use Y to denote the observation signal and X to denote the seizure component we are seeking to estimate, then the models are given by:
(5) (6)
We use Wiener filtering to find the optimal FIR for estimation of X given Y. That is, to find the filter that, when applied to Y is nearest to the seizure component, X, in the least-squares sense. More precisely,(7)
The following MATLAB code fragment illustrates the procedure:(8) % Wiener filter design%% Inputs: x_sz = vector of seizure training data% x_int = vector of non-seizure training data% N_B = number of coefficients desired for the filter% Get lengths of input training signal vectorsszlen = length(x_sz);intlen = length(x_int);min_len = min(szlen,intlen)% Compute cross-correlation functionsKss = xcorr(x_sz);Kii = xcorr(x_int);Ksi = xcorr(x_sz(1:min_len),x_int(1:min_len));Kss = Kss(sz_len:sz_len + N_B − 1);Ksi = Ksi(min_len:min_len + N_B − 1);Kii = Kii(int_len:int_len + N_B − 1);Kis = fliplr(Ksi);% The Wiener filter is the linear least squares estimate% of X(t) based on Y(t) where X(t) & Y(t) are defined as follows:% Model 1: Y(t) = x_sz + x_int; X(t) = x_szKyy = Kss + Kii + Ksi + Kis;Kxy = Kss + Ksi;b(:,1) = toeplitz(Kyy)\Kxy;% Model 2: Y(t) = Nx_sz + Nx_int; X(t) = Nx_sz% (where Nz = z/norm(z) is a unit vector)Kyy = Kss/Kss(1) + Kii/Kii(1) + (Ksi+Kis)/sqrt(Kss(1)×Kii(1));Kxy = Kss/Kss(1) + Ksi/sqrt(Kss(1)×Kii(1));b(:,2) = toeplitz(Kyy)\Kxy;% Model 3: Y(t) = x_int; S(t) = x_szKyy = Kii;Kxy = Ksi;b(:,3) = toeplitz(Kyy)\Kxy;
4 Examples
In this section we present examples illustrating the ability of the AOFA method to utilize recorded seizure and non-seizure signal information to improve performance. The data in each of these examples consists of single channel recordings obtained from intracranial (temporal depth) electrodes located in the primary epileptogenic zone of the subjects. In practice, for optimum detection speed, it is important that electrodes are placed at or near the site of seizure origination. Since this location may not be known in advance of implantation, typically multiple electrodes/sites are simultaneously monitored until one or more seizure foci are identified.
Example 1
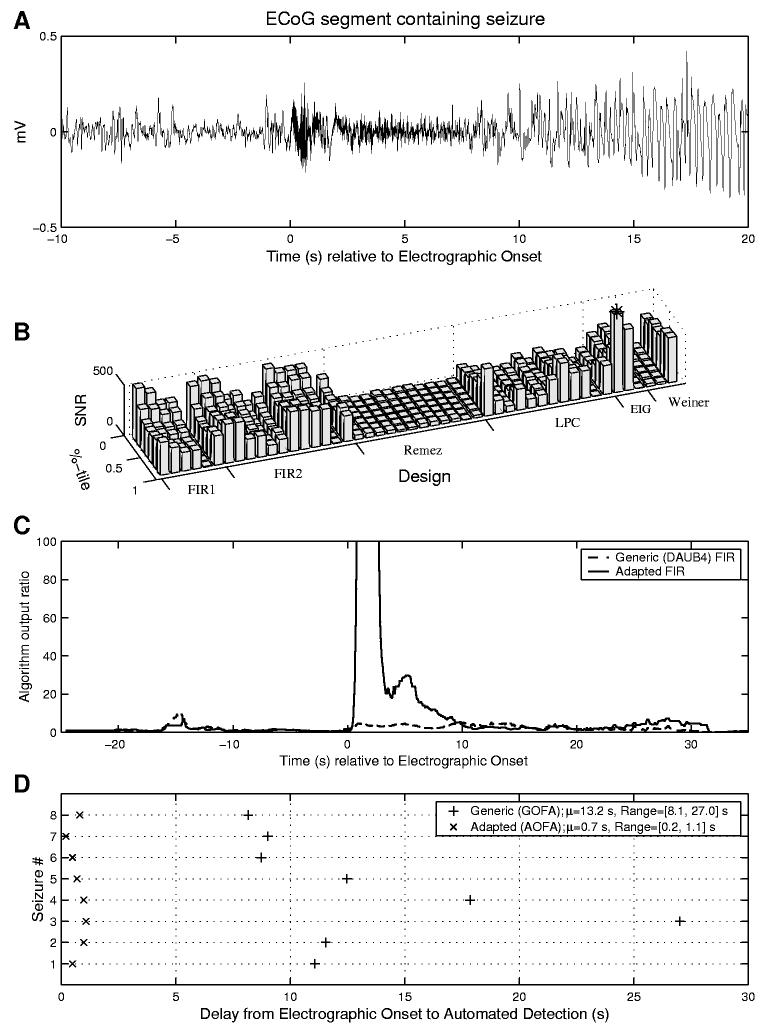
In a previous study [1] there was a single subject for which the GOFA method produced consistently late detections. All 8 seizures recorded for this subject began with a rhythmic high frequency discharge above the 40 Hz range. This explains the late detections of the GOFA method because the onset frequency was outside (above) the passband of the generic FIR filter. This data was re-examined using the methodology for adaptation proposed here. It consisted of 8 ten-minute segments of ECoG data recorded from the right mesial temporal lobe, each beginning 5 minutes before the seizure. Figure 3A shows a 30 s segment of data containing the first seizure for this subject, with t = 0 corresponding to the electrographic onset time determined by expert visual analysis. The data between t = 0 s and t = 2 s was used as representative ‘seizure’ input to the filter design software, and the 10s segment of data between t = −10 and t = 0 was used as representative ‘non-seizure’ input. Figure 3B shows the SNSR for each of the 48 candidate filter designs and 8 different percentiles equally spaced in [0, 1]. The optimal FIR design for this input was the first eigenfilter design method and the corresponding optimal percentile was 87:5. The outputs of the generic and optimal adapted algorithms are shown together in Figure 3C. Also of interest in Figure 3C are (a) the lack of consistency of performance changes across filter designs as the percentile varies from low to high, (b) the relatively poor behavior of the remez-based designs, (c) the significant advantage of Model 3 Weiner filtering over the other two Weiner filter models. The adaptation shows a clear improvement in seizure to non-seizure ratio, with the peak algorithm output reaching a value of 350 in the adapted method (not visible). Figure 3D shows the improvement in detection speed and consistency obtained by using this optimized filter on all eight seizures for this subject. The mean delay from electrographic onset to algorithm detection was reduced from 13:2 s for the generic algorithm to 0:7 s by the adaptation. The variability in detection delay was also significantly decreased (from a standard deviation of 6:35 s for GOFA to 0:31 s for AOFA) and the overall range of detection delays reduced from [8:1, 27:0] s to [0:2, 1:1] s. The adapted algorithm (as well as the generic algorithm) had no false positive detections over the 8 segments, each containing approximately 8 minutes of non-seizure data surrounding the seizure. However, longer, continuous recordings from this subject that would be required to more accurately determine false positive rates were not available for analysis.
Fig. 3.
(A) Single channel recording containing a seizure onset characterized by a burst of high frequency rhythmic activity (i.e., above 40 Hz); (B) Comparison of the performance (i.e., SNSR) of 48 candidate FIR filters and corresponding percentile levels designed using the seizure and pre-seizure data from (A). The optimal choice for this example is the first eigenfilter design (that maximized the ratio of mean squared filtered seizure to interictal) and a percentile choice of 87.5; (C) Comparison of the algorithm output ratios before and after adaptation; (D) Illustration of the adaptation-induced speedup in detection over 8 seizures for this subject. The mean delay from visually-marked electrographic onset to automated detection was reduced from 13:2s to 0:7s, the standard deviation from 6:35s to 0:31s., and the range from [8:1, 27:0] to [0:2, 1:1].
Example 2
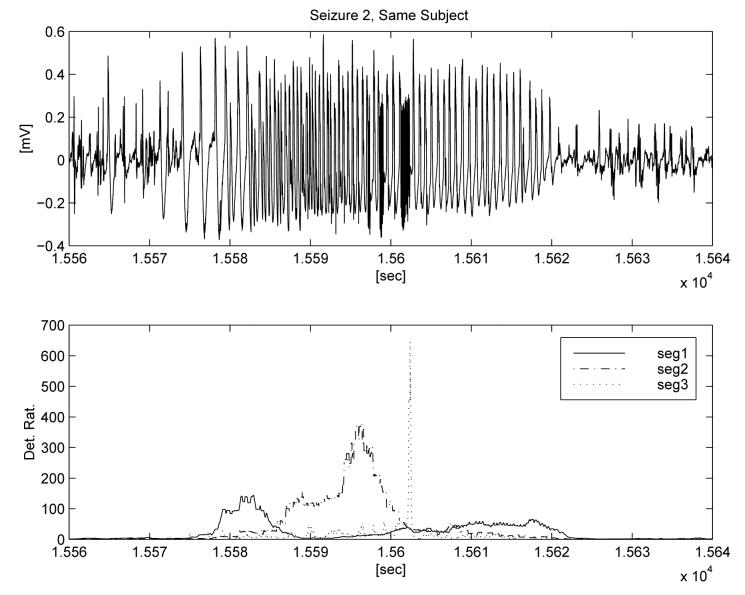
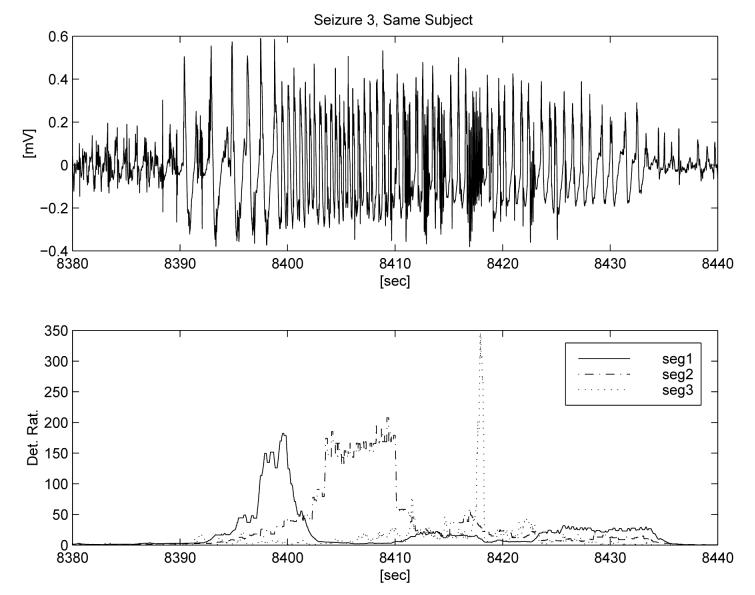
This example illustrates how the results of adaptation depend upon the choice of seizure segment used as input. In Figure 4 we show a seizure and annotate three different segments that were used for three separate adaptations. The first minute of interictal data from the recording (over one hour prior to seizure) was used as a representative non-seizure segment. The third segment (‘seg 3’) is representative of the seizure activity detected by the generic algorithm (∼ 30 Hz), while the frequencies of the two other segments that were tested as adaptation input are below those detectable by the generic algorithm. The first segment is somewhat arrhythmic, with less than 1 wave per second, while the second segment has a dominant PSD peak around 2 Hz. The lower panel displays the ratio outputs of the detection algorithms corresponding to the three separate adaptations. Each indicates an algorithm output ratio for detection that exceeds 100, and demonstrates the selectivity provided by the adaptation. Figures 5 and 6 show the outputs of the three adapted algorithms applied to two other seizures from the same subject. The stereotypical onset and evolution is apparent for all three events, as well as minor inter-seizure variability. In these two ‘testing seizures,’ the adaptations are able to detect only the type of seizure waveforms that are similar to the selected training segments and to quantify their intensity relative to background and time of occurrence. Once again the algorithm output ratio exceeds 100 for all three adaptations and all test seizures.
Fig. 5.
Testing of the three adaptations on a second seizure from same subject.
Fig. 6.
Testing of the three adaptations on a third seizure from same subject.
Example 3
As already stated, the generic algorithm mainly detects signal activity in the 8 – 42 Hz band. In some cases such activity is preceded by slower spike/slow-wave ‘precursor’ activity that can only be detected via adaptation (as in Example 2). Additionally, it is of interest to determine how the adaptation methodology presented here may perform over long time series when it is based only on single, short seizure and non-seizure training segments. To investigate these issues further, we applied the procedure to one continuous long time series (85.62 hr.) recorded from a subject during their epilepsy surgery evaluation. This recording had six clinical seizures, all originating from the same site in the left mesial temporal lobe.
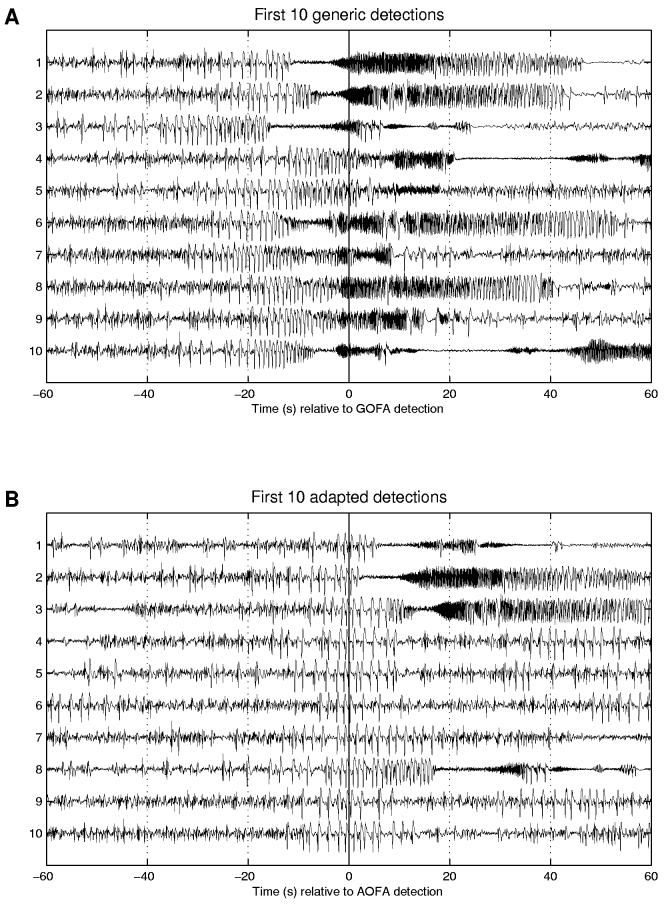
Application of GOFA to this time series yielded 33 detections.9 Figure 7A displays the first 10 of these detections, with the algorithm detection time (‘ADT’) corresponding to the vertical line at t = 0. Detections 1, 4, and 10 correspond to the first three clinical seizures. All six of the subject's clinical seizures were detected, along with 27 other events that were classified as ‘seizures with unknown clinical correlates’ via expert visual review. Since all the seizures were preceded by (undetected) spike/slow-wave trains beginning up to 40 s prior to detection, adaptation was performed to detect this type of activity. A 6 s segment of data beginning 17 s before the automated detection of the first clinical seizure (a rhythmic section of spike/slow-wave activity) and a 20 s segment of data beginning one minute before the first clinical seizure detection (and not readily visually distinguishable from interictal background data) were used as seizure and non-seizure training segments, respectively. Repeating the analysis of the entire time-series, this time using the adapted algorithm, resulted in 92 detections. Thirty-three of these were those seizures previously detected by the generic algorithm; the remainder (59) were new detections. All of the adapted algorithm detections were visually reviewed and found to correspond to trains of spike/slow-wave activity that often preceded (36 % of the time) the evolving seizures that had been detected by GOFA. The adapted algorithm sped up detections by an average of 20:6 s over GOFA, and increased the warning of clinical onset by 15:7 s (from 17:1 s by GOFA to 32:8 s after adaptation) for this subject. More detailed comparisons of available warning times for clinical seizures and speed of detection for evolving seizures are given in Tables 1 and 2, respectively.
Fig. 7.
This figure illustrates (A) the first 10 generic algorithm detections for one subject (Example 3) and (B) the first 10 detections after adaptation to detect the spike/slow-wave trains. The adapted method detects both earlier and more often, including the detection of spike/slow-wave trains that do not evolve into faster electrographic seizures (e.g., adapted detections 4-7, 9-10).
Table 1.
Comparison of detection speed between generic and adapted algorithms. EO-ADT indicates difference between electrographic onset of seizure and algorithm detection time (ADT) in seconds (positive indicates EO before ADT). Similarly, CO-ADT indicates difference between clinical onset of seizure and ADT.
| Clinical Sz. # |
Generic | Adapted | ||
|---|---|---|---|---|
| EO-ADT | CO-ADT | EO-ADT | CO-ADT | |
| 1 | 11.59 | −14.4 | −2.05 | −28.05 |
| 2 | 11.64 | −1.36 | 2.06 | −10.94 |
| 3 | 12.29 | −21.7 | −10.19 | −44.19 |
| 4 | 5.62 | −56.4 | −4.03 | −66.03 |
| 5 | 6.39 | −21.6 | −0.72 | −28.72 |
| 6 | 39.06 | 13.06 | 6.88 | −19.12 |
| Mean (s) | 14.4 | −17.1 | −1.3 | −32.8 |
| Median (s) | 11.6 | −18.0 | −1.4 | −28.4 |
| σ | 12.4 | 23.5 | 5.8 | 19.7 |
Table 2.
Improvement in detection speed between generic and adapted detection algorithm for subject in Example 3. Clinical seizures are denoted by ‘*’. Notice that the three smallest improvements over all (Det #s 4, 11, and 12) all correspond to clinical seizures. The reduced improvement indicates a shorter spike/slow-wave train before the high frequency onset, and possibly a more abrupt transition.
| Generic Detection # |
Adapted Improvement Over Generic (s) |
Generic Detection # |
Adapted Improvement Over Generic (s) |
|---|---|---|---|
| 1* | 13.6 | 18 | 29.8 |
| 2 | 18.5 | 19 | 28.3 |
| 3 | 32.9 | 20 | 19.2 |
| 4* | 9.6 | 21 | 28.6 |
| 5 | 17.6 | 22 | 15.5 |
| 6 | 24.8 | 23 | 22.8 |
| 7 | 21.4 | 24 | 28.3 |
| 8 | 14.8 | 25 | 31.9 |
| 9 | 13.3 | 26 | 13.3 |
| 10* | 22.5 | 27 | 13.8 |
| 11* | 9.6 | 28* | 32.2 |
| 12* | 7.1 | 29 | 25.2 |
| 13 | 14.9 | 30 | 23.3 |
| 14 | 14.4 | 31 | 27.7 |
| 15 | 13.7 | 32 | 30.2 |
| 16 | 25.5 | 33 | 13.8 |
| 17 | 21.6 | ||
| Mean (s) | 20.6 | ||
| Median (s) | 21.4 | ||
| σ | 7.4 | ||
| Min (s) | 7.1 | ||
| Max (s) | 32.9 | ||
In this example the adapted algorithm was designed to detect a type of signal activity (‘spike slow-wave train') not detected by the generic algorithm. In data for this particular subject, this activity always preceded the GOFA-detected seizures (which themselves evolved into clinical seizures only 6/33 of the time), but was also present at other times without being followed by the GOFA-detected seizures. Data for this subject emphasizes that evaluation of algorithm sensitivity, specificity, and detection speed critically depends upon the precise definition of what the user desires to be detected. For example, the adapted algorithm detections, or GOFA detections may be considered as false positives if one only desires to detect clinical seizures. On the other hand, if a user considers the detected spike slow-wave trains as subclinical seizures, then each occurrence of this activity could be considered as a false negative for the GOFA that can be eliminated via adaptation. The interested reader is referred to [2] for details of a recent large scale validation study of the generic and adapted seizure detection algorithms.
5 Conclusions
The nonstationary nature of electrical brain signals and the lack of widely accepted, objective criteria to determine which activity constitutes a seizure and its time of electrographic onset, make automated seizure detection optimization a problem with highly complex performance criteria. The strategy presented in this paper uses empirical means in an attempt to bridge the gap between existing spectral analysis tools, the majority of which were developed for non-biological applications, and those required for epileptic brain signals.
Among all deterministic design methods tested, the ratio eigenfilter design usually yielded the highest SNSR. We speculate that this is because it maximizes an expression similar to the SNSR of our approach, except it uses an average in place of the SNSR's percentile.
Although the filter bank used in this study consists of several well-known filter designs, the approach can be expanded to incorporate new ones that may be more useful for addressing the problem. For example, filters could be added that are designed via a trainable, feed-forward neural network using filter outputs as inputs. While not self-adaptive, our approach is completely automatic once the training segments and a small number of control parameters are chosen.
We have had further success beyond that afforded by the above listed deterministic design methods through the application of evolutionary random search techniques for filter coefficient design. These techniques can directly optimize both filter and percentile for any performance criteria that can be evaluated numerically, but can be computationally expensive when evaluation of the performance criteria is complex or the number of filter coefficients (and thus the space over which to conduct the search) is large. However, the computational complexity of this approach may be reduced through the use of deterministic designs (as described herein) to initialize the search. Caution must be exercised when applying random searches with non-convex performance criteria, as is the case here, as they may yield local, instead of global, extrema.
Since designing a real-time, universal seizure detection algorithm with perfect sensitivity and specificity, and excellent detection speed is an elusive objective, the focus should be on developing subject-specific algorithms that account for the marked inter-individual seizure heterogeneity and the subjectivity of visual seizure scoring by incorporating physician/user preference and the clinical application into the adaptation process. Additional refinements would include the simultaneous use of multiple AOFA algorithms, each with a different adaptation objective10 to detect, quantify, and classify different seizure patterns, including the onset, intensity, location, and duration of each of the three types of electrographic activity in Example 2. This would allow selective issuance of warnings or delivery of therapy according to the locus and type of activity detected and the probability of impairment or loss of function.
To be valid and meaningful, performance comparisons among seizure detections algorithms (‘SDAs’; see, e.g., [8], [9]) must be made on the same data based scored uniform rules. Since we did not have access to other SDAs, no such comparisons were possible. A recently published large validation study ([2]) that utilized this strategy to improve SDA performance (sensitivity, specificity or speed of detection), illustrates its usefulness. The procedure we described and the associated performance criterion for filter design can be applied to any detection algorithms which are modular and operate with spectral filters.
Acknowledgments
This research was supported by NIH Grant Number 5R44NS34630-03.
Appendix 1. Mathematical description of the Osorio-Frei detection algorithm
Let be the ith component of input signal (e.g., EEG/ECoG) to be monitored. Let A = {a1, a2,⋯, aNA} and B = {b1, b2; ⋯, bNB} be the coefficients of an IIR filter, and let be the output of the IIR filter applied to ith component of the input signal. More explicitly,
| (9) |
Define a “foreground sequence,” , for channel i, by
| (10) |
where denotes the pth percentile of the set , and oFG is the order of this order statistic filter. A “background sequence” , for channel i, is obtained by decimating, median filtering, then exponentially forgetting the corresponding foreground sequence, as follows:
| (11) |
where n = 0, 1, 2, …, s is an integer decimation factor, oBG is the order of the background median filter, and λ is the exponential forgetting factor. A dimensionless sequence of foreground-to-background ratios is then obtained for each channel as , and the maximum over all N data channels is given by
| (12) |
Detections are signaled whenever the output ratio, Rk, exceeds a threshold level, T, for at least D seconds.
In the generic Osorio-Frei algorithm, the filter given by (A, B) is a 22-coefficient FIR filter (NA = 1, a1 = 1, NB = 22 and the B coefficients are given by the DAUB4 level 3 wavelet), the foreground sequence is the output of a pth percentile filter11 obtained with oFG selected to correspond to 2 s of data, p = 0:50 (i.e., a median filter), oBG and the decimation factor are selected together for computational efficiency to correspond to a 30 minute background median (s = 900 @ 240 Hz, oBG = 480), λ is chosen to obtain a 30 minute half-life in the exponential forgetting, and the generic threshold and duration constraints for detection are T = 22 and D = 0:84 s.
Footnotes
This objective function was derived by examining the Osorio-Frei detection algorithm's architecture with the goal of maximizing the algorithm's output ratio during seizures and minimizing it at all other times.
Some physicians may wish to avoid detections of subclinical seizure activity that is brief in nature (e.g., less than 3 seconds) and instead limit detections to more prolonged activity. This is easily accomplished using an increased duration constraint, D, but this compromises detection speed. If the prolonged activity has different morphology at onset, adaptation of the filter and percentile can be used to preferentially detect the desired activity.
The approach can obviously be extended to IIR filter design methods, which we have found especially useful in detection of very low frequency activity, due to their increased computational efficiency. Our interest in FIR filters stems in part from their inherent stability, which will be an important consideration for future self-adaptive algorithms.
MATLAB Version 5.3.1.29215a (R11.1) on PCWIN. The filter design functions mentioned are found in MATLAB's Signal Processing Toolbox, Version 4.3. See http://www.mathworks.com for complete online documentation.
To compute the filter coefficients for these two variations, the eigenvectors and eigenvalues are obtained by replacing ‘[V,D] = eig(cintcsz)’ with ‘[V,D] = eig(csz)’ and ‘[V,D] = eig(cint\eye(size(cint)))’, respectively, in the code shown for the ratio eigenfilter.
Multiple algorithm detections separated by less than one minute were considered part of the same detection.
For example, adaptations could be performed separately for individual channels and/or seizure types.
Also known as an order statistic filter, rank order filter, or quantile filter.
Conflict of Interest
There are no conflicts of interest to report related to this work.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Osorio I, Frei MG, Wilkinson SB. Real-time automated detection and quantitative analysis of seizures and short-term prediction of clinical onset. Epilepsia. 1998;39(6):615–627. doi: 10.1111/j.1528-1157.1998.tb01430.x. [DOI] [PubMed] [Google Scholar]
- 2.Osorio I, Frei MG, Giftakis J, Peters T, Ingram J, Turnbull M, Herzog M, Rise MT, Schaffner S, Wennberg RA, Walczak TS, Risinger MW, Ajmone-Marsan C. Performance reassessment of a real-time seizure-detection algorithm on long ECoG series. Epilepsia. 2002;43(12):1522–1535. doi: 10.1046/j.1528-1157.2002.11102.x. [DOI] [PubMed] [Google Scholar]
- 3.Daubechies I. Ten Lectures on Wavelets. SIAM; Philadelphia, PA: 1992. [Google Scholar]
- 4.IEEE Press . Programs for Digital Signal Processing. John Wiley & Sons; Piscataway, NJ: 1979. [Google Scholar]
- 5.Proakis JG, Manolakis DG. Digital Signal Processing: Principles, Algorithms, and Applications. 3rd ed. Prentice Hall; Upper Saddle River, NJ: 1996. [Google Scholar]
- 6.Haykin S. Adaptive Filter Theory. 3rd ed. Prentice Hall; Upper Saddle River, NJ: 1996. [Google Scholar]
- 7.Ifeachor EC, Jervis BW. Digital Signal Processing: A Practical Approach. Addison-Wesley Publishers Ltd.; Wokingham, England: 1993. [Google Scholar]
- 8.Gotman J. Automatic recognition of epileptic seizures in the eeg. Electroencephalography and clinical Neurophysiology. 1982;54:530–540. doi: 10.1016/0013-4694(82)90038-4. [DOI] [PubMed] [Google Scholar]
- 9.Qu H, Gotman J. Improvement in seizure detection performance by automatic adaptation to the eeg of each patient. Electroencephalography and clinical europhysiology. 1993;86:79–87. doi: 10.1016/0013-4694(93)90079-b. [DOI] [PubMed] [Google Scholar]