Skip to main content
PMC home page
The Journal of Physiology logoLink to The Journal of Physiology
. 2002 Dec 6;546(Pt 3):931–942. doi: 10.1113/jphysiol.2002.029553

The effect of diazepam on motor cortical oscillations and corticomuscular coherence studied in man

Mark R Baker 1, Stuart N Baker 1
PMCID: PMC2342588  PMID: 12563016

Abstract

EEG recordings from sensorimotor cortex show oscillations around 10 and 20 Hz. These modulate with task performance, and are strongest during periods of steady contraction. The 20 Hz oscillations are coherent with contralateral EMG. Computer modelling suggests that oscillations arising within the cortex may be especially dependent on inhibitory systems. The benzodiazepine diazepam enhances the size of GABAA IPSPs; its effects are reversed by the antagonist flumazenil. We tested the effect of these drugs on spectral measures of EEG and EMG, whilst eight healthy human subjects performed a precision grip task containing both holding and movement phases. Either an auxotonic or isometric load was used. EEG changes following electrical stimulation of the contralateral median nerve were also assessed. The EEG power showed similar changes in all task/stimulation protocols used. Power around 20 Hz doubled at the highest dose of diazepam used (5 mg), and returned to control levels following flumazenil. EEG power at 10 Hz was by contrast little altered. The peak frequency of EEG power in both bands was not changed by diazepam. Corticomuscular coherence at ca 20 Hz was reduced following diazepam injection, but the magnitude of this effect was small (mean coherence during steady holding in the auxotonic task was 0.062 in control recordings, 0.051 after 2.5 mg and 5 mg doses of diazepam). These results imply that 20 Hz oscillations in the sensorimotor cortex are at least partially produced by local cortical circuits reliant on GABAA-mediated intracortical inhibition, whereas 10 Hz rhythms arise by a different mechanism. Rhythms generated during different tasks, or following nerve stimulation, are likely to arise from similar mechanisms. By examining the formulae used to calculate coherence, we show that if cortical oscillations are simply transmitted to the periphery, corticomuscular coherence should increase in parallel with the ratio of EEG to EMG power. The relative constancy of coherence even when the amplitude of cortical oscillations is perturbed suggests that corticomuscular coherence itself may have a functional role in motor control.

Field potential recordings made from the region of the central sulcus often show oscillatory activity. This has two main frequency ranges. Oscillations around 10 Hz may arise partly from the somatosensory cortex (Salmelin & Hari, 1994). Oscillations around 20–30 Hz (‘beta’ band) arise from the primary motor cortex (Murthy & Fetz, 1996; Baker et al. 1997; Donoghue et al. 1998; Kilner et al. 1999). Both bands show a task-dependent modulation. Oscillations are abolished during movements (Pfurtscheller & Neuper, 1992; Stancak & Pfurtscheller, 1996; Baker et al. 1997; Kilner et al. 1999), during motor imagery (Pfurtscheller & Neuper, 1997), and following somatosensory input (Salmelin & Hari, 1994; Salenius et al. 1997b). They are strongest during a steady contraction, especially if this directly follows a movement (Pfurtscheller et al. 1996; Baker et al. 1997; Kilner et al. 1999). There is some debate over whether the oscillations seen under different conditions are reflections of the same, or different, underlying phenomena (Pfurtscheller et al. 1997).

A number of authors have shown significant coherence between a motor cortical recording and the EMG of a contralateral muscle: this can be seen using magnetoencephalography (Conway et al. 1995; Salenius et al. 1997a; Kilner et al. 2000), electroencephalography (Halliday et al. 1998) and local field potential recordings made with a microelectrode (Baker et al. 1997). It is most prominent around 20–30 Hz; coherence close to 10 Hz is normally weak or absent (Conway et al. 1995; Salenius et al. 1997a; Baker et al. 1997; Kilner et al. 2000), although some authors have reported 10 Hz corticomuscular coherence (Marsden et al. 2001; Raethjen et al. 2002). Coherence at higher frequencies around 40 Hz can also be seen, especially during strong contractions (Brown et al. 1998). Corticomusular coherence is probably mediated by fast corticospinal axons and their monosynaptic cortico-motoneuronal connections (Farmer et al. 1993; Conway et al. 1995; Salenius et al. 1997a; Brown et al. 1998). In agreement with this, Baker et al. (2002) have shown that populations of pyramidal tract neurones effectively carry cortical oscillations within their discharge over a wide range of frequencies.

The functional role of cortical oscillations and their coherence with the periphery remain uncertain (for reviews, see Farmer, 1998; Hari & Salenius, 1999; Baker et al. 1999). One possibility was proposed by Kilner et al. (2000). They showed that corticomuscular coherence following a movement depended parametrically on the stiffness of the load. When subjects moved against a spring-like load with weak spring constant, coherence was high; it reduced with stiffer spring constants, and became small when contracting isometrically (equivalent to infinite spring constant). Kilner et al. (2000) proposed that corticomuscular coherence could be important in recalibrating the motor system after a movement; less recalibration might be needed after smaller rather than larger movements.

Several candidate mechanisms have been proposed by which synchronous cortical oscillations could be generated. Gray & McCormick (1996) showed that some pyramidal neurones in visual cortex were capable of spontaneous rhythmic firing due to their intrinsic membrane properties. Oscillations could also occur by resonance around processing loops which incorporate a delay; such loops could involve the thalamus, other cortical areas, subcortical structures, or the spinal cord. Finally, a number of studies have shown that an isolated cortical network can produce stable oscillatory discharge (Traub et al. 1996; Bush & Sejnowski, 1996; Wang & Buzsaki, 1996; Pauluis et al. 1999). In such a system, the inhibitory neurones play a critical role, acting to pace the network by periodically silencing bursts of firing from excitatory cells. In the simulations of Pauluis et al. (1999), the generation of a stable oscillating state was most sensitive to changes in the parameters of inhibition.

In this study, we have used the benzodiazepine diazepam to modify the properties of cortical inhibitory circuits in normal volunteer subjects. The benzodiazepines act on GABAA channels to increase the size of the IPSPs which they generate; their action can be specifically reversed by the antagonist flumazenil. It is well known in clinical practice that benzodiazepines enhance ‘beta band’ oscillatory activity in EEG recorded from the frontal cortex (e.g. Lindhardt et al. 2001). We investigated this further using the same motor tasks as in Kilner et al. (2000). We also measured the abolition and subsequent ‘rebound’ in oscillations following contralateral electrical stimulation of the median nerve (Salenius et al. 1997b). We show that diazepam has a selective effect on the amplitude of EEG oscillations around 20 Hz, but no effect on those at 10 Hz. Furthermore, following diazepam, corticomuscular coherence was either unchanged or slightly reduced. Consistent results were seen in both tasks studied, and following median nerve stimulation. These results have implications both for the mechanism underlying the generation of these rhythms, and for the functional role of oscillatory activity in motor control.

Methods

Experiments were conducted on 12 young adult subjects (two female), drawn from staff and students working in the department. One subject withdrew from the study due to a minor recognised side effect of diazepam, and three subjects showed no corticomuscular coherence around 20 Hz in the control recordings. Data are reported from the remaining eight subjects. All procedures were approved by the Local Ethical Committee, and written informed consent was obtained from each subject prior to commencing the experiment in accordance with the Declaration of Helsinki. Drugs were prescribed and administered by one of the authors who is a qualified physician (M.R.B.). All drug doses were within the range routinely used in clinical practice.

Recordings

Bipolar recordings of EMG from the right arm were made using adhesive surface electrodes (Biotrace 0713C, MSB Ltd, Marlborough, UK). Muscles recorded were first dorsal interosseous (1DI), abductor pollicis brevis (AbPB), abductor digiti minimi (AbDM), flexor digitorum superficialis (FDS) and extensor digitorum communis (EDC). EEG from left sensorimotor cortex was recorded differentially from two electrodes (Neuroline 720 00-S, Medicotest Ltd, Ølstykke, Denmark) placed 30 mm lateral to the midline and 20 mm anterior and posterior to the interaural line. Signals were amplified (gain 500–5000, EMG; 20 000–50 000, EEG) and filtered (bandpass 30 Hz-2 kHz, EMG; 3 Hz-2 kHz, EEG) before being digitised at 5681.8 Hz using a Power1401 interface (Cambridge Electronic Design Ltd, Cambridge, UK) connected to a PC running Spike2 software (Cambridge Electronic Design Ltd).

Task and experimental protocol

Subjects performed two different motor tasks. Both required them to squeeze two levers between the finger and thumb of the right hand using a precision grip. In the auxotonic task, the levers were free to move, but movement was opposed by springs. Lever displacement was monitored using potentiometers. An initial force of 1 N was required to move each lever from its end stop. Thereafter, movements were against a spring constant of 0.025 N mm−1. Subjects were required to move the levers to maintain cursors, representing the lever position, within target boxes on a computer screen. Targets first appeared at a location representing 12 mm displacement, and the subject made a rapid movement into target from rest. They held the levers at this displacement for 3 s (Hold 1 phase), before tracking a linear ramp increase in displacement to 24 mm over 2 s (Ramp phase). They then held at this new displacement for a further 3 s (Hold 2 phase), before releasing the levers. This is identical to the ‘COMP1′ task of Kilner et al. (2000).

In the isometric task, the levers were locked into place, and the cursors on the computer screen displayed force exerted on the levers, which was measured with strain gauges. The force display was low-pass filtered at 3 Hz to prevent tremor affecting the cursor display. Subjects were required to produce the same Hold-Ramp-Hold profile of force as they had generated during the auxotonic task (Hold 1, 1.3 N; Hold 2, 1.6 N). This is the ‘ISO’ task of Kilner et al. (2000).

Recordings were also made during electrical stimulation of the median nerve. Adhesive electrodes were placed over the median nerve at the wrist, and electrical stimuli (constant current, 0.2 ms pulse width, cathode proximal) were given using a Digitimer DS7 stimulator (Digitimer, Welwyn Garden City, UK). The intensity was chosen to be just above the motor threshold, as judged from the appearance of a small but consistent M-wave in the EMG recorded from the thenar muscles. Stimuli were given every 5 s whilst the subject relaxed.

Subjects were prepared for EEG and EMG recording as described above, and an intravenous catheter was inserted into a vein on the dorsum of the left hand. An order of the three experiments (auxotonic, isometric task and median nerve stimulation) was then determined at random; the same order was used subsequently in all recordings from that subject. Fifty trials of each task, and 50 responses to nerve stimulation, were recorded in each condition. A control dataset was firstly recorded prior to drug administration. Two 2.5 mg doses of diazepam (Diazemuls, Dumex-Alpharma, Copenhagen, Denmark) were then given intravenously (total dose 5 mg), followed by two 150 µg doses of flumazenil (Anexate, Roche; total dose 300 µg). Twenty seconds following the onset of each intravenous injection, recordings began. A complete dataset (auxotonic and isometric tasks, and median nerve stimulation) was recorded following administration of each drug dose. Subjects often reported considerable drowsiness at the highest level of diazepam used; this was usually completely reversed by the end of the experiment.

Analysis

Lever position and force traces were firstly examined by eye, and trials where the subject had failed to perform the task correctly were excluded from subsequent analysis. EMGs were full-wave rectified prior to analysis. A time-frequency representation of each signal was computed using a wavelet method:

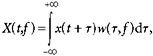graphic file with name tjp0546-0931-m1.jpg (1)

where t is time relative to the onset of a trial, x(t) is the original signal, X(t, f) is the time-frequency representation and w(t) is a complex Gabor function given by:

graphic file with name tjp0546-0931-m2.jpg (2)

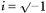where Inline graphic. A value of σ =0.128 s was used, which determined the amount of temporal smoothing of the analysis, and also the range of frequencies to which a given measurement was sensitive. We estimated numerically that using this value of σ, the measures were sensitive to a 2.5 Hz range of frequencies centred on f (i.e. 95 % of the power of w was within f ± 1.25 Hz). Measures separated by 2.5 Hz will therefore be approximately independent. We calculated all measures on a grid with 1.25 Hz spacing for improved clarity of display, from 1.25–50 Hz. Note that a wavelet analysis of this kind is equivalent to a more usual discrete Fourier transform based approach using a Gaussian window.

The power of a signal as a function of time and frequency was calculated as:

graphic file with name tjp0546-0931-m3.jpg (3)

where the index j refers to the jth trial out of N analysed and * indicates complex conjugation.

The coherence between two signals was calculated as:

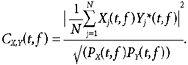graphic file with name tjp0546-0931-m4.jpg (4)

Coherence was considered significant (P < 0.05) if it exceeded C0.05, given by:

graphic file with name tjp0546-0931-m5.jpg (5)

This formula was given by Rosenberg et al. (1989) for Fourier transform based coherence calculations. We investigated whether this significance level is also valid for wavelet coherence analysis, using numerical simulation as follows. Wavelet coherence at a single frequency was calculated between two pseudo-random signals, generated to be normally distributed and independent. Ten thousand independent coherence estimates were determined, and how many exceeded the value given by eqn (5) determined. Using values of N (number of trials) between 10 and 100 in steps of 10, between 4.84 and 5.44 % of the coherence estimates between these random, unrelated signals exceeded the theoretical significance limit, confirming that eqn (5) also provides an appropriate significance level for wavelet coherence analysis at P < 0.05.

The absolute level of power in either EEG or EMG has little meaning, since it will depend on such uncontrolled factors as precise electrode placement relative to muscle or cortical generators. Accordingly, power was expressed relative to the average total power seen in the control recordings before administration of drugs:

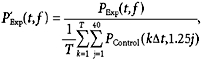graphic file with name tjp0546-0931-m6.jpg (6)

where P ‘indicates the normalised power and Δt represents the sampling period of the data.

To produce results which combined data from all experiments, EEG time-frequency relative power maps were averaged across subjects; EMG maps were averaged across subjects and the five muscles recorded from. EEG-EMG coherence maps were first transformed following Rosenberg et al. (1989) according to:

graphic file with name tjp0546-0931-m7.jpg (7)

If there is no coherence between the two signals, Z should be approximately normally distributed, with a standard deviation of 1 and a mean which will depend on the number of trials N (Benignus, 1969). We estimated this bias by averaging Z over all times t and between frequencies f = 45–50 Hz, a range with no significant coherence in any of our recordings. The bias was then subtracted from Z, to yield values which should be approximately normally distributed, with zero mean and unit variance, on the null hypothesis of no coherence between the two signals. Z-scores were combined across subjects and across muscles according to:

graphic file with name tjp0546-0931-m8.jpg (8)

These values should also be normally distributed with zero mean and unit variance on the null hypothesis.

All analysis was performed using custom written routines in the MATLAB (Mathworks Inc.) environment.

Results

Auxotonic task

Figure 1 shows results combined across eight subjects for the auxotonic task. Each column of this figure presents data for a different measurement: EEG power, EMG power, or EEG-EMG coherence. In Fig. 1B, each row shows data for a different drug condition through the experiment. All plots in this figure share a common time scale; the schematic illustrations of the lever position target levels in Fig. 1C show how this timescale relates to the different phases of task performance. The top row of Fig. 1B presents the results for the control recordings before drug administration. The EEG power in these control recordings showed peaks at multiple frequencies. The peak at 50 Hz reflects contamination at mains line frequency; the high power at very low frequencies probably reflects slow movement related potentials, and should be considered unreliable as it falls outside the region of flat bandpass of the amplifier. There was also a peak in EEG power at 10 Hz, and around 20 Hz; these represent oscillatory activity in the cortex underlying the recording electrodes. The power at ca 20 Hz reduced during the Ramp phase of the task; following this, there was a rebound so that ca 20 Hz power was transiently stronger in Hold 2 than it was during Hold 1. The 10 Hz power diminished slightly during the movement of the Ramp phase, and then showed a considerable increase during Hold 2. These task-dependent changes in the control data are shown more clearly in Fig. 1A, which plots the average of a given power band as a function of time (black, 10 Hz; red, 20 Hz; lines to the right of the control colour maps in Fig. 1B mark the bands used).

Figure 1. Auxotonic task.

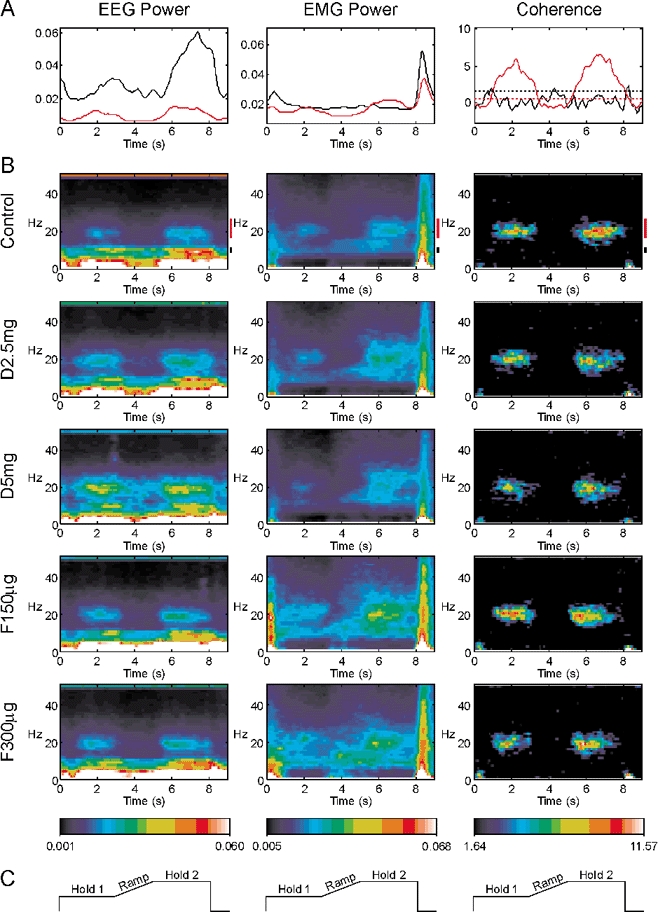
Figure 1

Open in a new tab

Each column presents a different measure: EEG power, EMG power or EEG-EMG coherence. Measures have been summed across all eight subjects recorded from, and across the five muscles recorded from (for EMG power and coherence). A, modulation of the power or coherence with task performance during the control experiment (before drug administration). Time is relative to the trial onset. The black line is for 8.75–11.25 Hz band, the red line for 17.5–27.5 Hz. Dotted lines in the coherence graph show the significance levels for each plot (P < 0.05). B, modulation of each measurement is shown as a function of both frequency and time, using the colour scale at the bottom of the figure. Each row shows the results for successive experiments with different drug dosages. Control, before drug administration; D2.5 mg, diazepam 2.5 mg; D5 mg, diazepam 5 mg; F150 µg, flumazenil 150 µg; F300 µg, flumazenil 300 µg. Black and red bars to the right of the control displays indicate the frequencies averaged to form the plots in A. C, schematic of lever target positions, in the same time frame as A and B.

The middle column of Fig. 1 shows the modulation of EMG power with task; this has been summed across all eight subjects and the five muscles per subject recorded from. The control data (top row of Fig. 1B) showed peaks in power over a wide range of frequencies at the onset and offset of each trial, corresponding to the phasic movements involved in gripping and releasing of the levers, respectively. There were also peaks in power at both 10 and 20 Hz. There was little modulation of the 10 Hz band with task performance; by contrast, the 20 Hz band showed considerable task dependence. Like the EEG power, it exhibited both a marked reduction during the Ramp phase of the task and a subsequent rebound to an elevated level during Hold 2. These changes can be clearly seen in the plot of power time course in Fig. 1A.

The right column of Fig. 1 shows the modulation of EEG-EMG coherence with task (expressed as a Z score summed across subjects and muscles as described in Methods). The colour scale of the time-frequency map has been chosen so that non-significant values of coherence will appear black. As previously observed, there was no significant coherence around 10 Hz, even though both EEG and EMG showed power in this band. Coherence was restricted to frequencies close to 20 Hz. As with EEG and EMG power, coherence was reduced during the Ramp phase of the task, and rebounded during Hold 2. The plot of Fig. 1A (right panel) shows this more clearly. The dotted lines in this plot are the relevant significance levels for each band; they are different since a different number of frequency bins were averaged for the ca 10 Hz compared to the ca 20 Hz band.

In the control data, the task-dependent modulation of the EEG and EMG power, the coherence between EEG and EMG, and the frequencies at which peaks are observed are all in agreement with the previous work of Kilner et al. (2000) using this task. However, by comparing the different rows of Fig. 1B, it is possible to see what effect increasing the efficacy of cortical inhibitory circuits has on this oscillatory activity.

Surprisingly, only one of the available measures showed an obvious change following drug administration. With increasing doses of diazepam (D2.5 mg, D5 mg), the proportion of the EEG power at 20 Hz increased during both the Hold 1 and Hold 2 phase of the task.

This effect was reversed as the actions of the diazepam were antagonised by increasing doses of flumazenil (F150 µg, F300 µg). However, the EEG power at 10 Hz, the EMG power at 10 and 20 Hz and the EEG-EMG coherence at 20 Hz showed no systematic changes with increasing doses of diazepam.

Figure 2 presents a statistical analysis of the findings shown graphically in Fig. 1. Figure 2A shows the results for the 10 Hz band of EEG power. The 10 Hz frequency bin was averaged for a 1 s period during the Hold 1, Ramp and Hold 2 phases of the task for each subject. The power in the Ramp and Hold 2 phases was 78 ± 5 % and 136 ± 15 % of that in Hold 1, respectively (mean ± s.e.m.). In Fig. 2A, the values for power have been expressed as a ratio of those seen in the control recordings during the same part of the task. The histogram bars show the mean ratios seen across all eight subjects; the error bars give the standard error of the mean. The 10 Hz power during Ramp was significantly reduced following 5 mg diazepam relative to control (P < 0.05, paired t test); the power was reduced to 72 % of the control level.

Figure 2. Comparison of different measures following successive drug doses with the same measures made during the control experiment, for the auxotonic task.

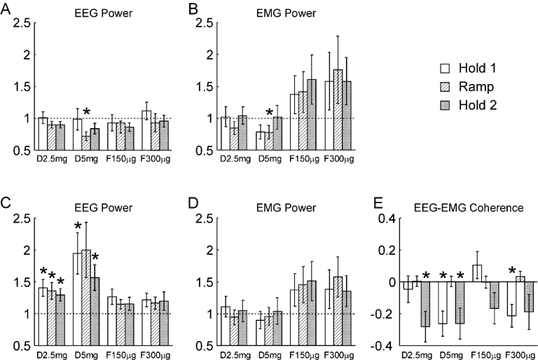
Figure 2

Open in a new tab

A and B refer to the 8.75–11.25 Hz band, C-E to the 17.5–27.5 Hz band. A and C, the EEG power; B and D, the EMG power. Power has been expressed relative to that seen in the control experiment; a ratio of one (dotted line) would indicate no change. E, EEG-EMG coherence, expressed as a difference between the Z-transformed values following drug administration and the control. Different shading indicates measurements made during the three phases of the task, according to the key at the top right of the figure. Labels D2.5 mg, etc. indicate different drug doses (see legend to Fig. 1). Error bars show 1 standard error of the mean; asterisks indicate a measure significantly different from that during the control period (P < 0.05). Analysis was across n = 8 subjects for A and C, n = 40 subjects and muscles for B, D and E.

Figure 2B shows a similar analysis for the EMG power at 10 Hz. Once again, the only significant effect was a slight reduction in the power with the largest diazepam dose tested during the Ramp phase, to 78 % of the control value.

Figure 2C shows how the EEG power around 20 Hz varied with the drug doses used. In this case, and for Fig. 2D and E, the seven frequency bins from 17.5–27.5 Hz have been averaged at each point of the task, since the peak was relatively broad. The power in the Ramp and Hold 2 task phases was 67 ± 7 % and 122 ± 9 % of the Hold 1 value, respectively (mean ± s.e.m.). In the figure, all values have once again been expressed relative to those seen in the control recordings at that task phase. There was clearly a substantial effect of diazepam on ca 20 Hz power, with 5/6 of the measurements following diazepam administration significantly different from the control. At the largest dose used, the EEG power in this band was approximately doubled in the Hold 1 and Ramp phases. The effective reversal of this increase in power by flumazenil provides confidence that this is a genuine pharmacological effect, and not due for example to increased practice on the task or subject fatigue.

Figure 2D shows the changes in EMG power within the ca 20 Hz band. There is a trend for the power to rise towards the end of the experiment, which was also seen for the data from the 10 Hz band. However, no measurements were significantly different from control.

Figure 2E shows how the EEG-EMG coherence at ca 20 Hz varies with drug dose. In this case, the values have been expressed as a difference of the Z-scores from the control measurements. There was a reduction in coherence following diazepam administration, which reached significance for Hold 2 at a dose of 2.5 mg diazepam, and both Hold 1 and Hold 2 at the 5 mg diazepam. However, these effects were small; for example, the mean coherence in the Hold 2 period was 0.062 during the control experiment, and 0.051 at both low and high diazepam doses. Effects did not completely reverse following flumazenil administration, and the coherence during Hold 1 in the final set of measurements was still significantly lower than during the control recordings. This may indicate that some of these changes were more due to fatigue or practice than pharmacological actions.

It was of interest to determine whether the drugs administered had any effect on the frequency of the peaks in the EEG power. The wavelet based analysis presented above was not suitable to investigate this, since it had poor frequency resolution. We therefore calculated conventional power spectra of the EEG using a 2 s window of data commencing 5 s into the task; this corresponded to the Hold 2 period, and was chosen since the power peaks are strongest during this time as assessed from the wavelet analysis. The results are shown in Fig. 3, which plots the proportion of power at different frequencies for each drug dose; this has been averaged across all eight subjects. There was no consistent change in the frequency of the peaks around 10 or 20 Hz. When peak frequency in each band was measured individually for each subject, there was no significant change from the control values following any drug dose tested (Wilcoxon signed rank test, n = 8, P > 0.05). Similar results were obtained using data from the Hold 1 or Ramp phases of the task.

Figure 3. EEG power spectra with high frequency resolution calculated over the Hold 2 period of the auxotonic task.

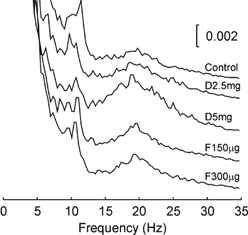
Figure 3

Open in a new tab

Power is expressed as a fraction of the total power at all frequencies, and is averaged across eight subjects. Each trace shows the result following a different drug dose, using the same labelling as in Fig. 1.

Isometric task

Figure 4 shows the results for the isometric task, in a similar format to Fig. 1. Both EEG and EMG power showed peaks at 10 and 20 Hz, as with the auxotonic task. However, the modulation with task was not so pronounced - for example, the EEG power at 20 Hz in the control recordings during the Ramp and Hold 2 phases was 86 ± 5 % and 98 ± 7 % of the Hold 1 value, respectively, compared to 67 ± 7 % and 122 ± 9 % in the auxotonic task (mean ± s.e.m., measured as described above for Fig. 2). The EEG-EMG coherence was confined to frequencies around 20 Hz, but it was much weaker than that observed in the auxotonic task (mean coherence during Hold 2 control recording 0.033, compared to 0.062 in auxotonic task). The coherence was not enhanced in Hold 2 compared to Hold 1, in contrast to the auxotonic task. These findings replicated those of Kilner et al. (2000). Once again, the only consistent change following the drug administration evident from this display was an increase in EEG power in the 20 Hz band.

Figure 4. Modulation of different measures with task performance during the isometric task.

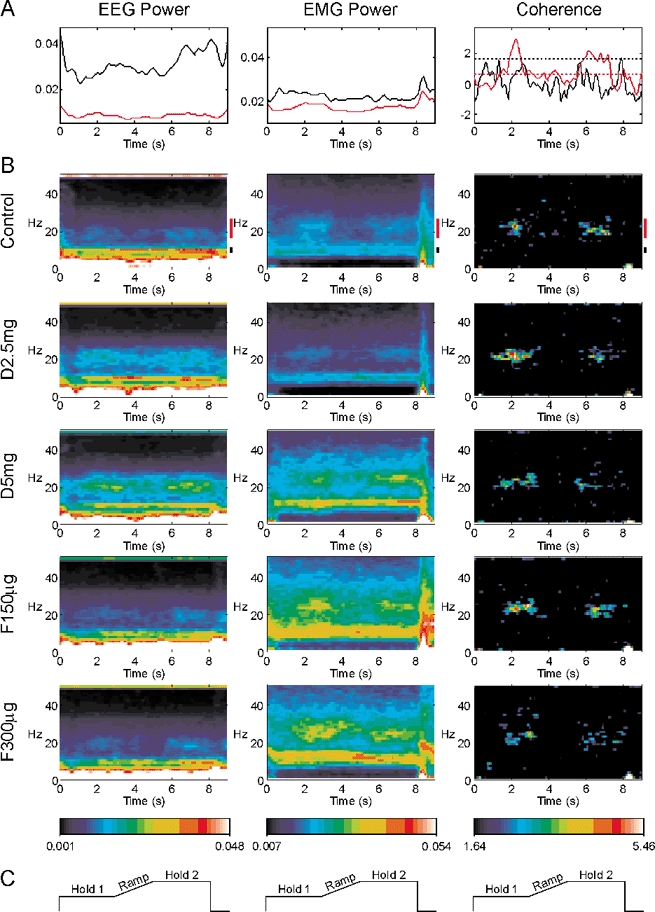
Figure 4

Open in a new tab

Display conventions as in Fig. 2. A, time course of 8.75–11.25 Hz band (black lines) and 17.5–27.5 Hz band (red lines) during the control experiment. B, time-frequency representation of each measurement. Different rows indicate results after each drug administration. C, schematic lever position target for orientation to the time scale, which is the same for all plots in the figure.

Figure 5 presents the statistical analysis of the data from the isometric task. The results were similar to those with the auxotonic task. The EEG power at 10 Hz declined slightly after diazepam administration; this reached significance only at the highest dose during Hold 2. The EEG power in the ca 20 Hz band was raised by diazepam. This reached significance during the Hold 2 period for both the low and high doses of diazepam used, and following the first dose of flumazenil. However, high inter-subject variability prevented the effects reaching statistical significance during other periods of the task. At the maximum dose of diazepam used, the EEG power around 20 Hz was approximately doubled, a quantitatively similar finding to that with the auxotonic task. There was no significant modulation of the EMG power in either band, although there was a clear trend for power to increase towards the end of the experiment, as in the auxotonic task. Figure 5E shows the changes in EEG-EMG coherence seen; only one measurement reached statistical significance, and this was following a dose of flumazenil, suggesting that as with the auxotonic task the effect may have been caused by fatigue or practice rather than a pharmacological action. The change in coherence in this case was small (mean coherence 0.020 compared with 0.024 for the control data).

Figure 5. Comparison between the measurements made following drug administration with those from the control experiment, for the isometric task.

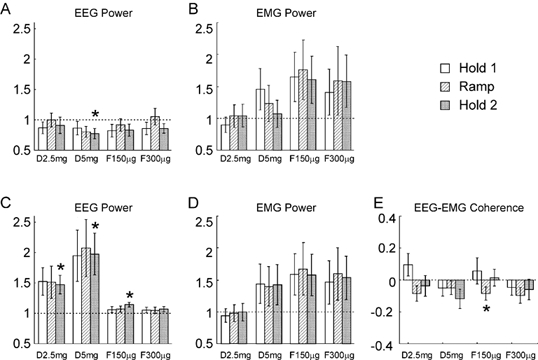
Figure 5

Open in a new tab

A and B refer to the 8.75–11.25 Hz band, C-E to the 17.5–27.5 Hz band. A and C, the EEG power, B and D, the EMG power, E, EEG-EMG coherence. Display conventions as in Fig. 2.

Median nerve stimulation

Median nerve stimulation produced a large stimulus artefact in the EMG recordings; this was followed by an M-wave in the AbPB recordings. These contaminants meant that it was unreliable to analyse either EMG power or EEG-EMG coherence, and accordingly results are only presented for the EEG power. Figure 6A and B shows the time course of 10 Hz (Fig. 6A) and ca 20 Hz (Fig. 6B) power in the EEG relative to a median nerve stimulus delivered at time 0 s, for the control recordings. These plots show the power averaged across all eight subjects recorded from. As has been previously reported, there was a desynchronisation immediately after the stimulus, which was followed by a rebound in power. The duration of the desynchronisation was slightly longer for the 10 Hz than for the 20 Hz bands.

Figure 6.

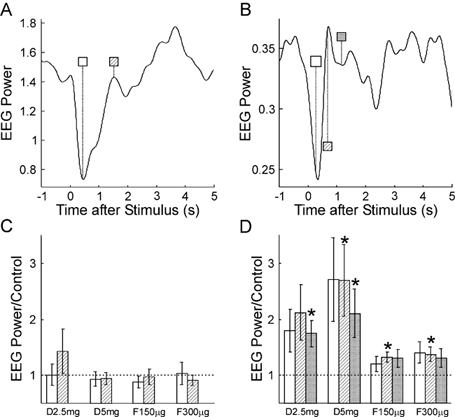
Figure 6

Open in a new tab

A and B, time course of EEG power in the 8.75–11.25 Hz and 17.5–27.5 Hz bands, respectively, following median nerve stimulation (time 0 s), in the control experiment prior to drug administration. Measurements have been averaged over 8 subjects. C and D, EEG power at different times post-stimulus following each drug dose, relative to that seen in the control experiment. The shading of the bars indicates the post-stimulus time used, and is the same as that used in the time markers in A and B. Dotted line indicates a ratio of 1, which is expected if there is no change from the control. Error bars show 1 standard error of the mean; asterisks mark a significant change from the control (P < 0.05).

Figure 6C and D shows the effect of drug administration on the power at selected times after the nerve stimulus. The times chosen have been marked on Fig. 6A and B; the shading of the markers there corresponds to the shading of the histogram bins in Fig. 6C and D. As in Fig. 2 and Fig. 5, power has been expressed relative to that seen in the control recordings. For the 10 Hz band, no significant changes were seen with drug administration. In the 20 Hz band, power at all three times after the stimulus rose with increasing dose of diazepam; this was significant for 3/6 measurements. The greatest increase was 2.69 times the control level. Power at ca 20 Hz remained slightly elevated when the effects of the diazepam were antagonised by flumazenil, and 2/6 of these measurements were significantly different from the control power levels.

Discussion

In this report, we have shown that a benzodiazepine known to enhance GABAA-mediated inhibition does affect electrophysiological measures of cortical activity during a behavioural task. The greatest change seen was in EEG power around 20 Hz; this could be more than doubled at the highest diazepam dose which we used. However, other measures often failed to show any significant changes, and in those cases where significant effects were seen, they were weak. These results have implications both for our understanding of the mechanisms which generate cortical oscillations, and for the functional role which they might play.

Mechanisms of generation of cortical oscillations

There are a number of candidate mechanisms which could produce oscillatory activity in cortical neurones. Some cortical cells have intrinsic membrane conductances biasing them towards firing at certain frequencies (Gray & McCormick, 1996). Oscillations could occur by reverberation around long-distance feedback loops which have a conduction delay. Finally, cortical circuits could generate oscillations as an emergent network property arising from their local circuit connectivity (Traub et al. 1996; Bush & Sejnowski, 1996; Wang & Buzsaki, 1996; Pauluis et al. 1999). There is no reason why these mechanisms should be mutually exclusive.

The modelling study of Pauluis et al. (1999) investigated how local cortical circuits produced oscillations. They showed that the inhibitory interneurones played a key role: the more inhibitory connections which were included, the stronger oscillations became. The oscillation frequency depended on parameters which modified the time course of inhibition; longer duration inhibitory post-synaptic currents (IPSCs) produced lower frequency oscillations. The data reported here for the ca 20 Hz band agree with the predictions which these simulations make, given the known actions of diazepam on cortical inhibitory synapses. Fluctuation analysis of intracellular recordings (Study & Barker, 1981) have shown that diazepam increases the probability of opening of the GABAA receptor, which leads to larger amplitude IPSCs. The predicted consequent rise in the amplitude of oscillations was clearly seen in our EEG data (Figs 2, 5 and 6). By contrast, the opening time of GABAA channels is only slightly affected, if at all, by diazepam (Study & Barker, 1981). The oscillation peak frequency remained stable at all drug doses tested (Fig. 3), which would be expected if the duration of the IPSCs is not changed (Pauluis et al. 1999). Our present results therefore support the hypothesis that local cortical circuits generate ca 20 Hz rhythmicity in the motor cortex. It is not possible to exclude an additional contribution by other mechanisms.

A very different result was seen for the ca 10 Hz oscillations. If anything, diazepam slightly reduced EEG power at 10 Hz; this only reached significance for the Ramp period in the auxotonic task and the Hold 2 period for the isometric task at the highest dose used (5 mg). Interestingly, there was also a significant reduction at this dose in the EMG 10 Hz power during the Ramp period of the auxotonic task. Diazepam has been used with some success clinically in the treatment of tremor (see Elble & Koller, 1990 for review); the mechanism by which it has this effect is not known. One possible explanation for our results is that diazepam reduced tremor around 10 Hz. The smaller EEG power at 10 Hz could then reflect the sensory sequelae of the reduced peripheral oscillation. This interpretation would be consistent with the claimed origin of the 10 Hz rhythm within the somatosensory rather than motor cortex (Salmelin & Hari, 1994). However, whether or not this interpretation is correct, the present results show that the 10 Hz rhythm is probably not generated by cortical local circuit interactions dependent on GABAA, as simulated by Pauluis et al. (1999).

It has previously been suggested that there may be more than one source of ca 20 Hz oscillations in the motor cortex (Pfurtscheller et al. 1997). In the present experiments, cortical oscillations were studied under a variety of conditions, such as different loads (auxotonic and isometric contractions), different task phases (steady holding or movement), and also following electrical stimulation of the contralateral median nerve. The broad similarity of the findings across these different conditions implies that the oscillations recorded in each case are generated by similar mechanisms.

Function of oscillations and corticomuscular coherence

A surprising finding of the present study was that doses of diazepam sufficient to double the power at ca 20 Hz in the EEG did not have great effects on corticomuscular coherence at this frequency. There was a significant reduction of coherence in the auxotonic task following diazepam administration, but the size of this decrease in coherence was small. A significantly reduced coherence was also seen after the benzodiazepine was almost completely antagonised with flumazenil. It is possible that the changes in coherence are a genuine pharmacological effect, and their persistence after flumazenil is due to the reversal of the diazepam actions not being complete. However, it is perhaps more likely that these small decreases in coherence result from a change in an uncontrolled variable over the course of the relatively long experiment, such as the subjects’ attention, fatigue, or practice in performing the task.

Coherence is a measure of correlation which is normalised for the amplitude of the two signals correlated. Careful examination of the formula used to calculate coherence can provide insight into the current result. Suppose that ca 20 Hz oscillations in the motor cortex performed a computational function within the cortex, akin to the ‘binding’ role proposed for 40 Hz oscillations in the visual cortex (Singer & Gray, 1995). In this case, corticomuscular coherence would simply be a ‘spill over’ effect, representing the unavoidable spreading of an essentially cortical phenomenon to the periphery. Let c represent the cortical oscillations recorded by the EEG, and m the EMG. Then a ‘spill over’ model would imply:

graphic file with name tjp0546-0931-m9.jpg (9)

where k is a constant and s is a source of input to the motoneurones uncorrelated with c. This assumes that a constant proportion of the oscillatory activity in the cortex recorded by the EEG is transmitted down the corticospinal tract to the motoneurones. This is a reasonable assumption, since the corticospinal neurones are embedded in the cortical network generating oscillations (Baker et al. 1997; Jackson et al. 2002; Baker et al. 2002). It has been shown that a small population of corticospinal cells could transmit the oscillations recorded in field potential measures with high fidelity (Baker et al. 2002).

Using capitalisation to indicate the Fourier transform, and E (•) for the expectation operator, the coherence between EEG and EMG is then:

graphic file with name tjp0546-0931-m10.jpg (10)

Hence if corticomuscular coherence is just an epiphenomenon of cortical rhythmicity, corticomuscular coherence should change as the ratio of EEG to EMG power. Careful examination of the present data shows that this was not the case. Using the auxotonic task, EEG power around 20 Hz was doubled at the maximum dose of diazepam used (Fig. 2C), whereas EMG power in this band was not significantly changed (Fig. 2D). Far from doubling, the coherence was actually reduced (Fig. 2E), albeit only slightly. Following flumazenil administration, the EMG power was systematically elevated, although in no case did this reach significance, whereas the EEG power was restored to close to baseline levels. The coherence was only slightly reduced in one of the six measurements made.

In the isometric task, examination of the EEG and EMG power changes shown in Fig. 5C and D suggests that the corticomuscular coherence should firstly have been increased by around 50 % after the initial dose of diazepam, and then reduced by around 30 % compared with the control recordings after flumazenil. In fact, only one coherence measurement showed a significant change (Fig. 5E), and this was small.

The assumption of eqn (9) cannot therefore be valid. Either the fraction of oscillatory activity transmitted by the corticospinal tract must vary, or the response of the spinal circuitry to this input changes. The result is to maintain coherence nearly constant.

The emphasis of previous work has been that oscillatory motoneurone activity is simply driven by rhythmic corticospinal inputs from the motor cortex, as implied by eqn (9). The phase difference between cortical recordings and EMG should then be consistent with a simple conduction delay, of similar size to known corticospinal conduction time. Some studies have produced evidence that this is the case (Salenius et al. 1997a; Brown et al. 1998; Gross et al. 2000); however, others have found that corticomuscular phase estimates do not behave as expected for a conduction delay (Halliday et al. 1998), or that they are highly variable between different parts of the same experiment (E.M. Pinches, S.N. Baker and R.N. Lemon, unpublished observations). The latter findings would be expected if the spinal response to oscillatory inputs is more complex than implied by eqn (9).

Taken on their own, our results could imply that mechanisms exist to fix corticomuscular coherence at a given value. However, Kilner et al. (2000) have shown that the size of corticomuscular coherence varies in a parametric manner according to the compliance of the load gripped. We replicated the results of Kilner et al. (2000), by showing that coherence was substantially lower in the isometric than auxotonic task (compare Fig. 1 and Fig. 4). Corticomuscular coherence is not therefore simply maintained at a constant preset level; instead it is task specific. It is this, task specific, value of coherence which is then maintained constant in the face of changes in cortical activity which otherwise might be expected to alter it. This suggests that the corticomuscular coherence itself is of functional relevance, rather than the oscillations in the cortex per se. One interpretation of our current findings is therefore that ca 20 Hz rhythmicity in the primate motor system does not have a role in purely cortical processing, but rather mediates some form of sensorimotor integration between the cortex and the periphery of which coherence is, fortuitously, the appropriate measure. The exact nature of this process remains to be elucidated.

Acknowledgments

The authors wish to thank Kyle Mitchell for assistance with the experiments, and all the volunteers who gave their time as subjects. Funded by The Wellcome Trust.

References

  1. Baker SN, Kilner JM, Pinches EM, Lemon RN. The role of synchrony and oscillations in the motor output. Exp Brain Res. 1999;128:109–117. doi: 10.1007/s002210050825. [DOI] [PubMed] [Google Scholar]
  2. Baker SN, Olivier E, Lemon RN. Coherent oscillations in monkey motor cortex and hand muscle EMG show task dependent modulation. J Physiol. 1997;501:225–241. doi: 10.1111/j.1469-7793.1997.225bo.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Baker SN, Pinches EM, Lemon RN. Synchronization in monkey motor cortex during a precision grip task. II. Effect of oscillatory activity on corticospinal output. J Neurophysiol. 2002. in the Press. [DOI] [PubMed]
  4. Benignus VA. Estimation of the coherence spectrum and its confidence interval using the fast fourier transform. IEEE Trans Acoust Speech Signal Proc. 1969;17:145–150. [Google Scholar]
  5. Brown P, Salenius S, Rothwell JC, Hari R. Cortical correlate of the Piper rhythm in humans. J Neurophysiol. 1998;80:2911–2917. doi: 10.1152/jn.1998.80.6.2911. [DOI] [PubMed] [Google Scholar]
  6. Bush P, Sejnowski T. Inhibition synchronizes sparsely connected cortical neurons within and between columns in realistic network models. J Comput Neurosci. 1996;3:91–110. doi: 10.1007/BF00160806. [DOI] [PubMed] [Google Scholar]
  7. Conway BA, Halliday DM, Farmer SF, Shahani U, Maas P, Weir AL, Rosenberg JR. Synchronization between motor cortex and spinal motoneuronal pool during the performance of a maintained motor task in man. J Physiol. 1995;489:917–924. doi: 10.1113/jphysiol.1995.sp021104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Donoghue JP, Sanes JN, Hatsopoulos NG, Gaal G. Neural discharge and local field potential oscillations in primate motor cortex during voluntary movements. J Neurophysiol. 1998;79:159–173. doi: 10.1152/jn.1998.79.1.159. [DOI] [PubMed] [Google Scholar]
  9. Elble RJ, Koller WC. Tremor. Baltimore: John Hopkins University Press; 1990. [Google Scholar]
  10. Farmer SF. Rhythmicity, synchronization and binding in human and primate motor systems. J Physiol. 1998;509:3–14. doi: 10.1111/j.1469-7793.1998.003bo.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Farmer SF, Bremner FD, Halliday DM, Rosenberg JR, Stephens JA. The frequency content of common synaptic inputs to motoneurones studied during voluntary isometric contraction in man. J Physiol. 1993;470:127–155. doi: 10.1113/jphysiol.1993.sp019851. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Gray CM, McCormick DA. Chattering cells: superficial pyramidal neurons contributing to the generation of synchronous oscillations in the visual cortex. Science. 1996;274:109–113. doi: 10.1126/science.274.5284.109. [DOI] [PubMed] [Google Scholar]
  13. Gross J, Tass PA, Salenius S, Hari R, Freund HJ, Schnitzler A. Cortico-muscular synchronization during isometric muscle contraction in humans as revealed by magnetoencephalography. J Physiol. 2000;527:623–631. doi: 10.1111/j.1469-7793.2000.00623.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Halliday DM, Conway BA, Farmer SF, Rosenberg JR. Using electroencephalography to study functional coupling between cortical activity and electromyograms during voluntary contractions in humans. Neurosci Lett. 1998;241:5–8. doi: 10.1016/s0304-3940(97)00964-6. [DOI] [PubMed] [Google Scholar]
  15. Hari R, Salenius S. Rhythmical corticomuscular communication. NeuroReport. 1999;10:1–10. [PubMed] [Google Scholar]
  16. Jackson A, Spinks RL, Freeman TC, Wolpert DM, Lemon RN. Rhythm generation in monkey motor cortex explored using pyramidal tract stimulation. J Physiol. 2002;541:685–699. doi: 10.1113/jphysiol.2001.015099. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Kilner JM, Baker SN, Salenius S, Hari R, Lemon RN. Human cortical muscle coherence is directly related to specific motor parameters. J Neurosci. 2000;20:8838–8845. doi: 10.1523/JNEUROSCI.20-23-08838.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kilner JM, Baker SN, Salenius S, Jousmäki V, Hari R, Lemon RN. Task-dependent modulation of 20–30 Hz coherence between rectified EMGs from human hand and forearm muscles. J Physiol. 1999;516:559–570. doi: 10.1111/j.1469-7793.1999.0559v.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Lindhardt K, Gizurarson S, Stefansson SB, Olafsson DR, Bechgaard E. Electroencephalographic effects and serum concentrations after intranasal and intravenous administration of diazepam to healthy volunteers. Br J Clin Pharmacol. 2001;52:521–527. doi: 10.1046/j.0306-5251.2001.01486.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Marsden JF, Brown P, Salenius S. Involvement of the sensorimotor cortex in physiological force and action tremor. NeuroReport. 2001;12:1937–1941. doi: 10.1097/00001756-200107030-00033. [DOI] [PubMed] [Google Scholar]
  21. Murthy VN, Fetz EE. Oscillatory activity in sensorimotor cortex of awake monkeys: synchronization of local field potentials and relation to behavior. J Neurophysiol. 1996;76:3949–3967. doi: 10.1152/jn.1996.76.6.3949. [DOI] [PubMed] [Google Scholar]
  22. Pauluis Q, Baker SN, Olivier E. Emergent oscillations in a realistic network: the role of inhibition and the effect of the spatiotemporal distribution of the input. J Comput Neurosci. 1999;6:27–48. doi: 10.1023/a:1008804916112. [DOI] [PubMed] [Google Scholar]
  23. Pfurtscheller G, Neuper C. Simultaneous EEG 10 Hz desynchronization and 40 Hz synchronization during finger movements. NeuroReport. 1992;3:1057–1060. doi: 10.1097/00001756-199212000-00006. [DOI] [PubMed] [Google Scholar]
  24. Pfurtscheller G, Neuper C. Motor imagery activates primary sensorimotor area in humans. Neurosci Lett. 1997;239:65–68. doi: 10.1016/s0304-3940(97)00889-6. [DOI] [PubMed] [Google Scholar]
  25. Pfurtscheller G, Stancak A, Edlinger G. On the existence of different types of central beta rhythms below 30 Hz. Electroenceph Clin Neurophysiol. 1997;102:316–325. doi: 10.1016/s0013-4694(96)96612-2. [DOI] [PubMed] [Google Scholar]
  26. Pfurtscheller G, Stancak A, Neuper C. Post-movement beta synchronization. A correlate of an idling motor area? Electroenceph Clin Neurophysiol. 1996;98:281–293. doi: 10.1016/0013-4694(95)00258-8. [DOI] [PubMed] [Google Scholar]
  27. Raethjen J, Lindemann M, Dumpelmann M, Wenzelburger R, Stolze H, Pfister G, Elger CE, Timmer J, Deuschl G. Corticomuscular coherence in the 6–15 Hz band: is the cortex involved in the generation of physiologic tremor? Exp Brain Res. 2002;142:32–40. doi: 10.1007/s00221-001-0914-7. [DOI] [PubMed] [Google Scholar]
  28. Salenius S, Portin K, Kajola M, Salmelin R, Hari R. Cortical control of human motoneuron firing during isometric contraction. J Neurophysiol. 1997a;77:3401–3405. doi: 10.1152/jn.1997.77.6.3401. [DOI] [PubMed] [Google Scholar]
  29. Salenius S, Schnitzler A, Salmelin R, Jousmaki V, Hari R. Modulation of human cortical rolandic rhythms during natural sensorimotor tasks. Neuroimage. 1997b;5:221–228. doi: 10.1006/nimg.1997.0261. [DOI] [PubMed] [Google Scholar]
  30. Salmelin R, Hari R. Spatiotemporal characteristics of sensorimotor neuromagnetic rythms related to thumb movement. Neuroscience. 1994;60:537–550. doi: 10.1016/0306-4522(94)90263-1. [DOI] [PubMed] [Google Scholar]
  31. Singer W, Gray CM. Visual feature integration and the temporal correlation hypothesis. Annu Rev Neurosci. 1995;18:555–586. doi: 10.1146/annurev.ne.18.030195.003011. [DOI] [PubMed] [Google Scholar]
  32. Stancak A, Pfurtscheller G. Mu-rhythm changes in brisk and slow self-paced finger movements. NeuroReport. 1996;7:1161–1164. doi: 10.1097/00001756-199604260-00013. [DOI] [PubMed] [Google Scholar]
  33. Study RE, Barker JL. Diazepam and (-)-pentobarbital: fluctuation analysis reveals different mechanisms for potentiation of gamma-aminobutyric acid responses in cultured central neurons. Proc Natl Acad Sci U S A. 1981;78:7180–7184. doi: 10.1073/pnas.78.11.7180. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Traub RD, Whittington MA, Colling SB, Buzsaki G, Jefferys JG. Analysis of gamma rhythms in the rat hippocampus in vitro and in vivo. J Physiol. 1996;493:471–484. doi: 10.1113/jphysiol.1996.sp021397. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Wang XJ, Buzsaki G. Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. J Neurosci. 1996;16:6402–6413. doi: 10.1523/JNEUROSCI.16-20-06402.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Physiology are provided here courtesy of The Physiological Society

RESOURCES