Developmental maturation of passive electrical properties in retinal ganglion cells of rainbow trout

Abstract

We investigated the electrotonic and anatomical features of the dendritic arbor in developing retinal ganglion cells (RGCs). Cell anatomy was studied by filling individual cells with fluorescent, membrane-bound dyes and using computer-assisted image reconstruction. Electrotonic properties were characterized through an analysis of charging membrane currents measured with tight-seal electrodes in the whole-cell mode. We studied developing RGCs in the peripheral growth zone (PGZ) of a fish retina. The PGZ presents a developmental time-line ranging from pluripotent, proliferating cells at the extreme edge, to mature, fully developed retina more centrally. In the PGZ, RGCs mature through three histologically distinct zones (in developmental sequence): bulge, transition and mature zones. In the most peripheral three-quarters of the bulge zone, cells have rounded somas, lack dendritic extensions and some are coupled so that membrane-bound dyes traverse from one cell to its immediate neighbours. In the more central quarter of the bulge, cells' dendrites are few, short and of limited branching. In the transition zone dendritic arbors becomes progressively more expansive and branched and we present a morphometric analysis of these changes. Regardless of the size and branching pattern of the developing RGC dendritic arbor, the ratio of the diameters of parent and progeny dendrites at any branching nodes is well described by Rall's 3/2 power law. Given this anatomical feature, the RGC passive electrical properties are well described by an equivalent electrical circuit consisting of an isopotential cell body in parallel with a single equivalent cylinder of finite length. We measured the values of the electrical parameters that define this equivalent circuit in bulge, transition and mature RGCs. As RGCs develop the electrical properties of their dendritic arbor change in an orderly and tightly regulated manner, not randomly. Electrically, dendritic arbors develop along either of two distinct modes, but only these modes: isoelectrotonic and isometric. In isoelectrotonic growth, electrotonic properties are constant regardless of the absolute dimensions of the dendritic arbor or its branching geometry. These cells maintain unvarying relative synaptic efficacy independently of the size or pattern of their dendritic arbor. In isometric growth, in contrast, electronic properties change, but the ratio of the changing electrotonic length to electrotonic diameter is constant. In these cells relative synaptic efficacy decreases linearly as dendrites extend.

In the course of embryologic development, retinal ganglion cells (RGCs) form part of early neuronal networks even while their dendritic arbor continues to grow in size and branching complexity. The RGC dendritic arbor, scant at first, grows exuberantly and only later is pruned to its mature state, in which dendrites stratify to form two distinct layers in the inner plexiform layer (Maslim et al. 1986; Maslim & Stone, 1988). The electrophysiological function of the cells matures in parallel with these structural changes. Even before they begin to respond to light, immature RGCs exhibit correlated bursts of action potentials that arise from the activity of early neuronal networks (review in Wong, 1999; Feller, 1999). The cell's response to light also progresses from initial stages with poorly defined visual fields to mature stages characterized by complex visual fields of defined spatial and dynamic features (Bowe-Anders et al. 1975; Masland, 1977; Tootle, 1993; Sernagor & Grzywacz, 1995).

It is well established that information processing in RGCs depends on the passive electrical properties of their dendrites. Synaptic signals generated in the dendrites sum at the cell's soma, and the spatial and temporal features of this summation are weighted by the dendritic electrotonic characteristics (Coleman & Miller, 1989; Taylor et al. 1996; Fohlmeister & Miller, 1997; Sheasby & Fohlmeister, 1999). These electrotonic characteristics, in turn, are determined by dendritic anatomy (Rall, 1959). Since dendritic structure is continuously changing as RGCs develop and since the cells are at the same time members of neuronal networks, are the cell's information processing capabilities changing?

Hill et al. (1994) have thoughtfully analysed possible consequences to information processing of developmental changes in dendritic structure. Developmental changes could be random; however, they have suggested that in the course of neural development the passive electrical properties of individual neurons change in precisely controlled ways, not randomly. Furthermore, these regulated changes can follow one of two alternative regimes – isoelectrotonic or isometric – with profound functional consequences associated with the choice. In isoelectrotonic growth, dendritic maturation is regulated to maintain constant passive properties, regardless of the absolute dimensions of the arbor or its branching geometry. Consequently, synaptic attenuation is essentially constant in the growing network and the efficacy of synapses near and far from the cell body do not change with respect to each other. In isometric growth, in contrast, passive electrical properties change following a single, well defined rule: the ratio of the changing electrotonic length to electrotonic diameter is constant. In isometric growth, therefore, there is a linear loss of the efficacy of synapses located in the periphery of a dendritic tree relative to that of more centrally located ones.

To investigate the electrotonic characteristics of developing RGCs we studied these cells in the peripheral growth zone (PGZ) of a fish retina. Uniquely among vertebrates, the eyes of fish continue to grow throughout the animal's life; the retina matches this growth both by stretching of the mature tissue and by the continuous development of new tissue (review in Fernald, 1991). New tissue differentiation occurs both at the edge of the mature retina, in the PGZ, and at the embryonic fissure, a crevice that runs ventrally from the retina's centre to its rim (Müller, 1952; Lyall, 1957; Grun, 1975; Kunz & Callaghan, 1989). The PGZ presents a developmental time-line ranging from pluripotent, proliferating cells at the extreme edge, to mature, fully developed retina more centrally (Lyall, 1957; Sharma & Ungar, 1980), and this time-line probably recapitulates the progression of embryonic development (Perron et al. 1998). In the PGZ, therefore, RGCs at all possible stages of differentiation are present, side-by-side.

The RGC layer in the PGZ of rainbow trout (the species we have studied) differentiates through three distinctive histological stages: bulge, transition and mature (Olson et al. 1999, 2000). The youngest cells form the bulge: a disorderly, yet anatomically distinct aggregate of cell bodies. Bulge RGCs have few dendritic processes, if any, they are not electrically excitable and their resting potential is relatively low. RGCs in the transition zone form a layered structure two to three nuclei thick, their dendritic arbors are elaborately branched and some of them extend over the entire span of the inner plexiform layer. These cells are electrically excitable and form networks with other retinal neurons, as evidenced by bursts of correlated spiking activity (S. C. Chung & J. I. Korenbrot, unpublished observation). Mature RGCs form a single row of cells; their dendritic arbors are stratified into distinct sublaminae in the inner plexiform layer according to their function (ON, OFF or ON/OFF; Famiglietti et al. 1977). We report here on the developmental maturation of the structural and electrotonic properties of the RGC dendritic arbor. We present a morphometric analysis of dendritic arbor structure and analyse their passive electrical properties. We find that developmental changes in electrotonic characteristics are not random, but regulated to preserve the cell's information-processing capacity. The information-processing capacity, furthermore, matures through either of only two regimes: isometric or isoelectrotonic.

Methods

Rearing rainbow trout in the laboratory

To control the developmental progress of the animals used in this study, we reared rainbow trout (Onchorynchus mykiss) indoors in a small aquaculture facility previously described (Julian et al. 1998; Olson et al. 1999). Eyed embryos (approximately 4 weeks post-fertilization) were obtained year-round from Mount Lassen Trout Farms (Red Bluff, CA, USA). Developing embryos and growing fish were fed ad lib. and maintained in 15 °C water under illumination that matched normal daylight spectrum (Vita-Lite, Duro-Test Corp., Fairfield, NJ, USA), with a daily 14 h-10 h light-dark cycle. Animals used in these experiments were juveniles 5–7 cm long, a size reached uniformly 5–10 weeks post-hatching. The Animal Care Committee at UCSF approved the protocols for animal care and use.

Retinal slices for electrophysiological studies

The procedures to obtain retinal slices that include the PGZ are detailed elsewhere (Olson et al. 1999). Briefly, fish were dark-adapted for about 45 min and then decapitated and pithed. Under dim red light an eye was removed, and incisions made in its temporal pole along a square 3–5 mm to the side. The square included the ora serrata. The square sector was lifted away from the eyeball and then positioned, retina side down, on Millipore filter membrane (Type HA, Millipore, Bedford, MA, USA). The sclera, choroid and pigment epithelium were hauled up, and the retina on its Millipore support immediately submerged under cold trout Ringer solution. The retina-Millipore was cut with a tissue chopper to yield 3–4 slices, each 240 μm thick. Slices were manoeuvred using the protruding ends of the filter membrane.

Retinal explants for anatomical studies

The initial tissue processing was just as described above, except that the square sector lifted from the temporal eye pole was immediately submerged under chilled Ringer solution. Under visual observation (dim red light), the retina was isolated from the rest of the tissue and then carefully layered, photoreceptor layer down, onto a square piece of Millipore filter membrane, about 5 mm to the side. The flattened retina was then forced to adhere to the Millipore membrane by absorbing excess solution with filter paper placed underneath the Millipore.

Electrical recordings

Retinal slices were held in a chamber on the fixed stage of an upright microscope equipped with DIC optics. The recording chamber was continuously perfused with oxygen-saturated trout Ringer solution at about 0.5 ml min⁻¹. Under visible light we observed the slices using a × 40, 0.75 NA water-immersion objective lens (Zeiss, Oberkochen, Germany) with × 1000 total magnification.

We measured whole-cell membrane currents at room temperature using an Axopatch 200A patch clamp amplifier (Axon Instruments, Foster City, CA, USA). Analogue signals were filtered at 5 kHz with an 8-pole low-pass Bessel filter (Frequency Devices, Haverhill, MA, USA) and digitized on-line with 12-bit accuracy at a sampling rate of 12.5 kHz (pClamp v8.0, Axon Instruments). We used tight-seal electrodes produced from aluminosilicate glass (Corning 1724, 1.5 mm × 1.0 mm o.d. × i.d.). Whole-cell mode was achieved by mechanical membrane disruption. In all figures inward currents are positive, contrary to typical convention but convenient for data analysis.

DiOlistics cell labelling and morphometric analysis

To label individual RGCs in the PGZ we used the technique developed by Gan et al. (2000). A retinal PGZ explant flat-mounted on Millipore (see above) was first incubated at room temperature for 5 min in 0.4 mg ml⁻¹ hyaluronidase (in Ringer solution) to remove adhering vitreous humour. It was then fixed for 10 min in fresh paraformaldehyde:glutaraldehyde (2 %:0.5 % v/v in 0.1 m PBS) and repeatedly rinsed with PBS. The retinal flat-mount, ganglion cell layer up, was bombarded with tungsten beads coated with the fluorescent dyes diO and diI (Molecular Probes, Eugene, OR, USA) and projected out of a Gene-Gun (BioRad, Richmond, CA, USA). The retina-Millipore was transferred out of PBS, placed about 20 mm from the gun's tip, bombarded and then rapidly returned to PBS. Fifty milligrams of tungsten beads (0.7 μm diameter) were coated with 1 mg dye (dissolved in 0.1 ml methylchloride), and projected at a pressure of 160–200 lbf in⁻² through a 0.4 μm PET. track-etched membrane (Falcon, BD Labware, Franklin Lakes, NJ, USA). After bombardment, we allowed at least 1 h (and up to 12 h) at room temperature for lateral membrane diffusion of the dye and then, without further processing, we cover-slipped the tissue and observed it with a confocal microscope (MRC 1024, BioRad).

After identifying well-labelled, isolated cells, we acquired successive confocal images at focal depths that systematically increased 1 μm at a time. Images were acquired over a depth range sufficient to include the cell's soma and full dendritic tree. With computer assistance (Confocal Assistant, shareware), the images were collapsed into a single final image that represents the plane projection of the entire dendritic tree. For morphometric analysis, each plane projection image was quantitatively analysed using image-analysis software (Neurolucida). To determine dendritic diameters at branching nodes, the diameter of each node's branch was measured over the 3 μm length nearest the node.

Salt solutions

Trout Ringer solution contained (mm): NaCl 120, NaHCO₃ 5, Na₂HPO₄ 1, KCl 2.5, CaCl₂ 1, MgCl₂ 1, glucose 10, Hepes 10 pH 7.5, minimal essential medium (MEM) vitamins, essential and non-essential amino acids (Gibco-BRL, Grand Island, NY, USA) and 0.1 % bovine serum albumin, osmolarity 276 mmol l⁻¹. Tight-seal electrodes were filled with a solution consisting of (mm): potassium gluconate 110, potassium aspartate 20, KCl 10, GTPNa₂ 1, ATPMg 1, Hepes 10 pH 7.3 adjusted with KOH, osmotic pressure 303 mmol l⁻¹.

In a subset of experiments we measured the cell's electrical properties under conditions designed to block all identified voltage-gated ionic currents (Olson et al. 2000). The trout Ringer solution was modified as follows (mm): NaCl 95, NaHCO₃ 5, Na₂HPO₄ 1, KCl 2.5, CaCl₂ 1, MgCl₂ 1, CoCl₂ 5, TEACl 20, TTX 0.001, 4-amino pyridine 5, DIDS (Cl⁻ channel blocker) 10, glucose 10, Hepes 10, pH 7.5 with MEM vitamins and amino acids. The electrode filling solution was (mm): caesium aspartate 95, NaCl 10, GTPNa₂ 2, ATPMg 2, EGTA 10 and Hepes 10, pH 7.3.

Data analysis

Our analysis is based on the theoretical and experimental framework developed by Jackson (1992), who applied to voltage-clamped neurons the cable conduction theory originally developed by Rall (1969). This analysis proposes that RGCs are well represented by a cell body with single R_s and C_s elements connected in parallel to a cylinder of finite electrotonic length, L, constituted by circuit elements R_p and C_p (Fig. 1). The cell body is accessed through the low resistance of a tight-seal electrode (R_a). Representing the equivalent circuit of the cell soma as single R_s, C_s elements follows the simple assumption that the body is isopotential, regardless of its shape. Rall (1959) first demonstrated that however extensive and intricate the anatomy of the dendritic arbor may be, its cable properties can always be mathematically represented by a single equivalent cylinder of finite length, provided dendrites terminate at equivalent electrotonic lengths and they obey the 3/2 power law:

Figure 1. Equivalent electrical circuit that represents the passive electrical properties of single ganglion cells in the rainbow trout retina.

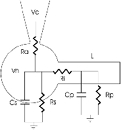
The soma is assumed to be isopotential and, therefore, it is represented by single lumped elements R_s and C_s. Dendritic processes are mathematically represented by a single cylindrical cable of finite length, of electrotonic length L and constituted by single lumped elements R_p and C_p. R_i is the cytoplasmic resistance connecting soma and cylindrical process. The tight-seal electrode holds the voltage-clamped cell at holding voltage V_h and delivers command steps, V_c, through access resistance R_a.

(1)

where d_p is the diameter of a parent branch and d_i is the diameter of the progeny branches.

In the Jackson-Rall analysis, the instantaneous charging current generated under voltage clamp is first separated into its constituent exponential components. The time constant of each of these exponential components is an eigenvalue that satisfies the cable equation:

(2)

where X = x/λ and T = t/τ_m. V is voltage, x is the distance along the axis of the equivalent cylinder, t is time, λ is the length constant of the cylinder and τ_m is the membrane time constant. The boundary conditions considered by Rall (1969) allow the assignment of specific elements in the Fig. 1 circuit to eigenvalues of eqn (2).

Jackson's (1992) analysis is based on the theoretical conclusion that, after correcting for the passive properties of the electrode, the elements R_a and C_s (Fig. 1) account for the largest and fastest of the current-charging components measured. As a corollary, therefore, the remaining, slower components reflect the features of the equivalent cable. To execute this analysis, then, multiple first-order exponentials are optimally fitted to charging currents generated in the linear range of the I-V curve. We achieved this aim through the following protocol. In each cell we analysed between three and seven individual current traces, and the results were averaged. Electrode transients were corrected off-line using time constants assessed experimentally immediately after forming an ‘on-cell’ seal and measured using the electronic cancellation circuits in the Axopatch amplifier. A single exponential function of adjustable initial amplitude, I_i, and time constant, τ_x, was then subtracted from the experimental current to obtain a residual current that was correctly compensated according to the criteria specified by Jackson (1992). Given I_i, and since τ_x = R_xC_x, we used these values to compute corrected values for R_a and C_s (Fig. 1):

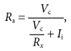(3)

(4)

where V_c is the amplitude of the command voltage. Next, the residual current was optimally fitted with the sum of three exponentials of initial amplitudes I₁, I₂ and I₃ and and time constants τ₁ < τ₂ < τ₃, respectively (non-linear, least-square minimization algorithm; Origin, MicroCal Software, Northampton, MA, USA). The electrotonic length of the equivalent cylinder, L, was computed from:

(5)

and the process resistance, R_p, and its time constant, τ_p, were computed from:

(6)

and

(7)

where α=π/2L. Given that the soma and equivalent process's time constant are the same, then τ_p = R_sC_s = R_pC_p, from which the values of all relevant parameters can be calculated. Finally, from the electrical data we computed anatomical features for the RGC soma and equivalent process by assuming the cell body is spherical, the specific membrane capacitance is C_m = 1 μF cm⁻² and the specific cytoplasmic conductivity is g_m = 9.1 mS cm⁻¹, values common to neuronal processes (Taylor et al. 1996). Thus, soma diameter, d_s, cylindrical process diameter, d_p, and process length, l_p, are given by (Taylor et al. 1996):

(8)

(9)

(10)

Results

To investigate the information-processing capabilities of developing RGCs in the rainbow trout's retina, we measured the passive electrical properties and anatomical characteristics of single cells in the ganglion cell layer of the PGZ. To compute the passive electrical properties of the cells we measured the kinetics of membrane-charging currents and analysed them using a method (Rall, 1969; Jackson, 1992) that assumes RGCs are adequately represented by an electrical equivalent circuit consisting of two parallel RC elements (Fig. 1). The soma is represented by one spherical RC element, while a single cylinder of finite length represents dendrites. The equivalent cylinder well represents the dendritic processes, regardless of their actual shape and branching complexity, as long as the dendrite's diameters at branching nodes obey the 3/2 power law (eqn (1); see Rall, 1959).

Dendritic tree structure in developing RGCs

We assessed the adequacy of the Rall approximation in the developing trout RGC by measuring the anatomical characteristics of its dendritic tree in flat-mounted tissue. Mature RGCs are not a single class of cells and complex schema have been developed to classify them on the basis of anatomical and/or physiological criteria (reviewed in Stone, 1983; fish retinal data in Hitchcock & Easter, 1986; Cook et al. 1992; Cook & Sharma, 1995). A limitation in this study is our inability to recognize subclasses of RGCs among bulge and transition cells. At this time, however, neither our anatomical observations nor studies of the membrane currents in these cells have allowed us to develop a specific scheme of subclass classification. Therefore, we have grouped all analysed bulge and transition RGCs into classes simply by their location within the histological distinct regions of the PGZ.

Microphotographs of individual, randomly selected RGCs in the trout PGZ are shown in Fig. 2. In flat-mounted tissue explants, cells were individually labelled with fluorescent dyes and two-dimensional plane projections of the entire dendritic tree were created by superimposition of multiple confocal images (see Methods). The cells were identified as being bulge, transition or mature RGCs by their location in the PGZ (Fig. 2, retinal section). For bulge cells, somas were round and mean cell diameter was 10.09 ± 2.12 μm (±s.d., n = 13). Among bulge cells, two anatomical classes were further distinguished: those located in the most peripheral three-quarters of the bulge, which we call ‘young bulge’, and those found in the more central quarter, which we call ‘old bulge’. Young bulge RGCs (Fig. 2, YB) were generally unremarkable and appeared as simple, nearly round somas without any apparent dendritic extensions. Most frequently, young bulge RGCs were labelled in clusters (Fig. 2, YB). Clusters of labelled cells were not observed in old bulge, transition or mature RGCs. Labelling as clusters suggests that the fluorescent dye can diffuse from cell to cell among young bulge RGCs, but not at any other developmental stage. It is improbable that multiple single pellets hit the tissue at a sufficient surface density to label independently so many neighbouring cells and to do so only over the young bulge cells. While diI diffusion is not an established indicator of gap junction coupling, it is possible that some young bulge cells may be electrically coupled to each other. Experimental data have previously suggested that very young RGCs in the mammalian (Penn et al. 1994) and fish retina (Hitchcock, 1993) are electrically coupled.

Figure 2. Plane projections of the RGC dendritic tree in flat-mounted retinal PGZ.

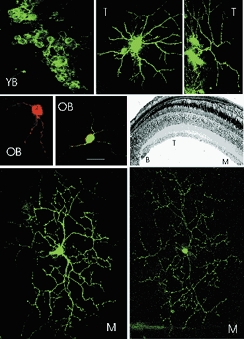
Single cells were fluorescently labelled using the DiOlistic method and observed under a confocal microscope. Shown are typical images of young bulge (YB), old bulge (OB), transition (T) and mature (M) cells. The location of the cells in the RGC layer of the PGZ is shown in the stained histological section in the middle, right panel. Young bulge cells frequently labelled as clusters, suggesting they are coupled and dye can diffuse among them. Old bulge cells located in the most central quarter of the bulge have short dendritic extensions scantly branched. Transition cells exhibited a more elaborate arbor with 1–3 primary dendrites, each branching several times (quantitative details in Table 1). Mature RGCs exhibited their well-known and complex dendritic arbor that is extensive, vigorously branched and stratified within the inner plexiform layer. The size marker shown in the OB panel corresponds to the following dimensions in each of the panels: Top YB = 30 μm. Top, middle T = 15 μm. Top, right T = 30 μm. Middle, left OB = 20 μm. Middle, middle OB = 25 μm. Bottom, left M = 30 μm. Bottom, right M = 50 μm.

The old bulge cells (Fig. 2, OB) exhibited one or two primary dendrites that were relatively short, branched once or twice and always two daughters formed at each branching node. Transition RGCs (Fig. 2, T) had round somas of mean diameter 7.65 ± 2.77 μm (±s.d., n = 9). To characterize the cells’ dendritic trees we measured the following parameters: number of primary dendrites (those emerging from the cell soma), number of branching nodes on each primary dendrite, total dendritic length (the sum of the lengths of all dendritic segments) and the diameter of each dendritic segment at each and every node. A summary of the anatomical characteristics of the developing RGCs is presented in Table 1. For comparison, the table includes data reported by Bloomfield & Hitchcock (1991) for a single class of mature RGCs in goldfish (type 1.2). We took advantage of Bloomfield & Hitchcock's (1991) elegant work, rather than repeat measurements in trout, because they report the features of only a single class of mature cells whereas our limited sampling of mature trout RGCs did not allow us to define specific classes. The dendritic tree in mature cells (Fig. 2, M) is much larger in extent and branches more extensively than any of the transition RGCs.

Table 1.

Anatomical features of developing RGC dendritic arbor in trout PGZ

	Number of primary dendrites
	Mean±s.d.	Most frequent	n
Young bulge	0	0	10
Old bulge	1.75 ± 1.29	1	12
Transition	2.8 ± 1.47	2	6
Mature (type 1.2)*	1 ± 0	1	6
	Number of branching nodes per primary dendrite
	Mean ± s.e.m.	Most frequent	n
Young bulge	0	0	10
Old bulge	1.83 ± 0.94	1	12
Transition	3.5 ± 2.07	2	6
Mature (type 1.2)*	13 ± 0	13	6
	Total dendritic length
	Mean ±s.d.	Range	n
	(μm)	(μm)
Young bulge	0	0	10
Old bulge	67.8 ± 21.7	49–108	12
Transition	393.7 ± 267.7	155–886	6
Mature (type 1.2 small)*	4353.1 ± 644	NA	3

n, number of cells; NA, not available.

^*Data from Bloomfield & Hitchcock (1991).

To analyse the applicability of Rall's 3/2 power law, we measured the diameter of parent and progeny dendrites at each and every branching node in six different old bulge RGCs, six transition RGCs and four mature RGCs. The diameter of each node's branch was measured over the 3 μm length nearest the node and the mean values measured are listed in Table 2. The nodes are named progressively with Greek alphabetical characters starting at the one nearest the cell body. At each node we exclusively found one parent and two progeny branches. At each individual branching node, we computed the ratio:

Table 2.

Branch diameter at progressive nodes in developing RGC dendritic arbor in trout retinal PGZ

	Old bulge (μm)	Transition (μm)	Mature (μm)
α parent	1.19 ± 0.16 (15)	1.17 ± 0.19 (16)	2.06 ± 0.38 (6)
α progeny 1	0.80 ± 0.11 (15)	0.96 ± 0.12 (16)	1.32 ± 0.18 (6)
α progeny 2	0.76 ± 0.11 (15)	0.80 ± 0.08 (16)	1.42 ± 0.11 (6)
β parent	–	0.98 ± 0.08 (14)	1.17 ± 0.26 (12)
β progeny 1	–	0.75 ± 0.10 (14)	0.77 ± 0.12 (12)
β progeny 2	–	0.71 ± 0.09(14)	0.79 ± 0.41 (11)
γ parent	–	0.86 ± 0.39 (11)	0.79 ± 0.09 (11)
γ progeny 1	–	0.55 ± 0.14 (11)	0.60 ± 0.07 (11)
γ progeny 2	–	0.64 ± 0.14 (11)	0.59 ± 0.07 (11)
δ parent	–	0.68 ± 0.15 (7)	–
δ progeny 1	–	0.51 ± 0.11 (7)	–
δ progeny 2	–	0.44 ± 0.12 (7)	–

Values are means ± S.E.M., with the number of branches given in parentheses.

(eqn (1)), and we then calculated the statistical distribution of these ratios only when at least five individual values could be measured at a given branching node. Figure 3 illustrates the mean and standard error of Rall's ratio at each branching node for all cell types. We also present our measurements of this ratio in the first three branching nodes of four unclassified mature RGCs of trout, as well as the results of Bloomfield & Hitchcock (1991), who thoroughly studied one defined anatomical class of mature RGC (Type 1.2) in goldfish. Our results show that dendrites in developing RGCs obey Rall's power law, and do so just as well as mature RGCs.

Figure 3. Value of Rall's ratio at each branching node in developing and mature RGC.

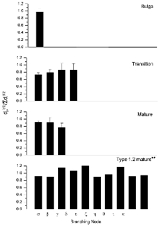
Rall's ratio (see eqn (1)) was computed at each branching node. The branching order follows the progression of the Greek alphabet, as listed. The number of individual branching nodes measured in each sample shown was: old bulge α= 15; transition α= 17; transition β= 13; transition γ= 11; transition δ= 5; mature α= 5; mature β= 10; mature γ= 12. **Data from Blomfield & Hitchcock (1991).

A test of the equivalent electrical circuit

To test the adequacy of the simplified equivalent circuit (Fig. 1) to describe RGCs in the trout retina, we measured charging membrane currents in two different mature RGCs, one under normal physiological solutions (Fig. 4A) and the other under modified intra- and extracellular solutions designed to block all the known voltage-dependent currents characteristic of these cells (Fig. 4B; Olson et al. 2000). From a holding potential of −70 mV, currents were activated by step changes to −80 mV. Inward currents are shown as positive. Under normal ionic solutions, the charging membrane currents exhibit complex kinetics that simply cannot be fitted by a single exponential function. In Fig. 4A, as a reference, the single exponential function shown (continuous line) describes the charging of the cell's soma (more details below). We posit that this kinetic complexity arises from the existence of several equivalent passive elements, each of characteristic time constant. If this thesis is correct, then electrically isolating the cell by blocking all the known voltage-gated ion channels in the neuron and its processes should transform the kinetics of the charging current into a single exponential process, one reflecting simply the features of the resting cell soma's membrane resistance and capacitance. Indeed, when all known voltage-gated currents were blocked, the charging current of the RGC was well described by a single exponential function (Fig. 4B). The same finding was made in every cell tested, (transition = 12 and mature = 15). This result indicates that under normal conditions a complex equivalent circuit must be used to describe the RGC electrotonic properties and, as we show below, the circuit illustrated in Fig. 1 is an adequate one.

Figure 4. Charging membrane currents in mature RGC.

Charging currents in two different cells were generated by −10 mV steps superimposed on −70 mV holding voltage. Inward current is positive. A illustrates current measured under physiological salt solutions. The experimental data (○) cannot be fitted by a single exponential function. The continuous line is a single exponential that describes the charging of the soma's electrical elements of the cell shown (details in text). The time axis is normalized by dividing time by the time constant of the soma's charging, in this case τ = 0.19 ms. B illustrates current measured in a different mature RGC in the presence of modified intra- and extracellular solution designed to block all known voltage-gated currents in the cell. The experimental data (○) are well fitted by a single exponential function (continuous line) of time constant τ = 2.38 ms (coefficient of correlation = 0.97).

Passive electrical properties of transition RGCs

Application of the Jackson-Rall analysis to a single RGC in the transition area of the trout retina is illustrated in Fig. 5. The experimental current shown has been corrected to remove charging of the tight-seal electrode. The complex time course of the current reflects charging of the elements of the cell's equivalent circuit. Shown in the figure are the constituent exponential components that add to make up the observed current, each computed as described under Methods. The largest and fastest single component, labelled S, reflects the charging features of the cell soma. The residual current, computed after subtracting the S component from the experimental datum, is labelled as P and reflects the charging features of the neuronal processes. We found that the sum of three exponentials fitted the residual current very well (coefficient of correlation R = 0.99). The sum of the four exponential functions fits the experimental data very well, as indicated in Fig. 5 by the nearly zero difference between the actual and computed data (error of fit shown by filled triangles). The optimized values of the equivalent circuit parameters that best-fit data in eight different mature and transition RGCs are presented in Table 3.

Figure 5. Analysis of charging membrane current in a transition RGC.

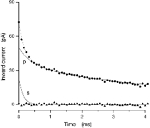
Current was activated by −10 mV steps superimposed on −70 mV holding voltage. Experimental data are shown as filled circles. Continuous lines illustrate the constituent exponential components that best fit the experimental data. The line labelled ‘s’ depicts charging of the cell soma (single exponential). The line labelled ‘p’ illustrates charging of the process (sum of three exponentials). The dotted line superimposed on the experimental points is the sum of ‘s’ and ‘p’. The error of fit (the difference between experimental and computed data) is illustrated by the filled triangles. Complete parameters for the cell shown are listed in Table 1 (transition T0903).

Table 3.

Electrotonic characteristics of developing RGC in the trout retinal PGZ

			Soma		Process				Soma	Cylindrical process
		Ra	τx	Cs	τ3/τ2	L	tp	Rp	ds	lp	dp
		(MΩ)	(ms)	(pF)			(ms)	(GΩ)	(μm)	(μm)	(μm)
Mature	M1906	9.17	0.20	21.26	1.429	6.599	3.17	0.01	4.76	2384.16	1.81
	M0607	74.20	0.16	2.09	3.784	2.150	3.04	0.68	4.59	317.63	0.32
	M1907	8.73	0.16	18.20	1.938	4.309	5.05	0.03	7.26	1692.11	1.34
	M2004	9.48	0.08	7.91	5.791	1.286	9.08	0.41	8.16	455.88	0.61
	M1004	24.56	0.10	4.11	7.907	0.625	26.86	8.83	8.67	246.43	0.25
	M1409	51.95	0.19	3.68	5.916	1.244	4.34	0.61	6.30	258.87	0.44
	M1003	20.21	0.43	21.03	7.395	0.787	66.54	4.39	19.72	680.45	0.49
	M1607	13.37	0.12	8.83	5.079	1.540	3.66	0.41	11.82	361.15	0.66
Transition	T0308	28.51	0.17	5.86	1.279	8.257	0.84	0.01	3.11	1240.04	1.18
	T0903	47.18	0.13	2.76	3.864	2.103	5.33	0.17	2.64	454.58	0.38
	T1903	15.14	0.16	10.24	2.128	3.878	6.19	0.06	5.51	1344.32	0.85
	T0902	41.93	0.14	3.22	3.377	2.416	1.57	0.57	7.43	289.57	0.40
	T0307	18.72	0.20	10.89	2.595	3.147	0.96	0.03	9.88	554.01	1.42
	T1506	25.37	0.25	9.85	8.536	0.390	64.01	23.07	15.64	252.01	0.29
	T0706	15.28	0.22	14.40	5.194	1.496	2.82	0.59	18.56	300.36	0.63
	T0708	15.77	0.31	19.66	2.167	3.800	7.23	0.06	9.04	1700.29	1.22
	T1403	13.09	0.06	4.43	1.367	7.163	0.67	0.03	4.60	876.74	0.98
Bulge	B0805	43.17	0.16	3.59	3.413	2.390	3.51	0.47	6.09	440.78	0.43
	B1606	17.95	0.08	4.18	1.820	4.648	4.79	0.48	6.28	177.00	0.43

Passive electrical properties of bulge RGCs

Of all bulge cells we investigated in detail (n = 9), only four cells could be successfully described with the same equivalent circuit used to analyse transition and mature RGCs. In the five other bulge cells, residual currents existed, but they could not be fitted with three exponentials or when fitted by the sum of three exponentials the theoretical demand that τ₃/τ₂ < 9 was violated (see eqn (5); Jackson, 1992). That is, the neural processes appeared to have developed sufficiently to be electrically apparent, but their passive electrical properties were different from that of older RGCs, and could not be described by a single equivalent cylinder. In two of the four cells described by the equivalent circuit, a single exponential (the S component) was necessary and sufficient to fit the experimental data; there were no residual currents and, therefore, no P components (Fig. 6). That is, the neural processes had not developed sufficient to be electrically detectable. These are almost certainly young bulge cells with round somas and lacking in dendritic extensions (Fig. 2, YB). Two other bulge cells could be reliably analysed by the Jackson-Rall method and their equivalent electrical parameters are shown in Table 3. These are probably old bulge cells.

Figure 6. Analysis of charging membrane current in a bulge RGC.

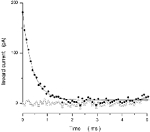
Current was activated by −10 mV steps superimposed on −70 mV holding voltage. We illustrate a cell that could not be fitted by the Jackson-Rall analytical method. Experimental data are shown as filled circles. In this instance, charging current was well fitted by a single exponential function (correlation coefficient = 0.97), shown as a continuous line, with time constant τ= 0.39 ms. That is, this bulge cell consisted of a single electrical compartment, presumably the cell body; dendritic processes had not developed sufficiently to become electrically detectable. The error of fit (the difference between experimental and simulated data) is illustrated by the open triangles.

Ganglion cell anatomical features inferred from their passive electrical properties

Under simplifying but reasonable assumptions, the RGC passive properties computed above can be used to calculate ‘equivalent’ soma diameter and processes length (eqns (8), (9) and (10)). The computed values of the equivalent anatomical features for each cell analysed are listed in Table 3.

The equivalent dendritic length and diameter can be analysed to determine whether electrotonic arbor growth is random or not and, if not, whether specific rules are followed. As described by Hill et al. (1994), if growth is not random, the cylindrical process diameter, d_p (eqn (9)), and its length, l_p (eqn (10)), change as a function of each other following well defined mathematical rules. If the electrotonic length of the growing dendrites, L (eqn (5)), remains constant, that is L_old/L_young, growth is isoelectrotonic and the ratio d_p/l_p² is constant. If, on the other hand, the growth is isometric then the ratio d_p/l_p should remain constant.

To analyse the electrotonic features of RGC dendritic development, we plot in Fig. 7 the electrical diameter for each process as a function of its length. To compare many different cells, diameter and length in each cell are normalized by dividing each value by the smallest value of these parameters measured in our cell universe. Specific symbols identify data measured in bulge (▵) and transition (▴) RGCs. Also shown in Fig. 7 is the relationship between process diameter and length anticipated theoretically for isoelectrotonic or isometric growth modes.

Figure 7. Mode of maturation of the electrical properties of dendritic processes in developing RGCs of the PGZ.

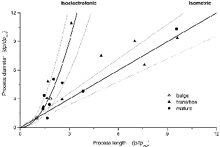
The normalized electrical equivalent diameter for the dendritic tree in each cell analysed is plotted as a function of the electrical length of the same tree. To compare among cells, the electrical diameter and length are normalized by dividing each by the smallest value of these parameters measured in the total universe of cells analysed. For transition RGCs, l_pmin = 252 μm and d_pmin = 0.38 μm. For bulge, l_pmin = 177 μm and d_pmin = 0.09 μm. The developmental stage of the RGC in which the data were measured is identified by specific symbols: transition (▴), bulge (▵) and mature (•) RGCs. The continuous lines are the predicted mathematical relationships when process growth is isoelectrotonic d_p/d_pmin = (l_p/l_pmin)² or isometric d_p/d_pmin = l_p/l_pmin, respectively. The dotted lines either side of the continuous ones indicate the 80 % confidence intervals.

In Fig. 7 there is no attempt to fit experimental data with theoretical lines. The theoretical lines are predicted behaviour of isometric or isoelectrotonic growth. About half of the transition cells fall accurately (within 0.9 probability) along the prediction of isoelectrotonic growth, while the other half are near prediction of isometric behaviour (within 0.8 probability). Since so few bulge cells could even be described by the equivalent cable formalism, little can be concluded about their mode of growth. Thus, dendritic growth in developing transition RGCs is not functionally random. It is tightly regulated and, remarkably, this orderly growth falls within either of only two alternative modes.

The dendritic arbor of mature RGCs also continues to grow after development to match the balloon-like stretching of the retina necessary to match eye growth. Bloomfield & Hitchcock (1991) have analysed the anatomical characteristic of this growth in Type 1.2 RGCs of the goldfish. Anatomical data indicate that this growth is isoelectrotonic. We also analysed dendritic growth in mature RGCs using the electrophysiological assay. In Fig. 7 we plot normalized dendritic process diameter as a function of its length for mature RGCs of different (and undefined) anatomical subclasses (•). As with developmental changes in transition RGCs, growth in mature RGCs is not random and can be either isoelectrotonic or isometric.

Discussion

The molecular mechanisms that regulate neuronal dendritic growth are the subject of the current investigation and an array of both intrinsic and extrinsic signals are now known to participate in this process (review in Wingate, 1996; McAllister, 2000; Sernagor et al. 2001). Among these signals, the strength and pattern of electrical activity in the developing dendrites are regulators of dendritic growth. Since the manner in which the information conveyed by electrical activity is processed depends on the anatomy and electrical properties of the dendrites, it is not surprising that the passive electrical properties of neuronal dendrites are carefully regulated in the course of development. Here we have investigated the structure and passive electrical properties of the changing dendritic tree in developing RGCs. We have observed that while both anatomy and passive electrical properties change, the changes in the electrotonic properties are well co-ordinated and follow either of only two functional modes: isoelectrotonic or isometric.

Taking advantage of the PGZ in trout retina, we studied the passive properties of RGC at three histologically defined developmental stages. The youngest cells – those in the bulge – are electrically immature. At one extreme, the cells are without dendrites and their electrotonic behaviour, correspondingly, consists only of the activity of the soma. Once the electrotonic behaviour reveals the presence of dendrites, it can be described by the equivalent circuit of Fig. 1 for some cells, but not for all. These electrical features match the anatomy of the cells: when dendrites begin to develop, they are short, thin and irregularly branched. The more developed transition and mature RGCs, on the other hand, are all well described by an equivalent electrical circuit consisting of an isopotential cell body in parallel with a single equivalent cylinder of finite length that well represents dendrites, however complex their branching pattern.

The success of the simplified electrical model used in our analysis is due to the fact that dendrites in fish RGCs obey Rall's 3/2 power law. This condition is necessary to justify the mathematical equivalency between branched dendrites and an equivalent cylinder of finite length (Rall, 1959). In the Jackson-Rall analysis the least accurate step is fitting the fast exponential component that reflects the soma's characteristics. Inaccuracies in this adjustment give rise to errors in the values of the somatic diameter, d_s. For example, in transition RGCs we measured the soma's diameter both histologically and electrically; the mean values are similar but the error in the electrical measurement is larger: anatomical d_s= 7.7 ± 2.8 μm (±s.d.), electrical d_s= 8.5 ± 5.5 μm (±s.d.). The electrical inaccuracy, however, introduces little error in defining the features of the equivalent cylindrical process because these features are derived from the values of the two slowest time constants, τ₂ and τ₃ These time constants were fitted to the data by strict least-square minimization algorithms. Moreover, empirical analysis demonstrated that changing the value of the fastest time constant by as much as 20 % did not change the values of τ₂ and τ₃.

Electrical equivalent circuits more complex than those assumed in the Rall analysis have been used in the analysis of RGC dendrites. These models are particularly accurate when the anatomy and physiology of the same cell are simultaneously known (Sheasby & Fohlmeister, 1999). An experimental limitation in our studies is that we did not label the cells we recorded from. Complete anatomical description of the RGC dendritic tree can only be carried out on flat-mounted tissue that includes the dendritic arbor in its fullest extent. However, we were unable successfully to use tight-seal electrodes to study RGCs in this preparation because the cell's soma is covered both by passing axons and by a fibrous and mucous membrane. This makes it practically impossible to obtain a giga-seal (our unpublished observation). In contrast, electrical recordings are possible in tissue slices, but anatomical studies are compromised because the dendritic trees are probably severed in the slice. While anatomical studies are compromised by the likely truncation of dendritic trees in retinal slices, this fact does not undervalue the conclusions of our electrical studies. This is because the dendrites in the remnant arbor of sliced RGCs continue to obey Rall's 3/2 power law. Hence, the electrotonic properties assessed in slices accurately represented the equivalent diameter and length of the dendritic process and their mathematical relationship.

A limitation of this study is our inability to recognize subclasses of RGCs among bulge and transition RGCs. Mature RGCs are not a single class of cells and complex schema have been developed to classify them on the basis of anatomical and/or physiological criteria (Stone, 1983). This limitation does not invalidate our conclusion on the orderly and bi-modal development of the electrical properties of RGCs. The two dissimilar developmental modes may correspond to different anatomical or physiological subclasses of transition and mature cells, and future work will investigate this possibility.

Developmental changes in the electrotonic properties of transition cells fell into one of two modes. The isoelectrotonic growth exhibited its canonical characteristics and was indistinguishable from that predicted by theory. The second mode of growth was distinct from the first, and appeared to follow the rules of isometric growth, but only with about 80 % confidence. These results may reflect the fact that the precision of growth control is itself maturing and it may transit through progressively more accurate stages.

The passive electrical properties of mature RGCs in fish, averaging all cells into a single population, are comparable to those reported in similar averaged populations of RGCs in other non-mammalian species. In our population (n = 9), τ_m = 13.8 ± 7.5 ms, L = 2.4 ± 0.7, d_s = 8.6 ± 1.7 μm, l_p = 743 ± 270 μm and d_p = 0.67 ± 0.19 μm. In tiger salamander (n = 13), for example, τ_m = 97 ± 72 ms, L = 0.34 ± 0.13, d_s = 18 ± 6 μm, l_p = 470 ± 90 μm and d_p = 1.4 ± 0.6 μm (Taylor et al. 1996). Developmental maturation of the passive electrical properties of RGC arbors has not been previously reported, although thorough anatomical investigations exist (see Introduction). Few electrophysiological studies of arbor development have been reported (Hochner & Spira, 1987; Ulfhake & Cullheim, 1988; Hill et al. 1994) and, although each neuron has its own characteristics, it is a common finding that dendritic development is not chaotic, and changes in passive properties can be either isometric or isoelectrotonic, but always well regulated.

Both impulse-encoding and synaptic efficacy in RGCs depend on the passive electrical properties of the cell (Coleman & Miller, 1989; Taylor et al. 1996; Sheasby & Fohlmeister, 1999). Hence, our results imply that in the course of development cell networks that include RGCs will continue to perform under remarkable control in spite of the fact that dendritic arbors are growing both in size and complexity. Isoelectrotonic maturation assures that the capability to generate action potentials by RGCs is robust and independent of their state of maturation. This is a desired feature given the fact that development of postsynaptic order in the CNS visual centres so depends on RGC impulse activity (review in Penn & Shatz, 1999; Wong, 1999). Isometric maturation is equally important, but serves a different purpose. This feature allows for the efficacy of synaptic inputs to change with development. This flexibility may be an important mechanism to allow varying input synaptic activity to modulate RGC maturation.