Abstract
We examined the tension (force) responses induced by rapid temperature jumps (T-jumps) in electrically stimulated, intact fibre bundles (5–10 fibres, fibre length ∼2 mm) isolated from a foot muscle (flexor hallucis brevis) of the rat; the muscle contains ∼90 % type 2 fast fibres. In steady state experiments, the temperature dependence of the twitch tension was basically similar to that previously described from other fast muscles; the tetanic tension increased 3- to 4-fold in raising the temperature from ∼2 to 35 °C and the relation between the tetanic tension and the reciprocal absolute temperature was sigmoidal with half-maximal tension at 9.5 °C. A rapid T-jump of 3–5 °C was induced during a contraction by applying an infrared laser pulse (λ= 1.32 μ, 0.2 ms) to the 50 μl trough containing the fibre bundle immersed in physiological saline. At ∼10 °C, a T-jump induced a large transient tension rise when applied during the rising phase of a twitch contraction, the amplitude of which decreased when the T-jump was delayed with respect to the stimulus; a T-jump probably perturbs an early step in excitation-contraction coupling. No transient increase was seen when a T-jump was applied during twitch relaxation. When applied during the plateau of a tetanic contraction a T-jump induced a tension rise to a higher steady tension level; the tension rise after a T-jump was 2–3 times faster than the corresponding phase of the initial tension rise in a tetanus. The approach to a new steady tension level after a T-jump was biphasic with a fast (phase 2b, ∼35 s−1 at 10 °C) and a slow component (phase 3, < 10 s−1). The rates of both components increased (Q10∼3) but their amplitudes decreased with increase of the steady temperature. These results from tetanised intact fibres are consistent with the thesis previously proposed from studies on Ca2+-activated skinned fibres, that the elementary force generation step in muscle is enhanced by increased temperature; the findings indicate that an endothermic molecular step underlies muscle force generation.
The basic event that underlies muscle contraction is an ATP-driven, cyclic, interaction of crossbridges (myosin heads) between thick (myosin) and thin (actin) filaments in a sarcomere (Huxley, 1957; Huxley & Simmons, 1971). Interpretation of the steady state contraction measurements from muscle is difficult because of the asynchrony of the cycling crossbridges during active muscle contraction and rapid perturbation methods have been used to induce crossbridge synchronisation. Following the original description by Ford et al. (1977) in intact frog muscle fibre, length perturbations applied to contracting muscle, have provided much of the background to our current knowledge of crossbridge force generation (see Piazzesi et al. 2002). The maximal active tension in mammalian muscle is sensitive to temperature and increases ∼2-fold in warming from 10 °C to more physiological temperatures (> 30 °C; see references in Ranatunga, 1994). Therefore, a rapid temperature jump (T-jump) also has been used to examine crossbridge kinetics in muscle fibres (Davis & Harrington, 1987; Goldman et al. 1987; Bershitsky & Tsaturyan, 1992). The experiments have shown that muscle force is generated in a temperature-sensitive (endothermic) step prior to the release of inorganic phosphate (Pi) during crossbridge cycling (Kawai & Halvorson, 1991; see references in Ranatunga, 1999a). The sigmoidal steady active force versus reciprocal temperature relation and its Pi sensitivity could be explained on the basis of such a scheme, where a single (force generation) step in the crossbridge cycle is enhanced by temperature (Coupland et al. 2001). Although considerable knowledge has been gathered using frog fibres (Bershitsky et al. 1997), mammalian fast skeletal (Davis & Harrington, 1987; Goldman et al. 1987; Bershitsky & Tsaturyan, 1992), slow skeletal and cardiac fibres (Ranatunga, 1996, 1999b), the rapid T-jump experiments to date have been limited to skinned muscle fibres.
Our primary aim in this study was to examine whether the general scheme proposed from skinned fibre experiments would account for experimental data from intact fibre preparations in which contractile activation is produced more physiologically by electrical excitation of the sarcolemma and involves the cellular processes of excitation-contraction coupling; moreover, intact fibres are mechanically more stable than skinned fibres so that many data could be collected over a wide range of temperatures from the same preparation. Experiments were done on bundles of 5–10 intact fibres isolated from the flexor hallucis brevis (FHB) muscle in the foot of the rat; fibres were short (∼2 mm), showed no deterioration during exposure to a wide range of temperatures and a preparation was small enough for laser T-jump experiments. Our data from intact fibres support the above thesis that the crossbridge force generation is endothermic and is particularly sensitive to temperature. Preliminary results from the study have been previously reported as abstracts (Coupland & Ranatunga, 2001a,b; Ranatunga & Coupland, 2002).
METHODS
Fibre bundle preparation
Experiments were performed on small bundles of fibres isolated from the FHB muscle of adult male rats (240–325 g body mass); FHB muscle was chosen because of its short fibres as required for laser temperature-jump (T-jump) experiments. Animals were killed with an i.p. injection of an overdose (∼150 mg (kg body weight)−1) of sodium pentobarbitone (Euthatal, Rhône Mérieux, France). Whole muscle was removed from the rat foot and placed in a petri-dish containing physiological saline solution (see below) bubbled with 95 % O2 and 5 % CO2 at room temperature. Small bundles of ∼5–10 intact excitable fibres were dissected from the mid-belly of the muscle under dark-field illumination. Small aluminium foil T-clips were fixed on the tendons within 0.2 mm of the fibre ends; resting fibre length was ∼2 mm and the major bundle width was ∼200 μm. Such a fibre bundle preparation was sufficiently small for laser T-jump experiments (see below).
Experimental methods
Steady state characterisation of the temperature dependence of force was done in a series of initial experiments using general methodology described previously (see Mutungi & Ranatunga, 2000). The preparation was set up in a 2 ml, flow through, stainless steel chamber for isometric tension recording. It was attached between two hooks, one connected to a force transducer (resonant frequency 6 kHz), the other to a servomotor, and was superfused with physiological saline solution containing (mm) NaCl 109; KCl 5; MgCl2 1; CaCl2 4; NaHCO3 24; NaH2PO4 1; sodium pyruvate 10 and 200 mg l−1 of bovine fetal serum. The solution was bubbled continuously with a mixture of 95 % O2 and 5 % CO2. The solution temperature (range 2–35 °C) was controlled by means of a Peltier device and monitored with a thermocouple in the muscle trough throughout the experiment.
The trough system previously used for skinned fibre experiments was modified for use in the T-jump experiments with intact fibre bundles (see Fig. 1). Thus, the 50 μl front glass trough housed a pair of platinum plates that acted as stimulating electrodes. The platinum foil electrodes were glued to the front window and the back wall of the trough, the front one being below the path of the neodymium-YAG (Nd-YAG; Schwartz Electro-Optics, Orlando, FL, USA) laser beam to avoid shadowing the fibres. The electrode lining the back wall replaced the aluminium lining that reflected the laser beam (see Ranatunga, 1996) in skinned fibre experiments. Oxygenated physiological saline solution within the trough was replaced manually with a pipette every 5–10 min. The resonant frequency of the force transducer used in the T-jump experiments was 14 kHz (see Ranatunga, 1999a).
Figure 1. A schematic diagram of the trough system used in laser T-jump experiments.
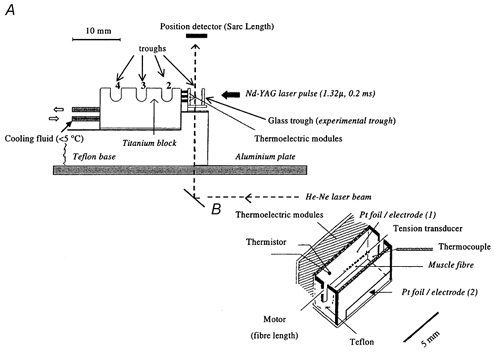
A, the system consists of three troughs milled in a titanium block and a front trough that was built with glass front and bottom windows and used as the experimental trough. Cooling fluid, circulated within the titanium block, acted as a heat sink. The trough system was fixed on a Teflon block (a heat insulator), that could be moved along the aluminium plate by a lever mechanism (not shown) to expose, in skinned fibre experiments, a preparation to different solutions. B, an enlarged view of the front glass experimental trough. An intact fibre bundle was attached, by aluminium foil clips, between two metal hooks, one connected to a force transducer and the other to a servomotor. The experimental trough temperature was clamped using thermoelectric modules that were under thermistor feedback control, and it was monitored by a thermocouple placed near the fibre bundle. Supramaximal voltage stimuli (0.2–0.5 ms) were delivered via two platinum foil electrodes glued to the front window and the back wall of the trough, the one in the front window being narrower to prevent fibre shadowing by the heating laser pulse. The Nd-YAG laser pulse (λ= 1.32 μ, pulse duration = 0.2 ms, elliptical cross-section ∼2 mm × 5 mm) entered through the front window, it was partially absorbed in solution and reflected by the platinum foil on the back wall. The transducer hooks and the aluminium T-clips were shadowed from the laser beam (not shown). The energy absorption of ∼50 % during the 0.2 ms pulse heated the solution and fibre bundle by 3–5 °C and the elevated temperature in the trough solution remained constant for ∼500 ms (for details see Ranatunga, 1996).
The basic technique of inducing T-jumps was as described previously (see Ranatunga, 1996; 1999a). Briefly, the whole trough assembly was kept <5 °C by cooling fluid, and the front trough temperature was clamped at a required initial temperature by means of thermoelectric modules on the back of the trough; the thermoelectric modules were under feedback control from a small (0.4 mm) thermistor in the trough (see Fig. 1). A T-jump of 3–4 °C was induced in the front trough by a 0.2 ms Nd-YAG laser pulse radiation (λ= 1.32 μm) applied through the front glass window. The beam was reflected back by the platinum foil on the back wall and its absorption increased solution temperature. When monitored with a small 20 μm thermocouple with a response time constant of ∼1–2 ms, the increased solution temperature remained constant for ∼500 ms after the laser pulse (see Ranatunga, 1996 for other details). For convenience, the solution temperature was measured using larger 0.2–0.4 mm thermocouples in the present experiments and the temperature at ∼300 ms after a laser pulse was taken to be the amplitude of a T-jump.
The method of electrical stimulation of intact mammalian fibre bundles was basically similar to that described previously (see Ranatunga, 1984). In the trough system used for steady state experiments, the electrodes were two 15 mm × 4 mm platinum plates, placed 7 mm apart, parallel to and on either side of the bundle. The electrodes in the T-jump apparatus were somewhat smaller and placed ∼3 mm apart (see Fig. 1). Unipolar square-wave voltage pulses from a stimulator were connected to the electrodes via a 6:1 stepdown transformer. The durations of stimulating pulses used were 200–500 μs and the intensity required for supramaximal stimulation was 30–50 V.
Experimental protocols
In a typical experiment, the bundle was first set up for tension recording at rest length at 20 °C by observing under a microscope, then adjusted if necessary for optimal twitch and tetanic contractions. The full range of resting sarcomere length determined by He-Ne laser diffraction was 2.49- 2.7 μm in different preparations. Continuous monitoring of sarcomere length by laser diffraction proved to be difficult with these preparations due to high light scattering from the fibre bundle surface. In some steady state experiments, however, sarcomere length was monitored using a diffractometer at various stages of an experiment; following an intial shortening phase during the tension rise, the sarcomere length remained approximately constant during the tension plateau of a tetanic contraction. Twitch contractions were elicited every 90 s using single supramaximal stimuli and tetanic contractions were elicited at longer intervals (>5 min). Following a minimum equilibration period of ∼30 min at 20 °C, we recorded twitch and tetanic contractions at 5 °C intervals during cooling and warming over a wide temperature range (∼5–35 °C), in order to determine steady state force behaviour. An equilibration period of about 10 min was allowed at each new temperature, and the tetanic stimulation frequency and train duration were adjusted to obtain fused tetanic contractions with tension plateaux at each temperature. Stimulation frequency ranged from 22.5 Hz at 5 °C to ∼300 Hz at 35 °C. At the end of the experiment, tetanic tension was remeasured at 20 °C. The total duration of the procedure was ∼3 h. Following some experiments, a fibre bundle was maintained in oxygenated physiological saline solution, and was found to remain excitable under these conditions for more than 24 h. In many of the T-jump experiments, a T-jump was induced on the plateau of a tetanic contraction at 10–12 °C; in each of three experiments, T-jump tension transients were examined over a wider temperature range (5–30 °C). In four experiments we examined the effect on the twitch of a T-jump applied during the twitch time course.
Recording, analyses and nomenclature
With either system, the outputs of the tension transducer and the thermocouple were observed on a digital cathode ray oscilloscope, collected via CED 1401 laboratory interface using Signal Averager software (Cambridge Design Ltd, Cambridge, UK) and stored on a personal computer. A chart recorder was also used to monitor overall changes in muscle tension throughout the experiment. Tension and time course measurements from stored traces were made using Signal Averager software and further analyses and curve fitting were done using Fig P software (Biosoft, Cambridge, UK). The tension transient induced by a T-jump applied on the plateau of a tetanus could be fitted with a double exponential function extracting two components. For compatibility with the nomenclature used in our previous studies (see Vawda et al. 1999; Ranatunga, 1999b; Ranatunga et al. 2002), the two components will be referred to as phases 2b (fast) and 3 (slow).
The rationale for adopting the nomenclature used here was to accommodate findings from different types of perturbation and it is briefly as follows. The tension change that occurs concomitant with a perturbation is referred to as phase 1, where the extreme force reached is T1, as used in the original length perturbation experiments (Huxley & Simmons, 1971). An instantaneous drop in tension is indeed seen in T-jump and pressure-release (P-jump) experiments, and is probably induced by expansion in some series elasticity. A T-jump or a P-jump induces a drop in force in rigor muscle fibres and this provides support for the expansion in some elasticity in muscle fibres (see Goldman et al. 1987; Ranatunga, 1994; Vawda et al. 1999). After a length perturbation, the tension recovers quickly from T1 to T2 level and this quick tension recovery can be resolved into two exponential components (Davis & Harrington (1993) - here referred to as phase 2a (very fast) and phase 2b. The force generation, i.e. tension rise above the pre-perturbation level, induced by a T-jump and a P-jump corresponds to phase 2b (see Ranatunga et al. 2002). In T-jump and P-jump experiments where a prominent phase 1 was seen (see Goldman et al. 1987; Ranatunga, 1999b; Vawda et al. 1999), a quick tension recovery corresponding to phase 2a is also seen which partially recovers the force drop during phase 1, as in length perturbation. In the T-jump experiments reported here, the phase 1 amplitude was small and it was not analysed. Consequently, the quick phase 2a was not obtained and the approach to a new higher steady tension level after a T-jump occurred in two phases, a moderately fast phase 2b and a slow phase 3; the phase 2b is considered to represent force generation in attached crossbridges.
General considerations: fibre type composition of FHB muscle
In a study of the fibre type composition of the entire hind limb of the rat, Armstrong & Phelps (1984) found the proportion of slow twitch fibres to be about 5 %, although no specific study of the FHB has been carried out. We therefore made a preliminary examination of the fibre type composition of FHB muscle. Frozen sections (10 μm thick) cut from approximately the same region as that used for bundle isolation, were stained for myosin ATPase using a method based on that of Guth & Samaha (1970). With alkaline pre-incubation (pH range 10.1–10.5), the light-stained fibres were classified as type 1 (slow), dark- and intermediate-stained were classified as type 2 (fast). A total of nine anatomically distinct fascicles, each containing 30–40 fibres, were used to determine the fibre type composition and fibre cross-sectional area. From a total of > 300 fibres, 9.5 % were light-stained, 6.0 % were intermediate-stained and 84.5 % were dark-stained. Complementary data were obtained with acid pre-incubation (pH range 4.1–4.7; 80–90 % fast). Mean ±s.e.m. fibre cross-sectional area, determined using a digitiser interfaced with a PC, was 1302 ± 56 μm2 for slow fibres (n = 35), 739 ± 44 μm2 for intermediate fibres (n = 21) and 751 ± 15 μm2 for fast fibres (n = 311). Thus, slow fibres had a larger cross-sectional area than fast fibres (ANOVA, P < 0.001). On the basis of the above findings, a fibre bundle used in our experiments would contain a majority of fast fibres. Since slow fibres were never grouped together, the number of slow fibres may have varied from zero to a maximum of two in a bundle (of 10 fibres) isolated from the fascicles. Although the cross-sectional area of slow fibres is larger (∼2-times that of fast), the force/cross-sectional area is smaller (∼0.5-times that of fast, M. E. Coupland & K. W. Ranatunga, unpublished observations from skinned fibre experiments) than in fast fibres. Thus, during force recording from a bundle, the force contribution from slow fibres in a bundle would have been less than 20 % and probably around 10 %.
RESULTS
Steady state force-temperature relations
Figure 2 shows superimposed twitch and tetanic contractions at a number of different temperatures from one fibre bundle. Contractions were first recorded in cooling from 20 to 5 °C (top row) and then during warming from 5 to 35 °C; the bottom row shows the recordings from 25 to 35 °C and the final contraction recordings at 20 °C. It can be seen that both twitch and tetanic tensions increase with increase of temperature from 5 to 25 °C. The tetanic tension increases little on further warming to 35 °C, whereas the twitch tension declines markedly on warming between 30 and 35 °C (see lower frames). The contractions became very prolonged at the low temperatures; for instance, the mean ±s.e.m. time-to-peak-twitch tension was 790 ± 116 ms at 5 °C and the half-relaxation time was 3907 ± 907 ms (n = 3) as compared with 33 ± 3 ms (time-to-peak) and 60 ± 9 ms (time to half-relaxation) at 35 °C.
Figure 2. Twitch and tetanic contractions at different temperatures.
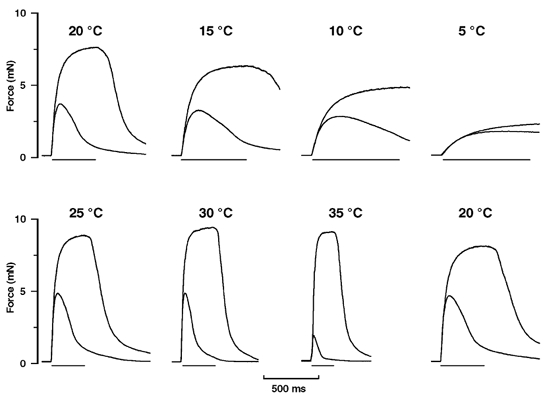
Superimposed twitch and tetanic contractions recorded from one preparation at various temperatures. The upper series of frames shows contractions first recorded at 20 °C and then at 5 °C intervals during cooling to 5 °C, and the lower series shows those during warming to 35 °C. Contractions recorded finally at 20 °C are shown in the bottom right frame; the duration of the whole experimental procedure was ∼3 h. Note that the peak twitch tension is highest at ∼25 °C and is lower at higher and lower temperatures. The increase of twitch tension from 35 to 20–25 °C, as obtained in fast mammalian muscles, is commonly referred to as ‘cooling potentiation’. The horizontal bar below each frame shows the duration of the tetanic stimulus train; frequency was adjusted to obtain fused tetanic contractions (see Methods). The tetanic tension increases with increased temperature but the relative increase is higher at temperatures below ∼20 °C.
Pooled data from eight fibre bundles were used to determine the steady state temperature dependence of tension over the range ∼5–35 °C. Fibre bundles remained in good condition during the course of an experiment, so that the ratio of the tetanic tension at the end of the experiment compared to that of the initial contraction at 20 °C was 1.01 ± 0.03 (mean ±s.e.m., n = 8). Figure 3A shows the mean ±s.e.m. twitch and tetanic tensions (in kN m−2) plotted against reciprocal absolute temperature (103 K/T). The specific tetanic tensions at 35, 25 and 10 °C were 371 ± 23, 359 ± 17 and 205 ± 13 kN m−2, respectively. These values are similar to data obtained from Ca2+-activated skinned fibres from rabbit psoas (Coupland et al. 2001) and they also compare well with specific tension of 375 kPa at 25 °C reported from intact single fibres from mouse muscle (Lannergren & Westerblad, 1987). The peak twitch tension in fast twitch muscles from several mammalian species has been shown to increase on cooling from 35–38 to 20 °C and this is referred to as ‘cooling potentiation’; twitch tension of a slow muscle decreases with a similar procedure (see Buller et al. 1984 and references therein). The twitch tension data from FHB muscle shown in Fig. 3A indeed show cooling potentiation between 35 and 25 °C; tension decreases in further cooling, as found in other rat fast muscle experiments (Wylie & Ranatunga, 1987). Figure 3B shows the pooled tetanic tension data from the same experiments where the tensions at other temperatures from a preparation were normalised to its tension at 35 °C; a sigmoidal curve is fitted to the data (see Coupland et al. 2001). It is seen that the tetanic tension versus reciprocal temperature relation is sigmoidal: the temperature at which the tension is half-maximal (from the curve) is 9.5 °C. The data below ∼5 °C seem not to be well fitted to the curve; we cannot rule out the possibility that some muscle fibres lose excitability at such low temperatures.
Figure 3. Temperature dependence of twitch and tetanic tensions.
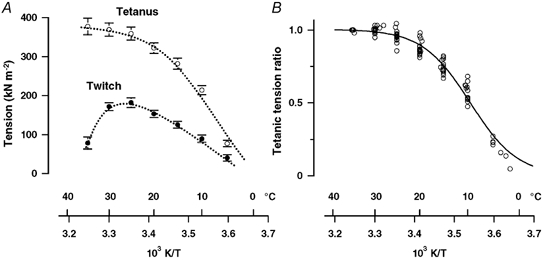
A, mean ±s.e.m. twitch tension (filled symbols) and tetanic tension (open symbols) from eight preparations. Tension per cross-sectional area is plotted on the ordinate and reciprocal absolute temperature on the abscissa. (Note that data for 5 °C and below are from three fibre bundles only.) The twitch tension increases linearly with temperature in the range 5–25 °C but declines at higher temperatures. Tetanic tension increases with increase of temperature, but the increase is less marked between ∼25 and 35 °C. B, tetanic tension data in A are plotted after normalisation to that at 35 °C. The relationship between tetanic tension and reciprocal temperature is approximately sigmoidal with half-maximal tension occurring at 9.5 ± 0.2 °C. The data at temperatures < 5 °C, however, are not well fitted to the curve.
The temperature dependence of the rate of tension rise and the rate of tension relaxation in tetanic contractions was also determined by using half-time measurements (not illustrated). As found in whole-muscle experiments (Ranatunga & Wylie, 1983), both the rate of tension rise (reciprocal half-time) and the rate of tension relaxation increased with rising temperature and were more temperature-sensitive below 20 °C. Similar differences in the temperature sensitivity between high and low temperature ranges were also found for twitch time course measurements.
T-jump experiments
Although the main aim of this study was to examine effects of a T-jump during tetanic contractions, tension changes induced during a twitch contraction were also examined in four experiments. The interesting observation made from these experiments was that the effect of a T-jump was dependent on its time of occurrence in relation to the twitch time course. Figure 4 shows sample records of twitch contractions from one preparation at 10 °C, where a T-jump is indicated in each frame by an arrow; a twitch without a T-jump is superimposed in the left frame. It is seen that following a T-jump the twitch tension relaxation becomes faster, but that a T-jump induces transient net rise of tension, the amplitude of which is larger when a T-jump is applied during the twitch rising phase. Indeed a net tension rise was barely discernible when a T-jump was applied during the twitch relaxation phase (see Fig. 4D).
Figure 4. Tension transients induced by T-jump during twitch contractions.
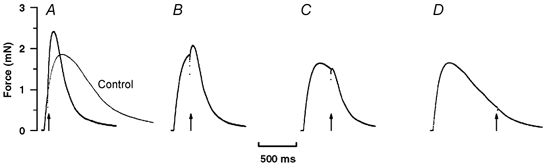
A T-jump of ∼4 °C was induced at different times during the course of a twitch, at a steady temperature of 10 °C; a superimposed control twitch (without T-jump) is also shown in A. Records show that a T-jump (arrow) induces an increased tension relaxation. Interestingly, a T-jump also produces a transient increase of tension that is very pronounced when the T-jump is applied on the rising phase of a twitch; it is considerably diminished or absent on the relaxation phase.
Figure 5A shows a tetanic contraction from one preparation elicited at 10 °C where a standard T-jump of 4 °C was applied during the tension plateau; it is seen that following a small instantaneous drop (phase 1) in tension, the tension rises to a new steady level after a T-jump. A T-jump-induced tension transient could be fitted with a bi-exponential curve as shown on the expanded time scale in Fig. 5B; the fast and the slow components so extracted are referred to as phases 2b and 3 respectively (see Methods). An initial quick recovery phase (phase 2a) was not seen, probably due to small amplitude of phase 1. The effect of a 3–4 °C T-jump was examined in seven fibre bundles at a steady temperature of 10 °C. The mean ±s.e.m. rates obtained by curve fitting from these experiments were 34 ± 4 s−1 and 8.3 ± 0.8 s−1, respectively for the fast (phase 2b) and slow (phase 3) phases. Expressed as percentages of steady tension prior to the T-jump, the mean ±s.e.m. amplitudes were 12 ± 1.9 % and 24 ± 2.3 %, respectively. There was a slow small creep in tension during the tension plateau in some cases but their occurrence was ignored in the analyses.
Figure 5. Tension responses induced by T-jump on tetanic contractions.
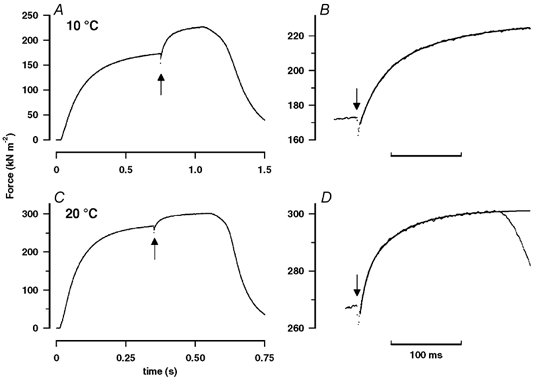
A, a temperature jump of ∼4 °C was induced by a laser pulse (indicated by the arrow), during the tension plateau of a tetanic contraction at 10 °C. The T-jump induces a small instantaneous drop in tension (phase 1) followed by a rise to a new steady level. B, the T-jump-induced tension rise is shown on an expanded time scale (horizontal bar is 100 ms). A bi-exponential curve is fitted to the tension transient and the exponential rates for phases 2b and 3 were 37 s−1 and 9 s−1, respectively. C and D, a corresponding pair of records from the same preparation but at 20 °C. The pre-T-jump tetanic tension is ∼1.5 times that at 10 °C, but the tension increment induced by the T-jump is smaller (∼0.6 times that at 10 °C). As a percentage of the pre-T-jump tension, the tension increment after a T-jump is ∼30 % at 10 °C (A) and only 10 % at 20 °C (C). Comparison of B with D shows that the tension rise to the new steady level is faster at 20 °C. The small slow creep in pre-T-jump tension as seen in D was ignored in the analyses.
The effect of a standard T-jump from the same fibre bundle, but at a higher steady temperature of 20 °C, is shown in Fig. 5C. As observed in steady state experiments (Fig. 3), the steady tension before the T-jump is 50–60 % greater at 20 than at 10 °C (compare Fig. 5A and C, note different tension scales on the ordinates). However, the T-jump-induced tension rise is faster but its relative amplitude smaller than at 10 °C (compare Fig. 5B and D). Tension transients induced by a standard T-jump (3–5 °C in different experiments) were recorded at a range of temperatures in experiments on four bundles. When the pre- and post-T-jump tensions were plotted against reciprocal absolute temperature, the tension data could be fitted with a single sigmoidal curve with half-maximal tension at 8.2 °C (not illustrated). Thus, the tension reached after a T-jump is similar to the steady tension recorded in a tetanic contraction elicited at the higher temperature. In order to analyse the data further, the temperature sensitivity of tension, i.e. the tension increment per °C T-jump, was calculated and it is plotted as a percentage of the pre-T-jump tension (see Fig. 9B in Goldman et al. 1987) against the reciprocal of absolute temperature in Fig. 6A (see legend). The data show that the temperature sensitivity of tension decreases sharply with increase of temperature, more or less as expected from the sigmoidal tension versus reciprocal temperature relation obtained from steady state experiments; the temperature sensitivity of tension per °C decreases from ∼10 % at ∼10 °C to < 3 % at high temperatures (>30 °C).
Figure 6. Characteristics of T-jump-induced tension rise.
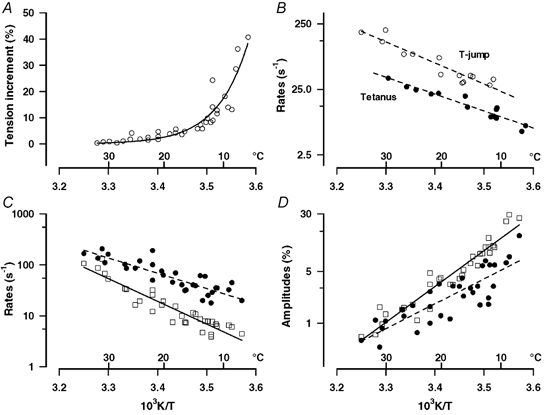
A, the tension increment per °C of T-jump is plotted on the ordinate as a percentage of the pre-T-jump tetanic tension and the mid-temperature of the T-jump as 103 K/T on the abscissa (as in Fig. 9B of Goldman et al. 1987). Note that the T-jump-induced tension enhancement decreases markedly as the temperature is increased; it is ∼10 % per °C at 10 °C whereas it is < 3 % per °C at high physiological temperatures (>30 °C). B, data from one experiment, comparing the rates of the tetanic tension rise (above ∼50 % tension level) and of the T-jump-induced tension generation; the faster of the two exponential components (from curve fitting to each trace) is plotted against pre-T-jump temperature for tetanus rise (filled symbols) and against post-T-jump temperature for T-jump tension rise (open symbols). The T-jump-induced force generation (phase 2b) is consistently (∼2.5 times) faster than the tetanic tension rise. The rate (C) and the amplitude (as percentage tension per °C of T-jump, D) of the two exponential components of the T-jump-induced transient (filled circles, phase 2b; squares, phase 3) extracted by curve fitting (as shown in Fig. 5C and D) are plotted on logarithmic ordinates against the post-T-jump reciprocal absolute temperature; lines through the points are the calculated regressions (n = 31; r > 0.8). Note that the rate constants of the two components increase with increase of temperature; for 20/10 °C, Q10 is 2.3 for phase 2b and 3.5 for phase 3. Their amplitudes decrease with increase of temperature.
It was observed that the tension rise after a T-jump in any given preparation was faster than the rising phase in the tetanus. The two events however occur at two different temperatures (post- and pre-T-jump temperatures). Moreover, the initial tension rise at the beginning of a tetanus may be limited by process(es) of contractile activation. Thus, in order to make a more quantitative comparison, a bi-exponential function was fitted to the tetanic tension rise (as for the T-jump transient) above ∼50 % tension level. Figure 6B shows data from one experiment comparing the rate of tension rise in a tetanus and the rate of tension rise after a T-jump applied on the tetanic tension plateau. The data show the rate of the fast component (filled circles) from tetanic rise plotted against the pre-T-jump temperature and the fast rate (phase 2b) from the T-jump transient (open circles) plotted against the post-T-jump temperature. The data show that the tension rise after T-jump is 2–3 times faster than in the corresponding phase of the initial tension rise in a tetanic contraction at all the temperatures. The temperature dependence of the characteristics of the T-jump-induced tension transient from four preparations is illustrated in Fig. 6C and D. The rate constants for fast (phase 2b, filled circles) and for slow (phase 3, squares) components are shown in Fig. 6C and their amplitudes normalised to the pre-T-jump steady tension (and per °C) are shown in Fig. 6D. The rates of both components increase with rising temperature (Q10= 2.3, 3.6 for the two rates); the amplitudes decrease with increase of temperature as would be expected from the data in Fig. 6A.
DISCUSSION
Comparison with previous studies
The potentiation of peak twitch tension in cooling from 35 to 25 °C is basically comparable to that of the more commonly used fast extensor digitorum longus (EDL, a calf muscle) of the rat (Wylie & Ranatunga, 1987); EDL muscle contains a predominance of type 2 histochemical fibre type. The comparison indicates that flexor hallucis brevis (FHB, a foot muscle) is a fast muscle, although it is not known whether it contains a predominance of type 2B fibres, as is the case in EDL muscle (see Ranatunga & Thomas, 1990). The marked non-linear temperature dependence of tetanic tension, obtained here from small bundles of intact fibres from FHB muscle, is basically similar to that reported in previous studies using muscle strips (Hadju, 1951; Isaacson et al. 1970), whole fast and slow muscles (Ranatunga & Wylie, 1983) and, also, single skinned muscle fibres (Stephenson & Williams, 1985). Additionally, the present results show that the temperature dependence of steady tetanic tension - when examined over a wide temperature range of 5–35 °C - is sigmoidal with a half-maximal tension occurring at ∼9.5 °C. This compares favourably with our recent finding from rabbit skinned psoas fibres, that the Ca2+-activated force versus reciprocal temperature relation is sigmoidal with a half-maximal tension at ∼8 °C (Coupland et al. 2001). It is relevant to note that, whereas the chemical/ionic composition (e.g. pH, Mg2+ etc.) around myofibrils is held approximately constant in skinned fibre experiments, it may have changed with temperature in intact fibres; the overall similarity between the data presumably implies that such temperature-dependent changes are not large in intact fibres with the experiment methods and protocols adopted here (see also Methods in Ranatunga, 1984).
Previous experiments on other mammalian fast and slow muscles have shown an increased temperature sensitivity of the rates of tension rise and relaxation in physiological tension responses (twitch and tetanic contractions) in cooling below ∼20 °C (see Ranatunga & Wylie, 1983). The same basic observation was made here, but the significance remains unclear. Compared to other muscle preparations used in previous studies, the FHB is a peripheral muscle in the mammalian body and it might be exposed to a wide temperature range during normal life (as suggested by Lannergren & Westerblad, 1987). Indeed, it has been shown experimentally that the temperature of in situ peripheral muscles (e.g. hand muscles) in the human body can change readily with changes in the skin temperature (see Ranatunga et al. 1987; De Ruiter et al. 1999). In contrast, the temperature in more centrally located muscles, such as psoas and cardiac, is likely to remain constant and near the core body temperature, which in mammals including rats would be 37–39 °C. It is therefore of considerable physiological interest to note the general similarity in the temperature dependence of the maximum muscle force, and other features, found in the different studies. Thus, it appears that the sigmoidal form of the tension versus reciprocal temperature relation and the temperature sensitivity differences at high and low temperatures are basic characteristics of all mammalian striated muscle, irrespective of their location in the body and whether or not they become exposed to large temperature changes.
T-jump experiments
It is of interest to note that exposure to infrared laser radiation did not produce deleterious effects in the excitability or the tension responses of intact muscle fibres, indicating that the absorption of the laser pulse energy only produces a rapid T-jump in the aqueous phase. When applied during a twitch, which represents a transient submaximal tension response initiated via a complex sequence of steps providing the excitation-contraction (E-C) coupling, the rate of tension relaxation was increased. T-jump induced enhancement of Ca2+ uptake by sarcoplasmic reticulum may underlie such a change. A pronounced transient increase of tension was observed when the T-jump was applied on the rising phase of a twitch. One may speculate that the rising phase of a twitch is limited by a step in E-C coupling (e.g. Ca2+ release/concentration) and this is accelerated by a T-jump. Previous experiments showed that an early event is sensitive to hydrostatic pressure changes (Vawda et al. 1995); whether these different experiments point to the same step, however, remains unclear. The tension rise occurs without a discernible delay and, hence, it may be partly due to enhancement of crossbridge force generation by a T-jump (see below). Thus, the laser T-jump technique may be a useful technique to dissect out the complex of processes involved in E-C coupling in intact muscle fibres.
When applied during the steady tension plateau of a tetanic contraction a T-jump induced a small concomitant tension drop (phase 1) as also found in skinned fibre experiments; this is thought to represent an effect of expansion in some series elasticity (Ranatunga, 1996). Phase 1 tension drop was followed by a tension rise to a new steady level above the pre-T-jump tension. In experiments on the same preparation, the amplitude of the tension rise induced by a standard T-jump was smaller, the higher the initial pre-T-jump temperature. Also, the tension rise began without any discernible delay after a T-jump and the tension level reached was similar to the plateau tension recorded in a tetanic contraction induced at the post-T-jump temperature. Consequently, the temperature dependence of tension determined from the steady state experiments, shown in Fig. 3B, and the temperature sensitivity of tension, i.e. tension increment per °C obtained from rapid T-jumps, shown in Fig. 6A, show considerable inter-correspondence. As expected from the sigmoidal steady state tension versus reciprocal temperature data with a half-maximal tension at 9.5 °C, the tension increment per °C rise of temperaure (i.e. the slope of the sigmoidal curve) increases nonlinearly in lowering the temperature, and the increase becomes pronounced below ∼10 °C. The findings indicate that the endothermic nature of muscle force generation underlies the sigmoidal relation between steady muscle force and reciprocal temperature. This was the sort of interpretation put forward from our skinned fibre experiments (Coupland et al. 2001; see also Davis, 1998). The present findings from intact fibre preparations, in which data at a range of temperatures could be obtained from the same preparation with and without T-jumps and without fibre deterioration, lend strong support to that thesis. It is also relevant to note that the skinned fibre experiments identified the particular force generation step as one preceding the release of inorganic phosphate (Pi) during acto-myosin ATP hydrolysis.
The tension transient induced by a laser T-jump in tetanised intact muscle fibres is biphasic and is basically similar to that reported in several previous studies on skinned fibres (see Davis & Harrington, 1987; Goldman et al. 1987; Bershitsky & Tsaturyan 1992; Ranatunga, 1996). An additional early quick recovery, phase 2a (see Methods) could not be identified probably because the tension drop during phase 1 was small; this was also the case in our recent skinned fibre experiments (Ranatunga, 1999a). In a recent study, Bershitsky & Tsaturyan (2002) found that the time course of the T-jump-induced tension transient in sarcomere-clamped skinned muscle fibres is not biphasic and cannot be described by exponential curve fitting. It is unclear whether this is due to the different techniques employed (see Davis, 1998); for instance, they employed large T-jumps from 5–6 °C to 16–33 °C in their experiments and the T-jumps were produced by passing a brief current through a fibre held in air, and also their experiments employed sarcomere length clamping. When small amplitude T-jumps from ∼9 °C to ∼12 °C were induced by laser pulses in skinned muscle fibres immersed in aqueous medium, we could clearly identify two phases - a fast phase (phase 2b, ∼50 s−1) and a slow phase (phase 3, < 10 s−1) by curve fitting (see also Goldman et al. 1987; Davis & Harrington, 1993; Davis & Rodgers, 1995). Moreover, the phase 2b became faster and the slow phase 3 became slower with increasing [Pi] (see Ranatunga, 1999a) suggesting their different origins.
Our present observations using small (∼4 °C) T-jumps on tetanised intact fast fibres compare favourably with our findings on maximally Ca2+-activated skinned fast fibres; thus, at ∼10 °C, the rate of phase 2b is ∼40 s−1 and that of the slow phase 3 is ∼9 s−1. Although the possibility cannot be completely excluded, the occurrence of two phases is probably not due to admixture of fast and slow fibres in a bundle. This is evident from the fact that a ∼20 % slow fibre component with low specific tension (50 % of fast fibre) would make only ∼10 % tension contribution, whereas the amplitude of the slow phase in a transient is ∼50 %. With increase of temperature, the rate increased and the amplitude decreased in both components. There is general agreement among different workers that the faster component arises from perturbation of attached crossbridges suggesting that crossbridge force generation is endothermic; thus the equilibrium between low force and high force crossbridge states is shifted towards the high force state when temperature is abruptly increased. The identity and existence of the slower phase 3 (see above), however, remain unclear. As suggested previously (see Ranatunga, 1999a) it may represent a slower step that the crossbridges pass through in completing the cycle after a temperature perturbation.
The difficulties in correlating T-jump force generation with quick (T1 to T2) tension recovery after length-release have been raised in a number of previous studies. T-jump force generation is slower than quick tension recovery in length-release (Ranatunga, 1999b; Bershitsky & Tsaturyan, 2002), the two events have different [Pi] sensitivities (Ranatunga et al. 2002) and, from X-ray diffraction experiments, the two events are associated with different structural changes (see Bershitsky et al. 1997). An original observation made here is that the T-jump force generation (phase 2b) was 2–3 times faster than the rate of tension rise in the corresponding rising phase of a tetanic contraction at the same (post-T-jump) temperature (see Fig. 6B). In their length perturbation experiments on intact frog fibres, Ford et al. (1977) observed that the final phase 4 of tension recovery after length-release was very similar to the late phase of tension rise in tetanus. The phase 4 after length-release is considered to reflect crossbridge cycling/re-attachment, and our results show that T-jump-induced force generation represents an event that is faster than phase 4. This is expected if, as postulated, a T-jump enhances force generation in attached crossbridges.
Conclusion/uncertainties
The two main uncertainties are, firstly, fibre bundles rather than single fibres were used in the experiments, and the exact fibre type composition of a bundle was not known. Secondly, sarcomere length recording and clamping were not done in these intact fibre bundles during T-jumps. Both these factors would have influenced the kinetics of the tension transients described and also contributed to the scatter in the data. Therefore the interpretations given above should be treated with some caution, although we consider that the basic similarity with the skinned fibre data is probably significant.
Acknowledgments
We thank the Wellcome Trust Foundation for support of our research.
references
- Armstrong RB, Phelps RO. Muscle fiber type composition of the rat hind limb. Am J Anat. 1984;171:259–272. doi: 10.1002/aja.1001710303. [DOI] [PubMed] [Google Scholar]
- Bershitsky SY, Tsaturyan AK. Tension responses to joule temperature jump in skinned rabbit muscle fibres. J Physiol. 1992;447:425–448. doi: 10.1113/jphysiol.1992.sp019010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bershitsky SY, Tsaturyan AK. The elementary force generation process probed by temperature and length perturbations in muscle fibres from the rabbit. J Physiol. 2002;540:971–988. doi: 10.1113/jphysiol.2001.013483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bershitsky SY, Tsaturyan AK, Bershitskaya ON, Mashanov GI, Brown P, Burns R, Ferenczi MA. Muscle force is generated by myosin heads stereospecifically attached to actin. Nature. 1997;388:188–190. doi: 10.1038/40651. [DOI] [PubMed] [Google Scholar]
- Buller AJ, Kean CJC, Ranatunga KW, Smith JM. Temperature dependence of isometric contractions of cat fast and slow skeletal muscles. J Physiol. 1984;355:25–31. doi: 10.1113/jphysiol.1984.sp015403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coupland ME, Puchert E, Ranatunga KW. Temperature dependence of active tension in mammalian (rabbit psoas) muscle fibres: effect of inorganic phosphate. J Physiol. 2001;536:879–891. doi: 10.1111/j.1469-7793.2001.00879.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coupland ME, Ranatunga KW. Temperature dependence of tetanic contraction of a small skeletal muscle (Flexor hallucis brevis) from rat. J Physiol. 2001a;536:162. P. [Google Scholar]
- Coupland ME, Ranatunga KW. Maximal active tension versus temperature relation in mammalian muscle fibres. J Musc Res Cell Motil. 2001b;22:599. [Google Scholar]
- Davis JS. Force generation simplified. Insights from laser temperature-jump experiments on contracting muscle fibres. In: Sugi H, Pollack GH, editors. Mechanisms of Work Production and Work Absorption in Muscle. New York: Blackwell Science Inc; 1998. pp. 343–352. [PubMed] [Google Scholar]
- Davis JS, Harrington W. Force generation by muscle fibers in rigor: a laser temperature-jump study. Proc Natl Acad Sci U S A. 1987;84:975–979. doi: 10.1073/pnas.84.4.975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis JS, Harrington W. A single order-disorder transition generates tension during the Huxley-Simmons phase 2 in muscle. Biophys J. 1993;65:1886–1898. doi: 10.1016/S0006-3495(93)81259-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis JS, Rodgers ME. Indirect coupling of phosphate release to de-novo tension generation during muscle contraction. Proc Natl Acad Sci U S A. 1995;92:10482–10486. doi: 10.1073/pnas.92.23.10482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeRuiter CJ, Jones DA, Sargeant AJ, De Haan A. Temperature effect on the rates of isometric force development and relaxation in fresh and fatigued human adductor pollicis muscle. Exp Physiol. 1999;84:1137–1150. doi: 10.1017/s0958067099018953. [DOI] [PubMed] [Google Scholar]
- Ford LE, Huxley AF, Simmons RM. Tension responses to sudden length change in stimulated frog muscle fibres near slack length. J Physiol. 1977;269:441–515. doi: 10.1113/jphysiol.1977.sp011911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman YE, McCray JA, Ranatunga KW. Transient tension changes initiated by laser temperature jumps in rabbit psoas muscle fibres. J Physiol. 1987;392:71–95. doi: 10.1113/jphysiol.1987.sp016770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guth L, Samaha FJ. Research note. Procedure for the histochemical demonstration of actomyosin ATPase. Exp Neurol. 1970;28:365–367. [PubMed] [Google Scholar]
- Hajdu S. Behaviour of frog and rat muscle at higher temperatures. Enzymologia. 1951;14:187–190. [PubMed] [Google Scholar]
- Huxley AF. Muscle structure and theories of contraction. Prog Biophys. 1957;7:285–318. [PubMed] [Google Scholar]
- Huxley AF, Simmons RM. Proposed mechanism of force generation in striated muscle. Nature. 1971;233:533–538. doi: 10.1038/233533a0. [DOI] [PubMed] [Google Scholar]
- Isaacson A, Hinkes MJ, Taylor SR. Contracture and twitch potentiation of fast and slow muscles of the rat at 20 and 37 °C. Am J Physiol. 1970;218:33–41. doi: 10.1152/ajplegacy.1970.218.1.33. [DOI] [PubMed] [Google Scholar]
- Kawai M, Halvorson HR. Two step mechanism of phosphate release and the mechanism of force generation in chemically skinned fibers of rabbit psoas muscle. Biophys J. 1991;59:329–342. doi: 10.1016/S0006-3495(91)82227-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lannergren J, Westerblad H. The temperature dependence of isometric contractions of single, intact fibres dissected from a mouse foot muscle. J Physiol. 1987;390:285–293. doi: 10.1113/jphysiol.1987.sp016700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mutungi G, Ranatunga KW. Sarcomere length changes during end-held (isometric) contractions in mammalina (rat) fast and slow muscle fibres. J Musc Res Cell Motil. 2000;21:565–575. doi: 10.1023/a:1026588408907. [DOI] [PubMed] [Google Scholar]
- Piazzesi G, Reconditi M, Linari M, Lucil L, Sun Y-B, Narayan T, Boesecke P, Lombardi V, Irving M. Mechanism of force generation by myosin heads in skeletal muscle. Nature. 2002;415:659–662. doi: 10.1038/415659a. [DOI] [PubMed] [Google Scholar]
- Ranatunga KW. The force-velocity relation of rat fast- and slow-twitch muscles examined at different temperatures. J Physiol. 1984;351:517–529. doi: 10.1113/jphysiol.1984.sp015260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranatunga KW. Thermal stress and Ca-independent contractile activation in mammalian skeletal muscle fibers at high temperatures. Biophys J. 1994;66:1531–1541. doi: 10.1016/S0006-3495(94)80944-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranatunga KW. Endothermic force generation in fast and slow mammalian (rabbit) muscle fibers. Biophys J. 1996;71:1905–1913. doi: 10.1016/S0006-3495(96)79389-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranatunga KW. Effects of inorganic phosphate on endothermic force generation in muscle. Proc R Soc B Biol Sci. 1999a;266:1381–1385. doi: 10.1098/rspb.1999.0791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranatunga KW. Endothermic force generation in skinned cardiac muscle from rat. J Musc Res Cell Motil. 1999b;20:489–490. doi: 10.1023/a:1005509731881. [DOI] [PubMed] [Google Scholar]
- Ranatunga KW, Coupland ME. Force generation induced by laser temperature-jumps in tetanized intact (rat) muscle fibers. Biophys J. 2002;82:367A. [Google Scholar]
- Ranatunga KW, Coupland ME, Mutungi G. An asymmetry in the phosphate dependence of tension transients induced by length perturbation in mammalian (rabbit psoas) muscle fibres. J Physiol. 2002;542:899–910. doi: 10.1113/jphysiol.2002.019471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranatunga KW, Sharpe B, Turnbull B. Contractions of a human skeletal muscle at different temperatures. J Physiol. 1987;390:383–395. doi: 10.1113/jphysiol.1987.sp016707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranatunga KW, Thomas PE. Correlation between shortening velocity, force-velicity relation and histochemical fibre type composition in rat muscle. Musc Res Cell Motil. 1990;11:240–250. doi: 10.1007/BF01843577. [DOI] [PubMed] [Google Scholar]
- Ranatunga KW, Wylie SR. Temperature-dependent transitions in isometric contractions of rat muscle. J Physiol. 1983;339:87–95. doi: 10.1113/jphysiol.1983.sp014704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephenson DG, Williams DA. Temperature-dependent calcium sensitivity changes in skinned muscle fibres of the rat and toad. J Physiol. 1985;360:1–12. doi: 10.1113/jphysiol.1985.sp015600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vawda F, Geeves MA, Ranatunga KW. Force generation upon hydrostatic pressure release in tetanized intact frog muscle fibres. J Musc Res Cell Motil. 1999;20:477–488. doi: 10.1023/a:1005565917768. [DOI] [PubMed] [Google Scholar]
- Vawda F, Ranatunga KW, Geeves MA. Pressure-induced changes in the isometric contractions of single frog muscle fibres at low temperatures. J Musc Res Cell Motil. 1995;16:412–419. doi: 10.1007/BF00114506. [DOI] [PubMed] [Google Scholar]
- Wylie SR, Ranatunga KW. Temperature dependence of contraction characteristics in developing rat muscles. Muscle Nerve. 1987;10:775–782. doi: 10.1002/mus.880100902. [DOI] [PubMed] [Google Scholar]


