Voltage-dependent gating and block by internal spermine of the murine inwardly rectifying K⁺ channel, Kir2.1

Abstract

The mechanism of inward rectification was investigated by recording single-channel currents through an inwardly rectifying K⁺ channel (Kir2.1). cDNA encoding a wild-type (WT) channel, a mutant replacing Asp 172 with Asn (D172N), and a tandem tetramer WT-(D172N)2-WT, was transfected into COS-1 cells using the liposome method, and after 48–72 h single-channel currents were recorded in the inside-out configuration at 150 mm internal and external K⁺. Steady-state open probability of outward currents decreased with larger depolarizations. The activation curve was fitted with a single Boltzmann equation. The voltages of half-activation in the absence of spermine were +35.9 mV (WT), +55.0 mV (WT-(D172N)2-WT) and +76.7 mV (D172N). Open-time and zero-current-time histograms were constructed. The open-time histogram was fitted with a single exponential function. Two exponential functions were necessary to fit the closed-time histogram. In each channel, internal spermine at a concentration of 1–100 nm reduced the open time of the outward currents in a concentration-dependent manner and produced one blocked state without affecting the inward currents, suggesting that spermine acts as an open channel blocker. The normalized steady-state open probability-spermine concentration curve was fitted by saturation kinetics with a Hill coefficient of 1. On the assumption of the linear sequential state model, the unblock and blocking rates were estimated in each channel. Unblock rates depended on the number of D172N mutant subunits, but blocking rates did not. The results suggest that closing gates work independently of the spermine block and D172 is involved in both intrinsic gating and the spermine block.

The phenomenon of inward rectification, whereby K⁺ conductance increases under hyperpolarization and decreases under depolarization, has been demonstrated in a variety of cell types (Katz, 1949; Hall et al. 1963; Kandel & Tauc, 1966; Hagiwara & Takahashi, 1974). This behaviour plays an important role in permitting long depolarizing responses. Inward rectification of cardiac inwardly rectifying K⁺ channels was ascribed to a voltage-dependent block of the channel pore by intracellular Mg²⁺ (Matsuda et al. 1987; Vandenberg, 1987; Matsuda, 1988) and an intrinsic gating mechanism that closes the channels under depolarization. Thereafter, blockade of cloned inwardly rectifying K⁺ channels (Kir2.1; Kubo et al. 1993) by internal polyamines such as spermine, spermidine and putrescine (Ficker et al. 1994; Lopatin et al. 1994) replaced the intrinsic gating mechanism, supported by the finding that Kir2.1 has no equivalent to the voltage sensor in voltage-dependent channels.

However, there are a few studies reporting an intrinsic gating mechanism independent of the block by polyamines (Shieh et al. 1996). In addition, in our previous studies, unitary outward currents through Kir2.1 channels expressed in COS-1 cells were barely recorded at holding potentials more positive than +50 mV, even after prolonged washing with Mg²⁺- and polyamine-free solution of inside-out patches (Omori et al. 1997; Oishi et al. 1998). Whether the voltage-dependent decrease of steady-state open probability is due to incomplete washout of residual polyamines or another mechanism remains unclear.

In the present study, we used an efficient Y-tube perfusion method (Murase et al. 1990), and recorded single-channel currents in the absence and presence of intracellular spermine through channels expressed by WT, D172N and tandem tetramers with two D172N subunits. These results suggest that closing gates work in Kir2.1 and that D172 is involved in such a gating mechanism. It was also shown that one spermine molecule binds to an open channel pore to induce one blocked state.

METHODS

Molecular biology

The Kir2.1 gene (Kubo et al. 1993) was digested with Hind III and Stu I. The Hind III-Stu I fragment (∼1.8 kb), which contains 5′ untranslated coding and part of the 3′ untranslated sequences, was subcloned into a pTZ19R vector (Pharmacia, Uppsala, Sweden) for mutagenesis or the construction of tandem multimers. Site-directed mutagenesis of the cDNA was performed using a QuikChange site-directed mutagenesis kit (Stratagene, La Jolla, CA, USA). The mutation was confirmed by sequencing. The DNA fragment containing the mutation was excised by restriction enzymes and used to replace the corresponding fragment in the wild-type cDNA. The method for construction of tetrameric cDNA has been described previously (Oishi et al. 1998).

For expression in COS-1 cells (Riken Gene Bank, Tsukuba, Japan), cDNA was subcloned into a pSVL expression vector (Pharmacia). The expression plasmid (1 μg per 35 mm dish) and cDNA of green fluorescent protein (pEGFP-N1, Clontech, Palo Alto, CA, USA; 0.1 μg) were co-transfected into COS-1 cells using lipofectamine (Gibco BRL, Gaithersburg, MD, USA), according to the manufacturer's protocol. Currents were recorded from cells exhibiting green fluorescence 48–72 h after transfection.

Electrophysiology

The coverslips (3 mm × 18 mm) on which COS-1 cells were grown were transferred to a recording chamber mounted on an inverted fluorescence microscope (IX–70, Olympus, Tokyo, Japan). Single-channel currents were recorded using a heat-polished patch electrode (Hamill et al. 1981) in the inside-out configuration with an EPC-7 patch clamp amplifier (List Electronics, Darmstadt, Germany). Pipettes were made from capillaries of hard borosilicate glass (G-1.5, Narishige, Tokyo, Japan), and were coated near the tips with silicone to reduce electrical capacitance. The electrode resistance ranged between 8 and 15 MΩ when filled with a pipette solution containing (mm): KCl 150; CaCl₂ 1; Hepes 5; pH was adjusted to 7.4 with KOH. The chamber was first perfused with Tyrode solution containing (mm): NaCl 140; NaH₂PO₄ 0.33; KCl 5.4; CaCl₂ 1.8; MgCl₂ 0.5; Hepes 5; glucose 5.5; pH was adjusted to 7.4 with NaOH. After Kir2.1 channel activity was identified in a patch, the solution perfusing the chamber was switched to a high-K⁺ solution and perfusion of the cell with this solution using a Y-tube was started. Then, the inside-out configuration was constructed. The high-K⁺ solution contained (mm): potassium aspartate 60; KCl 65; KH₂PO₄ 1; EDTA 5; K₂ATP 3; Hepes 5; pH was adjusted to 7.4 with KOH. Since the binding constant of spermine for ATP is 5.95 ×10²m⁻¹ (Watanabe et al. 1991), approximately two-thirds of spermine exists as complexes with ATP and the rest as free ions in the presence of 3 mm ATP. Spermine was diluted into an ATP-free, high-K⁺ solution on the day of the experiments. Experiments were carried out at 23–26°C.

Data were collected on digital audiotape using a PCM data recorder (RD-120TE, TEAC, Tokyo, Japan) and stored for subsequent computer analysis (PC-98XL, NEC, Tokyo, Japan). The unitary currents were filtered using a four-pole low-pass Bessel filter (FV-665, NF, Kanagawa, Japan) at a −3 dB corner frequency of 1 kHz and sampled at 5 kHz for steady-state kinetics, unless otherwise indicated. To make amplitude histograms, currents were filtered at 0.2–0.5 kHz and sampled at 1 kHz. The open probability was calculated from the amplitude histogram. Open and zero-current times were measured in patches where only one channel was active, using a cursor set mid-way between open and zero-current levels. Open- and zero-current-time histograms were formed and then fitted with exponential(s) using a least-squares algorithm. In another series of experiments, outward currents through WT channels were elicited by depolarizing steps of 200 ms every 1 s. Capacitive and leakage currents were removed by subtracting from each trace the average of current traces without events. Then average currents were calculated. When current traces without events were not available, 20 mm TEA-Cl was added to the high-K⁺ solution to block both inward and outward currents (Matsuda, 1991). Membrane potentials were corrected for liquid junction potential at the tip of the patch pipette in the Tyrode solution, and for that at the tip of the indifferent reference electrode filled with Tyrode solution and placed in the bathing solution.

Averaged results throughout this paper are given as means ±s.d.

RESULTS

Steady-state open probability depends on voltage

Figure 1A shows outward single-channel currents through WT Kir2.1 recorded in steady-state conditions in the absence of spermine. The equilibrium potential for K⁺, predicted from the 150 mm external and internal K⁺ concentration, is 0 mV. Outward currents with relatively long openings were recorded in the inside-out configuration. However, the open probability decreased with increasing holding potential and outward currents were hardly recorded at potentials more positive than +50 mV. The steady-state open probability was calculated from the amplitude histogram and plotted against the membrane potential (Fig. 2B). The data were fitted to Boltzmann distributions. The slope factor and voltage of half-activation in the control were 7.2 mV and +35.9 mV.

Figure 1. Outward single-channel currents through WT Kir2.1 channels and kinetic analysis in the control.

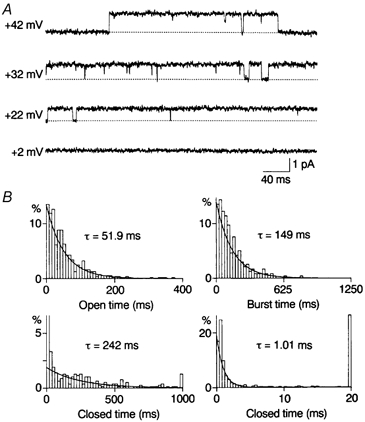
A, outward currents recorded from the inside-out patch in steady-state conditions. Numbers to the left of each current trace refer to the holding potential. The dotted line indicates the zero-current level. B, histograms of open, burst and closed times constructed for currents at +42 mV. The open time and burst time histograms were fitted with a single exponential function with the time constant (τ: the mean open time and mean burst time) indicated. The closed time histogram was fitted with two exponential functions; the slower mean closed time was 242 ms; the faster mean closed time was 1.01 ms. The value of the truncated first bin was 58%.

Figure 2. Effects of internal spermine on outward currents through WT channels.

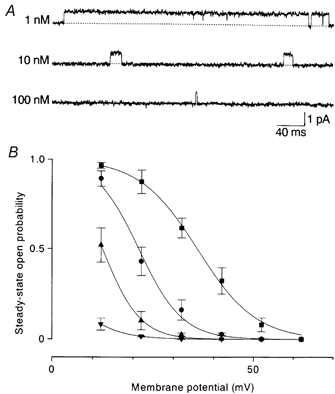
A, outward currents recorded at +22 mV in the presence of spermine. The open time decreased dependently on the spermine concentration. B, the steady-state open probability-membrane potential relations. Smooth lines are fits of a Boltzmann function to averaged data (n = 3–5). The voltages of half-activation and slope factors were +35.9 mV and 7.2 mV in the control (▪), +21.4 mV and 5.3 mV with 1 nm spermine (•), +12.4 mV and 4.5 mV with 10 nm spermine (▴), and − 2.1 mV and 5.8 mV with 100 nm spermine (▾).

Open-time and zero-current-time histograms were constructed for outward currents through WT channels recorded at +22 and +42 mV. Figure 1B shows open-, burst-, and closed-time histograms at +42 mV in the absence of spermine. The lifetimes of the openings were distributed according to a single exponential. The average of the mean open time was 52.8 ± 4.7 ms (n = 5) at +42 mV and 92.3 ± 9.6 ms (n = 3) at +22 mV. Closed times were fitted with two exponential functions. The average of the faster mean closed time was 1.24 ± 0.25 ms (n = 5) at +42 mV and 1.33 ± 0.04 ms (n = 3) at +22 mV. The slower mean closed time averaged 286 ± 35 ms (n = 5) at +42 mV and 25.9 ± 5.3 ms (n = 3) at +22 mV. The fraction of the faster component in the total closed events was 0.65 ± 0.04 (n = 5) at +42 mV and 0.62 ± 0.02 (n = 3) at +22 mV. Thus, the averaged probability density function for closed times at +42 mV was:

and that at +22 mV was:

where t represents time (ms). A burst was defined as any series of openings interrupted only by gaps shorter than 5 ms (four times the fast time constant). The burst-time histogram was fitted with a single exponential function with a time constant of 154 ± 5 ms (n = 5) at +42 mV.

Block of outward unitary currents through WT Kir2.1 channels by internal spermine

Intracellular spermine at a concentration of 1–100 nm did not affect the inward current amplitude (Fig. 4) or the open probability. However, it blocked the outward currents in a concentration- and voltage-dependent manner (Fig. 2A). The open probability-membrane potential relation shifted in the negative direction with increasing concentrations of spermine: the half-activation voltage was +21.4 mV with 1 nm, +12.4 mV with 10 nm and −2.1 mV with 100 nm (Fig. 2B). The open probability was normalized to that in the absence of spermine and plotted against the spermine concentration. The relations fitted well with the concentration-effect curves predicted by assuming one-to-one binding of spermine to a site. The dissociation constant was 11.4 nm at +12 mV and 1.00 nm at +22 mV.

Figure 4. Acceleration of the average outward current decay by internal spermine.

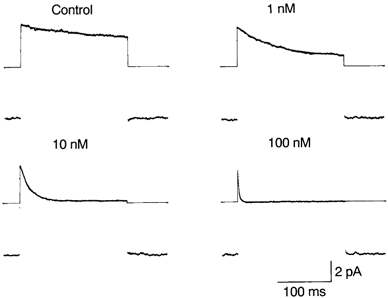
Outward currents through WT channels were elicited by depolarizing steps from −48 mV to +40 mV every 1 s. Capacitive and leakage currents were removed by subtracting from each trace the average of current traces with 20 mm TEA-Cl. The average current was obtained from 72–106 frames. The time constant of the exponential decay (shown by the continuous line) was 172 ms in the control, 71.9 ms with 1 nm spermine, 17.9 ms with 10 nm and 2.39 ms with 100 nm. The straight line before and after the step pulse corresponds to the zero-current level. The residual steady-state current during the pulse with 10 nm spermine is due to incomplete subtraction of leakage currents.

Most studies on the block by internal polyamines were performed by macroscopic current recording, and the results were interpreted by assuming more than one open state or blocked state (see Discussion for references). However, the present single-channel experiments showed that the open state is one at any time, and that spermine induces only one blocked state. Figure 3 shows open-time and zero-current-time histograms at +22 mV in the presence of 1–100 nm spermine. As evident in the figure, the open-time histogram at each spermine concentration could be fitted with a single exponential function. Spermine decreased the mean open time at +22 mV to 64.9 ± 4.9 ms (1 nm; n = 3), 22.6 ± 2.0 ms (10 nm; n = 4) and 2.43 ± 0.50 ms (100 nm; n = 4), indicating that internal spermine acts as an open channel blocker. The mean open time at +42 mV in three experiments was 39.1 ± 2.8 ms with 1 nm spermine and 11.7 ± 3.6 ms with 10 nm spermine. No outward currents were recorded in a steady-state at +42 mV with 100 nm spermine.

Figure 3. Analysis of blocking kinetics in WT channels.

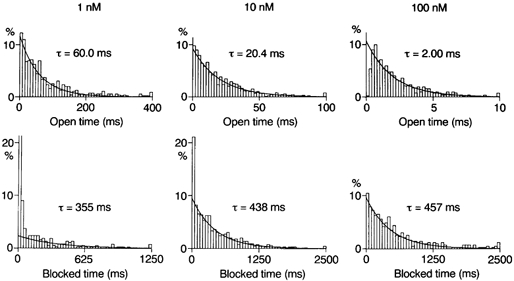
Histograms of open and zero-current times constructed for outward currents at +22 mV in the presence of spermine. The open-time histogram was fitted with a single exponential function. The mean open time decreased in a concentration-dependent manner. The zero-current-time histograms for currents filtered at 0.2 kHz and sampled at 1 kHz are shown. Spermine induced a component of zero-current times with the time constant indicated, which represents blocked times. The value of the truncated first bin in the zero-current-time histogram with 1 nm spermine was 57%.

As described in a previous section, the closed-time histogram at +22 mV in the control was fitted with two exponential functions with time constants of ∼1 ms and ∼30 ms. Spermine induced another component of zero-current times with a time constant of 350–450 ms: 346 ± 13 ms (1 nm; n = 3), 394 ± 36 ms (10 nm; n = 4) and 419 ± 39 ms (100 nm; n = 4). As evident in the lower panel of Fig. 3, the fraction of this component in the total zero-current events increased with increasing spermine, suggesting that this slowest component is attributable to the block by internal spermine. The unblock rate at +22 mV estimated from the mean blocked time was 2.5 s⁻¹. The mean blocked time at +42 mV with 1 and 10 nm spermine was ∼6.5 s, yielding an unblock rate of 0.15 s⁻¹.

To further clarify the spermine block, outward currents were elicited by depolarizing steps of 200 ms from -48 mV to +40 mV. Figure 4 shows the average of currents after removing capacitive and leakage currents. Decay of the average outward current could be fitted with a single exponential function. The time constant of the exponential decay (τ_decay) in seven experiments was 167 ± 30 ms (control), 86.9 ± 15.7 ms (1 nm), 18.7 ± 3.7 ms (10 nm) and 1.91 ± 0.50 ms (100 nm). τ_decay in the control was close to the mean burst time. Note that the amplitude of the inward currents was not affected by spermine.

WT-(D172N)2-WT channels show a higher open probability and less sensitivity to spermine

D172 is thought to be a binding site of internal Mg²⁺ and polyamines (Ficker et al. 1994; Lu & MacKinnon, 1994; Stanfield et al. 1994; Wible et al. 1994). We demonstrated previously that the number of D172N in tandem tetramers affects not only the substate behaviour in Mg²⁺ block, but also the steady-state open probability (Oishi et al. 1998). Figure 5A shows currents through WT-(D172N)2-WT channels recorded in a steady state in the control condition. Outward currents were observed at holding potentials more positive than in WT channels. Fitting the steady-state open probability-voltage relationship with the Boltzmann equation yielded a half-activation voltage of +55.0 mV and a slope factor of 9.9 mV in the control (Fig. 6B). The former was more positive by about 20 mV than in WT channels.

Figure 5. Outward single-channel currents through WT-(D172N)2-WT channels and kinetic analysis in the control.

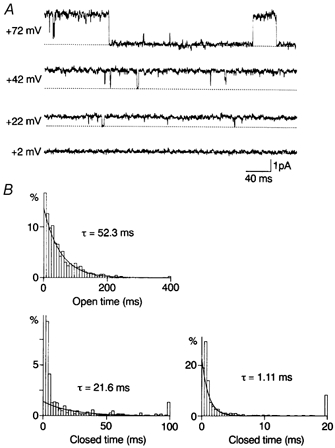
A, outward currents recorded from the inside-out patch in steady-state conditions. Outward currents were observed at potentials more positive than in WT channels. B, open-time and closed-time histograms for currents recorded at +42 mV. The slower mean closed time was shorter than that in WT channels. The value of the truncated first bin was 58%.

Figure 6. Effects of internal spermine on outward currents through WT-(D172N)2-WT channels.

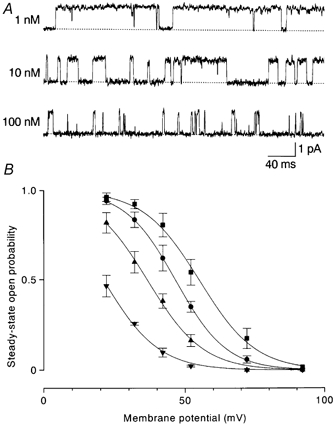
A, outward currents at +42 mV in the presence of spermine. The open time decreased with increasing spermine concentration. B, the averaged (n = 3–5) steady-state open probability was plotted against the membrane potential. The voltages of half-activation and slope factors were +55.0 mV and 9.9 mV in the control (▪), +46.5 mV and 8.9 mV with 1 nm spermine (•), +36.6 mV and 9.7 mV with 10 nm spermine (▴) and +20.9 mV and 9.7 mV with 100 nm spermine (▾).

Open-time and zero-current-time histograms were constructed for outward currents through WT-(D172N)2-WT channels. Figure 5B shows open- and closed-time histograms at +42 mV in the absence of spermine. The lifetimes of the openings were distributed according to a single exponential. The average of the mean open time was 46.3 ± 7.4 ms (n = 4) at +42 mV and 19.4 ± 1.9 ms (n = 5) at +72 mV. Closed times were fitted with two exponential functions. The averages of the faster and slower mean closed times were 1.05 ± 0.05 ms and 24.8 ± 3.4 ms (n = 4) at +42 mV and 1.19 ± 0.19 ms and 243 ± 31 ms (n = 5) at +72 mV. The fraction of the faster component in the total closed events was 0.61 ± 0.06 (n = 4) at +42 mV and 0.64 ± 0.08 (n = 5) at +72 mV. The averaged probability density function for closed times at +42 mV was:

and that at +72 mV was:

Depressive effects of spermine on the outward current were less marked in WT-(D172N)2-WT channels than in WT channels. Figure 6A shows steady-state outward currents recorded at +42 mV in the presence of spermine. Intracellular spermine decreased the open time in a concentration-dependent manner and induced a blocked state (see below). The open probability-membrane potential relationship shifted in the negative direction with increasing concentrations of spermine: the half-activation voltages were +46.5 mV with 1 nm, +36.6 mV with 10 nm and +20.9 mV with 100 nm (Fig. 6B). The dissociation constant obtained by fitting the normalized open probability-spermine concentration curve with a Hill coefficient of 1 was 7.8 nm at +42 mV.

Internal spermine decreased the mean open times (n = 3) to 34.7 ± 2.1 ms (1 nm), 10.9 ± 1.5 ms (10 nm) and 1.60 ± 0.18 ms (100 nm). It also produced a new component of zero-current times with a time constant of about 14 ms (Fig. 7). The time constants in three experiments averaged 13.7 ± 1.1 ms (1 nm), 14.4 ± 0.9 ms (10 nm) and 13.5 ± 0.8 ms (100 nm). The fraction of this component in the total zero-current events increased with the spermine concentration (0.25 ± 0.10 with 1 nm, 0.42 ± 0.17 with 10 nm and 0.60 ± 0.13 with 100 nm), suggesting that it represents a blocked state. The unblock rate at +42 mV was estimated to be 72 s⁻¹, much larger than that in WT channels.

Figure 7. Analysis of blocking kinetics in WT-(D172N)2-WT channels.

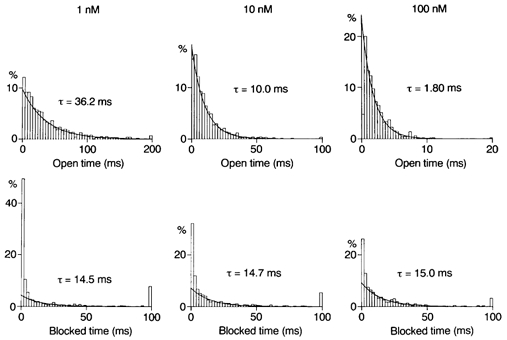
Histograms of open and zero-current times constructed for outward currents at +42 mV in the presence of spermine. Spermine decreased the mean open time in a concentration-dependent manner and induced a component of zero-current times with the time constant indicated. This component is ascribed to the spermine block.

D172N channels show the highest open probability and least sensitivity to spermine

The steady-state open probability at positive potentials in D172N channels was higher than in WT and WT-(D172N)2-WT channels (Fig. 8A and Fig. 9B). The voltage of half-activation was +76.7 mV, 40 mV more positive than in WT channels and 25 mV more than in WT-(D172N)2-WT channels. The slope factor was 14.5 mV.

Figure 8. Outward single-channel currents through D172N channels and kinetic analysis in the control.

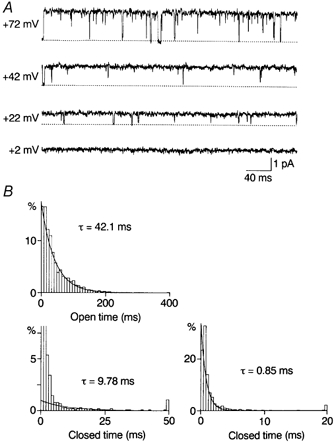
A, steady-state outward currents recorded in the inside-out configuration. The open probability was high even at +72 mV. B, open-time and closed-time histograms for currents recorded at +42 mV. The values of truncated first and second bins in the closed-time histogram were 58 and 18%, respectively.

Figure 9. Effects of internal spermine on outward currents through D172N channels.

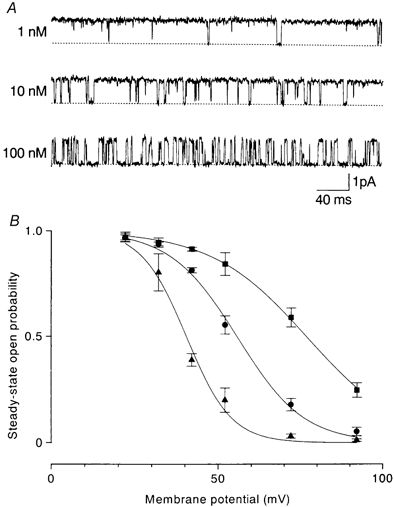
A, outward currents at +42 mV in the presence of spermine. Spermine decreased the open time in a concentration-dependent manner and induced a short-lived blocked state. B, the averaged (n = 3–10) steady-state open probability was plotted against membrane potential. The voltages of half-activation and slope factors were +76.7 mV and 14.5 mV in the control (▪), +55.6 mV and 10.0 mV with 10 nm spermine (•) and +40.4 mV and 6.6 mV with 100 nm spermine (▴).

Kinetic analysis of outward currents was carried out. Figure 8B shows open- and closed-time histograms at +42 mV in the control. As in other channels, the open-time histogram was fitted with a single exponential. The averages of the mean open time were 39.4 ± 3.1 ms (n = 3) at +42 mV, 19.7 ± 2.3 ms (n = 5) at +72 mV and 10.3 ± 0.7 ms (n = 4) at +92 mV. Closed times were fitted with two exponential functions. The averages of the faster and slower mean closed times and the fractions of the faster component in the total closed events were 0.93 ± 0.13 ms, 9.31 ± 0.73 ms and 0.68 ± 0.02 (n = 3) at +42 mV; 1.00 ± 0.18 ms, 29.2 ± 4.5 ms and 0.63 ± 0.04 (n = 5) at +72 mV; and 1.11 ± 0.34 ms, 73.8 ± 9.7 ms and 0.65 ± 0.12 (n = 4) at +92 mV. The averaged probability density function for closed times at +42 mV was:

that at +72 mV was:

and that at +92 mV was:

Inhibition of outward currents by spermine was lowest in D172N channels. Figure 9A shows outward current at +42 mV in the presence of spermine. Spermine decreased the open time in a concentration-dependent manner and produced a short-lived blocked state. The open probability-membrane potential relation shifted in the negative direction with increasing spermine concentration. The half-activation voltage was +55.6 mV with 10 nm and +40.4 mV with 100 nm (Fig. 9B). The dissociation constant at +42 mV was 75 nm.

Figure 10 shows open-time and zero-current-time histograms at +42 mV in the presence of spermine. The mean open time averaged 31.6 ± 2.7 ms with 1 nm (n = 4), 11.1 ± 0.6 ms with 10 nm (n = 5) and 1.70 ± 0.17 ms with 100 nm spermine (n = 4). Most zero-current times were distributed according to a single exponential function with time constants of 3.13 ± 0.51 ms (10 nm) and 3.51 ± 1.01 ms (100 nm), which is ascribed to a blocked state. A component with a similar time constant (3.38 ± 0.10 ms) was observed in the presence of 1 nm spermine, whose fraction in the total zero-current events was small (0.24 ± 0.05). The open probability with 1 nm spermine at +42 mV (0.92 ± 0.02; n = 4) was not different from the control (0.92 ± 0.01; n = 5). This was attributed to a high unblock rate of 300 s⁻¹ in these channels compared with the blocking rate (see below).

Figure 10. Analysis of blocking kinetics in D172N channels.

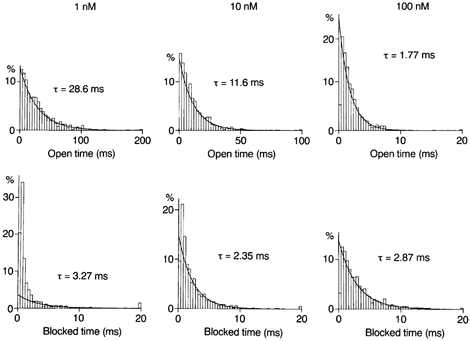
Histograms of open and zero-current times constructed for outward currents at +42 mV in the presence of spermine. Spermine decreased the mean open time in a concentration-dependent manner and induced a component of zero-current times with the time constant indicated.

DISCUSSION

We studied the single outward currents through Kir2.1 channels in the absence and presence of intracellular spermine. Steady-state open probability decreased with larger depolarization, even after prolonged wash-out of spermine with the high-K⁺ solution containing 3 mm ATP, which bound two-thirds of the total spermine. It is unlikely that this voltage-dependent decrease was due to residual polyamines (e.g. 0.1 nm spermine). Since the unblock rate is small in WT channels, the time constant of the exponential decay of the average outward current at higher spermine concentrations should approximate to the reciprocal of the blocking rate. Thus, τ_decay values with 10 nm (18.7 ms) and 100 nm (1.91 ms) spermine give blocking rates of 53.5 and 524 s⁻¹, respectively. The linear proportion between the blocking rate and the spermine concentration predicts blocking rates of ∼5 s⁻¹ with 1 nm and ∼0.5 s⁻¹ with 0.1 nm spermine (see below). Were it not for the voltage-dependent gating separate from the spermine block, the mean open times would be 200 ms with 1 nm and 2 s with 0.1 nm spermine (in the control). These were not observed.

The residual rectification independent of internal Mg²⁺ and polyamines has been ascribed to Hepes in recording solutions (Guo & Lu, 2000b). Although the steep voltage dependence observed in the present study was different from that reported in the study of Guo & Lu (2000b), we used an internal solution where 5 mm Hepes was replaced by 1 mmKH₂PO₄ and 4 mmK₂HPO₄ (pH 7.4). The steady-state open probabilities (0.27 at +42 mV and 0.021 at +52 mV) were not different from those obtained with Hepes. (Since it is unlikely that 5 mm affects the K⁺ efflux through Kir2.1 channels, we did not study the effect of replacing external Hepes with phosphate.) The internal solution used in the present study, containing 5 mm EDTA and buffered to pH 7.4, was similar to that recommended by Guo & Lu (2002). Therefore it is suggested that the voltage-dependent decrease of the steady-state open probability with larger depolarization results not from blocking by impurities contained in Hepes or EDTA but from gating of Kir2.1 channels. The reason behind the discrepancy between our conclusions and those of Guo & Lu (2002) denying intrinsic gating is unknown. It may be due to differences in the experimental procedures (single-channel recording vs. macroscopic current recording and steady-state kinetics vs. step pulse-induced current relaxations) or expression systems (mammalian cells vs. Xenopus oocytes).

One open state and two closed states were necessary for a description of the kinetics in the control condition. We consider the linear sequential model as in the inward currents through cardiac inwardly rectifying K⁺ channels (Kameyama et al. 1983; Sakmann & Trube, 1984) as:

where C₁ and C₂ are closed states, O is the open state, and the k symbols are rate constants. Colquhoun & Hawkes (1981) gave the probability density function of the closed lifetime for a linear scheme with two closed states (their eqn (2.32)). Rate constants were calculated from the mean open time and the observed probability density function of the closed time (Table 1). The open probability (P_O) was calculated from the equation:

Table 1.

Rate constants (s⁻¹) and P_o

	k1	k−1	k2	k−2	Po
+22 mV
WT	480	10.8	60.4	249	0.90(0.88)
+42 mV
WT	525	18.9	5.4	279	0.34(0.32)
WT-(D172N)2-WT	597	21.6	64.3	332	0.82(0.81)
D172N	765	25.4	150.9	266	0.92(0.92)
+72 mV
WT-(D172N)2-WT	539	51.5	6.4	299	0.18(0.18)
D172N	643	50.8	53.3	338	0.63(0.59)
+92 mV
D172N	591	97.1	20.7	303	0.28(0.25)

Rate constants were calculated from the averaged mean open time and the probability density function of the closed time. The open probabilities (P_o) were calculated from the relationship in the text. The observed P_o values are shown in parentheses.

The predicted values were close to the observed value (shown in parentheses). Rate constant k₋₁ increases and k₂ decreases with depolarization. The latter increases with the number of D172N subunits. The mean length of the burst (τ_burst) is (their eqn (2.23)):

The predicted value at +42 mV in WT channels was 155 ms, similar to the observed value (154 ± 5 ms). When the gaps within bursts (faster closed time) are brief, the time constant of relaxation of macroscopic currents corresponds approximately to the mean burst length (Colquhoun & Hawkes, 1995). Indeed, the average outward current in the control decayed with a time constant close to the τ_burst (167 ± 30 ms).

Block by internal polyamines of Kir2.1–2.3 channels, which show strong inward rectification, was mostly studied by macroscopic current recording with polyamines at concentrations higher than those used in the present study. The results were interpreted by assuming more than one open state or blocked state (Lopatin et al. 1995; Lee et al. 1999; Guo & Lu, 2000a; Xie et al. 2002). The present results obtained with single-channel recording suggest that (1) spermine acts as an open channel blocker, (2) both the open state and blocked state are one and (3) one spermine molecule binds to a site in the channel pore (cf. Lopatin et al. 1995; Yamashita et al. 1996).

Therefore, we consider the state model for the spermine block as:

where B is the blocked state, and μ and λ are blocking and unblocking rates. From the mean open time in the presence of spermine and k₋₁, the blocking rates at +42 mV were calculated: 6.7 s⁻¹ (1 nm) and 66.6 s⁻¹ (10 nm) in WT; 7.2 s⁻¹ (1 nm), 70.1 s⁻¹ (10 nm) and 603 s⁻¹ (100 nm) in WT-(D172N)2-WT; and 6.2 s⁻¹ (1 nm), 64.7 s⁻¹ (10 nm) and 563 s⁻¹ (100 nm) in D172N. τ_decay with 100 nm spermine (1.91 ms) gave a blocking rate of 524 s⁻¹ for WT channels. The blocking rate is linearly proportional to the spermine concentration and independent of the number of D172N mutant subunits. The blocking rate constant is approximately 6.4 ×10⁹ s⁻¹m⁻¹ at +42 mV and 4.0 ×10⁹ s⁻¹m⁻¹ at +22 mV. τ_decay with 1 nm spermine was approximated to be 1/(1/τ_burst+μ). The calculated value of 77.5 ms was close to the observed value (86.9 ± 15.7 ms). The unblocking rate depended closely on the number of D172N subunits. The dissociation constants calculated from the blocking rate constant and unblocking rate at +42 mV were 0.023 nm in WT channels, 11 nm in WT-(D172N)2-WT and 47 nm in D172N channels.

Recently, spermine at concentrations of 100 μm−1 mm was reported to reduce the unitary amplitude of the inward current (Xie et al. 2002). This was attributed to screening of negative surface charges by internal spermine, which binds to a region of the channel involving the negatively charged residues E224 and E229 (Yang et al. 1995; Kubo & Murata, 2001). The free intracellular spermine concentration was reported to be 20–80 μm (Watanabe et al. 1991; Igarashi & Kashiwagi, 2000). The amplitude of the inward current through Kir2.3 increased gradually after excision of a macropatch in Xenopus oocytes (Lopatin et al. 1994), while the inward current amplitude was not changed after formation of inside-out or open cell-attached patches in cardiac cells (Vandenberg 1987; Matsuda, 1991). Therefore, it appears that the physiological polyamine concentration is different between cells and, at least in cardiac cells, not high enough to decrease the inward current amplitude.

The present results show that voltage-dependent gating works in Kir2.1 channels in the outward current independently of spermine, though intracellular Mg²⁺ and polyamines at a physiological concentration block Kir2.1 almost completely, making its significance in inward rectification small. Voltage-dependent gating was also observed in the inward current through native inwardly rectifying K⁺ channels (Kameyama et al. 1983; Sakmann & Trube, 1984; Matsuda & Stanfield, 1989). Gating in the outward current through Kir2.1 channels depends strongly on the voltage and the number of D172N subunits. On the other hand, the steady-state open probability of inward currents is less voltage dependent and is not affected by neutralization of D172 (Omori et al. 1997; Oishi et al. 1998). It is likely that the gating mechanism in the outward direction is different from that in the inward direction. The intracellular pH-dependent gating mechanism reported by Shieh et al. (1996) works in D172N channels as well as in WT channels. Further studies will reveal how D172 is involved in the gating mechanism in the outward current.