The case for an internal dynamics model versus equilibrium point control in human movement

Abstract

The equilibrium point hypothesis (EPH) was conceived as a means whereby the central nervous system could control limb movements by a relatively simple shift in equilibrium position without the need to explicitly compensate for task dynamics. Many recent studies have questioned this view with results that suggest the formation of an internal dynamics model of the specific task. However, supporters of the EPH have argued that these results are not incompatible with the EPH and that there is no reason to abandon it. In this study, we have tested one of the fundamental predictions of the EPH, namely, equifinality. Subjects learned to perform goal-directed wrist flexion movements while a motor provided assistance in proportion to the instantaneous velocity. It was found that the subjects stopped short of the target on the trials where the magnitude of the assistance was randomly decreased, compared to the preceding control trials (P = 0.003), i.e. equifinality was not achieved. This is contrary to the EPH, which predicts that final position should not be affected by external loads that depend purely on velocity. However, such effects are entirely consistent with predictions based on the formation of an internal dynamics model.

Muscles are the motors responsible for limb movement. However, they are more than simple force generators. Their spring-like behaviour has long been recognized as a key element in the control of limb movement. One theory of motor control, the equilibrium point hypothesis (EPH), is predicated on the assumption that the central nervous system (CNS) can control the equilibrium position established by the balance of force in these muscle springs (Asatryan & Feldman, 1965; Feldman, 1966a, b; Bizzi & Polit, 1978, 1979; Bizzi et al. 1982). In the λ-model of motor control, proposed by Feldman (1986), motion of a joint arises through a reciprocal (R) command, which alters the relative activation of agonist and antagonist muscles to produce a shift in the equilibrium between the muscle force and external load. There is no consensus on the shape of the equilibrium point trajectory. However, regardless of the manner in which the equilibrium point shifts, the same final position will be achieved.

While the simplicity of the EPH is very appealing, there is abundant evidence that the ability to perform skilled movements in novel mechanical environments is only gradually acquired with practice. This suggests that motor learning is more complex than might be predicted under the EPH. Recent studies on motor learning provide convincing evidence for the formation of an internal dynamics model (IDM) of task dynamics as skill is acquired (Shadmehr & Mussa-Ivaldi, 1994; Conditt et al. 1997; Thoroughman & Shadmehr, 2000; Scheidt et al. 2000). The IDM encodes muscle activation patterns that compensate for the effects of predictable environmental forces.

According to the λ-model (Feldman, 1986), increased muscle activation through stretch reflex pathways should compensate for small, transient perturbations or loads that disappear once movement ceases, thereby preserving the final equilibrium position. For example, if a load, which depends only on velocity, is unexpectedly increased, the velocity of a joint will be reduced and the disparity between the joint angle and the pre-programmed equilibrium position will increase relative to movements which were not perturbed in this way. Consequently, the difference between the joint angle and stretch reflex threshold (λ) increases, which should result in an increase in agonist muscle activity that remains until the joint reaches the originally programmed final equilibrium position.

Contrary to this prediction, Lackner & Dizio (1994) found systematic errors in the final position of the hand during reaching movements in a rotating room that were consistent with the effects of the Coriolis force, a force present only during movement. Gomi & Kawato (1996) measured human arm stiffness by perturbing reaching movements in eight different directions. The equilibrium point trajectory was calculated using these stiffness estimations, the actual trajectory and computed muscle torques. The complexity of the equilibrium point trajectories, compared to the simplicity of the actual trajectories, was presented as evidence against a simple rate-controlled shift in equilibrium position. In defending the EPH, Feldman et al. (1998) argued that Lackner & Dizio's (1994) experiment entailed a change in the motor command, violating a necessary condition for equifinality under the EPH. Gomi & Kawato's (1996) results were dismissed because their estimated equilibrium trajectory did not arrive at the final position until some time after the actual movement had already ceased. Feldman et al. (1998) argued that this was not physically possible and attributed it to simplified assumptions about the force-generating mechanism (Gomi & Kawato, 1996).

Gribble et al. (1998) argued in defence of the EPH, showing that the complex trajectory found in the reaching experiment of Gomi & Kawato (1996), and cited as evidence against the EPH, could, in fact, be formed using simple monotonic changes in the equilibrium point. Although this appears to support the EPH, the authors point out that even though simple control signals, such as those under the λ-model, can control simple movements, movements with complex kinematics or movements requiring compensation for external loads may be controlled using more complex control signals.

In a study by Popescu & Rymer (2000), subjects made short (10 cm) reaching movements during which perturbations were applied in the direction of elbow flexion or extension. The persistence of endpoint error in extension perturbation trials was reported as evidence against the EPH. However, the study has several shortcomings. First, the stiffness of the arm was relatively low, favouring residual position error. Second, perturbations during small amplitude movements have been shown to have a greater effect on endpoint error than during large amplitude movements (Sanes & Evarts, 1983; Sanes, 1986). Third, the demonstrated lack of equifinality only for the extension perturbations is equivocal.

In addition to the aforementioned shortcomings of previous tests of the EPH, no test so far has been designed to compare alternative hypotheses, which predict distinct outcomes. We have designed an experiment for which formation of an IDM predicts that final position error will increase with the magnitude of an unexpected change in the environmental force. The EPH, in contrast, predicts that final position should not change. The environmental force was realized as an assisting torque, proportional to the velocity of wrist movement. Under the IDM framework, an unexpected reduction in the assisting torque would cause the movement to fall short of the intended goal by an amount directly proportional to the amount of the reduction. Under the EPH framework, regardless of the level of reduction in the assisting torque, and regardless of whether changes in the equilibrium point occur monotonically or in a more complex manner, the same final position should be achieved, albeit more slowly.

Our experimental design, unlike that of Gomi & Kawato (1996) requires no estimation of an equilibrium trajectory. It also addresses another issue raised by Feldman et al. (1998). Specifically, the property of equifinality is based on the premise that the pattern of central commands is not altered by a perturbation, something which Lackner & Dizio (1994) and Popescu & Rymer (2000) did not demonstrate. To deal with this issue, we recorded the activity of all of the primary muscles contributing to the movement to demonstrate maintenance of the same feedforward commands under all force perturbation conditions. Furthermore, to address the claim of Feldman et al. (1998) that the force perturbations in Lackner & Dizio's (1994) study, and possibly also in that of Popescu & Rymer (2000), may have been lower than a threshold, below which the EPH demonstrates no corrective muscle activation, we imposed perturbations of four different strengths, which included load changes of more than 100 %. The 30 deg flexion movements of the present study can be considered comparable to the large amplitude movements in Sanes' studies (Sanes & Evarts, 1983; Sanes, 1986), and the co-contraction of wrist flexor and extensor muscles required to perform the task successfully produced high stiffness (Milner & Cloutier, 1998), alleviating the ambiguity that the EPH may hold for high stiffness, large amplitude movements (Bizzi et al. 1978; Bizzi & Polit, 1978) but be prone to failure for low amplitude, low stiffness movements (Sanes & Evarts, 1983; Sanes, 1986; Popescu & Rymer, 2000).

METHODS

Experimental procedure

Six healthy, right-handed subjects (three men and three women aged 21–32 years) took part in the study. All subjects gave their informed, and written, consent to the protocol, which was approved by the Simon Fraser University Ethics Review Committee.

The apparatus and data acquisition system were the same as those described by Milner & Cloutier (1998). Briefly, a torque motor (PMI U16M4) with a fixture for securing the hand was used to apply an assisting torque to the wrist during flexion movements. Position, velocity and torque were measured together with surface EMG. Active bipolar surface electrodes (bandpass 20–500 Hz) were used to record activity from flexor carpi radialis (FCR), flexor carpi ulnaris (FCU), extensor carpi radialis (ECR) and extensor carpi ulnaris (ECU) muscles. All signals were sampled at 2000 Hz.

Subjects sat 0.70 m from a computer screen on which they viewed a display depicting wrist position as a vertical cursor. A 1 deg start window, centred on the subject's relaxed wrist position (0 deg), and a 3 deg target window, centred at 30 deg of flexion, were displayed as shaded regions above and below the position cursor, 0.18 m apart on the screen. The full screen represented 42 deg and had a resolution of 1/15 deg of wrist motion. Subjects could easily detect movement of 1/5 deg. The cursor was active only between trials to allow subjects to reposition the wrist in the start window. A box placed over the hand and apparatus prevented the subject from viewing the hand. Subjects were instructed to move the wrist from the start window to the centre of the target window at a prescribed peak velocity of 300 deg s⁻¹ ± 10 %. No visual feedback of wrist motion was available during the movement. The final position of the cursor and peak velocity during the movement were displayed only at the completion of the data acquisition, 1.5 s after movement onset. A horizontal bar at the bottom of the display screen reflected whether subjects had moved too slowly, too quickly, or in the desired range of peak velocity of 300 deg s⁻¹ ± 10 %. Subjects could make adjustments to the velocity on subsequent trials using this information. All trials were included in the analysis, regardless of the actual peak velocity.

Movement was assisted by the torque motor in proportion to angular velocity, ω. The control law used was τ = Bω. The velocity feedback gain, B, was positive, such that the torque, τ, assisted movement to the target. This produced negative damping of the torque motor, which resulted in underdamped oscillation of the wrist about the final position. The value of B was selected individually for each subject to ensure that the oscillation had completely subsided several hundred milliseconds before the end of data acquisition. Values ranged from 0.009 to 0.0011 N m s deg⁻¹.

Subjects performed 500–700 practice trials in sessions conducted prior to the day of the experiment to become familiar with the apparatus and to learn task dynamics. All practice trials were performed with the assisting torque. The experimental session began with an additional 100 practice trials with the assisting torque, followed by five sets of 100 trials in which the assisting torque was occasionally and unexpectedly reduced. There was a break between each set to prevent fatigue. Since trials were self-initiated subjects could rest within sets, if desired.

On 10 % of trials, selected randomly, the value of B was reduced prior to movement onset, without warning. The amount of the reduction was randomly chosen as 0 %, 25 %, 50 %, 75 % or 100 %. Each reduced value of B occurred 10 times. No feedback of wrist position or peak velocity was given on these trials, which are hereafter referred to as perturbation trials. Subjects were instructed to produce a single movement and not to react voluntarily to any changes in the assisting torque. Trials in which voluntary reaction was evident, i.e. as one or more late corrective movements, where zero crossings were present in the velocity trace, were excluded from later analysis (see below). This was detected in three perturbation trials for one subject and in four perturbation trials for another. In the statistical analysis, the data for these trials were replaced by the average of the remaining trials corresponding to the same perturbation condition.

One subject was consistently unable to suppress corrective reactions to changes in load during the perturbation trials. Late corrective movements towards the target were detected in 24 of the 50 perturbed trials. Because the subject was not able to adhere to the instructions, his data were not included in the subsequent analysis.

Analysis

This study enabled us to test the two very distinct hypotheses predicted under EPH and IDM control. Under the IDM framework, learning to move with the assisting torque would consist of a reduction in the joint torque produced by agonist muscles to accelerate the wrist to the required velocity and an increase in the torque produced by antagonist muscles to decelerate the limb and accurately locate the target. Under the EPH framework, learning would involve decreasing the rate of the shift in equilibrium position, which would now be augmented by the assisting torque. Both control models would predict that due to the underdamped nature of the wrist-motor system, initial overshoot of the final position, followed by underdamped oscillations about the target would ensue.

An IDM model predicts that an unexpected reduction in the assisting torque will cause the movement to fall short of the intended goal by an amount that would increase with the magnitude of the torque reduction. Assuming that the feedforward motor command is not altered, the speed of the movement will be reduced in relation to the amount by which the assisting torque is reduced. The slower the movement, the closer to the start position the extensor torque impulse will begin, and consequently the farther short of the target the movement will stop. Oscillation will still occur about the new final position if the assisting torque is not reduced to zero. Under the EPH, movement kinematics will be affected in a similar way when the assisting torque is reduced, i.e. the movement speed will be reduced. Assuming that the pre-programmed change in equilibrium position remains unaltered, the flexor muscles will be farther from their stretch reflex threshold (λ) than before, so their activation will increase, compensating for the reduction in the motor torque and driving the wrist to the same final position. The velocity profile may be skewed, reflecting a longer deceleration phase since flexor muscle activation will be reduced as the wrist approaches the programmed final equilibrium position. Depending on the level of torque reduction, some overshoot and oscillation about the target would be expected if the wrist-motor system remains underdamped. The predicted result of removing 100 % of the assisting torque is compared for IDM and EPH in Fig. l.

Figure 1. Theoretical predictions of the movement kinematics under IDM and EPH control.

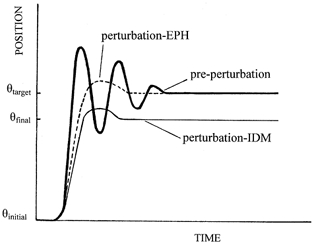
Movement under IDM and EPH results in identical movements after extensive learning of the control (pre-perturbation) movements (thick line) from Θ_initial to Θ_target, where Θ represents the wrist position. On a 100 % torque-removed perturbation trial, stretch reflex activity creates extra flexor torque such that the same final position, Θ_target, is achieved under the EPH (dashed line). In contrast, repetition of the feedforward motor command under IDM control results in an undershoot of the target (thin line) of Θ_target−Θ_final, directly proportional to the magnitude of the torque change.

Position errors were analysed by calculating the difference in final wrist position between perturbed trials and control trials immediately preceding (pre-perturbation) or following (post-perturbation) the perturbed trials. Final position was calculated as the average position during the final 100 ms of the data acquisition period, i.e. 1.4–1.5 s after movement onset. We confirmed that all motion had ceased before this time. Two-way repeated measures ANOVA and linear regression were used to establish the statistical significance of the differences. An a priori significance level of 0.05 was used in the ANOVA. Greenhouse-Geiser or Huynh-Feldt corrections were used where necessary to correct the degrees of freedom for low sphericity values (Howell, 1997).

To determine whether the motor commands to muscles were modified when the assisting torque was reduced, the cumulative EMG on pre-perturbation and perturbation trials was compared for each muscle. The EMG was rectified and smoothed using a 10-point moving average. The cumulative EMG at any point in time was calculated by summing the rectified EMG up to that point, starting 250 ms prior to movement onset. The mean cumulative EMG was calculated for each perturbation condition by averaging values for each of the 10 trials. Mean cumulative EMG for perturbation and pre-perturbation trials was compared using a non-parametric Kolmogorov-Smirnov test (Sokal & Rohlf, 1981) with an a priori significance level of 0.05. Using this test, the cumulative EMG for the two conditions could be compared up to any selected time to determine whether it differed significantly at any prior time.

The nature of the environmental force allowed us to analyse stretch reflex activity during the underdamped oscillations about the final position. We compared stretch reflex gain and threshold in pre-perturbation and post-perturbation trials. In both pre- and post-perturbation trials the wrist oscillated about the final position. These oscillations stretch and shorten the wrist muscles, producing phasic modulation of the EMG that can be attributed to the stretch reflex (Milner, 2002). If the stretch reflex was altered in any way during the random perturbation we would expect to see a change in the stretch reflex response in the post-perturbation trial. Although this is an indirect means of addressing the question of changes in reflex threshold (λ), the method can be applied to all levels of torque reduction, whereas direct analysis could only have been undertaken for trials corresponding to 0 % and 25 % reduction in the assisting torque, since with higher torque reductions there was no oscillation about the final position. EMG integrated over a period of 50 ms, beginning 20 ms after the onset of muscle stretch, as indicated by zero crossings of wrist velocity, was used as a measure of the monosynaptic stretch reflex. The amplitude of the wrist displacement, relative to its final position, was used as a measure of the magnitude of the muscle stretch. All pre- and post-perturbation trials were analysed. The 50 pre-perturbation trials for the five levels of torque reduction formed one set of data on which linear regression between cumulative EMG and displacement amplitude was performed for each subject. Similarly the 50 post-perturbation trials formed a second set of data on which linear regression was performed for each subject. By conducting a test of parallelism, an inference could be made about differences in stretch reflex gains, while testing for common intercepts provided information about differences in stretch reflex thresholds.

RESULTS

With extensive practice subjects adapted to the assisting torque and were able to perform accurate wrist flexion movements. The mean final position of pre-perturbation trials was 29.7 deg (s.d. 2.23), almost at the centre of the target window, while the mean peak velocity was 334 deg s⁻¹ (s.d. 49.4), approximately at the upper bound of the velocity target window. This was achieved without visual feedback during the movement. No secondary corrective movements were present in any of the trials included in the analysis.

The pre-perturbation trials (full assisting torque) are compared with the perturbation trials in which the assisting torque was reduced by 100 % in Fig. 2. There was a prominent overshoot and an underdamped oscillation of the wrist prior to stabilization at the final equilibrium position in pre-perturbation trials (thin lines) due to the assistance and negative damping of the torque motor. The positive velocity feedback control law, governing the behaviour of the torque motor, can be readily identified by comparing the recorded velocity and torque signals. The average final position was very close to the centre of the target window (30 deg), indicating that subjects accurately compensated for the dynamics of the torque motor. Muscle activity was characterized by prominent bursts in the FCR and FCU muscles to initiate movement. Bursts in the ECR and ECU muscles occurred shortly after movement onset to decelerate the wrist. There were later bursts which reflected stretch reflex responses during the oscillations about the final position.

Figure 2. Comparisons of EMG (normalized to peak), position and velocity for perturbation trials (thick lines) with 100 % reduction in assisting torque and the corresponding pre-perturbation trials (thin lines) for subject DM.

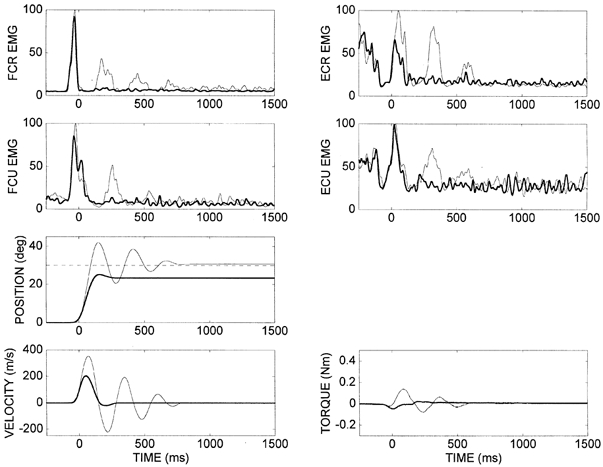
Data were averaged for the 10 trials under each condition. In the perturbation trials, the final position falls substantially short of the target. The patterns of muscle activation, associated with movements to the target are similar under the two conditions. They differ during the stabilization phase due to different kinematics with and without the assisting torque. Phasic stretch reflex activity is seen in the pre-perturbation trials as alternate phase-locked EMG bursts in flexors and extensors. The target is represented on the position plot as a dashed horizontal line.

The key feature of the perturbation trials (reduced assisting torque) was the prominent error in final position. The wrist always stopped short of the target. Without the assisting torque there was much less overshoot in the position and the wrist stabilized quickly at its final position. The peak velocity was much lower than the target value since there was no assisting torque. The initial EMG bursts in both flexor and extensor muscles were almost identical to those recorded in the pre-perturbation trials, although later bursts were generally undetectable due to the absence of oscillation.

Mean position traces for the perturbation trial at each level of torque reduction are shown in Fig. 3. As a higher percentage of the assisting torque is removed, the amount of oscillation about the final position is significantly reduced, reflecting a reduction in the negative damping of the wrist-motor system. To test whether the final position error was related to the percentage of the torque that had been removed, we calculated the difference in final position between each pre-perturbation trial and the subsequent perturbation trial. The differences were averaged for each perturbation condition. The average over all subjects is displayed as a linear regression in Fig. 4. It is clear that the error increased linearly with the percentage of assisting torque removed. Regression lines fitted to the data of individual subjects were highly linear with coefficients of variation (R²) between 0.74 and 0.94.

Figure 3. Position traces for the control perturbation trials (0 % torque reduction) and the 4 levels of torque reduction (25 %, 50 %, 75 % and 100 %).

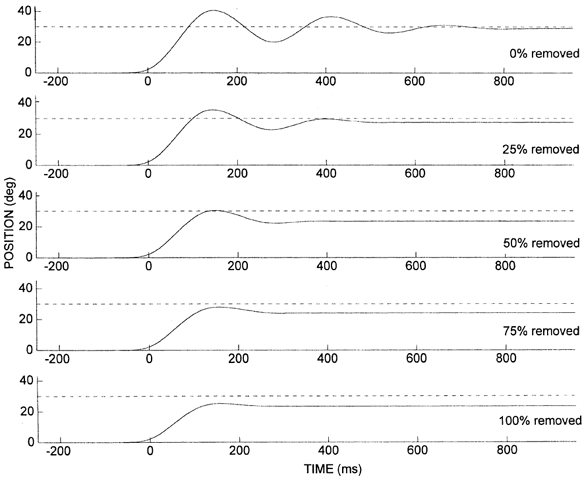
Endpoint error increases and the amplitude and number of oscillations about the target decrease as more of the assisting load is removed. Data are averaged over the 10 trials in each condition for subject DM.

Figure 4. Line fit of the difference in final position between the perturbation trials and corresponding pre-perturbation control trials, as a function of the percentage reduction in assisting torque.

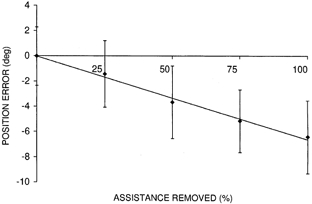
The data points represent the means for the five subjects. Error bars represent the standard deviation of all trials for each perturbation condition.

Two-way repeated measures ANOVA was used to compare final position in pre-perturbation and perturbation trials. The main effect of reducing the assisting torque was highly significant (F = 15.472, P = 0.003), showing that subjects stopped shorter of the target on the perturbation trials than the pre-perturbation trials. The trial main effect was not significant (F = 0.469, P = 0.648), i.e. as subjects were exposed to more and more perturbation trials, performance in the post-perturbation trial did not alter, relative to early exposures. The interaction between reduced assisting torque and trial number was not significant either (F = 1.131, P = 0.377).

ANOVA to compare pre- and post-perturbation trials did not reveal any difference in final position (mean −0.009 deg, s.d. 2.576 deg). There was no significant effect of the percentage of assisting torque removed in the intervening perturbed trial (F = 1.965, P = 0.195) or of the trial number (F = 0.507, P = 0.667), nor was there any significant interaction between the two (F = 1.179, P = 0.358). Figure 5 shows the pre- and post-perturbation trials corresponding to the 100 % torque removed perturbation. The amplitude of the overshoot and the number of oscillations were the same in the two cases as the torque motor provided full assistance on these trials. In fact, the kinematic traces correspond so precisely that the two traces are completely coincident for the duration of the movement. Furthermore, a two-way repeated measures ANOVA revealed no significant difference between the peak velocity in pre- and post-perturbation trials over all five subjects (F = 2.92, P = 0.160), nor was there any significant difference in peak velocity between trials under the five different load conditions (F = 1.939, P = 0.178. Stretch reflex activity was evident in all muscles during oscillations about the final position, and the reflex bursts were modulated with the oscillation amplitude in a similar manner for pre- and post-perturbation trials.

Figure 5. Comparisons of EMG (normalized to peak), position and velocity for pre-perturbation (thick lines) and post-perturbation trials (thin lines) corresponding to perturbation trials in which 100 % of the assistance was removed.

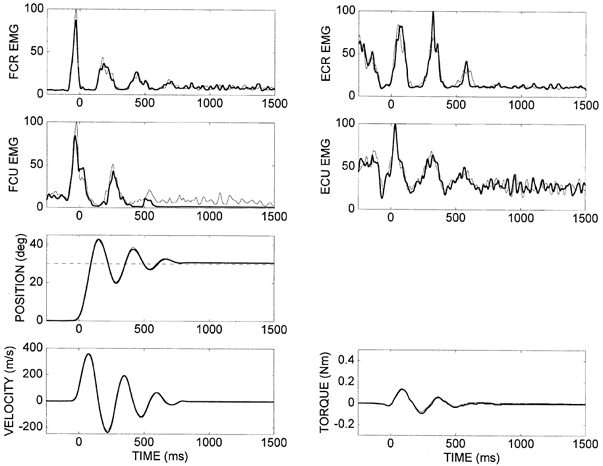
Data were averaged for the 10 trials under each condition for subject DM. EMG bursts during the period of stabilization are phase-locked to wrist displacement. The burst amplitudes can be seen to decrease as oscillation amplitude decreases. Note the distinct similarity in EMG and kinematic traces, and that the target is accurately located in both pre- and post-perturbation trials.

The cumulative EMG for one subject is shown in Fig. 6 for pre-perturbation trials and perturbation trials, where the assisting torque was reduced by 100 %. There were no significant differences in the cumulative EMG (P < 0.05) for any muscle for this subject or for any of the other four subjects, who did not make corrective movements, prior to the time at which stretch reflex responses occurred in the pre-perturbation trials during oscillations about the final position. Furthermore, regardless of the percentage of assisting torque reduction, no significant difference in the cumulative EMG during this period was found for any of these subjects. This indicates that subjects issued the same pattern of feedforward motor commands to wrist muscles in perturbation trials as in pre-perturbation trials.

Figure 6. Normalized cumulative EMG signals for the four muscles beginning 250 ms before movement onset.

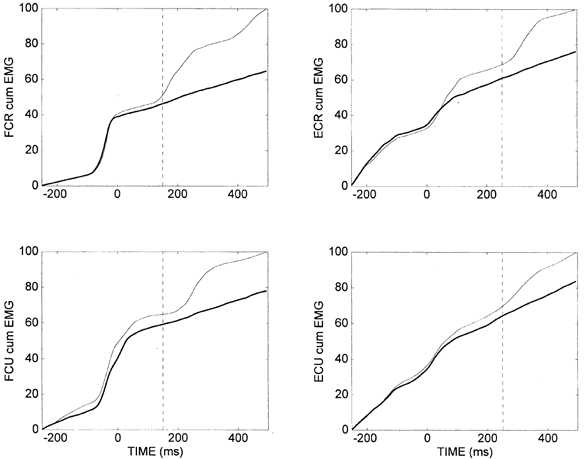
Data shown are for the perturbation trials with assisting torque reduced by 100 % (thick lines) and the corresponding pre-perturbation trials (thin lines), averaged over the 10 trials for subject DM. The vertical dashed lines on the flexor and extensor plots represent the time at which the first oscillation occurred in the pre-perturbation trials, causing muscle stretch in the flexors or extensors, respectively. Differences in cumulative EMG were not statistically significant from the start of data collection until the time of oscillation onset.

The preceding analysis might be interpreted as an incomplete characterization of the central motor commands because it does not address the state of the stretch reflex, which is integral to the λ-model. Under Feldman's λ-model, the stretch reflex threshold is crucial in determining muscle activation to correct for any error in final position. If a muscle, either flexor or extensor, is stretched to a length longer than at the corresponding threshold angle, λ_flexor or λ_extensor, stretch reflex activation will produce muscular force to move the joint until the muscles and the load are in equilibrium. To test whether the state of the stretch reflex was altered when the assisting torque was reduced, we compared the slope and intercept of the relationship between integrated EMG and wrist displacement during oscillation about the final position for pre- and post-perturbation trials (see Methods). There were generally two cycles of underdamped oscillation about the final position for each trial, such that each regression was performed on approximately 100 data points. Because subjects consistently undershot the target when the motor torque was reduced, an increase in flexor muscle activation would have been required to correct the error, so only the reflex response of flexor muscles was analysed. According to the λ-model, an increase in reflex activation should have occurred because the flexor muscles would have been at a longer length than that specified by the central command. Under the λ-model only if the central command were altered so as to increase the stretch reflex threshold could it be claimed that an error would occur due to inadequate reflex activation. For completeness, we also considered the effect of the perturbation trial on the stretch reflex gain, as measured by the slope of the regression lines. Although reflex threshold is central in the λ-model, both stretch reflex gain and threshold are central in the α-model of equilibrium point control (Bizzi et al. 1982).

Representative relationships between integrated EMG and wrist displacement are shown in Fig. 7. Table 1 lists the intercepts and slopes, together with the significance levels for the five subjects for both FCR and FCU.

Figure 7. Linear regression between cumulative EMG and wrist displacement.

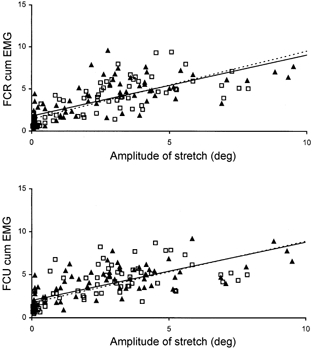
The 10 pre-perturbation trials (▴, continuous line) and 10 post-perturbation trials (□, dotted line) for all five levels of torque reduction on the intervening perturbation trial were combined. The data for FCR are shown in the upper panel and for FCU in the lower panel for subject AN.

Table 1.

Slope and intercept values for FCR and FCU for all five subjects

		Pre-perturbation trials		Post-perturbation trials		P values
	Subject	Slope	Intercept	slope	Intercept	Slope	Intercept
FCR	MH	0.4807	3.9190	0.5017	3.7350	0.6763	0.5967
	DM	0.3889	3.4141	0.3962	3.4389	0.8850	0.9898
	AN	0.7294	1.7823	0.8129	1.4225	0.3962	0.8484
	AL	0.4854	3.4876	0.5326	2.7879	0.6286	0.8522
	BM	0.3259	4.9161	0.2998	4.6700	0.6079	0.9451
FCU	MH	0.4985	3.8100	0.3877	4.4300	0.0105**	0.0272*
	DM	0.8223	2.3927	0.8733	2.9735	0.8811	0.9656
	AN	0.6788	2.0127	0.7166	1.7443	0.7144	0.9025
	AL	0.7570	2.8660	0.6165	2.8601	0.2009	0.9988
	BM	0.8857	4.1880	0.5914	5.8438	0.0218**	0.8323

Significant differences between pre- and post-perturbation trials are shown by asterisks:

^*significant at P = 0.05

^**significant at P = 0.05 after multiple-comparison adjustment.

Correlation coefficients for the 20 regressions (pre-perturbation and post-perturbation for both flexor muscles, for each of the five subjects) ranged from 0.55 to 0.83 (R² values 0.30–0.74), with an average of 0.71. Student's paired t tests revealed that for 9 of 10 comparisons (FCR and FCU for five subjects) there was no significant difference between the intercepts of the linear regressions for the pre- and post-perturbation trials (2-tailed test, a prioriα = 0.05, P values > 0.60). When a family-wise adjustment was made in the critical t value to account for multiple tests, i.e. testing for both slopes and intercepts using the same data set, none of the 10 comparisons produced a statistically significant difference.

Student's paired t tests for the slope (gradient) of the FCR regressions showed that in 8 out of 10 tests the slope in pre- and post-perturbation trials was not significantly different (2-tailed test, a prioriα = 0.05, P values > 0.20). The two cases where significant differences were found showed a decrease in the slope in post-perturbation trials relative to pre-perturbation trials. Both of these tests remained significant when a family-wise adjustment was made in the critical t value to account for multiple tests.

DISCUSSION

The results of our study clearly demonstrate that final equilibrium position is not preserved when the magnitude of an assisting torque, proportional to velocity, is unexpectedly reduced. This obviously violates the EPH. However, the strong correlation between the error in final position and the percentage by which the assisting torque was reduced matches the prediction based on the formation of an IDM of the specific task dynamics.

A fundamental prediction of the EPH is that final position should not be affected by a velocity-dependent perturbation if the pattern of central commands to agonist and antagonist muscles does not change (Feldman et al. 1998). In the λ-model, the equilibrium point specified by the λ state shifts from start to final position at some rate that determines the speed of the movement. An assisting torque that is proportional to velocity will affect the speed of the movement, but will not affect the final position specified by the λ state. Note that λ is not synonymous with final equilibrium position, which depends on load. The greater the load, the farther the final equilibrium position will be from λ because muscle torque must equal load torque. Once λ is fixed, muscle torque increases by moving the joint angle farther from λ. In the case where a velocity-dependent load is added, the added load disappears as movement is halted, leaving the final equilibrium position unaltered. Our results unequivocally demonstrate that not only did subjects stop short of the target when the assisting torque was reduced, but also the position error increased with the reduction in assisting torque. Endpoint error was as large as 6 deg, which represents 20 % of the movement amplitude. Although we cannot definitively state that subjects could perceive this error, it is more than 2.5 times greater than the standard deviation in final position on unperturbed trials. The relative error, as a proportion of movement distance, is the same whether the error is expressed in terms of joint position or endpoint (hand) position. Therefore, it is unlikely that errors as large as 6 deg could be considered as subthreshold for correction by the EPH. Endpoint errors could not be attributed to a change in the pattern of feedforward central commands since there was no difference in the cumulative EMG of any muscle until later in the movement when oscillations ensued about the final position.

As well as showing maintenance of the feedforward motor commands for all levels of torque reduction, we investigated changes in the stretch reflex during oscillations about the final position. We found no evidence of an increase in stretch reflex threshold (higher intercept) between pre- and post-perturbation trials for any subject in either the FCR or FCU. Similarly, when we considered the reflex gain, 8 out of 10 comparisons showed no evidence of a change. The average final position on pre-perturbation trials was 29.7 deg (s.d. 2.23), almost at the centre of the target window. A reduction in stretch reflex gain would, of course, produce lower muscular activity to correct for any residual endpoint error, relative to the programmed equilibrium position. Assuming that the programmed final equilibrium position was at the centre of the target window, i.e. 30 deg, then the residual error would have been 0.3 deg. Given that in the perturbation trial the final commanded equilibrium point defined by the R command remains unaltered, a change in the reflex gain would magnify the small residual error observed in pre-perturbation trials. A reduction in reflex gain of 50 % on the perturbation trial relative to the pre-perturbation trial, much larger than our results suggest, would increase the final position error from 0.3 to 0.6 deg. This is much smaller than the errors that we observed, indicating that observed changes in reflex gain could not be responsible for final position errors on the perturbation trials.

It might be argued that when the movement slowed, friction in the apparatus caused motion to stop and that the driving torque arising from the position error was insufficient to overcome the friction. This is unlikely for several reasons. First, the friction torque of the apparatus is small (0.05 N m). Second, under three of the perturbation conditions where endpoint errors occurred (25 %, 50 % and 75 % reduction in assisting torque) the assisting torque from the motor would have counteracted the friction torque. Furthermore, because of the negative damping effect of this assisting torque, there was often a transient overshoot of the target position even when position finally stabilized short of the target (Fig. 3). Third, wrist stiffness tends to be greater than 0.1 N m deg⁻¹ after adaptation to this type of assisting torque (Milner & Cloutier, 1998). Consequently, the final position error should have been reduced to less than 0.5 deg, according to the EPH, even without any compensation for friction. The fact that the average final position error ranged from about 1.5 to 6 deg belies such an explanation.

The results can be readily explained if the CNS employed an IDM of the dynamics of the assisting torque to control movement (Shadmehr & Mussa-Ivaldi, 1994; Conditt et al. 1997; Thoroughman & Shadmehr, 2000; Scheidt et al. 2000). In this case, we assume that subjects form an IDM of the relationship between velocity and assisting torque through practice. The CNS learns the muscle activation patterns to produce the torque needed to reach the target position. Specifically, it learns the requisite wrist flexor torque to accelerate toward the target at the specified speed and the requisite extensor torque to counteract the assisting torque during deceleration so as to stop in the target window. It also produces sufficient co-contraction of agonist and antagonist muscles to ensure stability (Milner, 2002). Because the assisting torque was reduced on perturbation trials, the flexor torque required to reach the target was increased while the extensor torque required to stop the movement was reduced. However, the CNS issued the same feedforward motor commands on all trials, as judged by the similarity in cumulative EMG up to the first velocity zero crossing. This is precisely as expected from a feedforward control scheme using an IDM and would result in the observed final position errors. There would be a deficiency in flexor torque and an excess extensor torque, equal to the reduction in assisting torque. Consequently, the movement would stop short of the target by an amount that increased with the percentage by which the assisting torque had been reduced.

Several previous studies have yielded evidence that casts doubt on the principle of equifinality. However, in none of them was equifinality completely violated nor was an alternative control hypothesis tested. Rothwell et al. (1982) found undershooting of the target position under conditions where muscle was areflexive. Since this only occurred during faster movements and did not occur when stretch reflexes were intact, it could not be considered as evidence against the λ-model of equilibrium point control. Similarly, Sanes & Evarts (1983) and Sanes (1986) found that unexpected changes in viscous loading produced final position errors, but only for small amplitude movements. Consequently, these errors may have been below some hypothesized threshold for stretch reflex compensation, as suggested by Feldman et al. (1998). This criticism, and the possibility of a change in motor command, weighs against the findings of Lackner & Dizio (1994) as providing definitive evidence against the EPH. The results of Popescu & Rymer (2000) were equivocal. They did not show that equifinality was consistently violated. Furthermore, their experimental protocol involved relatively small amplitude movements unopposed by any external load, where stiffness would have been low, a situation in which final position error would be expected given the elastic nature of the internal load (muscle and tendon).

Our test of the EPH is stronger than in any previous study. We created a situation where high joint stiffness was required and trained subjects to perform movements of moderate amplitude and speed. Furthermore, we rigorously examined the possibility of a change in motor command from the perspective of both change in feedforward command and change in stretch reflex threshold or gain. There should be no doubt that if the EPH was valid then equifinality should have held under our experimental conditions. The final position errors that we found were inconsistent with the EPH, but entirely consistent with a priori predictions based on feedforward control by an IDM. In addition, the similarity of the cumulative EMG on pre-perturbation and perturbation trials supports the use of such feedforward control. Comparison of the final position on pre-perturbation and post-perturbation trials provided more supportive evidence. Not only did we find no difference in final position, but also there was no effect of the magnitude of the intervening perturbation trial. This indicates that the feedforward motor commands were robust and could not be altered by occasional, unexpected changes in the relationship between assisting torque and velocity. Although we have not tried to show that the EPH fails universally since we examined only the case of wrist flexion under an assistive load, our results are in clear contradiction to the EPH. Furthermore, we have demonstrated that the results are compatible with an alternative movement control strategy, which postulates formation of an IDM.

We have presented evidence from both movement kinematics and patterns of muscle activation that provides strong support for the theory of IDM formation, but contradicts the EPH. This conclusion is not restricted to the λ-model, but applies generally to all formulations of the EPH. However appealing the EPH may be, we have shown that one of its fundamental predictions, equifinality, does not hold under certain conditions. We conclude that learning leads to the formation of an IDM of the load dynamics by the CNS, which is used for feedforward control of motor commands to muscles.