Abstract
Channels are water-filled membrane-spanning proteins, which undergo conformational changes as they gate, i.e. open or close. These conformational changes affect both the shape of the channel and the volume of the water-filled pore. We measured the changes in pore volume associated with activation, deactivation, C-type inactivation and recovery in an N-terminal-deleted mutant of the Kv1.4 K+ channel (Kv1.4ΔN) expressed in Xenopus oocytes. We used giant-patch and cut-open oocyte voltage clamp techniques and applied solutes which are too large to enter the pore mouth to exert osmotic pressure and thus favour smaller pore volume conformations. Applied intracellular osmotic pressure (300 mm sucrose) sped inactivation (time constants (τinactivation): control, 0.66 ± 0.09 s; hyperosmotic solution, 0.29 ± 0.04 s; n = 5, P < 0.01), sped deactivation (τdeactivation: control, 18.8 ± 0.94 ms; hyperosmotic solution, 8.01 ± 1.92 ms; n = 5, P < 0.01), and slowed activation (τactivation: control, 1.04 ± 0.05 ms; hyperosmotic solution, 1.96 ± 0.31 ms; n = 5, P < 0.01). These effects were reversible and solute independent. We estimated the pore volume change on inactivation to be about 4500 Å3. Osmotic pressure had no effect when applied extracellularly. These data suggest that the intracellular side of the pore closes during C-type inactivation and the volume change is similar to that associated with activation or deactivation. This is also similar to the pore volume estimated from the crystal structure of KcsA and MthK K+ channels. Intracellular osmotic pressure also strongly inhibited re-opening currents associated with recovery from inactivation, which is consistent with a physical similarity between the C-type inactivated and resting closed state.
C-type inactivation is the result of a major conformational change in K+ channels that can determine the ionic dependence, drug affinity and use-dependent drug binding properties of the channels (Lopez-Barneo et al. 1993; Baukrowitz & Yellen 1996a, b; Wang et al. 1997, 2003; Rasmusson et al. 1998; Ficker et al. 1998). C-type inactivation is the rate limiting step for recovery from inactivation of K+ channels and is thought to be closely related to the mechanism responsible for ‘slow’ inactivation of calcium and sodium channels (Zhang et al. 1994; Qu et al. 1999; Todt et al. 1999). C-type inactivation is sensitive to the concentration of extracellular permeant ions (Lopez-Barneo et al. 1993; Rasmusson et al. 1998), competes with extracellular TEA (Armstrong, 1971; Hoshi et al. 1990; Lipkind et al. 1995) and is sensitive to mutations near the extracellular mouth of the channel (Hoshi et al. 1991; Busch et al. 1991; Balser et al. 1996; Liu et al. 1996; Ficker et al. 1998). Based on this evidence, C-type inactivation was thought to arise from a closure of the extracellular mouth of the pore (Baukrowitz & Yellen, 1995, 1996b; Ficker et al. 1998). However, C-type inactivation is strongly influenced by events occurring at the intracellular side of the pore (Rasmusson et al. 1995; Wang et al. 2003; Li et al. 2003).
Channels are membrane-spanning water-filled pores. As the channel transitions between non-conducting and conducting states the structure, and therefore the volume, of the water-filled pore changes. If non-conducting osmolytes are introduced on one side of the membrane, there will be an increase in osmotic pressure. Frog oocyte membranes are relatively impermeable to water compared to other eukaryotic cells, which allows the osmotic pressure to be manipulated independently on either side of the membrane without major transmembrane flow artifacts and associated local unstirred layer effects (Starkus et al. 1995; Zeuthen et al. 2002). If osmolytes are chosen so that they are too large to enter the channel vestibule there will be an imbalance and an osmotic pressure gradient between the water-filled pore and the bath solution. If the volume of the water-filled pore is greater in the conducting state than the non-conducting state, an increase in osmotic pressure would favour the closed versus the open state (Zimmerberg & Parsegian, 1986). This is illustrated in Fig. 1.
Figure 1. The effect of osmostic pressure on ion channel behaviour.
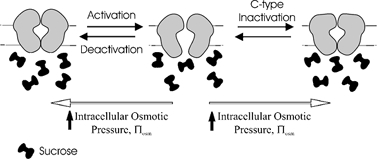
When a solute too large to enter the pore mouth is added to the solution on one side of the membrane osmosis will result in withdrawal of water from the pore. There will be a resulting osmotic pressure on the channel, which will make channel states with smaller pore volumes more energetically favourable. Activation of voltage-dependent cation channels is believed to result in the formation of a large intracellular vestibule but involve only relatively minor changes in volume on the extracellular face (Jiang et al. 2002). Activation, therefore, should be relatively insensitive to applied extracellular osmotic pressure. C-type inactivation is thought to involve closure of the extracellular side of the pore. If this closure involves a substantial change in volume, then extracellular osmotic pressure should promote C-type inactivation. Activation involves the formation of a large water-filled intracellular vestibule. Therefore it should be relatively sensitive to applied intracellular osmotic pressure, with higher osmotic pressure favouring the closed state. Deactivation is the reverse process to activation, so should be affected by osmotic pressure to a similar degree. If C-type inactivation involves a substantial change in intracellular pore volume, then intracellular osmotic pressure should promote C-type inactivation. If the volume changes involved in activation/deactivation and C-type inactivation are similar then the rates of activation, deactivation, and C-type inactivation should be changed proportionately, despite their vastly different time scales.
The process of activation is hypothesized to involve the formation of a water-filled intracellular vestibule (Jiang et al. 2002). The activation rate should, therefore, be slowed by application of large intracellular solutes. Similarly, an increase in osmotic pressure will favour the closed state and therefore enhance the rate of deactivation (Zimmerberg et al. 1990). If C-type inactivation involves a decrease in the volume of the intracellular pore, then an increase in intracellular osmotic pressure will promote the development of C-type inactivation. If the volume changes involved in activation and C-type inactivation are similar then the rates of activation, deactivation and C-type inactivation will be changed proportionately. The percentage change will depend only on the volume changes involved rather than the scale of the parameter values, which are orders of magnitude different.
In this study we demonstrate that the major physical conformational change in terms of pore volume associated with C-type inactivation occurs at the intracellular side of the channel.
METHODS
Mature female Xenopus laevis (Xenopus Express, FL, USA) were cared for in accordance with standards approved by the Institutional Animal Care and Use Committee of the University at Buffalo SUNY. Frogs were anaesthetized by immersion in tricaine solution (1 g l−1 Sigma). Oocytes were digested by placing in a collagenase-containing Ca2+-free OR2 solution (mm: 82.5 NaCl, 2 KCl, 1 MgCl2, 5 Hepes (pH 7.4); 1 mg ml−1 collagenase (type I, Sigma) added). The oocytes were gently shaken for 1.5–2 h, with an enzyme solution replacement at 1 h. Defolliculated oocytes (stage V–VI) were injected (using the Nanoject microinjection system; Drummond Scientific Co., Broomall, PA, USA) with up to 50 ng mRNA of a Kv1.4 channel clone (Kv1.4ΔN) originally isolated from ferret heart (Comer et al. 1994). Frogs were humanely killed by overdose of anaesthetic through immersion following the final collection of oocytes.
Currents were recorded at room temperature (∼22 °C). Two procedures were used: the cut-open oocyte voltage clamp and the giant-patch technique. Cut-open oocyte experiments (Bezanilla et al. 1991) were performed using a CA-1B Amplifier (Dagan Corp., Minneapolis, MN, USA). Oocytes were permeabilized with a 1 % saponin solution. Microelectrodes with resistances of 0.5–1.5 MΩ (when filled with 3 m KCl) were fabricated from 1.5 mm o.d. borosilicate glass tubing (TW150-4, WPI) using a two-stage puller. The control extracellular solution (98 K) contained (mm): 0 NaCl, 98 KCl, 1 MgCl2, 1.8 CaCl2, and 10 Hepes (pH adjusted to 7.4 with KOH). The intracellular solution contained (mm): 98 KCl, 1 MgCl2, 1.8 EGTA, and 10 Hepes (pH adjusted to 7.4 with KOH). Control cut-open oocyte currents averaged 3.75 ± 2.60 nA (mean ± s.d., n = 7).
Giant torn-off patches (Hilgemann, 1990) were taken from some oocytes and used as inside-out membrane patches in which intracellular solutions were controlled by a rapid solution-switching device (ALA Scientific Instruments Inc., NY, USA). Microelectrodes (0.5 MΩ) were coated with a mixture containing 5 % parafilm and light mineral oil. The giant-patch electrode solution contained (mm): 98 KCl, 1 MgCl2, 2.5 CaCl2, 10 Hepes (pH adjusted to 7.4 with KOH). For giant-patch experiments, the initial bath solution contained (mm): 98 KCl, 1.8 MgCl2, 1 EGTA, 10 Hepes (pH adjusted to 7.4 with KOH). Sucrose (300 mm) or N-methyl-d-glucamine methanesulfonate (NMDG, 300 mm) was added to the solutions to vary the osmotic pressure. Changes in kinetic properties with osmotic pressure were all measured relative to behaviour in the same patch under control conditions. Giant-patch peak currents at +30 mV were 3.19 ± 0.53 nA (mean ± s.d.) in control and 1.37 ± 0.36 nA (mean ± s.d.) in 300 mm NMDG (n = 5).
Data were digitized and analysed using pCLAMP 7 (Axon Instruments, CA, USA). Further analysis was performed using Clampfit (Axon Instruments, CA, USA), Excel (Microsoft Corp., WA, USA) and Origin (Microcal Software Inc., MA, USA). Data were filtered at 2 kHz and reported as means ± s.e.m. unless stated otherwise). Confidence levels were calculated using Student's paired t test. The null hypothesis was rejected when P < 0.05. Currents were inverted for clarity where necessary (see individual figure legends).
Structural modelling was performed using the Insight II 3D graphical environment for molecular modelling (Accelrys Inc., San Diego, CA, USA) running on a Silicon Graphics Indigo workstation (SGI, CA, USA) with a UNIX operating system. Atom co-ordinates were downloaded from the Research Collaboratory for Structural Bioinformatics. Side-chains were replaced using sequence homology modelling (Vector NTI, Informax, Inc., MD, USA) and energy minimized in Insight II. Cross-sectional areas of the pore were estimated in 1 Å (0.1 nm) steps along the axis of the pore of each channel type after side-chain substitution for Kv1.4 and energy minimization of side-chain orientation. Pore dimensions were estimated from the Van der Waal radius of the innermost side-chain carbon atom corrected for an attached hydrogen. These were summed to estimate the aqueous volume of the pore.
RESULTS
Electrophysiology
Kv1.4ΔN channels (amino acids 2–146 are deleted from the N-terminal which removes N-type inactivation) inactivate only by C-type inactivation, so providing an excellent system to study the effects of osmotic pressure on C-type inactivation. We studied these channels expressed in Xenopus oocytes. Osmotic pressure was manipulated by adding sucrose or NMDG to the intracellular or extracellular solutions, and the kinetic behaviour of Kv1.4ΔN was studied.
Figure 2 shows the effect of exposing Kv1.4ΔN channels to a hyperosmotic intracellular solution made with 300 mm sucrose. The time constant (τ) of activation was estimated by a single exponential fit to the late phase of current activation, which followed the initial sigmoid delay. Using the giant-patch voltage clamp technique to perfuse oocytes with a hyperosmotic intracellular solution resulted in a slowing of activation (Fig. 2A and B): the time constant of activation (τactivation) was increased from 1.04 ± 0.05 ms in control to 1.96 ± 0.31 ms in hyperosmotic solution (n = 5, P < 0.01). This is consistent with previous observations on a related delayed rectifier K+ channel (Zimmerberg et al. 1990) and a more distantly related Na+ channel (Rayner et al. 1992). This observation is also consistent with the hypothesis that activation involves the creation or opening of an intracellular water-filled vestibule.
Figure 2. Effect of intracellular hyperosmotic pressure on activation, C-type inactivation and deactivation in Kv1.4ΔN channels.
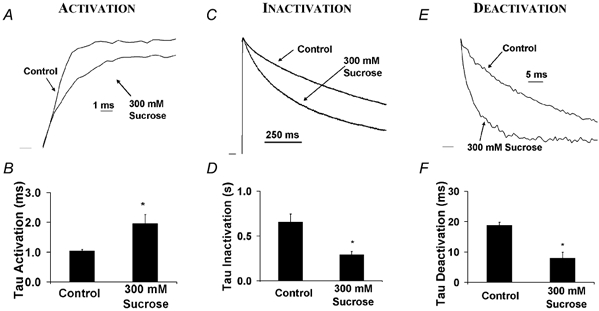
Currents were recorded from detached inside-out giant patches (Hilgemann, 1990) perfused with 300 mm (330 mosmol l−1) sucrose to increase osmotic pressure. Currents are normalized (and inverted where necessary) to emphasize changes in kinetic rates. Voltage clamp pulses (duration 1 s were applied from −90 to +50 mV. A, activation was slowed in the presence of an intracellular hyperosmotic solution. B, the activation time constant (τ) increased from 1.04 ± 0.05 ms in control to 1.96 ± 0.31 ms in hyperosmotic solution (n = 5, P < 0.01). C, the rate of C-type inactivation increased in intracellular hyperosmotic solution. D, the C-type inactivation time constant decreased from 0.66 ± 0.09 s in control to 0.29 ± 0.04 s in hyperosmotic solution (n = 5, P < 0.01). E, deactivation increased with intracellular hyperosmotic exposure. F, the fast time constant of deactivation decreased from 18.8 ± 0.94 ms in control to 8.01 ± 1.92 ms in hyperosmotic solution (n = 5, P < 0.01). Peak current was also suppressed by application of hyperosmotic pressure (see volume calculations). Peak current was 3.22 μA in control and 1.69 μA in 300 mm sucrose. Peak currents elicited in hyperosmotic solutions were 51 ± 6 % (at +50 mV) 46 ± 5 % (+40 mV) and 43 ± 6 % (+30 mV) of control (n = 5).
The rate of deactivation was increased by an intracellular hyperosmotic solution, with the fast time constant of deactivation (τdeactivation) reduced from 18.8 ± 0.94 ms in control to 8.01 ± 1.92 ms in hyperosmotic solution (n = 5, P < 0.01). This result is consistent with the opening and closing of an intracellular water-filled vestibule.
Surprisingly, the rate of C-type inactivation was also increased when the channel was exposed to an intracellular hyperosmotic solution. The time constant of inactivation (τinactivation) decreased from 0.66 ± 0.09 s in control to 0.29 ± 0.04 s in hyperosmotic solution (n = 5, P < 0.01). Even though these conformational changes occur on vastly different time scales, the relative changes in all time constants were of a similar size (see Fig. 2). This similarity of kinetic changes with osmotic pressure suggests that the intracellular pore volume change associated with all of these processes was similar. This is not surprising for activation and deactivation, since they are presumably the forward and reverse processes for the same conformational change. However, it is surprising for C-type inactivation. These results suggest that C-type inactivation involves a closure of the intracellular pore of the same physical size as deactivation.
In order to confirm that the effects of sucrose were due to changes in osmotic pressure and not to some specific interaction between sucrose and the channel, the giant-patch experiments shown in Fig. 2 were repeated with 300 mm NMDG as the osmolyte. The changes in gating kinetics were independent of the osmolyte used, with NMDG decreasing the rate of activation, and increasing the rate of deactivation and inactivation. The activation time constant increased from 0.73 ± 0.03 ms in control to 1.18 ± 0.09 ms in hyperosmotic conditions (n = 5, P < 0.01). The C-type inactivation time constant decreased from 0.72 ± 0.03 s in control to 0.38 ± 0.02 s in hyperosmotic conditions (n = 5, P < 0.01), and the fast time constant of deactivation decreased from 19.86 ± 1.57 in control to 12.34 ± 1.13 ms in hyperosmotic solution (n = 5, P < 0.01).
To ensure that the effects of the osmolytes were due to a change in pressure, and were not a result of the osmolyte binding to the channel, we tested the response of the channel to several osmolyte concentrations in the cut-open voltage clamp configuration. Figure 3 shows that over the range 0–600 mm NMDG there is a linear relationship between the rate of inactivation (1/τ) and the intracellular osmolyte concentration.
Figure 3. The effects of osmotic pressure were related to the osmolyte concentration.
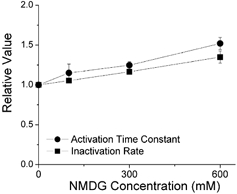
The cut-open oocyte voltage clamp technique was used to apply concentrations of NMDG between 0 and 600 mm, and determine the time constants of activation and inactivation. The oocyte was stepped from −90 to +30 mV for 5 s in 0, 100, 300 and 600 mm NMDG (n = 3). Activation and C-type inactivation rates are normalized to enable direct comparison.
Toxin binding near the external mouth of the pore is relatively unaffected by the activation or inactivation state of voltage-gated channels (Naranjo & Miller, 1996). Although the processes of activation and C-type inactivation undoubtedly result in changes in the structure of the outer mouth of the pore, the toxin binding data suggest that these changes are unlikely to be as physically large as the conformational changes associated with the intracellular gate. We confirmed this prediction through addition of 300 mm sucrose to the extracellular solution in the cut-open clamp configuration. External osmotic pressure had no effect on activation, only a small (but statistically significant) effect on deactivation, and no significant effect on C-type inactivation (Fig. 4). Similar results were observed for application of extracellular NMDG (results not shown). Starkus et al. (1995) observed a similar effect of intracellular, but not extracellular, sucrose addition on activation and deactivation rates in Shaker B channels. This is consistent with there being little or only very small physical changes in the water-filled volume of the external side of the pore (Perozo et al. 1999). In a related K+ channel, KcsA, an ‘external activation gate’ is reported to result in a minor change in solvent accessibility (Perozo et al. 1999), which is consistent with the extracellular changes that accompany C-type inactivation. However, a small change in solvent accessibility does not preclude significant changes in the orientation or conformation of residues on the extracellular face during C-type inactivation. We can only conclude that these changes do not result in a large alteration in the external aqueous permeation pathway, which is inaccessible to the added osmolytes. In other words, the lack of an effect of extracellular osmotic pressure suggests that changes in conformation are either very small, or do not result in a change in volume which excludes the applied osmolytes.
Figure 4. Effect of extracellular osmotic pressure on activation, C-type inactivation and deactivation measured using the cut-open oocyte voltage clamp technique.
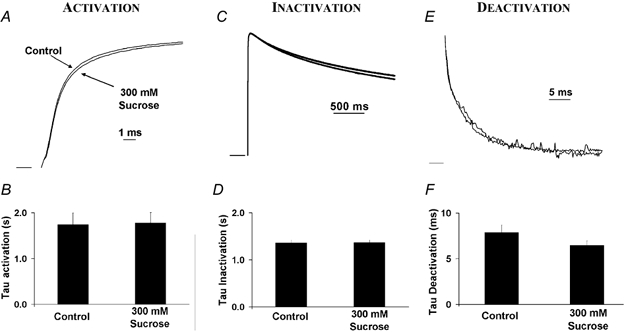
The hyperosmotic extracellular solution contained 300 mm sucrose, giving an increase in osmotic pressure of 330 mosmol l−1. The membrane was stepped from −90 to +50 mV for 1 s. Similar negative results were observed when NMDG was used as the extracellular osmolyte (results not shown). A, external hyperosmotic pressure had no effect on activation. B, the average time constant of activation was unchanged: τactivation = 1.74 ± 0.26 ms in control; τactivation = 1.78 ± 0.23 ms in hyperosmotic solution (n = 12, P > 0.05). C, extracellular hyperosmotic exposure had no effect on C-type inactivation. D, the average time constant of inactivation was unchanged: τinactivation = 1.36 ± 0.06 s in control; τinactivation = 1.37 ± 0.06 s in hyperosmotic solution (n = 12, P > 0.05) E, external hyperosmotic solution had a very small effect on deactivation. F, the time constant of deactivation decreased: τdeactivation = 7.86 ± 0.83 ms in control; τdeactivation = 6.46 ± 0.50 ms in hyperosmotic solution (n = 11, P < 0.01).
The similarity in the changes that osmotic pressure induces in activation, deactivation, and inactivation suggests that these processes are accompanied by similar changes in physical conformation. The Kv1.4ΔN channel has at least four closed states (C), one open (O) and one inactivated state (I), as shown in eqn (A1) in the Appendix (Comer et al. 1994):
Many channels can transition directly from non-conducting partially activated states to inactivated states, without passing through the open or conducting state. Similarly, recovery from inactivation can occur through two pathways: either as a direct transition from the inactivated state to a closed (non-conducting deactivated) state, as indicated by arrows in Fig. 5A, or through the open state (Demo & Yellen, 1991; Ruppersberg et al. 1991). Channels that follow this latter transition will re-open during recovery and produce a measurable re-opening current. The ratio of channels deactivating through these two pathways depends on channel type, inactivation mechanism, ionic conditions and the holding potential (Demo & Yellen, 1991; Ruppersberg et al. 1991). Since recovery occurs at approximately the same rate through both pathways (Demo & Yellen, 1991), the main manifestation of the electrically active pathway is a very slowly decaying ‘tail current’ (Itail) on repolarization, as shown in Fig. 5. If the C-type inactivated state involves closure of the intracellular mouth of the channel, then transitions through the open state, in which the channel mouth must open again will be less favourable when there is applied osmotic pressure. Intracellular osmotic pressure should therefore oppose re-opening and promote the electrically silent transition.
Figure 5. Effect of intracellular osmotic pressure on recovery from inactivation.
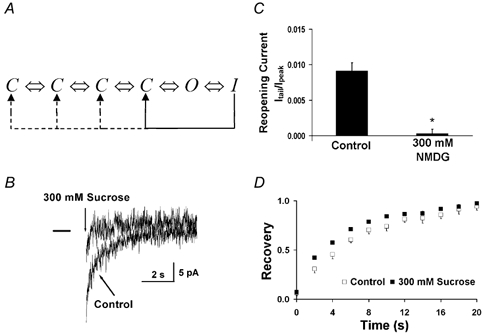
A, model of the Kv1.4ΔN channel, with four closed states, one open state, and an inactivated state. The channel can recover from the inactivated state by transitioning directly from the inactivated state to the closed state, or by passing through the open state. If the channel recovers by going through the open state, there will be a re-opening current. B, effect of applied intracellular pressure on re-opening currents measured using the giant-patch technique. A 5 s depolarizing pulse from −90 to +50 mV was applied to inactivate channels. In control conditions, there was a sustained inward re-opening current (which was a tiny fraction of the fully activated current) as channels slowly recovered from the inactivated state, passed through the open state and subsequently deactivated and returned to the closed state. The re-opening current was inhibited by intracellular osmotic pressure. Deactivation currents are not visible due to the time scale of the sampling rate. Traces were filtered at 40 Hz. C, average re-opening currents were inhibited by applied intracellular osmotic pressure. The magnitude of the re-opening current was normalized to the peak current measured during the preceding 500 ms activation pulse to +50 mV. D, effect of intracellular osmotic pressure (300 mm sucrose) on recovery from C-type inactivation in giant patches. Applied intracellular osmotic pressure had minimal effect on recovery from inactivation. A 5 s depolarizing pulse (P1) from −90 to +50 mV inactivated the channel. A second pulse to +50 mV (P2) was applied after a variable interval, Δt. Recovery (the ratio of the P2 peak current to the peak P1 current) was plotted against the inter-pulse interval, Δt (n = 5).
As predicted, re-opening currents are inhibited by applied intracellular pressure (see Fig. 5). In control conditions, Itail was 0.91 ± 0.11 % of the peak current (Ipeak), whereas when osmotic pressure was applied Itail was reduced to only 0.03 ± 0.06 % of Ipeak (n = 8, P < 0.01). Even though the slow re-opening tail was inhibited by applied intracellular osmotic pressure, the rate of channel recovery was relatively unchanged. This adds further support to the idea that the closed and C-type inactivated states can communicate directly, without requiring re-opening of the intracellular vestibule during deactivation.
Figure 5D shows that the recovery from inactivation is essentially unchanged by osmotic pressure. Recovery is controlled by C-type inactivation, so these data indicate that osmotic pressure has promoted normal C-type inactivation. The fact that the ratio of channels going through the closed pathway has been altered by osmotic pressure but the overall recovery from inactivation has not been changed is consistent with the observations in Shaker channels (Demo & Yellen, 1991) that recovery through both the electrogenic and electrically silent pathways occurs at the same rate (Ruppersberg et al. 1991).
Structural modelling
We examined the physical implications of our measurements using the Insight II Structural modelling software. We used data from the crystal structure of the open MthK channel (Jiang et al. 2002) and the open channel model of KcsA (Doyle et al. 1998; Perozo et al. 1999) to estimate the available water-filled intracellular volume of the open state (Fig. 6).
Figure 6. We used manual measurement of the KcsA and MthK intracellular pore dimensions and geometry to estimate the maximum water-filled volume of the entire permeation pathway.
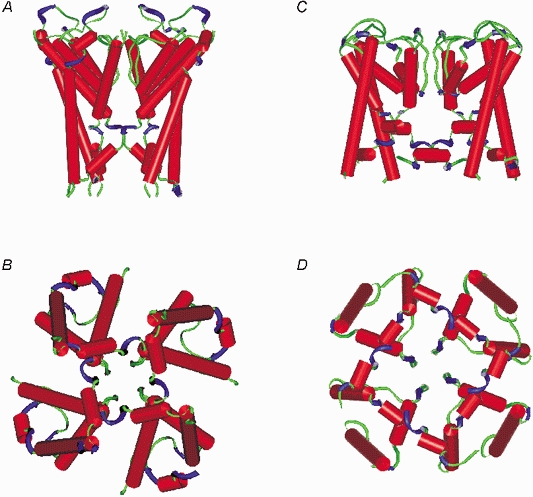
A and B, side and bottom views of the open KcsA channel (Doyle et al. 1998; Perozo et al. 1999). C and D, side and bottom views of the open MthK channel (Jiang et al. 2002).
We estimate the water-filled volume of the open KcsA pore to be 7431 Å3 and the open MthK pore to be 7852 Å3. The values we estimate from our electrophysiological results for the Kv1.4ΔN channel, using a variety of methods (see below) suggest a change of water-filled volume of approximately 55 % of this total, consistent with the notion of a small stable internal chamber in the closed KscA channel (Doyle et al. 1998). Volume estimates from the structural and mathematical approaches are summarized in Fig. 7.
Figure 7.
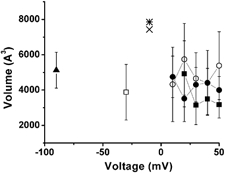
Data from five separate mathematical approaches were used to estimate the magnitude of the pore volume change associated with activation (▪, rate kinetics; □, current ratio), inactivation kinetics (•, rate kinetics; ○, steady state inactivation) and deactivation kinetics (▴). The estimates were voltage independent. Data from the crystal structure of the open MthK channel (Jiang et al. 2002) and the open channel model of KcsA (Doyle et al. 1998; Perozo et al. 1999) were used to give an estimate the available water-filled intracellular volume of the open state: the open KcsA pore was calculated to be 7431 Å3 (×) and the open MthK pore was calculated to be 7852 Å3 (⋇).
Mathematical modelling
We used three different approaches to estimate the volume change associated with conformational changes of the Kv1.4ΔN channel. The mathematical derivations are detailed in the Appendix, and only the final equations and estimates of volume changes are presented here.
1. Volume changes associated with C-type inactivation
An estimate of the change in solute-inaccessible aqueous volume can be calculated from the peak current, Ipeak, and the calculated final current, Ifinal (which is extrapolated from the exponential fit of the experimental current inactivation to infinite time), in the presence and absence of osmotic pressure (π):
| (A11) |
(see Appendix).
Using the values Ipeak and Ifinal at +30 mV, we estimate that the volume change associated with C-type inactivation is 4652 ± 1469 Å3 (n = 5). The volume change was independent of membrane voltage (see Fig. 7).
2. Volume changes associated with channel activation
For values of peak current near the threshold for activation, i.e. when Popen,π < Popen≪ 1, the change in pore volume accompanying activation is related to the peak current by the following equation:
| (A21) |
(see Appendix).
At −30 mV we estimate of the change in pore volume associated with activation to be 3878 ± 1574 Å3 (n = 5). This is similar to the volume calculated for C-type inactivation (see Fig. 7).
3. Kinetic estimates of volume changes
The relationship between rate constants (activation, inactivation and deactivation) and volume change is as follows:
| (A30) |
(see Appendix).
Using this relationship, we estimate that the volume change associated with inactivation is 4304 ± 980 Å3 (n = 5, measured at +30 mV), activation is 3141 ± 1099 Å3 (n = 5, measured at +30 mV) and deactivation is 5126 ± 1015 Å3 (n = 5, measured at −90 mV).
DISCUSSION
We studied a cloned K+ channel, Kv1.4ΔN, expressed in Xenopus oocytes (Comer et al. 1994). The gating kinetics of Kv1.4ΔN were sensitive to applied intracellular osmotic pressure: activation was slowed, whereas deactivation and C-type inactivation were speeded. This indicates that C-type inactivation is associated with a decrease in intracellular channel volume. Even though activation, deactivation and C-type inactivation occur on vastly different time scales, the effect of applied osmotic pressure resulted in a similar percentage change in time constants between all three kinetic variables. This suggests that the volume change associated with channel opening and closing is similar to that involved in C-type inactivation.
In contrast to the results seen with intracellular changes in osmotic pressure, manipulating extracellular osmotic activity had virtually no effect on activation and a small but statistically significant decrease in the time constant of deactivation. This is similar to observations from other voltage-gated channels, where little or no volume change occurred during activation on the extracellular face as measured both by osmotic pressure (Zimmerberg et al. 1990; Rayner et al. 1992) and toxin binding (Naranjo & Miller, 1996). Similarly, no change in the rate of C-type inactivation was measured, suggesting that little or no volume changes occur during C-type inactivation on this side of the membrane.
The similarity in changes in water-accessible volume between activation, deactivation and C-type inactivation strongly suggests that the intracellular pore volume change during C-type inactivation is similar to that undergone when the channel changes between the closed and open states.
What other data exist to support this view of C-type inactivation? Basically, the data parallel those used to implicate external pore mouth changes in C-type inactivation. For example, removal of [K+]o has been shown to speed C-type inactivation, an observation that led to the ‘foot in the door’ hypothesis of C-type inactivation (Armstrong, 1971). Reduction of [K+]i has been reported to increase the rate of C-type inactivation in N-terminal deleted Shaker potassium channels (Baukrowitz & Yellen, 1996b). These results were interpreted as being due to intracellular K+ diffusing through the pore to reach an unstirred layer near the extracellular domain of these channels. We performed similar substitution experiments in Kv1.4ΔN channels in the presence of 98 mm [K+]o (Li et al. 2003); the earlier experiments by Baukrowitz & Yellen (1996b) were performed with 0 mm [K+]o. With 98 mm [K+]o, the extracellular site for potassium modulation of C-type inactivation should be saturated and any effects of potassium removal should reflect changes in intracellular interactions. Substitution of intracellular 98 mm [K+]i with 98 mm[NMDG]i resulted in a significant increase in the rate of C-type inactivation (τinactivation: control, 0.84 ± 0.11 s; 0 KCl, 0.55 ± 0.09 s; n = 6, P < 0.01; Li et al. 2003). This modulation at an intracellular site can be considered a ‘foot in the back door’ mechanism or evidence for intracellular pore closure.
Previous results from other laboratories on closely related channels also show interactions that suggest C-type inactivation is accompanied by a significant intracellular conformational change. For a variety of voltage-gated K+ channels the development of C-type inactivation prevents the binding of drugs that act within the pore of the channel from the intracellular side (Castle et al. 1994; Wang et al. 1997; Ficker et al. 1998). This is similar to the interpretation that an extracellular conformational changes accompanies C-type inactivation because of the sensitivity to extracellular TEA (Armstrong, 1971; Hoshi et al. 1990, 1991; Choi et al. 1991; Yellen et al. 1991).
Mutations near the extracellular mouth of the pore which alter C-type inactivation are considered to be evidence that C-type inactivation involves closure of the extracellular mouth of the pore. Similarly, mutations near the intracellular mouth of the pore on S6 also change the properties of C-type inactivation (Castle et al. 1994; Wang & Wang, 1997; Li et al. 2003). Thus, all of the criteria that were used to demonstrate the involvement of the extracellular mouth of the pore in C-type inactivation are also fulfilled for implicating the intracellular mouth of the channel.
This study suggests that major physical changes in pore structure associated with C-type inactivation occur on the intracellular side of the channel. While this finding is surprising given the well-established involvement of the extracellular side, it should be somewhat expected. For example, cysteine scanning of the extracellular mouth of the channel has only revealed residues that become more, not less, accessible during C-type inactivation (Liu et al. 1996). The linkage between N-type inactivation (which involves intracellular N-terminal binding) and C-type inactivation is also indicative of some coupling of events on the intracellular side to events on the extracellular side of the membrane (for a review see Rasmusson et al. 1998).
In order to account for a change in volume of the putative pore, movement of the transmembrane domain S6 is required (Doyle et al. 1998; Jiang et al. 2002). If S6 is a relatively rigid structure, such a model has the added benefit of explaining why mutations on the intracellular side of S6 alter C-type inactivation (Li et al. 2003). Movement of S6 with C-type inactivation is also compatible with the observation of increased residue accessibility on the extracellular face of the channel during C-type inactivation (Liu et al. 1996). Similarly, either rotational or translational involvement of S6 can explain why mutations on the far extracellular side of S6 alter C-type inactivation (Hoshi et al. 1990, 1991; Busch et al. 1991) despite their putative physical remoteness from the extracellular mouth of the pore in the crystal structure. Perhaps most importantly, these results explain why channel blockers are excluded from binding by C-type inactivation (Castle et al. 1994).
An important question that remains is ‘How tightly closed is the intracellular pore mouth during C-type inactivation?’. The initial ‘closed’ crystal structure of KcsA was sufficiently ambiguous to spur debate as to whether or not it was an open or closed channel (Doyle et al. 1998). Our experiments demonstrate that a large change in pore volume is associated with development of C-type inactivation. Some investigators (Starkus et al. 1997, 1998; Kiss et al. 1999) have reported that Na+ ions, which have smaller hydrated radii than K+ ions, can permeate the C-type inactivated channel in the absence of potassium. It is possible that the pore closure measured here is incomplete enough to pass sodium ions. Alternatively, this may be a reflection of the differences between ion channel types, or the specific ionic conditions, which can alter the conformation, gating and selectivity properties of channels (Hille, 2001).
The term C-type inactivation was originally derived from the C-terminal splice variants, which determined the properties of inactivation that remained in the absence of N-type inactivation (Hille, 2001). In some channels, there may also be P-type inactivation (De Biasi et al. 1993), which may involve changes in the selectivity filter near the external pore mouth (Varga et al. 2002). Conventional C-type inactivation may occur later and stabilize the S4 domain (Olcese et al. 1997; Loots & Isacoff, 1998, 2000). The data presented in this paper were obtained from Kv1.4 channels, which in the wild-type exhibit only N- and C-type inactivation. The construct we examined, Kv1.4ΔN, has the N-terminal deleted, so the ‘ball and chain’ mechanism of N-type inactivation no longer functions. The inactivation that remains fulfills the criteria for C-type inactivation and has been well characterized (Rasmusson et al. 1995). The existence of re-opening currents in Kv1.4ΔN suggests that there may be immobilization of a portion of S4, which is consistent with the observed behaviour of C-type inactivation in Shaker channels (Olcese et al. 1997; Loots & Isacoff, 1998, 2000). Our data show that applied osmotic pressure promotes a return to the closed state through an electrically silent pathway, without altering the recovery rate. This is consistent with the hyposthesis that immobilization of S4 by C-type inactivation occurs in regions remote from the intracellular side of the membrane (Loots & Isacoff, 2000). Indeed, mutation near the extracellular side of S5 in Shaker K+ channels has been suggested to affect both the development of C-type inactivation and movement of S4 through alteration of the rotational movement of the S6 transmembrane spanning domain (Larsson & Elinder, 2000; Ortega-Saenz et al. 2000).
Slow, or C-type, inactivation is common to virtually all voltage-gated ion channels, including Na+, K+ and Ca2+ channels. The specific action of all antiarrhythmic drugs (except β-blockers) depends critically on the state of the channel. This is true for many other drugs which act on excitable cells in other tissues, such as smooth muscle and neurons. Virtually all clinically employed voltage-dependent cation channel blockers interact with the S6 residues lining the permeation pathway from the intracellular side of the membrane (for a review see Rasmusson et al. 1998). This region is critical in understanding binding specificity and use dependence. Understanding the large conformational change at the intracellular face of the channel which occurs during C-type inactivation is crucial to understanding the complex behaviour of antiarrhythmic drugs and their use dependence.
Acknowledgments
We thank Dr Harold C. Strauss for helpful comments. We thank Isidore Dinga Madou for technical assistance. This work was supported in part by NIH (R01 HL-062465), an Established Investigator Award (9940185N) from the American Heart Association, an NSF KDI Grant (DBI-9873173), and a Whitaker Foundation Biomedical Engineering Research Grant.
Appendix
Equilibrium analysis
1. Volume changes associated with inactivation
The Kv1.4ΔN channel can be modelled well with four closed states (C), an open state (O) and an inactivated state (I) (Comer et al. 1994; Wang et al. 2003):
| (A1) |
When a depolarization is applied to the channel the equilibrium will be well to the right in eqn (A1), so we considered only the dominant effect of osmotic pressure on inactivation. Following channel opening, C-type inactivation of Kv1.4ΔN channels is a single exponential process (Rasmusson et al. 1995) and can be simplified to a two-state process:
| (A2) |
where Kπ is the osmotic pressure-sensitive equilibrium constant describing the reaction.
The ratio of the statistical probability of finding the channel in either the open or the inactivated state, Popen/Pinactivated, according to the Boltzmann distribution is related to the difference in free energy between the two states:
| (A3) |
where G is the free energy difference between the two states under control conditions (Hille, 2001). When solutes too large to enter the mouth of the channel are introduced on one side of the membrane there will be a difference in osmotic pressure inside and outside the pore. This additional osmotic pressure leads to a change in the free energy difference between the two states, and the one with the smaller volume will be favoured. The extra energy term is equal to πosmΔV, where πosm is the difference in osmotic pressure inside and outside the channel, and ΔV is the change in solute-inaccessible volume between the open and closed states (Zimmerberg & Parsegian, 1986). The free energy change due to osmotic pressure is therefore:
| (A4) |
When the channel is subjected to osmotic pressure, the probability of finding the channel in either the open or inactivated state (cf. eqn (A3)) becomes:
| (A5) |
| (A6) |
Rearranging:
| (A7) |
Taking the natural logarithm (ln) of both sides:
| (A8) |
Rearranging:
| (A9) |
The ratio Popen/Pclosed for a given depolarization can be estimated from the initial peak current, Ipeak, and the steady-state current, Ifinal (extrapolated from the exponential fit of the inactivating experimental current to infinite time). This gives us the following equation (Hodgkin & Huxley, 1952):
| (A10) |
Substituting this in eqn (A9) gives:
| (A11) |
This allows us to estimate the change in solute-inaccessible aqueous volume associated with a change in osmotic pressure.
2. Volume changes associated with channel activation
Channel activation consists of multiple voltage-sensitive steps, and, generally, a final cooperative voltage-insensitive step (Hoshi et al. 1994). This complicates the analysis as applied to the simplified system described for inactivation described above. However, if we make the simplifying assumption that all of the volume change occurs at the final rate-limiting step of activation, the state model is simple:
| (A12) |
and the equation for calculating volume becomes similar to eqn (A9).
| (A13) |
Since probabilities must sum to one, we know that:
| (A14) |
This can be used to reformulate eqn (A13) to give:
| (A15) |
| (A16) |
The reduction in the probability of the channel being open once exposed to osmotic pressure, Popen,π, can be calculated from the accompanying reduction in peak current, which is a whole cell measure of this change in probability:
| (A17) |
One problem with the relationship given in eqn (A17) is that Popen is unknown for macroscopic currents, unless determined from single channel measurements. To date, only data from multichannel patches has been obtained from Kv1.4 or Kv1.4ΔN channels. In addition to the considerable uncertainty in our estimate of open probability and the simplifying assumption of a single step model of volume change, the measurement is subject to error if the open state as described in the model is a ‘bursting’ state that is a mixture of conducting and non-conducting states with similar volumes. However, if measurements are made only when:
| (A18) |
then:
| (A19) |
and so eqn (A16) simplifies to:
| (A20) |
Substituting eqn (A17) into eqn (A20) yields:
| (A21) |
If Popen is sufficiently small, this free energy analysis can be shown to be independent of assumptions in the activation model (Almers, 1978). Because this approach requires analysis of very small conductances, potential difficulties include miscalculations caused by undetected changes in leak current and difficulties in interpretation introduced by the model of activation, if Popen is not sufficiently small.
3. Kinetic estimates of volume changes
Estimates of volume based on equilibrium analysis of channel open probabilities predict that transition rates between states should also be dependent on applied osmotic pressure. Because such estimates are dependent on kinetic changes instead of equilibrium analysis, the interpretation of such data is highly model dependent. However, such estimates are important, because they provide an additional check on the assumptions of the equilibrium analysis. In general, because other steps may be rate limiting, kinetic estimates of volume changes may be less than or equal to the estimates obtained from equilibrium analysis.
The simplest model of transitions between a conducting and a non-conducting state is:
| (A22) |
where the transitions between the two states at a constant potential are governed by kopen, the rate constant for the closed-to-open transition, and kclose, which is the rate constant for the open-to-closed transition. The time constant associated for relaxation between these two states is given by:
| (A23) |
In the case of deactivation, where there are few, if any, re-openings and additional strongly voltage-dependent closed transitions are rapidly absorbing, eqn (A23) becomes well approximated by:
| (A24) |
or
| (A25) |
According to rate theory, kclose can be described as having an exponential dependence on a high-energy transition state:
| (A26) |
where A is a constant associated with specific reaction conditions. If we assume that the energy-limiting step in this reaction contains the free energy associated with dehydrating the open pore (Hummer et al. 2001), then for applied osmotic pressure we can use the approximation:
| (A27) |
| (A28) |
Substituting eqn (A25) into eqn (A28) gives:
| (A29) |
Rearranging:
| (A30) |
Similar arguments can be made for changes in the activation and inactivation rates.
Obviously, since the rate-limiting step may not involve the entire volume change, and the reverse transition also contributes to the time constant, kinetic estimates of volume changes from this equation may be an underestimate.
References
- Almers W. Gating currents and charge movements in excitable membranes. Rev Physiol Biochem Pharmacol. 1978;82:96–190. doi: 10.1007/BFb0030498. [DOI] [PubMed] [Google Scholar]
- Armstrong CM. Interaction of tetraethylammonium ion derivatives with the potassium channels of giant axons. J Gen Physiol. 1971;58:413–437. doi: 10.1085/jgp.58.4.413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balser JR, Nuss HB, Chiamvimonvat N, Perez-Garcia MT, Marban E, Tomaselli GF. External pore residue mediates slow inactivation in mu 1 rat skeletal muscle sodium channels. J Physiol. 1996;494:431–442. doi: 10.1113/jphysiol.1996.sp021503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baukrowitz T, Yellen G. Modulation of K+ current by frequency and external [K+]: tale of two inactivation mechanisms. Neuron. 1995;15:951–960. doi: 10.1016/0896-6273(95)90185-x. [DOI] [PubMed] [Google Scholar]
- Baukrowitz T, Yellen G. Two functionally distinct subsites for the binding of internal blockers to the pore of voltage-activated K+ channels. Proc Natl Acad Sci U S A. 1996a;93:13357–13361. doi: 10.1073/pnas.93.23.13357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baukrowitz T, Yellen G. Use-dependent blockers and exit rate of the last ion from the multi-ion pore of a K+ channel. Science. 1996b;271:653–656. doi: 10.1126/science.271.5249.653. [DOI] [PubMed] [Google Scholar]
- Bezanilla F, Perozo E, Papazian DM, Stefani E. Molecular basis of gating charge immobilization in Shaker potassium channels. Science. 1991;254:679–683. doi: 10.1126/science.1948047. [DOI] [PubMed] [Google Scholar]
- Busch AE, Hurst RS, North RA, Adelman JP, Kavanaugh MP. Current inactivation involves a histidine residue in the pore of the rat lymphocyte potassium channel RGK5. Biochem Biophys Res Commun. 1991;179:1384–1390. doi: 10.1016/0006-291x(91)91726-s. [DOI] [PubMed] [Google Scholar]
- Castle NA, Fadous SR, Logothetis DE, Wang GK. 4-Aminopyridine binding and slow inactivation are mutually exclusive in rat Kv1.1 and Shaker potassium channels. Mol Pharmacol. 1994;46:1175–1181. [PubMed] [Google Scholar]
- Choi KL, Aldrich RW, Yellen G. Tetraethylammonium blockade distinguishes two inactivation mechanisms in voltage-activated K+ channels. Proc Nat Acad Sci U S A. 1991;88:5092–5095. doi: 10.1073/pnas.88.12.5092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comer MB, Campbell DL, Rasmusson RL, Lamson DR, Morales MJ, Zhang Y, Strauss HC. Cloning and characterization of an Ito-like potassium channel from ferret ventricle. Am J Physiol. 1994;267:H1383–1395. doi: 10.1152/ajpheart.1994.267.4.H1383. [DOI] [PubMed] [Google Scholar]
- De Biasi M, Hartmann HA, Drewe JA, Taglialatela M, Brown AM, Kirsch GE. Inactivation determined by a single site in K+ pores. Pflugers Arch. 1993;422:354–363. doi: 10.1007/BF00374291. [DOI] [PubMed] [Google Scholar]
- Demo SD, Yellen G. The inactivation gate of the Shaker K+ channel behaves like an open-channel blocker. Neuron. 1991;7:743–753. doi: 10.1016/0896-6273(91)90277-7. [DOI] [PubMed] [Google Scholar]
- Doyle DA, Morais CJ, Pfuetzner RA, Kuo A, Gulbis JM, Cohen SL, Chait BT, MacKinnon R. The structure of the potassium channel: molecular basis of K+ conduction and selectivity. Science. 1998;280:69–77. doi: 10.1126/science.280.5360.69. [DOI] [PubMed] [Google Scholar]
- Ficker E, Jarolimek W, Kiehn J, Baumann A, Brown AM. Molecular determinants of dofetilide block of HERG K+ channels. Circ Res. 1998;82:386–395. doi: 10.1161/01.res.82.3.386. [DOI] [PubMed] [Google Scholar]
- Hilgemann DW. Regulation and deregulation of cardiac Na+-Ca2+ exchange in giant excised sarcolemmal membrane patches. Nature. 1990;344:242–245. doi: 10.1038/344242a0. [DOI] [PubMed] [Google Scholar]
- Hille B. Ion Channels of Excitable Membranes. 3. Sunderland, MA, USA: Sinauer Associates Inc.; 2001. [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoshi T, Zagotta WN, Aldrich RW. Biophysical and molecular mechanisms of Shaker potassium channel inactivation. Science. 1990;250:533–538. doi: 10.1126/science.2122519. [DOI] [PubMed] [Google Scholar]
- Hoshi T, Zagotta WN, Aldrich RW. Two types of inactivation in Shaker K+ channels: effects of alterations in the carboxy-terminal region. Neuron. 1991;7:547–556. doi: 10.1016/0896-6273(91)90367-9. [DOI] [PubMed] [Google Scholar]
- Hoshi T, Zagotta WN, Aldrich RW. Shaker potassium channel gating. I: Transitions near the open state. J Gen Physiol. 1994;103:249–278. doi: 10.1085/jgp.103.2.249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hummer G, Rasaiah JC, Noworyta JP. Water conduction through the hydrophobic channel of a carbon nanotube. Nature. 2001;414:188–190. doi: 10.1038/35102535. [DOI] [PubMed] [Google Scholar]
- Jiang Y, Lee A, Chen J, Cadene M, Chait BT, MacKinnon R. The open pore conformation of potassium channels. Nature. 2002;417:523–526. doi: 10.1038/417523a. [DOI] [PubMed] [Google Scholar]
- Kiss L, Loturco J, Korn SJ. Contribution of the selectivity filter to inactivation in potassium channels. Biophys J. 1999;76:253–263. doi: 10.1016/S0006-3495(99)77194-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larsson HP, Elinder F. A conserved glutamate is important for slow inactivation in K+ channels. Neuron. 2000;27:573–583. doi: 10.1016/s0896-6273(00)00067-2. [DOI] [PubMed] [Google Scholar]
- Li XY, Bett GKL, Jiang XJ, Bondarenko VE, Morales MJ, Rasmusson RL. Regulation of N- and C-type inactivation by pHo and potassium in normal and mutant Kv1.4 channels: evidence for transmembrane communication. Am J Physiol Heart Circ Physiol. 2003;284:H71–80. doi: 10.1152/ajpheart.00392.2002. [DOI] [PubMed] [Google Scholar]
- Lipkind GM, Hanck DA, Fozzard HA. A structural motif for the voltage-gated potassium channel pore. Proc Natl Acad Sci U S A. 1995;92:9215–9219. doi: 10.1073/pnas.92.20.9215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y, Jurman ME, Yellen G. Dynamic rearrangement of the outer mouth of a K+ channel during gating. Neuron. 1996;16:859–867. doi: 10.1016/s0896-6273(00)80106-3. [DOI] [PubMed] [Google Scholar]
- Loots E, Isacoff EY. Protein rearrangements underlying slow inactivation of the Shaker K+ channel. J Gen Physiol. 1998;112:377–389. doi: 10.1085/jgp.112.4.377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loots E, Isacoff EY. Molecular coupling of S4 to a K(+) channel's slow inactivation gate. J Gen Physiol. 2000;116:623–636. doi: 10.1085/jgp.116.5.623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez-Barneo J, Hoshi T, Heinemann SH, Aldrich RW. Effects of external cations and mutations in the pore region on C-type inactivation of Shaker potassium channels. Receptors Channels. 1993;1:61–71. [PubMed] [Google Scholar]
- Naranjo D, Miller C. A strongly interacting pair of residues on the contact surface of charybdotoxin and a Shaker K+ channel. Neuron. 1996;16:123–130. doi: 10.1016/s0896-6273(00)80029-x. [DOI] [PubMed] [Google Scholar]
- Olcese R, Latorre R, Toro L, Bezanilla F, Stefani E. Correlation between charge movement and ionic current during slow inactivation in Shaker K+ channels. J Gen Physiol. 1997;110:579–589. doi: 10.1085/jgp.110.5.579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ortega-Saenz P, Pardal R, Castellano A, Lopez-Barneo J. Collapse of conductance is prevented by a glutamate residue conserved in voltage-dependent K(+) channels. J Gen Physiol. 2000;116:181–190. doi: 10.1085/jgp.116.2.181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perozo E, Cortes DM, Cuello LG. Structural rearrangements underlying K+-channel activation gating. Science. 1999;285:73–78. doi: 10.1126/science.285.5424.73. [DOI] [PubMed] [Google Scholar]
- Qu Y, Rogers JC, Chen SF, McCormick KA, Scheuer T, Catterall WA. Functional roles of the extracellular segments of the sodium channel alpha subunit in voltage-dependent gating and modulation by beta1 subunits. J Biol Chem. 1999;274:32647–32654. doi: 10.1074/jbc.274.46.32647. [DOI] [PubMed] [Google Scholar]
- Rasmusson RL, Morales MJ, Castellino RC, Zhang Y, Campbell DL, Strauss HC. C-type inactivation controls recovery in a fast inactivating cardiac K+ channel (Kv1. 4) expressed in Xenopus oocytes. J Physiol. 1995;489:709–721. doi: 10.1113/jphysiol.1995.sp021085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasmusson RL, Morales MJ, Wang S, Liu S, Campbell DL, Brahmajothi MV, Strauss HC. Inactivation of voltage-gated cardiac K+ channels. Circ Res. 1998;82:739–750. doi: 10.1161/01.res.82.7.739. [DOI] [PubMed] [Google Scholar]
- Rayner MD, Starkus JG, Ruben PC, Alicata DA. Voltage-sensitive and solvent-sensitive processes in ion channel gating. Kinetic effects of hyperosmolar media on activation and deactivation of sodium channels. Biophys J. 1992;61:96–108. doi: 10.1016/S0006-3495(92)81819-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruppersberg JP, Frank R, Pongs O, Stocker M. Cloned neuronal IK(A) channels reopen during recovery from inactivation. Nature. 1991;353:657–660. doi: 10.1038/353657a0. [DOI] [PubMed] [Google Scholar]
- Starkus JG, Kuschel L, Rayner MD, Heinemann SH. Ion conduction through C-type inactivated Shaker channels. J Gen Physiol. 1997;110:539–550. doi: 10.1085/jgp.110.5.539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Starkus JG, Kuschel L, Rayner MD, Heinemann SH. Macroscopic Na+ currents in the ‘Nonconducting’ Shaker potassium channel mutant W434F. J Gen Physiol. 1998;112:85–93. doi: 10.1085/jgp.112.1.85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Starkus JG, Schlief T, Rayner MD, Heinemann SH. Unilateral exposure of Shaker B potassium channels to hyperosmolar solutions. Biophys J. 1995;69:860–872. doi: 10.1016/S0006-3495(95)79960-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todt H, Dudley SC, Jr, Kyle JW, French RJ, Fozzard HA. Ultra-slow inactivation in mu1 Na+ channels is produced by a structural rearrangement of the outer vestibule. Biophys J. 1999;76:1335–1345. doi: 10.1016/S0006-3495(99)77296-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varga Z, Rayner MD, Starkus JG. Cations affect the rate of gating charge recovery in wild-type and W434F Shaker channels through a variety of mechanisms. J Gen Physiol. 2002;119:467–485. doi: 10.1085/jgp.20028520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S, Morales MJ, Liu S, Strauss HC, Rasmusson RL. Modulation of HERG affinity for E-4031 by [K+]o and C-type inactivation. FEBS Lett. 1997;417:43–47. doi: 10.1016/s0014-5793(97)01245-3. [DOI] [PubMed] [Google Scholar]
- Wang S, Morales MJ, Qu Y, Bett GCL, Strauss HC, Rasmusson RL. Kv1.4 channel block by quinidine: evidence for a drug-induced allosteric effect. J Physiol. 2003;546:387–401. doi: 10.1113/jphysiol.2002.029512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang SY, Wang GK. A mutation in segment I-S6 alters slow inactivation of sodium channels. Biophys J. 1997;72:1633–1640. doi: 10.1016/S0006-3495(97)78809-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yellen G, Jurman ME, Abramson T, MacKinnon R. Mutations affecting internal TEA blockade identify the probable pore-forming region of a K+ channel. Science. 1991;251:939–942. doi: 10.1126/science.2000494. [DOI] [PubMed] [Google Scholar]
- Zeuthen T, Zeuthen E, Klaerke DA. Mobility of ions, sugar, and water in the cytoplasm of Xenopus oocytes expressing Na+-coupled sugar transporters (SGLT1) J Physiol. 2002;542:71–87. doi: 10.1113/jphysiol.2001.014530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang JF, Ellinor PT, Aldrich RW, Tsien RW. Molecular determinants of voltage-dependent inactivation in calcium channels. Nature. 1994;372:97–100. doi: 10.1038/372097a0. [DOI] [PubMed] [Google Scholar]
- Zimmerberg J, Bezanilla F, Parsegian VA. Solute inaccessible aqueous volume changes during opening of the potassium channel of the squid giant axon. Biophys J. 1990;57:1049–1064. doi: 10.1016/S0006-3495(90)82623-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimmerberg J, Parsegian VA. Polymer inaccessible volume changes during opening and closing of a voltage-dependent ionic channel. Nature. 1986;323:36–39. doi: 10.1038/323036a0. [DOI] [PubMed] [Google Scholar]


